Minimizers of convex functionals with small degeneracy set

Abstract

We study the question whether Lipschitz minimizers of $\int F(\nabla u)\,dx$ in $\mathbb {R}^n$ are $C^1$ when F is strictly convex. Building on work of De Silva–Savin, we confirm the $C^1$ regularity when $D^2F$ is positive and bounded away from finitely many points that lie in a 2-plane. We then construct a counterexample in $\mathbb {R}^4$, where F is strictly convex but $D^2F$ degenerates on the Clifford torus. Finally we highlight a connection between the case $n = 3$ and a result of Alexandrov in classical differential geometry, and we make a conjecture about this case.

Appendix

In the Appendix we record some properties of $\varphi$, and we prove the extension result Lemma 4.1.

1.1 Properties of $\varphi$

We recall from [22] that if we parametrize $\Gamma _1$ by the angle $\theta \in [\pi /4,\,3\pi /4]$ of its upward unit normal $\nu$, then its curvature is given by $\kappa = \frac{\sqrt{2}}{3}\sec (2\theta )$. It follows easily that $\varphi$ is smooth, even, and uniformly convex on $(-1,\,1)$, and $\varphi ''$ is increasing on $[0,\,1)$. We recall also the expansion

$$\begin{aligned} \varphi \left( -1 + \frac{3}{2}\theta ^2 + \theta ^3 + O(\theta ^4)\right) = 1-\frac{3}{2}\theta ^2 + \theta ^3 + O(\theta ^4) \end{aligned}$$

from [22]. By differentiating implicitly and using that $\varphi$ is even we obtain near $s = 1$ the expansions

$$\begin{aligned} \varphi '(s)= & {} 1 - 2\sqrt{\frac{2}{3}}(1-s)^{1/2} + O(1-s)\\ \varphi ''(s)= & {} \sqrt{\frac{2}{3}}(1-s)^{-1/2} + O(1)\\ \varphi '''(s)= & {} \frac{1}{2}\sqrt{\frac{2}{3}}(1-s)^{-3/2} + O((1-s)^{-1}). \end{aligned}$$

In particular, for $0< s < y$ the derivative of the weight $\varphi ''(s)(y-s)$ is bounded above by $\varphi '''(s)(1-s) - \varphi ''(s) = -\frac{1}{2}\sqrt{\frac{2}{3}}(1-s)^{-1/2} + O(1) < 0$ for s close to 1.

1.2 Proof of extension lemma

We now prove Lemma 4.1. Our strategy is to first construct G in a set containing a neighborhood of every point on $\Sigma _0$. We then apply a global $C^1$ extension result to this local extension. To complete the construction we use a mollification and gluing procedure.

1.2.1 Local extension

Lemma 5.1

There exists an open set $\mathcal {O}$ containing a neighborhood of each point on $\Sigma _0$ and a function $G_0 \in C^{\infty }(\mathcal {O})$ such that $G_0 = g$ and $\nabla G_0 = \mathbf{v}$ on $\Sigma _0$, and furthermore

$$\begin{aligned} G_0(\tilde{p}) - G_0(p) - \nabla G_0(p) \cdot (\tilde{p} - p) \ge \frac{\gamma }{2}|\tilde{p} - p|^2 \end{aligned}$$

(14)

for all $p,\,\tilde{p} \in \mathcal {O}$.

Proof

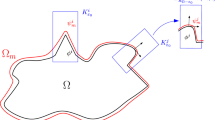
The squared distance function $d_{\Sigma _v}^2$ from $\Sigma _v$ is smooth in a neighborhood of each point on $\Sigma _0$, as is the projection $\pi _{\Sigma _v}$ to $\Sigma _v$. Let $\tau$ be a unit tangent vector field to $\Sigma _v$ in a neighborhood of a point on $\Sigma _0$, and $\nu$ a unit normal vector field. Then $D^2(d_{\Sigma _v}^2/2)$ projects in the normal direction $\nu$ on $\Sigma _0$. See e.g. [3] for proofs of these properties.

Let $A > 0$ be a smooth function on $\Sigma _0$ to be chosen, and define

$$\begin{aligned} G_0(x) := g(\pi _{\Sigma _v}(x)) + \mathbf{v}(\pi _{\Sigma _v}(x)) \cdot (x - \pi _{\Sigma _v}(x)) + A(\pi _{\Sigma _v}(x))d_{\Sigma _v}^2. \end{aligned}$$

It is elementary to check using (6) that $\nabla _{\Sigma _0}g$ is the tangential component of $\mathbf{v}$ on $\Sigma _0$, and as a consequence that $G_0 = g,\, \nabla G_0 = \mathbf{v}$ on $\Sigma _0$. Furthermore, it follows from (6) that $(G_0)_{\tau \tau } \ge 2\gamma$ on $\Sigma _0$. Since $D^2(A(\pi _{\Sigma _v}(x))d_{\Sigma _v}^2)$ is 2A times the matrix that projects in the direction $\nu$ on $\Sigma _0$, we have that $(G_0)_{\nu \nu } = 2A$ on $\Sigma _0$, and that $(G_0)_{\tau \nu }$ on $\Sigma _0$ depends only on $g,\,\mathbf{v}$, and the geometry of $\Sigma _0$ (in particular, not on A). By choosing A(p) sufficiently large depending on $\gamma$ and these quantities (and perhaps going to $\infty$ as $p \rightarrow S$), we have that

$$\begin{aligned} D^2G_0 \ge \frac{3}{2}\gamma I \end{aligned}$$

(15)

on $\Sigma _0$. In particular, (14) holds in a small neighborhood of each point on $\Sigma _0$.

Now, for $\delta ,\,\sigma > 0$ let $S_{\delta }$ be the closed $\delta$-neighborhood of S, and let $\Sigma _{\sigma }$ be the open $\sigma$-neighborhood of $\Sigma _v$. By (6), (15), and continuity, for each $\delta > 0$ there exists $\sigma (\delta ) > 0$ small and an open set $O_{\delta }$ containing $\Sigma _{\sigma (\delta )} \backslash S_{\delta }$ and a neighborhood of each point in $\Sigma _0$, such that (14) holds for all $p,\,\tilde{p} \in O_{\delta }$ such that at least one of $p,\,\tilde{p}$ is in $\Sigma _{\sigma (\delta )} \backslash S_{\delta }$. For $\delta = 1/k$ we may choose $\sigma (1/k)$ and $O_{1/k}$ such that $\Sigma _{\sigma (1/k)} \backslash S_{1/k} \subset O_{1/k} \subset O_{1/(k-1)}$ for $k > 1$. Taking

$$\begin{aligned} \mathcal {O} = \cup _{k > 1} (\Sigma _{\sigma (1/k)} \backslash S_{1/k}) \end{aligned}$$

completes the proof. $\square$

1.2.2 Global $C^1$ extension

Lemma 5.2

There exists a $C^1$ convex function $G_1$ on $\mathbb {R}^2$ such that $G_1 = G_0$ on an open set $\mathcal {U} \subset \mathcal {O}$ that contains a neighborhood of each point on $\Sigma _0$, such that $D^2G_1 \ge \frac{\gamma }{2}I$ on $\mathbb {R}^2$.

Proof

Let K be a compact set containing $\Sigma _v$ and a neighborhood of each point on $\Sigma _0$, such that $K \backslash S \subset \mathcal {O}$, and $G_0,\,\nabla G_0$ are continuous up to S in K. Let $H_0 := G_0 - \frac{\gamma }{4}|x|^2$. On S, define $H_0 = g - \frac{\gamma }{2},\, \nabla H_0 = \mathbf{v} - \frac{\gamma }{2}x$. Then by (14) we have

$$\begin{aligned} H_0(\tilde{p}) -H_0(p) - \nabla H_0(p) \cdot (\tilde{p} - p) \ge \frac{\gamma }{4}|\tilde{p} - p|^2 \end{aligned}$$

for all $p,\, \tilde{p} \in K$. We may thus apply Theorem 1.10 from [5] to obtain a global $C^1$, convex function $H_1$ on $\mathbb {R}^2$ such that $H_1 = H_0,\, \nabla H_1 = \nabla H_0$ on K. To finish take $G_1 = H_1 + \frac{\gamma }{4}|x|^2$. $\square$

1.2.3 Smoothing

Lemma 5.3

There exists a convex function $G \in C^1(\mathbb {R}^2) \cap C^{\infty }(\mathbb {R}^2 \backslash S)$ such that $G = G_1$ in a neighborhood of each point on $\Sigma _0$, and $D^2G \ge \frac{\gamma }{4}I$ on $\mathbb {R}^2$. In particular, $D_G = S$, and $(G,\,\nabla G) = (g,\,\mathbf{v})$ on $\Sigma _v$.

Proof

We begin with a simple observation. Let F be a $C^1$ convex function on $\mathbb {R}^n$ with $D^2F \ge \mu I$. Let $\rho _{\epsilon }$ be a standard mollifier, and let $F_{\epsilon } := \rho _{\epsilon } *F$. Then if $\varphi \in C^{\infty }_0(B_R)$ with $0 \le \varphi \le 1$ we have

$$\begin{aligned} \Vert (\varphi F_{\epsilon } + (1-\varphi ) F) - F\Vert _{C^1(\mathbb {R}^n)}&= \Vert \varphi (F_{\epsilon } - F)\Vert _{C^1(\mathbb {R}^n)} \\&\le C(\varphi )\Vert F_{\epsilon } - F\Vert _{C^1(B_R)} \end{aligned}$$

and

$$\begin{aligned} D^2(\varphi F_{\epsilon } + (1-\varphi ) F)&= \varphi D^2 F_{\epsilon } + (1-\varphi ) D^2 F + D^2\varphi \,(F_{\epsilon } - F) \\&+ \nabla \varphi \otimes (\nabla F_{\epsilon } - \nabla F) + (\nabla F_{\epsilon } - \nabla F) \otimes \nabla \varphi \\&\ge \left( \mu - C(\varphi )\Vert F_{\epsilon } - F\Vert _{C^1(B_R)}\right) I. \end{aligned}$$

Since F is $C^1$, by taking $\epsilon (\varphi )$ small we have that $\varphi F_{\epsilon } + (1-\varphi ) F$ is as close as we like to F in $C^1(\mathbb {R}^n)$, and we have a lower bound for $D^2(\varphi F_{\epsilon } + (1-\varphi ) F)$ that is as close as we like to $\mu I$. We will apply this observation to a sequence of mollifications of $G_1$.

Let $\{B_{r_i}(x_i)\}_{i = 1}^{\infty }$ be a Whitney covering of $\mathbb {R}^2 \backslash \Sigma _v$. That is, for

$$\begin{aligned} r(x) := \min \{1,\,d_{\Sigma _v}(x)\}/20, \end{aligned}$$

we have $r_i = r(x_i)$, the balls $B_{r_i}(x_i)$ are disjoint, $\cup _i B_{5r_i}(x_i) = \mathbb {R}^2 \backslash \Sigma _v$, and for each $x \in \mathbb {R}^2 \backslash \Sigma _v$ the ball $B_{10r(x)}(x)$ intersects at most $(129)^2$ of the $\{B_{10r_i}(x_i)\}$. For the existence of such a covering see for example [12].

Now take $\varphi _i \in C^{\infty }_0(B_{10r_i}(x_i))$ such that $\varphi _i = 1$ in $B_{5r_i}(x_i),\, 0 \le \varphi \le 1$. For $j \ge 1$ we define $G_{j+1}$ inductively as follows: If $B_{10r_j}(x_j) \subset \mathcal {U}$ then let $G_{j+1} = G_j$. If not, then let

$$\begin{aligned} G_{j+1} = \varphi _j (\rho _{\epsilon _j} *G_j) + (1-\varphi _j) G_j, \end{aligned}$$

with $\epsilon _j$ chosen so small that

$$\begin{aligned} \Vert G_{j+1} - G_j\Vert _{C^1(\mathbb {R}^2)} \le 2^{-j} \end{aligned}$$

(16)

and

$$\begin{aligned} D^2G_{j+1} \ge \left( \frac{\gamma }{2} - \frac{\gamma }{4}\sum _{i = 1}^j 2^{-i}\right) I. \end{aligned}$$

(17)

By the covering properties, for any $x \in \mathbb {R}^2 \backslash \Sigma _v$, we have that $G_j$ are smooth and remain constant in $B_{10r(x)}(x)$ for all j sufficiently large. In addition, for any point on $\Sigma _0$, every $B_{10r_j}(x_j)$ that intersects a small neighborhood of this point is contained in $\mathcal {U}$, so $G_j = G_1$ in a small neighborhood of every point in $\Sigma _0$. We conclude using (16) and (17) that $G := \lim _{j \rightarrow \infty } G_j$ is $C^1$, smooth on $\mathbb {R}^2 \backslash S$, agrees with $G_1$ in a neighborhood of every point on $\Sigma _0$, and satisfies

$$\begin{aligned} D^2G \ge \left( \frac{\gamma }{2} - \frac{\gamma }{4} \sum _{i = 1}^{\infty } 2^{-i}\right) I = \frac{\gamma }{4}I. \end{aligned}$$

$\square$