Introduction

Over the past three decades, scanning probe microscopy (SPM) has emerged as a primary tool for characterization of structure and functionality at the nanometer and atomic scales. Following the initial demonstration of topographic imaging in contact mode1, the intermittent and non-contact topographic imaging modes, as well as SPM modes for electrical2, magnetic3, mechanical4, and electromechanical imaging5,6 and spectroscopy7 followed. This rapid development of imaging modalities implemented on these benchtop tools have opened the nanoworld for exploration and was one of the key elements underpinning the explosive growth of nanoscience, nanotechnology, and many areas of fundamental and applied research8.

All SPM modes rely on the concept of the local probe interacting with the sample surface. Scanning the probe allows sequential measurements of materials response over a spatial grid, giving rise to images or hyperspectral images, i.e., multidimensional SPMs or SPM spectroscopic imaging modes. The data acquisition process in SPM can hence be represented as the combination of two elements—the SPM engine, or the excitation/detection scheme, and the spectroscopic mode. The spectroscopic modes define the sampling of the parameter space of interest at each spatial location, for example, classical force–distance and current–voltage curve mappings in atomic force microscopy9 and scanning tunneling microscopy, and complex time and voltage spectroscopies in piezoresponse force microscopy (PFM) and electrochemical strain microscopy10,11,12. In modern SPMs, the parameter space is usually sampled sequentially, albeit this limitation is not rigid.

The SPM engine defines the response at a single point in the parameter space, i.e., the nature of response at a single voxel. Classical SPM engines typically employ a combination of sinusoidal excitation and lock-in detection, e.g., as used in classical amplitude detection SPM, or a combination of sinusoidal excitation with the phase-locked loop detection in frequency detection schemes. These two engines yield (multimodal) scalar information, i.e., two response values per pixel. Examples of vector detection engines are the band excitation (BE)13, exciting and detecting multiple frequencies in parallel, and harmonic intermodulation methods14 that detect the mixing harmonics between the two excitation signals. In both cases, the engine compresses the data stream from the detector to a single parameter or a set of parameters corresponding to response vector components. Finally, more complex detection schemes such as G-mode SPM15,16,17 are based on detection and storage of the full data stream from the detector, obviating the data compression stage during scanning, after which in-depth data analysis can be performed. Both BE, and intermodulation and G-mode detection were extended to a broad variety of SPM modes, including topographic imaging, magnetic and electrostatic force imaging18, PFM19, and is expected to be universally applicable to all SPM modes.

The proliferation of BE, intermodulation, and G-Mode SPMs and their nascent adoption by the commercial vendors necessitates understanding basic image formation mechanisms in these techniques. To date, most of such analyses were based on the physics-based models, where the known (or postulated) physics of the imaging process was used to transform the high-dimensional data to a number of reduced, ideally material-specific (i.e., independent of imaging system), parameters. The examples of such analysis include the simple harmonic oscillator (SHO) fit in the BE methods20 or reconstruction of the intermodulation harmonics in intermodulation atomic force microscopy14,21. Here the measured resonance frequencies and force–distance curves describing salient features of tip–surface interaction can then be transformed into effective Young moduli.

At the same time, of interest is the amount of information contained in the multidimensional data as determined from a purely information theory viewpoint, as well as approaches to compress and visualize it for exploratory data analysis. This information will provide both insight into the fundamentals of imaging mechanisms and tip–surface interaction, can be correlated with materials’ structure to yield insight into materials’ behaviors, and suggest strategies for automated experimentation. Previously, hyperspectral data sets were explored using multivariate statistical methods such as principal component analysis22, more complex methods such as non-negative matrix factorization that allow for certain physics-based constraints23, or non-linear autoencoders24. However, these methods are based exclusively on the analysis of the spectral dimensions, whereas spatial correlations are explicitly ignored. In other words, the endmembers of spectral unmixing do not depend on the relative positions of the spatial pixels. Correspondingly, analysis of spatial features in the loading maps was used as a way to infer the understanding of the system23. Alternatively, neural network-based algorithms were suggested as an approach to identify the data based on labeled examples25 or to extract the parameters of a theoretical model26,27. However, in these cases as well analysis was essentially single-pixel based.

Here we explore the imaging mechanisms in the BE PFM using the Gaussian process (GP) regression28,29,30,31,32. This method allows exploration of the data structure from purely information theory perspective simultaneously in the spatial and parameter space. We apply this Bayesian machine learning approach to determine the characteristic length scale of the phenomena and information content in the hyperspectral images and suggest the strategies for automated experimentation based on exploiting sampling of space where maximum uncertainty is predicted.

Results and discussion

BE PFM on BiFeO3 film

The BE PFM measurements were performed on an Asylum Cypher microscope using an in-house built BE controller. The BE PFM is based on exciting and monitoring the cantilever/sample response within a continuous frequency band (instead of a single frequency as used in a classical set-up) using parallel multifrequency excitation and detection. This allows quantitative measurements via decoupling the material response from the changes in resonance frequency of the tip–surface junction.

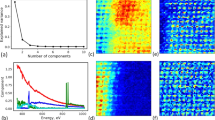
As a model system, we use an epitaxial BiFeO3 thin film of 100-nm thickness. The characteristic surface topography is shown in Fig. 1a. The BE data can be fitted to a SHO model to extract amplitude, phase, resonance frequency, and Q-factor maps as shown in Fig. 1b–e. These images clearly indicate a ferroelectric domain structure as expected for this material. Figure 1f shows the zoomed-in amplitude image at the top left corner of Fig. 1b.

Fig. 1: BE-PFM images in the BiFeO3 epitaxial film.
figure 1

a Topographic map. b BE-PFM amplitude, c phase, d resonance frequency, and e Q-factor maps. f Zoomed-in amplitude image at the top left corner of b.

Full size image

GP for reconstruction of BE PFM data

To explore the information distribution in the BE data set, we employ the GP method31,32. GP generally refers to an indexed collection of random variables, any finite number of which have a joint Gaussian distribution. More simply, a GP is a distribution over functions on a given domain and can be used for approximating continuous nonlinear functions. GP can be completely specified in terms of its mean function and covariance function (also referred to as kernel function). A common application of GP in machine learning is a GP regression analysis where one estimates an unknown function given noisy observations y = (y(x1), …, y(xn))T of the function at a finite number of points X = {x1, …, xn}. The marginal likelihood of the data is conditioned on the kernel hyperparameter θ as following:

$$\log p\left( {{\mathbf{y}}{\mathrm{|}}X,\theta } \right) \propto - \frac{1}{2}\log \left| {{\mathbf{K}}_{{\boldsymbol{\theta}}} + \sigma ^2{\mathbf{I}}} \right| - \frac{1}{2}{\mathbf{y}}^{\mathrm{T}}\left( {{\mathbf{K}}_{\boldsymbol{\theta}} + \sigma ^2{\mathbf{I}}} \right)^{ - 1}{\mathbf{y}}$$
(1)

where the first and second terms can be interpreted as the hyperparameter learning and the data fit, respectively31. Here σ2 is noise variance. Because the application of GP models to large data sets is intractable, we adapt a sparse GP regression method for constructing an approximation using a subset of observations called inducing points33. The inducing points are optimized together with kernel hyperparameters during model training. Maximizing the number of inducing points generally yields more accurate results, albeit at the cost of computation time and memory.

It is important to know that the signature aspect of GP method is that observations at different locations are assumed to be linked via the kernel function, defining the connection between the dissimilar locations. The kernel function can be either defined a priori, i.e., from the known physics of the system or additional information, or can be treated as a hyperparameter. In the latter case, the functional form of the kernel is defined and the corresponding parameters are determined as a part of the fitting process. Here we note that the kernel parameters determined self-consistently as a part of the regression process should provide robust information on the image formation mechanism in the technique and explore this proposition below.

To explore the applicability of the GP processing in BE, we first demonstrate its potential for reconstruction from partial data and subsequently show how exploratory analysis using information about maximum uncertainty as a guide for selecting the next measurement point can be performed. We selected a 32 × 32 × 102 subset of the original hyperspectral data (see Fig. 1f) in order to reduce computational time/costs and to make it easier to reproduce our results without a need to use high-performance computing. Our GP analysis code tailored toward the analysis of two- and three-dimensional (2D and 3D, respectively) image and spectroscopic data is based on Pyro probabilistic programming language32. We used a fixed number (1500) of inducing points (determined based on the limits of graphics processing unit (GPU) memory) for reconstruction of individual data sets, while for the “sample exploration” problem the number of inducing points was set to 5% of the overall data points. We also provide an executable Jupyter notebook for reproducing the paper’s results (available at https://colab.research.google.com/github/ziatdinovmax/GP/blob/master/notebooks/GP_BEPFM.ipynb). The notebook can be executed either using a standard Google Cloud Platform virtual machine with NIVIDIA’s Tesla P100 GPU and 15 GB of RAM (running the notebook one time from top to bottom costs ~2 USD) or in Google Colab with NVIDIA’s Tesla K80 GPU, which is free of charge but may require significantly longer computational times.

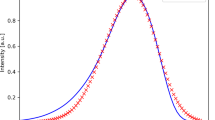
Here the original BE data set is considered to be the “known” ground truth. A part of the data is removed, creating the artificial data set. The GP regression is used to reconstruct the full data set, and the reconstruction error is evaluated. This process is illustrated in Fig. 2, showing the original data set as a response in the x, y, and frequency space (Fig. 2a), the reduced data set (Fig. 2b), the reconstructed data set (Fig. 2c), and the absolute error (Fig. 2d). Here the “Matern52” kernel is used31. The reconstruction error shown in Fig. 2d generally does not exceed ~20% despite the fact that 70% of the data was eliminated.

Fig. 2: Illustration of GP application to 3D spectroscopic data set.
figure 2

Original image (ground truth) in a is corrupted by removing 70% of observations (measured spectroscopic curves) as shown in b. The GP regression is then used to reconstruct the signal (c). The absolute error is shown in d. Note that the absolute error may be misleading when the ratio of signals of interest does not change (see Fig. 3). The data set dimensions are 32 × 32 × 102.

Full size image

To explore the robustness of this approach, we explore the veracity of reconstruction for the various degrees of image reduction. The 2D representation of the reconstruction of the BE data set for the full data set and for the data sets with removal of 70%, 90%, and 99% of the original data is shown in Fig. 3. Even for the data reduction by 90%, the reconstructed data sets maintain the characteristic features of the response, including both the general domain configuration and the behavior of the amplitude–frequency curves. Note that GP process yields not only estimated response values but also the confidence intervals at the given point in the parameter space, thus allowing for the formulation of optimal strategies for experiment automation, as will be explored later. Overall, we conclude that the BE data are strongly oversampled, and even without strong physics-specific priors, the GP process allows reconstruction of data from partial observations.

Fig. 3: Illustration of GP reconstruction on selected 2D data slices.
figure 3

Selected 2D representations corresponding to the application of GP regression to original (full) data (a) and data corrupted by removing 70% (b), 90% (c), and 99% (d) of observations. In each panel, the top row shows the input data (2D slices of hyperspectral data average over selected frequency range and spectroscopic curves extracted at A, B, and C points) and the bottom row shows the model output (the same averaged slices and the reconstructed curves from the same locations as in the input data). The vertical blue span in the plots indicate a slice used for 2D image plots (the same in all four panels). The spatial resolution in all the images is ~9.76 nm/px. The full 3D data sets are available from the notebook at https://colab.research.google.com/github/ziatdinovmax/GP/blob/master/notebooks/GP_BEPFM.ipynb.

Full size image

We further note that the key element of GP process is that it yields the insight into the structure of the data via the kernel parameters. Here we use the weakly informative 3D Matern kernel, with the characteristic length scales determined as a part of regression process. These length scales hence define the characteristic resolution in the spatial and frequency domains and do so in robust (with respect to noise) fashion. These behaviors are illustrated in Fig. 4a–d for the full data set and for the partially reduced data sets discussed in Fig. 3. Note that, for all cases discussed in Fig. 3, the frequency length scale converges to the similar value given by the width of the BE peak. For spatial length scales, the analysis of the full data set allows to establish characteristic spatial resolution as the kernel length scale. This length scale in turn provides robust estimate of the characteristic length scale of tip–surface interactions. We also showed trajectories of inducing points for each case, which were selected as a subset of the input data points by taking every nth point from the original data set. Here n was adjusted such that the total number of inducing points remained the same (1500, based on GPU memory limits) for all 4 scenarios. Notice that most inducing points in Fig. 4e–g stop their motion after ~500 stochastic variational inference iterations and that for data set with 99% of observations removed all the inducing points remain mostly at their original location. While the inducing points do not have a physical meaning, understanding their evolution during the optimization process is important for applying GP models to larger hyperspectral data sets and to the experiment automation.

Fig. 4: Evolution of GP parameters during training.
figure 4

Evolution of kernel length scales (a–d) and inducing points (e–h) during the stochastic variational inference (SVI)-based model training for full data set (a, e), and data corrupted by removing 70% of observations (b, f), 90% of observations (c, g), and 99% of observations (d, h). a The first two dimensions in a–d (dim 1 and dim 2) correspond to x and y coordinates, whereas the third dimension (dim 3) corresponds to frequency. The kernel length scales define the spatial resolution of the technique (assuming atomically thin domain wall width) in the spatial domain and the width of the resonance peak in the frequency domain.

Full size image

We further explored the robustness of the reconstruction with respect to the choice of the frequency range. In this case, the high-quality reconstruction is possible when the local resonance frequency is within the measurement range but start to deteriorate rapidly once outside (Supplementary Figs. 1 and 2). These observations suggest that introduction of GP in the imaging workflow favors the mapping over large frequency ranges but at the reduced spatial point densities. However, we expect that incorporation of physics-based kernels containing the information on the SHO model will allow to expand this approach further.

Uncertainty-guided sample exploration

We finally demonstrate that GP regression can be used for guiding the actual measurements. Here we start with just a few measured points along each edge in the xy plane (~1% of all the observations). A single exploration step consists of (i) performing a GP regression, (ii) doing a single “measurement” in a point with maximum uncertainty, and (iii) updating the previous input data with the data points associated with this measurement. The GP part of this process can be viewed as a “black box” that is effectively separated from the BE PFM acquisition software. It accepts the datacube of a fixed size containing the BE PFM response values (the size is determined by the scan size and frequency range) and the associated grid indices as the input and outputs the indices of the next point to be measured based on the GP uncertainty estimation. The points that are not yet measured are represented as NaNs in the datacube and are updated with the BE PFM response values once measured. The optimal frequency range (the third dimension of the datacube) is selected based on a prior knowledge of an operator and remains fixed during each measurement cycle.

Here we demonstrate this approach using a “synthetic” experiment, that is, we use the data from the actual but already completed experiment, with 99% of all the observations removed, which allows us to estimate the absolute error at each step. As one can observe from Fig. 5a, the absolute error is rapidly decreasing during the first ~30 exploration steps. The error is much higher when the next measurement point is selected just randomly, as demonstrated in Fig. 5b. We noticed that, if the edge points are not “opened” in the beginning, the algorithm typically spends the first ~10 iterations (for this particular data, dimensions) on measuring the edges since this is where the kernel diverges (and not because this is related to any sample properties) and then moves to the regions deeper inside the field of view. The selected inputs and outputs for this exploration range are shown in Fig. 6. Interestingly, one can get a good understanding of the sample domain structure already after 20–30 steps of such an autonomous experiment, which suggests that this approach can significantly reduce the data acquisition time. The remaining steps are typically spent on “refining” the uncovered structures (compare, for example, the third and the last column in Fig. 6b–d). The current approach can be improved by introducing a “cost function” determining which objects are of real physical interest (that, is “worth exploring”), in addition to a pure uncertainty-based exploration.

Fig. 5: Simulation of the GP-guided experimental measurements.
figure 5

The data are real (experimental). a The integrated absolute error versus exploration steps for measurements with (GP) and without (standard) GP regression-based reconstruction. b Comparison of the integrated absolute error when the next measurement point is selected using the maximal uncertainty in GP reconstruction versus when the next measurement point is selected randomly (for three different pseudo-random seeds). c Exploration path in xy coordinates for the first 60 steps.

Full size image
Fig. 6: Simulation of the GP-guided experimental measurements.
figure 6

The data are real (experimental). a Ground truth data in 2D representation for the selected frequency range and the individual spectroscopic curves from the selected locations. b Input data updated with a new single measurement at each step. c GP regression-based reconstruction of the entire field of view, integrated over a frequency range shown by a vertical blue span in Fig. 3. d Reconstructed individual spectroscopic curves from the locations shown by black, red, and green dots in c.

Full size image

To summarize, we have explored the applicability of the GP regression with weakly informative priors for the analysis of the BE PFM data. Here we explored the signal in the 3D (x, y, frequency) parameter space. Even for the weakly informative priors, the GP approach allows to unambiguously determine the characteristic length scales of the imaging process both in spatial and frequency domains. We further show that BE data set tend to be oversampled, with ~30% of original data set sufficient for high-quality reconstruction.

We further note that this analysis points at strong potential of GP for the development of the automated experiments, where the measurement points are chosen based on the results of previous measurements34,35,36. Here the Bayesian uncertainty along with the target-driven criteria can be used for balancing of the exploratory and exploitation activity. Furthermore, we believe that the analysis can be strongly improved with the addition of physics-based priors to reconstruction, where the kernel function incorporates the partially known physics of material (e.g., atomically resolved periodic features, sharp boundaries, Green’s function for known geometric domain, etc.) or imaging process (resolution function).