Multibody modeling for concept-level floating offshore wind turbine design

Abstract

Existing Floating Offshore Wind Turbine (FOWT) platforms are usually designed using static or rigid-body models for the concept stage and, subsequently, sophisticated integrated aero-hydro-servo-elastic models, applicable for design certification. For the new technology of FOWTs, a comprehensive understanding of the system dynamics at the concept phase is crucial to save costs in later design phases. This requires low- and medium-fidelity models. The proposed modeling approach aims at representing no more than the relevant physical effects for the system dynamics. It consists, in its core, of a flexible multibody system. The applied Newton–Euler algorithm is independent of the multibody layout and avoids constraint equations. From the nonlinear model a linearized counterpart is derived. First, to be used for controller design and second, for an efficient calculation of the response to stochastic load spectra in the frequency-domain. From these spectra the fatigue damage is calculated with Dirlik’s method and short-term extremes by assuming a normal distribution of the response. The set of degrees of freedom is reduced, with a response calculated only in the two-dimensional plane, in which the aligned wind and wave forces act. The aerodynamic model is a quasistatic actuator disk model. The hydrodynamic model includes a simplified radiation model, based on potential flow-derived added mass coefficients and nodal viscous drag coefficients with an approximate representation of the second-order slow-drift forces. The verification through a comparison of the nonlinear and the linearized model against a higher-fidelity model and experiments shows that even with the simplifications, the system response magnitude at the system eigenfrequencies and the forced response magnitude to wind and wave forces can be well predicted. One-hour simulations complete in about 25 seconds and even less in the case of the frequency-domain model. Hence, large sensitivity studies and even multidisciplinary optimizations for systems engineering approaches are possible.

1 Introduction

Floating wind turbine platforms can be grouped into the ones with taut mooring lines called Tension Leg Platforms (TLPs) and the ones with slack mooring lines. The latter are called spar in case of a single deep-drafted cylinder with a low center of gravity. Semisubmersibles or barges achieve the hydrostatic restoring moment from the waterplane area (barge effect), together with gravitational forces. To date, first full-scale prototype tests of FOWTs were successfully completed, such as Statoil’s Hywind spar with a 2.3 MW turbine [23], Principle Power’s WindFloat [71] with a 2 MW turbine, or the Japanese Kabashima project with a 2 MW turbine on two different platform types [86].

Currently, the design of FOWTs builds on the existing and established methodologies for onshore wind turbines on the one side and on the methodologies for offshore platforms on the other side. It is stated in [61] that the design process of the wind turbine and the substructure is currently rather independent. Only limited data are exchanged between the two designers due to confidentiality requirements. Coupled design tools include aerodynamics, hydrodynamics, structural dynamics, and control system dynamics. Although they build on engineering assumptions, they have a level of detail suitable for certification. Tools of lower order, for quick load analysis, on the other side, are not common. Consequently, an integrated design optimization is beyond the state-of-the-art, and the substructure is designed without considering the specific design requirements related to the wind turbine.

This work aims at providing a concept-level simulation methodology to facilitate an integrated design. The proposed simulation model includes all physical effects relevant for the dynamics of the overall system. In the same way as the physical effects are simplified, the necessary model parameters are less detailed than for common aero-hydro-servo-elastic models, easing the issue of confidentiality in practice. The holistic view on the system dynamics at an early stage of the development helps to improve the decision-making at early design stages, where most of the committed lifecycle costs are determined; see [27, p. 44].

1.1 Floating wind turbine dynamics and modeling

Nonlinear time-domain modeling with a number of realizations of the stochastic wind and wave conditions is common for FOWT load case simulations. Hydrodynamics, on the other side, are usually modeled in the frequency-domain in ocean engineering [63]. The currently consented method of a coupled modeling of FOWTs has its origins in the open-source FAST tool by National Renewable Energy Laboratory, Boulder, USA (NREL) [67], developed within the thesis project by Jason Jonkman [29]. This open-source tool is used as a reference model in this work. Other available FOWT models with comparable approaches are, among others, the commercial tools Bladed by Det Norske Veritas–Germanischer Lloyd (DNV-GL), Hawc2 by Technical University of Denmark (DTU), Simo-Riflex by Sintef Ocean, Norway, and Simpack by Dassault Systèmes. The structural model is commonly a flexible Multibody System (MBS) with modal shape functions, reducing the number of Degrees of Freedom (DoF) of a Finite Element (FE) representation. Some models include nonlinear beam models for the rotor blades to account for large deflections; see, for example, [21]. The floating platform is usually modeled as a rigid body. Studies were made recently to include the substructure flexibility in the dynamic system analysis; see [7, 10, 55].

For the aerodynamic forces, most models use Blade Element Momentum (BEM) theory [22], including semiempirical corrections to avoid computationally expensive high-fidelity fluid dynamic models. Recently, models were presented, which can better predict the unsteady effects from the fore-aft motion of the rotor due to the floating platform motion. A first increase of complexity is the potential flow free-wake vortex method, which was used in [16, 51, 59, 78], and [90]. An even higher fidelity can be expected from Computational Fluid Dynamics (CFD) simulations as done in [40, 85], and [53]. Experimental tests have also been conducted by [74] and [5]. In summary, the importance of these unsteady effects depends on the frequency of the fore-aft motion, the wind speed, and the aerodynamic loading of the rotor.

The control system is of critical influence to FOWTs because of the low-frequency fore-aft motion of the rotor. In above-rated conditions, the actuation of the blade pitch angle has the goal of reducing the aerodynamic torque when the controlled variable rotor speed has a positive error. However, if this overspeed results from an increase of the apparent wind speed due to a fore-aft motion of the floater, then this motion can become unstable. The reason is that the pitching of the blades decreases not only the aerodynamic torque but also the thrust. This effect yields a Right Half-Plane Zero (RHPZ) in the dynamics from the blade pitch angle to the rotor speed; see [17, 30, 39], and [47]. The results of this work are made with a robust Single-Input-Single-Output (SISO)-controller, which was developed using the presented model. The integrated controller design procedure was published first in [72] and automated and extended in [49].

The DoFs of common simulation models include, next to the platform rigid-body DoFs, elastic DoFs for the tower bending in fore-aft and side–side directions and multiple elastic DoFs per blade. FAST has two flapwise and one edgewise DoF. Additional DoFs are the rotor rotation, the drivetrain torsion, and the blade pitch actuator model DoFs, usually represented by a second-order dynamic system. Whereas the blade pitch actuator model is not included in FAST, the yaw drive actuator is included through a rotational spring-damper element. The total number of DoFs of the standard FAST v8.16 [67] configuration is 22. To focus on the overall system dynamics, the reduced-order model of this work limits the DoFs allowing only a planar platform motion in the vertical 2D plane, and it neglects the elasticity of the blades.

The hydrodynamic modeling in coupled FOWT models uses frequency-dependent coefficients, derived from potential flow panel codes with the Boundary Element Method. This methods assumes a linear superposition of the problem of a stationary floating body in waves including wave diffraction and the problem of a moving body in still water, radiating waves. Due to a frequency-dependency of the acceleration-dependent and velocity-dependent coefficients of the rigid body oscillator, a convolution integral is necessary in the time-domain [19]. Additionally, nonlinear effects can be of importance. For FOWTs, this is mainly viscous drag, which is neglected by potential flow theory and usually reintroduced through empirical Morison’s equation. Furthermore, free-surface effects represent nonlinearities, which yield slow-drift forces below the first-order wave frequencies; see [15] and for FOWTs, [14] and [20]. A summary on hydrodynamic FOWT modeling can be found in [50].

1.2 Reduced-order modeling

A number of researchers have made efforts in recent years to derive simplified numerical FOWT models. This was mostly done with the objective to derive linearized models for controller design. These models aimed in the first place at including the “soft” fore-aft motion of the floating platform in control design models. Only a single representative DoF of this fore-aft motion was considered in [11] and [17]. A dedicated model, specific to TLP-type FOWTs, was derived in [6]. It approximates the FAST response without modeling the tower flexibility. A more detailed structural model for control design was developed in [25] with semiempirical Morison’s equation for substructures composed of slender cylinders and regular wave conditions. The model has 16 states and couples the aero-hydro-servo dynamics but with a mechanical model of a single rigid body only. A recent control-oriented model [18] uses hydrodynamic coefficients from a panel code, valid also for nonslender structures. Both of the latter models, however, neglect the tower flexibility.

Reduced-order models were also developed for efficient concept-level load-case simulations. In [35], a model for spar-type platforms was presented. Here, a relatively detailed (BEM) aerodynamic model was employed but only a filter to represent the controller dynamics. The computational efficiency is only slightly increased, compared to FAST. Another rather detailed model is the one in [58], which is derived from a nonlinear FE-model including a potential flow model using classical Model Order Reduction (MOR) techniques. A comparable approach employing two different MOR techniques to a FAST model, with the goal of developing a wind farm model, was presented in [52]. Other authors also relied on the approximation of the FAST dynamics but more related to system identification techniques than linear MOR, like Pegalajar-Jurado et al. [68]. They approximate the controller dynamics by identifying the aerodynamic fore-aft damping from the nonlinear closed-loop FAST model. The present model was compared to the one by Pegalajar-Jurado et al. [43]. The model in [89] neglects the controller but features load-case dependent (or response-dependent) hydrodynamic drag and a dynamic mooring line model. The model in [70] also simplifies aerodynamics and neglects wind turbine structural flexibility and the controller dynamics, but it includes nonlinear hydrostatics and nonlinear wave excitation forces. A similar modeling approach for hydrodynamics and aerodynamics but with tower flexibility and wind turbine controller was presented in [1] with a comparison against various FOWT simulators. The results show differences between the models in terms of steady states and the response magnitude at the platform eigenfrequencies. Another dedicated model for the design of suction anchors in ultimate loading conditions was developed in [2]. It considers a spar-type FOWT and represents aerodynamics through a constant drag force.

Most models drastically simplify the aerodynamic part. For a linearized description, only a small number of simulation codes is able to derive the linearized aeroelastic equations for onshore wind turbines. The problem is complex, as the lift and drag depend quadratically on the wind speed and the correction models are mostly nonlinear, like dynamic stall models for large angles of attack; see [22]. Only one work on FOWTs addressed aerodynamic linearization techniques: In [57] the frequency-domain load response in deterministic environmental conditions is studied, as well as the errors through linearization of the blade-resolved aerodynamics, structural dynamics, and hydrodynamics. The hydrodynamic model also includes hydrodynamic second-order slow-drift forces.

In summary, many approaches for simplification of FOWT models have been proposed for different purposes. Most of them, however, simplify drastically either the aerodynamic or the hydrodynamic problem by neglecting the controller dynamics on the aerodynamic side, or diffraction effects, viscous effects, and second-order slow-drift forces on the hydrodynamic side. Often, codes are limited to a specific FOWT-type.

The motivation for the derivation of the present model is a system-oriented representation with a “fair” simplification of all disciplines. Thus, effects that do not drive the overall system are neglected equally in the structural model, the hydrodynamic model, and the aerodynamic model. Thereby an important consideration is the computational efficiency. It should be research-oriented, meaning that the MBS layout should not be hardcoded but defined by the users (allowing, for example, for additional bodies, like tuned mass dampers, or new DoFs, to model elastic members of the floater). The model should be control-oriented, with single (scalar) disturbance inputs (wind and wave) and a linear counterpart to a nonlinear time-domain model for model-based controller design. At the same time, it should allow a quick identification of critical load cases and integrated FOWT optimization. The equations should be exportable for model-predictive control applications as in [76]. It should be flexible with respect to the floater shape (not limited to slender cylinders).

A first development of the model was presented in [73] with a verification across different load cases in [62]. Earlier versions of the model were used in the European projects INNWIND.EU [87], LIFES50+ [43], and TELWIND [92] for controller design and preliminary load case analysis. A comparison of the model predictions with scaled experiments was made in [9]. The integrated optimization of the floating platform, including the wind turbine controller [44], showed a significant margin of the global tower load reduction. Another application of the model to 2-bladed onshore wind turbines was presented in [56].

The paper provides a review of different common engineering models for FOWTs for structural dynamics, aerodynamics, and hydrodynamics. Intermediate results of these submodels will be shown on the way, backing the selected approaches for the new low-order model, called Simplified Low-Order Wind Turbine (SLOW) in the following. Sections 2–7 address the derivation of the model, followed by its verification in Sects. 8–9 and final conclusions in Sect. 10.

2 Structural model

The derivation of the structural Equations of Motion (EQM) follows the Newton–Euler approach, as opposed to the Lagrangian approach, which is often found in wind turbine research [57, 93]. The method allows for a user-defined MBS layout, independent of the configuration of bodies and DoFs; see [75] or [79]. Therefore the derivation, which is here shown for a FOWT, holds also for any other multibody system with the same assumptions. This is different from the equations in FAST: Although the approach following Kane [34] is comparable to the current one, the FAST equations are exclusively derived for horizontal-axis wind turbines. The method chosen here follows Schiehlen [75] for rigid bodies and Schwertassek [77], specifically for flexible bodies. Symbolic programming will be used, which facilitates cross-platform applications of the EQM. The right-hand side of the EQM, formulated as Ordinary Differential Equation (ODE), is available symbolically and allows an efficient time-stepping because no matrix algebra is necessary. This is due to the formulation in minimal coordinates, meaning that not more second-order dynamic equations are necessary than the number of DoFs without constraint equations. Symbolic codes are efficient but limited by the size of the EQM. A large number of DoFs and kinematics involving several relative rotations result quickly in code, too large to compile efficiently. A discussion and possible alternatives can be found in [37]. Although the MBS equations can be found in the literature, a concise description will be given in this paper with particular additions, specific to FOWTs.

2.1 Equation of motion

The Newton–Euler equation can be written for an elastic body $i$ as the sum of inertial forces $\boldsymbol {M}_{i}\boldsymbol {z}_{\mathit{III},i}$, centrifugal, gyroscopic, and Coriolis forces $\boldsymbol {h}_{\omega ,i}$, gravitational forces $\boldsymbol {h}_{g}$, applied discrete forces $\boldsymbol {h}_{d,i}$, inner elastic forces $\boldsymbol {h}_{e,i}$ based on the selected deformation tensor, and the reaction forces $\boldsymbol {h}_{r,i}$. The accelerations $\boldsymbol {z}_{\mathit{III},i}=[\boldsymbol {a}_{i}, \boldsymbol {\alpha _{i}}, \ddot{\boldsymbol {q}}_{e,i}]^{T}$ include the rigid-body acceleration in translational and rotational directions $\boldsymbol {a}_{i}$ and $\boldsymbol {\alpha _{i}}$ and the generalized accelerations in $\ddot{\boldsymbol {q}}_{e,i}\in \mathbb{R}^{(f_{e,i}\times 1)}$ from the body deformation. The EQM results with a dimension of (${6+f_{e,i}}$) for each body $i$ as

$$ \boldsymbol {M}_{i} \boldsymbol {z}_{\mathit{III},i}+ \boldsymbol {h}_{\omega ,i} = \boldsymbol {h}_{g,i} + \boldsymbol {h}_{d,i} + \boldsymbol {h}_{e,i} + \boldsymbol {h}_{r,i}. $$

(1)

2.2 Kinematics

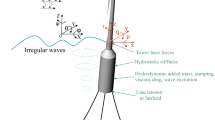
The vector of generalized coordinates $\boldsymbol {q}$ is a combination of rigid and flexible (elastic) DoFs $\boldsymbol {q}=[\boldsymbol {q}_{r}, \boldsymbol {q}_{e}]^{T}$. For the results in this paper, a model with 2D-motion of the floating platform rigid body in surge ($x_{p}$), heave ($z_{p}$), and pitch ($\beta _{p}$), a flexible tower with one representative coordinate $x_{t}$, the rotor speed $\Omega$, and the blade pitch actuator $\theta _{1}$ is selected; see Fig. 1. Thus the vector $\boldsymbol {q}$ of the generalized rigid and flexible coordinates is

$$ \boldsymbol {q}_{r} = [ x_{p}, z_{p}, \beta _{p}, \varphi , \theta _{1} ]^{T} \quad \text{and}\quad \boldsymbol {q}_{e} = [x_{t}]. $$

(2)

The $p=4$ bodies used in this work are the platform, tower, nacelle, and rotor; see Fig. 1. For FOWTs, the inertial frame $I$ is usually located at the Center of Flotation (CF) (at the intersection of the tower centerline with the Still Water Level (SWL)).

Fig. 1

Topology of the developed multibody model, reprinted from [48] with permission from MDPI, 2018

The limitation of the two-dimensional model, avoiding side-side DoFs, is justified by [4], who demonstrated that the dominant loads can be expected in the vertical plane of wind and wave direction, whereas lateral (side–side) loads are of lower magnitude. In [82, Fig. 10] the average variation of wind/wave misalignment angles over the considered US-sites is small. Consequently, it is reasonable to limit the present model to the two-dimensional plane in the predominant wind/wave direction.

2.2.1 Rigid bodies

The model includes the rigid bodies, platform, nacelle, and rotor. For these bodies, no generalized coordinate $\boldsymbol {q}_{e}$ for the body deformation exists, and thus $\boldsymbol {q}\equiv \boldsymbol {q}_{r}$. In this case the body accelerations $\boldsymbol {z}_{\mathit{III},i}$ are written for the body Center of Mass (CM) in inertial coordinates. The kinematic quantities of the translational velocity $\boldsymbol {v}_{i}$ and the translational acceleration $\boldsymbol {a}_{i}$ of each body’s CM in inertial coordinates can now be calculated from the position vectors $\boldsymbol {r}_{i}$ to each body’s CM. The velocity $\boldsymbol {v}_{i}$ is the time-derivative of the position vector $\boldsymbol {r}_{i}$. It can be expressed in terms of the generalized coordinates via the Jacobian matrix $\boldsymbol {J}_{\mathit{t,i}}$ following Schiehlen [75] as

$$ \boldsymbol {v}_{i}(\boldsymbol {q}, \dot { \boldsymbol {q}}) = \dot{\boldsymbol {r}}_{i}(\boldsymbol {q},\dot { \boldsymbol {q}}) = \frac{\partial \boldsymbol {r}_{i}(\boldsymbol {q},\dot {\boldsymbol {q}})}{\partial \boldsymbol {q}}\dot {\boldsymbol {q}}= \boldsymbol {J}_{\mathit{t,i}}(\boldsymbol {q},\dot {\boldsymbol {q}})\dot{\boldsymbol {q}}. $$

(3)

The partial differentiation with respect to time is omitted, since no time-dependent boundary conditions exist here (scleronomic system). Accordingly, the translational accelerations $\boldsymbol {a}_{i}$ are

$$ \boldsymbol {a}_{i} = \dot{\boldsymbol {v}}_{i}(\boldsymbol {q},\dot {\boldsymbol {q}}) = \frac{\partial \boldsymbol {v}_{i}(\boldsymbol {q},\dot {\boldsymbol {q}})}{\partial \dot {\boldsymbol {q}}}\ddot {\boldsymbol {q}}+\frac{\partial \boldsymbol {v}_{i}(\boldsymbol {q},\dot {\boldsymbol {q}})}{\partial \boldsymbol {q}}\dot { \boldsymbol {q}}=\boldsymbol {J}_{t,i}(\boldsymbol {q},\dot { \boldsymbol {q}})\ddot{\boldsymbol {q}} + \bar{\boldsymbol {v}}_{i}( \boldsymbol {q},\dot {\boldsymbol {q}}) $$

(4)

with the second summand $\bar{\boldsymbol {v}}_{i}$, called the local velocity [75].

2.2.2 Flexible bodies

The flexible bodies are described with respect to the “floating frame of reference”, according to Schwertassek [77] and Shabana [80]: It is an arbitrary body reference coordinate system for the definition of the flexible body. This formulation is useful for a precomputation of the elastic properties of the bodies. A standard format for these precomputed coefficients was developed in [88]. This Standard Input Data (SID) is used in the present model. As a consequence, the kinematics of an elastic body can be described by the motion of the reference frame and the body deformation.

The position vector $\boldsymbol {\rho }^{k}_{i}(t)$ to the flexible nodes $k$ can be written as the sum of the reference position ${{}^{R}}{\boldsymbol {r}}_{i}$, the relative undeformed reference coordinates ${{}^{R}}{\boldsymbol {R}}$, and the deformation field ${{}^{R}}{\boldsymbol {u}}^{k}_{i}(t)$, relative to the undeformed reference coordinates:

$$ {}^{R}\boldsymbol {\rho }^{k}_{i}(t)={{}^{R}}{\boldsymbol {r}}_{i}(t)+ {{}^{R}}{\boldsymbol {R}}^{k}_{i} + {{}^{R}}{\boldsymbol {u}}^{k}_{i}(t) = \boldsymbol {S}^{T}_{i}\:{{}^{I}}{\boldsymbol {\rho }}^{k}_{i}(t). $$

(5)

The rotation tensor $\boldsymbol {S}_{i}\equiv {{}^{I}}{\boldsymbol {S}}^{R}_{i}$ transforms the kinematics from the reference frame $R$ to the inertial frame $I$. All kinematics of the flexible bodies are described in the reference frame $R$. Therefore the superscript $R$ will be omitted in the following.

For the orientation, the same description holds: Equally to $\boldsymbol {R}^{k}_{i}$, the tensor $\boldsymbol {\Gamma }^{k}_{i}$ represents the orientation of node $k$ of the flexible body $i$ in the undeformed configuration with respect to the reference frame.

A deformed body has the nodal orientation

$$ \boldsymbol {D}^{k}_{i}=\boldsymbol { \Theta }^{k}_{i}(t)\boldsymbol {\Gamma }^{k}_{i}. $$

(6)

The additional rotation induced by the deformation is given by the linearized rotation tensor $\boldsymbol {\Theta }^{k}_{i}(t)$.

Shape functions

As with FE models, shape functions can be used with flexible MBS to characterize the body deformation through a limited number of coordinates. For wind turbine blades and the tower, the eigenmodes are usually used as shape functions. A discussion can be found in [24].

The shape function for translation $\boldsymbol {\Phi }^{k}_{i}\in \mathbb{R}^{(3\times f_{e,i})}$ for each node $k$ has $f_{e}$ columns, corresponding to the number of generalized elastic coordinates defined for flexible body $i$. The shape function for the rotation is $\boldsymbol {\Psi }^{k}_{i}\in \mathbb{R}^{(3\times f_{e,i})}$. The nodal rotation tensor $\boldsymbol {\Theta }^{k}_{i}(t)$ is calculated assuming small, linear displacements from the rotation shape function $\boldsymbol {\vartheta }^{k}_{i}$ with the identity matrix $\boldsymbol {E}$ and the cross-product operator $\tilde {\boldsymbol {S}} (\boldsymbol {x} )\boldsymbol {y}=\boldsymbol {x}\times \boldsymbol {y}$ as

$$ \boldsymbol {\Theta }^{k}_{i}(t)= \boldsymbol {E}+\tilde {\boldsymbol {S}} \bigl(\boldsymbol {\vartheta }^{k}_{i} \bigr). $$

(7)

The general relative deformation field for translation $\boldsymbol {u}^{k}_{i}(t)$ of Eq. (5) and for rotation $\boldsymbol {\vartheta }^{k}_{i}(t)$ of Eq. (6) can now be formulated as a function of the generalized coordinates $\boldsymbol {q}_{e,i}(t)$ of the elastic body as

$$ \boldsymbol {u}^{k}_{i}(t)=\boldsymbol {\Phi }^{k}_{i}\boldsymbol {q}_{e,i}(t) \quad \text{and}\quad \boldsymbol {\vartheta }^{k}_{i}(t)=\boldsymbol {\Psi }^{k}_{i} \boldsymbol {q}_{e,i}(t). $$

(8)

A wind turbine tower or a blade with zero sweep (blade sections are stacked along the axis of the aerodynamic center) has reference coordinates $\boldsymbol {R}$ with the first two elements $R_{1}=R_{2}=0$. The tower or beam longitudinal coordinates are given by $R_{3}$. The shape functions for a linear Bernoulli beam with only one DoF for bending are

$$ \boldsymbol {\Phi }_{i}(\boldsymbol {R})= \left [\textstyle\begin{array}{c} W_{i,1}(R_{3})\\ 0\\ -R_{2}W_{i,1}^{\prime}(R_{3}) \end{array}\displaystyle \right ], $$

(9)

where $W_{i,1}(R_{3})$ represents the lateral deflection of the beam axis for the first shape. The term $-R_{2}W_{i,1}^{\prime}(x)$ is a function of the lateral coordinate $R_{2}$. The third component of $\boldsymbol {\Phi }_{i}$ does not contain a function of $R_{3}$, as opposed to FAST. There, the latter component is named the axial reduction shape function [67]. The linearized shape function for the beam element rotations reads

$$ \boldsymbol {\Psi }_{i}(\boldsymbol {R})= \left [\textstyle\begin{array}{c} 0\\ W_{i,1}^{\prime}(x)\\ 0 \end{array}\displaystyle \right ]. $$

(10)

With these shape functions, the resulting nodal orientation ${}^{I}\boldsymbol {S}^{k}_{i}$ with respect to the inertial coordinate system $I$ can be calculated using Eqs. (7) and (8) as

$$ \boldsymbol {S}^{k}_{i}= \bigl( \boldsymbol {E}+ \tilde {\boldsymbol {S}} \bigl(\boldsymbol {\Psi }^{k}_{i}\boldsymbol {q}_{e,i}(t) \bigr) \bigr)\boldsymbol {\Gamma }^{k}_{i}\boldsymbol {S}_{i}(t). $$

(11)

The rotation of the reference system of body $i$ is $\boldsymbol {S}_{i}^{k=0}\equiv \boldsymbol {S}_{i}$. Equation (11) is needed for the definition of the orientation of the nacelle, attached to the top of the flexible tower. The upper node $\hat{k}$ of the tower determines the nacelle orientation $\boldsymbol {S}_{\mathit{nac}}=\boldsymbol {S}^{\hat{k}}_{\mathit{twr}}$. Accordingly, the angular velocity $\boldsymbol {\omega }^{k}_{i}$ can be calculated from the rotation tensor $\boldsymbol {S}^{k}_{i}$ using $\dot{\boldsymbol {S}}_{i}\boldsymbol {S}_{i}^{T}=\tilde {\boldsymbol {S}} (\boldsymbol {\omega }_{i} )$.

In the same way as for rigid bodies, the flexible body velocity and acceleration vectors $\boldsymbol {z}_{\mathit{II},i}$ and $\boldsymbol {z}_{\mathit{III},i}$ of Eq. (1) can be written in terms of the generalized coordinates $\boldsymbol {q}$ with the Jacobian matrices $\boldsymbol {J}_{t,i}$ and $\boldsymbol {J}_{r,i}$ following [79] as

$$\begin{aligned} \boldsymbol {z}_{\mathit{II},i} = \left [\textstyle\begin{array}{c} {}^{R}\boldsymbol {v}_{i}\\ {}^{R}\boldsymbol {\omega }_{i}\\ \dot{\boldsymbol {q}}_{e,i} \end{array}\displaystyle \right ] = \left [\textstyle\begin{array}{c} \boldsymbol {J}_{t,i}(\boldsymbol {q})\\ \boldsymbol {J}_{r,i}(\boldsymbol {q})\\ \boldsymbol {J}_{e,i}\\ \end{array}\displaystyle \right ]\dot{\boldsymbol {q}}, \quad \quad \boldsymbol {z}_{\mathit{III},i} = \left [\textstyle\begin{array}{c} {}^{R}\boldsymbol {a}_{i}\\ {}^{R}\boldsymbol {\alpha }_{i}\\ \ddot{\boldsymbol {q}}_{e,i} \end{array}\displaystyle \right ] = \left [\textstyle\begin{array}{c} \boldsymbol {J}_{t,i}(\boldsymbol {q})\\ \boldsymbol {J}_{r,i}(\boldsymbol {q})\\ \boldsymbol {J}_{e,i} \end{array}\displaystyle \right ]\ddot{\boldsymbol {q}} + \left [\textstyle\begin{array}{c} \dot{\boldsymbol {J}}_{t,i}(\boldsymbol {q},\dot{\boldsymbol {q}})\\ \dot{\boldsymbol {J}}_{r,i}(\boldsymbol {q},\dot{\boldsymbol {q}})\\ \boldsymbol {0} \end{array}\displaystyle \right ]\dot{\boldsymbol {q}}. \end{aligned}$$

(12)

The selection matrix $\boldsymbol {J}_{e,i}$ assigns the elastic coordinates $\boldsymbol {q}_{e,i}$ of $\boldsymbol {q}$ to the respective bodies. The rows of the generalized elastic deformation are unchanged when transforming the system into minimal coordinates. The global Jacobian matrix $\boldsymbol {J}$ for flexible bodies is

$$ \boldsymbol {J}= [\boldsymbol {J}_{t,1}, \boldsymbol {J}_{r,1}, \boldsymbol {J}_{e,1}, \ldots, \boldsymbol {J}_{t,p}, \boldsymbol {J}_{r,p}, \boldsymbol {J}_{e,p} ]^{T}. $$

(13)

2.3 Mass matrix

The mass matrix of Eq. (1) for a flexible body $i$ (subscript will be omitted in the following) related to the coordinates $\boldsymbol {z}_{I}$ is given by [77] as

$$ \boldsymbol {M}=\left [\textstyle\begin{array}{c@{\quad }c@{\quad }c} \boldsymbol {M}_{tt} && \mathit{{sym}}.\\ \boldsymbol {M}_{rt}& \boldsymbol {M}_{rr}& \\ \boldsymbol {M}_{et}& \boldsymbol {M}_{er}& \boldsymbol {M}_{ee} \end{array}\displaystyle \right ] = \left [\textstyle\begin{array}{c@{\quad }c@{\quad }c} \boldsymbol {m} && \mathit{{sym}}.\\ m\tilde {\boldsymbol {S}} (\boldsymbol {c} )& \boldsymbol {I}& \\ \boldsymbol {C}_{t}& \boldsymbol {C}_{r}& \boldsymbol {M}_{e} \end{array}\displaystyle \right ]. $$

(14)

Coupling elements between translations $(t)$, rotations $(r)$, and elastic coordinates $(e)$ are present. This means that inertial forces on the flexible body frame $R$ result from a generalized acceleration $\ddot {\boldsymbol {q}}_{e}$ and vice versa. No couplings occur between translations and rotations in the case of rigid bodies because their kinematics are in the present model written with respect to their CM, denoted $\boldsymbol {c}$ in reference coordinates. The inertial forces resulting from the beam deformation in translational directions are represented by $\boldsymbol {C}_{t}\in \mathbb{R}^{(f_{e}\times 3)}$ as

$$ \boldsymbol {C}_{t}= \int ^{l}_{0} \rho A \boldsymbol {\Phi }^{T}_{i}(R_{3})\,\mathrm{d}R_{3}. $$

(15)

The mass moment of inertia $\boldsymbol {I}=\boldsymbol {I}(\boldsymbol {q}_{e})$ is the sum of that of the undeformed body $\boldsymbol {I}_{0}$ and the contributions from elasticity $\boldsymbol {I}_{1}(\boldsymbol {q}_{e})$ and $\boldsymbol {I}_{2}(\boldsymbol {q}_{e})$:

$$\begin{aligned} \begin{aligned} \boldsymbol {I}(\boldsymbol {q}_{e})&=\boldsymbol {I}_{0}+\boldsymbol {I}_{1}(\boldsymbol {q}_{e})+\boldsymbol {I}_{2}(\boldsymbol {q}_{e})\quad \text{with } \\ \boldsymbol {I}_{1}&= \int _{0}^{l} \bigl(\tilde {\boldsymbol {S}} ( \boldsymbol {R} )\tilde {\boldsymbol {S}} (\boldsymbol {\Phi }\boldsymbol {q}_{e} )^{T} + \tilde {\boldsymbol {S}} (\boldsymbol { \Phi }\boldsymbol {q}_{e} )\tilde {\boldsymbol {S}} (\boldsymbol {R} )^{T} \bigr)\,\mathrm{d}m\quad \text{and} \\ \boldsymbol {I}_{2}&= \int _{0}^{l}\tilde {\boldsymbol {S}} ( \boldsymbol {\Phi }\boldsymbol {q}_{e} )\tilde {\boldsymbol {S}} ( \boldsymbol {\Phi }\boldsymbol {q}_{e} )^{T}\,\mathrm{d}m. \end{aligned} \end{aligned}$$

(16)

The coupling between elastic deformations and rotations $\boldsymbol {C}_{r}$ is given by

$$ \boldsymbol {C}_{r}= \int _{0}^{l}\boldsymbol {\Phi }^{T}\tilde {\boldsymbol {S}} (\boldsymbol {\Phi }\boldsymbol {q}_{e} )^{T}\,\mathrm{d}m. $$

(17)

The generalized elastic mass matrix $\boldsymbol {M}_{e}$ can be calculated by integrating over the squared shape functions

$$ \boldsymbol {M}_{e}= \int _{0}^{l}\boldsymbol {\Phi }\boldsymbol { \Phi }^{T}\,\mathrm{d}m. $$

(18)

2.4 Inner elastic forces

The elastic restoring forces $\boldsymbol {h}_{e}$ of Eq. (1) require a description of the strain $\epsilon$ in terms of the generalized elastic coordinates $\boldsymbol {q}_{e}$. To this end, the linear coefficient matrix $\boldsymbol {B}_{L}$ is introduced following [77]:

$$ \boldsymbol {\epsilon }=\boldsymbol {B}_{L} \boldsymbol {q}_{e}. $$

(19)

A derivation of the quadratic terms $\boldsymbol {B}_{N}$, resulting, for example, from geometric stiffening (centrifugal stiffening) of the rotor blades, can be found in [77, p. 356]. The linear restoring stiffness for mode $k=1$ can be calculated with Young’s modulus $E$ as

$$ \boldsymbol {K}_{eL}= \int _{V} \boldsymbol {B}_{L}^{T} E \boldsymbol {B}_{L}\,\mathrm{d}V= \int _{x=0}^{l} E J_{22}W_{1}^{\prime\prime\,2}(R_{3}) \,\mathrm{d}R_{3}. $$

(20)

The second moment of area $J_{22}$ about $R_{2}$ results from an integration over the cross-section $A$ with the lateral coordinate $R_{1}$. The linear generalized stiffness matrix $\boldsymbol {K}_{eL}\in \mathbb{R}^{\mathit{(f_{e}\times f_{e})}}$ has as many dimensions as elastic degrees of freedom defined for the body. The diagonal entries are the modal stiffnesses, which are a good approximation for simpler models, that is, tower-fore aft dynamics in the controller design model used in [76].

The modal damping matrix $\boldsymbol {D}_{e}\in \mathbb{R}^{(f_{e}\times f_{e})}$ can be obtained from the modal stiffness $\boldsymbol {K}_{eL}$ and the modal mass $\boldsymbol {M}_{e}$ for mode $k$ with a given structural damping ratio $\xi _{k}$:

$$ \boldsymbol {D}_{e} = \operatorname{diag}(D_{ek}) \quad \text{with } D_{ek}=2\xi _{k}\sqrt{K_{ek}M_{ek}}. $$

(21)

The modal damping ratios are user-defined inputs in FAST [67]. Finally, the vector of inner elastic forces $\boldsymbol {h}_{e}$ results as

$$ \boldsymbol {h}_{e}=\left [\textstyle\begin{array}{c} \boldsymbol {0}\\ \boldsymbol {0}\\ -\boldsymbol {K}_{eL}\boldsymbol {q}_{e}-\boldsymbol {D}_{e}\dot{\boldsymbol {q}}_{e} \end{array}\displaystyle \right ]. $$

(22)

2.5 Quadratic velocity vector

Centrifugal, gyroscopic, and Coriolis forces are combined in the quadratic velocity vector $\boldsymbol {h}_{\omega }$ of Eq. (1). For planar systems, as the present one, only centrifugal forces appear. Therefore we omit the derivation of $\boldsymbol {h}_{\omega }$. It can be found in [77, p. 296] (for a reference in English, see [79]). Nonetheless, in the present model, we implement the quadratic velocity vector.

2.6 External applied forces

Aerodynamic and hydrodynamic forces acting on a multibody system need to be transformed into the reference frame of the flexible body. The system transformation matrix given by Fossen [19, p. 176] is here of good use. The discrete applied forces $\boldsymbol {h}_{d}$ of Eq. (1) are again a combination of translational, rotational, and elastic forces, aligned with the coordinates $\boldsymbol {z}_{\mathit{I}}$ defined in Eq. (2). Based on the nodal forces $\boldsymbol {F}^{k}$ and torques $\boldsymbol {M}^{k}$ in the reference frame, the generalized forces are

$$ \boldsymbol {h}_{d}=\left [\textstyle\begin{array}{c} \boldsymbol {h}_{dt}\\ \boldsymbol {h}_{dr}\\ \boldsymbol {h}_{de}\end{array}\displaystyle \right ]= \sum _{k}\left(\left [\textstyle\begin{array}{c} \boldsymbol {E}\\ \tilde {\boldsymbol {S}} (\boldsymbol {R}^{k}+\boldsymbol {\Phi }^{k}\boldsymbol {q}_{e} )\\ \boldsymbol {\Phi }^{k^{T}} \end{array}\displaystyle \right ]\boldsymbol {F}^{k} + \left [\textstyle\begin{array}{c} \boldsymbol {0}\\ \boldsymbol {E}\\ \boldsymbol {\Psi }^{k^{T}} \end{array}\displaystyle \right ]\boldsymbol {M}^{k}\right). $$

(23)

The same transformation is necessary to obtain the generalized gravitational forces $\boldsymbol {h}_{g}$ of Eq. (1).

2.7 Nonlinear equations of motion

The global Newton–Euler equations for all bodies can now be assembled and transformed into minimal coordinates with the global Jacobian matrix $\boldsymbol {J}$ of Eq. (13) as

$$\begin{aligned} \boldsymbol {J}^{T} [\boldsymbol {M}\boldsymbol {z}_{\mathit{III}}+\boldsymbol {h}_{\omega } ] &= \boldsymbol {J}^{T} [\boldsymbol {h}_{g} + \boldsymbol {h}_{d} + \boldsymbol {h}_{e} + \boldsymbol {h}_{r} ] \\ &=\overline{\boldsymbol {M}}(\boldsymbol {q})\ddot{\boldsymbol {q}}+\overline{ \boldsymbol {h}}_{\omega}(\boldsymbol {q}, \dot {\boldsymbol {q}}) = \overline{\boldsymbol {h}}_{g}(\boldsymbol {q}) + \overline{ \boldsymbol {h}}_{d}(\boldsymbol {q},\dot {\boldsymbol {q}}) + \overline{\boldsymbol {h}}_{e}(\boldsymbol {q}_{e}). \end{aligned}$$

(24)

With this operation, the reaction forces $\overline{\boldsymbol {h}}_{r}$ of Eq. (1) vanish due to their orthogonality with $\boldsymbol {q}$. Thus the nonlinear EQM results with one dimension for each generalized coordinate of Eq. (2). The overline $(\overline{\cdot })$ indicates that the quantity is formulated in the space of generalized coordinates $\boldsymbol {q}$. The above derivation can be automated based on a user-defined MBS layout.

2.8 Linearized equations of motion

The structural EQM of Eq. (1) are linearized with respect to the states $\boldsymbol {x}$ and inputs $\boldsymbol {u}$. The control inputs are the blade pitch angle $\Delta \theta$ and the generator torque $\Delta M_{g}$, and the disturbance inputs are the rotor-effective wind $\Delta v$ and the incident wave height $\zeta \equiv \Delta \zeta$ collected in vector $\boldsymbol {u}$. The equations are linearized about the set point of the states $\boldsymbol {x}_{0}$ and the setpoint of inputs $\boldsymbol {u}_{0}$ as

$$\begin{aligned} \boldsymbol {x} = \boldsymbol {x}_{0} +\Delta \boldsymbol {x}, \quad \quad \boldsymbol {u} = \boldsymbol {u}_{0} + \Delta \boldsymbol {u}, \end{aligned}$$

(25)

where $\Delta \boldsymbol {x}$ and $\Delta \boldsymbol {u}$ are the new vectors of linear (differential) states and inputs, respectively. The coupled linearized equations of motion in state-space description can be separated for position- and velocity-dependent terms $\boldsymbol {Q}$ and $\boldsymbol {P}$. The state-space description with the input matrix $\boldsymbol {B}$ is

$$ \Delta \dot{\boldsymbol {x}} = \underbrace{\left [\textstyle\begin{array}{c@{\quad }c} \boldsymbol {0} & \boldsymbol {E}\\ -\boldsymbol {M}^{-1} \boldsymbol {Q} & -\boldsymbol {M}^{-1} \boldsymbol {P} \end{array}\displaystyle \right ]}_{\boldsymbol {A}} \Delta \boldsymbol {x} + \boldsymbol {B} \Delta \boldsymbol {u}. $$

(26)

The linearization takes advantage of the symbolic EQM: No perturbation analysis is necessary, but the Jacobians can be calculated analytically. The derivation of the force models and their linearization will be addressed in the following sections.

3 Aerodynamic model

Most engineering models for wind turbines rely on BEM theory, a combination of the momentum equation for annuli elements of the rotor and blade element theory (lift and drag as functions of the angle of attack). A difficulty of this model for implementation in the low-order model to be developed is the fact that the blade span needs to be divided into various sections and an iteration for the solution of the set of the BEM equations is necessary. The approach selected for this work neglects a calculation of distributed loads along the span but reduces the problem to the integral rotor loads. It has been applied previously to onshore turbines, for example, by [8, 41], and [76]. The method has proven to be computationally efficient, well suitable for linearization, and able to reproduce the forcing relevant for the system dynamics.

3.1 Nonlinear model

The aerodynamic torque about the shaft $M_{\mathit{{aero}}}$ and the thrust force in shaft-direction $F_{\mathit{{aero}}}$ can be calculated with the air density $\rho _{a}$ as

$$ M_{\mathit{{aero}}}=\frac{1}{2}\rho _{a}\pi R^{2} \frac{c_{p}(\lambda , \theta _{1})}{\Omega }v_{\mathit{{rel}}}^{3} \quad \text{and}\quad F_{\mathit{{aero}}}= \frac{1}{2}\rho _{a}\pi R^{2} c_{t}(\lambda , \theta _{1})v_{\mathit{{rel}}}^{2}. $$

(27)

The power and thrust coefficient $c_{p}$ and $c_{t}$, shown in Fig. 2, can be computed as the steady-state solution of a standard BEM code. Here FAST [67] is used with rigid blades of radius $R$ and a rotor shaft aligned with the global $x$-axis, requiring only few iterations for convergence. The coefficients are calculated for different Tip Speed Ratios (TSRs) $\lambda =\Omega R/\bar{v}_{\mathit{{hub}}}$ and blade pitch angles $\theta$ ($\bar{v}_{\mathit{{hub}}}$ is the mean free-stream wind speed) as shown in Fig. 2.

Fig. 2

Rotationally sampled wind $v_{\mathit{{eff}}}$ (left), rotor thrust coefficient from BEM simulation as a function of blade pitch $\theta$ and TSR $\lambda$ (right)

The relative rotor-effective wind speed $v_{\mathit{{rel}}}$ is a function of the component of the velocity of the rotor body $\boldsymbol {v}_{\mathit{{rotor}}}$ aligned with the global $x$-direction ${}^{I}\boldsymbol {e}_{I1}$:

$$ v_{\mathit{rel}}=v_{\mathit{{eff}}}-{{}^{I}}{\boldsymbol {e}_{I1}}\cdot {{}^{I}}{\boldsymbol {v}_{\mathit{{rotor}}}}, $$

(28)

where (⋅) denotes the dot-product. The two components $F_{\mathit{{aero}}}$ and $M_{\mathit{{aero}}}$ of the external aerodynamic force vector exert on the rigid rotor body in SLOW.

One way to obtain a representative wind speed $v_{\mathit{{eff}}}$ is to apply a weighted averaging of the full 3D turbulent wind field of, for example, TurbSim [28], over the rotor plane in each timestep. This averaging, however, yields to time series of $F_{\mathit{{aero}}}$ and $M_{\mathit{{aero}}}$ not representing the individual excitation of the blades. Mainly the azimuth-dependent excitation at the Three-Times-Per-Revolution (3p) frequency is important for the system response. A simple method to represent this forcing is to rotationally sample the turbulent wind at the rotor angular velocity of the operating point as illustrated in Fig. 2. Consequently, a “blade-effective” wind speed is used as $v_{\mathit{{eff}}}$ in Eq. (27).

3.2 Linearized model

The aerodynamic thrust force $F_{\mathit{{aero}}}$ and torque $M_{\mathit{{aero}}}$ can be written as a Taylor series up to the first order. The partial derivatives are calculated with respect to the differential rotor speed $\Delta \Omega$, the differential blade pitch angle $\Delta \theta _{1}$, and the differential relative wind speed $\Delta v$. The linearized formulations can be found in [72]. The linearized coefficients are obtained here with a fixed-size central difference scheme. In [57] the method of this work is called tangent linearization, which was compared to harmonic linearization, respecting the expected variation of model inputs. The next section shows that sufficiently accurate results can be obtained using the tangent linearization.

3.3 Verification

To verify the introduced structural and aerodynamic models, a comparison of the nonlinear and the linearized SLOW response against FAST to a deterministic gust at still water is shown in Fig. 3. This load case yields large transient rotor loads and an impulse response-like behavior (the duration of the gust is rather short in the time-scales of the FOWT). Nonetheless, the platform DoFs, the tower bending, and the rotor signals well follow the FAST results. The only visible difference is the steady state in surge ($x_{p}$). This is due to the neglected aerodynamic torque on the hub about the horizontal $y$-axis from wind shear and oblique inflow.

Fig. 3

Model verification: Extreme Operating Gust (EOG) at 14.0 m/s with linearized SLOW (dark blue), nonlinear SLOW (red), and FAST (light green) [42] (Color figure online)

The results show that a lumped rotor model with the inclusion of the controller dynamics in the model (with a blade pitch-dependent aerodynamic model) can well model the overall platform motion, the rotor speed, and the tower bending response.

4 Hydrodynamic model

In offshore engineering, it is common to model floating rigid bodies with the six DoFs of unconstrained motion $\boldsymbol {\xi }$ and the mass matrix $\boldsymbol {M}$ in the frequency-domain [60]:

$$ -\omega ^{2} \bigl[\boldsymbol {M}+\boldsymbol {A}( \omega ) \bigr]\boldsymbol {\xi } + j\omega \boldsymbol {B}(\omega )\boldsymbol { \xi } + \boldsymbol {C}\boldsymbol {\xi } = \boldsymbol {X}(\omega )\zeta _{0}(\omega )= \boldsymbol {F}_{\mathit{{wave}}}^{(1)}( \omega ). $$

(29)

With the SLOW model in 2D, the generalized rigid-body coordinates of the platform reduce to $\boldsymbol {\xi }=[x_{p}, z_{p}, \beta _{p}]^{T}$. The hydrostatic restoring stiffness $\boldsymbol {C}$ has only nonzero elements in $(1,1)$, $(3,3)$, and $(5,5)$ for point symmetric floaters. The frequency-dependent coefficients result from hydrodynamic potential flow programs. The added mass matrix $\boldsymbol {A}(\omega )$ and the potential damping matrix $\boldsymbol {B}(\omega )$ are the acceleration and velocity-dependent integrated hydrodynamic pressures of a body moving in all six DoFs at the frequency $\omega$. The calculation of the wave-induced forces $\boldsymbol {X}(\omega )$ results from the integrated pressure amplitudes and phases over the (stationary) wetted surface from a unit wave.

For a time-domain simulation of the hydrodynamics in the present model, Eq. (29) needs to be transformed from the frequency-domain. The frequency-dependency of the linear coefficients, however, yield a convolution integral; see Cummin’s equation [12]. For the present model, this is undesirable due to the computational effort required to compute the retardation forces from radiated waves. A method to overcome these challenges will be introduced in Sect. 4.1. The calculation of the exciting forces $\boldsymbol {F}_{\mathit{{wave}}}^{(1)}(t)$ in the time-domain is a subject of Sect. 4.2.

The linear potential flow forces excite the FOWT at the frequencies of linear waves (a peak spectral frequency $f_{\mathit{{wave}}}\approx 0.1~\mbox{Hz}$ is common for ocean waves). The linear potential flow solver can be augmented with the quadratic boundary condition for dynamic pressure [33, pp. 5–8] at the free surface. If the wave pressure on the body is integrated up to the instantaneous free surface, then the force model becomes nonlinear, and a frequency component off the linear wave spectrum appears. Assuming a bichromatic wave, a beat pattern arises, showing a low-frequency envelope of the peaks, the so-called bounded long waves. The forces at these frequencies are important because they often coincide with the low-frequency resonances of FOWTs; see [15]. The second-order force model will be the subject of Sect. 4.4.

Next to the hydrodynamic pressures from the potential flow solver, viscous forces need to be accounted for. These are inherently neglected by potential flow theory. Radiation damping $\boldsymbol {B}(\omega )$ is not a direct result of viscous effects but a result of the boundary condition of the BEM problem, imposing the condition of still water far away from the body. Viscous effects are, however, included in Morison’s equation [64]. Morison’s equation is a semiempirical alternative to Eq. (29) including a quadratic drag. It works without a numerical panel-code computation, assuming an undisturbed wave field but neglects diffraction effects and holds only for slender cylinders. In this work the linear panel-code coefficients are used in combination with the viscous drag term of Morison’s equation; see Sect. 4.3.

4.1 Radiation model

Most of the current FOWT tools use the above-mentioned convolution integral. One available alternative is a fitted state-space description, modeling the transfer dynamics from the body motion to the hydrodynamic forces acting back on the body [69]. In the course of the presented work an even simpler method has shown promising results: The added mass $\boldsymbol {A}(\omega )$ is interpolated at a single frequency, which avoids the frequency-dependent EQM. This “constant matrix” approach was already reported for offshore structures in [83]. A viable approach has been found, interpolating $\boldsymbol {A}(\omega )$ at the respective eigenfrequencies of the different DoFs. Figure 4 shows the frequency-dependent added mass with the interpolated values.

Fig. 4

Panel code added mass of TripleSpar platform with values interpolated at respective eigenfrequencies [42]

For the potential damping matrix $\boldsymbol {B}(\omega )$, an interpolation at a single frequency is not possible because, unlike $\boldsymbol {A}(\omega )$, it is strongly dependent on the frequency; see Fig. 5b. In the present model, potential damping is entirely neglected such that the only source of hydrodynamic damping is from Morison’s drag term. Nonetheless, the developed linearized model has the capability of solving Eq. (29) in the frequency-domain with both frequency-dependent coefficients. However, also in the frequency-domain, the sequential solution yields a significant computational effort due to the inversion of the mass matrix at each frequency. A comparison of the computational speed for the entire model will be shown in Sect. 8.

Fig. 5

Linear transfer function with frequency-dependent coefficients and with proposed simplification for TripleSpar platform

Neglecting potential damping can be justified through the hydrodynamic properties of most FOWT platforms. They are such that the potential damping is large at frequencies above their rigid-body natural frequencies. Damping forces are generally dominant at the natural frequencies and less important at other frequencies. Consequently, it is a reasonable simplification to neglect potential damping for FOWTs for the present modeling objectives. Note that the situation is different for ships because in their case potential damping is dominant over viscous damping and cannot be neglected; see [63, p. 387].

A comparison of the Response Amplitude Operator (RAO) in pitch direction, the linear transfer function from wave height $\zeta _{0}$ to the platform pitch displacement $\beta _{p}\equiv \xi _{5}$ is shown in Fig. 5a. The resonance frequency at $f_{\beta _{p}}\approx 0.04~\mbox{Hz}$ is clearly visible. It is below the frequencies where $B_{55}(\omega )$ (Fig. 5b) is large. The first two lines of Fig. 5a show results with and without potential damping, calculated for a rigid body in waves by the panel code. There is no visible difference between the two results, which supports the selected simplification. The third line is the same transfer function but here calculated with the full SLOW model, Fig. 1. Here the potential damping is again neglected, but the added mass is now constant, interpolated at a single frequency (Fig. 4). Additionally, all SLOW DoFs are enabled as in Eq. (2), and aerodynamics are included. Figure 5a shows the same resonance frequency with more damping due to the aerodynamic damping effects and the above-mentioned viscous drag from Morison’s equation. The amplification of SLOW above the resonance frequency deviates slightly from the rigid-body result, mainly due to the frequency-independent added mass. However, the overall agreement is satisfactory with a significant increase in computational efficiency by avoiding the convolution integral of the radiated waves.

4.2 First-order wave force model

The first-order wave forces $\boldsymbol {F}_{\mathit{{wave}}}^{(1)}$ result in the frequency-domain from a multiplication of the wave force transfer function $\boldsymbol {X}(\omega )$ with the wave height amplitude spectrum $\zeta _{0}(\omega )$. The forces are usually assumed to yield small motion responses such that the wave force model is independent from the rigid body states $\boldsymbol {\xi }$. The corresponding time series can be obtained from an Inverse Discrete Fourier Transform (IDFT).

For the SLOW model and especially for model-predictive controllers, a parametric transfer function has been fitted to $\boldsymbol {X}(\omega )$. As a result, the wave height $\zeta _{0}$ is an input to the linear system description; see Fig. 6. The procedure to obtain the force transfer function was presented in [45].

Fig. 6

Block diagram for parametric first-order wave excitation model

4.3 Viscous drag model

The drag properties of the floating platform are discretized through nodes as shown in Fig. 7. Each node $k$ has associated modified drag coefficients $C_{D,i}^{*}$ for all three directions $i$, which include the area $A_{ik}$ projected on direction $i$, associated with the node. Then the drag term of Morison’s equation is

$$ F_{\mathit{{drag},ik}} = C_{D,ik}^{*} (v_{w,ik}-v_{b,ik} ) \lvert v_{w,ik}-v_{b,ik} \rvert , $$

(30)

with the modified hydrodynamic coefficients $C_{D,ik}^{*}=\frac{1}{2}\rho _{w} A_{ik} C_{D,ik}$ and nodal body velocities $v_{b,ik}$. The wave particle velocities $v_{w,ik}$ can be calculated explicitly in time- or frequency-domain using linear wave theory [33]. For the TripleSpar platform, the horizontal and vertical drag coefficients are set according to Fig. 7: The vertical drag force is applied to the representative node of the heave plate at the keel $C_{D,hp}=C_{D,zk}$ and calculated with the heave plate cross-sectional area. The heave plates have no transverse drag forces, only the slender columns.

Fig. 7

Hull shape discretization for horizontal and vertical Morison drag coefficients [42] (Color figure online)

The linearization of the quadratic nodal viscous drag forces is a function of the relative velocity response Standard Deviation (STD) $\sigma$ of the nodes. Using Borgman linearization

$$ \bar{C}_{D,ik}^{*}=\sqrt{ \frac{8}{\pi }}\sigma (v_{w,ik} - v_{b,ik}) \frac{1}{2}\rho _{w} A_{i,k} C_{D,ik}, $$

(31)

we can obtain a linearized drag coefficient $\bar{C}_{D,ik}^{*}$. Here Eq. (30) is linearized with one linear coefficient of the wave velocity and one linear coefficient of the body velocity. Thus the first will be part of the external forcing in the input matrix $\boldsymbol {B}$, whereas the latter will contribute to the damping matrix $\boldsymbol {P}$ of Eq. (26). The result is the spectral density matrix $\boldsymbol {S}_{\mathit{FF}}^{\mathit{{mor}}}(\omega )$ of the Morison forcing and a generalized damping matrix $\boldsymbol {D}$ of the Morison damping. With the frequency-domain formulation of SLOW, the drag coefficients $\bar{C}_{D,ik}^{*}$ can be parameterized and iteratively determined, based on the dynamic response in the frequency-domain. This is the subject of the companion paper [48].

4.4 Second-order slow-drift force model

The slowly varying forces, introduced at the beginning of this section, have a strong influence on the scaled experiments. Figure 8 shows that the simulation significantly underpredicts the response at the platform pitch and surge eigenfrequencies if no slow-drift model is included.

Fig. 8

Experimental measurements [91] of platform response of scaled (1:60) TripleSpar of Fig. 1 with and without slow-drift model

The slowly varying drift force can be calculated based on the Quadratic Transfer Function (QTF), denoted by $\boldsymbol {T}(\omega ,\omega )$, which results from nonlinear panel codes [15]. The calculation of the QTF is computationally expensive, depending on the mesh, frequency resolution, and wave directions. The force spectral density matrix resulting from a wave spectrum $S_{\mathit{\zeta \zeta }}(\omega )$ in the frequency-domain was given by Pinkster [38] as

$$ \boldsymbol {S}^{(2)}_{\mathit{FF}}(\mu )=8 \int _{0}^{\infty }\boldsymbol {T}(\omega , \omega + \mu )S_{\zeta \zeta }(\omega )S_{\zeta \zeta }(\omega +\mu )\boldsymbol {T}( \omega , \omega +\mu )^{*T}\,\mathrm{d}\omega , $$

(32)

where $\mu$ is the difference-frequency of the bichromatic wave, $\mu=\omega _{i}-\omega _{j}$, and $(\cdot )^{*T}$ denotes the complex conjugate transpose. To simplify Eq. (32), Newman [66] proposed to obtain the second-order force spectrum $\boldsymbol {S}^{(2)}_{\mathit{FF}}$ with the diagonal $\boldsymbol {T}(\omega _{i}, \omega _{i})$ only, instead of the full QTF. This is reasonable because the QTF usually does not change much over the difference-frequency; see [15, p. 157], and it has the advantage that the diagonal of the QTF already results from a first-order panel code calculation. The force spectrum with Newman’s approximation results as

$$ \boldsymbol {S}^{(2)}_{\mathit{FF}}(\mu )=8 \int _{0}^{\infty }\boldsymbol {T} (\delta ,\delta )S_{\zeta \zeta }(\omega )S_{\zeta \zeta }(\omega +\mu )\boldsymbol {T} ( \delta , \delta )^{*T}\,\mathrm{d}\omega $$

(33)

with $\delta =\omega +\mu /2$. In the time-domain the forces result according to [66] from a double IDFT as

$$\begin{aligned} \boldsymbol {F}^{(2)}_{\mathit{{wave}}}(t) &= \sum_{i}\sum_{j} \zeta _{0}(\omega _{i})\zeta _{0}(\omega _{j})^{*}\boldsymbol {T}(\omega _{i}, \omega _{i})\cos \bigl[(\omega _{i}-\omega _{j}) t + \varphi _{\zeta ,i} - \varphi _{\zeta ,j} \bigr]. \end{aligned}$$

(34)

Newman [66] explains that the double summation over $\omega _{i}$ and $\omega _{j}$ of Eq. (34) can be expressed as the square of a single sum of suitably chosen frequencies of the arguments. In this case the time series result (formulation as in [14]) as

$$ \begin{aligned} \boldsymbol {F}^{(2)}_{\mathit{{wave}}}(t) &= \boldsymbol {\theta }^{2}\big\vert _{T(\omega _{i}, \omega _{i})>0} - \boldsymbol {\theta }^{2}\big\vert _{T(\omega _{i}, \omega _{i})< 0} \quad \text{with } \\ \boldsymbol {\theta } &=\sum_{i}{\big|\zeta (\omega_{i})\big|\sqrt{2\big|\boldsymbol {T}(\omega _{i}, \omega _{i})\big|}\cos (\omega _{i} t + \varphi _{\zeta ,i})}, \end{aligned} $$

(35)

where $\varphi _{\zeta ,i}$ is the phase angle at $\omega _{i}$. Although this formulation is computationally very efficient, its disadvantage is that it contains unphysical high frequencies, which need to be filtered. An improved formulation was proposed by [81] with the product of two sums as

$$\begin{aligned} \boldsymbol {F}^{(2)}_{\mathit{{wave}}}(t)={}&\operatorname{Re} \bigg( \biggl[\sum_{i}\big|\zeta (\omega _{i})\big|\operatorname{sgn}\bigl(\boldsymbol {T}(\omega _{i},\omega _{i})\bigr)\sqrt{\boldsymbol {T}(\omega _{i},\omega _{i})}\exp(\omega _{i} t +\varphi _{\zeta ,i}) \biggr] \\ &{} \times \biggl[\sum_{j}\big|\zeta ( \omega _{j})\big|\sqrt{\boldsymbol {T}(\omega _{j},\omega _{j})}\exp(-\omega _{j} t + \varphi _{\zeta ,i}) \biggr]\bigg). \end{aligned}$$

(36)

In Fig. 9 the different formulations for the slowly varying drift force, Eqs. (33)–(36), are compared for a load case of the experiments published in [91] with the $1/60$-scaled TripleSpar of Fig. 1. Comparing the wave spectrum $S_{\zeta \zeta }(\omega )$ on top, with the drift force spectrum $\boldsymbol {S}^{(2)}_{\mathit{FF}}(\omega )$, the fact that the drift forces are off the original wave frequencies becomes clear. The mean drift coefficients for the scaled TripleSpar are shown in surge-direction in the second plot. The plots below show the second-order force spectra and the corresponding time series. The direct frequency-domain calculation, Eq. (33), gives the largest response magnitude. The second largest response magnitude results from the double sum approach of Eq. (34). Comparing the original Newman formulation, Eq. (35), with the improved formulation by Standing, Eq. (36), the response magnitude is equal at the difference-frequency. The differences at higher frequencies are due to the above-mentioned unphysical frequencies.

Fig. 9

Wave spectrum (top), mean drift coefficients $T_{\mathit{11}}(\omega ,\omega )$, surge slow-drift force spectrum $S_{\mathit{FF,11}}^{(2)}(\omega )$, and time series $F_{\mathit{11}}^{(2)}(t)$ with frequency-domain calculation (Eq. (33)), double IDFT (Eq. (34)), original Newman approximation (Eq. (35)), and Standing et al.’s formulation (Eq. (36)) for scaled experiment [91] of TripleSpar (1:60) [42] (Color figure online)

The formulation implemented in SLOW is the one according to Standing et al., Eq. (36); the same is implemented in HydroDyn; see [32] and [14]. For the linearized frequency-domain model, the spectral densities $\boldsymbol {S}^{(2)}_{\mathit{FF}}(\omega )$ are computed through the Discrete Fourier Transform (DFT) of the force time series of Eq. (36) to ensure equal slow-drift models for both formulations. The implemented form of Newman’s approximation requires no more than a preprocessing of the second-order forces, which takes a comparable time as the first-order forces. Nonetheless, it has to be kept in mind that the model is only an approximation of the second-order forcing.

5 Mooring line model

The mooring lines are not modeled dynamically. Instead, the quasistatic equations for a catenary mooring line (e.g., [29]) are solved a priori for different horizontal and vertical excursions of the attachment point at the platform. The model solving for these forces is based on the formulation of FAST v7; see [31]. The resulting forces are subsequently summed and transformed into the generalized platform coordinates in each timestep. Dynamic effects of the mooring lines were a subject of the theses [3] and [59]. According to these works, dynamic effects can be important in certain conditions, but generally a dynamic model is most appropriate for a detailed design analysis of the lines themselves. For the linearized model, a generalized stiffness matrix $\boldsymbol {C}_{\mathit{{moor}}}|_{0}$ can be calculated for each operating point.

6 Code architecture

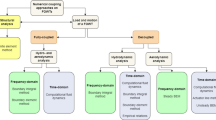
Figure 10 shows the workflow for the preparation of a time- or frequency-domain simulation with SLOW. The symbolic processor makes it possible to develop a user-defined MBS layout (1), with the input data highlighted with an underscore, resulting in a nonlinear and a linearized state-space description (Eq. (26)). The aerodynamic and hydrodynamic coefficients and the mooring line restoring forces (2) result from preprocessors (the IDFT method is shown for the hydrodynamic forces, Sect. 4.2). No black-box system identification is necessary as for other reduced-order models, all preprocessors are physical models. For the simulation of stochastic load cases turbulent wind speeds, irregular wave heights, and force time series need to be precomputed (3).

Fig. 10

Workflow of writing reduced-order model equations of motion and preparing simulation [42]

7 Frequency-domain response and load calculation

Load cases defined in standards, such as that by the International Electrotechnical Commission (IEC) [26], include deterministic wind and wave conditions but mostly more realistic stochastic ones. The latter are most important for fatigue assessments. In the frequency-domain the stochastic response can be efficiently obtained. For a Multi-Input-Multi-Output (MIMO) system $\boldsymbol {G}(s)$, the response autospectrum $\boldsymbol {S}_{\mathit{yy}}(\omega )$ to the matrix $\boldsymbol {S}_{\mathit{uu}}(\omega )$ of the input spectra is simply given by the multiplication:

$$ \boldsymbol {S}_{\mathit{yy}}(\omega ) = \boldsymbol {G}^{*T}(\omega )\boldsymbol {S}_{\mathit{uu}}(\omega ) \boldsymbol {G}(\omega ), $$

(37)

where $\boldsymbol {G}^{*T}(\omega )$ denotes the transfer function complex conjugate transpose. Consequently, no integration or “time-stepping” as in time-domain methods is necessary for solving the ODE of the state-space model, which can save orders of magnitude of computational time.

7.1 Fatigue

For fatigue assessments, the Damage-Equivalent Load (DEL) is usually calculated through a rainflow counting [54]. In the frequency-domain, it can be approximated with Dirlik’s method [13]. The method has been applied to wind turbine blades in [84]. It has not been yet applied to the sectional loads of a FOWT structure. Figure 11 shows the DEL for each of the chosen wind bins, calculated with the rainflow method of the tower-top displacement from elastic deformation of the nonlinear model, compared against Dirlik’s method. Dirlik’s method was applied twice: once to the Power Spectral Density (PSD) obtained from the time series through Welch’s method and once to the spectra directly obtained from the linear frequency-domain model. The DEL values are calculated for each bin and extrapolated for a lifetime of 20 years. We can see that the match is fairly good. There is a maximum deviation of only 0.4% for the time series data. This confirms that Dirlik’s method is valid for the nature of the tower-top bending signal under the given load conditions. The damage from the linear model data implies no larger deviations than Dirlik’s method itself.

Fig. 11

DEL for tower-top displacement $x_{t}$ for operational winds. Calculated with (1) rainflow counting, (2) Dirlik’s method with spectra obtained from the same time series data as (1), and (3) Dirlik’s method with spectra obtained from linearized frequency-domain model [42]

7.2 Short-term extremes

Next to the response STD and DEL, also the short-term extreme responses are important for the design. Especially, for the design of wind turbine controllers, the overshoot of the electrical power response or the generator torque is an important design criterion. A means to obtain these extremes from frequency-domain spectra has been implemented in the model. Assuming stationary Gaussian waves and a narrow-banded response signal, the response amplitudes are Rayleigh distributed [33]. The short-term probability density function $f_{\mathit{{st}}}$ of the response amplitudes $A_{y}$ is then

$$ f_{\mathit{{st}}}(A_{y})= \frac{A_{y}}{m_{0y}}\exp \biggl(-\frac{A_{y}^{2}}{2m_{0y}} \biggr). $$

(38)

The zeroth spectral moment $m_{0y}$ of the response is equal to the variance $\sigma _{y}^{2}$.

For a given time period $T$, the probability of exceedance of the amplitudes $A_{y}$ can be estimated with the Cumulated Distribution Function (CDF) $P_{\mathit{st}}$. It is the integral of Eq. (38)

$$ P_{\mathit{st}}(A_{y}>a) = \int _{a}^{\infty }\frac{A_{y}}{m_{0y}}\exp \biggl(- \frac{A_{y}^{2}}{2m_{0y}} \biggr)\,\mathrm{d}A_{y}. $$

(39)

The number of times $N_{T}$ of $A_{y}$ exceeding a limit $a$ can be estimated with the average zero-upcrossing period $T_{2r}$. This follows from the idea that “there is only one peak value between an upcrossing and a subsequent downcrossing of any level $a$” [65, p. 237]. It results in

$$ N_{T}=\frac{T}{T_{2r}}P_{st}(A_{y}>a). $$

(40)

For design tasks, the amplitude that is reached or exceeded $N_{T}$ times in a given time $T$ needs to be calculated. This can be done by solving Eq. (40) for the amplitude $a$. A comparison of this estimation with direct time-domain data is shown in Fig. 12 with the metocean conditions of Table 1. The graph shows that the estimation from the frequency-domain spectrum underpredicts the maximum around rated winds. This is likely because in these highly nonlinear response cases the signal is not normally distributed. In the other cases the method very well predicts the maximum amplitudes of the tower bending.

Fig. 12

Short-term extremes for tower-top displacement $x_{t}$ for operational winds. Calculated from (1) time series directly, (2) from PSD of time series, and (3) from linear frequency-domain model response spectrum using Eq. (38) [42]

Table 1 Environmental conditions for operational load cases of [36, Chap. 7]

7.3 Reference design

The FOWT design “TripleSpar”, used in this paper, was initially developed in the European project INNWIND.EU. It is an open concept design for the research community and can be downloaded [46]. It is a semisubmersible of deep draft with a large portion of the hydrostatic restoring coming from gravitational forces; see Fig. 1. The main parameters are listed in Table 2. The concept was already tested in a scaled experiment; see [9] and [91].

Table 2 Reference case parameters: INNWIND.EU TripleSpar platform and DTU10 MW wind turbine

8 Coupled model verification

In this section, the developed model will be compared to the widespread and verified FAST model (version 8.16) to assess its validity. A set of metocean conditions over operational wind speeds has been taken from the project LIFES50+ [36, Chap. 7] for the evaluation of the models. The conditions are shown in Table 1.

The most significant difference between the introduced concept-level SLOW and the reference model FAST is the aerodynamic model and the reduced number of structural DoFs (2D motion only). The modeling approaches are summarized and compared between SLOW and FAST in Table 3. For an improved computational efficiency, the results of the linearized model in this work are made with a constant added mass, neglecting the potential damping.

Table 3 Comparison of modeling approaches between FAST, SLOW nonlinear, and SLOW linear

Figure 13 shows the PSD of the response of the full-scale TripleSpar to stochastic wind and wave loads for a load case with mean wind $\bar{v}_{\mathit{hub}}=18~\mbox{m/s}$ and significant wave height $H_{s}=4.3~\mbox{m}$ with a peak period of $T_{p}=10~\mbox{s}$. SLOW proves to reproduce well the eigenfrequencies of the platform-DoFs surge $x_{p}$, heave $z_{p}$, and pitch $\beta _{p}$ and also their response magnitude. The forced response to the first-order wave loads at $f_{\mathit{{wave}}}=0.1~\mbox{Hz}$ can be clearly seen in the $x_{p}$ and $x_{t}$ signals. The tower-top displacement $x_{t}$ has a second peak above the wave frequency, below its coupled eigenfrequency of $0.42~\mbox{Hz}$ at about $0.18~\mbox{Hz}$. This effect has its origin in the wave force transfer function $\boldsymbol {X}(\omega )$ from the potential flow calculation. It has two peaks divided by an attenuation range. The slow drift force model of Sect. 4.4 is the main force exciting the amplitudes at the resonance frequencies of surge $x_{p}$ and pitch $\beta _{p}$, also reflected in the tower bending $x_{t}$. The rotor speed $\Omega$ responds to the $\beta _{p}$-motion, which is related to the discussed zeros in the right half-plane, induced by the controller dynamics. The generator torque is constant above rated ($v_{\mathit{{rated}}}=11.4~\mbox{m/s}$), and thus the rotor speed $\Omega$ is proportional to the electrical power $P$. The tower eigenfrequency is mainly excited by the 3p forces on the rotor, coming from the vertical wind shear. It is well captured by the reduced-order model with the rotational sampling method of Sect. 3. The tower-base bending moment $M_{\mathit{yt}}$ is widely proportional to the tower-top displacement $x_{t}$, except for the nonconservative structural damping forces.

Fig. 13

Model verification: PSD of response to LIFES50+ DLC 1.2 case @17.9 m/s. Linearized model (dark blue), nonlinear model (red), FAST (light green) [42] (Color figure online)

To realize a time-domain comparison of the same load case as Fig. 13, the same turbulent wind time series were input to SLOW and FAST, and the wave height time series $\zeta _{0}(t)$ of FAST were used in SLOW. The comparison of Fig. 14 shows that the transients and steady states (means) well compare between SLOW and FAST. The wind speed signal on top has more high-frequency oscillations for SLOW. This is because of the rotational sampling, introduced in Sect. 3, as opposed to the rotor-effective wind speed, shown for FAST. The steady-state deviation of surge ($x_{p}$) and the blade pitch angle $\theta$ are due to the same effects as in the deterministic case of Fig. 3.

Fig. 14

Model verification: Time-series of response to LIFES50+ DLC 1.2 case @17.9 m/s. Nonlinear model (dark red), FAST (light green) [42] (Color figure online)

Figure 15 shows a comparison against FAST of statistics of selected response signals over all metocean bins of Table 1. Again, the same stochastic process was used for the SLOW and FAST models to allow a valid assessment of short-term extremes. The wave conditions are rather severe with significant wave heights of up to 8 m. These conditions yield large deviations from the operating point of the linearized model. The STD $\sigma$ is shown for the rotor speed $\Omega$, the tower-top bending $x_{t}$, and the measured blade pitch angle $\theta _{1}$. The fatigue damage, condensed in the DEL, was calculated for the tower-base bending moment $M_{yt}$. Additionally, the one-hour maxima of the rotor speed $\Omega$, the tower-top deflection $x_{t}$, and the blade pitch angle $\theta _{1}$ are shown for the metocean conditions of Table 1. Most signals show to be driven by the significant wave height $H_{s}$. It increases with the mean wind speed $\bar{v}_{\mathit{{hub}}}$ as shown by Table 1. The other load driver are the aerodynamic forces, which increase up to rated wind $\bar{v}_{\mathit{hub}}=11.4~\mbox{m/s}$ and decrease above.

Fig. 15

Model comparison of STD, fatigue damage and short-term extremes over operational wind speeds of SLOW linear (dark blue), SLOW nonlinear (red), and FAST (light green) with environmental conditions of Table 1 (Color figure online)

The aerodynamic force model of Eq. (27) involves significant nonlinearities. Their effect can be observed in the rotor speed response $\sigma (\Omega )$. The signal agrees well between the nonlinear SLOW and FAST models, whereas the linear SLOW model deviates for severer conditions. Another nonlinear effect is the transition from below-rated to above-rated conditions. It involves a nonlinear switching of the controller. This effect cannot be modeled by the linear model, which leads to the shown differences in this wind speed range.

The agreement of the STDs of the tower-top displacement $x_{t}$ is remarkable with deviations of less than 10%. The tower bending is, opposed to the rotor speed, dominated by the wave loads equally to the tower-base bending $M_{yt}$. The wave force model involves less important nonlinearities than the aerodynamic model. The constant offset across the wind speed bins of $\sigma (x_{t})$ and $\mathrm{DEL}(M_{yt})$ is due to the rotor disk model of Sect. 3 with rotational sampling. The azimuth-dependent forcing from wind shear is only approximately included in SLOW. This forcing is particularly large for the TripleSpar design, because the rated 3p frequency is close to the tower eigenfrequency. The blade pitch angle $\theta _{1}$ does not respond to the wave frequencies due to the PI-controller bandwidth.

The model difference of the short-term extremes for $\Omega$ is comparable to the STD due to the controller switching and the nonlinear aerodynamic model, which cannot be accurately predicted by the linear model. The nonlinear SLOW model, however, shows deviations of less than 10%. The extremes of $x_{t}$ also have an agreement of around 10%, except for the switching around rated winds. The deviation for below-rated winds is again due to the approximate azimuth-dependent aerodynamic force model. The blade pitch angle extremes $\theta _{1}$ show small deviations of less than 10%.

Although the results are shown for the TripleSpar concept, another study [44] has shown that the model validity holds also for other semisubmersibles with larger column diameters and smaller drafts.

9 Computational efficiency

The main prospect of the presented modeling approach is a simplification for efficient concept-level design studies and optimization. A computational speed assessment is shown in Table 4. The simulation times are given for a PC with a 2.5 GHz processor and one hour simulations with $n=500$ frequencies for the linear frequency-domain computations. The preprocessing of wind and waves is necessary for each load case, but the preprocessing of the aerodynamic coefficients and the mooring line forces is only necessary when a new model is set up. The wave-preprocessing includes the first-order wave force time series and spectra, the Morison force spectra, and the slow-drift frequency spectra.

Table 4 Comparison of computational speed between SLOW and FAST for stochastic load case of 3600 s in time-domain. Linear SLOW model calculates response in frequency-domain. Preprocessing of mooring lines and aerodynamics only design-dependent, not load case-dependent [42]

10 Conclusions

The developed simulation method provides a new means to design, investigate, and optimize FOWT concepts. Unlike the widely used coupled models for FOWTs, the presented method enables more efficient concept-level studies on the dynamic behavior. Physical white-box instead of surrogate models are used. The comparison of the common approaches for structural dynamic, hydrodynamic, and aerodynamic modeling has led to the development of a reduced-order model, which includes effects of all disciplines, relevant for the system dynamics without focusing on one of the disciplines in more detail. This means that the design of the model has been done persistently aiming at the best tradeoff between accuracy and efficiency for a representation of system-level dynamics. Symbolic programming accelerates the model execution and makes real-time applications possible. The linear frequency-domain model is a counterpart to the nonlinear model, allowing a direct quantification of nonlinear effects. Different frequency-domain methods have been applied to estimate fatigue damage and short-term extremes from response spectra. The model is fully parameterized allowing for optimization tasks. Less detailed model parameters are necessary than for other models, which eases confidentiality issues in industrial design and an application at early conceptual design stages. The applied multibody system algorithm can be automated, which makes quick adjustments of the mechanical topology easily possible. All types of FOWTs can be simulated. The set of features and the level of development represents is a new contribution over existing reduced-order models.

The main findings on the modeling assumptions are on the structural side that a two-dimensional approach is sufficient to capture the dominant loads. On the aerodynamic side the controller is important to be included in the aerodynamic force model. Simplifying the blade forces to the integral rotor loads accelerates the model and simplifies linearization but still gives an accurate prediction of the low-frequency forces from turbulence. The simplification results in an approximate representation of the azimuth-dependent forcing from wind shear, influencing the high-frequency tower loads. On the hydrodynamic side the panel code coefficients enable a modeling across FOWT platform types. Neglecting the potential damping from wave radiation and the frequency-dependency of the fluid added mass is the major contribution to the computational efficiency without impairing significantly the accuracy.

It could be shown that it is possible to simulate the main FOWT dynamics of a 1 h load case in less than 30 s with only 6% of difference (STD) to the widespread FAST model in severe metocean conditions with significant wave heights of more than 8 m. The agreement is remarkable, considering that no system identification or order-reduction techniques are applied but only physical white-box models. The performance improvement allows for a better adaptation of future FOWT designs for a rejection of wind and wave forces and an increased lifetime. Also, an adaptation of the design to given site conditions is possible. Besides load simulations, the method has proven to be useful for model-based controller design. Due to the computational efficiency, a real-time prediction of the dynamics for model-predictive controllers or structural health and fault monitoring is a promising application. Generally, the research contributes a new level of fidelity for FOWT modeling, completing the range of available numerical approaches from preliminary static to high-fidelity methods.