Applicability of pulsed 2cLIF-EET for micro-droplet internal thermometry under evaporation conditions

Abstract

The relatively new thermometry technique “pulsed 2cLIF with MDR-enhanced energy transfer” is tested for the first time on micro-droplet streams in a heated air flow. The method allows simultaneous measurements of the droplet internal temperature-field, droplet size and droplet velocity. Plausibility of the measurement results is evaluated by comparing results of various experimental conditions among each other and by comparison with analytic modeling. Overall, measurement results are plausible. However, measured temperature-fields are biased by the integral fluorescence signal and initial conditions of the models are limited by the Rayleigh jet breakup that creates the droplet stream.

Graphic abstract

1 Introduction

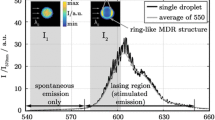
“Pulsed 2-color Laser-Induced Fluorescence with MDR-enhanced energy transfer” (pulsed 2cLIF-EET) was recently introduced for instantaneous temperature imaging of micro-droplets (Palmer et al. 2016, 2017, 2018a). The method is based on conventional 2cLIF thermometry, but uses a pulsed laser for imaging without motion-blur. The pulsed laser enables simultaneous measurements of the droplet’s temperature-field, its size and velocity. Detrimental influences from optical resonances of the laser light (morphology dependent resonances (MDRs), Chen et al. 1996) and the temperature sensitive fluorophore (lasing,¹ Mazumder et al. 1995) are controlled by a second dye that enables a special radiative energy transfer. This Enhanced Energy Transfer (EET, Folan et al. 1985) allows to red-shift lasing at the droplet surface to irrelevant wavelengths. Spontaneous emission of the temperature dye remains mostly unchanged (Arnold et al. 1996). Therefore, 2cLIF thermometry capabilities are restored. Some minor remaining spatial artifacts of the EET can be corrected using an “error-mask method” (Palmer et al. 2018a).

Pulsed 2cLIF-EET also avoids nonlinear fluorescence signals associated with small droplet sizes (Labergue et al. 2010, 2012), because MDRs in fluorescence—the preliminary stage of lasing (Eversole et al. 1995) that limits CW-laser setups with low dye excitation intensity—can be excluded. As a consequence, pulsed 2cLIF-EET enables investigations even of droplets with diameters smaller than $100 \,\upmu$m. Until now, droplet internal thermometry was restricted to droplet diameters of 180 $\upmu$m, applying conventional point-wise 2cLIF thermometry and complex data post-processing. Those experiments are usually time consuming and limited by lasing-effects to the inner droplet region. Other experimental methods, e.g., laser-induced phosphorescence (Abram et al. 2018) or infrared thermometry (Saha et al. 2010), are even more restricted regarding the droplet size.

In this work, pulsed 2cLIF-EET is tested for the first time in a realistic scenario, where a droplet stream is placed in a hot air flow. The droplet stream is based on a frequency-stabilized Rayleigh jet breakup by a Vibrating Orifice Droplet Generator (VODG, Fig. 1A). The VODG produces a mono-disperse droplet stream with a constant inter-droplet spacing² ($\lambda _\mathrm {b}$) a few millimeters downstream the orifice. In this mono-disperse droplet measurement zone, which is typically some centimeters long, droplet heating and evaporation can be investigated. Purpose of this experiment is a plausibility check of the results measured by pulsed 2cLIF-EET as there are droplet temperature-fields, droplet size and droplet velocity. Plausibility is evaluated by comparing the transient process at various ambient temperatures and by highlighting differences to analytic droplet heating and evaporation modeling.

Fig. 1

Schematic illustration of a frequency-stabilized droplet stream controlled by a vibrating orifice droplet generator (VODG, A). The relative motion between droplet and air causes liquid circulation inside the droplet with a strong effect on the heat transport and evaporation (B). Evaporation processes of isolated droplet differ from droplets in a stream

A suitable droplet heating and evaporation model for the comparison is given by the effective thermal conductivity (ETC) approach introduced by Abramzon and Sirignano (1989), because it can be implemented in a reasonable amount of time, has a short computational duration and includes the effect of liquid circulation inside droplet’s by an ad hoc factor despite its simplification to radial symmetry. Liquid circulation (see Fig. 1B) is induced by the relative velocity between droplet and air. The liquid movement can be imagined as toroidal vortex with a possibly accelerating effect on the liquid heat transport and subsequent evaporation. The mechanism is often referred to as “Hill’s Vortex” (Hill 1894). The strength of the liquid circulation and its impact on the liquid convection depend certainly on the droplet properties, but latest publications also stress the flow and vapor field surrounding the droplet (Castanet et al. 2016). Experiments with droplet streams indicated that droplets indirectly interact among each other through the flow and vapor field. Each droplet accelerates the surrounding air³ and thereby hinders the vapor transport and reduces the droplet–air shearing for subsequent droplets. Liquid heat transport and evaporation are slowed down.

Conventional ETC models are designed for isolated (single) droplets only, but some authors already suggested modified ETC models for droplet streams (e.g., Deprédurand et al. 2010 or Castanet et al. 2016): The Hill vortex is assumed to remain present regardless of the droplet interaction (Abramzon and Sirignano 1989). The interaction affects the heat, mass and momentum transfer. Influence can be modeled by appropriate formulations of the Nusselt number, the Sherwood number and the droplet drag and friction coefficients. In general, a closer inter-droplet spacing is connected with lower Nusselt and Sherwood numbers (Chiang and Sirignano 1993). According to Castanet et al. (2002), the Hill vortex can be diffusion-limited for high inter-droplet spacing.

The following steps are carried out in this work: Sect. 2 explains the fundamentals of pulsed 2cLIF-EET. Section 3 introduces a single droplet ETC evaporation model according to⁴ Abramzon and Sirignano (1989) and an adjusted ETC model for droplet streams according to Castanet et al. (2016). Section 4 shows the details of the used experimental setup and the 2cLIF-EET calibration. Section 5 contains an evaluation of the variables measured by the pulsed 2cLIF-EET method. First, measured droplet velocities, sizes and average droplet temperatures are compared among each other based on a variation of ambient temperature. Secondly, measured droplet internal temperature-fields are studied in a similar manner and also evaluated regarding peculiarities of the LIF measurement. Thirdly, results are compared with the two ETC models, which employ measured droplet velocities as initial condition. The comparison involves several variables that can only be deduced from the measured droplet temperature-fields including the droplet surface temperature and the surface temperature gradient. These values can only be determined by pulsed 2cLIF-EET. The comparison also includes the measured droplet sizes and further characteristics that allow an evaluation of the heat and mass transfer process including evaporation mass flow, Sherwood number, heat transfer coefficient and heating rate as well as the Peclet number. Finally, results of the work are summarized in Sect. 6.

2 Theory of pulsed 2cLIF-EET thermometry

Pulsed 2cLIF-EET is based on conventional 2cLIF thermometry theory, where a temperature sensitive fluorescent dye is excited by a laser with an intensity $I_\mathrm {0}$ (${\hbox {W}/\hbox {m}^2}$). Assuming negligible attenuation (small optical thickness), the non-saturated spontaneous fluorescence intensity I (W) of a measurement volume V is calculated as (Lemoine et al. 1996; Palmer et al. 2018a):

$$\begin{aligned} I = K_\mathrm {opt}(\lambda ) I_\mathrm {0} \phi (\lambda ,T) \varepsilon (\lambda _0,T) C V g(\lambda ,x,y) \end{aligned}$$

(1)

where $K_\mathrm {opt}(\lambda )$ (−) is an optical calibration constant of the setup and the dye is characterized by its molar attenuation coefficient $\varepsilon$ (L/(mol cm)) at excitation wavelength ($\lambda _0$), quantum yield $\phi (\lambda )$ and concentration C (mol/L). Factor g is a variable of the pulsed 2cLIF-EET approach that comprises all wavelength and spatially dependent photon density influences with an impact on energy transfer (MDR-EET; self-absorption; attenuation, droplet-lens and shadow-zone effects, etc.). Temperature sensitivity of the fluorophore affects both, absorption ($\varepsilon$) and emission ($\phi$). Together, influences are modeled by an Arrhenius approach (Lemoine et al. 1999; Palmer et al. 2018a):

$$\begin{aligned} I = K_{\mathrm {opt}}(\lambda ) K_{\mathrm {spec}}(\lambda ) I_\mathrm {0} C V \exp \left( \frac{\beta (\lambda )}{T}\right) g(\lambda ,x,y) \end{aligned}$$

(2)

Equation 2 contains $\beta (\lambda )$ (K) as wavelength-dependent temperature sensitivity and constant $K_{\mathrm {spec}}(\lambda )$ (1/mol) as parameter for the dye’s spectral properties. Integration of Eq. 2 allows to describe fluorescence intensity of a narrow wavelength band $\lambda _\mathrm {i1}$ to $\lambda _\mathrm {i2}$. 2cLIF requires the selection of two of these color channels (Lavieille et al. 2000). Color channel $I_1$ must have a low temperature dependency and acts as reference signal. Wavelength band $I_2$ requires a high temperature dependency. Detrimental influence of dye-lasing within droplets is avoided by enabling EET from the temperature sensitive dye to a second absorber. EET ensures that only stimulated emission and lasing is red-shifted through the second dye, but not spontaneous emission which is required for thermometry.

Calculating an intensity ratio $R_{12}$ (−) of the color channels allows elimination of disruptive influences, including volumetric effects V, excitation intensity $I_{0}$ and concentration C (based on Lemoine et al. 1999):

$$\begin{aligned} R_\mathrm {12}&= \frac{I_{1}}{I_{2}} = \frac{K_{\mathrm {opt},1} K_{spec,1}}{K_{\mathrm {opt},2} K_{\mathrm {spec},2}} \exp \left( \frac{\varDelta \beta _{12}}{T}\right) \frac{g_{1}(x,y)}{g_{2}(x,y)} \end{aligned}$$

(3)

$$\begin{aligned}&= \underbrace{\exp \left( \frac{\varDelta \beta _{12}}{T} + \log (K_{12})\right) } \underbrace{\frac{g_{1}(x,y)}{g_{2}(x,y)}} \nonumber \\&= f_\mathrm {12}(T) \cdot g_\mathrm {12}(x,y) \end{aligned}$$

(4)

After summarizing Eq. 3, intensity ratio $R_{12}$ can be described by only two dimensionless functions $f_{12}$ and $g_{12}$. Measurements require a temperature calibration to determine both. The exponent of function $f_{12}$ relies only on temperature and can be calibrated by a low order polynomial. $g_{12}$ is a spatially resolved error-mask of the photon density of state across the droplet. The function is independent of temperature and droplet size. Changes of dye concentration are tolerable within certain limits (Palmer et al. 2018a).

3 Droplet evaporation modeling

The following description of droplet evaporation is based on the effective thermal conductivity (ETC) model introduced by Abramzon and Sirignano (1989). The ETC model is designed for isolated droplets, but droplet streams can be simulated with some adjustments. ETC models rely on some assumptions: Droplets are radially symmetric and surface tension influences, i.e., the Marangoni effect, are neglected (Castanet et al. 2011; Sirignano 1999). Convective heat transfer from the surrounding ambiance to the moving droplet is modeled by employing “film-theory” (Abramzon and Sirignano 1989). Most importantly, influences from liquid circulation inside the droplet are included by a simple ad hoc procedure that evaluates in how far the droplet’s streamlines resemble with the Hill vortex (Abramzon and Sazhin 2006). The procedure gives the ETC model its name, because the thermal conductivity of the liquid is adjusted to include influences of the three-dimensional Hill vortex in a one-dimensionally modeled droplet.

The following nomenclature is used to describe the four phases involved in the evaporation: liquid (no index), the free air stream (index a), pure vapor (index v) and a mixed gas phase (index g) of air and vapor.⁵ Liquid properties are calculated using polynomials according to Daubert and Danner (1989). Gas phase properties and vapor concentrations are calculated by applying the well-established 1/3-rule (Hubbard et al. 1975).⁶

3.1 Modeling the liquid phase

The Peclet number is one measure to describe in how far the temperature-field of a moving droplet is determined by its internal liquid circulation (Sirignano 1999; Castanet et al. 2011). The number is defined as the ratio of the rate of thermal advection to the rate of thermal diffusion (Castanet et al. 2005, 2016):

$$\begin{aligned} \mathrm{Pe}_\mathrm{s}&= \frac{2r_\mathrm{d} u_\mathrm{s}}{\kappa } = \frac{2r_\mathrm{d} u_\mathrm{s}}{\nu }\cdot \frac{\nu }{\kappa } = \mathrm{Re}_\mathrm{s}\cdot \mathrm{Pr}_\mathrm{s} \end{aligned}$$

(5)

$u_\mathrm{s}$ is the droplet surface velocity, $2r_\mathrm {d}$ equals the droplet diameter (d), and $\kappa =\rho c_{\mathrm{p}}/k$ is the thermal diffusivity ($\rho$, $c_\mathrm{p}$ and k are the density, specific heat capacity and thermal conductivity). Extending with the kinematic viscosity $\nu$ allows to express the Peclet number as the product of the liquid’s Reynolds ($\mathrm{Re}_\mathrm{s}$) and Prandtl number ($\mathrm{Pr}_\mathrm{s}$). For low Peclet numbers (< 10), liquid heat transport is dominated by conductivity and the droplet’s temperature-field is characterized by radial symmetry. For high Peclet numbers (> 100), strong liquid circulation improves the heat transport and characterizes the temperature-field. Calculating the Peclet number requires a friction model to estimate the droplet surface velocity (Abramzon and Sirignano 1989):

$$\begin{aligned} u_\mathrm{s} = \frac{1}{32}\left( \frac{\eta _\mathrm {g}}{\eta }\right) \mathrm {Re} (u - u_\mathrm {a}) C_\mathrm{F} \end{aligned}$$

(6)

with $\eta$ and $\eta _\mathrm {g}$ as the dynamic viscosity of the liquid and the gas phase. $\mathrm {Re} = 2r_\mathrm {d} \rho _\mathrm {a} \left( u-u_\mathrm {a}\right) /\eta _\mathrm {g}$ is the droplet’s gas Reynolds number (with u and $u_\mathrm {a}$ as droplet and air stream velocity).⁷ The friction coefficient $C_\mathrm{F}$ is modeled according to Abramzon and Sirignano (1989) with $B_\mathrm {M}$ as Spalding mass transfer number:

$$\begin{aligned} C_\mathrm{F} = \frac{12.69 K_\mathrm {F}}{\mathrm {Re}^{2/3} (1+B_\mathrm {M})} \quad \mathrm {with} \quad B_\mathrm {M} = \frac{Y_\mathrm {vs} - Y_\mathrm {va}}{1-Y_\mathrm {vs}} \end{aligned}$$

(7)

Variable $K_\mathrm {F}$ is assumed to be 1 for isolated droplets. For droplet streams, Castanet et al. (2011, 2016) derived an empirical equation for $K_\mathrm {F}$ that depends on the Reynolds number and the dimensionless droplet spacing $C=uf/d$ (with f as droplet generation frequency):

$$\begin{aligned} K_\mathrm {F}&= 0.67 \left[ 1 - \exp \left( -a-b\left( C-1\right) \right) \right] - 1\nonumber \\ a&= 0.0988 + 0.00339\mathrm {Re} \quad b = 0.0988 - 0.00339\mathrm {Re} \end{aligned}$$

(8)

Abramzon and Sirignano (1989) introduced an effective thermal conductivity $k_\mathrm {eff}$ that models improved heat transfer by liquid circulation based on Peclet number:

$$\begin{aligned} k_\mathrm {eff}&= k \left[ 1.86+0.86\tanh \left( 2.245\log _{10}\left( \mathrm{Pe}_\mathrm{s}/30\right) \right) \right] \end{aligned}$$

(9)

For a given value of k, Eq. 9 is an s-shaped function with a turning point at $\mathrm{Pe}_\mathrm{s}\approx 70$. The maximum enhancement of the liquid heat transfer (a factor of 2.72) is slowly reached for Peclet numbers larger than 100. The enhanced thermal conductivity improves the thermal diffusivity ($\kappa _\mathrm {eff}=k_\mathrm {eff}/(c_\mathrm{p}\rho )$), which in turn is required to solve the heat equation that estimates a droplet temperature profile (Sazhin 2014):⁸

$$\begin{aligned} \frac{\partial T}{\partial t}&= \kappa _\mathrm {eff} \left( \frac{\partial ^2 T}{\partial r^2} + \frac{2}{r} \frac{\partial T}{\partial r} \right) \end{aligned}$$

(10)

In this differential equation, temperature T is a function of time t and radial position $0<r<r_\mathrm {d}$. Initial and boundary conditions for solving the equation include a uniform initial temperature, a symmetry condition at the droplet centrum and a temperature gradient at the droplet surface due to ambient convection and evaporation. The latter boundary condition requires an energy balance at the droplet surface (Sazhin et al. 2010, 2011; Sazhin 2006, 2014):

$$\begin{aligned} h \left( T_\mathrm {a} - T_\mathrm {s} \right)&= -\rho \varDelta h_\mathrm {v} {\dot{r}}_\mathrm {d} + k \frac{\partial T}{\partial r}\Bigr |_{r_\mathrm {d}} \end{aligned}$$

(11)

Here, $\varDelta h_\mathrm {v}$ is the heat of vaporization and h is the convective heat transfer coefficient that is linked to the Nusselt number ($\mathrm {Nu} = 2r_\mathrm {d}h/k_\mathrm {g}$).⁹ Variable ${\dot{r}}_\mathrm {d}$ describes the change of droplet size over a time step ($\varDelta t$). Thus, ${\dot{r}}_\mathrm {d}$ can be modeled to include the effects of evaporation and thermal swelling:

$$\begin{aligned} {\dot{r}}_\mathrm {d}&= \frac{{\dot{m}}_d}{4\pi r_\mathrm {d}^2 \rho } + \frac{r_\mathrm {d}({\bar{T}}_0)}{\varDelta t}\left[ \left( \frac{\rho ({\bar{T}}_0)}{\rho ({\bar{T}}_1)}\right) ^{1/3} - 1\right] \end{aligned}$$

(12)

This equation models thermal swelling with the second summand. The liquid densities ($\rho$) are based on average droplet temperatures of the current (${\bar{T}}_1$) and previous time step (${\bar{T}}_0$). The first summand describes evaporation with a mass flow based on film-theory (Sazhin 2006; Abramzon and Sirignano 1989):

$$\begin{aligned} {\dot{m}}_d&= -2\pi r_\mathrm {d}D_\mathrm {va}\rho _\mathrm {g}B_\mathrm {M}\mathrm {Sh} \end{aligned}$$

(13)

with $D_\mathrm {va}$ as diffusion coefficient of vapor in air, $\rho _\mathrm {g}$ as gas density and $\mathrm {Sh}=2r_\mathrm {d}k_\mathrm {c}/(\rho _\mathrm {a}D_\mathrm {va})$ as Sherwood number ($k_\mathrm {c}$ is the mass transfer coefficient). Evaporation usually starts after a short period of thermal swelling due to liquid heating. During steady state evaporation, a thermodynamic equilibrium is reached at the droplet surface and the squared droplet diameter decreases linearly with time ($d^2$-law). The steady state is characterized by the wet-bulb temperature of the liquid. If the wet-bulb temperature lies below the boiling point, evaporation is diffusion-controlled (Kneer et al. 1993).

3.2 Modeling the gas phase of isolated droplets

This work renounces a spatial and temporal resolution of the gas phase, but uses Nusselt (Nu) and Sherwood (Sh) numbers that summarize the processes instead. The well-established correlations of Clift et al. (2013) apply to non-evaporating droplets without Stefan flow and low Reynolds numbers:

$$\begin{aligned} \begin{aligned} \mathrm{Nu}_\mathrm{0}&= 1 + \left( 1 + \mathrm {Re}\mathrm {Pr}\right) ^{1/3} \mathrm {max}\left[ 1,\mathrm {Re}^{0.077}\right] \\ \mathrm{Sh}_\mathrm{0}&= 1 + \left( 1 + \mathrm {Re}\mathrm {Sc}\right) ^{1/3} \mathrm {max}\left[ 1,\mathrm {Re}^{0.077}\right] \end{aligned} \end{aligned}$$

(14)

with the Schmidt and Prandtl number defined as:

$$\begin{aligned} \mathrm {Sc}&= \frac{\eta _\mathrm {g}}{\rho _\mathrm {a} D_\mathrm {va}} \mathrm {Pr} = \frac{\eta _\mathrm {g} c_{p\mathrm {,g}}}{k_\mathrm {g}} \end{aligned}$$

(15)

According to Abramzon and Sirignano (1989), evaporation under consideration of the Stefan flow can be included by applying film-theory, where two film thicknesses $\delta _\mathrm {T}$ and $\delta _\mathrm {M}$ are used to describe the thermal and mass transport in the droplet’s boundary layer. Nusselt and Sherwood numbers of a moving, isolated droplet are than (Sazhin et al. 2011):

$$\begin{aligned} \mathrm{Nu}_\mathrm{iso}&= \frac{\ln \left( 1+B_\mathrm{T}\right) }{B_\mathrm{T}} \underbrace{\left[ 2 + \frac{\mathrm{Nu}_\mathrm{0}-2}{F(B_\mathrm{T})}\right] }_{\mathrm{Nu}^*}\\ \mathrm{Sh}_\mathrm{iso}&= \frac{\ln \left( 1+B_\mathrm{M}\right) }{B_\mathrm{M}} \underbrace{\left[ 2 + \frac{\mathrm{Sh}_\mathrm{0}-2}{F(B_\mathrm{M})} \right] }_{\mathrm{Sh}^*} \end{aligned}$$

(16)

The index $^*$ labels the modified Nusselt and Sherwood numbers, which account for a value of two for a droplet in a quiescent ambiance. Function F is defined by the film thicknesses with and without (index 0) evaporation and applies for the Spalding numbers of mass ($B_\mathrm {M}$) and heat transfer ($B_\mathrm {T}$):

$$\begin{aligned} F(B_\mathrm {M,T})&= \frac{\delta _\mathrm {M,T}}{\delta _\mathrm {M0,T0}} = \frac{\ln \left( 1+ B_\mathrm {M,T} \right) }{B_\mathrm {M,T}} \left( 1 + B_\mathrm {M,T} \right) ^{0.7} \end{aligned}$$

The Spalding number of heat transfer $B_\mathrm {T}$ is defined as:

$$\begin{aligned} B_\mathrm {T}&= c_{\mathrm{p}\mathrm {,v}}\left( T_\mathrm {a} - T_\mathrm {s} \right) /\varDelta h_\mathrm {v,eff} \end{aligned}$$

(17)

Here, $c_{\mathrm{p}\mathrm {,v}}$ is the specific heat capacity of the vapor and $\varDelta h_\mathrm {v,eff}$ is the effective heat of vaporization that links the heat and mass transfer processes by connecting the power spend on droplet heating $Q_\mathrm {L}$ with the evaporation mass flow:

$$\begin{aligned} \varDelta h_\mathrm {v,eff}&= \varDelta h_\mathrm {v} + Q_\mathrm {L}/{\dot{m}}_\mathrm {d} \end{aligned}$$

(18)

Both Spalding numbers are related:

$$\begin{aligned} B_\mathrm {T}&= \left( 1 + B_\mathrm {M}\right) ^{\phi } - 1\nonumber \\ \phi&= \left( \frac{c_{\mathrm{p}\mathrm {,v}}}{c_{\mathrm{p}\mathrm {,g}}}\right) \left( \frac{\mathrm {Sh}^*}{\mathrm {Nu}^*}\right) \left( \frac{1}{\mathrm {Le}}\right) \end{aligned}$$

(19)

The Lewis number $\mathrm {Le}=\mathrm {Sc}/\mathrm {Pr}$ describes the ratio between heat and mass transfer. For small Reynolds numbers the ratio $\mathrm {Sh}^*/\mathrm {Nu}^*=1$, while for large values $\mathrm {Sh}^*/\mathrm {Nu}^*=\mathrm {Le}^{1/3}$. In the most important intermediate range, calculations require an iterative procedure, because Spalding numbers are linked and dependent on the evaporation mass flow (Sazhin et al. 2011).

3.3 Modeling the gas phase of droplet streams

The previous definition of the Nusselt and Sherwood numbers is not applicable for droplet streams. In a droplet stream, both numbers reduce with a shorter inter-droplet distance. First modeling approaches by Atthasit et al. (2003) and Castanet et al. (2005) were soon discarded, because they foresee the influence of the droplet stream on an entirely empirical basis. A first sophisticated model based on film-theory was introduced by Deprédurand et al. (2010): the film thicknesses of the stream’s boundary layer were adjusted by a radial Stefan-flow velocity and a characteristic time of diffusion that is based on the dimensionless droplet spacing and forced convection. The model was refined by Castanet et al. (2016), who included a travel-distance of the droplet stream to describe the growing boundary layer thickness with a further droplet flight-time. The approach was verified with experimental results and numerical studies. The new Nusselt and Sherwood correlations are similar to the famous Ranz and Marshall (1952) equations, but feature the influence of the adjusted Stefan flow for the droplet stream:

$$\begin{aligned} \mathrm{Nu}_\mathrm{{st}}&= \frac{\ln \left( 1+B_\mathrm{T}\right) }{B_\mathrm{T}} \left[ e + a\left( \frac{z}{2r_\mathrm{d}}\right) ^b \frac{\mathrm{Re}^{0.58+c} \mathrm{Pr}^d}{F(B_\mathrm{T})}\right] \\ \mathrm {Sh}_\mathrm{{st}}&= \frac{\ln \left( 1+B_\mathrm{M}\right) }{B_\mathrm{M}} \left[ e + a\left( \frac{z}{2r_\mathrm{d}}\right) ^b \frac{\mathrm{Re}^{0.58+c} \mathrm{Sc}^d}{F(B_\mathrm{M})}\right] \end{aligned}$$

(20)

with a modified function $F(B_\mathrm {T,M})$), where the exponent of 0.7 is replaced with a more appropriate value of 0.655. Coefficients $a-e$ depend on the dimensionless inter-droplet spacing C of the stream and can be found in Castanet et al. (2016).¹⁰ Applicability of Eq. 20 is limited to $10\le \mathrm {Re}\le 100$, $0.5\le \mathrm {Sc}\le 4$, $0\le B_\mathrm {M}\le 4$ and $3\le z/(2r_\mathrm {d}C)\le 76$. For $z\gg 2r_\mathrm {d}$, the model comes down to motionless droplets and Nu- and Sh-numbers are simplified to $e(C) \cdot \ln (1+B_\mathrm {M,T})/B_\mathrm {M,T}$. For typical experiments where the droplet flight-distances account for only a few centimeters, the factor $[z/(2r_\mathrm {d})]^b$ lies in the range from 0.4 to 0.7. Therefore, the convective term in Eq. 20 reduces slowly with z due to the thickening of the boundary layer. However, due to the values of Re of a few tenths, convection should still plays a significant role in the experimental results compared to an isolated droplet.

4 Experimental setup

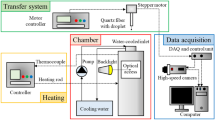
Micro-droplets are produced with a VODG equipped with an orifice with a pinhole diameter of $46.9\,\upmu$m. The liquid volume flow rate through the orifice accounts for roughly ${\dot{V}}_\mathrm {inj}=21\,\upmu$ l/s. The piezo-actuator of the VODG is operated with a frequency of $f=40.2\,\hbox {kHz}$. The VODG is positioned centrally in the head of a constant-pressure flow (CPF) vessel (see Fig. 2). Dry air flows through the vessel from top to bottom with a velocity of $u_\mathrm {a}=0.03\hbox { m/s}$. The ambient pressure accounts for $p_\mathrm {a}=1.285\hbox { bar}$.¹¹ Air temperature inside the CPF-vessel is varied during the experiments. Temperature losses across the main flow direction of air (vessel height $h=100 \hbox { mm}$, $\varDelta T_\mathrm {a}=$ max. $10\hbox { K}$) are neglected. Different vertical measurement positions along the droplet stream are accessed by traversing vessel up or down.

Fig. 2

The setup consists of a vibrating orifice droplet generator (VODG) positioned in a constant-pressure flow (CPF) vessel. A pulsed 2cLIF-EET thermometry imaging setup is applied to study droplet stream heating and evaporation

Droplets consist of n-dodecane. The liquid is characterized by a low volatility and a high thermal conductivity. These properties allow to limit evaporation and focus on the heat transfer inside the droplet. The liquid is seeded with $2\, \upmu$M of the temperature sensitive dye pyrromethene 597-8C9 (PM597) and $0.5\,\upmu$M of the energy transfer partner Oil Blue N (OBN).¹² The low concentration of PM597 keeps the magnitude of the spatial error-field $g_{12}$ across the droplet small (negligible attenuation) and simultaneously ensures a high temperature sensitivity (see also Palmer et al. 2018a, b). The lower concentration of OBN compared to PM597 ensures a full exploitation of the EET, where PM597-lasing at the droplet surface is fully shifted to OBN, but the magnitude of spontaneous PM597 emission from all over the droplet remains high. Only PM597 is excited by a pulsed Nd:YAG laser with a wavelength of 532nm and a pulse duration of 4 ns. The dye excitation intensity accounts for $I_0=10.8\hbox { MW}/\hbox {cm}^2$.

Light emission of the droplet stream is collected with a self-developed microscope. The microscope features a working distance of 128mm and a numerical aperture of 0.192 (optical resolution of $1.9\,\upmu$m according to the Rayleigh-limit). The microscope consists of only two achromats, one aperture and one stop, to ensure the highest possible optical transmittance. After passing a Notch filter (Thorlabs NF533-17), fluorescence enters a self-developed 2-way image splitter though an optical slit. The slit allows adjustments of the image-width and lies in the focal plane of an achromatic relay-lens. A dichroic filter splits fluorescence at a wavelength of 561 nm (Chroma ZT561rdc). Each color channel is band pass filtered ($I_1$: Semrock 549/15 nm BL; $I_2$: Semrock, 586/15 nm BL). Subsequent mirrors direct the light to a single EMCCD (Andor iXon3 DU-888). Before reaching the camera sensor, a second achromatic relay-lens restores the virtual image observable in the optical slit. The EMCCD that is operated with a frame rate of 2.5 Hz, an exposure duration of 10 $\upmu$s (minimum) and its maximum gain factor of 1000 x. The sensor of the EMCCD is cooled to 178 K to reduce the dark noise contribution of high gain settings and ensure a high signal-to-noise ratio. Droplet stream images of both color channels appear on the camera sensor side-by-side, each with a magnification of 6.27$\times$ (scale: 482 px/mm). Thus, six to seven droplets are observed at the same time. At each measurement position, 1000 droplets are recorded and post-processed. Fluorescence, or rather temperature information of the liquid, as well as droplet size and velocity, are extracted from images as explained in a Palmer et al. (2018b), whereas spatial errors across the droplet ratio-image are corrected by applying the error-mask method.

Due to the small depth of field of the imaging system (40 $\upmu$m) and the oblique propagation of the droplet stream (600 $\upmu$m over 90 mm), the detection system is positioned on a translation stage that ensures a constant focal distance.¹³ The translation stage is calibrated once for every measurement position. Once the measurement positions are calibrated, fluorescence imaging can be carried out without detriments effects on the measured droplet size and intensity ratio.¹⁴

Fig. 3

An increasing standard deviation of the droplet velocity (u) indicates a growing instability of the stream (A). The oblique droplet stream is anticipated using a translation stage, which allows to keep the focal distance constant and measure a correct constant droplet sizes for all vertical positions under atmospheric conditions (B)

Figure 3 shows the measured droplet velocity (A) and droplet diameter (B) along the droplet stream under isothermal conditions with an active translation stage calibration. Diagram A indicates a linearly decreasing droplet velocity with further flight-distance. An increasing standard deviation indicates a growing instability of the stream. Smallest droplet oscillations and aerodynamic forces lead to a reduction and fluctuation of the inter-droplet spacing ($\lambda _\mathrm {b}$). At 80 mm downstream the orifice, the stream is not reproducible anymore due to satellite and coalescent droplets. For positions closer than 20 mm below the orifice, inter-droplet spacing is stable, but droplets are still affected by detrimental oscillations from the jet breakup. The measured droplet velocity ($u=f\lambda _\mathrm {b}$) is also used to calculate the droplet flight-time to each position ($t=\int _{0}^h \! \frac{1}{u(y)} \, \mathrm {d}y$). Figure 3B shows measured droplet diameters of the stream. The mean droplet diameter, the maximum deviation of the mean value along the stream’s height and the mean standard deviation account for 98.4 $\upmu$m, 0.18 $\upmu$m and 0.38 $\upmu$m, respectively. A constant droplet size is a necessary result of the translation stage calibration. The deviations must be judged carefully, because they are much smaller than the optical resolution of the microscope. In fact, measurement accuracy relies on a high number of evaluated droplets and a droplet diameter calculation based on the area-footprint in the droplet images. The latter fact implies diameter changes on a pixel basis, whereas a droplet consists of about 1770 pixels. Thus, diameter changes of about 28 nm become measurable that are actually physically impossible to detect.¹⁵ However, this entirely statistical process is the only reason why measurements of thermal swelling and an evaporation mass flow are possible at all.

Fig. 4

Diagram A highlights the necessity of the isothermal conditions during the temperature calibration. The correct 2cLIF calibration has a higher temperature sensitivity of 0.29%/K. The corresponding planar droplet error-mask $g_{12}$ is shown in image B

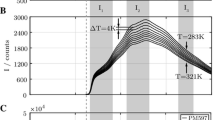
The 2cLIF-EET calibration is performed under isothermal conditions at a measurement position 30 mm below the orifice. For a measurement position close to the outlet, evaporation of n-dodecane is assumed to be negligible. However, there is no thermodynamic equilibrium with non-evaporation conditions during calibration, because a saturated ambiance cannot be realized with the used test rig. During the isotherm calibration, injection temperature is varied from 300 to 340 K in steps of 10 K. The average measured droplet intensity ratio $R_{12}$ is shown in Fig. 4A. The temperature sensitivity accounts for 0.29 %/K. The value is much higher compared to previous studies, due to the reduced dye concentration of PM597 (Palmer et al. 2018a, b).¹⁶ The diagram also includes a reference measurement conducted for a constant ambient temperature of 290 K. The lower sensitivity of only 0.24 %/K is certainly invalid and stresses the necessity of isothermal conditions during the temperature calibration. An image of the calibrated error-mask $g_{12}$ is depicted in Fig. 4B. The pattern differs significantly from previous studies (Palmer et al. 2018a). The error-field shows symmetry toward the vertical droplet axis. Signs of attenuation or a droplet-lens-effect are probably not visible due to the low dye concentration.

Fig. 5

Image of a typical average droplet temperature-field (T(x, y), arithmetic mean values based on 1000 droplets). The average droplet temperature $T_\mathrm {d}$ is the arithmetic value of the image. A droplet surface temperature ($T_\mathrm {s}$) is calculated as arithmetic value of all temperature values at $r>0.9r_\mathrm {d}$. A droplet layer model is applied to determine the surface temperature gradient dT/d$r|_{r_\mathrm {d}}$

Error-mask $g_{12}$ is applied to determine the droplet temperature-fields (see Palmer et al. 2018b). Only average droplet temperature-fields (T(x, y))¹⁷ are studied, which are calculated by stacking 1000 single droplet images and computing their arithmetic mean image. Figure 5 shows an exemplary average droplet temperature-field, from which several information can be extracted:

• Average droplet temperature ${{{\varvec{T}}}}_{\text {d}}$: The value is the arithmetic mean value of the average droplet temperature-field.

• Average droplet surface temperature ${{{\varvec{T}}}}_\text {s}$: The value is the arithmetic mean value of all pixels with a radial coordinate large than 90% of the droplet radius ($r_\mathrm {d}$). Averaging to a single value allows comparison with the one-dimensional ETC model.

• Droplet surface gradient $\mathbf{d }{{\varvec{T}}}/\mathbf{d }{{\varvec{r}}}|_{{{{\varvec{r}}}}_\mathbf{d }}$: By assuming that a droplet consists of 20 equally spaced layers ($d_r=0.05r_\mathrm {d}$), a mean temperature can be calculated for each layer by averaging corresponding regions of the temperature-field. The outer two layers are used to determine the surface gradient. The averaging to a single value also allows the comparison with the ETC model.

Temperature measurement accuracy of the LIF-setup can be estimated during the temperature calibration, when droplets are expected to be isothermal. The average droplet temperature can be determined with a standard deviation of 0.4 K (based on 1000 droplets) and the average median spatial deviation across the average droplet temperature-field accounts for 1.3 K. Maximum spatial deviations do not exceed ± 5.6 K.

For the plausibility check of the measurement results, experiments are conducted at air temperatures ($T_\mathrm {a}$) from 400 to 600 K in steps of 50 K. During this variation, injection temperature is set to $T_\mathrm {inj}= 310$ K. For each air temperature, transient droplet heating is studied at the five equally distant positions between 30 and 70 mm downstream the orifice (Fig. 3). Due to the discussion of this section, subsequent diagrams do not contain standard deviations.

5 Results

5.1 Average droplet characterization

This section presents average droplet results of the pulsed 2cLIF-EET measurements including average droplet velocity (v), average droplet diameter (d) and average droplet temperature ($T_\mathrm {d}$). The data are evaluated based on droplet flight-time (t) and ambient temperature ($T_\mathrm {a}$).

5.1.1 Dynamics of the droplet stream

Figure 6A shows the average droplet velocity (d) as a function of flight-time (t) and ambient temperature ($T_\mathrm {a}$). Droplets are decelerated constantly with about − 450 m/$\hbox {s}^2$, regardless of the ambient temperature. There is an offset between the graphs measured at different ambient temperatures: A higher ambient temperature is connected with a higher droplet velocity level. The offset is presumably caused by a slight drift of the liquid flow rate (see Fig. 6) that behaves proportional to air temperature. The drift is unexpected, because the speed of the piston pump remained constant and the thermocouple showed a constant temperature of 310 K. However, the thermocouple is positioned about 1 mm above of the orifice, which itself has a thickness of another millimeter. Therefore, heat conductivity from the ambient air into the VODG and onto the liquid could be an issue.

Fig. 6

Droplet velocity (u) of the stream reduces constantly, regardless of the ambient temperature (A). The magnitude of deceleration can be explained by the drag coefficient ($C_\mathrm {D}$) that is much lower compared to an isolated droplet (B). The lower drag coefficient is caused by a low inter-droplet spacing (C) that affects the boundary layer of the stream (C)

The constant deceleration of the droplets in a row is in contrast to the continuously preceding deceleration of isolated droplets (Abramzon and Sirignano 1989; Miller et al. 1998). A possible explanation can be found in the droplet drag coefficient, which can be calculated by balancing the droplet drag force with the deceleration force (Sirignano 1999).¹⁸ Figure 6B shows the results in a typical $C_\mathrm {D}$-Re-diagram with a reference curve for the isolated moving droplet.¹⁹ The droplet stream drag coefficients are more than five times smaller than for isolated droplets and thus droplets are about five times less decelerated. This finding is in accordance with several available studies (Mulholland et al. 1988; Poo and Ashgriz 1991; Fieberg et al. 2009): All approaches agree that the droplet drag coefficient in an infinite stream depends on aerodynamic forces (Reynolds number), the inter-droplet distance (spacing parameter C) and evaporation (a factor that includes the Spalding mass transfer number). The inter-droplet spacing is the crucial factor for modeling the influence of the stream. A smaller distance between the droplets always reduces the drag coefficient. However, none of the mentioned studies presents a model that fits to experimental results of this work. It is likely that the generation of the droplet stream by a stabilized Rayleigh breakup is responsible for this finding. Since the jet breakup requires some time and space, initial conditions of the droplet stream 30 mm downstream the outlet are uncertain and application of a droplet deceleration model is difficult.

Figure 6C illustrates the inter-droplet spacing of the experiments. The dependency on Reynolds number (Re) represents the decreasing inter-droplet distance with a further droplet flight-duration. Each droplet in the stream can be imagined as an additional force that participates in an acceleration of the surrounding boundary layer. In difference to an isolated droplet, where the air is basically quiescent, ambient air in the boundary layer is dragged into the traveling direction of the stream and droplets are less decelerated. Thus, friction between air and droplet stream remains almost constant (for results see Sect. 5.3). The same yields for the droplet surface velocity. In turn, the Peclet number of a stream should be lower than for an isolated droplet and heat transfer is dominated by diffusivity. Several studies have investigate the influence of the inter-droplet spacing on the heat and mass transfer processes and tried to model the effect for 0-dimensional droplets (see Sect. 3). However, the mechanism is still not fully understood.

5.1.2 Average size and temperature development

Slight unforeseen variations in the liquid volume flow rate due to the elevated ambient temperatures (see previous section Fig. 6) also affect the measured droplet diameter (Fig. 7A).

Fig. 7

The low volatility of n-dodecane causes an increasing droplet diameter (d) during the heating phase due to thermal expansion (A) and a linearly increasing average droplet temperature (B). Effects become stronger for higher ambient temperatures ($T_\mathrm {a}$)

With increasing ambient temperature, the initial droplet diameter (d) increases also with the increasing flow rate and causes an offset between the measurements. Overall, the evolution of the measured droplet diameter is smooth (low error), because of the planar measurement approach features an accuracy of presumable less than 100 nm (see also Sect. 4). Results also align well with the initial droplet size. For all temperatures, droplet size increases linearly with a longer flight-time. This finding could be an indicator for a strong effect of thermal swelling that outweighs influences of evaporation. If it is the other way around, droplet size would be characterized by a digressive trend over time. In fact, a high linearity of the graphs also implies that the droplet heating phase just started (with a negligible evaporation mass flow) and that n-dodecane is a liquid with low volatility.

The average measured droplet temperature $T_\mathrm {d}$ increases linearly for all ambient temperatures (Fig. 7B). The trend is characteristic for a heating phase with weak evaporation. For the low volatile fuel n-dodecane, this is certainly applicable. An evaporation equilibrium with a wet-bulb temperature is not reached in any case. High linearity and a large offset between the graphs allow an assessment of the droplet heating rate (d$T_\mathrm {d}$/dt), which increases from 2.58 (400 K) to 8.36 K/ms (600 K). Absolute values of the heating rates are reasonable when compared to literature (Kristyadi et al. 2010). Measured temperatures are also reasonably above the injection temperature (310 K). The data gap between injection and the first measurement is difficult to judge due to the uncertainty of the injection temperature and the formation of the droplet stream. Uncertainties of the injection temperature could be avoided in a future work by performing thermometry also directly at the outlet of the VODG.²⁰

5.2 Droplet internal temperature-fields

This section contains the most important measurement result of the pulsed 2cLIF-LIF method—the average droplet temperature-fields (T(x, y)). Figure 8 summarizes the influence in dependency of air temperature ($T_\mathrm {a}$), droplet flight-time (t) and droplet flight-distance (h). For the lowest ambient temperature, droplet heating is hardly observable due to the low heating rate. For ambient temperatures of 450 and 500 K, heating of the entire droplet becomes observable, but spatial variations are hardly detectable. For the high ambient temperature of 550 and 600 K, strong droplet heating is visible and spatial temperature variations are significant, especially for a long flight-duration.

Fig. 8

Momentarily droplet temperature-fields as a function of flight-time (t) and ambient temperature ($T_\mathrm {a}$). All images use the same temperature scaling

For a better perception of the droplet’s temperature distribution, average droplet temperature images are normalized each by its own overall average value (Fig. 9). Maximum deviations from the average droplet temperature account for ±5% and are found for the highest ambient temperature and the longest flight-time. Figure 9 shows that the droplet temperature is mostly uniform for the lowest ambient temperature of 400 K with only some variations at random surface positions. Increasing ambient temperature (450 and 500 K) causes a detectable heating in the surface regions at the stagnation point and the droplet shoulders. Even higher ambient temperature raises the stagnation point temperature significantly. In general, an ambient temperature increment of 50 K appears to have a stronger effect on the spatial temperature distribution than an additional flight-time of another millisecond.

Fig. 9

Normalized droplet temperature-fields as a function of flight-time (t) and ambient temperature ($T_\mathrm {a}$). Each image is normalized by its own average droplet temperature

A qualitative description of the liquid circulation inside the droplets only based on Figs. 8 and 9 is inconclusive: For low ambient temperatures, uniform droplet temperature-fields indicate negligible impact of spatially improved heat transport by liquid circulation. At high ambient temperature, increased stagnation point and shoulder temperatures could indicate improved heat transfer by a liquid vortex. Whether this is substantiated quantitatively should show a comparison with evaporation modeling (see Sect. 5.3).

5.2.1 Influence of the integral fluorescence signal

Identification and quantification of improved heat transfer due to a liquid vortex is a difficult task. There is no standard procedure to link measured droplet temperature images to a single Peclet number or liquid circulation. For the given results, the main challenge arises from the fact that the illustrated average droplet temperature images do not correspond to a central cut-out section of the droplet (compared with Fig. 1). Instead, images correspond to some integral result that is biased by the ratiometric LIF approach and the use of the error-mask method. This raises the question: at which temperatures are we actually looking at in Fig. 8.

In pulsed 2cLIF-EET thermometry, droplets are illuminated entirely by laser light, which causes fluorescence emission from all positions inside the droplet. The EMCCD records the intensity signal and produces a planar projection of the three-dimensional droplet. This basically means that the surface regions ($r>0.9r_\mathrm {d}$) are based on a small integral depth and results are likely reliable. Contrarily, measured temperatures at the center of the temperature-field (e.g., $r<0.1r_\mathrm {d})$) entail contributions from the fluorescence emission along the entire droplet diameter ($2r_\mathrm {d}$). Thus, measured temperatures at this position must be some volumetrically average that are higher than the actual local temperature in the droplet centrum.

There are several mechanisms that could have an impact on the averaging of the integral fluorescence signal, such as the LIF-calibration procedure including the error-mask method, the small depth of field of the fluorescence detection optics (about 40 $\upmu$m or the optical process inside the droplet (e.g., the droplet-lens effect). Since all these effect have a spatial dependency, it appears difficult to reconstruct the actual local temperature in the droplet centrum from the measured temperature-fields. A suitable procedure could be based on optical ray tracing and Mie-theory simulations. However, such effort is beyond the scope of this work. Investigations of the local temperature in the droplet centrum are therefore not possible at this point.

5.3 Comparison with evaporation modeling

The third result section contains the comparison of the measured droplet temperatures and diameters with the two analytic ETC models introduced in Sect. 3. One model is used to predict evaporation and heating of an isolated droplet, and the other model predicts the behavior of a droplet stream.

Both models require initial conditions to run the simulation. Aside from the values that define the ambient and injection conditions, initial droplet size, velocity and the temperature profile must be set. The selection of these values is an issue, because the actual droplet stream is generated by Rayleigh jet breakup a few millimeters downstream the VODG. Thus, there are no droplets directly at the outlet with known conditions. In order to adjust the model to the actual experiment, measured droplet velocities are used as an initial or rather boundary condition.²¹ The initial droplet diameter at the nozzle outlet is deduced from the liquid flow rate though the VODG and the temperature-field is assumed to be uniform with the injection temperature of the experiment.

Focus of the following comparison lies on the plausibility of the measured temperature-fields and droplet diameters and in how far the results correspond to the heat and mass transfer predicted by the ETC models. Therefore, several additional droplet quantities must be deduced from the measurement variables:

• Droplet surface temperature (${{\varvec{T}}_\mathbf{s} }$) and surface temperature gradient (${\mathbf {d}{{\varvec{T}}}/\mathbf {d}{{\varvec{r}}}|_{{{\varvec{r}}}_\mathbf {d}}}$): Both values are deduced from the measured temperature-fields as explained in Sect. 4. The surface temperature is required to determine physical properties. The surface temperature gradient is used for determination the heat transfer into the droplet.

• Evaporation mass flow (${{\dot{{{\varvec{m}}}}}_\mathbf{d} }$): Corresponding values are calculated from the measured droplet size under consideration of thermal swelling (Eq. 12).

• Sherwood number (Sh): The dimensionless mass transfer number is calculated from the evaporation mass flow (Eq. 13) under consideration of the Spalding mass transfer number ($B_\mathrm{M}$ with $Y_\mathrm {va}=0$). Calculation of the latter value requires an average droplet surface temperature to determine the diffusion coefficient, vapor pressure and the heat of vaporization at the gas-liquid interphase.

• Heat transfer coefficient (${{{\varvec{h}}}}$) and Nusselt number (Nu): The convective heat transfer coefficient is calculated directly by solving the droplet surface energy balance (Eq. 11). Calculations require knowledge of the average droplet surface temperature gradient, whose measurement is enabled by pulsed 2cLIF-EET. Once the heat transfer coefficient is known, the corresponding Nusselt number can be determined.²²

• Peclet number ($\mathbf{Pe }_\mathbf{s }$):  Peclet numbers of the experiment are calculated under consideration of the surface friction coefficient $C_\mathrm{F}$ (Eq. 7) of a droplet stream. This involves application of Eq. 8, which deals with the inter-droplet spacing. The Peclet number evaluates the heat transport inside the droplets.

5.3.1 Droplet size and evaporation

Results of the droplet size measurements are compared in Fig. 10A with the isolated droplet model and in (B) with the stream model. Experimental results deviate clearly from the isolated droplet model, where presumably thermal swelling due to higher droplet temperatures causes a stronger expansion of the droplet. However, measurement results are almost in accordance with the stream model. There appears to be only a different gradient in the change of the droplet size, which causes a slight underestimation at an early point of the measurements and a small overestimation at the end.

Fig. 10

Both diagrams include the measured droplet diameter (d) as a function of time (t) and ambient temperature ($T_\mathrm {a}$). Diagram A shows a comparison with the isolated droplet model and B with the droplet stream model. Measurement results agree mostly with the stream model

The droplet’s evaporation mass flow can be calculated from the measured droplet size change (${\dot{r}}_\mathrm {d}$) under consideration of thermal swelling (Eq. 12). Figure 11A shows that the evaporation mass flow is low and similar for all tested ambient temperatures. Results align rather with the stream model than with the isolated droplet model. Evaporation mass flow must be small and comparable for all tested conditions, because of the hampered heat and mass transfer induced by the droplet stream as well as the low volatility of n-dodecane. The magnitude of the evaporation mass flow is constantly increasing due to the heating of the droplets. Slight uncertainties in the calculation of the mass flow cause a nonphysical positive results for an early measurement ($t<$ 5 ms) at the lowest ambient temperature of 400 K. The error is not surprising, because droplet size changes are in the same magnitude as the optical resolution of the detection hardware.

Fig. 11

Diagrams show the droplet’s evaporation mass flow (${\dot{m}}_\mathrm {d}$) and its Sherwood number (Sh) as a function of time (t) and ambient temperature ($T_\mathrm {a}$). Both diagrams include a comparison with evaporation models. Weak evaporation leads to a Sherwood number close to zero

Once the measured evaporation mass flow is determined, Eq. 13 can be applied to calculate the droplet Sherwood number (Sh). Figure 11B shows corresponding results for the different tested ambient temperatures. The graph for the experiment with the lowest ambient temperature (400 K) is not shown, because Sherwood values are negative and thus nonphysical. This finding is a consequence of the nonphysical evaporation mass flow that is shown in Fig. 11A. The Sherwood numbers of the other experimental conditions are slightly larger than the predictions by the droplet stream model and clearly lower than the results of the isolated droplet model. However, values are strongly fluctuating and results from different ambient temperatures are much further apart than the model predictions.

Sherwood numbers of the experiment are mostly larger than Sh=2. This threshold describes droplets, where only diffusive mass transport is present. As indicated by the values of the stream model, additional convective transport allows Sherwood numbers slightly lower than 2. An explanation why the Sherwood numbers of the experiment are larger than the stream model relies on the measurement result of the droplet temperature. As Sect. 5.3.2 will show, measured droplet temperatures are generally higher than predicted by the stream model. The higher temperature causes a larger vapor mass fraction at the droplet surface and an increased Spalding mass transfer number ($B_\mathrm {M}$). Since Fig. 11A illustrates that the evaporation mass flow of the experimental data is slightly larger compared to the prediction by the droplet stream model, Sherwood numbers of the experiments are also overestimated when applying Eq. 13. However, it should be remembered that the evaporation mass flow measurements are connected with some uncertainty, due to the low volatility of n-dodecane.

Difference between the Sherwood numbers measured for different ambient temperatures is presumably related to the use of the arithmetically averaged droplet surface temperature. By principle, arithmetic averaging becomes less suitable with higher ambient temperature, because of the larger temperature spread across the droplet. By applying a different averaging procedure or a spatially resolved approach, post-processing could be improved.

5.3.2 Droplet heating

Figure 12 shows a comparison of the average measured droplet temperature ($T_\mathrm {d}$) with the isolated droplet evaporation model (A) and the droplet stream model (B). Measurement results are sufficiently above the injection temperature and match for all tested ambient temperatures with the first measurement point, at about 2.5 ms, with the isolated droplet evaporation model. This finding is convincing to some degree due to the negligible level of evaporation at this moment. During the further flight-time of the droplet, differences between the average measured temperatures and the isolated droplet model increase continuously. The measured heating rates (gradients) are lower than for the isolated droplet model due to the growing vapor film around the stream that hampers further heating and evaporation. Figure 12B shows that the measured heating rates are similar to the stream model, which basically implies that the heating process is generally captured correctly. Nevertheless, average droplet temperatures of the stream model are much lower than the measured values. There are two possible explanations:

• 1. The temperature measurement is incorrect. An explanation could be the integral fluorescence signal that leads in general to an overestimation of temperature (see Sect. 5.2.1). However, the explanation lacks credibility due to the temperature calibration of the LIF method, where no temperature gradient across the droplet is present.

• 2. The temperature prediction by the stream model is inappropriate for comparison, because of a false assumption regarding the initial magnitude and profile of the droplet temperature. This hypothesis is strengthened by two facts: (1) The Rayleigh jet breakup improves the heating of the liquid and simultaneously impresses a temperature profile significantly deviating from a uniform distribution. (2) The injection temperature of the droplet stream could be higher than the planned 310 K due to heat conduction from the hot air flow into the VODG and liquid.

Fig. 12

Diagrams show the average measured droplet diameter ($T_\mathrm {d}$) as a function of time (t) and ambient temperature ($T_\mathrm {a}$) in comparison with the evaporation models

Additional information about the magnitude and transient behavior of the droplet temperature is given by Fig. 13A. The plot contains the average droplet temperature ($T_\mathrm {d}$) and the average droplet surface temperature ($T_\mathrm {s}$) of the experiment and the predictions of the models for an air flow temperature of 600 K. The surface temperature is always higher than the average droplet temperature and in a constant offset. Both results appear reasonable for droplets that are exposed to a hot air flow. The offset values are different for the experiments and models. The largest offset is given for the single droplet model (roughly 10 K). The second largest difference is found for the stream model with about 6-7 K. The smallest offset between surface and average droplet temperature is given for the measurement results (roughly 5-6 K). Since the stream model and the experiment show a similar temperature spread, it is likely that the physics of the droplet internal heat transfer are captured mostly correctly. The slight difference between the stream model and experimental values is presumably caused by the arithmetic averaging of the experimental values (see Sect. 4). A detrimental influence by the integral fluorescence signal is not assumed due to the small optical thickness of the evaluated surface regions of the droplet projection (see Sect. 5.2.1).

Fig. 13

Diagram A shows droplet internal temperatures as a function of time (t) in comparison with the models. Diagram B depicts the comparison for the surface temperature gradient as a function of time (t) and ambient temperature ($T_\mathrm {a}$)

Droplet heating is also characterized by the temperature gradient at the droplet surface (dT/d$r|_{r_\mathrm {d}}$). The surface temperature gradient is a variable that can only be measured by planar 2cLIF-EET thermometry (see also Sect. 4). Figure 13B shows the average droplet surface temperature gradients of the experiment and models. Despite some uncertainties, results agree mostly with the isolated droplet model, which has a slightly higher magnitude than the stream model. The higher gradient implies a hotter droplet and more evaporation. However, the measured droplet temperatures and evaporation rates are not comparable with the isolated droplet model. This contradiction could be solved, if the injection temperature in the experiment would be higher than expected. The same hypothesis was already given in the previous subsection, which makes it even more likely. Regardless, the results of this section generally seem plausible as the energy conservation considerations are consistent.

5.3.3 Droplet internal heat transfer

Droplet internal heating can be discussed by studying parameters of the ETC model. Figure 14 illustrates the droplet friction coefficient ($C_\mathrm{F}$) as a function of time (t) and ambient temperature ($T_\mathrm {a}$). The diagram shows a high agreement between the measurement and the stream model. The result is reasonable, because both apply the empiric droplet streams friction model (Eq. 8) introduced by Castanet et al. (2016). The stream-friction model foresees a significant friction reduction compared to the isolated droplet model due to indirect droplet interaction. The friction coefficient of the stream is almost insensitive to the tested ambient temperatures. An explanation could be the insulating vapor film surrounding the stream. Thermal circulations inside the droplets of a stream are therefore much easier influenced by a variation of the dimensionless droplet spacing than by a change of the ambient temperature.

Fig. 14

The diagrams show the droplet friction coefficient ($C_\mathrm{F}$) as a function of time (t) and ambient temperature ($T_\mathrm {a}$). The zoom region highlights the high agreement of the stream model with the values deduced from the measurement results

The droplet friction coefficient is required to calculate the droplet surface velocity which in turn is used to determine the Peclet numbers.²³ In the ETC models, the Peclet number is used to compute the effective thermal diffusivity of the liquid. According to Fig. 15, Peclet numbers of the experiment are comparable with the prediction of the droplet stream model. Slightly higher values of the experiments Peclet numbers could be attributed to the higher droplet temperatures that affect the physical properties of the liquid.

Fig. 15

The diagram compares measured Peclet numbers ($\mathrm{Pe}_\mathrm{s}$) with the evaporation models. Results mostly agree with the stream model, which is highlighted by the zoom region

Measurement results show a slightly increasing Peclet number over time with values between about 15 and 40. The increasing trend is presumably the result of a slowly developing liquid circulation hindered by inertia. According to Abramzon and Sirignano (1989), the ETC model assumes a maximum impact of the Hill vortex for $\mathrm{Pe}_\mathrm{s}>100$. Therefore, Peclet numbers of the experiment seem to agree well with the visual inspection of the temperature-fields (Fig. 8), which indicate only a low level of liquid circulation. This basically confirms the applied empiric friction model for droplet streams introduced by Castanet et al. (2016). However, so far it was not possible to correlate the Peclet number reasonably with a dimensionless temperature coefficient that describes the measured temperature-field.

5.3.4 Convective heat transfer

Convective heating of droplets can be described by the Nusselt number (Nu), which is deduced from the convective heat transfer coefficient (h). The average convective heat transfer coefficient of a droplet is calculated according to Eq. 11, by using the measured droplet surface temperature gradient. Results of both parameters h and Nu are given in Fig. 16.

Fig. 16

Diagrams show the droplet’s convective heat transfer coefficient (h) and its Nusselt number (Nu) as a function of time (t) and ambient temperature ($T_\mathrm {a}$)

The measured heat transfer coefficient shows reasonable values in the magnitude of 350 to 1300 W/($\hbox {m}^2$ K). Values decrease slowly with a further droplet flight-time due to the hindering surrounding vapor film and the increasing droplet diameter. This finding is similar for both models. Contrary, influences from different ambient temperatures are much more distinct for the experimental results. The explanation for this finding is assumed to be similar to the Sherwood numbers. The general trend, that a hotter ambiance leads to a lower heat transfer coefficient, is also present for the isolated droplet model. Nevertheless, absolute values are rather comparable with the stream model. Figure 16B indicates that statements regarding the heat transfer coefficient are similar for the Nusselt number. However, measurement results are in the magnitude of $\hbox {Nu}=2$, which fulfills the expectations for droplets in a stream. In total, results of the droplet internal heat transfer appear plausible.

6 Summary and outlook

This work presents a first application of the new thermometry method called “pulsed 2cLIF-EET”, which was specifically developed to measure simultaneously temperature-fields, size and velocity of micro-droplets without motion-blur. The application comprehends transient heating and evaporation of micro-droplet streams at several different ambient temperatures up to 600 K. Aim of the study is a plausibility check of the measurement results. Results are evaluated by comparison among each other and by highlighting differences to two analytic effective thermal conductivity (ETC) models: One model is implemented for a single isolated droplet, and the other is adjusted for droplet streams.

Comparison of the measurement results among each other indicates that the measured droplet velocity is strongly influenced by the Rayleigh jet breakup that generates the droplet stream. As a consequence, both ETC models apply the measured droplet velocity as boundary condition. Furthermore, measurement results show negligible evaporation, strong thermal expansion and significant heating of the droplet stream due to the utilization of n-dodecane as liquid. Droplet temperature-fields that were measured at these conditions appear with a uniform temperature distribution at low ambient temperature and a high temperature gradient from the droplet surface to the droplet center for high ambient temperatures. In addition, the highest temperature is measured correctly at the stagnation point of the droplet. Measured temperature-fields do not indicate a significant influence of a Hill vortex. Further examinations reveal that the temperature-fields are partially affected by the integral fluorescence signal of the pulsed 2cLIF-EET method. Due to the integral signal, temperature determination depends on the optical thickness of the particular region in of the recorded droplet projection. At the droplet surface, where the optical thickness is low, temperature is presumably measured correctly. At the center of the temperature image, where the optical thickness corresponds to the droplet diameter, significant temperature averaging takes place. Consequently, temperature in the image center appears much higher than the actual local temperature in the droplet centrum. Therefore, temperature in the droplet center is not further evaluated.

Comparison of the experimental results with the ETC simulations shows a high agreement with the droplet stream model. Droplet sizes and thermal expansion are similar. The same yields for the evaporation mass flow. Sherwood numbers of the experiments are slightly higher, presumably due to deviant temperatures that have an indirect influence through the Spalding mass transfer number and physical properties. In difference to the prediction of the droplet stream model, average and surface droplet temperatures are higher. However, they are not as high as predicted by the isolated droplet model. Additional evaluation of the droplet surface temperature gradient and the Nusselt number suggest that the measurement results could be correctly and the initial temperature conditions of the model are inappropriate. In fact, it is assumed that the Rayleigh breakup and an imprecisely measured injection temperature in the injector by a thermocouple lead to the described differences. Regardless, further investigations of the Peclet number, which are in the range of 15 to 40, confirm the perception that the investigated droplets are hardly affected by improved droplet internal heat transfer via liquid circulation.

In conclusion, this work has not only highlighted the invaluable benefits of “pulsed 2cLIF-EET thermometry”, but also stressed the need of further studies of the heat and mass transfer of closely spaced droplets. However, future measurements need to clarify influence of the injection temperature as well as the influence of the integral fluorescence signal on the thermometry. Moreover, post-processing of the measurement results should exploit the spatial results further, especially regarding the droplet surface temperature and its gradient.