Influence of wetting conditions on bubble formation from a submerged orifice

Abstract

The formation of gas bubbles by submerged orifices is a fundamental process encountered in various industrial applications. The dynamics of the contact line and the contact angle may have a significant influence on the detached bubble size depending on the wettability of the system. In this study, the influence of wetting conditions on the dynamics of bubble formation from a submerged orifice is investigated experimentally and numerically. The experiments are performed using a hydrophobic orifice plate and a series of ethanol–water solutions to vary the wettability where the key characteristics of the bubbles are measured using a high-speed, high-resolution camera. An extensive analysis on the influence of wetting conditions on the bubble size, bubble growth mechanism and the behavior of the contact line is given. Bubble growth stages, termed (1) hemispherical spreading, (2) cylindrical spreading, (3) critical growth and (4) necking, are identified based on key geometrical parameters of the bubble and relevant forces acting on the bubble during the growth. The experimental results show that the apparent contact angle varies in a complicated manner as the bubble grows due to the surface roughness and heterogeneity. The experimental findings are finally used to validate the local front reconstruction method with a contact angle model to account for the contact angle hysteresis observed in the experiments.

Graphic abstract

1 Introduction

The formation of gas bubbles by submerged orifices is a fundamental phenomenon encountered in many processes found in the chemical, nuclear and metallurgical industries. In most of these processes, the bubble size control is essential since it determines the bubble rise velocity, its trajectory in the liquid, and the mass and heat transfer characteristics. However, the bubble formation from submerged orifices is still not completely understood since it is governed by many operating parameters (e.g., gas flow rate and liquid flow), system properties (e.g., orifice dimensions and orifice material) and fluid properties (e.g., surface tension, liquid viscosity and liquid density). One of the main challenges is the movement of the three-phase (gas, liquid and solid) contact line during the bubble growth.

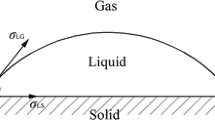
Generally, the wettability is captured by the contact angle, which is defined as the angle between the solid surface plane and the tangent to the liquid surface at the contact line (see Fig. 1). By convention, the contact angle is measured from the liquid side. For a liquid droplet on a flat, smooth and ideal surface, it is well established that the contact angle ($\theta _{\mathrm{Y}}$) obeys Young’s equation (Young 1805):

$$\begin{aligned} \sigma _{\mathrm{SG}} = \sigma _{\mathrm{SL}} + \sigma _{\mathrm{LG}} \mathrm {cos} \, \theta _{\mathrm{Y}} \end{aligned}$$

(1)

Here, $\sigma _{\mathrm{SG}}$ is the solid–gas surface tension, $\sigma _{\mathrm{SL}}$ the solid–liquid tension and $\sigma _{\mathrm{LG}}$ (or $\sigma$) the liquid–gas tension. This angle between the surface of the droplet and the solid surface indicates whether the surface is hydrophilic ($\theta < 90^\circ$) or hydrophobic ($\theta > 90^\circ$). Most solid surfaces are rough on the $\upmu \hbox {m}$ scale. At the local sub-roughness scale, the equilibrium contact angle given by Young’s equation might hold. However, when measuring contact angles using low-power optics ($\sim 0.01\,\hbox {mm}$), these local angles are not observed. Instead, ‘apparent’ contact angles are measured on this macroscopic scale, which, depending on the roughness, can be different from the equilibrium contact angle (Drelich 2019). Due to the surface heterogeneity and roughness, there can be many stable contact angles for a given system, of which the largest is called the advancing angle ($\theta _{\mathrm{adv}}$) and the smallest the receding angle ($\theta _{\mathrm{rec}}$) (Eick et al. 1975; Schwartz and Garoff 1985). In addition, when the contact line is moving, deviations of Young’s equation can be observed due to high local stresses near the contact line where the apparent contact angle depends on the history of the contact line motion.

Fig. 1

A schematic illustration of the contact angle $\theta$ between a fluid drop on a solid surface for a hydrophilic and b hydrophobic surfaces

The dynamics of the contact line and the contact angle may have a significant influence on the detached bubble size depending on the wettability of the system. In case of good wetting conditions ($\theta < 90^{\circ }$), the contact line sticks to the orifice inner rim (Fig. 2a, b). In this case, the behavior of the contact angle has little influence on the size of the detached bubble. On the other hand, in case of poor wetting conditions ($\theta > 90^{\circ }$), both the contact angle and the contact line radius vary as the bubble grows in size and thereby affect the detached bubble size (Fig. 2c).

Fig. 2

Sequence of bubble formation in water under quasi-static regime on three different orifice plates: a stainless steel ($\theta _{\mathrm{s}} = 75^{\circ }$), b polyether ether ketone (PEEK) ($\theta _{\mathrm{s}} = 89^{\circ }$), and c Teflon ($\theta _{\mathrm{s}} = 105^{\circ }$). The orifice inner diameter is 1 mm

Several authors have studied the influence of wetting conditions on the bubble volume. Corchero et al. (2006) investigated the influence of different surface materials ($68^{\circ } \le \theta \le 123^{\circ }$) on the detached bubble volume under various gas flow rates. All their data can be approximated by a single curve when a scaled bubble volume is plotted against a scaled gas flow rate. Byakova et al. (2003) performed experiments on bubble formation in water and a water–soap solution at a wide range of contact angles ($15^{\circ } \le \theta \le 110^{\circ }$). They discussed the discrepancies between theoretical prediction and experimental results at low gas flow rates when the surface tension force is dominant. Liow and Gray (1988) performed numerical simulations on bubble formation in the steel-argon system using a non-spherical bubble model and showed that the influence of contact angle on bubble size becomes less significant at high gas flow rates.

Significant progress in computational resources and numerical methods over the last two decades has made it possible to perform detailed direct numerical simulations (DNS) of multiphase flows by using either interface capturing or front tracking approaches. Both approaches assume a one-fluid formulation, in which the flow phenomena in all phases are described by a single set of Navier–Stokes equations. In interface capturing methods, the interface is reconstructed from an indicator function, which is advected by the fluid velocity on a fixed Eulerian grid. The most widely used interface capturing approaches are the volume of fluid (VOF) method (Hirt and Nichols 1981), the level set (LS) method (Osher and Sethian 1988) and a combination of these two, known as the CLSVOF method (Sussman and Puckett 2000). In the front-tracking-type methods, the interface is explicitly tracked using Lagrangian marker elements, which results in more accurate interface tracking and surface tension calculation (Unverdi and Tryggvason 1992; Shin et al. 2011). All these methods have been used to simulate bubble formation from an orifice (Gerlach et al. 2007; Buwa et al. 2007; Quan and Hua 2008; Chakraborty et al. 2009; Yujie et al. 2012; Albadawi et al. 2013; Xu et al. 2015; Mirsandi et al. 2018, 2019; Kong et al. 2019). However, only a few numerical studies have taken into account the influence of the moving contact line (Kandlikar and Steinke 2002; Gerlach et al. 2007; Buwa et al. 2007; Chen et al. 2013) and the majority of them assumed a constant contact angle.

Once the three-phase moving contact line is involved, the predictive capabilities of these numerical techniques are limited due to the difficulty in specifying the boundary conditions at the contact line. In addition, it is well known that the no-slip boundary condition yields a stress singularity at the contact line since the fluid velocity is finite at the free surface but zero at the wall (Huh and Scriven 1971). This singularity is usually removed by relaxing the no-slip boundary condition with a slip model. The most common approach is to use an empirical dynamic contact angle model that gives the apparent contact angle based on the slip velocity (Cox 1986; Blake 2006; Kistler 1993), which is used to specify the location of the contact line. Several authors have incorporated these dynamic contact angle models for the simulation of droplet spreading (Sui et al. 2014). For the simulations of bubble formation, several authors have used static receding and advancing contact angles for the dynamic contact angle model, which results in a stick-slip behavior at the contact line during the growth (Mukherjee and Kandlikar 2007; Chen et al. 2013; Mirsandi et al. 2018).

Despite the large number of studies reported so far, the detailed physics of bubble formation that involves a moving contact line is still lacking. Therefore, in the present work we focus on advancing the current understanding of the dynamics of bubble formation from a submerged orifice, particularly focusing on the contact line behavior, and to provide detailed experimental data for validating the numerical simulations. In this study, the experiments of bubble formation on a hydrophobic Teflon surface are performed using several water–ethanol solutions to vary the wetting conditions. The details of the transient shape, contact line diameter and apparent contact angle of the bubbles are measured using a combination of a high-speed, high-resolution camera and an accurate digital image processing technique. The experimental results are used to validate the in-house front-tracking-type technique called the local front reconstruction method (LFRM) incorporated with a contact angle model to account for the contact angle hysteresis observed in the experiments. This paper is organized as follows. The description of the experimental setup and measurement techniques is given in Sect. 2. Section 3 provides a description of the numerical model. In Sects. 4.1–4.3, an extensive analysis of the dynamics of the bubble formation in poor wetting systems is provided. In Sect. 4.4, the numerical simulations and a comparison between experimental and numerical results are presented. Finally, a summary of the main conclusions of the present study is provided.

2 Experimental method

2.1 Experimental setup

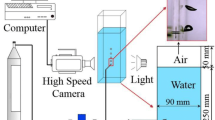
The experimental setup is schematically shown in Fig. 3. The column is 100 mm in width and 500 mm in height. For each experiment, the liquid height is set to 100 mm. The air bubbles are formed from a submerged orifice plate made of hydrophobic Teflon attached to the lower wall of the column. This circular orifice plate with an inner diameter of 1 mm and outer diameter of 10 mm is processed using a high-precision diamond-headed lathe to minimize the surface roughness. The surface roughness is measured using Mitutoyo SJ-210, and the roughness average (RA) is found to be $0.211 \pm 0.007\,\upmu \hbox {m}$. For low gas flow rates ($Q \le 10\,\hbox {ml/min}$), the gas is controlled using a combination of a KD Scientific LEGATO 100 syringe pump and a 2.5-ml Hamilton 1000 series GASTIGHT syringe, while for higher gas flow rates a Bronkhorst EL-FLOW F-201 CV mass flow controller is used to introduce the gas.

Fig. 3

Schematic diagram of the experimental setup of bubble formation in water–ethanol solution. All dimensions are shown in millimeter

In order to achieve the constant gas flow rate condition throughout the bubble formation process, the total pressure drop across the orifice needs to be sufficiently large compared to the pressure variations occurring during the bubble formation. Muilwijk and Van den Akker (2019) suggested that the constant laminar flow rate can be achieved when the non-dimensional orifice constant defined as:

$$\begin{aligned} k_{\mathrm{or}}^{*}=k_{\mathrm{or}} \, g^{0.8} \rho _{g} Q^{-0.6} \end{aligned}$$

(2)

where

$$\begin{aligned} k_{\mathrm{or}}=\frac{Q}{\Delta P}=\frac{\pi d_{\mathrm{cap}}^{4}}{128 \mu _{g} l_{\mathrm{cap}}} \end{aligned}$$

(3)

approaches zero. Here, $l_{\mathrm{cap}}$ and $d_{\mathrm{cap}}$ are the length and the inner diameter of the capillary, respectively. In the present work, a capillary with $l_{\mathrm{cap}} = 150\,\hbox {cm}$ and $d_{\mathrm{cap}} = 0.5\,\hbox {mm}$ is used to satisfy this criterion. To ensure the constant flow conditions further, the individual bubble volume is determined for at least three consecutive formed bubbles. The result for the lowest gas flow rate is shown in Fig. 4.

Fig. 4

Evolution of bubble volume with time. The validity of constant flow rate condition is confirmed from the linearity of the bubble volume growth

To study the effects of wettability, a series of aqueous solutions of ethanol, ranging from 0 to 10 wt%, is used. By increasing the concentration of ethanol, the surface tension of the liquid phase is reduced and therefore the interaction between the liquid and the orifice material shifts to a more pronounced wetting type of interaction. All experiments are performed at a temperature of $20\,^{\circ }\text {C}$. The properties of the liquid at this temperature are determined using a Brookfield DV-E viscometer for measuring the viscosity and a DataPhysics DCAT-25 with the Wilhelmy plate method for measuring the surface tension. Each of the measurements is repeated multiple times to test reproducibility and obtain more accurate data. The properties of the fluids are summarized in Table 1. It should be noted here that as the ethanol concentration is increased from 0 wt% to 10 wt%, the surface tension is reduced by 34%, whereas the liquid viscosity is increased by 68%. However, several studies revealed that the influence of liquid viscosity on bubble formation is negligible, especially at low gas flow rates (Kumar and Kuloor 1970; Gerlach et al. 2007; Mirsandi et al. 2019).

Table 1 Fluid properties of water–ethanol solutions (Khattab et al. 2012)

The apparent contact angle between the liquid phases and the orifice material for each solution is measured using a DataPhysics OCA-30 contact angle goniometer equipped with a TBU 90E tilting base unit. Droplets with a volume of $10\,\upmu \hbox {l}$ prepared with a micropipette are used for the measurements. The advancing and receding contact angles are determined at the time right before the droplet starts moving. The accuracy of the contact angle goniometry through direct measurement with a telescope-goniometer is generally recognized to be approximately $\pm 2 ^\circ$ and twice of this value for the dynamic contact angles (Bracco and Holst 2013). The measured static ($\theta _{\mathrm{s}}$), advancing ($\theta _{\mathrm{adv}}$) and receding ($\theta _{\mathrm{rec}}$) contact angles are shown in Fig. 5. It can be seen that $\theta _{\mathrm{s}}$ increases with increasing surface tension. This trend is also followed by the advancing and receding contact angles. On the other hand, the contact angle hysteresis ($\theta _{\mathrm{adv}} - \theta _{\mathrm{rec}}$) is approximately constant at $10 ^\circ$. This may be explained from the fact that contact angle hysteresis is a surface roughness phenomenon and the same orifice sample is used for each measurement.

Fig. 5

Influence of surface tension on the measured static ($\theta _{\mathrm{s}}$), advancing ($\theta _{\mathrm{adv}}$) and receding ($\theta _{\mathrm{rec}}$) contact angles

2.2 Visualization and image processing

The experimental images are captured using a pco.dimax HD high-speed digital video camera with a frame rate of 2200 Hz and a resolution of $1920\,\hbox {pixels}\,\times \,1440\,\hbox {pixels}$. The recordings are performed with the aid of back lighting, which is only employed during image capturing to limit the heating of the liquid by the illumination. To avoid direct reflections on the bubble interface, the illuminated side of the channel is covered with a white plastic diffusion screen improving the measurements of geometrical parameters of the bubble.

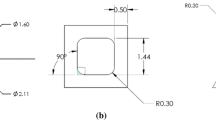
The captured images are processed by using an in-house code, which utilizes the image processing toolbox from Matlab. The main image processing steps are the determination of the grayscale image, background removal, binarization of the images with a threshold value, and then determination of the bubble characteristics, which include the bubble volume $V_{\mathrm{b}}$, bubble height H, apparent contact angle $\theta$, radius of curvature at the bubble apex $R_{0}$ and the contact diameter D (Fig. 6). In the present study, the bubbles are axisymmetric. This allows the implementation of calculation of bubble volume using Pappus second theorem (Legendre et al. 2012). A calibration plate with known size and distance is used to obtain the pixel size. The pixel size used for image capturing is typically 90 pixels/mm. The spatial resolution is high enough to capture the bubble interface without using any interpolative reconstruction. The calibration generates an error about one pixel ($\pm\, 0.011\,\hbox {mm}$). In addition, binarization may introduce one pixel error when the edge of the bubble is not exactly detected.

Fig. 6

Sequence of image processing: a grayscale image, b background removal, c creation of a binary picture, and d definition of edge and calculation of geometrical parameters

3 Numerical method

The numerical model used in the present work is based on the LFRM, originally developed by Shin et al. (2011) and extended by Mirsandi et al. (2018) and Rajkotwala et al. (2018). The main characteristics of the numerical model are described in the section below.

3.1 Governing equations and solution methodology

In the numerical model, the fluids are assumed to be incompressible, immiscible and Newtonian. Furthermore, a one-fluid formulation is used to describe the fluid flow for both phases. The governing equations for mass and momentum conservation are expressed as follows:

$$\begin{aligned} \nabla \cdot {\mathbf {u}}&= 0 \end{aligned}$$

(4)

$$\begin{aligned} \rho \frac{\partial {\mathbf {u}}}{\partial t}&= -\nabla p - \rho \nabla \cdot \left( {\mathbf {u}}{\mathbf {u}}\right) - \nabla \cdot \varvec{\tau }+\rho {\mathbf {g}} + {\mathbf {F}}_{\sigma } \end{aligned}$$

(5)

where ${\mathbf {u}}$ is the fluid velocity, p is the pressure, and $\varvec{\tau }$ is the stress tensor given by $- \mu \big [ \nabla {\mathbf {u}} + \big (\nabla {\mathbf {u}}\big )^{T} \big ]$. The local averaged density $\rho$ and dynamic viscosity $\mu$ depend on the local fluid phase distribution and therefore are calculated from the local phase fraction, F, using normal and harmonic averaging, respectively (Prosperetti 2002). The local volumetric force accounting for the effect of surface tension, ${\mathbf {F}}_{\sigma }$, is obtained by employing the hybrid Lagrangian–Eulerian formulation representation of Shin et al. (2005), which eliminates unphysical parasitic currents in the vicinity of the interface using:

$$\begin{aligned} {\mathbf {F}}_{\sigma } = \sigma \kappa _{H} \nabla F \end{aligned}$$

(6)

where $\sigma$ is the surface tension coefficient and $\kappa _{H}$ is twice the mean interface curvature field calculated on the Eulerian grid using the Lagrangian interface.

Once the flow field is solved, the Lagrangian marker points, which are used to track the interface, are moved using a fourth-order Runge–Kutta time stepping scheme with the locally cubic spline interpolated fluid velocities. Finally, the phase fraction in each Eulerian cell is updated using a geometrical method based on the location of the marker elements (Dijkhuizen et al. 2010).

Due to the separate advection of the marker points, the size of the marker elements changes, decreasing the quality of the interface mesh. To prevent this deterioration of the mesh quality, the LFRM reconstruction procedure is periodically performed to ensure a sufficient resolution for the entire interface. Moreover, a smoothing procedure of Kuprat et al. (2001) is employed to prevent small-scale surface instabilities and volume errors due to advection of marker points and interface reconstruction, which can otherwise accumulate significantly during a simulation. A more detailed description of the reconstruction and smoothing procedures can be found in Mirsandi et al. (2018).

The dynamics of the contact line during the bubble formation process is incorporated in the current framework by applying the appropriate contact angle boundary condition at the contact line. The effect of the contact angle is taken into account by modifying the geometry of the interface near the contact region, as illustrated in Fig. 7. In the present work, to take into account the contact angle hysteresis, a stick-slip model defined as

$$\begin{aligned} \theta _{\mathrm{rec}} \le \theta \le \theta _{\mathrm{adv}} \end{aligned}$$

(7)

is incorporated in the LFRM. In this contact angle model, there is no explicit relationship between the apparent contact angle and contact line velocity. The contact line sticks when the contact angle is in between these receding and advancing values. When the angle reaches either the receding or advancing value, the contact angle is fixed at this value and the contact line slips. However, when the contact line coincides with the orifice rim, the contact angle is allowed to have any value between $\theta _{\mathrm{rec}}$ and $180^{\circ }$ ($\theta _{\mathrm{rec}} \leqslant \theta \leqslant 180^{\circ }$), ensuring that the contact angle will start to spread outward when $\theta < \theta _{\mathrm{rec}}$ and preventing the contact line to recede beyond the orifice rim, respectively. The details of the contact line modeling in LFRM and the stick-slip model can be found in our previous work [see model-A in Ref. (Mirsandi et al. 2018)].

Fig. 7

Schematic illustration of the contact line modeling in LFRM

3.2 Computational setup

The schematic of the computational domain is shown in Fig. 8. The gas bubble is injected through an orifice of inner diameter $D_{\mathrm{in}}$ located at the bottom wall. The gas injection is assumed to be at a constant flow rate Q. The flow in the orifice is assumed fully developed laminar. A parabolic profile is imposed for the axial velocity. A constant pressure boundary condition is imposed at the top wall, and no-slip boundary condition is imposed at the side and bottom walls. The numerical domain has a width and height of approximately five equivalent bubble diameters to ensure that liquid circulations close to the wall do not affect the bubble formation.

Fig. 8

Schematic representation of the computational domain for the simulations of bubble formation

For all simulations presented in this paper, the time step $\Delta t$ is chosen such that it satisfies both Courant–Friedrichs–Lewy (CFL) and capillary time step restrictions as follows (Brackbill et al. 1992):

$$\begin{aligned} \Delta t < \min \left( \Delta t_{\mathrm {CFL}}, \Delta t_{\sigma }\right) =\min \left( \frac{\Delta }{v_{\max }}, \sqrt{\frac{\left( \rho _{l}+\rho _{g}\right) \Delta ^{3}}{4 \pi \sigma }}\right) \end{aligned}$$

(8)

Here, $\Delta$ is the size of the computational grid and $v_{\max }$ is the maximum fluid velocity in the computational domain.

4 Results and discussion

4.1 Detached bubble volume and bubbling regime

In this section, the experiments are performed over a wide range of gas flow rates, ranging from 1 to 350 ml/min, to investigate the influence of the gas flow rate on the detached bubble volume and the bubbling regime under various wetting conditions.

Figure 9a shows the maximum contact diameter reached during formation for four different water–ethanol solutions, which are indicated by their surface tension values. The maximum contact diameter tends to be constant at low gas flow rates and increases slightly at high gas flow rates ($Q > 130\,\hbox {ml/min}$) for each case. Moreover, the value slightly varies at high gas flow rates, which indicates that the bubble formation becomes aperiodic. It can be observed that the maximum contact diameter increases with increasing surface tension at all gas flow rates. This can be explained by the fact that the contact angle also increases with increasing surface tension, as shown previously in Fig. 5.

The surface tension affects the bubble formation via the capillary force ($F_{\mathrm{s}} = \pi \sigma D \, \mathrm {sin} \, \theta$), which restrains the bubble from the detachment. Therefore, it affects the bubble volume in two ways, i.e., through the capillary force and the contact diameter for the case of bubble formation that involves a moving contact line. Figure 9b shows that the bubble volume increases with increasing surface tension since the values of both $\sigma$ and D increase. The figure also shows that the influence of surface tension decreases with increasing gas flow rate. At the lowest gas flow rate of $Q = 1\,{\mathrm {ml}}/{\mathrm {min}}$, the bubble volume increases by 135% when the surface tension is increased from $47.8\,\hbox {mN/m}$ to $72.5\,\hbox {mN/m}$, which reduces to 35% at $Q = 350\,{\mathrm {ml}}/{\mathrm {min}}$. This indicates that the inertia force also affects the bubble formation at high gas flow rates.

Fig. 9

Influence of surface tension on a the maximum contact diameter and b the detached bubble volume under various gas flow rates

Two different bubbling regimes are observed under the considered gas flow rates. At low gas flow rates, the bubble formation process is in the period-1 (single) bubbling regime, where the bubbles detach in a periodic fashion with a constant volume. At higher gas flow rates, the bubble formation process switches to period-2 bubbling regime, where the wake of the preceding bubble significantly affects the formation of the succeeding bubble such that the succeeding bubble is smaller and two constant formation periods exist. It can be observed from the regime map shown in Fig. 10 that the transition from period-1 bubbling regime to period-2 bubbling regime is shifted to higher gas flow rates as the surface tension increases. The delay in the transition of bubbling regime for increasing surface tension is due to the fact that the bubble volume increases with increasing surface tension so that the bubble formation period also increases and thus the interaction between the preceding and succeeding bubbles is reduced.

Fig. 10

Bubble formation regime map for bubble formation in water–ethanol solutions

It is well known that for bubble formation without a moving contact line, e.g., bubbles formed from a thin walled nozzle, the transition from surface tension controlled regime to inertia controlled detachment can be predicted using the critical gas flow rate proposed by Oguz and Prosperetti (1993) defined as follows:

$$\begin{aligned} Q_{\mathrm {crit}} = \pi \Big ( \frac{16}{3g^2} \Big )^{1/6} \Big ( \frac{\sigma D_{\mathrm{in}}}{2\rho _{l}} \Big )^{5/6} \end{aligned}$$

(9)

They also concluded that the relation between the bubble volume at detachment and the gas flow rate is universal when the volume is scaled by the critical bubble volume $V_{\mathrm{crit}}$ and the flow rate is scaled by the critical flow rate $Q_{\mathrm{crit}}$. The bubble volume is then given by:

$$\begin{aligned} \frac{V_{\mathrm{b}}}{V_{\mathrm{crit}}} = \left\{ \begin{array}{ll} 1 & \quad \mathrm {if} \, Q < Q_{\mathrm{crit}} \,\,\,\,\,\,(\mathrm {a})\\ (Q / Q_{\mathrm{crit}})^{6/5} & \quad \mathrm {if} \, Q > Q_{\mathrm{crit}} \,\,\,\,\,\,(\mathrm {b}) \end{array}\right. \end{aligned}$$

(10)

Here, $V_{\mathrm{crit}}$ is derived from the balance of buoyancy and surface tension forces:

$$\begin{aligned} V_{\mathrm{crit}} = \frac{4}{3} \pi \Bigg ( \frac{3 \sigma D_{\mathrm{in}}}{4 \rho _{l} g} \Bigg ) \end{aligned}$$

(11)

According to Eq. (9), the critical gas flow rate for the case of $\sigma = 47.8\,\hbox {mN/m}$ is 53 ml/min. However, the bubble formation process is still in single bubbling regime even beyond this value, as shown in Fig. 10. The reason is that the usage of orifice diameter $D_{\mathrm{in}}$ in Eqs. (9) and (11) is not appropriate since the bubble shape differs significantly from spherical shape due to the widening of the contact line (Gnyloskurenko et al. 2003; Corchero et al. 2006). If the orifice diameter is replaced with the maximum contact diameter measured during the growth of a bubble at the low gas flow rates, the critical gas flow rate becomes 170 ml/min, which is similar to Fig. 10. To further test the validity of this approach, the bubble formation regime map shown in Fig. 10 is scaled by the modified critical gas flow rate $Q_{\mathrm{crit}}^{\prime }$ in Fig. 11. It can be observed that the transition of bubbling regime from single bubbling regime to period-2 bubbling regime happens at $Q/Q_{\mathrm{crit}}^{\prime } \approx 1$.

Fig. 11

Bubble formation regime map for bubble formation in water–ethanol solutions given in terms of the non-dimensional volumetric flow rate ($Q/Q_{\mathrm{crit}}^{\prime }$) and surface tension

The measured bubble volumes and gas flow rates shown in Fig. 9b are scaled by the modified critical gas flow rate $Q_{\mathrm{crit}}^{\prime }$ and critical bubble volume $V_{\mathrm{crit}}^{\prime }$, respectively, and the results are shown in Fig. 12. It can be observed that the experimental data fall approximately on a single curve when this modified scaling is used. The figure also shows that the dimensionless bubble volume is constant and independent of the dimensionless gas flow rate at the surface tension controlled regime ($Q/Q_{\mathrm{crit}}^{\prime } < 1$) and subsequently it increases significantly with the gas flow rate at the inertia controlled regime ($Q/Q_{\mathrm{crit}}^{\prime } > 1$). As pointed out by Corchero et al. (2006), even though the collapse of experimental data in Fig. 12 is promising, the figure is not easy to use in practice because it requires a prior knowledge on the maximum contact diameter for the system of interest.

Fig. 12

Non-dimensional volumetric flow rate ($Q/Q_{\mathrm{crit}}^{\prime }$) versus the non-dimensional bubble volume ($V_{\mathrm{b}}/V_{\mathrm{crit}}^{\prime }$)

4.2 Bubble growth stages

As the bubble grows, it passes through several stages, which can be identified based on several geometric parameters. These phases are identified for the surface tension force controlled regime, where the quasi-static approximation is reasonable. An example is shown in Fig. 13 for bubble formation in water under $Q = 21.8\,\hbox {ml/min}$. The dimensionless time $t/t_{\mathrm{det}}$ is used in presenting the data, where $t_{\mathrm{det}}$ is the moment at which the bubble detaches.

Four stages can be identified based on the key geometrical parameters and relevant forces acting on the bubble during growth: hemispherical spreading, cylindrical spreading, cylindrical growth, and necking. The transition to each following stage is represented by vertical dashed lines in Fig. 13. The first stage is the hemispherical spreading, where the bubble attains the shape of an almost perfectly hemispherical shape witnessed from the radius of the curvature at the bubble apex $R_{0}$ being nearly identical to the bubble height H. The bubble spreads for some time while retaining a hemispherical shape. The first stage ends when $R_{0}/H \approx 0.95$. At the cylindrical spreading stage, the bubble spread further as its height keeps increasing. This stage ends when the maximum contact diameter is reached, coinciding with an inflection point in the height curve. The third stage is the cylindrical growth, where the values of $R_{0}$ and D remain almost constant as the volume growth is captured in the height growth. The value of contact angle $\theta$ increases significantly as the bubble grows further. The third stage ends when the buoyancy force ($F_{\mathrm{b}} = (\rho _{l} - \rho _{g}) V_{\mathrm{b}} g$) exceeds the surface tension force ($F_{\mathrm{b}}/F_{\mathrm{s}} > 1$). The last stage is the necking stage. Finally, a force balance between restraining (primarily $F_{\mathrm{s}}$) and lifting forces (primarily $F_{\mathrm{b}}$) is achieved. The contact line continuously shrinks to the orifice rim. The bubble height and radius of curvature at the bubble apex increase as all the volume is displaced from a cylindrical shape into a spherical shape due to the formation of bubble neck. This stage ends at the detachment.

Similar stages of bubble growth in non-wetting systems under surface tension dominated regime have been identified and described by Gnyloskurenko et al. (2003). The under critical growth, critical growth and necking phases are comparable to the spreading stages, cylindrical growth stage and necking stage. However, the nucleation period, which is defined as very sharp and sudden increase of all geometrical parameters at the initial stage of bubble growth, is not observed in the present study. Although Gnyloskurenko et al. (2003) stated that a constant flow rate device was used, the volume growth was nonlinear.

The radius of the curvature at the bubble apex, $R_0$, attains an almost constant value for a long period during the bubble growth. The behavior seems comparable to what was numerically predicted by Gerlach et al. (2005) using the Young–Laplace equation. However, the increase in $R_{0}$ that occurs in the detachment stage was not described by Gerlach et al. (2005) since the method cannot simulate the last phase of the neck pinch-off at detachment.

Fig. 13

The evolution of a key geometrical parameters and relevant forces and b bubble shape during growth for the case of $\sigma = 72.5\,\hbox {mN/m}$ under $Q = 21.8\,\hbox {ml/min}$. The formation time $t_{\mathrm{det}}$ is $351 \pm 0.6\,\hbox {ms}$

4.3 Contact line behavior

In this section, the behavior of the contact line during the bubble formation process at the single bubbling regime ($Q/Q_{\mathrm{crit}}^{\prime } < 1$) is presented. Figure 14 shows the evolution of contact diameter and contact angle with the dimensionless time $t/t_{\mathrm{det}}$ under the considered gas flow rates. The overall trend of the contact diameter during the process of bubble formation is similar for all surface tension values selected in this study. The contact line begins to extend beyond the orifice rim until it reaches the maximum diameter. The contact line holds on to this maximum value for a relatively long period, and then, it shrinks back to the value of the orifice inner diameter. The maximum contact diameter shows little change with increasing gas flow rate. However, a higher gas flow rate leads to a slower shrinkage of the contact line during the necking stage.

The evolution of the contact angle is more complex than the contact diameter. When the contact line recedes, the contact angle decreases to a minimum value for all surface tension values. However, no clear relationship is observed between the contact angle and the gas flow rate. The minimum contact angles are comparable for all gas flow rates for $\sigma \ge 65.2\,\hbox {mN/m}$ (Fig. 14a, b), whereas the minimum contact angle tends to decrease with increasing gas flow rate for $\sigma \le 55.7\,\hbox {mN/m}$ (Fig. 14c, d). After the minimum contact angle value is reached, the contact angle increases as the contact line advances back to the orifice. For $Q < 130\,\hbox {ml/min}$, an increase in contact angle is observed during the cylindrical growth and necking stages. On the other hand, at higher gas flow rate ($Q \approx 130\,\hbox {ml/min}$), the contact angle increases only during the cylindrical growth stage, while it is almost constant during the necking stage. Despite this, the maximum contact angle during the advancing phase shows little change with increasing gas flow rate.

Fig. 14

The evolution of contact diameter (left) and contact angle (right) during growth under various gas flow rates for: a $\sigma = 72.5\,\hbox {mN/m}$, b $\sigma = 65.2\,\hbox {mN/m}$, c $\sigma = 55.7\,\hbox {mN/m}$ and d $\sigma = 47.8\,\hbox {mN/m}$

Figure 15 shows the variation of contact angle with contact line velocity under various surface tension values. It can be observed from the figure that during the receding phase, there is no clear relationship between contact line velocity and contact angle since the same contact line velocity can have multiple contact angle values. However, during the advancing phase, the contact angle seems to be independent of the contact line velocity since the value is almost constant. Moreover, the value is almost the same for all gas flow rates since the differences are within the experimental errors.

The contact angle during the formation process tends to increase as the surface tension increases. For example, under $Q = 1\,\hbox {ml/min}$, the minimum contact angle increases from $91^{\circ }$ to $100^{\circ }$ when the surface tension is increased from 45.8 to 72.5 mN/m. However, as can be seen in Fig. 15, no clear relationship is observed between the contact angle during the bubble formation and the receding and advancing contact angles measured using the tilting plate method, $\theta _{\mathrm{rec}}$ and $\theta _{\mathrm{adv}}$. The contact angle tends to be larger than $\theta _{\mathrm{rec}}$ during the receding phase, and it can exceed beyond the limit given by $\theta _{\mathrm{adv}}$ during the advancing phase. Therefore, the contact angle hysteresis, defined as the difference between the minimum and maximum contact angle when the contact line velocity is zero, tends to be different than the one measured using the tilting plate method.

Fig. 15

The variations of the contact line velocity with contact angle for: a $\sigma = 72.5\,\hbox {mN/m}$, b $\sigma = 65.2\,\hbox {mN/m}$, c $\sigma = 55.7\,\hbox {mN/m}$ and d $\sigma = 47.8\,\hbox {mN/m}$

4.4 Comparison of simulations and experiments

In this section, three simulation examples using the LFRM with a stick-slip model to account for the contact angle hysteresis observed in the experiments are presented. As explained in the previous section, once the contact diameter reaches the maximum, the contact angle gradually increases while the contact line shifts from the receding phase to the advancing phase. The experimental contact angle values at the time when the contact line reaches the maximum and at the time when the contact line starts to advance back to the orifice rim are used as $\theta _{\mathrm{rec}}$ and $\theta _{\mathrm{adv}}$ in the stick-slip model, respectively. The simulation results are compared with the results obtained using a static contact angle ($\theta _{\mathrm{s}} = \theta _{\mathrm{rec}}$) and the experimental results of bubble formation at the single bubbling regime shown in the previous section.

The first example is the bubble formation in a water under a gas flow rate of 132.1 ml/min. The receding and advancing contact angles are set to $97^{\circ }$ and $114^{\circ }$, respectively. The dependency of the simulation results on the grid resolution is checked by performing the simulation using three different grid sizes: $\Delta _{1}=2.0\times 10^{-4}\,\hbox {m}$, $\Delta _{2}=1.0\times 10^{-4}\,\hbox {m}$, and $\Delta _{3}=5.0\times 10^{-5}\,\hbox {m}$. The effect of grid resolution on the bubble shape at the final instant prior to bubble pinch-off ($t/t_{\mathrm{det}} = 1$) is shown in Fig. 16. It can be seen that the bubble shapes for $\Delta _{2}$ and $\Delta _{3}$ are identical. However, the bubble shape obtained using the coarsest grid of $\Delta _{1}$ is significantly smaller. The detached bubble volume $V_{\mathrm{b}}$ and formation time $t_{\mathrm{det}}$ obtained by the finest grid are $192.5\,{\mathrm {mm}}^3$ and $87.1\,\hbox {ms}$, respectively. The differences in $V_{\mathrm{b}}$ and $t_{\mathrm{det}}$ compared to the finest grid for $\Delta _{1}$ and $\Delta _{2}$ are 27.6% and 1.1%, respectively. Therefore, the grid $\Delta _{2}$ is good enough to produce accurate results.

Fig. 16

Effect of grid resolution on bubble shape at $t/t_{\mathrm{det}} = 1$ for $\sigma = 72.5\,\hbox {mN/m}$ under $Q = 132.1\,\hbox {ml/min}$. The point coordinates of the interface position are extracted by slicing the 3D-bubble at the center of the orifice

Figure 17 shows the comparison of several geometrical parameters of the bubble between the simulations and experiments for this case. The experiments show that the bubble spreads until it reaches the maximum contact diameter at $t \approx 33\,\hbox {ms}$. The bubble base remains almost constant, while the bubble height increases until $t \approx 68\,\hbox {ms}$. Then, the bubble base continuously decreases to the value of $D_{\mathrm{in}}$ and bubble departs at $t = 85.6\,\hbox {ms}$ with a departure volume of $188.4\,{\mathrm {mm}}^3$. It can be observed that the occurrence of the contact line pinning can be reproduced by the numerical simulation with the stick-slip model. On the other hand, with a static contact angle the contact diameter immediately advances toward the orifice rim once it reaches the maximum value. As a consequence, the predicted departure time and thereby the volume of the detached bubble are smaller compared to the experiments. The simulations agree well with the experiments when the stick-slip model is employed. The differences in the departure time compared to the experiments for simulations obtained using a static contact angle and the stick-slip model are 7.1% and 1.8%, respectively.

Figure 18 shows the comparison between the simulations and experiments for the case of bubble formation in a 10 wt% ethanol–water mixture under a gas flow rate of $21.9\,\hbox {ml/min}$. The prescribed receding and advancing contact angles for the stick-slip model are $86^{\circ }$ and $98^{\circ }$, respectively. In this case, the bubble departs at $t = 156\,\hbox {ms}$ with a departure volume of $56.7\,{\mathrm {mm}}^3$. Similarly, the stick-slip model causes the bubble base to exhibit a stick/slip pattern during bubble growth whereas the base promptly shrinks to the orifice rim when the static contact angle model is used. Overall, the variations of contact angle, contact diameter and bubble shape obtained using the stick-slip model agree well with the experiments. The predicted maximum contact diameter is also in a good agreement with the experimental value despite the slightly higher contact angles seen in the experiments in the initial 50 ms. The differences in $t_{\mathrm{det}}$ compared to the experiments for simulations obtained using a static contact angle and the stick-slip model for this case are 15.4% and 1.9%, respectively.

The last case is the bubble formation in a 5 wt% ethanol–water mixture under a low gas flow rate of $5.0\,\hbox {ml/min}$. The comparison of the geometrical parameters of the bubble between the simulations and experiments for this case is shown in Fig. 19. The bubble departs at $t = 855\,\hbox {ms}$ with a departure volume of $71.1\,{\mathrm {mm}}^3$ in the experiments. The receding and advancing contact angles for the stick-slip model are set to $94^{\circ }$ and $103^{\circ }$, respectively. Again, the stick-slip model provides better results compared to the static contact angle. The differences in $t_{\mathrm{det}}$ compared to the experiments for simulations obtained using a static contact angle and the stick-slip model in this case are 16.7% and 1.1%, respectively. It should be noted here that the difference in $t_{\mathrm{det}}$ between the experiments and simulations obtained using a static contact angle tends to increase as the gas flow rate decreases. This indicates that the stick-slip model is essential for obtaining good agreement with the experiments, especially at low gas flow rates where the surface tension force is more important.

Fig. 17

Comparisons of the contact angle, bubble height, contact diameter and bubble shape for bubble formation in a water under a gas flow rate of 132.1ml/min

Fig. 18

Comparisons of the contact angle, bubble height, contact diameter and bubble shape for bubble formation in a 10 wt% ethanol–water mixture under a gas flow rate of 21.9 ml/min

Fig. 19

Comparisons of the contact angle, bubble height, contact diameter and bubble shape for bubble formation in a 5 wt% ethanol–water mixture under a gas flow rate of 5.0 ml/min

5 Conclusions

In the present work, we presented a study on the formation of bubbles from a submerged hydrophobic orifice plate. Several different wetting conditions were obtained by varying the surface tension value using a series of ethanol–water solutions. The significant observations are as follows:

• 1. The maximum contact diameter increases with increasing surface tension because the interaction between the liquid and the orifice material becomes more wetting. The bubble size is therefore affected by the surface tension value in two ways: via the capillary force and via the contact diameter for the case of bubble formation that involves a moving contact line.

• 2. Based on the relevant forces and the key geometrical parameters of the bubble, bubble growth stages, termed (1) hemispherical spreading, (2) cylindrical spreading, (3) critical growth and (4) necking, are identified during the process of bubble formation in a surface tension controlled regime.

• 3. The contact line and the apparent contact angle vary in a complicated manner as the bubble grows due to the surface roughness and heterogeneity. No explicit relationship is found between the contact angle and the contact line velocity. A significant increase in the contact angle from the receding value to the advancing one is observed when the contact line is pinned to the surface once it attains the maximum value.

• 4. The simulation results show a good agreement with the experiments when a stick-slip model is used to account for the contact angle hysteresis. This is attributed to the fact that the contact line pinning observed in the experiments can be reproduced by the stick-slip model, whereas the usage of a static contact angle leads to an immediate shrinks of the contact diameter. For a good comparison, it is required to use the advancing and receding angles observed from bubble formation experiments, which deviate from the angles measured by the means of the sliding drop experiment.