1 Introduction

While advances in deep learning [25] have been been unprecedented, many researchers know that the capabilities of this methodology are being at times overestimated [38]. Some works have been published where performance reported with DL surpass that obtained by humans on the same task (see [14] and [34]). Despite this, some studies have also shown that DL networks have a weird behavior which is very different from human responses when confronted with the same task [23, 32]. Perhaps the best example to describe it is the case of the so-called “adversarial examples” [32], see Fig. 1. Adversarial examples are apparently identical to the original example versions except for a very small change in pixels of the image. Despite being perceived by humans as completely equal to the originals, DL techniques fail miserably at classifying them.

Fig. 1
figure 1

Adversarial example. “Person” is the so-called target class

Full size image

Thus, while apparently having superhuman capabilities, DL also seems to have weaknesses that are not coherent with human performance. Not only that, from the structure of DL (essentially an interconnected network of neurons with numerical weights), it is unclear what gives rise to that behavior. The problem is not also in maliciously-selected noise, since some transformations involving rescaling, translation, and rotation produce the same results [2]. Likewise, physical changes in the objects (graffiti or stickers) have been shown to produce the same effect [9]. While not strictly adversarial examples, in video processing it often happens that the object of interest is recognized in one frame but not in the next one, even if there is no noticeable difference in the frames. Such implausible ’stability’ issues are exemplified in real-life cases, like Uber’s self-driving vehicle in which a pedestrian was killed in Arizona (USA). The preliminary report released by the NTSBFootnote 1 states: “As the vehicle and pedestrian paths converged, the self-driving system software classified the pedestrian as an unknown object, as a vehicle, and then as a bicycle with varying expectations of future travel path…”. Other real-life examples have been shown in the contexts of optical flow-based action recognition [15], vision for robots [20] and even in other domains such as machine learning-based malware detection [19]. If the safety of a DL system depends on the classifier never making obvious mistakes then the system must be considered intrinsically unsafe.

On the other hand, while the prevailing trend in the scientific community is currently in proposing variant architectures for DL, it has been demonstrated that for a given dataset the same adversarial examples persist even after training with different architectures [24].

The goal of this paper is not to introduce a novel method, but to advance our knowledge about the phenomenon, its root causes and implications. The contributions of this paper are as follows. While other underlying reasons have been proposed in the literature for the existence of adversarial examples, in this paper we contend that the phenomenon of adversarial examples is tied to the inescapable trade-off that exists in machine learning between fitting and generalization. This idea is supported by experiments carried out in which the robustness to adversarial examples is measured with respect to the degree of fitting to the training samples.

This paper is an extended version of conference paper [8]. The contributions in this paper are: new correct methodology used, removal of the concept of ’cognitively adversarial examples’ introduced in [8] and new set of experiments with a deep network (experiments in [8] were carried out with K-NN), plus a more detailed analysis of the results and implications.

2 Previous work

The two major lines of research around adversarial examples have been: (1) generating AEs and (2) defending against AEs. This paper will not cover either, and the reader is referred to recent surveys [1, 6, 40]. In parallel to those two lines, however, a significant body of work has been carried out to delve into the root causes of AEs and their implications.

In early work, the high nonlinearity of deep neural networks was suspected as a possible reason explaining the existence of adversarial examples [32]. On the other hand, later in [13] it is argued that high-dimensional linearities cause the adversarial pockets in the classification space. This suggests that generalization (as implied by the less complex linear discrimination boundaries) has a detrimental effect that produces AEs. In the same line, in [10] it is stated: “Unlike the initial belief that adversarial examples are caused by the high non-linearity of neural networks, our results suggest instead that this phenomenon is due to the low flexibility of classifiers”.

In [32] the authors had suggested a preliminary explanation for the phenomenon, arguing that low-probability adversarial “pockets” are densely distributed in input space. In later work [33] the authors probed the space of adversarial images using noise of varying intensity and distribution. They showed that adversarial images appear in large regions in the pixel space instead.

In [27] the existing literature on the topic is reviewed, showing that up to 8 different explanations have been given for AEs. The prevailing trend, however, seems to focus on the linear/non-linear and in general in the overfitting problems of the classifier. Under two interpretations (the boundary tilting hypothesis [35] and in [11]) the authors argue that the phenomenon of AEs is essentially due to overfitting and can be alleviated through regularisation or smoothing of the classification boundary.

Recent work has linked low test error with low robustness to AEs. In [31] it is shown that a better performance in test accuracy in general reduces robustness to AEs. In [12] the authors perform experiments on a synthetic dataset and state that low (test) error classification and AEs are intrinsically linked. They argue that this does not imply that defending against adversarial examples is impossible, only that success in doing so would require improved model generalization. Thus, they argue that the only way to defend against AEs is to massively reduce that error. However, we note that this would be in apparent contradiction with the main finding in that paper (that AEs appear with low classification error). Thus, while generalization may help reduce error in general, without additional considerations it would not necessarily remove AEs.

In [26] the authors point out that an implicit assumption underlying most of the related work is that the same training dataset that enables good standard accuracy also suffices to train a robust model. The authors argue that the assumption may be invalid and suggest that, for high-dimensional problems, adversarial robustness can require a significantly larger number of samples. Similar conclusions are drawn in [30], where it is stated that adversarial vulnerability increases with input dimension. Again, all of this would point to overfitting as the primary cause.

On the other hand, despite the several methods that have been proposed to increase robustness to AEs, the phenomenon appears to be difficult or impossible to avoid [3, 10, 12, 28, 29, 36].

In summary, despite significant research on the topic, the cause of the phenomenon remains elusive. It is not clear whether the phenomenon is due to overfitting or, on the contrary, to underfitting. Some researchers have also tied the phenomenon to the (limited) amount of training samples that are available or a large input dimension (or the relationship between these two).

3 Datasets and methods

Our reasoning is based on two simple facts:

  1. 1.

    Adversarial examples can be generated from training samples (just as they can be generated from test samples)

  2. 2.

    The adversarial example can be arbitrarily close to the original sample

During training, we always try to minimize both bias (by reducing training set error) and variance (by applying some form of regularization). It is well known that reducing variance increases bias and vice versa.

Thus, if we consider facts 1 and 2 in the limit of distance towards 0 (with respect to the training examples), the situation is equivalent to a model that has been trained with high bias (high training error). In other words, this would equate to a model in which the source of error in the adversarial examples is due to high bias. This situation is depicted in Fig. 2, where regularization near the known training sample causes the adversarial example.

Fig. 2
figure 2

Adversarial example caused by regularization in the vicinity of a training sample

Full size image

If the error can be attributed to bias, then reducing it should reduce that error. In other words, this means that reducing model bias (and therefore increasing model variance) should reduce error in adversarial examples. That is exactly the hypothesis that we address below in the experiments. The bias and variance errors are in general controlled by the classifier’s trade-off between fitting and generalization. Our aim is to test if such change in the fitting-generalization trade-off point reflects in the robustness to AEs.

In the experiments below we used the MNIST [18], CIFAR-10 [16] and ImageNet [17] datasets, arguably the three most common datasets used in research on the nature of adversarial examples (these three datasets were used in 46 of the 48 papers reviewed in [27]). MNIST is a dataset of handwritten grayscale 28x28 images representing the digits 0–9. Typically, 60,000 images are used for training and 10,000 for testing. The CIFAR-10 dataset consists of 60,000 32 \(\times\) 32 colour images in 10 classesFootnote 2, with 6000 images per class (50,000 training images and 10,000 test images). The CIFAR-10 dataset is in general considered more challenging than MNIST. On the other hand, compared to MNIST and CIFAR-10 datasets, ImageNet is much more challenging in terms of images and classes (1000 classes) and it has been shown in previous work that ImageNet images are easier to attack but harder to defend than images from MNIST and CIFAR.

To validate our hypothesis and show that accuracy in the AE set is linked to the fitting capability, we need a classifier working under various points of the fitting-generalization regime. In a first set of experiments, we used a K-Nearest Neighbor Classifier, for K values equal and greater than 1, to control the point in the trade-off between fitting and generalization. The K-NN classifier is a natural choice here. It is widely known that large values of K are used to achieve better generalization, while lower values (down to K = 1) may produce overfitting. Given the dimensionalities involved, an efficient KD-tree-based implementation was used for the K-NN classifier.

In the second set of experiments we used a LENET-5 CNN for classification. The architecture of this network is shown in Fig. 3. Note that we did not use any pre-trained models in any of the experiments with deep networks.

Fig. 3
figure 3

Network architecture used in the experiments (for MNIST)

Full size image

Attack methods are iterative optimization algorithms based on trained deep networks. They essentially optimize a norm or distance to the original sample and a change in label from that of the original sample to that of the target class. In our experiments, the AEs were obtained using four methods: the Fast Gradient Sign Method (a so-called white-box targeted attack, introduced in [13]), DeepFool [22] targeting all classes, Carlini-Wagner [5] and the recent HopSkipJump method [7]. For FGSM we fixed the attack step size (input variation) to \(\epsilon =0.1\). For DeepFool the maximum number of iterations was set at 100. For all methods we used the aforementioned LENET-5 network architecture to generate the adversarial examples (also in the first set of experiments with the K-NN classifier). Figs. 4 and 5 show some examples of the AEs generated.

Fig. 4
figure 4

Sample AEs generated with FGSM for the MNIST dataset

Full size image
Fig. 5
figure 5

Sample AEs generated with DeepFool for the CIFAR-10 dataset. Best viewed in color

Full size image

4 Experimental results

Experiments were performed with two different classifiers: (1) K-NN classifier and (2) Convolutional Neural Network. Our objective in the experiments is to bring those two classifiers to overfitting and show the accuracy trends in three sets of samples: (a) the test set, (b) an adversarial set and (c) a so-called fail subset.

In the following we describe the results obtained in each case.

4.1 K-NN classifier

For the K-NN classifier, Fig. 6 shows how the three aforementioned subsets are obtained. To get to the adversarial subset we first obtained the test samples that were correctly classified by the K-NN, for a \(K=Z\) (for a fixed \(Z>1\), Z odd). The attack method (FGSM, DeepFool, Carlini-Wagner and HopSkipJump) was then used to generate a set of AEs from those. Note that at this point AE generation was done with the CNN network (since all attack methods are based on trained CNN networks and backpropagation), and therefore this set has to be filtered to discard samples that were correctly classified by the Z-NN. Thus the Z-NN accuracy in this final AE set is 0%.

Fig. 6
figure 6

How the three sets of samples used in the experiments with K-NN are obtained

Full size image

Then we measured the K-NN classifier accuracy on this AE set, for values of K smaller than Z, down to K = 1. Again, our hypothesis is that accuracy in this AE set should increase as K gets smaller. As can be seen in Fig. 7, the classifier is, for both datasets, overfitting as K gets smaller.

Fig. 7
figure 7

K-NN train and test accuracies for MNIST (left) and CIFAR10 (right) datasets

Full size image

In order to discard the possibility of this being a general trend with lower values of K, we also obtained the accuracy for the whole test set and for the subset of test samples in which the classifier gave a wrong decision for K = Z. We call the latter fail subset, see Fig. 6. Note that, by definition, the fail subset and the adversarial set both give 0% accuracy for K = Z. The fail subset is a sort of worst-case set in which accuracy is also expected to grow as K gets smaller (since it starts with an accuracy of 0% for K = Z).

We repeated the experiment a number of times, each run performing a stratified shuffling of the dataset between the training and test sets (always leaving 60,000 samples for training and 10,000 samples for test for MNIST, and 50,000 samples for training with 10,000 samples for test in CIFAR-10). The results are shown in Fig. 8.

Fig. 8
figure 8

Accuracy values for the datasets used. Left: Accuracy values for the MNIST dataset, using \(\hbox {Z}=7\). Right: Accuracy values for the CIFAR-10 dataset, using \(\hbox {Z}=7\). Best viewed in color

Full size image

The results show that accuracy in the adversarial set has the highest increase rate as K gets smaller. The accuracy values obtained in the whole test set are always very stable (and very close 100% in the case of MNIST) which makes it difficult to establish a trend in that case. For the other two sets, in order to check if there was a statistically significant difference of trends we applied hypothesis testing in the following way. Let \(A_i\) be the accuracy obtained using \(K=i\). We calculated the slope between accuracies for successive values of K in the following way: \(S_j = A_j/A_{j+2}\), for \(j=\{1, 3, 5\}\). Then we used the slopes as the random variables to perform a paired Welch’s t testFootnote 3. In Fig 9 we show the p values of the test.

Fig. 9
figure 9

p values obtained. Left: p values (represented in logarithmic scale) obtained by the paired Welch’s t test between results in the Adversarial set and those in the misclassified test samples, for MNIST. The dashed horizontal lines represent the 95% and 99% confidence thresholds. Right: idem for CIFAR-10

Full size image

The values in Fig. 9 show that the trends in the two sets are statistically different. Note also that for \(S_5\) the value is not meaningful since \(A_7\) is 0 in both cases so the slope is actually infinite.

4.2 CNN classifier

In the experiments carried out with the CNN classifier, the number of epochs is the parameter that will control the degree of overfitting (with more epochs increasing overfitting). Thus, instead of using K as in the previous experiment we will use E, which here is the number of epochs, in this case varying from 1 to 35. The adversarial examples in this case are obtained from test samples that are correctly classified (by the CNN classifier) for \(E=M\), where M is the number of epochs for which the test accuracy was the highest. Thus, for \(E=M\) the accuracy in this set of adversarial examples is zero. Likewise, we also consider the subset of test samples that are not correctly classified when \(E=M\). This is what we have been calling the fail subset (the accuracy for this subset for \(E=M\) is also zero). This part of the experimental workflow is shown in Fig. 10.

Fig. 10
figure 10

How the three sets of samples used in the experiments with CNN are obtained. Note that the two CNN boxes are the same model

Full size image

This set of experiments was only carried out with the CIFAR-10 dataset since MNIST with CNN provided test accuracies near 100%, which did not allow to obtain meaningful results. To obtain the results from \(E=1\) to \(E=35\) we used model checkpointing. We repeated the experiment a number of times, each run performing a stratified shuffling of the dataset between the training and test sets. The Adam optimizer was used with batch size of 32 and learning rate of 0.003.

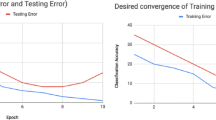
The results are shown in Fig. 11.

Fig. 11
figure 11

Results with the CNN for the CIFAR-10 dataset

Full size image

The results show that the accuracy in the training set is always improving. The accuracy in the test set initially increases to a maximum value (approximately at \(M=5\) epochs) and then slowly decreases. This region shows overfitting, which is the regime of interest in our case. As for the other sets, from the figure it is difficult to compare trends. To measure them, for each run of the experiment we obtained the point (i.e. number of epochs) that provided the maximum test set accuracy, again let this be \(E=M\). Then we calculated the delta accuracy as: \(ACC(E=35) - ACC(E=M)\). The boxplot of deltas thus obtained is shown in Fig. 12.

Fig. 12
figure 12

Boxplots of the deltas for the sets considered

Full size image

Welch’s t test between test set and adv FGSM and between test set and adv DeepFool sets gave p values of \(4.8 \cdot 10^{-4}\) and \(5.7 \cdot 10^{-2}\) respectively, so the difference in trends is statistically significant.

Note also that the adv FGSM and adv DeepFool sets gave trends that were very different from each other. This should not come as a surprise, since the methods are different and they produce different sets of AEs. To further analyze this, we obtained the L2 norm between each original test sample and the corresponding AE generated by either method, see Fig. 13. The lower norms of DeepFool’s AEs are coherent with the lower trend observed in Fig. 12 for adv DeepFool vs adv FGSM. Again, the induced overfitting improves results for samples that lie closer to the originals.

Fig. 13
figure 13

L2 norms between original test sample and corresponding AE generated by the two attack methods

Full size image

Note that in Figs. 11 and 8 show that the the performance change trends are very similar in the fail subset and the adversarial subset. However, it is the magnitude of the increase what is statistically different. The increase in the adversarial subset is statistically higher than in the fail subset. On the other hand, note again that the two subsets represent qualitatively different data. The adversarial subset contains samples that have been failed and we know that there is a close sample which has been correctly classified. The fail subset contains samples that have been failed and they do not have a close sample which has been correctly classified (therefore not qualifying as AEs). In summary, one subset represents AEs while the other only represent non-AE fails, and the accuracy results show trends of statistically different magnitudes, which we find it supports our hypothesis.

We also conducted experiments with the ImageNet dataset. The results, see Fig. 14, show the same general trend as with the other datasets. Figure 15 shows the the boxplot of deltas.

Fig. 14
figure 14

Results with the CNN for the ImageNet dataset. In this case we used an InceptionV3 architecture trained from scratch with a learning rate of 0.05, 10 randomly selected classes, 13,000 training images and 500 test images. Averages of 3 runs

Full size image
Fig. 15
figure 15

Boxplots of the deltas for the sets considered

Full size image

5 Discussion

Our hypothesis that AEs are intrinsic to the bias-variance dilemma has been supported by experiments in which a classifier moving towards the variance extremum showed increased robustness to the AEs. This increase was, with statistical significance, higher than in the test set, meaning that the increased robustness to AEs was not associated with a higher accuracy in general. Overall this is essentially the expected behavior for the well-know bias-variance dilemma: good generalization and robustness to AEs are not achieved simultaneously.

We note that our work is coherent with some defensive methods such as feature squeezing [37], whereby the input is transformed to make similar samples coalesce into a single point in the feature space. One example of such transformation is bit depth reduction. In this respect, simple binarization on the inputs has been shown to add robustness against AEs. In fact, other squeezers have been proposed, such as image denoising [21] and learnable bit depth reduction [4]. In our context, such transformations are in fact helping the standard classifier decide for samples that lie near the training samples.

In the light of the results, we postulate that the existence of AEs do not reflect a problem of either overfitting or lack of expressive power, as suggested by previous work. Rather, AEs exist in practice because our models lack both aspects simultaneously. Rather than being an impossibility statement, this actually calls for methods that have more flexibility to reflect both aspects. While practically all machine learning methods already incorporate some form of trade-off between generalization and fitting, we hypothesize that such trade-offs may be fundamentally different from any such trade-off used by human perceptual learning (since the latter presumably allows for both good generalization and robustness to AEs simultaneously).

Based on our reasoning at the beginning of Sect. 3, it can be argued that the “overfitting” argument will not hold for deeper networks, as for deeper networks the training loss can be made close to 0, see for example [39]. However, we have to emphasize that in this paper we are not claiming that AEs exist just because of a high training error. Our reasoning is that the presence of AEs is akin to a situation of high training error. In this respect, note that in fact this same reasoning can be applied to test samples, meaning that the presence of AEs is also akin to a situation of high test error. The only logical conclusion is the one already put forward, i.e. that AEs exist because our algorithms suffer from high training error and/or high test error. In other words, the only way to remove AEs is to have an algorithm with both low training error and low test error. For this to happen, the algorithm must be such that it has both overfitting (in the sense of good fitting to training samples) and good generalization *at the same time*. This contrasts with extant machine learning which implicitly assumes an unavoidable trade-off between fitting and generalization. Our work points to the need for methods with enough expressibility to accommodate both aspects simultaneously. In machine learning the focus on generalization aims at answering the question ‘how can we generalize to unseen samples?’. In the light of our results the question would be more a ‘how can we generalize equally well while keeping good fitting at the same time?’.

Our analysis suggests that the existence of AEs is a manifestation of the implicit trade-off between fitting and generalization. While the emphasis in machine learning is typically focused on improving generalization, here we argue that the generalization-fitting trade-off is also important. Ideally, while the classifier must have generalization power, it should be also flexible enough to accommodate the good effects of overfitting.

6 Conclusions

Despite the biological plausibility of deep neural networks, adversarial examples are an incontrovertible demonstration that a certain fundamental difference between human and machine learning exists. In this paper we have considered the possible causes of this intriguing phenomenon. While many methods have been proposed to make classifiers more robust to AEs, apparently the phenomenon essentially persists and cannot be definitely avoided.

Our results support the notion that the phenomenon is rooted in the inescapable trade-off that exists in machine learning between fitting and generalization. This is supported by experiments carried out in which the robustness to adversarial examples is measured with respect to the degree of fitting to the training samples, showing an inverse relation between generalization and robustness to adversarial examples. As far as the authors know, this is the first time that such reason is proposed as the underlying cause for AEs. This hypothesis should in any case receive additional support through future work.

While the bias-variance dilemma is posited as the root cause, that should not be considered an impossibility statement. Rather, this would actually call for methods that have more flexibility to reflect both aspects. Current trade-offs between bias and variance or equivalently between fitting and generalization would seem to be themselves biased towards generalization.