Comparison of Evidential Reasoning Algorithm with Linear Combination in Decision Making

Abstract

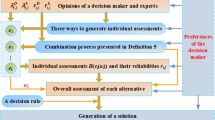
Evidential reasoning (ER) approach is a representative method for analyzing uncertain multi-criteria decision-making (MCDM) and multi-criteria group decision-making (MCGDM) problems. Its core is ER algorithm used to combine belief distributions on criteria, which is developed based on Dempster’s rule of combination and probability theory. The ER algorithm is nonlinear and more computationally complex than linear combination of belief distributions. To address the necessity of the ER algorithm in MCDM and MCGDM, it is compared with linear combination from three perspectives by simulation. The first is to examine differences between the aggregated assessments derived from the ER algorithm and linear combination. The second is to examine error rates of best alternatives derived from two combination ways. The third is to examine alternative ranking differences derived from two combination ways. To facilitate the comparison, difference between aggregated assessments is designed and score function of alternative is developed from the expected utilities of alternative. Simulation experiments show that differences between the aggregated assessments are influenced by the number of assessment grades, and error rates of best alternatives and alternative ranking differences are influenced by the numbers of criteria and alternatives.

Appendix

1.1 Proof of Proposition 1

From the two assessments B(a_l) and $\bar{B}(a_{l} )$ and the constraint 0 = u(H₁) < u(H₂) < ··· < u(H_N) = 1, it can be known that

$$0 \le \Delta \beta_{n} (a_{l} ) \le 1\quad \left( {n = 1, \ldots ,N} \right),$$

(A.1)

$$0 \le \Delta \beta_{m} (a_{l} ) \; \le 1\quad \left( {m = 1, \ldots ,N} \right),$$

(A.2)

$$0 \le u(H_{m} ) - u(H_{n} ) \le 1,\quad \left( {m,\;n = 1, \ldots ,N} \right),{\text{ and}}$$

(A.3)

$$0 \le \Delta \beta_{\varOmega } (a_{l} ) \le 1.$$

(A.4)

Meanwhile, Eq. (14) shows that the larger the values of $\Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )$ and $\Delta \beta_{\varOmega } (a_{l} )$ are, the larger the value of $\Delta D(a_{l} )$ is. To compare the contributions of $\Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )$ and $\Delta \beta_{\varOmega } (a_{l} )$ to the value of $\Delta D(a_{l} )$, the partial derivatives of $\Delta D(a_{l} )^{2}$ with respect to $\Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )$ and $\Delta \beta_{\varOmega } (a_{l} )$ are calculated as

$$\frac{{\partial \Delta D(a_{l} )^{2} }}{{\partial \left( {\Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )} \right)}} = u(H_{m} ) - u(H_{n} )\;{\text{and}}$$

(A.5)

$$\frac{{\partial \Delta D(a_{l} )^{2} }}{{\partial \Delta \beta_{\varOmega } (a_{l} )}} = 1.$$

(A.6)

From Eqs. (A.3) and (A.5–A.6), it can be obtained that $\frac{{\partial \Delta D(a_{l} )^{2} }}{{\partial \Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )}} \le \frac{{\partial \Delta D(a_{l} )^{2} }}{{\partial \Delta \beta_{\varOmega } (a_{l} )}}$, which deduces that $\Delta \beta_{\varOmega } (a_{l} )$ contributes more than $\Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )$ to the value of $\Delta D(a_{l} )$. Due to this fact, to obtain the maximum value of $\Delta D(a_{l} ),\quad \Delta \beta_{\varOmega } (a_{l} )$ is first expected to reach its maximum value, 1. There are two situations to make $\Delta \beta_{\varOmega } (a_{l} ) = 1$, which are $\left( {\beta_{\varOmega } (a_{l} ),\;\bar{\beta }_{\varOmega } (a_{l} )} \right) = (1,\;0)$ and $\left( {\beta_{\varOmega } (a_{l} ),\;\bar{\beta }_{\varOmega } (a_{l} )} \right) = (0,\;1).$ Without loss of generality, under the assumption that $\left( {\beta_{\varOmega } (a_{l} ),\;\bar{\beta }_{\varOmega } (a_{l} )} \right) = (1,\;0),\;\Delta D(a_{l} )$ is calculated as

$$\Delta D^{1} (a_{l} ) = \sqrt {\sum\limits_{n = 1}^{N - 1} {\sum\limits_{m = n + 1}^{N} {\Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )\left( {u(H_{m} ) - u(H_{n} )} \right)} + 1} } .$$

(A.7)

From Eq. (A.5), it can be known that the maximum value of $\frac{{\partial \Delta D(a_{l} )^{2} }}{{\partial \Delta \beta_{n} (a_{l} )\Delta \beta_{m} (a_{l} )}}\quad \left( {n,\;m = 1, \ldots ,N} \right)$ is $\frac{{\partial \Delta D(a_{l} )^{2} }}{{\partial \Delta \beta_{1} (a_{l} )\Delta \beta_{N} (a_{l} )}}$. According to this, $\Delta \beta_{1} (a_{l} )\Delta \beta_{N} (a_{l} )\left( {u(H_{N} ) - u(H_{1} )} \right)$ can make $\Delta D^{1} (a_{l} )$ maximum, which means that belief degrees included in $\bar{B}(a_{l} )$ should be assigned to $\bar{\beta }_{1} (a_{l} )$ and $\bar{\beta }_{N} (a_{l} )$. When $\left( {\beta_{\varOmega } (a_{l} ),\;\bar{\beta }_{\varOmega } (a_{l} )} \right) = (1,\;0)$, we have

$$\bar{\beta }_{1} (a_{l} ) + \bar{\beta }_{N} (a_{l} ) = 1\;{\text{and}}$$

(A.8)

$$\beta_{n} (a_{l} ) = 0\quad \left( {n = 1, \ldots ,N} \right),$$

(A.9)

from which $\Delta D^{1} (a_{l} )$ shown in Eq. (A.7) is transformed into

$$\Delta D^{2} (a_{l} ) = \sqrt {\bar{\beta }_{1} (a_{l} )^{2} \bar{\beta }_{N} (a_{l} )^{2} \left( {u(H_{N} ) - u(H_{1} )} \right) + 1} .$$

(A.10)

According to the inequality of arithmetic and geometric means [33], $\bar{\beta }_{n} (a_{l} )^{2} \bar{\beta }_{m} (a_{l} )^{2} \left( {u(H_{N} ) - u(H_{1} )} \right)$ reaches its maximum value if and only if

$$\bar{\beta }_{n} (a_{l} )^{2} = \bar{\beta }_{m} (a_{l} )^{2} .$$

(A.11)

Equations (A.8) and (A.11) show that $\Delta D^{2} (a_{l} )$ and $\Delta D^{1} (a_{l} )$ reach their maximum values when $\bar{\beta }_{1} (a_{l} ) = \bar{\beta }_{N} (a_{l} ) = 0.5.$

As a result, when $B\left( {a_{l} } \right) = \{ (\varOmega ,1)\}$ and $\bar{B}(a_{l} ) = \left\{ {\left( {H_{ 1} , \, 0. 5} \right), \, \left( {H_{N} , \, 0. 5} \right)} \right\}$, the maximum value of $\Delta D(a_{l} )$ is reached, which is

$$\Delta D^{ + } (a_{l} ) = \sqrt {0.5^{2} 0.5^{2} \left( {u(H_{N} ) - u(H_{1} )} \right) + 1^{2} } = \sqrt {1.0625} .$$

When $\left( {\beta_{\varOmega } (a_{l} ),\;\bar{\beta }_{\varOmega } (a_{l} )} \right) = (0,\;1)$, the same conclusion can be drawn.

As a whole, the proposition is verified.□