Topological Asymptotic Expansion for a Thermal Problem

Abstract

In this paper, we propose an approach based on the topological sensitivity notion for solving an inverse design problem. The presented procedure can be applied for finding the optimal design of cooling holes in a turbine blade. Our proposed method uses a simplified and rigorous mathematical analysis related to the unsteady state heat transfer equation. We start our analysis by establishing a preliminary estimate describing the asymptotic behavior of the heat equation solution with respect to the presence of small hole. The obtained estimate will play a crucial role in the derivation of a topological asymptotic formula valid for a large class of design functions. Based on the derived theoretical results, we build a one-iteration numerical algorithm for solving an inverse design problem. To point out the efficiency and accuracy of the proposed approach, some numerical experiments are presented.

1 Introduction

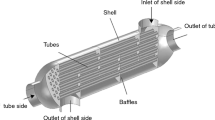
The design of turbine blade is only one of many challenges facing design engineers. To ensure the best performance of the turbine, every component and assembly should be maintained within expected temperature ranges. This process is achieved by injecting cooling air through discrete holes created in the blade, see Fig. 1.

Fig. 1

Optimal shaped turbine blade (see [1])

The design of the turbine blade can be formulated as an inverse problem in which the inner boundaries that realizes the cooling process are unknown. In this context, various approaches and techniques have been developed [1,2,3,4,5,6,7]. In this work, an approach based on the topological sensitivity analysis method is proposed to solve this design problem.

The idea of topological sensitivity analysis is to give the sensitivity of a design function with respect to the presence of a small cooling hole inside the blade. Precisely, let ${\mathcal {B}}$ be a two-dimensional cross-section of a blade containing strictly a small cooling hole ${\mathcal {C}}_{z,\varepsilon } := z + \varepsilon {\mathcal {C}}$, where $z \in {\mathcal {B}}$ is an arbitrary location, ${\mathcal {C}} \subset {\mathbb {R}}^2$ is a fixed open and bounded smooth domain containing the origin and $\varepsilon \in ]0, 1[$ is a small parameter. The topological sensitivity analysis method would provide an asymptotic expansion of the form

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )=j({\mathcal {B}})+\rho (\varepsilon ) {\mathcal {S}}(z) + o (\rho (\varepsilon )),\, \forall z \in {\mathcal {B}}, \end{aligned}$$

where $\varepsilon \mapsto \rho (\varepsilon )$ is a scalar positive function going to zero with $\varepsilon$. The function ${\mathcal {S}}$ is called the topological sensitivity function or the topological gradient.

Hence, to minimize the design function, one has to create hole at some point where the function ${\mathcal {S}}$ is negative. The presented concept has been applied for several applications: geometric control problem for fluid flow [8], identification of gas bubbles [9], optimization of injectors locations [10].

The theoretical aspect of the topological sensitivity function has been obtained for various operators: Guillaume and Idris [11] for the Laplace equation, Garreau et al. [12] for the elasticity problem, Guillaume and Idris [13] for the stokes systems, Samet et al. [14] for the Helmholtz equation and Bonnet [15] for the acoustic problem.

But, most of the contributions are limited to the steady-state case and associated with elliptic operators. In this work, we exploit this idea for solving a topological optimization in the transient regime. In this context, one can cite the existing works ([16] or [17]) which are focused on the sensitivity analysis with respect to the presence of a small inhomogeneity ${\mathcal {C}}_{z,\varepsilon }$ inside the background domain ${\mathcal {B}}$. In this particular case the perturbed solution of the considered PDE is defined in the entire domain ${\mathcal {B}}$ with a continuity condition on the inhomogeneity boundary $\partial {\mathcal {C}}_{z,\varepsilon }$. In [18], the authors established a near reversibility estimate for the non stationary wave equation. The proposed approach, making use of the Fourier transform with respect to time, is more adapted for time-reversible problems.

In this work, we generalize the topological sensitivity analysis notion for a parabolic problem. We will deal with a more singular geometric hole where the solution of the perturbed problem is defined in the modified domain ${\mathcal {B}}_{z,\varepsilon }:= {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$ with a Dirichlet condition on the inner boundary $\partial {\mathcal {C}}_{z,\varepsilon }$.

This paper concerns the calculus of the topological derivative associated to a parabolic operator. We will consider the heat equation as a model problem and we will derive a topological sensitivity analysis valid for a large class of design functions and arbitrary shaped holes. Our approach is based on a preliminary estimate describing the temperature field variation caused by the presence of a small internal cooling hole inside the blade ${\mathcal {B}}$. The obtained estimate leads to a very simplified mathematical analysis for the derivation of the topological asymptotic expansion. Besides, we will propose a one-iteration algorithm for solving the inverse design problem. Based on the topological sensitivity analysis method, the scalar function ${\mathcal {S}}$ is used for locating the unknown domains.

The plan of this article is as follows: in the next section, we present the mathematical model. In Sect. 3, we examine the influence of a small internal cooling hole on the heat transfer problem’s solution. In Sect. 4, we extend the topological sensitivity analysis notion for the parabolic case and we derive a topological asymptotic expansion valid for a large class of design functions. Particularly, we present some design functional examples and we calculate their topological sensitivity function ${\mathcal {S}}$. Section 5 is devoted to some numerical experiments.

2 Model Setting and Regularity Assumptions

Let ${\mathcal {B}}$ be a two-dimensional bounded domain with smooth ($C^\infty$) boundary $\partial {\mathcal {B}}$ representing a cross-section of a turbine blade. The physical properties of the medium ${\mathcal {B}}$ is described by a smooth scalar function $\nu$. For sake of simplicity, we assume that $\nu \in {C}^1 ({\overline{{\mathcal {B}}}})$ and that there exists two constants $\nu _{min}>0$ and $\nu _{max}>0$ such that $\nu _{min} \le \nu (x) \le \nu _{max}$. The temperature distribution ${{\varvec{u}}}_0$ inside the blade is governed by the unsteady-state heat conduction equation. The simplified mathematical model can be represented by the following system:

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}_0}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}_0) &{} =F &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}_0 &{}= g_D &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}_0 (.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}, \end{array} \right. \end{aligned}$$

(2.1)

where $\nu$ is a given positive function describing the physical properties of the material ${\mathcal {B}}$, $F \in L^2(0,T;H^1({\mathcal {B}}))$ is a given function describing the heat generated source, $g_D \in L^2(0,T;H^{1/2}(\partial {\mathcal {B}}))$ is a given boundary temperature on the outer surface of the blade and $T>0$ is the computational time.

The optimal design problem that we consider can be formulated as follows. Let j be a given design function measuring the temperature distribution inside the turbine blade in the presence of some well separated cooling holes ${\mathcal {C}} ^i,\, 1\le i\le m$.

The aim is to find the best locations and sizes of the holes ${\mathcal {C}} ^i,\, 1\le i\le m$ solution to the following optimal shape design problem:

$$\begin{aligned} ({\mathcal {P}}) \displaystyle \min _{{\mathcal {H}} \subset {\mathcal {B}}}j({\mathcal {B}}\backslash {\overline{{\mathcal {H}}}}), \end{aligned}$$

(2.2)

where $\displaystyle {\mathcal {H}} = \displaystyle \cup _{i=1}^{m}{\mathcal {C}} ^i$.

To solve this problem, we will use the topological sensitivity analysis method.

2.1 Topological Sensitivity Analysis

It consists in studying the variation of the design function j with respect to the insertion of a small cooling hole inside the initial turbine blade domain ${\mathcal {B}}$. As it is mentioned in the introduction, the cooling hole will be modeled by a small geometric perturbation of the form ${\mathcal {C}}_{z,\varepsilon } := z + \varepsilon {\mathcal {C}}$, where $z \in {\mathcal {B}}$ is an arbitrary location, $\varepsilon \in ]0, 1[$ is a small parameter describing the perturbation size and the shape is defined by an open and bounded smooth domain ${\mathcal {C}} \subset {\mathbb {R}}^2$ containing the origin. It is interesting to note that from this assumption on ${\mathcal {C}}$, one can check that there exist $r>0$ and $R>0$ such that $\overline{B(0,r)}\subset {\mathcal {C}}$ and ${\overline{{\mathcal {C}} }}\subset B(0,R)$.

Let ${{\varvec{u}}}_\varepsilon$ be the solution to the heat transfer problem in the perforated domain ${\mathcal {B}}_{z,\varepsilon }:= {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$ with a Dirichlet boundary condition on $\partial {\mathcal {C}}_{z,\varepsilon } .$ In other words, the perturbed temperature distribution ${{\varvec{u}}}_\varepsilon$ satisfies the following system

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}_\varepsilon }{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}_\varepsilon )&{} =F &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ {{\varvec{u}}}_\varepsilon &{}= g_D &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T) , \\ {{\varvec{u}}}_\varepsilon &{}= 0 &{} \text{ on } &{} \partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) ,\\ {{\varvec{u}}}_\varepsilon (.,0)&{}=0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } }. \end{array} \right. \end{aligned}$$

(2.3)

Our aim is to derive a topological sensitivity analysis for the heat transfer equation. To this end, we will derive an asymptotic formula describing the behavior of the shape function variation $j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})$ with respect to the created hole size. More precisely, we will establish an asymptotic expansion of the form

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})=\rho (\varepsilon ){\mathcal {S}}(z)+ o(\rho (\varepsilon )), \end{aligned}$$

valid for all design functions j having the form

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )=\displaystyle \int _0^{T} J_\varepsilon ( {{\varvec{u}}}_\varepsilon (.,t)) dt, \end{aligned}$$

where ${{\varvec{u}}}_\varepsilon$ is the solution to (2.3) and $J_\varepsilon$ is a design function defined on $H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )$ and satisfying the following hypothesis:

Hypothesis (H)

• For each $\varepsilon \ge 0$ such that ${\overline{{\mathcal {C}}_{z,\varepsilon } }} \subset {\mathcal {B}}$, the function $t \mapsto J_\varepsilon ({{\varvec{u}}}_\varepsilon (.,t))$ belongs to $L^1(0,T)$.

• The function $J_0$ is differentiable at ${{\varvec{u}}}_0(.,t)$ for almost every $t \in (0,T)$, its derivative is being denoted by $DJ_0({{\varvec{u}}}_0(.,t))$.

• There exist two scalar functions $\delta {\mathcal {J}} : {\mathcal {B}}\rightarrow {\mathbb {R}}$ and $\rho : {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+$ such that

  $$\begin{aligned} \int _0^{T} \big [ J_{\varepsilon }({{\varvec{u}}}_\varepsilon (.,t))- J_0({{\varvec{u}}}_0(.,t))\big ] dt= & {} \displaystyle \int _0^{T} D J_0({{\varvec{u}}}_0(.,t))({{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0) (.,t)dt \nonumber \\&+ \rho (\varepsilon ) \delta {\mathcal {J}}(z)+ o(\rho ( \varepsilon )) ,\nonumber \\&\text{ and } \lim _{\varepsilon \rightarrow 0}\rho (\varepsilon )=0. \end{aligned}$$

  (2.4)

Before starting our analysis, it is interesting to consider the following remark.

Remark 2.1

In (2.4), the function $\displaystyle \rho (\varepsilon )$ describes the asymptotic behavior of the shape function variation with respect to the geometric perturbation size $\varepsilon$. As we will show in Sect. 4, the expression of $\rho$ will be dictated by the asymptotic behavior of the perturbed solution.

The hypothesis (H) implies that the variation of the design function j reads

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})&= \int _0^T D J_0({{\varvec{u}}}_0)({{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0) dt + \rho (\varepsilon ) \delta {\mathcal {J}}(z)+ o(\rho (\varepsilon )). \end{aligned}$$

To study the integral term, we introduce the adjoint state ${{\varvec{v}}}_0$ solution to the following boundary value problem

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial {{\varvec{v}}}_0}{\partial t} - div (\nu (x) \nabla {{\varvec{v}}}_0) &{} =- D J_0({{\varvec{u}}}_0) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0&{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0(.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(2.5)

As one can observe, the adjoint state can be computed by solving a heat type equation. In fact, the solution ${{\varvec{v}}}_0$ can be defined as ${{\varvec{v}}}_0(x,t)={\widetilde{{{\varvec{v}}}_0}}(x,T-t),\,\forall (x,t)\in {\mathcal {B}}\times (0,T)$, with ${\widetilde{{{\varvec{v}}}_0}}$ is the solution to

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {\widetilde{{{\varvec{v}}}_0}} }{\partial t} - div (\nu (x) \nabla {\widetilde{{{\varvec{v}}}_0}}) &{} =- D J_0({{\varvec{u}}}_0(T-t,.)) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {\widetilde{{{\varvec{v}}}_0}} &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {\widetilde{{{\varvec{v}}}_0}} (.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

To derive the expected topological sensitivity analysis, we need to add additional regularity assumptions.

2.2 Regularity Assumptions

To enable the mathematical analysis, we introduce additional regularity assumptions, namely there exist two neighborhoods ${\mathcal {O}}_F$ and ${\mathcal {O}}_J$ of z such that

$$\begin{aligned} F \in L^2(0,T;H^4({\mathcal {O}}_F))&\cap&H^2(0,T; L^2 ({\mathcal {O}}_F)), \end{aligned}$$

(2.6)

$$\begin{aligned} DJ_0(u_0) \in L^2(0,T;H^4({\mathcal {O}}_J))&\cap&H^2(0,T; L^2 ({\mathcal {O}}_J)). \end{aligned}$$

(2.7)

The assumption (2.7) will be checked for the considered cost functional examples. The condition (2.6) will be assumed throughout the rest of this paper. It leads to the following regularity results for the direct and adjoint problem solutions.

Proposition 2.2

Under the assumptions (2.6) and (2.7), the solutions of the direct and adjoint problems satisfy the regularity result: for all subdomain ${\widetilde{{\mathcal {O}}}}$ containing z, such that

$$\begin{aligned} {\widetilde{{\mathcal {O}}}} \subset \subset {\mathcal {O}}_F \cap {\mathcal {O}}_J, \end{aligned}$$

we have

$$\begin{aligned} {{\varvec{u}}}_0,{{\varvec{v}}}_0\in L^2(0,T,H^6( {\widetilde{{\mathcal {O}}}} ) ) \cap H^3(0,T,L^2( {\widetilde{{\mathcal {O}}}}) ). \end{aligned}$$

(2.8)

As a consequence of Proposition 2.2, it is interesting to make the following remark.

Remark 2.3

Assuming that the conditions (2.6) and (2.7) hold. By interpolation, one can deduce that

$$\begin{aligned} {{\varvec{u}}}_0,{{\varvec{v}}}_0\in H^1(0,T,H^4( {\widetilde{{\mathcal {O}}}}) ). \end{aligned}$$

For more details, one can consult Lions and Magenes [19, Chap. 4, Prop. 2.3].

The presented regularity result in Proposition 2.2 follows straightforwardly from the following Lemma.

Lemma 2.4

Let ${\widetilde{{\mathcal {O}}}} \subset \subset {\mathcal {B}}$, k be a positive integer, $f \in L^2(0,T,H^{-1}({\mathcal {B}})) \, \cap L^2(0,T,H^k({\widetilde{{\mathcal {O}}}})) \cap \, H^{k/2}(0,T,L^2({\widetilde{{\mathcal {O}}}})),$ $g \in L^2(0,T,H^{1/2} (\partial {\mathcal {B}}))$ and $\theta$ be the solution of the system

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial \theta }{\partial t} - div( \nu \nabla \theta ) &{} = f &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \theta &{} = g &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ \theta (.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}. \end{array} \right. \end{aligned}$$

(2.9)

Then for all subdomain ${\mathcal {O}}_k \subset \subset {\widetilde{{\mathcal {O}}}}$, we have

$$\begin{aligned} \theta \in L^2(0,T,H^{k+2} ({\mathcal {O}}_k) ) \cap H^{k/2+1}(0,T,L^2 ({\mathcal {O}}_k) ) . \end{aligned}$$

(2.10)

The same result holds if we replace the Dirichlet boundary condition on $\partial {\mathcal {B}}$ by a Neumann condition of the form $\nabla \theta . n =g$, with $g\in L^2(0,T,H^{-1/2} (\partial {\mathcal {B}}))$.

Proof

The difficulty comes from the fact that the so-called compatibility conditions required to apply the standard parabolic regularity theorems are not satisfied here. We will construct auxiliary functions for which those conditions hold. Our analysis is based on the following steps:

• Step 1: Let ${\mathcal {O}}_0$ be a domain such that ${\mathcal {O}}_k \subset \subset {\mathcal {O}}_0 \subset \subset {\widetilde{{\mathcal {O}}}}$. Let $\eta _0$ be a smooth function defined in ${\mathcal {B}}$ and satisfying

  $$\begin{aligned} \eta _0=\left\{ \begin{array}{r l l l} 0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\widetilde{{\mathcal {O}}}}} , \\ 1 &{} \text{ in } &{} {\mathcal {O}}_0 . \\ \end{array} \right. \end{aligned}$$

  (2.11)

  We introduce the function $\theta _0 = \eta _0 \theta$. One can easily check that $\theta _0$ is solution to

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{ \partial \theta _0 }{\partial t} - div( \nu \nabla \theta _0 ) &{} = f_0 &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \theta _0 &{} = 0 &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T), \\ \theta _0(.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}. \end{array} \right. \end{aligned}$$

  (2.12)

  with

  $$\begin{aligned} f_0=\eta _0 f -2 \nu \nabla \eta _0 \nabla \theta - \nu \theta \Delta \eta _0. \end{aligned}$$

  Since $\nu$ and $\eta _0$ are smooth in ${\mathcal {B}}$, from the fact that $\theta \in L^2(0, T ;H^1({\mathcal {B}}))$, we deduce that $f_0 \in L^2(0, T ;L^2({\mathcal {B}}))$. Then using [19, Chap. 4, Theorem 1.1], one can derive that $\theta _0 \in L^2(0,T,H^2({\mathcal {B}}) ) \cap H^1(0,T,L^2({\mathcal {B}}))$. Consequently

  $$\begin{aligned} \theta \in L^2(0,T,H^2({\mathcal {O}}_0)) \cap H^1(0,T,L^2({\mathcal {O}}_0)). \end{aligned}$$

• Step 2: Assume that, given an integer $p \in \{ 0, ..., k-1\}$, there exists a domain ${\mathcal {O}}_p$ satisfying ${\mathcal {O}}_k \subset \subset {\mathcal {O}}_p \subset \subset {\widetilde{{\mathcal {O}}}}$ such that

  $$\begin{aligned} \theta \in L^2(0,T,H^{p+2}({\mathcal {O}}_p)) \cap H^{p/2+1}(0,T,L^2({\mathcal {O}}_p)) . \end{aligned}$$

  (2.13)

  If $p+1< k$, we define a domain ${\mathcal {O}}_{p+1}$ such that ${\mathcal {O}}_k \subset \subset {\mathcal {O}}_{p+1} \subset \subset {\mathcal {O}}_p$. We consider a smooth function $\eta _{p+1}$ verifying

  $$\begin{aligned} \eta _{p+1}=\left\{ \begin{array}{r l l l} 0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {O}}_p} , \\ 1 &{} \text{ in } &{} {\mathcal {O}}_{p+1} . \\ \end{array} \right. \end{aligned}$$

  (2.14)

  and we define the function

  $$\begin{aligned} \theta _{p+1} =\eta _{p+1} \theta . \end{aligned}$$

  It solves

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{ \partial \theta _{p+1} }{\partial t} - div( \nu \nabla \theta _{p+1} ) &{} = f_{p+1} &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \theta _{p+1} &{} = 0 &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T), \\ \theta _{p+1}(.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}. \end{array} \right. \end{aligned}$$

  (2.15)

  with

  $$\begin{aligned} f_{p+1}=\eta _{p+1} f -2 \nu \nabla \eta _{p+1} \nabla \theta - \nu \theta \Delta \eta _{p+1}. \end{aligned}$$

  Thanks to [19, Chap. 4, Proposition 2.3], one can obtain that $f_{p+1} \in L^2(0,T,H^{p+1} ({\mathcal {O}}_p)) \cap H^{(p+1)/2}(0,T, L^2({\mathcal {O}}_p)) .$ Making use of [19, Chap. 4, Theorem 5.3], it follows that

  $$\begin{aligned} \theta _{p+1} \in L^2(0,T,H^{p+3} ({\mathcal {O}}_p)) \cap H^{(p+3)/2}(0,T, L^2({\mathcal {O}}_p)). \end{aligned}$$

  Then, we have

  $$\begin{aligned} \theta \in L^2(0,T,H^{p+3}( {\mathcal {O}}_{p+1})) \cap H^{(p+3)/2} (0,T,L^2({\mathcal {O}}_{p+1})). \end{aligned}$$

  Hence the relation (2.13) holds true at rank $p+1$. The relation (2.10) is obtained by repeating this procedure up to the rank $p+1=k$. $\square$

3 Estimate of the Perturbed Solution

In this section, we will study the influence of the presence of a small cooling hole ${\mathcal {C}}_{z,\varepsilon }$ on the temperature distribution. To this end, we will derive the asymptotic behavior of the variation $\xi _\varepsilon := {{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0$ with respect to the hole size $\varepsilon$.

From (2.1) and (2.3) one can easily check that $\xi _\varepsilon$ is solution to

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial \xi _\varepsilon }{\partial t} - div( \nu (x) \nabla \xi _\varepsilon )&{} =0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ \xi _\varepsilon &{}= 0 &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T) , \\ \xi _\varepsilon &{}= -{{\varvec{u}}}_0&{} \text{ on } &{} \partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) ,\\ \xi _\varepsilon (.,0)&{}=0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } }. \end{array} \right. \end{aligned}$$

(3.1)

Next, we will prove that the leading term of the variation ${{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0$ is defined as

$$\begin{aligned} \mathbf{U }(x,t)= 2 \pi {{\varvec{u}}}_0 (z,t) \Gamma (x-z), \, \forall (x,t) \in {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T), \end{aligned}$$

(3.2)

where $\Gamma$ is the fundamental solution of the Laplace operator in ${\mathbb {R}}^2$

$$\begin{aligned} \Gamma (y)=\frac{-1}{2 \pi } \log |y| ,\forall y \in {\mathbb {R}}^2. \end{aligned}$$

To establish this result, we need some preliminary results.

3.1 Preliminary Lemmas

Here, we present two preliminary estimates. The first one is described by Lemma 3.1 and gives an energy estimate for the non-stationary heat problem. For similar results, one can consult Theorem 8.2.3 in [20, p. 237] or Proposition 7.9 in [21, p. 235] or [22, p. 27]. The second one is concerned with an estimate of the perturbed solution of the stationary heat equation, one can see [23] for similar result.

Lemma 3.1

Consider $F \in L^2(0,T;H^1({\mathcal {B}}))$, $p \in ]1,+\infty [$ and let ${{\varvec{u}}}\in H^1(0,T;H^1({\mathcal {B}}))$ be the solution of the following parabolic problem

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}}{\partial t} - div( \nu (x) \nabla {{\varvec{u}}}) &{} =F &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ {{\varvec{u}}}&{} = 0 &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T), \\ {{\varvec{u}}}(.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}. \end{array} \right. \end{aligned}$$

There exists a constant $c>0$ such that

$$\begin{aligned} \Arrowvert {{\varvec{u}}}\Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert {{\varvec{u}}}\Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}&\le c \Arrowvert F \Arrowvert _{L^2(0,T;L^{p}( {\mathcal {B}}))} , \end{aligned}$$

Proof

Using the weak formulation associated to the previous system, we get

$$\begin{aligned} \int _{{\mathcal {B}}} \displaystyle \frac{\partial {{\varvec{u}}}}{\partial t}(x,t) {{\varvec{u}}}(x,t) dx +\int _{{\mathcal {B}}} \nu (x) | \nabla {{\varvec{u}}}(x,t)|^2 dx&= \int _{{\mathcal {B}}} F(x,t) {{\varvec{u}}}(x,t) dx. \end{aligned}$$

Let $t_0 \in [0,T]$. Using the fact that $\displaystyle \frac{\partial {{\varvec{u}}}}{\partial t}(x,t) {{\varvec{u}}}(x,t)= \frac{1}{2} \frac{d}{dt}({{\varvec{u}}}(x,t))^2 ,$ and $\,{{\varvec{u}}}(.,0) = 0 \text{ in } {\mathcal {B}},$ one can obtain

$$\begin{aligned} \frac{1}{2} \int _{{\mathcal {B}}} |{{\varvec{u}}}(.,t_0)|^2 dx + \int _0^{t_0} \int _{{\mathcal {B}}} \nu (x) | \nabla {{\varvec{u}}}(x,t)|^2 dx dt&= \int _0^{t_0} \int _{{\mathcal {B}}} F(x,t) {{\varvec{u}}}(x,t) dx dt \nonumber \\&\le \int _0^{T} \int _{{\mathcal {B}}} | F(x,t) {{\varvec{u}}}(x,t) | dx dt. \end{aligned}$$

(3.3)

Let $q\in {\mathbb {N}}^*$ be such that $\frac{1}{p}+\frac{1}{q} =1$. Using Cauchy Schwarz inequality, one can derive

$$\begin{aligned} \int _0^{T}\int _{{\mathcal {B}}} | F(x,t) {{\varvec{u}}}(x,t) | dx dt&\le || F ||_{L^2(0,T;L^p({\mathcal {B}}))} || {{\varvec{u}}}||_{L^2(0,T;L^q({\mathcal {B}}))}. \end{aligned}$$

Since $p\in ]1, + \infty [$, we have $q \in ]1, + \infty [$, which implies that $H^1({\mathcal {B}}) \hookrightarrow L^q({\mathcal {B}}).$ Then, there exits a constant $c_1>0$ independent of $\varepsilon$ such that

$$\begin{aligned}&\frac{1}{2} \int _{{\mathcal {B}}} |{{\varvec{u}}}(.,t_0)|^2 dx + \int _0^{t_0} \int _{{\mathcal {B}}} \nu (x) | \nabla {{\varvec{u}}}(x,t)|^2 dx dt \nonumber \\&\quad \le c_1 || F ||_{L^2(0,T;L^p({\mathcal {B}}))} || {{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))} \end{aligned}$$

(3.4)

• Estimate of $|| {{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))}$: Choosing $t_0=T$ in (3.4), we get

  $$\begin{aligned} \nu _{min} || \nabla {{\varvec{u}}}||^2_{L^2(0,T;L^2({\mathcal {B}}))}&\le c_1 || F ||_{L^2(0,T;L^p({\mathcal {B}}))} || {{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))}. \end{aligned}$$

  (3.5)

  Similarly, for each $t_0\in [0,\,T]$ we have

  $$\begin{aligned} \int _{{\mathcal {B}}} | {{\varvec{u}}}(.,t_0)|^2 dx&\le 2 c_1 || F ||_{L^2(0,T;L^p({\mathcal {B}}))} || {{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))}. \end{aligned}$$

  (3.6)

  Integrating between 0 and T, we get

  $$\begin{aligned} ||{{\varvec{u}}}||^2_{L^2(0,T;L^2({\mathcal {B}}))}&\le 2 T c_1 \, || F ||_{L^2(0,T;L^p({\mathcal {B}}))} || {{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))}. \end{aligned}$$

  (3.7)

  Then, combining (3.7) and (3.5), it follows that there exists $c_2>0$ such that

  $$\begin{aligned} ||{{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))}&\le c_2 \, || F ||_{L^2(0,T;L^p({\mathcal {B}}))} . \end{aligned}$$

  (3.8)

  Here, one can choose $c_2=(\frac{1}{\nu _{min}}+2T)\, c_1.$

• Estimate of $||{{\varvec{u}}}||_{L^\infty (0,T;L^2({\mathcal {B}}))}$: Now, we examine the term $||{{\varvec{u}}}||_{L^\infty (0,T;L^2({\mathcal {B}}))}$. Based on the estimates (3.6) and (3.8), we get

  $$\begin{aligned} \int _{{\mathcal {B}}} |{{\varvec{u}}}(.,t_0)|^2 dx&\le 2 c_1 c_2 || F ||^2_{L^2(0,T;L^p({\mathcal {B}}))} ,\, \forall t_0 \in [0,T]. \end{aligned}$$

  Then, we have

  $$\begin{aligned} ||{{\varvec{u}}}(.,t_0)||_{L^2({\mathcal {B}})}&\le 2 c_1 \sqrt{T+\frac{1}{2 \nu _{min}}} || F ||_{L^2(0,T;L^p({\mathcal {B}}))} ,\, \forall t_0 \in [0,T]. \end{aligned}$$

  Consequently, there exists a constant $c_3>0$ such that

  $$\begin{aligned} ||{{\varvec{u}}}||_{L^\infty (0,T;L^2({\mathcal {B}}))}&\le c_3 || F ||_{L^2(0,T;L^p({\mathcal {B}}))} . \end{aligned}$$

  (3.9)

• The desired estimate: Finally, using (3.8) and (3.9), one can deduce that there exists a constant $c=max(c_2,c_3)$ such that

  $$\begin{aligned} ||{{\varvec{u}}}||_{L^\infty (0,T;L^2({\mathcal {B}}))} +||{{\varvec{u}}}||_{L^2(0,T;H^1({\mathcal {B}}))} \le c || F ||_{L^2(0,T;L^p({\mathcal {B}}))}. \end{aligned}$$

  (3.10)

$\square$

Lemma 3.2

Consider two functions $\varphi _1 \in H^{1/2}(\partial {\mathcal {B}})$, $\varphi _2 \in H^{1/2}(\partial {\mathcal {C}}_{z,\varepsilon } )$ and let ${{\varvec{u}}}\in H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )$ be the solution of the following system

$$\begin{aligned} \left\{ \begin{array}{r l l l} - div( \nu (x) \nabla {{\varvec{u}}}) &{} =0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } , \\ {{\varvec{u}}}&{} = \varphi _1 &{} \text{ on } &{} \partial {\mathcal {B}}, \\ {{\varvec{u}}}&{} = \varphi _2 &{} \text{ on } &{} \partial {\mathcal {C}}_{z,\varepsilon } . \end{array} \right. \end{aligned}$$

Then, there exists a constant $c>0$, independent of $\varepsilon$, such that

$$\begin{aligned} \Arrowvert {{\varvec{u}}}\Arrowvert _{H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}&\le c \Big ( \Arrowvert \varphi _1 \Arrowvert _{H^{1/2}( \partial {\mathcal {B}}))} + \frac{1}{\sqrt{|\log \varepsilon }|} \Arrowvert \varphi _2 (z+\varepsilon x) \Arrowvert _{H^{1/2}( \partial {\mathcal {C}} ))} \Big ) . \end{aligned}$$

(3.11)

Proof

This estimate has been proven in [23] for the case $\nu (x)=1$. Using the fact that $\nu \in {C} ( {\overline{{\mathcal {B}}}})$, one can adapt the same techniques and prove the same results. $\square$

3.2 Estimates of the Fundamental Solution

In this paragraph, we present some estimate related to the fundamental solution $\Gamma$ (see (3.2)) of the Laplace operator.

Lemma 3.3

The fundamental solution of the Laplace operator $\Gamma$ admits the following estimates

$$\begin{aligned} \Arrowvert \Gamma (x) \Arrowvert _{H^{1/2}( \partial {\mathcal {C}} ) }&\le c, \end{aligned}$$

(3.12)

$$\begin{aligned} \Arrowvert \Gamma (x-z) \Arrowvert _{H^{1/2}( \partial {\mathcal {B}}) }&\le c , \end{aligned}$$

(3.13)

$$\begin{aligned} \Arrowvert \Gamma (x-z)\Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}&\le c , \end{aligned}$$

(3.14)

$$\begin{aligned} \Arrowvert \nabla \Gamma (x-z)\Arrowvert _{L^p( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}&\le c ,\, \forall p \in ]1,2[ , \end{aligned}$$

(3.15)

$$\begin{aligned} \Arrowvert \nabla \Gamma (x-z)\Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}&\le c \sqrt{| \log \varepsilon |} . \end{aligned}$$

(3.16)

Proof

Next, we will prove the estimates (3.12)–(3.16) successively.

• The estimates (3.12) follows from the fact that ${\mathcal {C}}$ is an open domain containing the origin. Let $r_1>0$ such that the $\overline{\mathbf{B }(0,r_1) }\subset {\mathcal {C}}$. Then, the function $y\mapsto \Gamma (y)$ belongs to ${C}^\infty (\overline{ {\mathcal {C}} _{r_1}} )$ where ${\mathcal {C}} _{r_1} := {\mathcal {C}} \backslash \overline{\mathbf{B }(0,r_1) }$. One can deduce

  $$\begin{aligned} \Arrowvert \Gamma \Arrowvert _{H^{1/2}( \partial {\mathcal {C}} ) }&:= \inf \{ || \upsilon ||_{H^1( {\mathcal {C}} _{r_1})} , \, \upsilon =\Gamma \text{ on } \partial {\mathcal {C}} \} \\&\le \Arrowvert \Gamma \Arrowvert _{L^2( {\mathcal {C}} _{r_1})} + \Arrowvert \nabla \Gamma \Arrowvert _{L^2( {\mathcal {C}} _{r_1}) } =O(1). \end{aligned}$$

• Let $r_2>0$ such that $\overline{\mathbf{B }(z,r_2)} \subset {\mathcal {B}}$. Since $z \notin \mathbf{B }_{r_2}:= {\mathcal {B}}\backslash \overline{\mathbf{B }(z,{r_2})}$, the function $x \mapsto \Gamma (x-z)$ belongs to ${C}^\infty ( \overline{\mathbf{B }_{r_2}} )$ and the term $\Arrowvert \Gamma (x-z) \Arrowvert _{H^{1/2}( \partial {\mathcal {B}})}$ is uniformly bounded, i.e. there exists $c>0$ such that

  $$\begin{aligned} \Arrowvert \Gamma (x-z) \Arrowvert _{H^{1/2}( \partial {\mathcal {B}})} \le c. \end{aligned}$$

• To estimate the term $|| \Gamma (x-z) ||_{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}$, we use the fact that the domain ${\mathcal {B}}$ is bounded in such a way that there exists $R>0$ such that ${\overline{{\mathcal {B}}}} \subset \mathbf{B }(z, R), \, \forall z \in {\mathcal {B}}.$

  Then, we have

  $$\begin{aligned} {\mathcal {B}}\backslash {\overline{{\mathcal {C}}_{z,\varepsilon } }}-z:= & {} \{ x-z, \, x \in {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \} \subset \mathbf{C }(0,r_1 \varepsilon , R) \nonumber \\:= & {} \{ y \in {\mathbb {R}}^2 ,\, r_1 \varepsilon< |y| < R \}. \end{aligned}$$

  (3.17)

  From the fact that $\overline{\mathbf{C }(0,r_1 \varepsilon , R)}\subset {\mathbb {R}}^2 \backslash \{0\},$ it follows that the function $x \mapsto \Gamma (x-z)$ is smooth in $\mathbf{C }(0,r_1 \varepsilon , R)$. Using the polar coordinates, one can deduce that

  $$\begin{aligned} \Arrowvert \Gamma (x-z)\Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}&\le \frac{1}{\sqrt{2\pi }} \Big ( \int _{r_1 \varepsilon }^R r (\log r)^2 dr \Big )^{ \frac{1}{2} }. \end{aligned}$$

  Using the fact that the function $r \mapsto r \, (\log r)^2$ is integrable near the origin, one can deduce that there exists a positive constant $c>0$, independent of $\varepsilon$, such that

  $$\begin{aligned} \Arrowvert \Gamma (x-z)\Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}&\le c. \end{aligned}$$

• To justify the estimates (3.15) and (3.16), we deal with an explicit calculus. Using (3.17), one can derive for all $p \in ]1,2]$ that

  $$\begin{aligned} \Arrowvert \nabla \Gamma (x-z)\Arrowvert _{L^p( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}\le & {} \Arrowvert \nabla \Gamma (x)\Arrowvert _{L^p(\mathbf{C }(0,r_1 \varepsilon , R))}\nonumber \\= & {} \Big ( \frac{1}{(2 \pi )^p } \int _{\mathbf{C }(0,r_1 \varepsilon , R)} \Big | \frac{1}{x} \big |^p dx \Big )^{1/p} \nonumber \\= & {} \Big ( (2 \pi )^{1-p} \int _{r_1\varepsilon }^R r^{1-p} dr \Big )^{1/p} . \end{aligned}$$

  (3.18)

  Consequently, if $p \in ]1,2[$ and $\varepsilon >0$ sufficiently small we have

  $$\begin{aligned} \Arrowvert \nabla \Gamma (x-z)\Arrowvert _{L^p( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}\le \Big ( \frac{(2 \pi )^{1-p}}{2-p} [ R^{2-p} - (r_1 \varepsilon )^{2-p}]\Big )^{1/p}=O(1). \end{aligned}$$

  In the particular case when $p=2$, the norm $\Arrowvert \nabla \Gamma (x-z)\Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}$ admits the following behavior

  $$\begin{aligned} \Arrowvert \nabla \Gamma (x-z)\Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}\le \frac{1}{\sqrt{2 \pi }} \Big ( \log (R)-\log (r_1 \varepsilon ) \Big )^{1/2} =O\big ( \sqrt{| \log \varepsilon | } \big ). \end{aligned}$$

$\square$

3.3 The Asymptotic Behavior of the Perturbed Solution

The asymptotic behavior of the perturbed solution ${{\varvec{u}}}_\varepsilon$ with respect to $\varepsilon$ is given by the following proposition.

Proposition 3.4

Let ${\mathcal {C}}_{z,\varepsilon }$ be a small internal cooling hole created inside the domain ${\mathcal {B}}$, with a Dirichlet boundary condition on $\partial {\mathcal {C}}_{z,\varepsilon }$. Then, there exists a constant $c>0$, independent of $\varepsilon$, such that the perturbed temperature field satisfies the following estimate

$$\begin{aligned}&\Arrowvert {{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }\Arrowvert _{L^{\infty }(0,T;L^2({\mathcal {B}}\backslash {\overline{{\mathcal {C}}_{z,\varepsilon } }}))} + \Arrowvert {{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0 \\&\quad - \frac{1}{ \log \varepsilon } \mathbf{U }\Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} \le \frac{ c}{|\log \varepsilon | } , \end{aligned}$$

for small $\varepsilon >0$.

Proof

To estimate the quantity ${{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }$, we introduce the following function

$$\begin{aligned} w_{\varepsilon } = {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }. \end{aligned}$$

Using (3.1) and (3.2), one can easily check that $w_{\varepsilon }$ is solution to the following system

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial w_{\varepsilon } }{\partial t} - div( \nu \nabla w_{\varepsilon } ) &{} = - \frac{2 \pi }{\log \varepsilon } \big [ \displaystyle \frac{\partial {{\varvec{u}}}_0 }{\partial t}(z,t) \Gamma (x-z) + {{\varvec{u}}}_0 (z,t) \nabla \nu . \nabla \Gamma (x-z) \big ] &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ w_{\varepsilon } &{} = - \frac{2 \pi }{\log \varepsilon } \displaystyle {{\varvec{u}}}_0 (z,t) \Gamma (x-z) &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ w_{\varepsilon } &{} = -{{\varvec{u}}}_0 (x,t) - \frac{2 \pi }{\log \varepsilon } \displaystyle {{\varvec{u}}}_0 (z,t) \Gamma (x-z) &{} \text{ on } &{}\partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) ,\\ w_{\varepsilon } (.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } . \end{array} \right. \nonumber \\ \end{aligned}$$

(3.19)

From the fact that $\Gamma (x-z)= \Gamma ((x-z) / \varepsilon )-\frac{1}{2 \pi } \log \varepsilon$, the boundary condition on $\partial {\mathcal {C}}_{z,\varepsilon }$ can be rewritten as

$$\begin{aligned} w_{\varepsilon } (x,t) = -{{\varvec{u}}}_0 (x,t)+{{\varvec{u}}}_0 (z,t) - \frac{2 \pi }{\log \varepsilon } \Gamma ((x-z)/\varepsilon ) \displaystyle {{\varvec{u}}}_0 (z,t) , \, \forall (x,t) \in \partial {\mathcal {C}}_{z,\varepsilon } \times (0,T). \end{aligned}$$

Our aim is to prove that there exists a constant $c>0$, independent of $\varepsilon$, such that

$$\begin{aligned} || w_{\varepsilon } ||_{L^\infty (0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}+ || w_{\varepsilon } ||_{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}\le \frac{ c}{ | \log \varepsilon | }. \end{aligned}$$

(3.20)

To this end, we will introduce four functions $w^{1}_{\varepsilon }$, $w^{2}_{\varepsilon }$, $w^{3}_{\varepsilon }$ and $w^{4}_{\varepsilon }$ in such a manner that we get the decomposition $w_{\varepsilon } := w^{1}_{\varepsilon }+w^{2}_{\varepsilon }+w^{3}_{\varepsilon }+w^{4}_{\varepsilon }$. We will define and estimate the terms $w^{1}_{\varepsilon }$, $w^{2}_{\varepsilon }$, $w^{3}_{\varepsilon }$ and $w^{4}_{\varepsilon }$ separately.

• The first term $w^{1}_{\varepsilon }$: The first term ${ w}^{1}_{\varepsilon }$ is chosen as the solution to the following system

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial w^{1}_{\varepsilon } }{\partial t} - div( \nu (x) \nabla w^{1}_{\varepsilon }) &{} =0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ w^{1}_{\varepsilon } &{} = 0 &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ w^{1}_{\varepsilon }&{} = -{{\varvec{u}}}_0 (x,t) + {{\varvec{u}}}_0 (z,t) &{} \text{ on } &{}\partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) ,\\ w^{1}_{\varepsilon } (.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } . \end{array} \right. \end{aligned}$$

  (3.21)

  Let $\widetilde{{ w}^{1}_{\varepsilon }}$ be an extension of $w^{1}_{\varepsilon }$ in ${\mathcal {B}}$, defined by

  $$\begin{aligned} \widetilde{{ w}^{1}_{\varepsilon }}(x,t)= \left\{ \begin{array}{r l l l} &{} w^{1}_{\varepsilon }(x,t) &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ &{}-{{\varvec{u}}}_0 (x,t) + {{\varvec{u}}}_0 (z,t) &{} \text{ in } &{} {\mathcal {C}}_{z,\varepsilon } \times (0,T) .\\ \end{array} \right. \end{aligned}$$

  (3.22)

  One can remark that $\widetilde{{ w}^{1}_{\varepsilon }}$ is constructed using a continuity boundary condition on $\partial {\mathcal {C}}_{z,\varepsilon } .$ From the smoothness of ${ w}^{1}_{\varepsilon }$ and ${{\varvec{u}}}_0$, it follows that $\widetilde{{ w}^{1}_{\varepsilon }} \in H^1(0,T;H^1({\mathcal {B}}))$ and satisfies the following system

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial \widetilde{{ w}^{1}_{\varepsilon }} }{\partial t} - div( \nu (x) \nabla \widetilde{{ w}^{1}_{\varepsilon }}) &{} =F_\varepsilon ^1 &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \widetilde{{ w}^{1}_{\varepsilon }}&{} = 0 &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ \widetilde{{ w}^{1}_{\varepsilon }}(.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}, \end{array} \right. \end{aligned}$$

  (3.23)

  with $F_\varepsilon ^1(x,t)= \Big [ F(x,t)- \frac{\partial {{\varvec{u}}}_0 (z,t)}{\partial t} \Big ] \chi _{{\mathcal {C}}_{z,\varepsilon } }(x)$, where $\chi _{{\mathcal {C}}_{z,\varepsilon } }$ is the characteristic function of the domain ${\mathcal {C}}_{z,\varepsilon }$. Using Lemma 3.1, we derive that there exists a constant $c>0$, independent of $\varepsilon$, such that

  $$\begin{aligned} \Arrowvert \widetilde{{ w}^{1}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{1}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}&\le c \, \Arrowvert F_\varepsilon ^1 \Arrowvert _{L^2(0,T;L^{2}( {\mathcal {B}}))} . \end{aligned}$$

  Using the smoothness of ${{\varvec{u}}}_0$ and the Cauchy Schwarz inequality, the term $F_\varepsilon ^1$ can be estimated as

  $$\begin{aligned} \Arrowvert F_\varepsilon ^1 \Arrowvert _{L^2(0,T;L^{2}( {\mathcal {B}}))}&\le | {\mathcal {C}}_{z,\varepsilon } |^{1/4} || F(x,t) ||_{L^{2}(0,T;L^4({\mathcal {B}}))} +| {\mathcal {C}}_{z,\varepsilon } |^{1/2} || \frac{\partial {{\varvec{u}}}_0 (z,t)}{\partial t} ||_{L^{2}(0,T )} , \end{aligned}$$

  where $| {\mathcal {C}}_{z,\varepsilon } |= |{\mathcal {C}} |\varepsilon ^2$ denotes the Lebesgue measure of ${\mathcal {C}}_{z,\varepsilon }$. Then, we get

  $$\begin{aligned} \Arrowvert \widetilde{{ w}^{1}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{1}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}&=o \big (\frac{1}{|\log \varepsilon |} \big ) . \end{aligned}$$

  Since $\widetilde{{ w}^{1}_{\varepsilon }} = { w}^{1}_{\varepsilon }$ in ${\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$, one can deduce that

  $$\begin{aligned} \Arrowvert { w}^{1}_{\varepsilon } \Arrowvert _{L^\infty (0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} + \Arrowvert { w}^{1}_{\varepsilon } \Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}&= o \big (\frac{1}{|\log \varepsilon |} \big ). \end{aligned}$$

  (3.24)

• The second term $w^{2}_{\varepsilon }$: The term $w^{2}_{\varepsilon }$ is constructed as

  $$\begin{aligned} w^{2}_{\varepsilon }(x,t)=- \frac{2 \pi }{\log \varepsilon } T_\varepsilon (x) {{\varvec{u}}}_0(z,t) , \, \forall (x,t) \in {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times ]0,T[, \end{aligned}$$

  (3.25)

  where the function $T_\varepsilon$ is defined as the solution of the following Laplace problem

  $$\begin{aligned} \left\{ \begin{array}{r l l l} - div( \nu (x) \nabla T_{\varepsilon }) &{} =0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } , \\ T_{\varepsilon } &{} = \Gamma (x-z) &{} \text{ on } &{}\partial {\mathcal {B}}, \\ T_{\varepsilon } &{} = \Gamma ((x-z)/\varepsilon ) &{} \text{ on } &{}\partial {\mathcal {C}}_{z,\varepsilon } . \\ \end{array} \right. \end{aligned}$$

  (3.26)

  Using Lemma 3.2, one can deduce that there exists a constant $c>0$, independent of $\varepsilon$, such that

  $$\begin{aligned} \Arrowvert T_\varepsilon \Arrowvert _{ H^{ 1}( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) } \le c \Big ( \Arrowvert \Gamma (x-z) \Arrowvert _{H^{ 1/2}(\partial {\mathcal {B}}) } + \frac{1}{\sqrt{|\log \varepsilon |}} \Arrowvert \Gamma (x) \Arrowvert _{H^{ 1/2}(\partial {\mathcal {C}} ) } \Big ) .\nonumber \\ \end{aligned}$$

  (3.27)

  Using (3.25), one can derive

  $$\begin{aligned}&\Arrowvert { w}^{2}_{\varepsilon } \Arrowvert _{L^\infty (0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} + \Arrowvert { w}^{2}_{\varepsilon } \Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} \\&\quad \le \frac{c}{|\log \varepsilon | } || {{\varvec{u}}}_0(z,t)||_{L^2(0,T) } \\&\qquad \Big [ \frac{1}{\sqrt{|\log \varepsilon |}} \Arrowvert \Gamma (y) \Arrowvert _{H^{ 1/2}(\partial {\mathcal {C}} ) } + \Arrowvert \Gamma (x-z) \Arrowvert _{H^{ 1/2}(\partial {\mathcal {B}}) } \Big ] . \end{aligned}$$

  Using Lemma 3.3, one can deduce that there exists $c>0$ such that

  $$\begin{aligned} \Arrowvert w^{2}_{\varepsilon } \Arrowvert _{L^\infty (0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} + \Arrowvert w^{2}_{\varepsilon } \Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} \le \frac{c }{| \log \varepsilon | }. \end{aligned}$$

  (3.28)

• The third term $w^{3}_{\varepsilon }$: We define the function $w^{3}_{\varepsilon }$ as the solution to the following system

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial w^{3}_{\varepsilon } }{\partial t} - div( \nu \nabla w^{3}_{\varepsilon }) &{} = \frac{-2 \pi }{\log \varepsilon } {{\varvec{u}}}_0 (z,t) \nabla \nu (x) .\nabla \Gamma (x-z) &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ w^{3}_{\varepsilon } &{} = 0 &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ w^{3}_{\varepsilon }&{} = 0 &{} \text{ on } &{}\partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) ,\\ w^{3}_{\varepsilon } (.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } . \end{array} \right. \nonumber \\ \end{aligned}$$

  (3.29)

  Let $\widetilde{{ w}^{3}_{\varepsilon }}$ be the extension by zero of $w^{3}_{\varepsilon }$ on ${\mathcal {C}}_{z,\varepsilon }$ i.e.

  $$\begin{aligned} \widetilde{{ w}^{3}_{\varepsilon }} =\left\{ \begin{array}{r l l l} w^{3}_{\varepsilon } &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times ]0,T[ , \\ 0 &{} \text{ in } &{} {\mathcal {C}}_{z,\varepsilon } \times ]0,T[ . \end{array} \right. \end{aligned}$$

  (3.30)

  Using the continuity condition $w^{3}_{\varepsilon }=0$ on $\partial {\mathcal {C}}_{z,\varepsilon } \times ]0,T[$, the function $\widetilde{{ w}^{3}_{\varepsilon }}$ belongs to $H^1(0,T;H^1({\mathcal {B}}))$ and satisfies the system

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial \widetilde{{ w}^{3}_{\varepsilon }} }{\partial t} - div( \nu (x) \nabla \widetilde{{ w}^{3}_{\varepsilon }} ) &{} = F^3_\varepsilon (x,t) &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \widetilde{{ w}^{3}_{\varepsilon }} &{} = 0 &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ \widetilde{{ w}^{3}_{\varepsilon }} (.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}, \end{array} \right. \end{aligned}$$

  (3.31)

  with $F^3_\varepsilon (x,t)=\frac{-2 \pi }{\log \varepsilon } {{\varvec{u}}}_0 (z,t) \nabla \nu (x). \nabla \Gamma (x-z) \chi _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } }(x),$ where $\chi _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } }$ is the characteristic function of the domain ${\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$. Using Lemma 3.1 and choosing $p=\frac{6}{5}$, one can derive that there exists a constant $c>0$, independent of $\varepsilon$, such that

  $$\begin{aligned}&\Arrowvert \widetilde{{ w}^{3}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{3}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}\\&\quad \le \frac{c }{|\log \varepsilon | } || {{\varvec{u}}}_0 (z,t) \nabla \nu .\nabla \Gamma (x-z) ||_{L^2(0,T;L^{6/5}({\mathcal {B}}))} . \end{aligned}$$

  Since $\nu$ and ${{\varvec{u}}}_0$ are sufficiently smooth, it follows

  $$\begin{aligned}&\Arrowvert \widetilde{{ w}^{3}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{3}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))} \nonumber \\&\quad \le \frac{c }{|\log \varepsilon | } ||\nabla \Gamma (x-z) ||_{L^2(0,T;L^{6/5}({\mathcal {B}}))} . \end{aligned}$$

  (3.32)

  Using (3.32) Lemma 3.3, we obtain

  $$\begin{aligned} \Arrowvert \widetilde{{ w}^{3}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{3}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}&\le \frac{c }{ |\log \varepsilon | }. \end{aligned}$$

  Since ${{ w}^{3}_{\varepsilon }}= \widetilde{{ w}^{3}_{\varepsilon }}$ in ${\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$, we deduce

  $$\begin{aligned} \Arrowvert {{ w}^{3}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} + \Arrowvert {{ w}^{3}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}&\le \frac{c }{ |\log \varepsilon | }. \end{aligned}$$

  (3.33)

• Fourth term $w^{4}_{\varepsilon }$: The term $w^{4}_{\varepsilon }$ is chosen such that $w^{4}_{\varepsilon } = w_{\varepsilon } -w^{1}_{\varepsilon }-w^{2}_{\varepsilon }-w^{3}_{\varepsilon }$. From (3.19) (3.21), (3.25) and (3.29) it follows that the term $w^{4}_{\varepsilon } \in H^1(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))$ and satisfies the following system

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial w^{4}_{\varepsilon } }{\partial t} - div( \nu \nabla w^{4}_{\varepsilon }) &{} = \frac{2 \pi }{\log \varepsilon } \displaystyle \frac{\partial {{\varvec{u}}}_0 }{\partial t}(z,t) \big [ T_\varepsilon (x) -\Gamma (x-z) \big ] &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T) , \\ w^{4}_{\varepsilon } &{} = 0 &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ w^{4}_{\varepsilon }&{} = 0 &{} \text{ on } &{}\partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) ,\\ w^{4}_{\varepsilon } (.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } . \end{array} \right. \nonumber \\ \end{aligned}$$

  (3.34)

  Similarly to the previous term, we define the extension of $w^{4}_{\varepsilon }$ by zero on ${\mathcal {C}}_{z,\varepsilon }$

  $$\begin{aligned} \widetilde{w^{4}_{\varepsilon }} =\left\{ \begin{array}{r l l l} w^{4}_{\varepsilon } &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times ]0,T[ , \\ 0 &{} \text{ in } &{} {\mathcal {C}}_{z,\varepsilon } \times ]0,T[ . \end{array} \right. \end{aligned}$$

  (3.35)

  Using the continuity condition $w^{4}_{\varepsilon }=0$ on $\partial {\mathcal {C}}_{z,\varepsilon } \times ]0,T[$, the function ${\widetilde{w}}^{4}_{\varepsilon }\in H^1(0,T;H^1({\mathcal {B}}))$ satisfies

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial \widetilde{w^{4}_{\varepsilon } }}{\partial t} - div( \nu (x) \nabla \widetilde{w^{4}_{\varepsilon } }) &{} = F^4_\varepsilon (x,t) &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \widetilde{w^{4}_{\varepsilon } } &{} = 0 &{} \text{ on } &{}\partial {\mathcal {B}}\times (0,T), \\ \widetilde{w^{4}_{\varepsilon } }(.,0) &{} = 0 &{} \text{ in } &{} {\mathcal {B}}, \end{array} \right. \end{aligned}$$

  (3.36)

  where the source term is defined by

  $$\begin{aligned} F^4_\varepsilon (x,t)= \frac{2 \pi }{\log \varepsilon } \displaystyle \frac{\partial {{\varvec{u}}}_0 }{\partial t}(z,t) \big [ T_\varepsilon (x) -\Gamma (x-z) \big ] \chi _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } (x), \, \forall (x,t) \in {\mathcal {B}}\times ]0,T[ . \end{aligned}$$

  Using Lemma 3.1 with $p=2$, one has

  $$\begin{aligned} \Arrowvert \widetilde{{ w}^{4}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{4}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}&\le \frac{c}{ | \log \varepsilon | } || F^4_\varepsilon ||_{L^2(0,T;L^2({\mathcal {B}}))} . \end{aligned}$$

  Since $\frac{\partial {{\varvec{u}}}_0 }{\partial t}(z,t)$ is sufficiently smooth and the triangle inequality, it follows

  $$\begin{aligned} || F^4_\varepsilon ||_{L^2(0,T;L^2({\mathcal {B}}))}&\le c \big ( || T_\varepsilon (x)||_{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )} + ||\Gamma (x-z) ||_{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )} \big ) . \end{aligned}$$

  (3.37)

  Using Lemma 3.3 and (3.27), we have

  $$\begin{aligned} \Arrowvert \widetilde{{ w}^{4}_{\varepsilon }} \Arrowvert _{L^\infty (0,T;L^2({\mathcal {B}}))} + \Arrowvert \widetilde{{ w}^{4}_{\varepsilon }} \Arrowvert _{L^2(0,T;H^1({\mathcal {B}}))}&\le \frac{c}{ | \log \varepsilon | } . \end{aligned}$$

  (3.38)

  Since $w^{4}_{\varepsilon }$ coincides with $\widetilde{{ w}^{4}_{\varepsilon }}$ on ${\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$, we deduce

  $$\begin{aligned} \Arrowvert w^{4}_{\varepsilon } \Arrowvert _{L^\infty (0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} + \Arrowvert w^{4}_{\varepsilon } \Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}&\le \frac{c}{ | \log \varepsilon | } . \end{aligned}$$

  (3.39)

• The desired estimate: Combining the estimates (3.24), (3.28), (3.33) and (3.39), one can deduce that there exists $c>0$, independent of $\varepsilon$, such that the function $w_{\varepsilon } = {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }$ satisfies the following estimate

  $$\begin{aligned} \Arrowvert w_{\varepsilon } \Arrowvert _{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} + \Arrowvert w_{\varepsilon } \Arrowvert _{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} \le \frac{ c}{|\log \varepsilon | } . \end{aligned}$$

  $\square$

Next, we will use this estimate and we will derive a topological asymptotic expansion valid for a large class of shape functions j.

4 Topological Asymptotic Expansion

We are now ready to present the main results of this section. Starting from the established estimate for the perturbed solution (see Sect. 3.3), we will prove that the asymptotic behavior of the term $\int _0^T D J_0({{\varvec{u}}}_0)({{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0) dt$ with respect to $\varepsilon$ is given by the function $\displaystyle \rho (\varepsilon )=-\frac{1}{\log (\varepsilon )}$.

In this section, we will derive a topological asymptotic expansion valid for all shape function j verifying the Hypothesis (H), with $\rho (\varepsilon )=-1/\log (\varepsilon )$. The following theorem summarizes the main theoretical results of this work. Some shape function examples are considered in Sects. 4.1, 4.2, 4.3 and 4.4 .

Theorem 4.1

Let $J_\varepsilon$ be a given function satisfying the hypothesis (H), with $\rho (\varepsilon )=-1/\log (\varepsilon )$. Then, for small $\varepsilon >0$, the design function

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )=\displaystyle \int _0^{T} J_\varepsilon ( {{\varvec{u}}}_\varepsilon (.,t)) dt, \end{aligned}$$

admits the following expansion

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{1}{ \log \varepsilon } {\mathcal {S}}(z) + o \left( \frac{-1}{ \log \varepsilon } \right) , \end{aligned}$$

with ${\mathcal {S}}$ is the topological sensitivity function defined by

$$\begin{aligned} {\mathcal {S}} (x) = 2 \pi \nu (x) \displaystyle \int _0^{T} {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) dt + \delta {\mathcal {J}}(x) , \forall x \in {\mathcal {B}}. \end{aligned}$$

Before giving the detailed proof, we make the following remark.

Remark 4.2

As one can note here, the leading term ${\mathcal {S}}$ of the obtained topological asymptotic expansion is not dependent on the shape ${\mathcal {C}}$ of the geometric perturbation. The results here comply with those of several authors (see for example [11,12,13, 24]) who have shown, in the case of elliptic problems with Dirichlet boundary condition in 2D, that the first order of the topological expansion does not depend on the shape of the created hole, in the case of holes with non-empty interiors. The shape ${\mathcal {C}}$ of the hole matters usually when dealing with Neumann boundary condition.

Proof

With the help of the weak formulation of (2.5), the design function variation can be rewritten as

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})&= - \int _0^T \int _{{\mathcal {B}}} \frac{\partial ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 )}{\partial t} {{\varvec{v}}}_0dx dt \\&\quad -\int _0^T \int _{{\mathcal {B}}} \nu (x) \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0) . \nabla {{\varvec{v}}}_0dx dt + \rho (\varepsilon ) \delta {\mathcal {J}}(z)+ o(\rho (\varepsilon )). \end{aligned}$$

Using the fact that ${{\varvec{u}}}_\varepsilon =0$ in ${\mathcal {C}}_{z,\varepsilon }$, it follows

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})&= \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \frac{\partial {{\varvec{u}}}_0 }{\partial t} {{\varvec{v}}}_0dx dt + \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla {{\varvec{u}}}_0 . \nabla {{\varvec{v}}}_0dx dt\\&\quad -\int _0^T \int _{ {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon }} \frac{\partial ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 )}{\partial t} {{\varvec{v}}}_0dx dt\\&\quad -\int _0^T \int _{ {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon }} \nu (x) \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) . \nabla {{\varvec{v}}}_0dx dt \\&\quad +\rho (\varepsilon ) \delta {\mathcal {J}} (z)+ o(\rho (\varepsilon )). \end{aligned}$$

Applying Green formula to system (3.1), we get

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})&= \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \frac{\partial {{\varvec{u}}}_0 }{\partial t} {{\varvec{v}}}_0dx dt + \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla {{\varvec{u}}}_0 . \nabla {{\varvec{v}}}_0dx dt \end{aligned}$$

(4.1)

$$\begin{aligned}&\quad - \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) \mathbf . n {{\varvec{v}}}_0ds dt +\rho (\varepsilon ) \delta {\mathcal {J}} (z)\nonumber \\&\quad + o(\rho (\varepsilon )). \end{aligned}$$

(4.2)

In order to derive the expected asymptotic expansion, we will examine the terms (4.1) and (4.2) separately.

• Estimate of the term (4.1): Using the change of variable $x=z+ \varepsilon y$, the first integral term in (4.1) can be written as

  $$\begin{aligned} \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \frac{\partial {{\varvec{u}}}_0 }{\partial t} {{\varvec{v}}}_0dx dt&= \varepsilon ^2 \int _0^T \int _{{\mathcal {C}} } \big ( \frac{ \partial {{\varvec{u}}}_0 }{\partial t} ( z+ \varepsilon y ,t) {{\varvec{v}}}_0(z+ \varepsilon y,t )\\&\quad - \frac{ \partial {{\varvec{u}}}_0 }{\partial t} (z,t) {{\varvec{v}}}_0(z,t) \big ) dy dt\\&\quad + \varepsilon ^2 |{\mathcal {C}} | \int _0^T \frac{\partial {{\varvec{u}}}_0 }{\partial t} (z,t) {{\varvec{v}}}_0(z,t) dt, \end{aligned}$$

  where $|{\mathcal {C}} |$ denotes the Lebesgue measure of the domain ${\mathcal {C}}$.

  From the fact that ${{\varvec{u}}}_0$ and ${{\varvec{v}}}_0$ are smooth near z, one can derive

  $$\begin{aligned} \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \frac{\partial {{\varvec{u}}}_0 }{\partial t} {{\varvec{v}}}_0dx dt = \varepsilon ^2 |{\mathcal {C}} | \int _0^T \frac{ \partial {{\varvec{u}}}_0 }{\partial t} (z,t) {{\varvec{v}}}_0(z,t) dt +o(\varepsilon ^2)=O(\varepsilon ^2). \end{aligned}$$

  The second integral term in (4.1) can be estimated using the same arguments. Therefore, the smoothness of ${{\varvec{u}}}_0$ and ${{\varvec{v}}}_0$ leads to

  $$\begin{aligned} \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla {{\varvec{u}}}_0 . \nabla {{\varvec{v}}}_0dx dt&=O( \varepsilon ^2 ). \end{aligned}$$

  Then, the integral terms in (4.1) satisfy the asymptotic behavior

  $$\begin{aligned} \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \frac{\partial {{\varvec{u}}}_0 }{\partial t} {{\varvec{v}}}_0dx dt + \int _0^T \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla {{\varvec{u}}}_0 \nabla {{\varvec{v}}}_0dx dt =O(\varepsilon ^2). \end{aligned}$$

  (4.3)

• Estimate of the term (4.2): We have

  $$\begin{aligned}&\int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) \mathbf . n {{\varvec{v}}}_0ds dt\\&\quad = \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla \left( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }\right) \mathbf . n {{\varvec{v}}}_0ds dt\\&\qquad +\frac{1}{ \log \varepsilon } \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla \mathbf{U }\mathbf . n {{\varvec{v}}}_0ds dt . \end{aligned}$$

  Applying trace theorem, the smoothness of ${{\varvec{v}}}_0$ and Proposition 3.4 one can easily check that

  $$\begin{aligned} \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu \nabla \left( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }\right) \mathbf . n {{\varvec{v}}}_0ds dt = o \left( \frac{-1}{ \log \varepsilon } \right) . \end{aligned}$$

  Consequently, the integral terms in (4.2) satisfy the estimate

  $$\begin{aligned}&\int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) \mathbf . n {{\varvec{v}}}_0ds dt\\&\quad = \frac{1}{ \log \varepsilon } \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla \mathbf{U }\mathbf . n {{\varvec{v}}}_0ds dt + o \left( \frac{-1}{ \log \varepsilon } \right) . \end{aligned}$$

• The desired asymptotic expansion: From the last estimates, one can deduce

  $$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})&= \frac{-1}{ \log \varepsilon } \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla \mathbf{U }\mathbf . n {{\varvec{v}}}_0ds dt - \frac{1}{ \log \varepsilon } \delta {\mathcal {J}}(z) \\&\quad + o \left( \frac{-1}{ \log \varepsilon } \right) . \end{aligned}$$

  Using (3.2), the integral term can be rewritten as

  $$\begin{aligned}&\int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla \mathbf{U }\mathbf . n {{\varvec{v}}}_0ds dt \nonumber \\&\quad = 2 \pi \int _0^T {{\varvec{u}}}_0(z,t) \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nabla \Gamma (x-z) \mathbf . n \Big [ \nu (x){{\varvec{v}}}_0(x,t) - \nu (z){{\varvec{v}}}_0(z,t) \Big ] ds (x) dt \nonumber \\&\qquad + 2 \pi \nu (z) \int _0^T {{\varvec{u}}}_0(z,t) {{\varvec{v}}}_0(z,t) dt \Big [ \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nabla \Gamma (x-z) . n ds (x) \Big ] . \end{aligned}$$

  (4.4)

  In the one hand, the functions ${{\varvec{v}}}_0$ and $\nu$ are sufficiently smooth near z, in such a way one can deduce

  $$\begin{aligned} \Arrowvert \nu (x) {{\varvec{v}}}_0(x,t) - \nu (z) {{\varvec{v}}}_0(z,t) \Arrowvert _{L^2(0,T;L^2(\partial {\mathcal {C}}_{z,\varepsilon } ))} =O(\varepsilon ). \end{aligned}$$

  In the other hand, we have

  $$\begin{aligned} \Arrowvert \nabla \Gamma (x-z) \mathbf . n \Arrowvert _{L^2 ( \partial {\mathcal {C}}_{z,\varepsilon } )} = \Arrowvert \frac{1}{\Vert x-z\Vert }\Arrowvert _{L^2 ( \partial {\mathcal {C}}_{z,\varepsilon } )}\le c\,\varepsilon ^{-1/2}. \end{aligned}$$

  Consequently, the first term in (4.4) can be neglected and the variation of j reads

  $$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}})&= - \frac{ 2 \pi \nu (z) }{ \log \varepsilon } \Big ( \int _0^T {{\varvec{u}}}_0(z,t) {{\varvec{v}}}_0(z,t) dt \Big ) \Big ( \int _{\partial {\mathcal {C}}_{z,\varepsilon } }\nabla \Gamma (x-z)\mathbf . n ds (x) \Big ) \\&\quad - \frac{1}{ \log \varepsilon } \delta {\mathcal {J}}(z) + o \Big ( \frac{-1}{ \log \varepsilon } \Big ). \end{aligned}$$

  Finally, using the fact that

  $$\begin{aligned} - \Delta \Gamma (x-z)= \delta _z \, \text{ in } {\mathcal {C}}_{z,\varepsilon } , \end{aligned}$$

  and taking into account of the normal orientation, one can deduce

  $$\begin{aligned} \int _{\partial {\mathcal {C}}_{z,\varepsilon } }\nabla \Gamma (x-z)\mathbf . n ds (x)=1 . \end{aligned}$$

  Then, we derive the desired asymptotic expansion

  $$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )-j({\mathcal {B}}) = -\frac{2 \pi \nu (z) }{ \log \varepsilon } \int _0^T {{\varvec{u}}}_0(z,t) {{\varvec{v}}}_0(z,t ) dt - \frac{1}{ \log \varepsilon } \delta {\mathcal {J}}(z) + o \Big ( \frac{-1}{ \log \varepsilon } \Big ). \end{aligned}$$

$\square$

The term $\delta {\mathcal {J}}$ depends on the considered function $J_\varepsilon$. In the next sections, we will present some cost functional examples verifying the hypothesis (H) and we calculate their variations $\delta {\mathcal {J}}$.

4.1 First Example

We consider the quadratic function $J_\varepsilon$ defined on the outer boundary $\partial {\mathcal {B}}$ by

$$\begin{aligned} J_\varepsilon ({{\varvec{u}}})=\int _{\partial {\mathcal {B}}} | {{\varvec{u}}}- \varphi _m |^2ds, \, \forall {{\varvec{u}}}\in H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ), \end{aligned}$$

(4.5)

where $\varphi _m \in L^2(0,T;H^{1/2}(\partial {\mathcal {B}}))$ is a given measured datum on $\partial {\mathcal {B}}$. The associated design function j is defined by

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )= \int _0^{T} \int _{\partial {\mathcal {B}}} | {{\varvec{u}}}_\varepsilon - \varphi _m |^2 ds dt, \end{aligned}$$

(4.6)

with ${{\varvec{u}}}_\varepsilon$ is the perturbed temperature distribution defined in ${\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$.

This cost function example has been used for solving various optimal design and geometric inverse problems. One can cite for examples; detection of inclusion [25], detection of cavities [26] and the reconstruction of a source term support [27, 28].

Proposition 4.3

The quadratic function (4.5) satisfies the hypothesis (H) and the associated design function j admits the following expansion

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{1}{ \log \varepsilon } {\mathcal {S}}(z) + o \left( \frac{-1}{ \log \varepsilon } \right) , \end{aligned}$$

with ${\mathcal {S}}$ is the topological sensitivity function defined by

$$\begin{aligned} {\mathcal {S}} (x) = 2 \pi \nu (x) \displaystyle \int _0^{T} {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) dt , \forall x \in {\mathcal {B}}, \end{aligned}$$

where ${{\varvec{v}}}_0$ is the solution to the associated adjoint problem.

Proof

The considered design function j can be written as

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )= \int _0^T J_\varepsilon ({{\varvec{u}}}_\varepsilon (.,t)) dt , \end{aligned}$$

with

$$\begin{aligned} J_\varepsilon ({{\varvec{u}}})= \int _{\partial {\mathcal {B}}} |{{\varvec{u}}}- \varphi _m(.,t)|^2 dx , \, \forall {{\varvec{u}}}\in H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) . \end{aligned}$$

From the fact that $\varphi _m \in L^2(0,T;H^{1/2}(\partial {\mathcal {B}}))$ and ${{\varvec{u}}}_\varepsilon \in L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))$, it follows that the function $t\mapsto J_\varepsilon ({{\varvec{u}}}_\varepsilon (.,t))$ belongs to $L^1(0,T)$. Moreover, one can easily check that the function $J_0$ is differentiable at ${{\varvec{u}}}_0(.,t)$ and we have

$$\begin{aligned} DJ_0({{\varvec{u}}}_0(.,t)) h=2 \int _{\partial {\mathcal {B}}} \big [{{\varvec{u}}}_0(.,t)-\varphi _{m}(.,t)\big ] h dx , \, \forall h \in H^1({\mathcal {B}}). \end{aligned}$$

Let us note here that, under the assumption (2.6), the solutions ${{\varvec{u}}}_0$ and ${{\varvec{v}}}_0$ satisfy the regularity result (2.8). The regularity of ${{\varvec{v}}}_0$ comes from the fact the right hand side term in the adjoint equation vanishes near the point z.

In order to derive the expected topological asymptotic expansion, we start our analysis by describing the variation of the design function j with respect to the presence of the hole ${\mathcal {C}}_{z,\varepsilon }$ in ${\mathcal {B}}$. We have

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j({\mathcal {B}})&= \int _0^{T} \int _{\partial {\mathcal {B}}} | {{\varvec{u}}}_\varepsilon - \varphi _m |^2 ds(x) dt - \int _0^{T} \int _{\partial {\mathcal {B}}} | {{\varvec{u}}}_0 - \varphi _{m} |^2 ds(x) dt \\&= \int _0^{T} DJ_0({{\varvec{u}}}_0(.,t)) ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) ds(x) dt \\&\quad + \int _0^{T} \int _{\partial {\mathcal {B}}} |{{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 |^2 ds(x) dt . \end{aligned}$$

Due to trace theorem and the fact that $\mathbf{B }_{r_2} \subset {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$ (see Sect. 3.2), we get

$$\begin{aligned} \int _0^{T} \int _{\partial {\mathcal {B}}} |{{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 |^2 ds(x) dt&\le \Arrowvert {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 \Arrowvert ^2_{L^2(0,T;H^1(\mathbf{B }_{r_2}))} . \end{aligned}$$

By the triangle inequality, we have

$$\begin{aligned}&\int _0^{T} \int _{\partial {\mathcal {B}}} |{{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 |^2 ds(x) dt \\&\quad \le 2 \Big ( \Arrowvert {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }\Arrowvert ^2_{L^2(0,T;H^1(\mathbf{B }_{r_2}))} + \frac{1}{(\log \varepsilon )^2} \Arrowvert U \Arrowvert ^2_{L^2(0,T;H^1(\mathbf{B }_{r_2}))} \Big ). \end{aligned}$$

From (3.2), we get

$$\begin{aligned} \Arrowvert U \Arrowvert ^2_{L^2(0,T;H^1(\mathbf{B }_{r_2} ))} =2 \pi \Arrowvert {{\varvec{u}}}_0 (z,t) \Arrowvert ^2_{L^2(0,T)} \Arrowvert \Gamma (x-z) \Arrowvert ^2_{H^1(\mathbf{B }_{r_2})} =O(1). \end{aligned}$$

The last estimate is due to the fact that $z \notin \mathbf{B }_{r_2}:= {\mathcal {B}}\backslash \overline{\mathbf{B }(z,{r_2})}$, which implies that the function $x \mapsto \Gamma (x-z)$ belongs to ${C}^\infty ( \overline{\mathbf{B }_{r_2}} )$.

Moreover, using the fact that $\mathbf{B }_{r_2} \subset {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon }$ and Proposition 3.4, it follows

$$\begin{aligned} || {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0- \frac{1}{ \log \varepsilon } \mathbf{U }||^2_{L^2(0,T;H^1(\mathbf{B }_{r_2}))} =o\big ( \frac{-1}{ \log \varepsilon } \big ). \end{aligned}$$

Then, we deduce that

$$\begin{aligned} \int _0^{T} \int _{\partial {\mathcal {B}}} |{{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 |^2 ds(x) dt =o\big ( \frac{-1}{ \log \varepsilon } \big ), \end{aligned}$$

which implies that the considered function $J_\varepsilon$ satisfies the hypothesis (H) with

$$\begin{aligned} \delta {\mathcal {J}} (x)=0,\, \forall x \in {\mathcal {B}}. \end{aligned}$$

Consequently, one has

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{2 \pi \nu (z)}{ \log \varepsilon } \displaystyle \int _0^{T} {{\varvec{u}}}_0(z,t) {{\varvec{v}}}_0(z,t) dt + o \left( \frac{-1}{ \log \varepsilon } \right) . \end{aligned}$$

$\square$

4.2 Second Example

We consider the standard design function example defined by the $L^2$-norm

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )= \int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}_\varepsilon - \varphi _{d} |^2 dx dt. \end{aligned}$$

where $\varphi _{d}\in L^2(0,T;H^1( {\mathcal {B}}))$ is a given desired temperature distribution verifying the regularity assumptions, namely there exists a neighborhood ${\mathcal {O}}\subset {\mathcal {B}}$ of z such

$$\begin{aligned} \varphi _{d}\in L^2(0,T;H^6({\mathcal {O}})) \cap H^3(0,T; L^2 ({\mathcal {O}})). \end{aligned}$$

(4.7)

This kind of shape functions has been used in various shape optimization and geometric inverse problems. In our case, it can be used for achieving an optimal design that approximating a given desired temperature within the blade.

The associated cost function $J_\varepsilon$ is given by

$$\begin{aligned} J_\varepsilon ({{\varvec{u}}})=\int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}- \varphi _{d} |^2 dx , \, \forall {{\varvec{u}}}\in H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ), \end{aligned}$$

(4.8)

Proposition 4.4

The cost function (4.8) satisfies the hypothesis (H) and the associated design function j admits the following expansion

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{1}{ \log \varepsilon } {\mathcal {S}}(z) + o \left( \frac{-1}{ \log \varepsilon } \right) , \end{aligned}$$

with ${\mathcal {S}}$ is the topological sensitivity function defined by

$$\begin{aligned} {\mathcal {S}} (x) = 2 \pi \nu (x) \displaystyle \int _0^{T} {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) dt , \forall x \in {\mathcal {B}}, \end{aligned}$$

where ${{\varvec{v}}}_0$ is the solution to the associated adjoint problem.

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial {{\varvec{v}}}_0}{\partial t} - div (\nu (x) \nabla {{\varvec{v}}}_0) &{} = - 2 ( {{\varvec{u}}}_0 - \varphi _{d} ) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0&{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0(.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}, \end{array} \right. \end{aligned}$$

Proof

Based on the fact that ${{\varvec{u}}}_\varepsilon$ and $\varphi _{d}$ belong to $L^2(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))$, it follows that the function $t \mapsto J_\varepsilon ({{\varvec{u}}}_\varepsilon (.,t))$ belongs to $L^1(0,T)$. It is easy to see that the function $J_0$ is differentiable at ${{\varvec{u}}}_0(.,t)$ and we have

$$\begin{aligned} DJ_0({{\varvec{u}}}_0(.,t)) h=2 \int _{\mathcal {B}}\big ({{\varvec{u}}}_0(.,t)-\varphi _{d} \big ) h dx , \, \forall h \in H^1({\mathcal {B}}). \end{aligned}$$

We note here that under the assumptions (2.6) and (4.7), the direct and the adjoint problems solutions satisfy the regularity result (2.8). The regularity of the adjoint state ${{\varvec{v}}}_0$ follows from Proposition 2.2 and the fact that $DJ_0({{\varvec{u}}}_0)= - 2 ( {{\varvec{u}}}_0 - \varphi _{d} )$.

The design function variation reads

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j({\mathcal {B}})&=2\int _0^{T} \int _{{\mathcal {B}}} ( {{\varvec{u}}}_0 - \varphi _{d} ) ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) dx dt +\int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } |{{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0|^2 dx dt \\&\quad + \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } |{{\varvec{u}}}_0|^2 dx dt - \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } | \varphi _{d} |^2 dx dt. \end{aligned}$$

The smoothness of ${{\varvec{u}}}_0$ and $\varphi _{d}$ implies

$$\begin{aligned} \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } |{{\varvec{u}}}_0|^2 dx dt = O(|{\mathcal {C}}_{z,\varepsilon } |)=o(\varepsilon ), \end{aligned}$$

and

$$\begin{aligned} \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } | \varphi _{d} |^2 dx dt= O(|{\mathcal {C}}_{z,\varepsilon } |)=o(\varepsilon ). \end{aligned}$$

Furthermore, we have

$$\begin{aligned}&\int _{0}^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 |^2 dx dt \nonumber \\&\quad \le 2\int _{0}^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0- \frac{1}{ \log \varepsilon } \mathbf{U }|^2 dx dt +\frac{2}{(\log (\varepsilon ))^2} \int _{0}^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | \mathbf{U }|^2 dx dt. \end{aligned}$$

(4.9)

From Propositions 3.4, we have

$$\begin{aligned} \Arrowvert {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0- \frac{1}{ \log \varepsilon } \mathbf{U }\Arrowvert ^2_{L^2(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}= o\big ( \frac{-1}{ \log \varepsilon } \big ). \end{aligned}$$

From Lemma 3.3, it follows

$$\begin{aligned} \Arrowvert \mathbf{U }\Arrowvert _{L^2(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}= 2 \pi \Arrowvert {{\varvec{u}}}_0 \Arrowvert _{L^2(0,T)} \Arrowvert \Gamma (x-z) \Arrowvert _{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )} = O ( 1 ). \end{aligned}$$

Consequently, we have

$$\begin{aligned} \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 |^2 dxdt = o\left( \frac{-1}{ \log \varepsilon }\right) . \end{aligned}$$

(4.10)

Combining the above estimates, one can deduce that the chosen function $J_\varepsilon$ satisfies the hypothesis (H) with

$$\begin{aligned} \delta {\mathcal {J}} (x)=0,\, \forall x \in {\mathcal {B}}. \end{aligned}$$

$\square$

4.3 Third Example

The third example is concerned with the $H^1$-semi norm function

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )= \int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \nu | \nabla {{\varvec{u}}}_\varepsilon - \nabla \varphi _w |^2 dx dt, \end{aligned}$$

(4.11)

where $\varphi _w \in L^2(0,T;H^2( {\mathcal {B}}))$ is a given wanted state, verifying the regularity assumptions, namely there exists a neighborhood ${\mathcal {O}}\subset {\mathcal {B}}$ of z such

$$\begin{aligned} \varphi _w\in L^2(0,T;H^6({\mathcal {O}})) \cap H^3(0,T; L^2 ({\mathcal {O}})). \end{aligned}$$

The associated cost function $J_\varepsilon$ is given by

$$\begin{aligned} J_\varepsilon ({{\varvec{u}}}) =\int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \nu | \nabla {{\varvec{u}}}- \nabla \varphi _w |^2dx, \, \forall {{\varvec{u}}}\in H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ). \end{aligned}$$

(4.12)

The obtained topological asymptotic expansion related to this design functional example is illustrated by the following proposition.

Proposition 4.5

The design function j defined by (4.11) admits the following expansion

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{1}{ \log \varepsilon } {\mathcal {S}}(z) + o \left( \frac{-1}{ \log \varepsilon } \right) , \end{aligned}$$

where ${\mathcal {S}}$ is the topological sensitivity function, defined as

$$\begin{aligned} {\mathcal {S}} (x) = 2 \pi \nu (x) \displaystyle \int _0^{T} \Big [ {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) + | {{\varvec{u}}}_0(x,t) |^2 \Big ] dt , \forall x \in {\mathcal {B}}, \end{aligned}$$

with ${{\varvec{v}}}_0$ is the solution to the associated adjoint problem.

Proof

Similarly to the previous case, one can easily see that the function $J_0$ is differentiable at ${{\varvec{u}}}_0 (.,t)$ and we have

$$\begin{aligned} DJ_0({{\varvec{u}}}_0 (.,t))h = 2 \int _{\mathcal {B}}\nu \big [ \nabla {{\varvec{u}}}_0 -\nabla \varphi _w \big ] . \nabla h dx , \forall h \in H^1({\mathcal {B}}). \end{aligned}$$

The variation of the design function j is given by

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j({\mathcal {B}})&=2\int _0^{T} \int _{{\mathcal {B}}} \nu ( \nabla {{\varvec{u}}}_0 - \nabla \varphi _{w} ) . (\nabla {{\varvec{u}}}_\varepsilon - \nabla {{\varvec{u}}}_0 )dx dt \\&\quad +\int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \nu |\nabla {{\varvec{u}}}_\varepsilon - \nabla {{\varvec{u}}}_0|^2 dx dt\\&\quad + \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu |\nabla {{\varvec{u}}}_0 |^2 dx dt \\&\quad - \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu | \nabla \varphi _{w} |^2 dx dt. \end{aligned}$$

Thanks to the regularity of $\nabla {{\varvec{u}}}_0$ and $\nabla \varphi _w$, we get

$$\begin{aligned} \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu |\nabla {{\varvec{u}}}_0 |^2 dx dt- \int _0^{T} \int _{ {\mathcal {C}}_{z,\varepsilon } } \nu | \nabla \varphi _{w} |^2 dx dt = o\big (\frac{-1}{ \log \varepsilon }\big ). \end{aligned}$$

(4.13)

Furthermore, using (4.13) and the weak formulation of (3.1), the variation of j becomes

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j({\mathcal {B}})&= \int _0^{T} DJ_0( {{\varvec{u}}}_0 (.,t)) ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) dt \nonumber \\&\quad -\int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \frac{\partial ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0) }{\partial t} ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0)dx dt \end{aligned}$$

(4.14)

$$\begin{aligned}&\quad - \int _0^{T} \int _{ \partial {\mathcal {C}}_{z,\varepsilon } } \nu \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 )\mathbf . n {{\varvec{u}}}_0 dx dt +o\big (\frac{-1}{ \log \varepsilon }\big ) . \end{aligned}$$

(4.15)

Taking the supremum for all $t \in [0,T]$, we have

$$\begin{aligned} \int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \frac{\partial ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0) }{\partial t} ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0)dx dt&= \frac{1}{2} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}_\varepsilon (.,T) - {{\varvec{u}}}_0(.,T) |^2 dt \\&\le c || {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0||^2_{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))} . \end{aligned}$$

By the triangle inequality and the identity $(a+b)^2 \le 2(a^2 +b^2)$, we get

$$\begin{aligned} || {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0||^2_{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}&\le 2 || {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }||_{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}^2 \\&\quad +\frac{2}{(\log \varepsilon )^2} || \mathbf{U }||_{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}^2 . \end{aligned}$$

From Propositions 3.4, we have

$$\begin{aligned} || {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }||_{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}^2 = o\left( \frac{-1}{ \log \varepsilon }\right) . \end{aligned}$$

(4.16)

We recall that the function ${{\varvec{u}}}_0(.,T)$ is sufficiently smooth, then Lemma 3.3 implies

$$\begin{aligned} || \mathbf{U }||_{L^{\infty }(0,T;L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))}^2 = 2 \pi || {{\varvec{u}}}_0 (z,t)||_{L^{\infty }(0,T)}^2 || \Gamma ||_{L^2( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } )}^2 =O(1) . \end{aligned}$$

Then, we deduce

$$\begin{aligned} \int _0^{T} \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \frac{\partial ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0) }{\partial t} ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0)dx dt = o\left( \frac{-1}{ \log \varepsilon }\right) . \end{aligned}$$

(4.17)

Consequently

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j({\mathcal {B}})&= \int _0^{T} DJ_0( {{\varvec{u}}}_0 (.,t)) ( {{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 ) dt\nonumber \\&\quad - \int _0^{T} \int _{ \partial {\mathcal {C}}_{z,\varepsilon } } \nu \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 )\mathbf . n {{\varvec{u}}}_0 dx dt +o \big ( \frac{- 1}{ \log \varepsilon } \big ) . \end{aligned}$$

(4.18)

Moreover, the second integral term in (4.18) can be decomposed as

$$\begin{aligned} \int _0^{T} \int _{ \partial {\mathcal {C}}_{z,\varepsilon } } \nu \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 )\mathbf . n {{\varvec{u}}}_0 dx dt&= \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla \left( {{\varvec{u}}}_\varepsilon -{{\varvec{u}}}_0 - \frac{1}{ \log \varepsilon } \mathbf{U }\right) \mathbf . n {{\varvec{u}}}_0 ds dt \\&\quad + \frac{ 1}{ \log \varepsilon } \int _0^T \int _{\partial {\mathcal {C}}_{z,\varepsilon } } \nu \nabla \mathbf{U }\mathbf . n {{\varvec{u}}}_0 ds dt . \end{aligned}$$

Using the same technique developed in the proof of Theorem 4.1, the last integral terms can be estimated as follows

$$\begin{aligned} \int _0^{T} \int _{ \partial {\mathcal {C}}_{z,\varepsilon } } \nu (x) \nabla ({{\varvec{u}}}_\varepsilon - {{\varvec{u}}}_0 )\mathbf . n {{\varvec{u}}}_0 dx dt = - \displaystyle \frac{2 \pi \nu (z) }{ \log \varepsilon } \int _0^{T} | {{\varvec{u}}}_0(z,t) |^2 dt +o \big ( \frac{-1}{ \log \varepsilon } \big ) . \end{aligned}$$

Then, we deduce that the design function j satisfies the hypothesis (H) and its topological sensitivity function reads

$$\begin{aligned} {\mathcal {S}} (x)= 2 \pi \nu (x) \displaystyle \int _0^{T} \Big [ {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) + | {{\varvec{u}}}_0(x,t) |^2 \Big ] dt , \forall x \in {\mathcal {B}}. \end{aligned}$$

$\square$

4.4 Fourth Example

In this example, we derive a topological asymptotic expansion for the Kohn–Vogelius type functional. In many industrial applications, the detection of the unknown inclusion ${\mathcal {H}} \subset {\mathcal {B}}$ (solution to (2.2) is done using the non-destructive inspection technique, such as ultrasound, radiography, eddy current etc.

As a possible application in non-destructive testing, we mention the detection of ${\mathcal {H}}$ from applying a heat flux (denoted by $g_N$) to the boundary of the background domain ${\mathcal {B}}$ and measuring the temperature response over time (denoted by $g_D$). In this context, the optimization problem (2.2) can be formulated as: determine ${\mathcal {H}} \subset {\mathcal {B}}$ such that the temperature distribution ${{\varvec{u}}}_{{\mathcal {H}}}$ in the perforated domain ${\mathcal {B}}\backslash \overline{{\mathcal {H}}}$ satisfies the following overdetermined boundary value problem

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}_{{\mathcal {H}}}}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}_{{\mathcal {H}}}) &{} =F &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {H}}} \times (0,T)}, \\ \nu \nabla {{\varvec{u}}}_{{\mathcal {H}}} \mathbf . n &{}= g_N &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}_{{\mathcal {H}}} &{}= g_D &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}_{{\mathcal {H}}} (.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {H}}}}. \end{array} \right. \end{aligned}$$

(4.19)

To determine the unknown domain ${\mathcal {H}}$, Kohn and Vogelius proposed in [29] an interesting approach reformulating the geometric inverse problem into a shape optimization one. To define the function to be minimized (the criteria), they exploited the overdetermined boundary data and introduced two auxiliaries problems:

$$\begin{aligned}&\left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}^N_{{\mathcal {H}}}}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}^N_{{\mathcal {H}}}) &{} =F &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {H}}} \times (0,T)}, \\ \nu (x) \nabla {{\varvec{u}}}^N_{{\mathcal {H}}} \mathbf . n &{}= g_N &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}^N_{{\mathcal {H}}} (.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {H}}}}. \end{array} \right. \\&\left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}^D_{{\mathcal {H}}}}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}^D_{{\mathcal {H}}}) &{} =F &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {H}}} \times (0,T)}, \\ {{\varvec{u}}}^D_{{\mathcal {H}}} &{}= g_D &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}^D_{{\mathcal {H}}} (.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {H}}}}. \end{array} \right. \end{aligned}$$

In their concept, Kohn and Vogelius characterized the unknown domain ${\mathcal {H}}$ as the solution to a shape optimization problem minimizing the difference between the Neumann and Dirichlet solutions:

$$\begin{aligned} \displaystyle \min _{{\mathcal {H}} \subset {\mathcal {B}}}\left\| {{\varvec{u}}}^N_{{\mathcal {H}}}-{{\varvec{u}}}^D_{{\mathcal {H}}}\right\| . \end{aligned}$$

This approach has been successfully used for solving various applications; crack detection [30], obstacle reconstruction [31], image restoration and edge detection [32], cavities identification in Stokes flow [9], Reconstruction of contact regions in semiconductor transistors [33], inverse source problem [34], ...etc.

Next, we will derive a topological sensitivity analysis for two examples of Kohn–Vogelius type functional. In the first case, we consider a shape function j defined by the $L^2$-norm. The second case is devoted to the $H^1$-semi norm.

4.4.1 The $L^2$-Norm

In the presence of a small geometric perturbation, the considered shape function is defined by

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) = \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | {{\varvec{u}}}_\varepsilon ^N- {{\varvec{u}}}_\varepsilon ^D|^2 dx dt , \end{aligned}$$

(4.20)

with ${{\varvec{u}}}_\varepsilon ^N\in H^1(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))$ is the solution of the perturbed Neumann problem

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}_\varepsilon ^N}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}_\varepsilon ^N)&{} =F &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T)}, \\ \nu (x) \nabla {{\varvec{u}}}_\varepsilon ^N\mathbf . n &{}= g_N &{} \text{ on } &{} {\partial {\mathcal {B}}\times (0,T) }, \\ {{\varvec{u}}}_\varepsilon ^N&{}= 0 &{} \text{ on } &{} {\partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) }, \\ {{\varvec{u}}}_\varepsilon ^N(.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } }, \end{array} \right. \end{aligned}$$

(4.21)

and ${{\varvec{u}}}_\varepsilon ^D\in H^1(0,T;H^1( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ))$ is the solution of the perturbed Dirichlet problem related to the measured heat temperature $g_D$

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}_\varepsilon ^D}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}_\varepsilon ^D)&{} =F &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } \times (0,T)}, \\ {{\varvec{u}}}_\varepsilon ^D&{}= g_D &{} \text{ on } &{} {\partial {\mathcal {B}}\times (0,T) }, \\ {{\varvec{u}}}_\varepsilon ^D&{}= 0 &{} \text{ on } &{} {\partial {\mathcal {C}}_{z,\varepsilon } \times (0,T) }, \\ {{\varvec{u}}}_\varepsilon ^D(.,0)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } }. \end{array} \right. \end{aligned}$$

(4.22)

In the absence of any perturbation (i.e. $\varepsilon =0$), we have ${\mathcal {C}}_{z,\varepsilon } = \emptyset$ and ${\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } = {\mathcal {B}}$. The non-perturbed states ${{\varvec{u}}}^N_0$ and ${{\varvec{u}}}^D_0$ satisfies the following Neumann and Dirichlet problems

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}^N_0}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}^N_0)&{} =F &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ \nu (x) \nabla {{\varvec{u}}}^N_0\mathbf . n &{}= g_N &{} \text{ on } &{} {\partial {\mathcal {B}}\times (0,T) }, \\ {{\varvec{u}}}^N_0(.,0)&{}= 0 &{} \text{ in } &{} {{\mathcal {B}}}, \end{array} \right. \end{aligned}$$

(4.23)

and

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}^D_0}{\partial t} - div(\nu (x) \nabla {{\varvec{u}}}^D_0)&{} =F &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {{\varvec{u}}}^D_0&{}= g_D &{} \text{ on } &{} {\partial {\mathcal {B}}\times (0,T) }, \\ {{\varvec{u}}}^D_0(.,0)&{}= 0 &{} \text{ in } &{} {{\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(4.24)

Proposition 4.6

The Kohn–Vogelius function defined by the $L^2$-norm (4.20) admits the following asymptotic expansion

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{1}{ \log \varepsilon } {\mathcal {S}}(z) + o \left( \frac{-1}{ \log \varepsilon } \right) , \end{aligned}$$

with ${\mathcal {S}}$ is the topological sensitivity function given by

$$\begin{aligned} {\mathcal {S}} (x) =2 \pi \int _0^T \Big [ {{\varvec{u}}}^N_0(x,t) {{\varvec{v}}}_0^N (x,t) +{{\varvec{u}}}^D_0(x,t) {{\varvec{v}}}_0^D (x,t) \Big ] dt , \, x \in {\mathcal {B}}\end{aligned}$$

(4.25)

where ${{\varvec{v}}}_0^N$ and ${{\varvec{v}}}_0^D$ are the adjoint states, solutions to

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial {{\varvec{v}}}_0^N }{\partial t} - div (\nu (x) \nabla {{\varvec{v}}}_0^N) &{} = - 2 ( {{\varvec{u}}}^N_0- {{\varvec{u}}}^D_0) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ \nu (x) \nabla {{\varvec{v}}}_0^N \mathbf . n &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0^N (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}, \end{array} \right. \end{aligned}$$

(4.26)

and

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial {{\varvec{v}}}_0^D }{\partial t} - div (\nu (x) \nabla {{\varvec{v}}}_0^D) &{} = - 2 ( {{\varvec{u}}}^D_0- {{\varvec{u}}}^N_0) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0^D &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0^D (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(4.27)

Proof

The variation of the Kohn Vogelius function can be written as

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j ({\mathcal {B}})= & {} \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \arrowvert {{\varvec{u}}}_\varepsilon ^D\arrowvert ^2 dx dt - \int _0^T \int _{{\mathcal {B}}} \arrowvert {{\varvec{u}}}^D_0\arrowvert ^2 dx dt + \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \arrowvert {{\varvec{u}}}_\varepsilon ^N\arrowvert ^2 dx dt \\&- \int _0^T \int _{{\mathcal {B}}} \arrowvert {{\varvec{u}}}^N_0\arrowvert ^2 dx dt \\&-2 \big [ \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } {{\varvec{u}}}_\varepsilon ^N{{\varvec{u}}}_\varepsilon ^Ddx dt - \int _0^T \int _{{\mathcal {B}}} {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0dx dt \big ]. \end{aligned}$$

Applying Proposition 4.4, one can derive

$$\begin{aligned}&\int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \arrowvert {{\varvec{u}}}_\varepsilon ^D\arrowvert ^2 dx dt - \int _0^T \int _{{\mathcal {B}}} \arrowvert {{\varvec{u}}}^D_0\arrowvert ^2 dx dt \nonumber \\&\quad = \frac{- 2 \pi }{\log ( \varepsilon ) } \int _0^T {{\varvec{u}}}^D_0(z,t) w_0^D (z,t) dt + o \big ( \frac{-1}{\log ( \varepsilon ) } \big ) , \end{aligned}$$

(4.28)

where $w_0^D$ is the associated adjoint state, solution to

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial w_0^D }{\partial t} - div (\nu (x) \nabla w_0^D) &{} = - 2 {{\varvec{u}}}^D_0&{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ w_0^D &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ w_0^D (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(4.29)

Similar to the previous term, Proposition 4.4 implies

$$\begin{aligned}&\int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \arrowvert {{\varvec{u}}}_\varepsilon ^N\arrowvert ^2 dx dt - \int _0^T \int _{{\mathcal {B}}} \arrowvert {{\varvec{u}}}^N_0\arrowvert ^2 dx dt \nonumber \\&\quad = \frac{- 2 \pi }{\log ( \varepsilon ) } \int _0^T {{\varvec{u}}}^N_0(z,t) w_0^N (z,t)dt + o \big ( \frac{-1}{\log ( \varepsilon ) } \big ), \end{aligned}$$

(4.30)

with $w_0^N$ solves

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial w_0^N }{\partial t} - div (\nu (x) \nabla w_0^N) &{} = - 2 {{\varvec{u}}}^N_0&{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ \nu (x) \nabla w_0^N \mathbf . n &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ w_0^N (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(4.31)

The mixed terms can be decomposed as

$$\begin{aligned}&\int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } {{\varvec{u}}}_\varepsilon ^N{{\varvec{u}}}_\varepsilon ^Ddx dt - \int _0^T \int _{{\mathcal {B}}} {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0dx dt\\&\quad = \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } ( {{\varvec{u}}}_\varepsilon ^D- {{\varvec{u}}}^D_0) ( {{\varvec{u}}}_\varepsilon ^N- {{\varvec{u}}}^N_0) dx dt - \int _0^T \int _{{\mathcal {C}}_{z,\varepsilon } } {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0dxdt \\&\qquad + \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } {{\varvec{u}}}_\varepsilon ^N{{\varvec{u}}}^D_0dx dt - \int _0^T \int _{{\mathcal {B}}} {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0dx dt + \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } {{\varvec{u}}}^N_0{{\varvec{u}}}_\varepsilon ^Ddx dt \\&\qquad - \int _0^T \int _{{\mathcal {B}}} {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0dx dt . \end{aligned}$$

Due to the fact that ${{\varvec{u}}}^N_0$ and ${{\varvec{u}}}^D_0$ are uniformly bounded on ${\mathcal {C}}_{z,\varepsilon } \times (0,T)$, one can deduce

$$\begin{aligned} \int _0^T \int _{{\mathcal {C}}_{z,\varepsilon } } {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0dxdt= & {} o \big ( \frac{-1}{\log ( \varepsilon ) } \big )\quad { and } \\ \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } ( {{\varvec{u}}}_\varepsilon ^D- {{\varvec{u}}}^D_0) ( {{\varvec{u}}}_\varepsilon ^N- {{\varvec{u}}}^N_0) dxdt= & {} o \big ( \frac{-1}{\log ( \varepsilon ) } \big ) \end{aligned}$$

As one can remark, the function $v\mapsto J_\varepsilon (v)=\displaystyle \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } v {{\varvec{u}}}^D_0$ is linear satisfying the hypothesis (H) with $\delta {\mathcal {J}}(z)=0$ and $DJ_0({{\varvec{u}}}^N_0)={{\varvec{u}}}^D_0$. Then, by Theorem 4.1 it follows

$$\begin{aligned}&\int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } {{\varvec{u}}}_\varepsilon ^N{{\varvec{u}}}^D_0dx dt - \int _0^T \int _{{\mathcal {B}}} {{\varvec{u}}}^N_0{{\varvec{u}}}^D_0\nonumber \\&\quad = \frac{- 2 \pi }{\log ( \varepsilon ) } \int _0^T {{\varvec{u}}}^N_0(z,t) z_0^N (z,t) + o \big ( \frac{-1}{\log ( \varepsilon ) }) , \end{aligned}$$

(4.32)

where $z_0^N$ is solution to

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial z_0^N }{\partial t} - div (\nu (x) \nabla z_0^N) &{} = - {{\varvec{u}}}^D_0&{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ \nu (x) \nabla z_0^N \mathbf . n &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ z_0^N (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(4.33)

Similarly, one can check that

$$\begin{aligned}&\int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } {{\varvec{u}}}_\varepsilon ^D{{\varvec{u}}}^N_0dx dt - \int _0^T \int _{{\mathcal {B}}} {{\varvec{u}}}^D_0{{\varvec{u}}}^N_0dx dt \nonumber \\&\quad = \frac{ -2 \pi }{\log ( \varepsilon ) } \int _0^T {{\varvec{u}}}^D_0(z,t) z_0^D (z,t) dt + o \big ( \frac{-1}{\log ( \varepsilon ) } \big ), \end{aligned}$$

(4.34)

where $z_0^D$ is solution to

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial z_0^D }{\partial t} - div (\nu (x) \nabla z_0^D) &{} = - {{\varvec{u}}}^N_0&{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ z_0^D &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ z_0^D (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

(4.35)

Setting ${{\varvec{v}}}_0^N = w_0^N - 2 z_0^N$ and ${{\varvec{v}}}_0^D = w_0^D - 2 z_0^D$. Combining (4.28) (4.30) (4.32) and (4.34), one gets

$$\begin{aligned} {\mathcal {S}} (x) =2 \pi \int _0^T \big ( {{\varvec{u}}}^N_0(x,t) {{\varvec{v}}}_0^N (x,t) +{{\varvec{u}}}^D_0(x,t) {{\varvec{v}}}_0^D (x,t) \big ) dt. \end{aligned}$$

From (4.29), (4.31), (4.33) and (4.35) one can check that ${{\varvec{v}}}_0^N$ and ${{\varvec{v}}}_0^D$ are solution to (4.26) and (4.27). $\square$

4.4.2 The $H^1-$Semi Norm

In this paragraph, we consider a Kohn–Vogelius type functional j defined by the $H^1-$semi norm. In the presence of a small geometric perturbation, the considered shape function reads

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) = \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } | \nabla {{\varvec{u}}}_\varepsilon ^N- \nabla {{\varvec{u}}}_\varepsilon ^D|^2 dx dt, \end{aligned}$$

(4.36)

with ${{\varvec{u}}}_\varepsilon ^N$ and ${{\varvec{u}}}_\varepsilon ^D$ solve the systems (4.21) and (4.22).

In order to simplify the presentation of the adjoint problems related to the Neumann and Dirichlet cases, we introduce the following cost functions:

$$\begin{aligned} J_0^D(u)=\int _{ {\mathcal {B}}} | \nabla u - \nabla {{\varvec{u}}}^D_0|^2 dx \text{ and } J_0^N(u)=\int _{ {\mathcal {B}}} | \nabla u - \nabla {{\varvec{u}}}^N_0|^2 dx \end{aligned}$$

The topological sensitivity analysis, describing the variation of this shape functional example with respect to the presence of a small geometric perturbation, is illustrated by the following proposition.

Proposition 4.7

The Kohn–Vogelius type functional (4.36) admits the asymptotic expansion

$$\begin{aligned} j( {\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{z,\varepsilon })=j({\mathcal {B}})- \frac{1}{ \log \varepsilon } {\mathcal {S}}(z) + o \left( \frac{-1}{ \log \varepsilon } \right) , \end{aligned}$$

where ${\mathcal {S}}$ is the topological sensitivity function, given by

$$\begin{aligned} {\mathcal {S}} (x)= & {} 2 \pi \int _0^T \Big [ {{\varvec{u}}}^N_0(x,t) ({{\varvec{v}}}_0^N (x,t) \nonumber \\&- {{\varvec{u}}}^N_0(x,t)) +{{\varvec{u}}}^D_0(x,t) ( {{\varvec{v}}}_0^D (x,t) -{{\varvec{u}}}^D_0(x,t) ) \Big ] dt , \, x \in {\mathcal {B}}. \end{aligned}$$

(4.37)

Here ${{\varvec{v}}}_0^N$ and ${{\varvec{v}}}_0^D$ are the adjoint states, solutions to the following adjoint problems:

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial {{\varvec{v}}}_0^N }{\partial t} - div (\nu (x) \nabla {{\varvec{v}}}_0^N) &{} = - DJ_0^D({{\varvec{u}}}^N_0) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ \nu (x) \nabla {{\varvec{v}}}_0^N \mathbf . n &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0^N (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle - \frac{\partial {{\varvec{v}}}_0^D }{\partial t} - div (\nu (x) \nabla {{\varvec{v}}}_0^D) &{} = - DJ_0^N({{\varvec{u}}}^D_0) &{} \text{ in } &{} { {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0^D &{}= 0 &{} \text{ on } &{} { \partial {\mathcal {B}}\times (0,T)}, \\ {{\varvec{v}}}_0^D (.,T)&{}= 0 &{} \text{ in } &{} { {\mathcal {B}}}. \end{array} \right. \end{aligned}$$

Proof

The variation of the Kohn–Vogelius type functional (4.36) can be written as

$$\begin{aligned} j( {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } ) - j ({\mathcal {B}})= & {} \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \arrowvert \nabla {{\varvec{u}}}_\varepsilon ^D\arrowvert ^2 dx dt - \int _0^T \int _{{\mathcal {B}}} \arrowvert \nabla {{\varvec{u}}}^D_0\arrowvert ^2 dx dt + \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \arrowvert \nabla {{\varvec{u}}}_\varepsilon ^N\arrowvert ^2 dx dt \\&- \int _0^T \int _{{\mathcal {B}}} \arrowvert \nabla {{\varvec{u}}}^N_0\arrowvert ^2 dx dt\\&-2 \big [ \int _0^T \int _{ {\mathcal {B}}\backslash \overline{{\mathcal {C}}}_{z,\varepsilon } } \nabla {{\varvec{u}}}_\varepsilon ^N. \nabla {{\varvec{u}}}_\varepsilon ^Ddx dt - \int _0^T \int _{{\mathcal {B}}} \nabla {{\varvec{u}}}^N_0. \nabla {{\varvec{u}}}^D_0dx dt \big ]. \end{aligned}$$

Adaping the analysis presented in the previous section with the help of Proposition 4.5, one can derive that

$$\begin{aligned} {\mathcal {S}} (x) =2 \pi \int _0^T \big ( {{\varvec{u}}}^N_0(x,t) ({{\varvec{v}}}_0^N (x,t) - {{\varvec{u}}}^N_0(x,t) ) +{{\varvec{u}}}^D_0(x,t) ({{\varvec{v}}}_0^D (x,t) - {{\varvec{u}}}^D_0(x,t) ) \big ) dt. \end{aligned}$$

$\square$

5 Numerical Experiments

This section is concerned with some numerical investigations. The numerical procedure is mainly based on the topological sensitivity analysis presented in Theorem 4.1. The time discretization is based on the Crank–Nicolson schema, and the space discretization is based on the ${\mathbb {P}}_1$-finite elements method. The numerical simulations are computed under the free software Freefem++ [35].

5.1 The Proposed Algorithm

Now we present a one-iteration algorithm based on the obtained theoretical results for solving the considered inverse design problem (2.2). It consists in finding the best locations and sizes of some cooling holes ${\mathcal {C}} ^i,\, 1\le i\le m$, solution to the following optimal design problem

$$\begin{aligned} ({\mathcal {P}}) \quad \min _{{\mathcal {H}} \subset {\mathcal {B}}} j({\mathcal {B}}\backslash \overline{{\mathcal {H}}}), \end{aligned}$$

where $\displaystyle {\mathcal {H}} = \displaystyle \cup _{i=1}^{m}{\mathcal {C}} ^i$, $m \in {\mathbb {N}}^*$ is a known integer, and j is a given design function satisfying the hypothesis (H) and defined by

$$\begin{aligned} j({\mathcal {B}}\backslash \overline{{\mathcal {H}}})=\int _0^T J_{{\mathcal {B}}\backslash \overline{{\mathcal {H}}}} ({{\varvec{u}}}(.,t)) dt , \end{aligned}$$

with ${{\varvec{u}}}$ is the solution to the following heat transfer problem in ${\mathcal {B}}\backslash \overline{{\mathcal {H}}}$

$$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}}{\partial t} - div ( \nu \nabla {{\varvec{u}}}) &{} = Q &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {H}}} \times (0,T) , \\ \nu \nabla {{\varvec{u}}}\mathbf . n &{}= g_N &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T) , \\ {{\varvec{u}}}&{}= 0 &{} \text{ on } &{} \partial {\mathcal {H}} \times (0,T) , \\ {{\varvec{u}}}(.,0)&{}=0 &{} \text{ in } &{} {\mathcal {B}}\backslash \overline{{\mathcal {H}}} . \end{array} \right. \end{aligned}$$

Here Q is a given source term and $g_N$ is an imposed flux on the external boundary $\partial {\mathcal {B}}$.

Based on Theorem 4.1, the topological sensitivity function ${\mathcal {S}}$, measuring the variation of j with respect to the presence of a small internal cooling hole ${\mathcal {C}}_{z,\varepsilon }$, is given by

$$\begin{aligned} {\mathcal {S}} (x)=2 \pi \nu \int _0^T {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) dt+ \delta {\mathcal {J}}(x ) , \, \forall x \in {\mathcal {B}}, \end{aligned}$$

where

• ${{\varvec{u}}}_0$ is the solution to the heat transfer problem in the non perturbed domain ${\mathcal {B}}$

  $$\begin{aligned} \left\{ \begin{array}{r l l l} \displaystyle \frac{\partial {{\varvec{u}}}_0}{\partial t} - div ( \nu \nabla {{\varvec{u}}}_0 )&{} = Q &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \nu \nabla {{\varvec{u}}}_0 \mathbf . n &{}= g_N &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T) , \\ {{\varvec{u}}}_0(.,0)&{}=0 &{} \text{ in } &{} {\mathcal {B}}. \end{array} \right. \end{aligned}$$

  (5.1)

• ${{\varvec{v}}}_0$ is the solution to the associated adjoint problem

  $$\begin{aligned} \left\{ \begin{array}{r l l l} - \displaystyle \frac{\partial {{\varvec{v}}}_0}{\partial t} - div ( \nu \nabla {{\varvec{v}}}_0)&{} = - D J_0 ( {{\varvec{u}}}_0 ) &{} \text{ in } &{} {\mathcal {B}}\times (0,T) , \\ \nu \nabla {{\varvec{v}}}_0\mathbf . n &{}=0 &{} \text{ on } &{} \partial {\mathcal {B}}\times (0,T) , \\ {{\varvec{v}}}_0(.,T)&{}=0 &{} \text{ in } &{} {\mathcal {B}}. \end{array} \right. \end{aligned}$$

  (5.2)

We present a fast and efficient detection procedure to solve the design problem $( {\mathcal {P}})$. The unknown cooling holes will be located at spots where the topological sensitivity function ${\mathcal {S}}$ is most negative. The main steps of the proposed detection procedure are summarized by the following one-iteration algorithm.

The One-Iteration Algorithm

• Solve the problem (5.1) and its adjoint problem (5.2) computed in the initial domain ${\mathcal {B}}$.

• Compute the topological sensitivity function ${\mathcal {S}} (x), \forall x\in {\mathcal {B}}$,

• Determine $\zeta ^* \in [0,1]$ such that $j({\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{\zeta ^*}) \le j({\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}_{\zeta }), \, \forall \zeta \in [0,1]$, where ${\mathcal {C}} _{\zeta }= \{ x \in {\mathcal {B}}; {\mathcal {S}}(x) < \zeta \delta _{min} \}$ with $\delta _{min}$ the most negative value of the function ${\mathcal {S}}$ in ${\mathcal {B}}.$

Next, we will present some numerical investigations. Two design function examples will be considered. The first one concerns the quadratic boundary function (4.6). The second one is associated with the $H^1-$semi norm function (4.11).

5.2 First Numerical Example

Here, we apply the previous algorithm for locating the unknown cooling holes ${\mathcal {H}} = \cup _{i=1}^m {\mathcal {C}}^i \subset {\mathcal {B}}$ solution to

$$\begin{aligned} \min _{{\mathcal {H}} \subset {\mathcal {B}}} \int _0^T \int _{\partial {\mathcal {B}}} | {{\varvec{u}}}-\varphi _m |^2 ds dt, \end{aligned}$$

(5.3)

where $\varphi _m$ is the measured data $\varphi _m = {{\varvec{u}}}^*_{| \partial {\mathcal {B}}\times (0,T)}$ on the outer boundary with ${{\varvec{u}}}^*$ is the temperature field computed using the exact hole locations.

From Theorem 4.1 and Proposition 4.3, one can deduce that the topological sensitivity function ${\mathcal {S}}$ associated to this inverse design problem is given by

$$\begin{aligned} {\mathcal {S}}(x) = 2 \pi \nu \int _0^{T} {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) dt , \, \forall x \in {\mathcal {B}}. \end{aligned}$$

Next, we present the obtained numerical experiments. In each test case, we present the iso-value of the topological sensitivity function and the optimal design.

In Fig. 2, we present the numerical results for circular shaped holes ${\mathcal {C}}^*$ having different sizes. In Fig. 3, we illustrate the detection results for elliptical shaped cooling holes having different sizes.

Fig. 2

Reconstruction of circular shaped holes with different sizes

Fig. 3

Reconstruction of elliptical shaped cooling holes

Fig. 4

Detection of elliptical shaped hole

Fig. 5

Detection of well separated internal holes

Fig. 6

Reconstruction of complex-shaped holes

As one can observe, the unknown hole ${\mathcal {C}} ^*$ is located at the zone where the topological sensitivity function ${\mathcal {S}}$ is most negative. The boundary $\partial {\mathcal {C}} ^*$ is described by a level set curve of the scalar function ${\mathcal {S}}$ i.e.

$$\begin{aligned} \partial {\mathcal {C}} ^* = \{ x \in {\mathcal {B}}, \, {\mathcal {S}}(x)= \zeta ^* \delta _{min} \}. \end{aligned}$$

5.3 Second Numerical Example

Now, we consider a second example of design problem related to the $H^1$-semi norm. It is given by

$$\begin{aligned} \min _{{\mathcal {C}} \subset {\mathcal {B}}} \int _0^T \int _{{\mathcal {B}}\backslash {\overline{{\mathcal {C}} }}} \nu | \nabla {{\varvec{u}}}- \nabla \varphi _w |^2 dx dt, \end{aligned}$$

(5.4)

where $\varphi _w$ is a given wanted state $\varphi _w = {{\varvec{u}}}^*_{| {\mathcal {B}}\times (0,T)} .$

From Theorem 4.1 and Proposition 4.5, it follows that the topological sensitivity function is given by

$$\begin{aligned} {\mathcal {S}}(x)= 2 \pi \nu (x) \int _0^{T} \big [ {{\varvec{u}}}_0(x,t) {{\varvec{v}}}_0(x,t) + | {{\varvec{u}}}_0(x,t) |^2 \big ] dt , \, \forall x \in {\mathcal {B}}. \end{aligned}$$

Next, we present some numerical results for different test examples.

We start by the detection of elliptical shaped cooling holes. The iso-values of the topological sensitivity function ${\mathcal {S}}$ and the optimal design are described in Fig. 4. As one can observe, the unknown holes ${\mathcal {C}} ^*$ (black line) is approximated by a level set curve of ${\mathcal {S}}$.

Next, we apply our one-iteration procedure for locating well separated multiple internal holes. The obtained result is depicted in Fig. 5. As one can observe, each geometry component’s location is described by a local minimum of the topological sensitivity function ${\mathcal {S}}$.

The last numerical example is concerned with a complex-shaped hole. The obtained results are presented in Fig. 6.

As one can remark, the domain to be detected is located at the zone where the topological sensitivity function ${\mathcal {S}}$ is minimal. The unknown domain is well located but its boundary is not well approximated by a level set curve of ${\mathcal {S}}$.

6 Conclusion

A topological sensitivity analysis, with respect to the creation of a small geometric perturbation, is derived for the unsteady state heat transfer equation. The mathematical analysis is general and can be applied for various parabolic operators. The derived asymptotic formula is valid for a large class of design functions. Based on the obtained theoretical results, we have proposed a one-iteration numerical algorithm for solving the turbine blade optimal design problem. The obtained numerical simulations show the efficiency and accuracy of the proposed approach.