Stabilization Results for Well-Posed Potential Formulations of a Current-Controlled Piezoelectric Beam and Their Approximations

Abstract

Hysteresis is highly undesired for the vibration control of piezoelectric beams especially in high-precision applications. Current-controlled piezoelectric beams cope with hysteresis substantially in comparison to the voltage-controlled counterparts. However, the existing low fidelity current-controlled beam models are finite dimensional, and they are either heuristic or mathematically over-simplified differential equations. In this paper, novel infinite-dimensional models, by a thorough variational approach, are introduced to describe vibrations on a piezoelectric beam. Electro-magnetic effects due to Maxwell’s equations factor in the models via the electric and magnetic potentials. Both models are written in the standard state-space formulation (A, B, C), and are shown to be well-posed in the energy space by fixing the so-called Coulomb and Lorenz gauges. Different from the voltage-actuated counterparts, the control operator B is compact in the energy space, i.e. the exponential stabilizability is not possible. Considering the compact $C=B^*-$type state feedback controller (induced voltage), both models fail to be asymptotically stable if the material parameters satisfy certain conditions. To achieve at least asymptotic stability, we propose an additional controller. Finally, the stabilizability of infinite-dimensional electrostatic/quasi-static model (no magnetic effects) is analyzed for comparison. The biggest contrast is that the asymptotic stability is achieved by an electro-mechanical state feedback controller for all material parameters. Our findings are simulated by the filtered semi-discrete Finite Difference Method.

1 Introduction

Piezoelectric materials have become more and more promising in aeronautic, civil, defense, biomedical, and space structures [8, 47] due to their small size and high power density. These materials can be used as both sensors and actuators since they have the ability to interchange mechanical energy, electrical energy, and magnetic energy during the motion. The amount of magnetic energy produced/stored can be minor or major in certain applications [55, Chap. 8]. Recent cutting-edge applications include cardiac pacemakers [7], course-changing bullets [10], structural health monitoring [17], nano-positioners [18], ultrasound imagers [45], ultrasonic welders and cleaners [51], energy harvesting [14] due to the excellent advantages of the fast response time, large mechanical force, and extremely fine resolution [18, 42].

Fig. 1

A piezoelectric beam extents or contracts by supplying surface current $i_s(t)$ to its electrodes since the charges separate and line up in the vertical direction

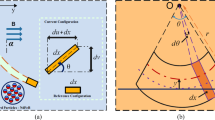
There are mainly three ways to electrically actuate piezoelectric materials: supplying voltage, current or charge to its electrodes, see Fig. 1. Piezoelectric materials have been traditionally activated by a voltage source [4, 13, 41, 47, 48, 50]. In fact, it is stated in [1] that “From the very beginning of applying piezoelectric materials as actuators, they are voltage-controlled, and this is still the standard way of electrical steering.” However, the biggest disadvantage of voltage-controlled piezoelectric materials is that there is huge hysteresis between voltage source and mechanical strain [9]. An empirical approach to avoid hysteresis is simply applying only low voltages, but this prevents these structures from being used at their maximum potential. Another approach, which is gaining popularity [3], is current or charge-control designs since these types of actuation lead to considerably less hysteresis [5, 15, 24,25,26]. In fact, charge or current control enhances the dynamics, reduces the costs, and performs better at low frequencies [39]. This motivates the consideration of current-actuated piezoelectric beams.

Accurate modeling of piezoelectric beams are critical to achieve control objectives for high-precision motion [4]. However, the existing current-controlled beam models in the literature are generally based on ordinary differential equations, and these equations model only the first several vibrational models of devices. Moreover, majority of existing models considers only electrostatic or quasi-static assumptions due to Maxwell’s equations). Involving electrical effects in the modeling is done by coupling a circuit equation to the mechanical equations. This way, the current input is accounted for, see [19].

Even though it is known that the electrostatic theory is sufficient for many applications in piezoelectric acoustic wave devices, there are situations in which the full electro-magnetic coupling needs to be considered [21, 55, 56]. To our knowledge, there is no fully-dynamic infinite-dimensional model for “current-controlled” piezoelectric beams in the literature accounting for the full electro-magnetic effects. By incorporating mathematically-thorough Lagrangian formalism involving all electro-magneto-mechanical interactions, and using the variational approach [23], “partial” differential equations (PDE) can be used to accurately model vibrational dynamics of these devices. In this approach, the states of the electro-magnetic interaction due to the Maxwell’s equations are chosen in terms of the scalar electric potential and vector magnetic potential. However, it is well-known that the electric and magnetic potentials are not uniquely determined for this formulation (for instance see [11, p. 80]). To obtain a unique solution to the initial-boundary value problem, an appropriate gauge condition is chosen. Once a gauge condition is fixed, the electro-magnetic coupling in the charge equation is eliminated. There are many gauges used for Maxwell’s equations [12]. One of the most commonly-used one is called Coulomb gauge, and it assumes that electrical potential has infinite velocity. The other commonly-used one is called Lorenz gauge which assumes that the electrical field equation is a wave-type equation so electrical field propagates with the speed of light. In many applications, Coulomb gauge is preferred since proving uniqueness of the solutions is less challenging [29].

The controllability of piezoelectric beams is mostly studied for voltage control in finite or infinite dimensional setting [4, 9]. Letting $\mathbf{y}, \mathcal A, B, u$ be the system state, system operator, control operator, and electric controllers, the PDE models can be transformed into the state-space formulation

$$\begin{aligned} {\dot{\mathbf{y}}}=\mathcal A\mathbf{y}+ B u(t). \end{aligned}$$

The control operator B is unbounded in the infinite dimensional energy space if the piezoelectric material is controlled by a voltage or a charge source with [27, 28] or without [2, 20, 33, 47] magnetic effects. The controllability of electrostatic, quasi-static and fully dynamic models for voltage control is thoroughly studied in [27]. It is shown that only electrostatic/quasi-static model is exponentially stable by a $B^*-$type feedback controller. The fully dynamic model is not exponentially stabilizable by any state feedback, and not even asymptotically stable for many combinations of material parameters by the $B^*-$feedback controller [27, 30]. On the other hand, the control operator B is compact in the energy space if the piezoelectric material is controlled by a current source. This is first observed in [28, 37] where a piezoelectric beam model is considered in the standard state-space formulation with electromagnetic potentials and the Coulomb gauge. The current-driven piezoelectric beams have different controllability characteristics though since B is compact. Exponential stability is not possible. A lack of asymptotic stability is shown with the $B^*-$feedback controller provided that a number-theoretical condition is satisfied for certain subclass of material parameters. In this work, a thorough analysis for the description of the spectrum is not possible due to the complexity of coupling and the gauge condition. For the finite dimensional circuit-model setting, there are several results available in the literature [9, 19, 24, 25].

Following the modeling and control methodology of [27, 34, 35, 37], modeling and stabilization current and charge-controlled smart composites are also studied with the Coulomb gauge formalism in [32]. For the inclusion of electro-magnetic effects in piezoelectric layers, all three approaches: electrostatic, quasi-static, and fully dynamic, are considered. Even though a dramatic reflection of magnetic effects on the stabilizability characteristics of the composite with the $B^*-$type feedback is shown, the models provided alternate electro-magnetic feedback controllers. For the electrostatic and quasi-static approaches, exponential stability (charge control) and asymptotic stability (current control) results are proved.

There are also recent Port-Hamiltonian models of piezoelectric beams where the electro-magnetic modeling of the piezoelectric modeling is based on the models for the transmission lines. These models are automatically passive and with the extra dissipation these model can be made strictly passive. When these models are obtained, purely mechanical part can be interconnected to the piezoelectric part. In [54], it is shown that quasi-static Port-Hamiltonian modeling does not fulfill the necessary conditions of stabilization. In [52], fully dynamic model is obtained by blending the full set of Maxwell’s equations to the P-H structure for mechanical equations but without using the potential theory or gauge formalism. In [53], a nonlinear piezoelectric beam model is obtained with and without magnetic effects. This model is shown to fulfill the stability conditions with full mechanical controllers. Agreeing with the results of [27, 32], it is shown that the fully dynamic models of piezo-patch system with electro-magnetic and mechanical controllers, beams achieves stability [52].

To the best of our knowledge, there are no other results reported in the literature for the infinite dimensional models including all types of electro-magnetic effects. The fundamental goals of this paper are

• (i) to introduce fully-dynamic and electrostatic/quasi-static current-controlled PDE models obtained by a consistent variational approach. Novelty of the models is due to the inclusion of electro-magnetic effects by scalar electric and vector magnetic potentials.

• (ii) to prove that Lorenz gauge and Coulomb gauge models have well-posed state-space formulations in the corresponding energy spaces with compatibility conditions. In particular, the proposed Lorenz gauge formulation is quite new yet requires a special class of initial conditions for the electric potential. Analogous to [27, 37], both models provide alternative measurable electro-magnetic $B^*-$feedback controllers.

• (iii) to show that the closed-loop system for each model with the corresponding $B^*-$feedback controller lacks asymptotic stability for certain combinations of material parameters as in [32, 37]. Those combinations correspond to high-frequency vibrational modes. In this paper, we propose a remedial mechanical boundary controller to achieve at least asymptotic stability.

• (iv) to introduce the current-actuated electrostatic/quasi-static model which can never be exponentially stable. However, a feedback controller, requiring measurements of both mechanical and electrical states, can be designed to achieve polynomial stability. This type of control law has much to do with energy harvesting applications [14, 46].

• (v) to simulate vibrations with proposed control laws by the semi-discrete Finite Difference method with indirect filtering by adding relevant viscosity terms to each equation. This is a discretization technique where the so-called spill-over issue and the effects of spurious vibrational modes are discarded [49]. It is also safe to say that, to our knowledge, the numerical schemes using the filtering technique for a piezoelectric beam are preliminary and have never been proposed for the current-actuated piezoelectric beam models with the gauge formalism. However, further analysis is necessary.

Note that the compatibility condition arises for both gauges. The one found in the Lorenz gauge is quite new and it results from the semigroup formulation. Note that compatibility conditions are very similar to the “incompressibility condition” in hydrodynamics. This also lines up with the $H(curl, \varOmega )$ and $H(div, \varOmega )$ spaces in [11, 12] for which the global existence and uniqueness theorems are proved for Maxwell’s equations.

Note also that fully-dynamic modeling and stabilizability results for Coulomb gauge and free-free boundary conditions are first presented in [28, 37]. However, in this paper, we include the discussion of well-posed semigroup formulation with the Lorenz gauge, the model with the electrostatic/quasi-static assumptions, and the related numerical investigations for clamped-free boundary conditions. The numerical investigations are all based on the filtering technique developed in [49].

2 Modeling Assumptions and Gauge Conditions

Consider a piezoelectric beam of dimensions $\varOmega =[0,L]\times [-r,r]\times [-\frac{h}{2}, \frac{h}{2}]$ where $L> > h.$ Let x, y be the longitudinal directions, z the transverse direction, and $\partial \varOmega$ the boundary. Since $L>>h$, beam theory is appropriate and Euler-Bernoulli small displacement assumptions are good enough to model mechanical effects. To model the electro-magnetic properties, there are mainly three approaches [48]: electrostatic, quasi-static, and dynamic. Here, a fully dynamic approach is used. The Gauss’s law of magnetism $\nabla \cdot B=0$ implies that there exists a magnetic potential vector A such that $B=\nabla \times A$ by Poincáre’s lemma (p. 214, [12]). Substituting B into the Faraday’s law $\dot{B}= -\nabla \times E$ yields the existence of a scalar electric potential $\phi$ such that

$$\begin{aligned} E+\dot{A}=-\nabla \phi . \end{aligned}$$

(1)

To include the induced effects of the electromagnetism, we assume a quadratic-through thickness scalar electrical potential distribution and a linear-through thickness magnetic potential vector distribution:

$$\begin{aligned}&\phi (x,z)=\phi ^0(x)+z \phi ^1(x)+ \frac{z^2}{2} \phi ^2(x), \end{aligned}$$

(2)

$$\begin{aligned}&A(x,z) = \left( \begin{array}{c} A_1(x,z) \\ 0 \\ A_3(x,z) \\ \end{array} \right) =\left( \begin{array}{c} A_1^0(x) + z A_1^1(x) \\ 0 \\ A_3^0(x) + z A_3^1(x) \\ \end{array} \right) . \end{aligned}$$

(3)

Therefore, (1) is rewritten as the following:

$$\begin{aligned} \nonumber&E_1= - \left( \dot{A}_1^0 +z \dot{A}_1^1 \right) -\left( ({\phi }^0)_x+z (\phi ^1)_x+ \frac{z^2}{2} (\phi ^2)_x\right) ,\\&E_3= -\left( \dot{A}_3^0 + z \dot{A}_3^1 \right) -\left( \phi ^1 + z \phi ^2 \right) . \end{aligned}$$

(4)

We also assume that there are no mechanical external forces acting on the beam, and polarization and isotropy are taken in the transverse direction. Denoting v the stretching of the centerline of the beam in $x-$direction (longitudinal vibrations), the application of the Hamilton’s principle to the Lagrangian (kinetic energy-enthalpy+work due to $i_s(t)$) with respect to all possible admissible displacements yields two decoupled systems of equations; one set of equations for stretching another set of equations for bending. For details about modeling, refer to [28, 32, 37]. The applied current $i_s(t)$ at the electrodes affects only the stretching motion. Therefore, only stretching equations are considered in this paper:

$$\begin{aligned} (Stretching)\left\{ \begin{array}{l l} \rho \ddot{v} -{\alpha } v_{xx} -{\gamma } \left( \phi + {\dot{\eta }} \right) _x= 0 &{} \\ -\xi \left( \phi _{xx}+ {\dot{\theta }}_x\right) + {\dot{\eta }}+ \phi -\frac{\gamma }{{\varepsilon _{3}}}v_x= 0&{} \\ \ddot{\theta }+ {\dot{\phi }}_x -\frac{\mu }{\xi {\varepsilon _{3}}} \left( \eta _x- \theta \right) =\frac{i_s(t)}{\xi {\varepsilon _{3}} h} &{} \\ \ddot{\eta }+ {\dot{\phi }}-\frac{\gamma }{{\varepsilon _{3}}}\dot{v}_x -\frac{\mu }{{\varepsilon _{3}}} \left( \eta _{xx}-\theta _x\right) =0&{} \end{array}\right. \end{aligned}$$

(5)

where $\phi :=\phi ^1, \theta :=A_1^1,$ $\eta :=A_3^0,$ $\xi :=\frac{\varepsilon _{1}h^2}{12{\varepsilon _{3}}},$ and $\rho , \alpha , \gamma , \varepsilon _1, {\varepsilon _{3}}, \mu$ denote the mass density per unit volume, elastic stiffness, piezoelectric coupling coefficient, permittivity in x and z directions, and magnetic permeability, respectively. It will also be assumed the surface electrical continuity condition [27, 50] is satisfied

$$\begin{aligned} \frac{di_s(x,t)}{dx}=0.\end{aligned}$$

(6)

since there is no external body charge or current applied to the beam. We consider the beam clamped on the left end, i.e. $v(0)=0,$ and free on the right end. By the Hamilton’s principle, the natural boundary conditions are

$$\begin{aligned} \left\{ \begin{array}{l r} \left| {\alpha }v_x +{\gamma }\left( \phi +{\dot{\eta }} \right) \right| _{x=L}=0 \quad \mathrm{{(Lateral ~ force)}} \\ \left| \xi {\varepsilon _{3}}\left( {\dot{\theta }} + \phi _x\right) \right| _{x=0,L}=0 \quad \mathrm{{(First~ charge ~ moment)}}\\ \left| \mu \left( \theta -\eta _x\right) \right| _{x=0,L}=0 \quad \mathrm{{(Current). }}\\ \end{array} \right. \end{aligned}$$

(7)

The PDE system (5)–(7) does not yield a unique solution since (i) the magnetic potential vector components $\theta ,\eta$ and the electric potential $\phi$ are not uniquely defined due to (1) [11, 27], (ii) the Lagrangian is invariant under certain transformations [27, 37]. The ambiguity arising from this invariance must be fixed. To obtain a unique solution, particular gauge conditions are presented in electro-magnetic theory to completely decouple the electromagnetic equations in (5). Two of the most widely-used gauges are Lorenz and Coulomb gauges [12, 27, 29, 37, 44]. For the piezoelectric beam model, these gauges are

$$\begin{aligned}&\left\{ \begin{array}{ll} - \xi \theta _x + \eta = \frac{\xi {\varepsilon _{3}} }{\mu }{\dot{\phi }} &{}\quad \mathrm{(Lorenz ~gauge~ condition)} \\ -\xi \theta _x + \eta = 0 &{}\quad \mathrm{(Coulomb~ gauge~ condition)} \end{array} \right. \end{aligned}$$

(8)

with the boundary conditions $\theta (0)=\theta (L)= 0.$ The difference between these two gauges arise from assumption whether the electric potential $\phi$ is static or dynamic.

Notice that the Coulomb gauge (8) makes the term $-\xi {\dot{\theta }}_x+ {\dot{\eta }}$ in the $\phi -$equation in (5) zero. Therefore, $\phi -$equation in (5) is transformed into an elliptic equation:

$$\begin{aligned} -\xi \phi _{xx}+\phi = \frac{\gamma }{{\varepsilon _{3}}}v_x. \end{aligned}$$

(9)

Defining the operator $P_\xi$ by

$$\begin{aligned} P_{\xi }:=\left( -\xi D_x^2+I\right) ^{-1}.\end{aligned}$$

(10)

It can be shown that ${P_\xi }$ is a compact and non-negative operator on ${\mathcal {L}}_{2} (0,L)$. Therefore, the equation (9) has the solution $\phi =\frac{\gamma }{{\varepsilon _{3}}}P_\xi v_x.$

In the case of Lorenz gauge (8), the term $-\xi {\dot{\theta }}_x+ {\dot{\eta }}$ in the $\phi -$equation in (5) is transformed into $\frac{\xi {\varepsilon _{3}}}{\mu } \ddot{\phi }.$ As well, the terms ${\dot{\phi }}_x -\frac{\mu }{\xi {\varepsilon _{3}}} \left( \eta _x- \theta \right)$ and ${\dot{\phi }}-\frac{\mu }{{\varepsilon _{3}}} \left( \eta _{xx}-\theta _x\right)$ in $\theta$ and $\eta$ equations in (5) are transformed into $-\frac{\mu }{\xi {\varepsilon _{3}}} \left( \xi \theta _{xx}- \theta \right)$ and $-\frac{\mu }{\xi {\varepsilon _{3}}} \left( \xi \eta _{xx}- \eta \right)$, respectively. This transformation not only converts the $\phi -$equation to a wave equation but also the $\theta$ and $\eta$ equations. Therefore, both electric and magnetic equations are wave equations.

Taking into the argument above, the equations of motion (5)–(10) respectively reduce to

$$\begin{aligned}&{(\mathrm{Lorenz})} \left\{ \begin{array}{ll} \rho \ddot{v} -{\alpha } v_{xx} -{\gamma } \left( \phi _x + {\dot{\eta }}_x \right) = 0 &{} \\ \ddot{\phi }-\frac{\mu }{{\varepsilon _{3}}}\phi _{xx} +\frac{\mu }{\xi {\varepsilon _{3}}}\phi -\frac{\gamma \mu }{\xi {\varepsilon _{3}}^2}v_x=0 &{} \\ \ddot{\theta }- \frac{\mu }{{\varepsilon _{3}}} \theta _{xx}+\frac{\mu }{ \xi {\varepsilon _{3}} } \theta =\frac{i_s(t)}{\xi {\varepsilon _{3}} h} &{} \\ \ddot{\eta }- \frac{\mu }{{\varepsilon _{3}}} \eta _{xx} + \frac{\mu }{\xi {\varepsilon _{3}}} \eta -\frac{\gamma }{{\varepsilon _{3}}} \dot{v}_x=0,\quad (x,t)\in (0,L) \times {\mathbb {R}}^+,&{} \\ \left\{ \begin{array}{ll} v(0,t)={\alpha } v_{x}(L,t) + \gamma \phi (L,t) +\gamma {\dot{\eta }}(L,t)=0, &{} \\ \left\{ \phi _x, \theta , \eta _x\right\} (0,t)=\left\{ \phi _x, \theta , \eta _x\right\} (L,t)=0, &{}\\ (v,\phi ,\theta ,\eta ,\dot{v}, {\dot{\phi }}, {\dot{\theta }}, {\dot{\eta }})(x,0)=(v^0, \phi ^0, \theta ^0, \eta ^0, v^1, \phi ^1, \theta ^1,\eta ^1).&{} \end{array}\right.&\end{array} \right. \end{aligned}$$

(11)

$$\begin{aligned}&{(\mathrm{Coulomb})} \left\{ \begin{array}{ll} \rho \ddot{v}-{\alpha } v_{xx} -\frac{{\gamma }^2}{{{\varepsilon _{3}}}}(P_{\xi } v_x)_x- {\gamma }{\dot{\eta }}_x= 0 &{} \\ \xi {\varepsilon _{3}} \ddot{\theta }+\mu \left( \theta - \eta _x\right) +\xi \gamma (P_{\xi } \dot{v}_x)_x=\frac{i_s(t)}{h} &{} \\ {{\varepsilon _{3}}} \ddot{\eta }+ \mu \left( \theta -\eta _x\right) _x- {\gamma }\left( \dot{v}_x-(P_\xi \dot{v}_x)\right) = 0, ~ (x,t)\in (0,L) \times {\mathbb {R}}^+,&{} \\ \left\{ \begin{array}{ll} v(0,t)={\alpha } v_{x}(L,t) +\frac{{\gamma }^2 }{{\varepsilon _{3}}}{P_\xi } v_x(L,t) + {\gamma } {\dot{\eta }}(L,t)=0, &{} \\ \left\{ \theta , \eta _x\right\} (0,t)=\left\{ \theta , \eta _x\right\} (L,t)=0, &{}\\ (v,\theta ,\eta ,\dot{v}, {\dot{\theta }}, {\dot{\eta }})(x,0)=(v^0, \theta ^0, \eta ^0, v^1,\theta ^1,\eta ^1).&{} \end{array}\right.&\end{array} \right. \nonumber \\ \end{aligned}$$

(12)

Note that distributed mechanical damping such as viscous damping $\delta \dot{v}$ or Kelvin-Voigt damping $-\delta \dot{v}_{xx}$ with $\delta > 0,$ can also be considered in both models. However, the goal of the paper is to see the effect of the active electrical controller $i_s(t)$ on the stabilization of the piezoelectric beam model.

3 Well-Posedness of the Lorenz Gauge Model (11)

The natural energy E(t) associated with (11) is the sum of kinetic, potential, magnetic, and electrical energies, respectively:

$$\begin{aligned} \mathbf {K}= & {} \frac{\rho }{2} \int _0^L \left| \dot{v} \right| ^2~dx,\quad \mathbf {P}= \frac{\alpha }{2} \int _0^L |v_x|^2 ~dx,\quad \mathbf {B}=\frac{\mu }{2} \int _0^L\left| \theta -\eta _x \right| ^2~dx.\\ \mathbf {E}= & {} \frac{1}{2} \int _0^L \left[ \xi {\varepsilon _{3}} \left| {\dot{\theta }}+\phi _x \right| ^2 + {{\varepsilon _{3}}} \left| {\dot{\eta }}+\phi ) \right| ^2 \right] ~dx \end{aligned}$$

where $\theta -\eta _x,$ ${\dot{\theta }}+\phi _x,$ and ${\dot{\eta }}+\phi$ refer to magnetic field component in $y-$direction, electrical field component in $x-$direction, and electric field component in $z-$direction. Therefore,

$$\begin{aligned} \mathrm {E}(t)=\frac{1}{2}\int _0^L \left\{ \mu \left| \theta -\eta _x\right| ^2+ \xi {\varepsilon _{3}}|{\dot{\theta }}+\phi _x |^2 + {\varepsilon _{3}} \left| {\dot{\eta }}+\phi \right| ^2 +{\alpha } |v_x|^2 +\rho |\dot{v}|^2 \right\} dx.\quad \nonumber \\ \end{aligned}$$

(13)

For any scalar $C^1-$function $\chi =\chi (x, t),$ consider the transformation

$$\begin{aligned}&\theta \mapsto {\tilde{\theta }}:= \theta + \chi _x,\quad \eta \mapsto {\tilde{\eta }}:= \eta + \chi ,\quad \phi \mapsto {\tilde{\phi }}:= \phi -{\dot{\chi }}.&\end{aligned}$$

(14)

Since

$$\begin{aligned} \begin{array}{ll} {\tilde{\theta }} - {\tilde{\theta }}_x= \theta +\chi _x -\eta _x-\chi _x=\theta -\eta _x&{} \\ {\dot{{\tilde{\theta }}}} + {\tilde{\phi }}_x= {\dot{\theta }} +{\dot{\chi }}_x + \phi _x -{\dot{\chi }}_x&{} \\ {\dot{{\tilde{\eta }}}} + {\tilde{\phi }}= {\dot{\eta }} +{\dot{\chi }} + \phi -{\dot{\chi }},&{} \end{array} \end{aligned}$$

(15)

E(t) is invariant under the transformation (14). Once the Lorenz gauge (8) is used for $\{{\tilde{\theta }},{\tilde{\eta }},{\tilde{\phi }}\}:$

$$\begin{aligned} \begin{array}{ll} -\xi {\tilde{\theta }}_x + {\tilde{\eta }}=\frac{\xi {\varepsilon _{3}}}{\mu }{\dot{{\tilde{\phi }}}} &{}\\ -\xi \left( \theta _x +\chi _{xx}\right) + \left( \eta +\chi \right) =\frac{\xi {\varepsilon _{3}}}{\mu }\left( {{\dot{\phi }}}-\ddot{\chi }\right) &{}\\ \frac{\xi {\varepsilon _{3}}}{\mu } \ddot{\chi }-\xi \chi _{xx}+\chi =0. \end{array} \end{aligned}$$

(16)

By (14), the boundary conditions for $\chi$ is chosen in such a way that they align with the boundary conditions of $\theta$ and $\eta$ in (11)and the gauge condition (8). Therefore, $\chi$ in (16) is considered together with the Neumann boundary conditions:

$$\begin{aligned} \chi _x(0,t)=\chi _x(L,t)\equiv 0. \end{aligned}$$

(17)

By (14), ${\tilde{\theta }} (x,0)= \theta (x,0)+ \chi _x (x,0),\quad {\tilde{\eta }}(x,0)= \eta (x,0)+ \chi (x,0),\quad {\tilde{\phi }} (x,0)= \phi (x,0)-{\dot{\chi }} (x,0).$ To obtain a zero solution for (16)–(17), we choose the zero initial conditions $\phi$:

$$\begin{aligned} \phi (x,0)={\dot{\phi }}(x,0)=0, \end{aligned}$$

(18)

This implies that $\chi (x,0)={\dot{\chi }}(x,0)=0.$ Therefore, the initial conditions for $\{\theta ,\eta \}$ satisfy the following condition:

$$\begin{aligned} -\xi \theta _x(x,0) + \eta (x,0)=0. \end{aligned}$$

By (13), $E(t)\equiv 0$ implies that

$$\begin{aligned}&\theta -\eta _x={\dot{\theta }}+\phi _x={\dot{\eta }}+\phi =\dot{v}=v_x\equiv 0. \end{aligned}$$

Finally, we obtain two sets of equations for $\theta$ and $\phi :$

$$\begin{aligned}&\left\{ \begin{array}{ll} \frac{\xi {\varepsilon _{3}}}{\mu }\ddot{\phi }-\xi \phi _{xx} +{\dot{\phi }}=0&{}\\ \phi _x(0,t)=\phi _x(L,t) ~~\mathrm{and}~~ \phi (x,0)={\dot{\phi }}(x,0)=0, \end{array}\right. \end{aligned}$$

(19)

$$\begin{aligned}&\left\{ \begin{array}{ll} \theta -\xi \theta _{xx}+\frac{\xi {\varepsilon _{3}}}{\mu }{\dot{\phi }}=0&{}\\ \theta (0,t)=\theta (L,t)=0. \end{array}\right. \end{aligned}$$

(20)

The solution of (19) is $\phi \equiv 0.$ Feeding $\phi \equiv 0$ into (20) yields $\theta \equiv 0.$ Finally by (8), $\eta =0.$

Note that, in the case of a Coulomb gauge in Sect. 4, we obtain in Sect. 4 that $\chi$ satisfies an elliptic equation, not a wave equation, with the same boundary conditions. The extra condition is not needed (18).

Considering the components of E(t) in (13), now define the states

$$\begin{aligned} \mathbf{y}=[y_1, y_2, y_3, y_4, y_5]^{\mathrm{T}}=[\theta -\eta _x, {\dot{\theta }}+\phi _x, {\dot{\eta }} +\phi , v_x, \dot{v}]^{\mathrm{T}} \end{aligned}$$

(21)

with $\mathbf{y}(x,0)=\mathbf{y}_0=[\theta (x,0)-\eta _x(x,0), {\dot{\theta }}(x,0), {\dot{\eta }}(x,0), v_x(x,0), \dot{v}(x,0) ]^{\mathrm{T}}.$

By these choices of the states, note that the following compatibility condition arises

$$\begin{aligned} \xi (y_2)_x-y_3+\frac{\gamma }{{\varepsilon _{3}}}y_4=0\end{aligned}$$

(22)

due to the second equation in (11) and the gauge condition (8); taking the time derivative of (8) and substituting it in the second equation in (11) and using (21) yields

$$\begin{aligned} \begin{array}{ll} {\ddot{\phi }}&{}=\frac{\mu }{{\varepsilon _{3}}}\phi _{xx}-\frac{\mu }{{\varepsilon _{3}}\xi }\phi + \frac{\gamma \mu }{\xi {\varepsilon _{3}}^2}y_4 \\ &{}= \frac{\mu }{{\varepsilon _{3}}} ((y_2)_x-{\dot{\theta }}_x)- \frac{\mu }{{\varepsilon _{3}}\xi } (y_3-{\dot{\eta }}) + \frac{\gamma \mu }{\xi {\varepsilon _{3}}^2 }y_4 \\ &{}= \frac{\mu }{{\varepsilon _{3}}} ((y_2)_x- \frac{\mu }{{\varepsilon _{3}}\xi } y_3 + \frac{\gamma \mu }{\xi {\varepsilon _{3}}^2 }y_4 + \frac{\mu }{\xi {\varepsilon _{3}}}\left( -\xi {\dot{\theta }}_x + {\dot{\eta }}\right) \\ &{}= \frac{\mu }{{\varepsilon _{3}}} ((y_2)_x- \frac{\mu }{{\varepsilon _{3}}\xi } y_3 + \frac{\gamma \mu }{\xi {\varepsilon _{3}}^2 }y_4 + {\ddot{\phi }}. \end{array} \end{aligned}$$

Let $H^1_L(0,L)=\{f\in H^1(0,L)~:~ f(0)=0 \}.$ Define the linear space

$$\begin{aligned} \begin{array}{l} \mathrm H= \left\{ \mathbf{y}\in ({\mathcal {L}}_{2} (0,L))^5: (y_2)_x\in {\mathcal {L}}_{2} (0,L), \quad y_2(0)=y_2(L)=0, \right. \\ \left. \quad \quad \quad \quad \xi (y_2)_x -y_3+\frac{\gamma }{{\varepsilon _{3}}}y_4=0\right\} \end{array} \end{aligned}$$

(23)

and the bilinear form on $\mathrm H\times \mathrm H:$

$$\begin{aligned} a(\mathbf{y}, \mathbf{z})= & {} \int _0^L \left\{ \mu y_1 {\bar{z}}_1+ \xi {\varepsilon _{3}} y_2{\bar{z}}_2 + {\varepsilon _{3}} y_3{\bar{z}}_3 + {\alpha } y_4 {\bar{z}}_4 + \rho y_5 {\bar{z}}_5 \right\} dx. \end{aligned}$$

(24)

The term ${\varepsilon _{3}} y_3{\bar{z}}_3$ in (23) can be replaced by the compatibility condition in (23) so that

$$\begin{aligned} {\varepsilon _{3}} y_3{\bar{z}}_3 ={\varepsilon _{3}}\left( \xi (y_2)_x + \frac{\gamma }{{\varepsilon _{3}}}y_4\right) \left( \xi ({\bar{z}}_2)_x + \frac{\gamma }{{\varepsilon _{3}}}{\bar{z}}_4\right) . \end{aligned}$$

The bilinear form (24) is therefore symmetric, continuous and coercive on $\mathrm H\times \mathrm H$. Continuity of $a(\cdot ,\cdot )$ follows from the Poincare’s inequlaity for the $y_2$-term. The coercivity of $a(\cdot ,\cdot )$ follows from the generalized Young’s inequality $ab\le \frac{a^2}{\kappa } + \kappa b^2$ as the following

$$\begin{aligned} a(\mathbf{y}, \mathbf{z})= & {} \int _0^L \left\{ \mu |y_1|^2 + \xi {\varepsilon _{3}} |y_2|^2+ + \frac{{\varepsilon _{3}}}{2} |y_3|^2 + \frac{\xi ^2{\varepsilon _{3}}}{2} |(y_2)_x|^2 \right. \\&\left. +\,\gamma \xi \mathrm{Re} (y_4 ({\bar{y}}_2)_x )+ ({\alpha }+\frac{\gamma ^2}{2{\varepsilon _{3}}}) |y_4|^2+\rho |y_5|^2 \right\} ~dx\\\ge & {} \int _0^L \left\{ \mu |y_1|^2 + \xi {\varepsilon _{3}} |y_2|^2+ + \frac{{\varepsilon _{3}}}{2} |y_3|^2 \right. \\&\left. +\,\left( \frac{\xi ^2{\varepsilon _{3}}}{2}-\gamma \xi \kappa \right) |(y_2)_x|^2 + ({\alpha }+\frac{\gamma ^2}{2{\varepsilon _{3}}}-\frac{\gamma \xi }{\kappa }) |y_4|^2+\rho |y_5|^2 \right\} ~dx\\\ge & {} C\Vert y\Vert _{\mathrm H}^2 \end{aligned}$$

where $\kappa$ is chosen as $\frac{\gamma \xi }{\alpha +\frac{\gamma ^2}{{\varepsilon _{3}}}}<\kappa < \frac{\xi {\varepsilon _{3}}}{2\gamma }$ so that the coefficients $\frac{\xi ^2{\varepsilon _{3}}}{2}-\gamma \xi \kappa , {\alpha }+\frac{\gamma ^2}{2{\varepsilon _{3}}}-\frac{\gamma \xi }{\kappa }>0,$ and $C=\mathrm{min}(\mu , \xi {\varepsilon _{3}}, \left( \frac{\xi ^2{\varepsilon _{3}}}{2}-\gamma \xi \kappa \right) , \frac{{\varepsilon _{3}}}{2}, ({\alpha }+\frac{\gamma ^2}{2{\varepsilon _{3}}}-\frac{\gamma \xi }{\kappa }), \rho ).$

Therefore, the bilinear form (24) defines an inner product on the linear space $\mathrm H$. The following result is immediate:

Theorem 1

The energy E in (13) is the norm induced by this inner product, and $\mathrm H$ is a Hilbert space with this norm.

Proof

We only prove the completeness of $\mathrm H$ here. Let $\mathbf{y}^k$ be a Cauchy sequence in $\mathrm H$ so that $y_1^k, y_2^k, (y_2^k)_x, y_3^k, y_4^k, y_5^k$ are Cauchy sequences in ${\mathcal {L}}_{2} (0,L)$ with $y_2^k(0)=y_2^k(L)=0.$ By the completeness of ${\mathcal {L}}_{2} (0,L)$ and $H^1_0(0,L)$ there exists $z_1, z_2, z_{22}, z_3, z_4, z_5\in {\mathcal {L}}_{2} (0,L)$ such that $y_1^k\rightarrow z_1,$ $y_2^k\rightarrow z_2,~(y_2^k)_x\rightarrow z_{22}, ~y_3^k\rightarrow z_3,~ y_4^k\rightarrow z_4,~ y_5^k\rightarrow z_5$ as $k\rightarrow \infty .$ Moreover, $z_2(0)=z_2(L)=0.$ Therefore, for $\varphi \in C^\infty _0(0,L),$

$$\begin{aligned} \lim _{k\rightarrow \infty }\int _0^L (y_2^k)_x ~\varphi ~dx=-\lim _{k\rightarrow \infty }\int _0^L y_2^k ~\varphi _x ~dx = -\int _0^L z_{2} ~\varphi _x ~dx. \end{aligned}$$

(25)

Therefore, $z_2\in H^1(0,L)$ with $(z_2)_x=z_{22}$ as distributions, and by construction, $z_{22}\in {\mathcal {L}}_{2} (0,L).$ Therefore, $z_2, (z_2)_x \in {\mathcal {L}}_{2} (0,L).$ Similarly, for all $\varphi \in C^\infty _0(0,L),$

$$\begin{aligned} 0=\int _0^L \left[ \xi (y_2^k)_x -y_3^k+\frac{\gamma }{{\varepsilon _{3}}}y_4^k\right] ~\varphi ~dx \rightarrow \int _0^L \left[ \xi z_{22} -z_3+\frac{\gamma }{{\varepsilon _{3}}}z_4\right] ~\varphi ~dx=0 \end{aligned}$$

as $k\rightarrow \infty .$ Hence, $\xi (z_2)_x -z_3+\frac{\gamma }{{\varepsilon _{3}}}z_4=0$ as distributions. $\square$

Define the operator

$$\begin{aligned}&\mathcal A= \left( {\begin{array}{*{20}c} 0 &{} I &{} -D_x &{} 0 &{} 0 \\ -\frac{\mu }{\xi {\varepsilon _{3}}}I &{} 0 &{} 0 &{} 0 &{} 0 \\ -\frac{\mu }{{\varepsilon _{3}}}D_x &{} 0 &{} 0 &{} 0 &{} \frac{\gamma }{{\varepsilon _{3}}}D_x \\ 0 &{} 0 &{} 0 &{} 0 &{} D_x \\ 0 &{} 0 &{} \frac{\gamma }{\rho }D_x &{} \frac{\alpha }{\rho }D_x &{}0 \\ \end{array}} \right) \end{aligned}$$

(26)

with

$$\begin{aligned}&\mathrm{Dom}(\mathcal A)= \left[ H^1_0(0,L) \times H^1_0(0,L) \times (H^1(0,L))^2\times H^1_L(0,L)\right] \\&\quad \quad \bigcap \left\{ \mathbf{y}\in \mathrm H :~\left( {\alpha } y_4 + \gamma y_3\right) (L)=0 \right\} , \end{aligned}$$

and the B and $B^*$ operators with the new state are

$$\begin{aligned} \left\langle \mathcal B u(t), \psi \right\rangle _{{\mathrm H}}= & {} \frac{1}{h}\int _0^L u(t) ~\psi _2 ~dx =u(t)\frac{1}{h}\int _0^L ~ \psi _2 ~dx=\left\langle u, \mathcal B^*\psi \right\rangle _{\mathcal U} \end{aligned}$$

and $\mathcal B \mathcal B^*\in \mathcal L( \mathrm H, \mathrm H).$

Lemma 1

The operator $\mathcal A : \mathrm{Dom} ({\mathcal A}) \rightarrow \mathrm H.$

Proof

Let $\mathbf{y}\in \mathrm{Dom}(\mathcal A).$ Then

$$\begin{aligned} \mathcal A \mathbf{y}= & {} \begin{bmatrix} y_2-(y_3)_x \\ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1\\ -\frac{\mu }{{\varepsilon _{3}}}(y_1)_x+\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x\\ (y_5)_x \\ \frac{\gamma }{\rho }(y_3)_x+\frac{\alpha }{\rho }(y_4)_x \end{bmatrix}. \end{aligned}$$

For given $\mathbf{y}\in \mathrm{Dom}(\mathcal A),$ it is obvious that $y_2-(y_3)_x\in {\mathcal {L}}_{2} (0,L), -\frac{\mu }{\xi {\varepsilon _{3}}}y_1\in H^1_0(0,L), ~ -\frac{\mu }{{\varepsilon _{3}}}(y_1)_x+\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x,~ (y_5)_x,~ (y_3)_x+\frac{\alpha }{\rho }(y_4)_x \in {\mathcal {L}}_{2} (0,L).$ Next we check if $\mathcal A \mathbf{y}$ satisfies the compatibility condition (22) for $\mathcal A \mathbf{y}:$

$$\begin{aligned} \xi ((\mathcal A y)_2)_x -(\mathcal A y)_3+\frac{\gamma }{{\varepsilon _{3}}} (\mathcal A y)_4= -\frac{\mu }{{\varepsilon _{3}}}(y_1)_x+\frac{\mu }{{\varepsilon _{3}}}(y_1)_x-\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x+\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x=0. \end{aligned}$$

This completes the proof of $\mathcal A \mathbf{y}\in \mathrm H.$ $\square$

Theorem 2

For any $\mathbf{g}\in \mathrm {H}$ there is $\mathbf{y}\in \mathrm{Dom}(\mathcal {A} )$ so that $\mathcal {A} \mathbf{y}=\mathbf{g}.$ That is, $0\in \rho (\mathcal A).$

Proof

This is equivalent to solving the system of equations for $\mathbf{y}\in \text {Dom}(\mathcal {{\tilde{A}}} ).$ Simplifying the equations leads to

$$\begin{aligned} \begin{bmatrix} y_2-(y_3)_x=g_1 \\ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1=g_2\\ -\frac{\mu }{{\varepsilon _{3}}}(y_1)_x+\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x=g_3\\ (y_5)_x=g_4 \\ \frac{\gamma }{\rho }(y_3)_x+\frac{\alpha }{\rho }(y_4)_x=g_5 \end{bmatrix} \end{aligned}$$

Since $\mathbf{g}\in \mathrm H,$ the gauge condition $\xi (g_2)_x -g_3+\frac{\gamma }{{\varepsilon _{3}}}g_4=0$ is satisfied. By using the Green’s function theory, we obtain $\mathbf{y}\in \text {Dom}(\mathcal {{\tilde{A}}} )$ where

$$\begin{aligned} \begin{array}{ll} y_1(x)=-\frac{\xi {\varepsilon _{3}}}{\mu }g_2&{}\\ y_2(x)=-\frac{\left( \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) g_1+\gamma \rho g_5 \right) e^{-\frac{(L+x) \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha \xi {\varepsilon _{3}} }}} \left( e^{\frac{L \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha \xi {\varepsilon _{3}} }}}-e^{\frac{x \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha \xi {\varepsilon _{3}} }}}\right) ^2}{2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ y_3(x)=\frac{\rho \gamma }{\alpha {\varepsilon _{3}} +\gamma ^2}\int _x^L g_5(s)ds &{} \\ \quad + \frac{\sqrt{\alpha \xi {\varepsilon _{3}} } \left( g_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +\gamma \rho g_5 \right) e^{-\frac{(L+x) \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha \xi {\varepsilon _{3}} }}} \left( e^{\frac{2 L \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha \xi {\varepsilon _{3}} }}}-e^{\frac{2 x \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha \xi {\varepsilon _{3}} }}}\right) }{2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) ^{3/2}}&{}\\ y_4(x)=\frac{\rho {\varepsilon _{3}}}{\alpha {\varepsilon _{3}} +\gamma ^2}\int _x^L g_5(s)ds + &{}\\ \quad +\frac{\gamma \sqrt{\xi } \sqrt{{\varepsilon _{3}} } \left( g_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +\gamma \rho g_5 \right) e^{-\frac{(L+x) \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha } \sqrt{\xi } \sqrt{{\varepsilon _{3}} }}} \left( e^{\frac{2 L \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha } \sqrt{\xi } \sqrt{{\varepsilon _{3}} }}}-e^{\frac{2 x \sqrt{\alpha {\varepsilon _{3}} +\gamma ^2}}{\sqrt{\alpha } \sqrt{\xi } \sqrt{{\varepsilon _{3}} }}}\right) }{2 \sqrt{\alpha } \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) ^{3/2}}&{}\\ y_5(x)=\int _0^x g_4(s)ds. \end{array} \end{aligned}$$

(27)

where $\mathbf{y}$ clearly satisfies the compatibility condition $\xi (y_2)_x -y_3+\frac{\gamma }{{\varepsilon _{3}}}y_4=0.$ $\square$

Theorem 3

The operator $\mathcal A$ satisfies $\mathcal {A}^*=-\mathcal {A}$ on $\mathrm {H},$ and

${\mathcal {A}}: \mathrm{Dom} (\mathcal A) \subset \mathrm H \rightarrow \mathrm H$ defined by (26) is the generator of a unitary semigroup $\{e^{{\mathcal {A}}t}\}_{t\ge 0}.$

Proof

Let $\mathbf{y}, \mathbf{z}\in \mathrm{Dom}({\mathcal {A}}).$ Then, by integration by parts and rearranging the terms, we have

$$\begin{aligned} \nonumber&\left\langle {\mathcal {A}}\mathbf{y}, \mathbf{z}\right\rangle _{\mathrm {H}} = \left\langle \begin{bmatrix} y_2-(y_3)_x \\ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1\\ -\frac{\mu }{{\varepsilon _{3}}}(y_1)_x+\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x\\ (y_5)_x \\ \frac{\gamma }{\rho }(y_3)_x+\frac{\alpha }{\rho }(y_4)_x \end{bmatrix}, \left[ \begin{array}{c} z_1 \\ z_2 \\ z_3\\ z_4\\ z_5\\ \end{array} \right] \right\rangle _{\mathrm {H}}\\ \nonumber&\quad = \int _0^L \left\{ \mu (y_2-(y_3)_x){\bar{z}}_1-\mu y_1{\bar{z}}_2+(-\mu (y_1)_x)+\gamma (y_5)_x){\bar{z}}_3 \right. \\ \nonumber&\qquad \left. +\,\alpha (y_5)_x{\bar{z}}_4+ (\gamma (y_3)_x+\alpha (y_4)_x){\bar{z}}_5\right\} ~dx\\ \nonumber&\quad = -\int _0^L \left\{ \mu ({\bar{z}}_2-({\bar{z}}_3)_x) y_1-\mu {\bar{z}}_1 y_2+(-\mu ({\bar{z}}_1)_x)+\gamma ({\bar{z}}_5)_x) y_3 \right. \\ \nonumber&\qquad \left. +\,\alpha ({\bar{z}}_5)_x y_4+ (\gamma ({\bar{z}}_3)_x+\alpha ({\bar{z}}_4)_x) y_5\right\} ~dx\\&\quad = \left\langle \mathbf{y}, -{\mathcal {A}}\mathbf{z}\right\rangle _{\mathrm {H}}= \left\langle \mathbf{y}, \mathcal A^*\mathbf{z}\right\rangle _{\mathrm {H}} \end{aligned}$$

(28)

with $\mathrm{Dom}(\mathcal A^*)=\mathrm{Dom}(\mathcal A).$ By Theorem 2, is the generator of a unitary semigroup.

$\square$

The system (11) can be written as

$$\begin{aligned} {\dot{\mathbf{y}}}=\mathcal A\mathbf{y}+ Bi_s(t), \quad \mathbf{y}(0)=y_0, \end{aligned}$$

(29)

where $\mathbf{y}_0$ is defined by (18) and (21), the control operator B is defined by

$$\begin{aligned} B=[0\quad \frac{1}{\xi {\varepsilon _{3}} h}I\quad 0 \quad 0 \quad 0]^{\mathrm{T}} \end{aligned}$$

where I is the identity operator.

Theorem 4

Let $T>0,$ and $i_s(t)\in L^2(0,T).$ For any $\mathbf{y}_0 \in \mathrm { H},$ $\mathbf{y}\in C[[0,T]; \mathrm H],$ and there exists a positive constants c(T) such that (29) satisfies

$$\begin{aligned} \Vert \mathbf{y}(T) \Vert ^2_{\mathrm H}\le & {} c (T)\left\{ \Vert \mathbf{y}^0\Vert ^2_{\mathrm H} + \Vert i_s\Vert ^2_{{\mathcal {L}}_{2} (0,T)}\right\} . \end{aligned}$$

(30)

Proof

The operator $\mathcal A: {\mathrm{Dom}}(\mathcal A) \rightarrow \mathcal H$ is a unitary semigroup by Lemma 3. Therefore, it is an infinitesimal generator of $C_0-$semigroup of contractions by Lümer-Phillips theorem [38]. Since with $\frac{di_s}{dx}=0$ by the surface continuity condition (6), B is admissible for $\{e^{\mathcal A t}\}_{t\ge 0}:$

$$\begin{aligned} \left\langle B i_{s}(t), {\tilde{\psi }}\right\rangle _{\mathrm {H},\mathrm {H}}=\frac{1}{h}\int _{0}^{L} i_{s}(t)\psi _{2}(x) dx<\infty . \end{aligned}$$

Hence the conclusion (30) follows. $\square$

3.1 Lack of Stabilization of the Lorenz Gauge Model (11)

Along the trajectories of (11), the energy (13) satisfies

$$\begin{aligned} \frac{d{{\mathrm {E}}}(t)}{dt}=i_s(t) \left( \int _0^L \psi _2(x) dx\right) . \end{aligned}$$

The adjoint operator $B^*$ of B is found by

$$\begin{aligned} \left\langle B i_{s}, \mathbf{y}\right\rangle _{\mathrm {H}, \mathrm {H}}= \frac{i_{s}(t)}{h} \int _{0}^{L} 1\cdot {\bar{y}}_{2}(x) dx = \left\langle i_{s}, B^{*}\mathbf{y}\right\rangle _{{\mathbb {C}}} \end{aligned}$$

where $B^*\mathbf{y}= \frac{1}{h}\int _0^L {\bar{y}}_2(x) dx.$ We investigate the asymptotic stability of the closed-loop system with the $B^*-$feedback.

$$\begin{aligned} B^*\mathbf{y}= \frac{1}{ h}\int _0^L y_2(x) dx. \end{aligned}$$

(31)

This leads to the feedback control

$$\begin{aligned} i_s(t)=-K_1 h^2 \int _0^L ~ ({\dot{\theta }}+\phi _x) dx \end{aligned}$$

(32)

where $K_1 >0$ is arbitrary. This can be regarded as induced total charge (voltage) accumulated at the electrodes of the beam.

The uncontrolled system (11) has an infinite number of eigenvalues on the imaginary axis. Moreover, the feedback control operator is compact and rank 1. Thus, it is not possible to exponentially stabilize the piezo-electric beam; see for instance [6].

The abstract state-space description (29) with (32) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{\mathbf{y}}} = \mathcal {{\tilde{A}}} \mathbf{y}= \mathcal A\mathbf{y}- K_1 \xi ^2 {\varepsilon _{3}}^2h^2 B B^*\mathbf{y},&{}\\ \mathbf{y}(x,0) = \mathbf{y}^{\mathbf{0}}.&{} \end{array} \right. \end{aligned}$$

(33)

The operator $\mathcal {{\tilde{A}}}: \mathrm{Dom}(\mathcal {{\tilde{A}}})\subset \mathrm H \rightarrow \mathrm H$ defined by (33) with domain $\mathrm{Dom}(\mathcal {{\tilde{A}}})=\mathrm{Dom}(\mathcal { A})$ is densely defined in $\mathrm H.$

Lemma 2

The infinitesimal generator $\mathcal {{\tilde{A}}}$ satisfies $\mathcal {{\tilde{A}}}^*=-\mathcal {{\tilde{A}}}(-K_1)$ on $\mathrm {H}.$ Moreover it is dissipative and it satisfies $\mathrm{Re}\left\langle \mathcal {{\tilde{A}}} \mathbf{y}, \mathbf{y}\right\rangle _{{\mathrm H}}\le 0.$

Theorem 5

$\mathcal {{\tilde{A}}}: \mathrm{Dom}( {\mathcal A}) \rightarrow {\mathrm H}$ is the infinitesimal generator of a $C_0-$semigroup of contractions. Therefore for every $T\ge 0,$ and $\mathbf{y}^{\mathbf{0}}\in \mathrm{Dom}( {\mathcal A})$ solves (33) and $\mathbf{y}\in C([0,T]; \mathrm{Dom}( {\mathcal A}))\cap C^1\left( [0,T]; {\mathrm H}\right) .$ Moreover, the spectrum $\sigma ({\mathcal {{\tilde{A}}}})$ of $\mathcal {{\tilde{A}}}$ has all isolated eigenvalues.

Proof

(outline): The domain $\mathrm{Dom}({\mathcal {{\tilde{A}}}})$ is densely defined and is compact in ${\mathrm H}$ due to the compact embedding of $H^1(0,L)\subseteq L^2(0,L),$ and $H^2(0,L)\subseteq H^1(0,L).$ Moreover, $0\in \rho ({ \mathcal A} )$ by Theorem 2. Therefore, $(\lambda I -{\mathcal {{\tilde{A}}}})^{-1}$ is compact at $\lambda =0,$ (and thus compact for all $\lambda \in \rho (\tilde{\mathcal A})$). Hence the spectrum of ${\mathcal {{\tilde{A}}}}$ has all isolated eigenvalues. $\square$

Theorem 6

Let $a_1=\frac{ 2n\pi }{L}, a_2=\frac{ 2m \pi }{L},$ and $m^2+ n^2>\frac{\mu \rho L^2 }{16 \alpha \xi {\varepsilon _{3}} \pi ^2}$ for $m,n\in {\mathbb {N}}$ where $a_1$ and $a_2$ are defined by (41). For $\mathbf{y}^{\mathbf{0}}\in \mathrm H ,$ the semigroup $\{e^{\mathcal {{\tilde{A}}}t}\}_{t\ge 0}$ corresponding to (33) is not asymptotically stable in $\mathrm {H}$, i.e. $\Vert e^{\mathcal {{\tilde{A}}}t}\mathbf{y}^{\mathbf{0}}\Vert _{\mathrm {H}}\nrightarrow 0, ~~~ t\rightarrow \infty .$

Proof

Since $0\in \rho (\mathcal {{\tilde{A}}}),$ we show that there are eigenvalues on the imaginary axis, or in other words, the set

$$\begin{aligned} \left\{ \mathbf{y}\in \mathrm{Dom}({\tilde{{\mathcal {A}}}}) ~|~ \mathrm{Re} \left\langle {\mathcal {{\tilde{A}}}}\mathbf{y}, \mathbf{y}\right\rangle _{{\mathrm H}} = -K_1\left( \int _0^L y_2(x) ~dx\right) ^2= 0\right\} \end{aligned}$$

(34)

has nontrivial solutions $\mathbf{y}\ne 0.$ It will then follow that the system (33) is NOT strongly stable.

Let $\lambda =\imath \tau .$ The eigenvalue problem is

$$\begin{aligned}&\left\{ \begin{array}{ll} y_2-(y_3)_x=\imath \tau y_1&{} \\ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1=\imath \tau y_2 &{}\\ -\frac{\mu }{{\varepsilon _{3}}}(y_1)_x+\frac{\gamma }{{\varepsilon _{3}}}(y_5)_x=\imath \tau y_3 &{}\\ (y_5)_x=\imath \tau y_4 &{}\\ \frac{\gamma }{\rho }(y_3)_x+\frac{\alpha }{\rho }(y_4)_x=\imath \tau y_5 &{} \end{array} \right. \end{aligned}$$

(35)

together with the boundary conditions

$$\begin{aligned} y_5(0)=y_2(0)=y_1(L)=\alpha y_4(L)+\gamma y_3(L)=0. \end{aligned}$$

(36)

and the compatibility condition (22). By using (22), we can eliminate the variables $y_1, y_3, y_4,$ and the system (35) can be reduced to

$$\begin{aligned}&\left\{ \begin{array}{ll} (y_2)_{xx}=\frac{1}{\xi {\varepsilon _{3}}}\left( 1-\frac{\xi \tau ^2}{\mu }\right) (\frac{\gamma ^2}{\alpha }+{\varepsilon _{3}})y_2-\frac{\rho \tau \imath }{\alpha \xi {\varepsilon _{3}} }y_5&{}\\ (y_5)_{xx}=-\frac{\gamma \tau \imath }{\alpha }\left( 1-\frac{\xi {\varepsilon _{3}}\tau ^2}{\mu }\right) y_2-\frac{\rho \tau ^2}{\alpha }y_5&{} \\ y_2(0)=y_5(0)=y_2(L)=\gamma \xi \imath \tau (y_2)_x(L)+(\alpha +\frac{\gamma ^2}{{\varepsilon _{3}}})(y_5)_x(L)=0 \end{array} \right. \end{aligned}$$

(37)

Now we let $Z=[y_2~ (y_2)_x~ y_5 ~(y_5)_x]^{\mathrm{T}}.$ We write the system (37)

$$\begin{aligned} \frac{dZ}{dx}=\mathcal D Z=\left( \begin{array}{cccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \frac{\left( \frac{\gamma ^2}{\alpha }+\epsilon _3\right) \left( 1-\frac{\xi \tau ^2 \epsilon _3}{\mu }\right) }{\xi \epsilon _3} &{}\quad 0 &{}\quad -\frac{\imath \gamma \rho \tau }{\alpha \xi \epsilon _3} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ -\frac{\imath \gamma \tau \left( 1-\frac{\xi \tau ^2 \epsilon _3}{\mu }\right) }{\alpha } &{}\quad 0 &{}\quad -\frac{\rho \tau ^2}{\alpha } &{}\quad 0 \\ \end{array} \right) Z. \end{aligned}$$

(38)

with the boundary conditions

$$\begin{aligned}&z_1(0)=z_3(0)=z_1(L)=\gamma \xi \imath \tau z_2(L)+(\alpha +\frac{\gamma ^2}{{\varepsilon _{3}}})z_4(L)=0. \end{aligned}$$

(39)

The solution to (38) is $Z=e^{\mathcal D x} C$ where $C=[c_1 ~ c_2 ~ c_3 ~ c_4]^{\mathrm{T}}$ is a vector of arbitrary coefficients. The characteristic equation for $\mathcal D$ is

$$\begin{aligned}&\alpha \mu \xi {\varepsilon _{3}} {\tilde{\lambda }}^4 + \left( \xi \tau ^2 {\varepsilon _{3}} \left( \alpha {\varepsilon _{3}} +\gamma ^2+\mu \rho \right) -\mu \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) \right) {\tilde{\lambda }}^2\\&\quad +\,\rho \tau ^2 {\varepsilon _{3}} \left( \xi \tau ^2 {\varepsilon _{3}} -\mu \right) =0. \end{aligned}$$

Let

$$\begin{aligned} \nonumber&A=\alpha \mu \xi {\varepsilon _{3}},\quad B=-(\alpha {\varepsilon _{3}} + \gamma ^2)(\mu -{\varepsilon _{3}} \xi \tau ^2)+\alpha \xi \mu \rho {\varepsilon _{3}} \tau ^2\\&C=-\rho \tau ^2 {\varepsilon _{3}} \left( \mu -{\varepsilon _{3}}\xi \tau ^2 \right) , \end{aligned}$$

(40)

and

$$\begin{aligned} a_1=\sqrt{\frac{B+ \sqrt{B^2-4AC}}{2A}}, \quad a_2 = \sqrt{\frac{B- \sqrt{B^2-4AC}}{2A}}. \end{aligned}$$

(41)

Note that in the description of $B^2-4AC,$ the term ${\varepsilon _{3}}\left( \alpha -\frac{\gamma ^2}{{\varepsilon _{3}}}\right) >0$ since $\frac{\gamma ^2}{{\varepsilon _{3}}}$ is due to the quadratic-through thickness electrical field assumption. Indeed, the piezoelectric beam becomes relatively less-stiff even though $\frac{\gamma ^2}{{\varepsilon _{3}}} \ll \alpha .$ We consider the case

$$\begin{aligned} \mu -\xi {\varepsilon _{3}} \tau ^2<0, \end{aligned}$$

(42)

and therefore, $B^2-4AC>0.$ This generates four complex conjugate roots of the characteristic equation:

$$\begin{aligned} {\tilde{\lambda }}_1=\imath a_1, ~~{\tilde{\lambda }}_2=-\imath a_1, ~~ {\tilde{\lambda }}_3=\imath a_2, ~~ {\tilde{\lambda }}_4=-\imath a_2. \end{aligned}$$

(43)

The solution of (38) is written as $Z=P e^{Jx}P^{-1} C$ where

$$\begin{aligned} P=\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 \\ \imath a_1 &{} -\imath a_1 &{} \imath a_2 &{} -\imath a_2 \\ b_1 &{} b_1 &{} b_2 &{} b_2 \\ \imath a_1 b_1 &{} -\imath a_1 b_1 &{} \imath a_2 b_2 &{} -\imath a_2 b_2 \\ \end{array} \right] , e^{Jx}=\left[ \begin{array}{cccccc} e^{\imath x a_1} &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{-\imath x a_1} &{} 0 &{} 0 \\ 0 &{} 0 &{} e^{\imath x a_2} &{} 0 \\ 0 &{} 0 &{} 0 &{} e^{-\imath x a_2} \\ \end{array} \right] , \end{aligned}$$

(44)

the constants $b_1,b_2$ are defined as in

$$\begin{aligned}&b_1=\frac{ \gamma \tau (\mu -\xi {\varepsilon _{3}}\tau ^2)\imath }{\mu (\alpha a_1^2-\rho \tau ^2)},\quad b_2=\frac{ \gamma \tau (\mu -\xi {\varepsilon _{3}}\tau ^2)\imath }{\mu (\alpha a_2^2-\rho \tau ^2)} \end{aligned}$$

(45)

where $b_1-b_2\ne 0.$ By using the boundary conditions $z_1(0)=z_3(0)=0$ in (39), we get $c_1=c_3=0.$ Therefore, the solution to (38) is

$$\begin{aligned} z_1(x)= & {} \frac{c_2 \left( a_1 b_1 \sin \left( a_2 x\right) -a_2 b_2 \sin \left( a_1 x\right) \right) }{a_1 a_2 \left( b_1-b_2\right) }+\frac{c_4 \left( a_2 \sin \left( a_1 x\right) -a_1 \sin \left( a_2 x\right) \right) }{a_1 a_2 \left( b_1-b_2\right) }\\ z_3(x)= & {} \frac{b_1 b_2 c_2 \left( a_1 \sin \left( a_2 x\right) -a_2 \sin \left( a_1 x\right) \right) }{a_1 a_2 \left( b_1-b_2\right) }+\frac{c_4 \left( a_2 b_1 \sin \left( a_1 x\right) -a_1 b_2 \sin \left( a_2 x\right) \right) }{a_1 a_2 \left( b_1-b_2\right) }. \end{aligned}$$

Choosing $a_1$ and $a_2$ as in the statement of the theorem, we immediately get $c_2=\mathrm{free}:$

$$\begin{aligned}\left( \begin{array}{cc} \frac{\left( -i \xi \tau {\varepsilon _{3}} ^2-\left( \gamma ^2+\alpha {\varepsilon _{3}} \right) b_1\right) b_2+b_1 \left( i \xi \tau {\varepsilon _{3}} ^2+\left( \gamma ^2+\alpha {\varepsilon _{3}} \right) b_2\right) }{{\varepsilon _{3}} \left( b_1-b_2\right) } &{} \frac{\gamma ^2+\alpha {\varepsilon _{3}} }{{\varepsilon _{3}} } \\ 0 &{} 0 \end{array} \right) \left( \begin{array}{c} c_2 \\ c_4 \end{array}\right) =\mathbf {0}. \end{aligned}$$

For simplicity take $c_2=1.$ Therefore, a family of nontrivial solutions of the overdetermined eigenvalue problem (together with the feedback condition $\int _0^L z_1 (x)dx=0$) is

$$\begin{aligned} \begin{array}{ll} z_1(x)=\frac{a_1 \sin \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) -a_2 \sin \left( a_1 x\right) \left( b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) }{a_1 a_2 \left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ z_2(x)=\frac{\left( \alpha {\varepsilon _{3}} +\gamma ^2\right) \left( b_1 \cos \left( a_2 x\right) -b_2 \cos \left( a_1 x\right) \right) -i \xi \tau {\varepsilon _{3}} ^2 \left( \cos \left( a_1 x\right) -\cos \left( a_2 x\right) \right) }{\left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ z_3(x)=\frac{a_1 b_2 \sin \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) +a_2 b_1 \sin \left( a_1 x\right) \left( -b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) -i \xi \tau {\varepsilon _{3}} ^2\right) }{a_1 a_2 \left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ z_4(x)=\frac{b_2 \cos \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) +b_1 \cos \left( a_1 x\right) \left( -b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) -i \xi \tau {\varepsilon _{3}} ^2\right) }{\left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }\end{array} \end{aligned}$$

(46)

and therefore, the solution of the system (35) is

$$\begin{aligned} \begin{array}{ll} y_1(x)=\frac{-\imath \tau \xi {\varepsilon _{3}}}{\mu }\frac{a_1 \sin \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) -a_2 \sin \left( a_1 x\right) \left( b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) }{a_1 a_2 \left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ y_2(x)=\frac{a_1 \sin \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) -a_2 \sin \left( a_1 x\right) \left( b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) }{a_1 a_2 \left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ y_3(x)=\frac{\gamma \left( a_2 b_2 \left( -\sin \left( a_2 x\right) \right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) -a_1 b_1 \sin \left( a_1 x\right) \left( -b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) -i \xi \tau {\varepsilon _{3}} ^2\right) \right) }{\left( b_1-b_2\right) {\varepsilon _{3}} \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ \quad -\frac{i \xi \tau \left( a_1 a_2 \cos \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) -a_1 a_2 \cos \left( a_1 x\right) \left( b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) \right) }{a_1 a_2 \left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }&{}\\ y_4(x)=\frac{i \left( b_2 \cos \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) +b_1 \cos \left( a_1 x\right) \left( -b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) -i \xi \tau {\varepsilon _{3}} ^2\right) \right) }{\left( b_1-b_2\right) \tau \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) } &{}\\ y_5(x)=\frac{a_1 b_2 \sin \left( a_2 x\right) \left( b_1 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) +i \xi \tau {\varepsilon _{3}} ^2\right) +a_2 b_1 \sin \left( a_1 x\right) \left( -b_2 \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) -i \xi \tau {\varepsilon _{3}} ^2\right) }{a_1 a_2 \left( b_1-b_2\right) \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) }. \end{array} \end{aligned}$$

(47)

Note that for the choices of $a_1=\frac{2n \pi }{L}$ and $a_2=\frac{ 2m \pi }{L},$ $\tau _{nm}$ can be determined as the following

$$\begin{aligned} \tau _{nm}=\sqrt{\frac{\mu }{\xi {\varepsilon _{3}}}}\frac{ \sqrt{\alpha {\varepsilon _{3}} _3+\gamma ^2+16 \pi ^2 \alpha \xi {\varepsilon _{3}} _3 \left[ m^2+n^2\right] }}{L\sqrt{\alpha {\varepsilon _{3}} _3+\gamma ^2 +\mu \rho }}. \end{aligned}$$

The condition (42) is equivalent to

$$\begin{aligned} m^2+ n^2>\frac{\mu \rho L^2 }{16 \alpha \xi {\varepsilon _{3}} \pi ^2}. \end{aligned}$$

(48)

Let the initial condition of the control-free problem (29) be

$$\begin{aligned}\mathbf{y}_{0,nm}(x)=[y_{1,nm}(x)~~y_{2,nm}(x) ~~ y_{3,nm}(x)~~ y_{4,nm}(x)~~ y_{5,nm}(x)]^{\mathrm{T}}\end{aligned}$$

where $y_{i,nm}$’s are defined by (47). Then the solution of the initial value problem (29) is

$$\begin{aligned} \mathbf{y}_{nm}(x,t)= \mathbf{y}_{0,nm} (x)e^{i\tau _{nm} t} \end{aligned}$$

(49)

where n, m can be chosen to satisfy (48). This type of solution results in $B^*\mathbf{y}_{nm} \equiv 0.$

$\square$

Remark 1

Note that the wave speeds of mechanical and electro-magnetic equations in (11) are $\left\{ \sqrt{\frac{\alpha }{\rho }},\sqrt{\frac{\mu }{{\varepsilon _{3}}}}\right\} ,$ respectively, where $\sqrt{\frac{\mu }{{\varepsilon _{3}}}}\sim 10^8$ is the speed of light with the material parameters in (70), and $\frac{\mu }{{\varepsilon _{3}}}>> \frac{\alpha }{\rho }.$ Since $\xi$ in (70) is around $10^{-6}$ the condition $\tau>\frac{\mu }{\xi {\varepsilon _{3}}}>>\frac{\mu }{{\varepsilon _{3}}}$ implies the high-frequency eigenvalues $\lambda =\imath \tau$ in (35). Thus, Theorem (5) proves the lack of stability for the high-frequency vibration modes. As $\tau <\frac{\mu }{\xi {\varepsilon _{3}}},$ the form of the eigenvalues don’t look as good. For that reason, the lack of stability for these modes are shown through simulations in Sect. 6.

3.2 Additional Remedial Controller

In addition to the current controller $i_s(t)$, an additional mechanical controller g(t),  as in [22], can be considered at the tip $x=L$ so that the boundary condition ${\alpha } v_{x}(L) + \gamma \phi (L) +\gamma {\dot{\eta }}(L)=0$ in (11) is replaced by

$$\begin{aligned} {\alpha } v_{x}(L) + \gamma \phi (L) +\gamma {\dot{\eta }}(L)=\frac{g(t)}{h}. \end{aligned}$$

(50)

Then the system (29) is replaced by

$$\begin{aligned} {\dot{\mathbf{y}}}=\mathcal A\mathbf{y}+ B \left[ \begin{array}{c} i_s(t)\\ g(t) \end{array} \right] \quad \mathbf{y}(0)=y_0, \end{aligned}$$

where $B= \left[ \begin{array}{cc} 0 &{} 0 \\ \frac{1}{ \xi {\varepsilon _{3}} h} &{} 0 \\ 0 &{} 0 \\ 0 &{} 0 \\ 0 &{} \frac{1}{h}\delta (x-L) \end{array} \right] ,$ with $B^*\mathbf{y}= \left[ \begin{array}{ccccc} 0 &{} \frac{1}{ \xi {\varepsilon _{3}} h} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{h}\delta (x-L) \end{array} \right] \mathbf{y}= \left[ \begin{array}{c} \frac{1}{\xi {\varepsilon _{3}} h}\int _0^L y_2(x) dx\\ \frac{1}{h}y_5(L) \end{array} \right] ,$ and $\delta (x-L)$ is the Dirac-Delta distribution at $x=L.$ Then, the energy of the closed-loop system

$$\begin{aligned} {\dot{\mathbf{y}}}=\mathcal A\mathbf{y}+ K B B^* \mathbf{y}\quad \mathbf{y}(0)=y_0, \end{aligned}$$

where $K= \left[ \begin{array}{ccccc} 0 &{} 0 &{}0&{}0 &{}0\\ -\xi ^2 {\varepsilon _{3}}^3 h^2 K_1&{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 0&{} 0 &{}0\\ 0 &{} 0 &{} 0&{} 0 &{}0\\ 0 &{} 0&{} 0&{} 0&{} -h^2 K_2\end{array} \right]$ with $K_1,K_2>0$ satisfies $\frac{d{{\mathrm {E}}}(t)}{dt}=-K_1 \left( \int _0^L \psi _2(x) dx\right) ^2 -K_2 |y_5(L)|^2.$ By using the similar methodology in Sect. 3.1, it can be shown that there are no eigenvalues on the imaginary axis, or in other words, the set

$$\begin{aligned} \left\{ \mathbf{y}\in {\mathrm H} ~|~ \mathrm{Re} \left\langle {\mathcal {{\tilde{A}}}}\mathbf{y}, \mathbf{y}\right\rangle _{{\mathrm H}} = -K_1\left( \int _0^L y_2(x) dx\right) ^2-K_2 |y_5(L)|^2= 0\right\} \end{aligned}$$

has only the trivial solution $\mathbf{y}=0.$ Hence, the following theorem is immediate:

Theorem 7

For $a_1\ne \frac{n \pi }{L}$ and $a_2\ne \frac{ m \pi }{L}$ for $m,n\in {\mathbb {N}},$ and $\mathbf{y}^{\mathbf{0}}\in \mathrm H ,$ the semigroup $\{e^{(\mathcal A + K B B^*)t}\}_{t\ge 0}$ corresponding to (33) is asymptotically stable in $\mathrm {H}$, i.e. $\Vert e^{(\mathcal A + K B B^*)t}\mathbf{y}^{\mathbf{0}}\Vert _{\mathrm {H}}\rightarrow 0, ~~~ t\rightarrow \infty .$

Remark 2

Following up with Remark 1, the additional remedial controller help asymptotically stabilize both mechanical and electro-magnetic states. This includes both high and low-frequency vibration modes. See Sect. 6 for the power of the remedial controller.

Remark 3

An additional feedback controller can be considered in the distributed (stronger) sense, i.e., viscous damping [40] or fractional damping [16]. This type of feedback controller makes the voltage-controlled beam equations exponentially stable. It is an open problem whether the exponential stability is retained for the current-controlled beam equations (33).

4 Well-Posedness of the Coulomb Gauge Model (12)

Note that a similar analysis of this section is carried out for (12) with free-free boundary conditions [27, 37] and different choice of states. Our paper deals with clamped-free boundary conditions. For $t\in {\mathbb {R}},$ the natural energy associated with (12) is

$$\begin{aligned} {{{\mathrm {E}}}(t)}= & {} \frac{1}{2}\int _0^L \left\{ \mu \left| \theta -\eta _x\right| ^2+ \xi {\varepsilon _{3}}|{\dot{\theta }}|^2 + {\varepsilon _{3}} \left| {\dot{\eta }}\right| ^2 +\rho |\dot{v}|^2\right. \\ \nonumber \quad \quad&\left. +\,{\alpha } |v_x|^2 + \frac{{\gamma }^2 }{{\varepsilon _{3}}}({P_\xi } v_x) {\bar{v}}_x \right\} dx. \end{aligned}$$

(51)

Define the linear space

$$\begin{aligned}&{\mathrm H}= \left[ {\mathcal {L}}_{2} (0,L))\times H^1_0(0,L)\times ({\mathcal {L}}_{2} (0,L))^3\right] \bigcap \left\{ \mathbf{y}: \xi (y_2)_x-y_3=0\right\} \end{aligned}$$

(52)

with the bilinear form

$$\begin{aligned} \left\langle \mathbf{y}, \mathbf{z}\right\rangle _{{\mathrm {H}}}=\int _0^L \left\{ \mu y_1 {\bar{z}}_1 + \xi {\varepsilon _{3}} y_2 {\bar{z}}_2 + {\varepsilon _{3}}y_3{\bar{z}}_3 + {\alpha } y_4{\bar{z}}_4 + \frac{{\gamma }^2 }{{\varepsilon _{3}}}({P_\xi } y_4) {\bar{z}}_4+\rho y_5 {\bar{z}}_5 \right\} dx.\nonumber \\ \end{aligned}$$

(53)

Since $P_\xi$ is a nonnegative operator, the following result is straightforward as in Theorem 1:

Lemma 3

The form (24) defines an inner product on the linear space $\mathrm H$. Moreover, E is the norm induced by this inner product and $\mathrm H$ is complete.

Let

$$\begin{aligned} \mathbf{y}=[y_1,y_2,y_3,y_4,y_5]^{\mathrm{T}}=[\theta -\eta _x, {\dot{\theta }}, {\dot{\eta }}, v_x,\dot{v}]^{\mathrm{T}}. \end{aligned}$$

(54)

Then (12) can be written as the following

$$\begin{aligned} {\dot{\mathbf{y}}} = A \mathbf{y}- \mathcal B i_s^1(t),~~~ \mathbf{y}(x,0) = \mathbf{y}^{\mathbf{0}}=(\theta ^0-\eta _x^0, \theta ^1,\eta ^1, v^0_x, v^1) \end{aligned}$$

(55)

where $A= \left( {\begin{array}{*{20}c} 0 &{} I &{} -D_x &{} 0 &{} 0 \\ \frac{-\mu }{\xi {\varepsilon _{3}}} I &{} 0 &{} 0 &{} 0 &{} \frac{-\gamma }{{\varepsilon _{3}}}D_xP_\xi D_x \\ \frac{-\mu }{{\varepsilon _{3}}}D_x &{} 0 &{} 0 &{} 0&{} \frac{\gamma }{{\varepsilon _{3}}} (D_x-D_x P_\xi ) \\ 0&{} 0 &{} 0 &{} 0 &{} D_x \\ 0&{} 0 &{} \frac{\gamma }{\rho } D_x &{} \frac{\alpha }{\rho } D_x +\frac{\gamma ^2}{\rho {\varepsilon _{3}}} P_\xi D_x &{} 0 \\ \end{array}} \right) \quad \mathrm{and}$

$$\begin{aligned}&\mathrm{Dom}({A})\nonumber \\&\quad = \left[ H^1_0(0,L) \times (H^2(0,L)\cap H^1_0(0,L)) \times H^1(0,L) \times H^1(0,L)\times H^1_L(0,L)\right] \nonumber \\&\qquad \bigcap \left\{ \mathbf{y}\in \mathrm {H} : \left| ~\left( {\alpha } I + \frac{{\gamma }^2}{{\varepsilon _{3}}} {P_\xi }\right) y_4 +{\gamma } y_3~\right| _{x=L}=0 \right\} , \end{aligned}$$

(56)

and the B and $B^*$ operators with the new state are

$$\begin{aligned} \left\langle \mathcal B u(t), \psi \right\rangle _{{\mathrm H}}= & {} \frac{1}{\xi {\varepsilon _{3}} h}\int _0^L u(t) ~\psi _2 ~dx =u(t)\frac{1}{\xi {\varepsilon _{3}} h}\int _0^L ~ \psi _2 ~dx=\left\langle u, \mathcal B^*\psi \right\rangle _{\mathcal U} \end{aligned}$$

and $\mathcal B \mathcal B^*\in \mathcal L( \mathrm H, \mathrm H).$ We recall the following result from [27]:

Lemma 4

Let $\mathrm{Dom} (D_x^2)=\{w\in H^2(0,L) ~:~ w_x(0)=w_x(L)=0\}.$ The operator $\frac{1}{\xi }(P_\xi -I)$ is continuous, self-adjoint and non-positive on ${\mathcal {L}}_{2} (0,L).$ Moreover, for all $w\in \mathrm{Dom} (P_\xi ),$ $J=D_x^2 ~P_\xi = D_x^2 (I-\xi D_x^2)^{-1}w.$

Lemma 5

The operator A maps $\mathrm{Dom}(A)\subset \mathrm H$ to H,  and is densely defined in $\mathrm H.$

Proof

Let $\mathbf{y}\in \mathrm{Dom}(A).$ Then

$$\begin{aligned}A \mathbf{y}=\left( \begin{array}{c} y_2- (y_3)_x \\ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1 -\frac{\gamma }{{\varepsilon _{3}}} (P_\xi (y_5)_x)_x\\ -\frac{\mu }{{\varepsilon _{3}}} (y_1)_x +\frac{\gamma }{{\varepsilon _{3}}} (I - P_\xi ) (y_5)_x\\ (y_5)_x\\ \frac{\gamma }{\rho } (y_3)_x + \frac{\alpha }{\rho } (y_4)_x +\frac{\gamma ^2}{{\varepsilon _{3}}\rho } (P_\xi y_4)_x\\ \end{array} \right) . \end{aligned}$$

Since $\mathbf{y}\in W_1,$ $y_1\in H^1(0,L)$ and $y_4\in H^1_0(0,L),$ $(y_1)_x\in {\mathcal {L}}_{2} (0,L),$ and by the definition of the operator in (10) $P_\xi (y_1)_x\in H^2(0,L).$ Therefore $({P_\xi } (y_1)_x)_x + y_4\in H^1_0(0,L).$ Hence, $A \mathbf{y}\in W_1.$ $\square$

Let’s also verify that the gauge condition (52) for $A\mathbf{y}$ is satisfied:

$$\begin{aligned} \left[ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1 -\frac{\gamma }{{\varepsilon _{3}}} (P_\xi (y_5)_x)_x\right] _x= & {} -\frac{\mu }{\xi {\varepsilon _{3}}}(y_1)_x -\frac{\gamma }{{\varepsilon _{3}}} (P_\xi (y_5)_x)_{xx}\\= & {} -\frac{\mu }{\xi {\varepsilon _{3}}}(y_1)_x -\frac{\gamma }{{\varepsilon _{3}}\xi } (P_\xi - I)(y_5)_x \end{aligned}$$

where we use Lemma 4.

The following result is immediate, and it can obtained in a similar fashion as in Sect. 3:

Theorem 8

The operator ${A}: \mathrm{Dom} (A)\subset \mathrm H \rightarrow \mathrm H$ satisfies ${A}^*=-{A}$ on $\mathrm H,$ and A

defined by (26) is the generator of a unitary semigroup $\{e^{{A}t}\}_{t\ge 0}$ on $\mathrm H.$ Letting $T>0$ and $i_s(t)\in L^2(0,T),$ for any $\mathbf{y}_0 \in \mathrm { H},$ $\mathbf{y}\in C[[0,T]; \mathrm H],$ and there exists a positive constants c(T) such that (55) satisfies

$$\begin{aligned} \Vert \mathbf{y}(T) \Vert ^2_{\mathrm H}\le & {} c (T)\left\{ \Vert \mathbf{y}^0\Vert ^2_{\mathrm H} + \Vert i_s\Vert ^2_{{\mathcal {L}}_{2} (0,T)}\right\} . \end{aligned}$$

4.1 Lack of Stabilization of the Coulomb Gauge Model (12)

Similar to the Lorenz gauge case, along the trajectories of (12), the energy (51) satisfies $\frac{d{{\mathrm {E}}}(t)}{dt}=i_s(t) \left( \int _0^L \psi _2(x) dx\right) .$

We investigate the asymptotic stability of (12) for the same $B^*$-feedback (31). This leads to the feedback control $i_s^1(t)=-K_1 h^2 \xi ^2{\varepsilon _{3}}^2 \int _0^L ~ {\dot{\theta }}(z)dz$ where $K_1 >0$ is arbitrary.

The abstract state-space description (29) becomes

$$\begin{aligned}&\left\{ \begin{array}{ll} {\dot{\mathbf{y}}} = {{\tilde{A}}} \mathbf{y}- K_1 h^2 \xi ^2{\varepsilon _{3}}^2 B B^*\mathbf{y},&{}\\ \mathbf{y}(x,0) = \mathbf{y}^{\mathbf{0}}. \end{array}\right. \end{aligned}$$

(57)

The operator ${{\tilde{A}}}: \mathrm{Dom}( {{\tilde{A}}})\subset \mathrm H \rightarrow \mathrm H$ defined by (57) with domain $\mathrm{Dom}({{\tilde{A}}})=\mathrm{Dom}({ A})$ is densely defined in $\mathrm H.$

Lemma 6

The infinitesimal generator ${{\tilde{A}}}$ satisfies ${{\tilde{A}}}^*=- {{\tilde{A}}}(-K_1)$ on $\tilde{\mathrm H}.$ Moreover it is dissipative and it satisfies ${\mathrm{Re}}\left\langle {{\tilde{A}}} \mathbf{y}, \mathbf{y}\right\rangle _{\tilde{\mathrm {H}}}\le 0.$

Theorem 9

$\tilde{{\mathcal {A}}}: \mathrm{Dom}( {{\tilde{A}}}) \rightarrow \tilde{\mathrm H}$ is the infinitesimal generator of a $C_0-$semigroup of contractions. Therefore for every $T\ge 0,$ and $\mathbf{y}^{\mathbf{0}}\in \mathrm{Dom}( {{\tilde{A}}})$ we have $\mathbf{y}\in C\left( [0,T]; \mathrm{Dom}({{\tilde{A}}})\right) \cap C^1\left( [0,T]; {\mathrm H}\right) .$ Moreover, the spectrum $\sigma (\tilde{{A}})$ of $\tilde{{\mathcal {A}}}$ has all isolated eigenvalues.

Proof

By Lemma 6, $\tilde{{A}}: \mathrm{Dom}( {{\tilde{A}}}) \rightarrow {\mathrm H}$ is the infinitesimal generator of a $C_0-$semigroup of contraction by Lümer-Phillips theorem [38]. Therefore for every $T\ge 0,$ and $\mathbf{y}^{\mathbf{0}}\in \mathrm{Dom}(\tilde{{A}})$ solves (55), and we have $\mathbf{y}\in C\left( [0,T]; \mathrm{Dom}(\tilde{{A}})\right) \cap C^1\left( [0,T]; \tilde{{\mathrm H}}\right) .$

Finally, since $\mathrm{Dom}(\tilde{ A})$ is densely defined and compact in ${\mathrm H},$ $0\in \rho ({\tilde{A}}),$ we have $(\lambda I -{\tilde{ A}})^{-1}$ is compact at $\lambda =0,$ thus compact for all $\lambda \in \rho ({\tilde{ A}}).$ Hence the spectrum of ${\tilde{A}}$ has all isolated eigenvalues. $\square$

We have the following result that lists some choices of material parameters causing instabilities.

Theorem 10

Let $a_1=\frac{2n\pi }{L}, a_2=\frac{2m\pi }{L}$ in (41), and $m^2+ n^2>\frac{\mu \rho L^2 }{16 \alpha \xi {\varepsilon _{3}} \pi ^2}$ for $m,n\in {\mathbb {N}}$ where $a_1$ and $a_2$ are defined by (41). For $\mathbf{y}^{\mathbf{0}}\in { {\mathrm H}},$ the semigroup $\{e^{ {{\tilde{A}}}t}\}_{t\ge 0}$ corresponding to (33) is not asymptotically stable in ${\mathrm {H}}$, i.e. $\Vert e^{{{\tilde{A}}}t}\mathbf{y}^{\mathbf{0}}\Vert _{\tilde{\mathrm {H}}}\nrightarrow 0, ~~~ t\rightarrow \infty .$

Proof

Since $0\in \rho ( {{\tilde{A}}}),$ we show that there are eigenvalues on the imaginary axis, or in other words, the set

$$\begin{aligned} \left\{ \mathbf{y}\in {\mathrm H} ~|~ \mathrm{Re} \left\langle {{{\tilde{A}}}}\mathbf{y}, \mathbf{y}\right\rangle _{{\mathrm H}} = -K_1\left( \int _0^L y_2(x) dx\right) ^2= 0\right\} \end{aligned}$$

(58)

has nontrivial solutions. It will then follow that the system (33) is not strongly stable. This is equivalent to saying that the current-controlled problem is not approximately controllable on $\mathrm H.$ $\square$

Let $\lambda =\imath \tau .$ The the eigenvalue problem ${\tilde{A}} \mathbf{y}=\lambda \mathbf{y}=\imath \tau \mathbf{y}$ is

$$\begin{aligned}&\left\{ \begin{array}{ll} y_2- (y_3)_x=\imath \tau y_1 \\ -\frac{\mu }{\xi {\varepsilon _{3}}}y_1 -\frac{\gamma }{{\varepsilon _{3}}} (P_\xi (y_5)_x)_x=\imath \tau y_2\\ -\frac{\mu }{{\varepsilon _{3}}} (y_1)_x +\frac{\gamma }{{\varepsilon _{3}}} (I - P_\xi ) (y_5)_x=\imath \tau y_3\\ (y_5)_x=\imath \tau y_4\\ \gamma (y_3)_x + \alpha (y_4)_x +\frac{\gamma ^2}{{\varepsilon _{3}}} (P_\xi y_4)_x=\imath \tau \rho y_5\\ \end{array} \right. \end{aligned}$$

(59)

with the boundary conditions

$$\begin{aligned} y_1(0)=y_1(L)=\gamma y_3(L) + \alpha y_4(L) +\frac{\gamma ^2}{{\varepsilon _{3}}} P_\xi y_4(L)=y_5(0)=y_2(0)=y_2(L)=0. \end{aligned}$$

As well, (58) implies that $\int _0^L y_2 (x) dx=0.$ Let $r:=P_\xi (y_5)_x.$ By (10), $r-\xi r_{xx}=(y_5)_x.$ By using the gauge condition, i.e. $y_3=\xi (y_2)_x$, (59) reduces to

$$\begin{aligned}&\left\{ \begin{array}{ll} \alpha (y_5)_{xx} + \tau ^2 \rho y_5 + \frac{{\gamma }^2}{{\varepsilon _{3}}} r_x +\imath \tau \gamma \xi (y_2)_{xx}=0 &{}\\ -\gamma \imath \tau r_x - \frac{\mu }{\xi }(y_2-\xi (y_2)_{xx})+ \tau ^2 {\varepsilon _{3}} y_2=0 &{}\\ r - \xi r_{xx}=(y_5)_x&{} \end{array} \right. \end{aligned}$$

(60)

with the boundary conditions

$$\begin{aligned} y_5(0)&={\alpha } (y_5)_x (L)+\frac{{\gamma }^2 }{{\varepsilon _{3}}}r(L) + \imath \tau \gamma \xi (y_2)_x(L)=r_x(0)=r_x(L)=y_2(0)\\&=y_2(L)=0, \end{aligned}$$

and $\int _0^L y_2(x)dx=0.$

Solving (60) for $r_{xx}, (y_1)_{xx}$ and $(y_3)_{xx}$ yields

$$\begin{aligned}&\left\{ \begin{array}{ll} (y_5)_{xx}= -\frac{\tau ^2 \rho }{\alpha } y_5+\left( \frac{\gamma ^2\tau ^2\xi }{\alpha \mu } -\frac{\gamma ^2}{\alpha {\varepsilon _{3}}}\right) r_x + \left( \frac{\imath \tau ^3 \gamma \xi {\varepsilon _{3}}}{\alpha \mu }-\frac{\imath \tau \gamma }{\alpha }\right) y_2. &{}\\ (y_2)_{xx}= \frac{1}{\mu }\left( \gamma \imath \tau r_x + \frac{\mu }{\xi } y_2 -\tau ^2 {\varepsilon _{3}} y_2\right) &{}\\ r_{xx}=\frac{1}{\xi }\left( r-(y_5)_x\right) &{} \end{array}.\right. \end{aligned}$$

(61)

Now we let $Z=[y_5~ (y_5)_x~ y_2 ~(y_2)_x~ r ~r_x]^{\mathrm{T}}.$ We write the system (61)

$$\begin{aligned} \frac{dZ}{dx}= & {} {\tilde{\mathcal D}} Z=\left( {\begin{array}{*{20}c} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -\frac{\tau ^2\rho }{\alpha } &{}\quad 0&{}\quad \frac{-\imath \tau \gamma }{\alpha } + \frac{\imath \tau ^3\gamma \xi {\varepsilon _{3}}}{\alpha \mu } &{}\quad 0 &{}\quad 0 &{}\quad -\frac{\gamma ^2}{\alpha {\varepsilon _{3}}} + \frac{\gamma ^2 \tau ^2 \xi }{\alpha \mu } \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \frac{1}{\xi }-\frac{\tau ^2 {\varepsilon _{3}}}{\mu }&{}\quad 0 &{}\quad 0 &{}\quad \frac{\gamma \tau \imath }{\mu }\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad -\frac{1}{\xi } &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{\xi } &{}\quad 0 \end{array}} \right) Z.\nonumber \\ z_1(0)= & {} {\alpha } z_2(L) +\frac{{\gamma }^2 }{{\varepsilon _{3}}} z_5 (L)+ \imath \tau \gamma \xi z_4(L)=z_6(0)=z_6(L)=0\nonumber \\ z_3(0)= & {} z_3(L)=\int _0^L z_3(x)dx=0. \end{aligned}$$

(62)

The solution to (62) is $Z=e^{{\tilde{\mathcal D}} x} C$ where $C=[c_1 ~ c_2 ~ c_3 ~ c_4~c_5 ~c_6]^{\mathrm{T}}$ is a vector of arbitrary coefficients. The characteristic equation is

$$\begin{aligned}&\left( \xi {{\tilde{\lambda }}}^2-1\right) \\&\quad \times \left( \alpha \mu \xi {\varepsilon _{3}} {{\tilde{\lambda }}}^4 +\left( \xi \tau ^2 {\varepsilon _{3}} \left( \alpha {\varepsilon _{3}} +\gamma ^2+\mu \rho \right) {{\tilde{\lambda }}}^2 -\mu \left( \alpha {\varepsilon _{3}} +\gamma ^2\right) \right) \right. \\&\quad \left. +\rho \tau ^2 {\varepsilon _{3}} \left( \xi \tau ^2 {\varepsilon _{3}} -\mu \right) \right) =0. \end{aligned}$$

For the same A, B, C in (40), and real $\tau$, define

$$\begin{aligned} \nonumber a_1= & {} \sqrt{\frac{B+ \sqrt{B^2-4AC}}{2A}}, \quad a_2 = \sqrt{\frac{B- \sqrt{B^2-4AC}}{2A}},\\ \nonumber b_1= & {} -\frac{\alpha \mu \imath }{\gamma \tau (\mu -{\varepsilon _{3}} \xi \tau ^2) }\left( -\frac{\tau ^2\rho }{\alpha } + \frac{a^2}{a^2+a_3^2} \frac{\gamma ^2}{\alpha {\varepsilon _{3}} \mu } (\mu -{\varepsilon _{3}}\xi \tau ^2) a_3^2 +a_3^2 \right) ,\\ \nonumber b_2= & {} -\frac{\alpha \mu \imath }{\gamma \tau (\mu -{\varepsilon _{3}} \xi \tau ^2) }\left( -\frac{\tau ^2\rho }{\alpha } + \frac{a^2}{a^2+a_4^2} \frac{\gamma ^2}{\alpha {\varepsilon _{3}} \mu } (\mu -{\varepsilon _{3}}\xi \tau ^2) a_4^2+a_4^2 \right) \\ b_{11}= & {} \frac{\imath a^2 a_3}{a^2+a_3^2},\qquad b_{22}=\frac{\imath a^2 a_4}{a^2+a_4^2} \end{aligned}$$

(63)

For

$$\begin{aligned} \mu -\xi {\varepsilon _{3}} \tau ^2<0, \end{aligned}$$

(64)

the first four eigenvalues turn to be similar to those obtained in Sect. 3.1:

$$\begin{aligned} {\tilde{\lambda }}=\mp \imath a_1, \mp \imath a_2, \mp a \end{aligned}$$

where $a=\frac{1}{\sqrt{\xi }},$ and $a_1,a_2$ are defined in (41). Since $a_3 \ne a_4$, in (63), $b_3-b_4\ne 0, b_{33}-b_{44}\ne 0,$ the solution of (62) is written as $Z=P e^{Jx}P^{-1} K$ where $P,e^{Jx}$ are defined by

$$\begin{aligned} P= & {} \left( \begin{array}{cccccc} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1 \\ 0 &{} 0 &{} \imath a_1 &{} -\imath a_1 &{} \imath a_2 &{} -\imath a_2 \\ 1 &{} 1 &{} b_1 &{} b_1 &{} b_2 &{} b_2 \\ a &{} -a &{} \imath a_1 b_1 &{} -\imath a_1 b_1 &{} \imath a_2 b_2 &{} -\imath a_2 b_2 \\ b &{} -b &{} b_{11} &{} - b_{11} &{} b_{22} &{} -b_{22} \\ ab &{} a b &{} \imath a_1 b_{11} &{} \imath a_1 b_{11} &{} \imath a_2 b_{22} &{} \imath a_2 b_{22} \\ \end{array} \right) \nonumber \\ e^{Jx}= & {} \left( \begin{array}{cccccc} e^{x a} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{-x a} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} e^{\imath x a_1} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} e^{-\imath x a_1} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} e^{\imath x a_1} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} e^{-\imath x a_2} \\ \end{array} \right) \end{aligned}$$

(65)

where $b=\frac{-\imath \tau {\varepsilon _{3}}a}{\gamma }.$ Using the boundary conditions at $x=0$ yields $c_1=c_3=c_6=0.$ By using the other three boundary conditions at $x=L,$ the feedback condition $\int _0^L z_3 (x)dx=0,$ and $a_1 =\frac{2n\pi }{L}$ and $a_2=\frac{2m\pi }{L}$, we obtain an overdetermined system of equations for the unknowns $\{c_2,c_4,c_5\}.$ After row reducing it, we obtain that $c_5$ is a free variable. The solution of the eigenvalue problem

$$\begin{aligned} \mathbf{y}=\left( \begin{array}{cc} C(a_1)b_1\imath \left( a_1^2 \xi +1\right) \sin \left( a_1 x\right) -b_2 C(a_2)\imath \left( a_2^2 \xi +1\right) \sin \left( a_2 x\right) &{}\\ \tau b_2 C(a_1)\sin \left( a_2 x\right) +\tau b_1 \sin \left( a_1 x\right) C(a_2)&{}\\ \xi \tau b_2 C(a_1)\sin \left( a_2 x\right) +\xi \tau b_1 \sin \left( a_1 x\right) C(a_2)&{}\\ -\imath C(a_1)\sin \left( a_2 x\right) -\imath \sin \left( a_1 x\right) C(a_2)&{}\\ \tau C(a_1) \sin \left( a_2 x\right) +\tau \sin \left( a_1 x\right) C(a_2)\end{array}\right) \end{aligned}$$

where $C(a_k)\ne 0,$

$$\begin{aligned} C(a_k):=(-1)^k\left( b_{kk} \gamma ^2+a_k {\varepsilon _{3}} \left( \imath \alpha -b_k \gamma \xi \tau \right) \right) ,\quad k=1,2 \end{aligned}$$

This implies that the eigenvalue problem has nontrivial solutions. It is the same conclusion in Sect. 3.1 that the integral-type observation $\int _0^L z_3(x)dx$ does not help to show approximate controllability. Since $c_3$ can be chosen to be a free variable, the solution of the eigenvalue problem can be chosen.

For $a_1\ne \frac{n \pi }{L}$ and $a_2\ne \frac{ m \pi }{L},$ the remedial controller (50) discussed in Sect. 3.2 can be also considered here to obtain exactly the same asymptotic stability result, see Theorem 7.

5 Electrostatic/Guasi-Static Model

To see the difference between the electrostatic/quasi-staic and fully magnetic models, the charge or voltage-controlled model [27], obtained by a thorough variational approach, is chosen to start with. The magnetic effects are totally freed. The mechanical equation is coupled to the dynamic charge equation:

$$\begin{aligned} {}\left\{ \begin{array}{l l} \rho \ddot{v} -\left( {\alpha +\frac{\gamma ^2}{{\varepsilon _{3}}}}\right) v_{xx} = 0, &{} \\ v(0)=0,\quad (\alpha +\frac{\gamma ^2}{{\varepsilon _{3}}}) v_{x}(L,t)=-\frac{\gamma }{{\varepsilon _{3}} h}\sigma _s(t),&{}\\ {\dot{\sigma }}_s(t)=i_s(t),&{}\\ (v,\dot{v})(x,0)=(v_0,v_1), \quad {\dot{\sigma }}_s(0)=\sigma _0. \end{array}\right. \end{aligned}$$

(66)

Here $\sigma _s(t)$ is the applied charge to the electrodes on the top and bottom surfaces of piezoelectric beam. The model (66) is a well-studied wave-equation with a dynamic boundary controller. This type of model is first proposed and analyzed by [43].

Table 1 Non-dimensionalization of fully-dynamic Eqs. (11) and (12)

Table 2 Non-dimensionalization of the electrostatic/quasi-static equation (66)

The natural energy associated with (66) is

$$\begin{aligned} \mathrm {E}(t)= & {} \frac{1}{2}\left\{ \int _0^L \left( \left( \alpha + \frac{\gamma ^2}{{\varepsilon _{3}}}\right) |v_x|^2 +\rho |\dot{v}|^2 \right) ~dx + |\sigma _s|^2 \right\} . \end{aligned}$$

(67)

Define the linear space $H^1_L(0,L)\times L^2(0,L)\times {\mathbb {C}}$ and the bilinear form

$$\begin{aligned} \left\langle \mathbf{y}, \mathbf{z}\right\rangle _{\mathrm {H}}= & {} \int _0^L \left\{ \left( \alpha + \frac{\gamma ^2}{{\varepsilon _{3}}}\right) y_1 {\bar{z}}_1 + \rho y_2 {\bar{z}}_2 \right\} dx + y_3 {\bar{y}}_3 . \end{aligned}$$

(68)

Let $\mathbf{y}=[y,\dot{y}, \sigma _s]^{\mathrm{T}}$ be the states, $\mathcal A\mathbf{y}= [y_2, \frac{\alpha +\frac{\gamma ^2}{{\varepsilon _{3}}}}{\rho }(y_1)_{xx}, 0],$ and $B=[0 ~0 ~ 1]$ where

$$\begin{aligned} \mathrm{Dom}(\mathcal A)=\{\mathbf{y}\in \mathrm H, y_1\in H^2(0,L), ~y_2 \in H^1_L(0,L),~ (y_1)_x(L)+y_3=0 \}. \end{aligned}$$

Then (66) can be written as

$$\begin{aligned} {\dot{\mathbf{y}}}=\mathcal A \mathbf{y}+ B i_s(t),\quad \mathbf{y}(0)=\mathbf{y}_0. \end{aligned}$$

(69)

The model (69) is well studied in the literature. This model is never exponentially stabilizable [57]. However, by the designing the feedback controller $i_s(t)=\frac{\gamma }{{\varepsilon _{3}} h}\left( \dot{v}(L,t)-K_3\sigma _s(t)\right) ,~~K_3>0,$ we have the following optimal polynomial decay result

Theorem 11

(Thm. 2.1, [57]) Let $T>0,$ and $i_s(t)=\left( \dot{v}(L,t)-K_3\sigma _s(t)\right) ,$ $K_3\in {\mathbb {R}}^+.$ For any $\mathbf{y}_0 \in \mathrm{Dom}(\mathcal A),$ there exists a constant $C(\mathbf{y}_0,K_3)>0$ such that (67) satisfies

$$\begin{aligned} E(t)\le \frac{2C}{t+C}, \forall t>0. \end{aligned}$$

Note that the feedback $i_s(t)=-K_3B^*\mathbf{y}=-K_3\sigma _s$ does not make the energy dissipative at all.

6 Simulations

Now, we illustrate a numerical experiment by a sample example for the material parameters

$$\begin{aligned} \left\{ \begin{array}{ll} L=1 \mathrm{m}, ~~h=0.01\mathrm{m}, ~~\rho =7600 \mathrm{kg}/{\mathrm{m}^3}, \alpha =1.21\times 10^9 \mathrm{N}/\mathrm{m}^2,&{}\\ \varepsilon _1={\varepsilon _{3}}= 0.25 \times 10^{-12} \mathrm{F/m} ,~~ \mu =1.2\times 10^{6}\mathrm{H/m}, ~~\gamma =10^{-3} \mathrm{C}/\mathrm{m}^2,&{} \\ \beta = 10^{6} \mathrm{m/F},~~\xi =\frac{\varepsilon _1h^2}{{\varepsilon _{3}} 12}=8.3\times 10^{-6}\mathrm{m}^2. \end{array}\right. \end{aligned}$$

(70)

Our goal is to simulate the low-frequency vibrational states. First, to carry out numerical calculations, we non-dimensionalize the systems of Eqs. (11)–(12) as in Table 1. We also non-dimensionalize the model (66) in Table 2.

Table 3 Control strategies to suppress vibrations on a piezoelectric beam where $K_1,K_2,K_3$ are positive feedback gains

Table 4 The state $y_1$ refers to the magnetic field component in $y-$direction. In Case II, the current controller $i_s(t)$ performs better in the Lorenz gauge model than the Coulomb gauge model. It is simply because amplitudes of waves are higher without any controller (Case I), and the controller suppresses them good enough

Table 5 The state $y_2$ refers to the electric field component in $x-$direction. In Case II, the current controller $i_s(t)$ performs better in the Lorenz gauge model. The same controller in Coulomb gauge model does not contribute at all in controlling this state. In Case III, the remedial controller g(t) by itself is good enough to stabilize $y_2.$ In Case IV, both controllers do not improve the performance much

Table 6 The state $y_3$ refers to the electric field component in $z-$direction. In Case II, the current controller $i_s(t)$ performs good enough for both models. In Case III, the remedial controller g(t) by itself is good enough to stabilize $y_3.$ In Case IV, both controllers do not improve the performance much

Table 7 The state $y_4$ refers to the mechanical strains in the $x-$direction. In Case II, the current controller $i_s(t)$ performs really bad for both models. In fact, it is not able to stabilize this state at all. In Case III, the remedial controller g(t) by itself is good enough to stabilize $y_4.$ In Case IV, both controllers act a little better. The electrostatic/quasi-static model is known to be polynomially stable, see Theorem 11. This can be seen in the simulations. The proposed feedback controller, which requires a mechanical and an electrical measurement, perform well enough

Table 8 The state $y_5$ refers to the velocity of displacements in the $x-$direction. In Case II, the current controller $i_s(t)$ performs really bad for both models. In fact, it is not able to stabilize this state at all. In Case III, the remedial controller g(t) by itself is good enough to stabilize $y_5.$ In Case IV, both controllers act a little better. The feedback controller for electrostatic/quasi-static model performs well enough

Table 9 In Case II, the current controller $i_s(t)$ performs really bad for both models. In fact, it is not able to stabilize the tip velocity. In Case III, the remedial controller g(t) by itself is good enough, and in Case IV, the current control’s contribution can not observed. The proposed feedback controller for the electrostatic/quasi-static model is able to stabilize the tip velocity

Consider the discretization of the interval [0, L] as the following

$$\begin{aligned} 0=x_0< x_1<x_2, \ldots < x_N = L, \quad x_i=i\cdot dx, ~~dx=\frac{L}{N}. \end{aligned}$$

The following are the second order finite differences where $i=,0,1,\ldots , N.$ Henceforth, to simplify the notation, we use $z(x_{i})=z_i.$ The approximations for different order derivatives are

$$\begin{aligned} z_{x}= & {} \frac{z_{i+1}-z_{i-1}}{2dx}+O(dx^2), \quad \mathrm{or}\quad z_x=\frac{3z_i-4z_{i-1}+z_{i-2}}{2dx}+O(dx^2),\nonumber \\ z_{xx}= & {} \frac{z_{i+1}-2z_i+z_{i-1}}{dx^2}+O(dx^2), \end{aligned}$$

(71)

We consider simulations for $N=40,$ and $T_{\mathrm{final}}=300.$ We adopt the methodology to derive a filtered semi-discrete scheme in finite differences as it is applied successfully for a boundary-controlled wave equation [49]. The high frequency spurious solutions, causing artificial instability (unobservability), are filtered by adding a viscosity term to the wave equation. After this type of filtering, the discrete control-free problem becomes uniformly exactly observable with respect to the mesh parameter, and therefore, the controlled problem mimics the same exponential stability behavior of the original PDE problem. By adopting the same strategy, additional viscosity terms

$$\begin{aligned}(dx)^2 v_{xxt}, (dx)^2, (dx)^2\phi ^2_{xxt}, (dx)^2\theta _{xxt}, (dx)^2\eta _{xxt}\end{aligned}$$

are added to the $\{v,\phi , \theta ,\eta \}-$equations with appropriate coefficients in Tables 1 and 2, respectively.

The simulations for the models in Tables 1 and 2are performed for four different control strategies as shown in Table 3. The effect of numerical viscosity terms can be seen in Tables 4, 5, 6, 7, 8 and 9. The effect of these terms diminishes as the mesh size N increases. These effects are getting bigger in the Coulomb and Lorenz gauge models since there are viscosity terms as many as the equations.

One general observation in Tables 4, 5, 6, 7 and 8 that the integral controller $i_s^1(t)=-K_1\int _0^L y_2(x,t) dx,~ K_1>0$ itself is not even able to stabilize any state with low-frequency vibration modes for the Coulomb and Lorenz gauge models. The remedial mechanical feedback controller $g(t)=-K_2 \dot{v}(L,t), ~K_2>0$ acting on the boundary in each case is able to stabilize the vibrations very fast by itself. In some cases, the current controller has a minor effect to improve the controllers’ performance for the electro-magnetic states $y_1, y_2, y_3.$ The polynomial stability of the electrostatic/quasi-static model reflects in the simulations, see Tables 7 and 8.

The mechanical states are stabilized faster for the electrostatic/quasi-static equations regardless of optimal choice of the feedback gain $K_3>0$ in Table 2.

7 Conclusion

In this paper, we consider two well-posed models for current-controlled piezoelectric beams including full electro-magnetic effects; one uses the Coulomb gauge and the other one uses Lorenz gauge. Both models are shown to be not asymptotically stable with only one feedback controller if the material parameters satisfy certain conditions. These conditions correspond to the high-frequency vibration modes. This is due to the addition of the magnetic effects back into to the model; these effects are minor in comparison to the mechanical and electrical effects. The lack of stability for the low-frequency modes is almost impossible to show. Therefore, low frequency vibrational modes are chosen as initial conditions for simulations. It is observed that the choice of a gauge condition does not play an important role in terms of the stabilization, which is good since one can go with either model depending on the physical assumptions for the electromagnetic equations (hyperbolic or elliptic).

A parallel discussion is carried out in [52,53,54] where both quasi-static and fully dynamic cases are handled for voltage or mechanical actuation in the port-Hamiltonian framework. It is shown that asymptotic stability is at stake for the quasi-static model whereas the asymptotic stability can be achievable by retaining the magnetic effects in the model and with additional feedback controllers. Relevant problems have been studied in [31, 32, 36] in details where the quasi-static model with enough number of controllers provide an asymptotic stability result.