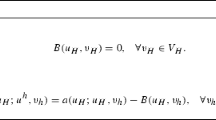Abstract
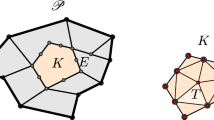
This work extends the general form of the multiscale hybrid-mixed (MHM) method for the second-order Laplace (Darcy) equation to general non-conforming polygonal meshes. The main properties of the MHM method, i.e., stability, optimal convergence, and local conservation, are proven independently of the geometry of the elements used for the first level mesh. More precisely, it is proven that piecewise polynomials of degree k and \(k+1\), \(k \ge 0\), for the Lagrange multipliers (flux), along with continuous piecewise polynomial interpolations of degree \(k+1\) posed on second-level sub-meshes are stable if the latter is fine enough with respect to the mesh for the Lagrange multiplier. We provide an explicit sufficient condition for this restriction. Also, we prove that the error converges with order \(k+1\) and \(k+2\) in the broken \(H^1\) and \(L^2\) norms, respectively, under usual regularity assumptions, and that such estimates also hold for non-convex; or even non-simply connected elements. Numerical results confirm the theoretical findings and illustrate the gain that the use of multiscale functions provides.















Similar content being viewed by others
References
Achdou, Y., Japhet, C., Maday, Y., Nataf, F.: A new cement to glue non-conforming grids with Robin interface conditions: the finite volume case. Numer. Math. 92(4), 593–620 (2002)
Araya, R., Harder, C., Paredes, D., Valentin, F.: Multiscale hybrid-mixed method. SIAM J. Numer. Anal. 51(6), 3505–3531 (2013)
Araya, R., Harder, C., Poza, A., Valentin, F.: Multiscale hybrid-mixed method for the Stokes and Brinkman equations—the method. Comput. Methods Appl. Mech. Eng. 324, 29–53 (2017)
Arbogast, T., Pencheva, G., Wheeler, M.F., Yotov, I.: A multiscale mortar mixed finite element method. SIAM Multiscale Model. Simul. 6, 319–346 (2007)
Babuska, I., Osborn, E.: Generalized finite element methods: their performance and their relation to mixed methods. SIAM J. Numer. Anal. 20(3), 510–536 (1983)
Beirão da Veiga, L., Brezzi, F., Marini, L.D., Russo, A.: The hitchhiker’s guide to the virtual element method. Math. Models Methods Appl. Sci. 24(8), 1541–1573 (2014)
Beirao da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., Marini, L.D., Russo, A.: Basic principles of virtual element methods. Math. Models Methods Appl. Sci. 23(1), 199–214 (2013)
Cangiani, A., Dong, E.H., Georgoulis, A., Houston, P.: hp-Version Discontinuous Galerkin Methods on Polygonal and Polyhedral Meshes. Springer, Berlin (2017)
Cangiani, A., Georgoulis, E., Houston, P.: \(hp\)-version discontinuous Galerkin methods on polygonal and polyhedral meshes. Math. Models Methods Appl. Sci. 24(10), 2009–2041 (2014)
Cockburn, B., Di Pietro, D., Ern, A.: Bridging the hybrid high-order and hybridizable discontinuous Galerkin methods. ESAIM Math. Model. Numer. Anal. 50(3), 635–650 (2016)
Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)
Coutinho, A.L.G.A., Franca, L.P., Valentin, F.: Numerical multiscale methods. Int. J. Numer. Methods Fluids 70(4), 403–419 (2012)
Crouzeix, M., Raviart, P.A.: Conforming and nonconforming finite element methods for solving the stationary Stokes equations. I. Revue française d’automatique, informatique, recherche opérationnelle. Mathématique 7(3), 33–75 (1973)
Di Pietro, D.A., Droniou, J.: A hybrid high-order method for Leray–Lions elliptic equations on general meshes. Math. Comput. 86(307), 2159–2191 (2017)
Duran, O., Devloo, P.R.B., Gomes, A.T.A., Valentin, F.: A multiscale hybrid method for Darcy’s problems using mixed finite element local solvers. Technical report HAL-01868853, INRIA (2018)
E, W., Engquist, B.: The heterogeneous multi-scale methods. Commun. Math. Sci. 1, 87–133 (2003)
Efendiev, Y.R., Hou, T.Y., Wu, X.H.: Convergence of a nonconforming multiscale finite element method. SIAM J. Numer. Anal. 37(3), 888–910 (2000)
Ern, A., Guermond, J.-L.: Theory and Practice of Finite Alements. Applied Mathematical Sciences, vol. 159. Springer, New York (2004)
Ern, A., Pietro, D.D.A.: Arbitrary-order mixed methods for heterogeneous anisotropic diffusion on general meshes. IMA J. Numer. Anal. 37(1), 40–63 (2017)
Farhat, C., Harari, I., Franca, L.P.: The discontinuous enrichment method. Comput. Methods Appl. Mech. Eng. 190(48), 6455–6479 (2001)
Farhat, C., Mandel, J., Roux, F.-X.: Optimal convergence properties of the FETI domain decomposition method. Commun. Numer. Methods Eng. 115, 365–385 (1994)
Gander, M.J., Japhet, C., Maday, Y., Nataf, F.: A new cement to glue nonconforming grids with Robin interface conditions: the finite element case. In: Erhel, J., Gander, M.J., Halpern, L., Pichot, G., Sassi, T., Widlund, O.B. (eds.) Domain Decomposition Methods in Science and Engineering. Volume 40 of Lecture Notes in Computational Science and Engineering, pp. 259–266. Springer, Berlin (2005)
Glowinski, R., Wheeler, M.F.: Domain decomposition and mixed finite element methods for elliptic problems. In: Glowinski, R., Golub, G.H., Meurant, G.A., Périaux, J. (eds.) First International Symposium on Domain Decomposition Methods for Partial Differential Equations, pp. 144–172. SIAM, Philadelphia (1988)
Grisvard, P.: Elliptic Problems in Non-smooth Domains. Pitman Publishing, London (1985)
Harder, C., Madureira, A.L., Valentin, F.: A hybrid-mixed method for elasticity. ESAIM Math. Model. Numer. Anal. 50(2), 311–336 (2016)
Harder, C., Paredes, D., Valentin, F.: A family of multiscale hybrid-mixed finite element methods for the Darcy equation with rough coefficients. J. Comput. Phys. 245, 107–130 (2013)
Harder, C., Paredes, D., Valentin, F.: On a multiscale hybrid-mixed method for advective-reactive dominated problems with heterogenous coefficients. SIAM Multiscale Model. Simul. 13(2), 491–518 (2015)
Harder, C., Valentin, F.: Foundations of the MHM method. In: Barrenechea, G.R., Brezzi, F., Cangiani, A., Georgoulis, E.H. (eds.) Building Bridges: Connections and Challenges in Modern Approaches to Numerical Partial Differential Equations. Lecture Notes in Computational Science and Engineering. Springer, Berlin (2016)
Hou, T.Y., Wu, X., Cai, Z.: Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients. Math. Comput. 68(227), 913–943 (1999)
Hughes, T.J.R.: Multiscale phenomena: Green’s functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origin of stabilized methods. Comput. Methods Appl. Mech. Eng. 127, 387–401 (1995)
Lanteri, S., Paredes, D., Scheid, C., Valentin, F.: The multiscale hybrid-mixed method for the Maxwell equations in heterogeneous media. SIAM Multiscale Model. Simul. 16(4), 1648–1683 (2018)
Malqvist, A., Peterseim, D.: Localization of elliptic multiscale problems. Math. Comput. 83(290), 2583–2603 (2014)
Paredes, D., Valentin, F., Versieux, H.M.: On the robustness of multiscale hybrid-mixed methods. Math. Comput. 86(304), 525–548 (2017)
Raviart, P.A., Thomas, J.M.: Primal hybrid finite element methods for 2nd order elliptic equations. Math. Comput. 31(138), 391–413 (1977)
Sangalli, G.: Capturing small scales in elliptic problems using a residual-free bubbles finite element method. SIAM Multiscale Model. Simul. 1(3), 485–503 (2003)
Veeser, A., Verfurth, R.: Poincaré constants for finite element stars. IMA J. Numer. Anal. 32(1), 30–47 (2012)
Zheng, W., Qi, H.: On Friedrichs–Poincaré-type inequalities. J. Math. Anal. Appl. 304(2), 542–551 (2005)
Funding
GRB’s work is funded by the Leverhulme Trust through the Research Fellowship No. RF-2019-510. The third author was supported by FONDECYT Project 1181572. The fourth author was partially supported by CNPq/Brazil No. 301576/2013-0, EU H2020 Program and from MCTI/RNP-Brazil under the HPC4E Project, Grant Agreement No. 689772, and by CAPES/Brazil No. 88881.143295/2017-01 under the PHOTOM Project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Lemma 4
Let \(k\ge 0\), and let us define the following space
Then, if \(\mu \) satisfies
then \(\mu =0\) in [0, 1].
Proof
The case \(k=0\) will be treated first. For \(k=0\) let
Then, \(q\in \mathscr {X}\). Thus, if \(\mu \in \mathbb {R}{\setminus }\{0\}\), then
which contradicts the hypothesis.
Now, let \(k\ge 1\), and let \(\mu \in \mathbb {P}_{k}^{}(0,1)\) satisfying (101). Let \(q_1^{},q_2^{}\in \mathscr {X}\) be defined by
Since
and \(q_1^{}(x)\ge 0\) in (0, 0.5), then \(\mu \) changes sign in (0, 0.5), which implies that \(\mu \) has at least one root \(x_1^{}\in (0,0.5)\). Analogously, since
then \(\mu \) has also a root \(x_2^{}\in (0.5,1)\). So, if \(k=1\), then \(\mu \in \mathbb {P}_{1}^{}(0,1)\) has two roots in (0, 1), and thus it needs to be identically zero. If \(k\ge 2\), we define the following functions in \(\mathscr {X}\):
If \(\mu \) does not have any other root in (0, 0.5), then, since \(\mu \) and \(q_3^{}\) change signs at the exact same points in (0, 0.5), then
which contradicts (101). In an analogous way, using the function \(q_4^{}\), we deduce the existence of a fourth root \(x_4^{}\in (0.5,1)\). If \(k=3\), then \(\mu \) is a quadratic polynomial with four distinct roots in (0, 1), and then it needs to be identically zero.
For \(k\ge 3\), following completely analogous steps to the ones just described, we deduce that \(\mu \) needs to vanish at, at least, \(2(k+1)-2\) different points in (0, 1), which, for a polynomial \(\mu \in \mathbb {P}_{k}^{}(0,1)\), is impossible unless \(\mu =0\). This finishes the proof. \(\square \)
The following result extends the previous result to the \(\mathbb {P}_{k+1}^{}(F)\times \mathbb {P}_{k+1}^{}(\mathfrak {T})\) case.
Lemma 5
Let \(k\ge 0\). Then, if \(\mu \) satisfies
then \(\mu =0\) in [0, 1], where the space \(\mathscr {X}\) is defined as:
For \(k=0\):
$$\begin{aligned}&\mathscr {X}=\left\{ q\in H^1_0(0,1): \text {the restriction of }\;q\;\text {to}\;(0,1/4),(1/4,1/2),(1/2,3/4), \right. \\&\quad \,\,\quad \qquad \left. \text {and} \;(3/4,1)\;\text {belongs to}\; \mathbb {P}_1^{}\right\} . \end{aligned}$$For \(k=1\):
$$\begin{aligned}&\mathscr {X} = \left\{ q\in H^1_0(0,1): \text {the restriction of }\;q\;\text {to}\;(0,1/3),(1/3,2/3), \right. \\&\quad \,\,\quad \qquad \left. \text {and} \;(2/3,1)\;\text {belongs to}\; \mathbb {P}_2^{}\right\} . \end{aligned}$$For \(k\ge 2\):
$$\begin{aligned} \mathscr {X}=\left\{ q\in H^1_0(0,1): q|_{(0,0.5)}^{}\in \mathbb {P}_{k+1}^{}\left( 0,0.5\right) \;\text {and}\; q|_{(0.5,1)}^{}\in \mathbb {P}_{k+1}^{}\left( 0.5,1\right) \right\} . \end{aligned}$$
Proof
We split the proof in the three cases described above:
\({k=0}\): Let \(\mu \in \mathbb {P}_1^{}(0,1)\) satisfying (101), and let \(\ell _1^{},\ell _2^{}\in \mathscr {X}\) be defined as follows:
Since \(\mu \) satisfies (101) then
which implies that \(\mu \) has a root in (0, 0.5) since \(\ell _1^{}\) is positive in that interval. Analogously, since
and \(\ell _2^{}\) is positive in (0.5, 1), we deduce that \(\mu \) has a root also in (0.5, 1). Since \(\mu \in \mathbb {P}_1^{}(0,1)\) and has two different roots in (0, 1), then it is identically zero.
\({k=1}:\) Let \(\mu \in \mathbb {P}_2^{}(0,1)\) satisfying (101), and let \(\ell _3^{},\ell _4^{}, \ell _5^{}\in \mathscr {X}\) be defined as follows:
Since \(\mu \) satisfies (101) then
which, due to the positivity of \(\ell _3^{}\) implies the existence of \(x_1^{}\in (0,1/3)\) such that \(\mu (x_1^{})=0\). In a completely analogous way, we deduce there exist \(x_2^{}\in (1/3,2/3)\) and \(x_3^{}\in (2/3,1)\) such that \(\mu (x_2^{})=\mu (x_3^{})=0\). Thus, \(\mu \) must necessarily vanish.
\({k\ge 2}\): From the proof of Lemma 4, any function \(\mu \) that satisfies (107) has at least 2k different roots in (0, 1). Now, for \(k\ge 2\), \(2 k \ge k+2\), and thus, if \(\mu \in \mathbb {P}_{k+1}^{}(0,1)\) satisfies (107) it will vanish at at least \(k+2\) different points in (0, 1), which implies that \(\mu \) is identically zero. This finishes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Barrenechea, G.R., Jaillet, F., Paredes, D. et al. The multiscale hybrid mixed method in general polygonal meshes. Numer. Math. 145, 197–237 (2020). https://doi.org/10.1007/s00211-020-01103-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-020-01103-5