Discrete-time survival forests with Hellinger distance decision trees

Abstract

Random survival forests (RSF) are a powerful nonparametric method for building prediction models with a time-to-event outcome. RSF do not rely on the proportional hazards assumption and can be readily applied to both low- and higher-dimensional data. A remaining limitation of RSF, however, arises from the fact that the method is almost entirely focussed on continuously measured event times. This issue may become problematic in studies where time is measured on a discrete scale $t = 1, 2, ...$, referring to time intervals $[0,a_1), [a_1,a_2), \ldots$. In this situation, the application of methods designed for continuous time-to-event data may lead to biased estimators and inaccurate predictions if discreteness is ignored. To address this issue, we develop a RSF algorithm that is specifically designed for the analysis of (possibly right-censored) discrete event times. The algorithm is based on an ensemble of discrete-time survival trees that operate on transformed versions of the original time-to-event data using tree methods for binary classification. As the outcome variable in these trees is typically highly imbalanced, our algorithm implements a node splitting strategy based on Hellinger’s distance, which is a skew-insensitive alternative to classical split criteria such as the Gini impurity. The new algorithm thus provides flexible nonparametric predictions of individual-specific discrete hazard and survival functions. Our numerical results suggest that node splitting by Hellinger’s distance improves predictive performance when compared to the Gini impurity. Furthermore, discrete-time RSF improve prediction accuracy when compared to RSF approaches treating discrete event times as continuous in situations where the number of time intervals is small.

1 Introduction

Random survival forests (RSF, Ishwaran et al. 2008) have become an established tool to model right-censored data in observational research. They provide a valuable nonparametric alternative to classical Cox regression in longitudinal studies, being able to deal with higher-order interactions between covariates, higher-dimensional covariate spaces, and non-proportional hazards when configured appropriately (Korepanova et al. 2019). In recent years, RSF have been increasingly used in practice (e.g. Fantazzini and Figini 2009; Pan et al. 2017; Banerjee et al. 2018; Ingrisch et al. 2018; Verschut and Hambäck 2018), and there are numerous methodological advances and additions, for example regarding variable selection (Ishwaran et al. 2010, 2011) and improved split criteria (Schmid et al. 2016b; Moradian et al. 2017; Wright et al. 2017).

A remaining limitation of the RSF methodology arises from the fact that RSF are almost entirely focussed on continuously measured event times. This limitation is particularly relevant in observational studies with fixed follow-up intervals where it is only known that events have occurred between two consecutive points in time. In these cases, event times are grouped (constituting a special case of interval censoring), and time is measured on a discrete scale $t = 1,2,\ldots , k$, referring to time intervals $[0,a_1), [a_1,a_2), \ldots , [a_{k-1},\infty )$ with fixed boundaries $a_1,\ldots , a_{k-1}$. A similar situation occurs in studies where event times are “intrinsically” discrete, for example, when analyzing time to pregnancy, which is usually measured by the number of menstrual cycles (Scheike and Keiding 2006; Fehring et al. 2013). As argued by many authors (e.g. Tutz and Schmid 2016; Bogaerts et al. 2017; Berger et al. 2018), the application of statistical models designed for continuous time-to-event data is not appropriate when interval censoring and/or grouping effects are ignored.

The aim of this work is therefore to develop a random forest algorithm that is specifically designed for the analysis of (possibly right-censored) discrete time-to-event data. Discrete-time survival trees and RSF have been first considered in Bou-Hamad et al. (2009) and Bou-Hamad et al. (2011), respectively. The main building block of the algorithm proposed here is a discrete-time survival tree method developed by Schmid et al. (2016a): Conditional on the values of a set of covariates $X = (X_{(1)},\ldots , X_{(p)})^{\top }$, the method by Schmid et al. (2016a) results in nonparametric estimates of the discrete hazard function

$$\begin{aligned} \lambda (t|X) := \mathrm{P}(T = t \, | \, T \ge t, X) \, , \ \ \ t = 1, 2, \ldots , k \, , \end{aligned}$$

(1)

which is the discrete-time equivalent to the hazard function considered in continuous-time survival analysis. As with classical random forest approaches (Breiman 2001; Ishwaran et al. 2008), a discrete-time RSF estimate of $\lambda (t|X)$ is obtained by averaging the discrete hazard estimates derived from a set of survival trees that have been applied to bootstrap samples of the available data.

The key features of the new RSF algorithm can be briefly summarized as follows:

• (i) Based on the definition of the discrete hazard function (1), the idea is to fit probability estimation trees (PETs, Provost and Domingos 2003; Schmid et al. 2016a) to bootstrap samples of re-shaped data sets with a binary outcome $Y \in \{0,1\}$. To generate these re-shaped data, the original time-to-event data are converted to sets of augmented data, in which each individual is represented by multiple data lines. Each of these data lines refers to a specific time point $t = 1, 2, \ldots$, and the outcome value $Y =0$ indicates survival of the individual beyond the respective time point. Conversely, each data line with $Y=1$ indicates an event at the respective time point. Details on data re-shaping will be provided in Sect. 2.2.

• (ii) A major problem of tree building with re-shaped data is that Y is typically highly imbalanced, as by definition each individual is represented by at most one data line with $Y=1$ but multiple data lines with $Y=0$. This problem is known to severely degrade tree performance and evaluation when not accounted for (Menardi and Torelli 2014; Fernandez et al. 2018). To address this issue, we propose to use Hellinger’s distance criterion (Cieslak et al. 2012) for tree building, which is insensitive to the skewness of the distribution of Y and has been shown to be highly effective when used for imbalanced classification tasks (“Hellinger Distance Decision Trees”, Cieslak et al. 2012). Details on split criteria and tree building will be given in Sect. 2.3.

• (iii) Unlike Schmid et al. (2016a), who proposed to fit discrete-time survival trees using cardinality pruning in combination with the Gini impurity split criterion, we propose to build discrete-time RSF using unpruned trees with a small minimum node size. This strategy follows the original approach to random forest classification for binary outcome variables proposed by Breiman (2001). Details on building the random forest ensemble, along with a formal definition of the RSF estimates of $\lambda (t|X)$, will be given in Sect. 2.4.

In Sects. 3 and 4 we will analyze the properties of the discrete-time RSF algorithm using simulation studies and a data set on the duration of unemployment spells of U.S. citizens (Cameron and Trivedi 2005). Our numerical results suggest that node splitting by Hellinger’s distance improves predictive performance when compared to skew-sensitive split criteria such as the Gini impurity. Furthermore, discrete-time RSF tend to improve prediction accuracy when compared to continuous-time RSF algorithms ignoring discreteness in situations where the number of time intervals is small.

The findings of this paper will be summarized and discussed in Sect. 5. The supplementary materials contain the results of additional simulations as well as another real-world application on the analysis of the time to first childbirth in German women (German Family Panel, Huinink et al. 2011).

2 Methods

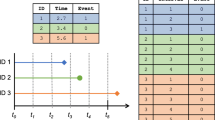
Throughout this paper, we denote by $T \in \{ 1, 2,\ldots , k\}$ a discrete survival outcome and by $C \in \{ 1, 2,\ldots , k\}$ a discrete censoring time independent of T. The aim of the discrete-time RSF algorithm is to obtain a nonparametric estimate of the discrete hazard function $\lambda (t|X)$ defined in (1). It is assumed that the RSF algorithm is applied to a set of i.i.d. learning data with n independent observations and p covariates $(\tilde{T}_i, \varDelta _i, X_i)$, $i=1,\ldots , n$, where $\tilde{T}_i$ and $\varDelta _i$ denote the sample variables of the (possibly right-censored) observed survival time $\tilde{T}_i:= \min (T_i, C_i)$ and the status indicator $\varDelta _i := \mathrm{I}(T_i \le C_i)$, respectively. Figure 1 provides a schematic overview of the discrete-time RSF algorithm. The various steps of the algorithm will be described in detail in the next subsections. For a general description of the rationale of the random forest methodology, see e.g. Breiman (2001) and Ishwaran et al. (2008).

2.1 Initialization

Before the algorithm starts, one needs to specify the number of trees of the RSF (termed ntree) and the number of covariates available for splitting at each node (termed mtry). Common choices are $mtry = \lfloor \sqrt{p}\rfloor$ and $ntree = 500$. These values have been pre-specified in the R package ranger (Wright and Ziegler 2017) and will also be used here.

2.2 Data re-shaping

Instead of fitting the discrete-time RSF directly to the learning data $(\tilde{T}_i, \varDelta _i, X_i)$, $i=1,\ldots , n$, we propose to define the input of the RSF algorithm by a set of re-shaped (“augmented”) data with binary outcome variable. This approach is motivated by parametric and semiparametric discrete time-to-event modeling (e.g., Berger and Schmid 2018), which is based on the optimization of the log-likelihood of the data-generating process described above. The main idea is to express the log-likelihood of a discrete-time survival model in terms of the hazards $\lambda (t|X)$, which results in a binomial log-likelihood function

$$\begin{aligned} \ell =\sum _{i=1}^n \sum _{t = 1}^{\tilde{T}_i} y_{it} \log \left( \lambda (t|X_i) \right) +(1 - y_{it}) \log \left( 1 - \lambda (t|X_i) \right) \end{aligned}$$

(2)

with the sequences $y_i = (y_{i1}, \dots , y_{i\tilde{T}_i})$ of length $\tilde{T}_i$ that are defined by $y_i := (0, \dots , 0, 1)$ if $\varDelta _i = 1$ and $y_i := (0, \dots , 0, 0)$ if $\varDelta _i = 0$. Note that each entry of $y_i$ corresponds to one of the time points $t = 1,2,\ldots , \tilde{T}_i$, where $y_{it}=0$ indicates survival beyond t and $y_{it}=1$ indicates an event at t.

Based on the result stated in (2), estimates of $\lambda (t|X)$ can generally be obtained by fitting a statistical model with binary outcome to the set of augmented data, which are defined for each individual by

$$\begin{aligned} M_i := \left( \begin{array}{ccc} 0 &{} 1 &{} X_i^{\top } \\ 0 &{} 2 &{} X_i^{\top } \\ 0 &{} 3 &{} X_i^{\top } \\ \vdots &{} \vdots &{} \vdots \\ 1 &{} \tilde{T}_i &{} X_i^{\top } \\ \end{array}\right) \end{aligned}$$

(3)

if $\varDelta _i = 1$ and

$$\begin{aligned} M_i := \left( \begin{array}{ccc} 0 &{} 1 &{} X_i^{\top } \\ 0 &{} 2 &{} X_i^{\top } \\ 0 &{} 3 &{} X_i^{\top } \\ \vdots &{} \vdots &{} \vdots \\ 0 &{} \tilde{T}_i &{} X_i^{\top } \\ \end{array}\right) \end{aligned}$$

(4)

if $\varDelta _i = 0$. The first columns of the matrices (3) and (4) contain the binary values $y_{it}$ whereas the third columns contain copies of the covariate values. The values in the second columns of (3) and (4) refer to the time intervals $1,\ldots ,\tilde{T}_i$; the role of these columns will be explained later. The augmented data matrix of the whole sample is obtained by concatenating the individual augmented data matrices $M_i$, $i=1,\ldots , n$, resulting in a matrix with $m:=\sum _{i=1}^n \tilde{T}_i$ rows. Each row refers to one of the $\sum _{i=1}^n \tilde{T}_i$ summands in the binomial log-likelihood function (2). For further details on data augmentation we refer to Tutz and Schmid (2016) and Schmid et al. (2016a).

An important consequence of the structure of the log-likelihood function in (2) is that it allows the model fitting algorithm to treat the values $y_{it}$ as realizations of a binary outcome variable Y. The idea of the proposed RSF algorithm is therefore to augment the available learning data analogously to (3) and (4) (“Data Preparation” step in Fig. 1), to generate a set of ntree bootstrap samples from the augmented data, and to fit ntree probability estimation trees with binary outcome variable Y to the augmented data sets (“Tree Building” step in Fig. 1).

2.3 Tree building

Following Schmid et al. (2016a), we propose to base tree building on the classification and regression trees (CART) approach by Breiman et al. (1984). Starting with the root node (referring to the whole covariate space), the idea of CART is to recursively subdivide the support of X into a set of terminal nodes. Partitioning of the covariate space is done by recursively optimizing a split criterion, which is computed from the learning data and is chosen according to the type of outcome variable. For each of the splits a single variable $X_{(j)}$, $j \in \{1, \dots , p\}$ is selected. Then the support of $X_{(j)}$ is subdivided into two mutually exclusive subsets termed children nodes. Generally, partitioning is done such that within-node homogeneity with respect to the distribution of the outcome variable is maximized. The choice of the split criterion generally depends on the scale of the outcome variable. If the outcome is a categorical variable, a popular strategy is to construct a classification tree or a probability estimation tree (PET) by minimizing the Gini criterion or some other impurity measure in the children nodes. If the outcome is a continuous survival time, a survival tree can be constructed by maximizing the log-rank statistic obtained from the survival times in the children nodes. The latter strategy is e.g. used in the continuous-time RSF method by Ishwaran et al. (2008). Node splitting in CART has been the topic of many articles and books; for details, we refer to Breiman et al. (1984).

Fig. 1

Schematic overview of the discrete-time RSF algorithm

Based on the definition of the log-likelihood in (2), Schmid et al. (2016a) developed a discrete-time survival tree algorithm that applies the CART approach with binary outcome variable Y to the augmented data matrix defined in Sect. 2.2. For this, the rows of the matrices (3) and (4) are subject to recursive partitioning, implying that (i) each individual is represented by multiple rows in the augmented learning data, and that (ii) each terminal node of the discrete-time survival tree contains a set of zeros and ones. Estimates of the discrete hazard $\lambda (t|X)$ are then obtained by the proportions of ones in the terminal nodes. Since the discrete hazard function does not only condition on the values of the covariates X but also on the event “$T \ge t$”, the idea is to use both X and the values $\tilde{t}_i := (1,2,\ldots , \tilde{T}_i)$ contained in the second columns of (3) and (4) for node splitting. This strategy implies that the vector $(\tilde{t}_1, \ldots , \tilde{t}_n)^{\top }$ is treated like an ordinal covariate during tree building, so that the estimates of the discrete hazard function capture interactions between the covariates and time. Also, by definition of the augmented data matrix and the recursive partitioning procedure, each terminal node refers to a hazard estimate that is constant within a node-specific time interval ${\mathcal {T}} \subset \{1, \ldots , k\}$ (cf. Schmid et al. 2016a). Estimates of the discrete hazard function $\lambda (t|X)$ over the whole time range $t=1,\ldots , k$ are obtained for each individual by concatenating the hazard estimates (i.e., the proportions of ones) in the terminal nodes. For example, assume that an individual $i \in \{1,\ldots , n\}$ has a covariate combination $X_i$ and an observed survival time $\tilde{T}_i$ resulting in $\tilde{T}_i$ rows in the augmented data matrix. The values of these rows are then dropped down the discrete-time survival tree and result in a set of hazard estimates that are defined within mutually exclusive time intervals ${\mathcal {T}}$. Concatenating these time intervals and their associated hazard estimates defines an estimate of the individual’s hazard function across the whole time range $t=1,\ldots , k$. As illustrated in Schmid et al. (2016a) and Berger and Schmid (2018), this strategy results in a flexible nonparametric estimator of $\lambda (t|X)$ that is able to incorporate both higher-order interactions and time-dependent covariate effects.

The discrete-time RSF proposed in this paper is based on a similar tree-building algorithm, which differs from the method in Schmid et al. (2016a) mainly by the choice of the split criterion. With regard to the latter, Schmid et al. (2016a) argued that the focus of a discrete-time survival tree is not on the correct classification of the values $y_{it} \in \{ 0, 1\}$ but on the accurate estimation of the probabilities${\lambda } (t|X)$ (“probability estimation tree”, PET, Provost and Domingos 2003). For this reason, Schmid et al. (2016a) proposed to use the Gini impurity (Breiman et al. 1984) for node splitting, as this criterion is asymptotically equivalent to the Brier score (Gneiting and Raftery 2007) for evaluating the accuracy of probabilistic binary forecasts. Schmid et al. (2016a) demonstrated that the Gini-based splitting approach works well in single trees, in particular when combined with a cardinality pruning strategy that guarantees sufficiently large numbers of observations in the terminal nodes (thereby controlling the variance of the discrete hazard estimates). Unlike Schmid et al. (2016a), however, we do not propose to use cardinality pruning in the development of the discrete-time RSF algorithm, as the aim is to control the variance of the hazard estimates by averaging the predictions of an ensemble of unpruned trees with small terminal node sizes. Moreover, it is well known that the Gini split criterion, which was also considered in the original random forest algorithm for binary outcome variables by Breiman (2001), may heavily deteriorate the performance of CART when the distribution of the outcome variable is imbalanced (Cieslak and Chawla 2008). This issue is particularly problematic in discrete-time survival analysis, which is based on the binary outcome sequences $y_{i}$ containing multiple numbers of zeroes but at most one value with $y_{it}=1$ each (see Sect. 2.2). For example, under the assumption of independent uniformly distributed discrete event and censoring times with $k=10$ intervals (resulting in a moderately high censoring rate of $45\%$), data augmentation will yield only approximately $14\%$ values with $y_{it}=1$.

We therefore propose to replace the Gini impurity by Hellinger’s distance, which has been recommended by Cieslak et al. (2012) as a split criterion in decision trees with a highly imbalanced outcome. For any pair of children nodes ${\mathcal {M}}, {\mathcal {N}} \subset \{1, \ldots , m\}$, ${\mathcal {M}} \cap {\mathcal {N}}= \emptyset$, that result from splitting the support of a covariate $X_{(j)}$, the idea is to consider all observations in ${\mathcal {M}}$ as “positive” instances and all observations in ${\mathcal {N}}$ as “negative” instances. Based on this concept, Hellinger’s distance is defined by

$$\begin{aligned} d_H ({\mathcal {M}}, {\mathcal {N}}) :=\sqrt{\left( \sqrt{tpr} - \sqrt{fpr} \right) ^2 +\left( \sqrt{1-tpr} - \sqrt{1-fpr} \right) ^2} \, , \end{aligned}$$

(5)

where tpr and fpr refer to the pair of true and false positive rates defined by

$$\begin{aligned} tpr&:= \big |{\mathcal {M}} \cap {\mathcal {O}} \big | \, / \, \big | {\mathcal {O}}\big | \, , \end{aligned}$$

(6)

$$\begin{aligned} fpr&:= \big |{\mathcal {M}} \cap \big ( ({\mathcal {M}} \cup {\mathcal {N}}) \backslash {\mathcal {O}}\big ) \big | \, / \, \big | ({\mathcal {M}} \cup {\mathcal {N}}) \backslash {\mathcal {O}}\big | \, , \end{aligned}$$

(7)

and ${\mathcal {O}} \subset ({\mathcal {M}} \cup {\mathcal {N}})$ is the set of elements with outcome value $y_{it}=1$ in the joint set ${\mathcal {M}} \cup {\mathcal {N}}$. In each node of the ntree trees, splitting is done such that Hellinger’s distance in (5) is maximized over all possible binary partitions of the supports of the mtry covariates (“Hellinger Distance Decision Tree”, HDDT, Cieslak et al. 2012).

By definition, HDDTs capture deviations in the class conditionals, implying that they are skew-insensitive and work well even when the distribution of the binary outcome Y is highly imbalanced. For an in-depth discussion and analysis of HDDTs, see Cieslak and Chawla (2008) and Cieslak et al. (2012).

2.4 Ensemble estimation

The discrete-time RSF ensemble is obtained by collecting the ntree Hellinger Distance Decision Trees constructed from the bootstrap samples generated in the “Data Preparation” step in Fig. 1. Generally, there are two options for generating bootstrap samples: One could either draw bootstrap samples from the original time-to-event data and augment them afterwards (“bootstrapping before augmentation”), or one could augment the time-to-event data first and draw bootstrap samples from the concatenated data matrices (3) and (4) (“bootstrapping after augmentation”, as proposed in Fig. 1). Both options are explored in more detail in Sects. 3 and 4. Following the idea of Breiman (2001), we propose to build unpruned trees with a small terminal node size, i.e., tree building is continued until a pre-specified minimum node size is reached. In the remainder of this paper, the minimum node size of all RSF algorithms will be set to 10, which is the default value for fitting PETs in the R package ranger.

After having built the ensemble, estimates of the discrete hazard $\lambda (t|X)$ are obtained as follows: For each new observation with covariate data $X_{\mathrm{new}}$, one considers the augmented data matrix

$$\begin{aligned} M_{\mathrm{new}} := \left( \begin{array}{cc} 1 &{} X_{\mathrm{new}}^{\top } \\ 2 &{} X_{\mathrm{new}}^{\top } \\ 3 &{} X_{\mathrm{new}}^{\top } \\ \vdots &{} \vdots \\ k-1 &{} X_{\mathrm{new}}^{\top } \\ \end{array}\right) \end{aligned}$$

(8)

covering the time range $t = 1, \ldots , k-1$. Next, the $k-1$ data lines are dropped down each of the ntree trees, resulting in sets of estimates $\hat{\lambda }_b (1|X_{\mathrm{new}})$, $\hat{\lambda }_b (2|X_{\mathrm{new}})$, $\ldots$, $\hat{\lambda }_b (k-1|X_{\mathrm{new}})$, $b=1,\ldots , ntree$, which are given by the proportions of ones (computed from the learning data) in the respective terminal nodes. Note that it is not necessary to include a k-th row in the augmented matrix (8), as $\lambda (k|X_{\mathrm{new}}) = 1$ by definition. Finally, the discrete-time RSF estimate of ${\lambda }(t|X_{\mathrm{new}})$ is computed by averaging over the ntree trees, i.e.,

$$\begin{aligned} \hat{\lambda }_{\mathrm{RSF}} (t|X_{\mathrm{new}}) := \frac{1}{{ ntree}} \sum _{b=1}^{{ ntree}} \hat{\lambda }_b (t|X_{\mathrm{new}}) \, , \ \ \ t=1,\ldots , k-1 \, . \end{aligned}$$

(9)

When the aim is to measure the performance of the discrete-time RSF using a single real-valued score, it is useful to aggregate the set of discrete hazard estimates in (9) over time. Analogous to continuous-time RSF (Ishwaran et al. 2008), this can be done by computing the sum of the cumulative discrete hazard estimates, which is given by

$$\begin{aligned} \hat{\varLambda }_{\mathrm{RSF}} (X_{\mathrm{new}}) := \sum _{t=1}^{k-1} \, (k-t) \cdot \hat{\lambda }_{\mathrm{RSF}} (t|X_{\mathrm{new}}) \, . \end{aligned}$$

(10)

The estimate in (10), which can be computed separately for each individual in a set of independent test data, will be used as a predictive marker to evaluate the performance of discrete-time RSF in Sect. 4.

3 Simulation study

3.1 Experimental design

To investigate the properties of the discrete-time RSF method, we carried out a simulation study with 100 Monte Carlo replications. The aims of the study were (i) to compare discrete-time RSF to alternative methods, in particular to random forests using the Gini split criterion, and (ii) to analyze the effects of the censoring rate and the number of intervals k on the performance of discrete-time RSF.

The data-generating process for the simulation study was defined as follows: In each Monte Carlo replication, we generated a learning data set with $n=1,000$ observations and $p=50$ independent standard uniformly distributed covariates. Event times were generated according to the logistic discrete hazard model

$$\begin{aligned} \log \left( \frac{\lambda (t|X)}{1-\lambda (t|X)} \right) =\eta _{0t} + \eta (X) \, , \ \ \, t=1,\ldots , k-1 \, , \end{aligned}$$

(11)

where $\eta _{0t} \in {\mathbb {R}}$ was a set of baseline coefficients independent of X and $\eta (X) \in {\mathbb {R}}$ was an additive predictor independent of t (“proportional continuation ratio model”, cf. Tutz and Schmid 2016). The baseline coefficients were defined by the linear trend function $(\eta _{01}, \ldots , \eta _{0,k-1})^{\top } := ( -1, -1-{1}/{(k-2)}$, $-1-{2}/{(k-2)}, -1-{3}/{(k-2)}, \ldots , -2)^{\top }$, and the values of $\eta (X)$ were obtained by multiplying the standardized sum of ten independently generated three-way interactions of the covariates $X_1,\ldots , X_{25}$ (defined as $X_{(j)}\cdot X_{(k)} \cdot X_{(l)}$, $j \ne k \ne l \in \{1,\ldots , 25\}$, (j, k, l) drawn ten times with replacement) by the factor two. Depending on the value of k, this data-generating process resulted in Spearman correlations between T and $\eta (X)$ ranging from $-0.75$ to $-0.70$. The covariates $X_{26},\ldots , X_{50}$ served as noise variables in the simulation study.

Censoring times were generated independently from a continuous exponential distribution with right-shifted support $(1, \infty )$. Based on the values of the continuous censoring times (denoted by $C_{\mathrm{cont},i}$, $i=1,\ldots , n$), the observed discrete event times were calculated as $\tilde{T}_i = \lfloor \min (T_i, C_{\mathrm{cont},i}) \rfloor$, $i=1,\ldots , n$. For each value of k, the rate of the exponential distribution was adjusted such that the censoring rate (defined as $\sum _{i=1}^n (1-\varDelta _i) / \sum _{i=1}^n \mathrm{I}(T_i > 1)$) became either $30\%$ (“low censoring” scenario) or $70\%$ (“high censoring” scenario).

In each Monte Carlo replication, we applied the discrete-time RSF algorithm to the learning data using varying numbers of time points ($k=5, 6, \ldots , 10$). Prediction accuracy was evaluated by applying the 100 RSF fits to an independent test sample of size $n_{\mathrm{test}} = 1000$ that followed the same data-generating process as the learning data. In each Monte Carlo replication, we calculated the time-dependent average squared difference between the values of the predicted survival function $\hat{S}(t|X)$ and the respective values of the true survival function S(t|X). Based on these differences (which in the following will be denoted by err(t)), we computed a time-independent measure of prediction error that was defined by $Err := {\sum _{t=1}^{k-1} \hat{\mathrm{P}} (\tilde{T} = t) \cdot err(t) }$.

For each value of k we compared the following modeling approaches:

• (i) discrete-time RSF with splitting by Hellinger’s distance (HD),

• (ii) discrete-time RSF with splitting by the Gini impurity (GI),

• (iii) discrete-time RSF with splitting by the Gini impurity, combined with synthetic minority over-sampling (“SMOTE”) in the data preparation step (Fernandez et al. 2018; GI_SMOTE),

• (iv) continuous-time RSF with splitting by the log-rank statistic (LeBlanc and Crowley 1993; Ishwaran et al. 2008; RSF_cont),

• (v) RSF for interval-censored continuous time-to-event data (Yao et al. 2019a, ICcforest), and

• (vi) the correctly specified logistic discrete hazard model (11).

For the discrete-time RSF methods (i) and (ii), we additionally considered a modified version of the data preparation step in which the original time-to-event data were re-shaped after bootstrapping (“Bootstrapping before Augmentation”, HD_BA and GI_BA). With this strategy, PETs were fitted to ntree augmented data sets that were generated from bootstrap samples of the original learning data. The SMOTE method in (iii) was applied to compare splitting by Hellinger’s distance with an alternative method for addressing class imbalance in tree-based models. The ICcforest method in (v) is based on a likelihood function that represents discrete event times as interval-censored continuous event times. The logistic discrete hazard model in (vi) was used as a benchmark model reflecting the true data-generating process. All RSF models except ICcforest were fitted using the R add-on package ranger, which is available on GitHub at https://github.com/imbs-hl/ranger. For the continuous-time RSF method in (iv) we set the minimum terminal node size to three observations, which is the default value for log-rank splitting in ranger. RSF for interval-censored continuous time-to-event data were fitted using the implementation in the R add-on package ICcforest (Yao et al. 2019b). Synthetic minority over-sampling was done using the ubSMOTE function of the R add-on package unbalanced (Dal Pozzolo et al. 2015). To achieve class balance, we adjusted the SMOTE method such that the number of ones in the binary outcome of the re-shaped data became approximately equal to $\sum _{i=1}^n \sum _{t=1}^{\tilde{T}_i} (1-y_{it})$.

3.2 Results

Figure 2 shows the average values of the time-dependent squared prediction error err(t) obtained in the low censoring scenario with $k=7$. It is seen that the HD method (discrete-time RSF with splitting by Hellinger’s distance) resulted in smaller prediction errors than the GI method (discrete-time RSF with splitting by the Gini criterion) at all time points. The same result was observed for the alternative methods HD_BA and GI_BA, which, however, performed worse than their respective counterparts HD and GI. Compared to the RSF_cont method (continuous-time RSF), the HD method resulted in smaller prediction errors at early time points and larger prediction errors at later time points. This finding may be attributed to the fact that the HD method considers the time points $\tilde{t}_i = (1,2,\ldots , \tilde{T}_i)$ as an additional variable during node splitting, which results in an increased accuracy of the hazard estimates at (early) time points that are more frequently observed in the learning data. In contrast, the log-rank criterion used by the RSF_cont method is based on the whole time range in each split, resulting in hazard estimates that show less variability (compared to the HD method) at later time points with smaller observed frequencies. The ICcforest method behaved similar to the RSF_cont method, but its prediction errors were smaller than the respective prediction errors of RSF_cont at almost all time points. As expected, the estimates obtained from the correctly specified logistic discrete hazard model resulted in the smallest prediction errors in Fig. 2. Similar results (not shown) were obtained in the high censoring scenario with $k=7$.

Fig. 2

Results of the simulation study. The plot shows the average values of the time-dependent squared difference between the predicted survival function $\hat{S}(t|X)$ and the true survival function S(t|X), as obtained from 100 Monte Carlo replications in the low censoring scenario ($k=7$, $30\%$ censoring). The gray bars visualize the relative frequencies of the observed event times ($\hbox {true model} = \hbox {correctly specified logistic discrete hazard model}$)

Figure 3 presents the values of the summary measure Err obtained from the HD and GI methods in the low censoring scenarios. It is seen that the prediction error of the HD method was smaller than the respective prediction error of the GI method for all values of k (panel (a) of Fig. 3). Larger values of k (implying an increased class imbalance in the binary outcome variable Y) resulted in higher prediction errors of both methods. Panel (b) of Fig. 3, which depicts the differences in Err between the GI and HD methods, shows that the benefit obtained from splitting by Hellinger’s distance increased with the value of k. This finding confirms the results by Cieslak et al. (2012), who argued that using Hellinger’s distance for node splitting is particularly beneficial in situations where class imbalance in the binary outcome variable is high.

Fig. 3

Results of the simulation study. The boxplots in panel a visualize the values of the summary measure Err obtained from the GI and HD methods in the low censoring scenario (100 Monte Carlo replications, $30\%$ censoring). The boxplots in panel b visualize the respective differences in Err between the GI and HD methods

A comparison of the HD and RSF_cont methods (referring to discrete-time and continuous-time RSF, respectively) is presented in Fig. 4. It is seen that the prediction error of the HD method was smaller than the respective prediction error of the RSF_cont method for all values of k (panel (a) of Fig. 4). However, the differences between the two methods became smaller with increasing value of k (panel (b) of Fig. 4). This result justifies the use of the continuous-time RSF approach in situations where k is large and where the discrete time scale may be well approximated by a continuous time scale. On the other hand, the discrete-time RSF approach performed best when the value of k was small and the time scale was distinctly discrete. Similar results (not shown) were obtained in the high censoring scenarios.

Fig. 4

Results of the simulation study. The boxplots in panel a visualize the values of the summary measure Err obtained from the RSF_cont and HD methods in the low censoring scenario (100 Monte Carlo replications, $30\%$ censoring). The boxplots in panel b visualize the respective differences in Err between the RSF_cont and HD methods

Figure 5 presents a comparison of the differences in prediction error that were obtained in the high and low censoring scenarios. Panel (a) of Fig. 5 shows that the differences in Err between the GI and HD methods were essentially insensitive to variations in the censoring rate (although there appeared to be a very slight decrease in the Err difference at some values of k when the censoring rate was increased from $30\%$ to $70\%$). In contrast, the differences in Err between the RSF_cont and HD methods became larger as the censoring rate increased (panel (b) of Fig. 5). This result confirms earlier findings by Ishwaran et al. (2008) who stated that “the performance of [log-rank-based] RF regression depended strongly on the censoring rate”, with the prediction accuracy of continuous-time RSF being “poor” in high-censoring scenarios. The HD method appeared to be more robust against high censoring rates, which might be attributed to the definition and the properties of Hellinger’s distance (being insensitive to class imbalance).

Fig. 5

Results of the simulation study. The boxplots in panel a visualize the differences in Err between the GI method and the HD method for different values of k and different censoring rates. The boxplots in panel b visualize the respective differences in Err between the RSF_cont method and the HD method. Censoring rates were $30\%$ in the low censoring scenario and $70\%$ in the high censoring scenario

3.3 Effect of the minimum node size on prediction accuracy

To analyze the sensitivity of the various RSF methods with regard to choice of the minimum node size, we repeated the simulation study with minimum node sizes ranging between 3 and 100. The prediction errors of the resulting ICcforest, HD and GI fits are summarized in Fig. 6 (low censoring scenario, $k = 7$). Obviously, the prediction accuracy of the methods could be improved by optimizing the minimum node sizes of the algorithms. On the other hand, the benefits of this additional tuning step appear to be rather small, especially when compared to the differences in prediction accuracy between the various RSF algorithms and split criteria. Similar results were obtained for other values of k (see Section A of the supplementary materials).

Fig. 6

Results of the simulation study. The boxplots visualize the effect of the minimum node size on the values of the summary measure Err obtained from the ICcforest, HD and GI methods (100 Monte Carlo replications, $30\%$ censoring, $k=7$)

4 Application: duration of unemployment

To illustrate the use of the discrete-time RSF approach, we analyzed a data set on the duration of unemployment spells of $n = 3,343$ U.S. citizens. The data, which were originally analyzed by McCall (1996) and Cameron and Trivedi (2005), were collected in the years 1986, 1988, 1990 and 1992 as part of the January Current Population Survey’s Displaced workers supplements (DWS). Unemployment duration was measured in two-week intervals. Analogous to the analysis by Cameron and Trivedi (2005), Example 17.11, and Schmid et al. (2018), we defined the outcome variable as the time to re-employment at either a part-time or a full-time job. Furthermore, we set $k = 14$ and summarized all unemployment spells $> 26$ weeks into one category. This strategy resulted in a censoring rate of $31.11\%$ (see Table 1).

For RSF analysis we used the publicly available version of the data, which is part of the R add-on package Ecdat (Croissant 2016). The covariates considered for RSF analysis were (i) age at baseline (years), (ii) filing of an unemployment claim (yes/no), (iii) eligible replacement rate (defined as the weekly benefit amount divided by the amount of weekly earnings in the lost job), (iv) eligible disregard rate (defined as the disregard, i.e. the amount up to which recipients of unemployment insurance who accept part-time work can earn without any reduction in unemployment benefits, divided by the weekly earnings in the lost job), (v) log weekly earnings ($) in the lost job, and (vi) tenure in the lost job (years). A descriptive summary of the covariates is presented in Table 1. Ninety observations were excluded from statistical analysis because of missing values in at least one of the variables. This resulted in an analysis data set containing $n=3253$ observations.

Table 1 Descriptive summary statistics of the variables that were used to model time to re-employment (data frame UnempDur contained in the R package Ecdat, Croissant 2016)

To investigate the performance of the discrete-time RSF approach, we conducted a benchmark experiment that was based on 100 random partitions of the data. Each partition consisted of a learning data set of size $n=2602$ and a test data set of size $n_{\mathrm{test}}=651$. For model comparison we considered the same RSF approaches as in Sect. 3 and applied them to the 100 learning data sets. Furthermore, we considered a logistic discrete hazard model (Tutz and Schmid 2016) that was fitted to the 100 learning data sets using the default implementation of the elastic net method in the R package glmnet (Friedman et al. 2019), E_net). The penalty parameter $\lambda$ of the elastic net method was determined using ten-fold cross-validation, as implemented in the cv.glmnet function of the glmnet package.

To evaluate the predictive performance of the RSF fits, we computed the aggregated hazard estimates defined in (10) and assessed the concordance between $\hat{\varLambda }_{\mathrm{RSF}}$ and T in each of the 100 test samples. This was done by applying the estimator of the discrete concordance index (“C-index”) proposed in Schmid et al. (2018). Generally, the C-index is defined by the probability $\mathrm{P}(\zeta _i > \zeta _s \, |\, T_i < T_s)$, where $\zeta$ is a continuous marker (here, $\zeta \equiv \hat{\varLambda }_{\mathrm{RSF}}$), and i and s refer to two independent individuals in the test data. By definition, the C-index compares the rankings of the survival times and the marker values. It takes the value 1 in case of “perfect disagreement”, which, in case of discrete-time RSF, implies that a larger value of the aggregated hazard is associated with a shorter event time. For the elastic net fits, we defined $\zeta$ in the same way as the marker $\hat{\varLambda }_{\mathrm{RSF}}$ in (10). In addition to the C-index, we computed estimates of the integrated squared prediction error in each test data set. Generally, the integrated squared prediction error is defined by the time-integrated squared deviation between the predicted survival functions and the observed survival functions (for each observation defined by a step function dropping from one to zero at time point $T_i$) in the test data. It is thus similar to the time-independent measure Err used in Sect. 3, which is based on the true data-generating process instead of the observed survival functions. Unlike the C-index, which solely measures the discriminatory power of a time-to-event model, the integrated squared prediction error also accounts for how well a model is calibrated. For details, we refer to Tutz and Schmid (2016), Chapter 4, and Schmid et al. (2018). The evalCindex and evalIntPredErr functions of the R package discSurv (Welchowski and Schmid 2019) were used to compute the estimates of the C-index and the integrated squared prediction error, respectively.

The estimates of the integrated squared prediction error are presented in panel (a) of Fig. 7. It is seen that, in contrast to the simulation study presented in Sect. 3, the ICcforest method outperformed the discrete-time RSF approaches and resulted in the smallest values of the summary measure Err. Apart from this finding, the results of the simulation study were largely confirmed: Again, the discrete-time RSF approaches with splitting by Hellinger’s distance (HD and HD_BA) performed better than the respective approaches with splitting by the Gini impurity (GI_BA and GI_BA). The median values of the integrated squared prediction error (as estimated from the 100 test data sets) were 0.203 (RSF_cont), 0.194 (ICcforest), 0.198 (HD), 0.203 (HD_BA), 0.201 (GI), 0.207 (GI_BA), 0.201 (E_net), and 0.285 (GI_SMOTE). Similar results were obtained from the estimates of the C-index presented in panel (b) of Fig. 7: Again, the ICcforest method performed best, and the HD approach performed better than the GI approach, although, with regard to the C-index, the alternative methods HD_BA and GI_BA showed a slightly higher discriminatory power than their respective counterparts HD and GI. The median values of the C-index (as estimated from the 100 test data sets) were 0.664 (RSF_cont), 0.683 (ICcforest), 0.663 (HD), 0.665 (HD_BA), 0.660 (GI), 0.660 (GI_BA), 0.656 (E_net), and $0.623$ (GI_SMOTE).

Fig. 7

Analysis of time to re-employment. The boxplots in panel a visualize the estimates of the integrated squared prediction error, as obtained from fitting various RSF models to 100 pairs of learning and test samples generated from the UnempDur data. The rightmost boxplot in panel a refers to a discrete-time RSF model that included the time intervals $1,\ldots , \tilde{T}_i$ (second columns of (3) and (4)) as only covariate. This model served as a “null” model that would have been used in the absence of any covariate information. Note that the boxplot referring to the GI_SMOTE method was excluded from panel a, as the respective estimates of the integrated squared prediction error (median $= 0.285$, range $= [0.246, 0.327]$) were far higher than the values of the null model. The boxplots in panel b visualize the estimated values of the C-index. A reference value for the C-index is given by the value 0.5 (not depicted in the right panel), which corresponds to the C-index of the covariate-free null model

Fig. 8

Analysis of time to re-employment. The barplots in panel a visualize the permutation-based variable importance values, as obtained from fitting the discrete-time RSF model with splitting by Hellinger’s distance to the full UnempDur data. The barplots in panel b visualize the respective importance values obtained from the discrete-time RSF model with splitting by the Gini impurity

In the final step we applied the HD and GI methods to the whole data set and computed permutation-based variable importance values, as implemented in the importance function of the R package ranger. In case of the HD method (panel (a) of Fig. 8), filing an unemployment claim was estimated to be the most important covariate along with the amount of weekly earnings in the lost job. Conversely, in the case of the GI method (panel (b) of Fig. 8), the amount of weekly earnings in the lost job was estimated to be clearly the most important covariate, followed by the eligible replacement rate. While an in-depth analysis of the underlying predictor-response relationships is out of the scope of this paper, the results presented in Fig. 8 clearly show that differences in the choice of the split criterion (Hellinger’s distance vs. Gini impurity) do not only affect prediction accuracy but may also lead to differences in the interpretation of a RSF fit.

4.1 Application: time to first childbirth

In Section B of the supplementary materials, we present the results of another real-world application in which we analyzed the time to first childbirth in German women (German Family Panel, “pairfam”, Huinink et al. 2011). The results of this analysis largely confirmed the results obtained from the analysis of the UnempDur data: Again, the discrete-time RSF approaches with splitting by Hellinger’s distance outperformed the respective approaches with splitting by the Gini impurity. In contrast to the analysis of the UnempDur data presented in Fig. 7, the ICcforest method did not perform better than the HD method with regard to the summary measure Err and the estimated C-index (see Fig. 3 in Section B of the supplementary materials.)

5 Summary and discussion

The random forest method proposed in this paper provides a flexible approach to prediction modeling in situations where the outcome variable of interest is measured on a discrete time scale. By operating on an augmented data matrix with binary outcome, it directly relates to the CART-based classification forest methodology by Breiman (2001). Furthermore, our method may be viewed as an alternative to an earlier discrete-time RSF approach by Bou-Hamad et al. (2011) that performs node splitting by maximizing the sum of the log-likelihood values of two covariate-free discrete hazard models fitted to the data in the children nodes.

Unlike parametric discrete hazard models (such as the complementary log-log model or the proportional continuation ratio model, cf. Tutz and Schmid 2016), discrete-time RSF do not require the pre-specification of a link function relating the discrete hazard to the covariates. By including the time variable as an additional candidate variable, our approach accounts for time-varying effects of the covariates on the discrete hazard rate. As demonstrated in Sect. 4, variable importance measures can be calculated in the same way as in “classical” random forest methods for classification and regression.

In our simulation study, the RSF approach with splitting by Hellinger’s distance (HD) performed consistently better in terms of prediction accuracy than the respective RSF approach with splitting by the Gini impurity (GI). This result clearly demonstrates the benefit of accounting for class imbalance in tree-based modeling of discrete time-to-event data. Surprisingly, random oversampling of the minority class via the SMOTE method did not improve the performance of Gini-based RSF but resulted in a strong decrease in prediction accuracy. This finding might be explained by the fact that oversampling distorts the ratio of ones and zeros in the binary outcome variable Y which is inherent in the definition of the log-likelihood function (2).

Compared to continuous-time RSF, the discrete-time RSF approach with splitting by Hellinger’s distance resulted in a better prediction accuracy when the number of unique time points was small and the time scale was “distinctly” discrete. As expected, the differences in prediction accuracy between the discrete-time and the continuous-time methods vanished when the number of unique time points increased and when the discrete time scale could be well approximated by a continuous time scale. When compared to the ICcforest approach that accounts for discrete time measurements by representing them as interval-censored continuous event times, the discrete-time RSF approach resulted in a better prediction accuracy in the simulations and in the analysis of the pairfam data. On the other hand, ICcforest outperformed RSF with splitting by Hellinger’s distance in the analysis of the unemployment data. These results suggest that the appropriate use of the ICcforest and HD methods depends on the characteristics of the data at hand, and that a properly designed comparison study (using validation data or re-sampling procedures) is essential to decide on the application of the methods in practice.

A remaining limitation of the discrete-time RSF approach arises from the size of the augmented data matrices (3) and (4), which may lead to storage and/or run time issues when the number of unique time points is large. Despite the fact that RSF are ideally suited for parallel computing, this problem might restrict the application of discrete-time RSF to “big data” sets in some situations. On the other hand, it is likely that the increasing availability of large-scale storage solutions and high-performance computing facilities will help to settle this problem in the near future.

We finally emphasize that all numerical results presented in this paper are based on the default values of the minimum node size and the mtry parameter specified in the ranger package. While these parameters are supposed to work well in practice, and while relying on the default values ensured the comparability of the methods in the simulations, one might expect additional tuning steps for the minimum node size and the mtry parameter to further improve the predictive performance of the discrete-time RSF method (cf. Fig. 6).