State estimation of T–S fuzzy Markovian generalized neural networks with reaction–diffusion terms: a time-varying nonfragile proportional retarded sampled-data control scheme

Abstract

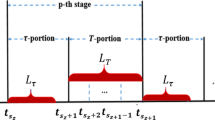
This paper focuses on the state estimation issue of T–S fuzzy Markovian generalized neural networks (GNNs) with reaction–diffusion terms. An estimator-based nonfragile time-varying proportional retarded sampled-data controller that permits norm-bounded indeterminacy and contains a time-varying delay is designed to guarantee the asymptotical stability of the error system. By establishing a novel Lyapunov–Krasovskii functional that involves positive indefinite items and discontinuous items, meanwhile, by combining the reciprocally convex combination method, Jenson’s inequality and Wirtinger inequality, a less conservative stability criterion can be derived. Moreover, the principle for the number of selected variables in the process of deriving main results is also analyzed. Finally, two numerical examples are given to demonstrate the validity and advantages of the results proposed in this paper.

Appendix

1.1 Appendix 1: Crucial Lemmas

Lemma 1

[45] If there exists a matrix $X \in {{\mathbb {R}}^{n \times n}}$, $X = {X^\mathrm{T}} > 0$ and $c \le s \le d$, then one has

$$\begin{aligned} -\int _c^d {{\alpha ^\mathrm{T}}(s)X\alpha (s)\mathrm{d}s} \le -&\frac{1}{{d - c}}{\left( {\int _c^d {\alpha (s)} \mathrm{d}s} \right) ^\mathrm{T}}\\&X\int _c^d {\alpha (s)} \mathrm{d}s \end{aligned}$$

Lemma 2

[46] Let $\Omega$ be a cube $\left| {{x_k}} \right| < {\tilde{l}_k}(k = 1,2,\ldots ,m)$, $\nu (x)$ be a real-valued function belonging to ${C^1}(\Omega )$ which satisfies $\nu (x)\left| {_{\partial \Omega }} \right. = 0$. Then

$$\begin{aligned} \int _\Omega {\nu ^2(x)\mathrm{d}x} \le \tilde{l}_k^2\int _\Omega {\left| {\frac{{\partial \nu (x)}}{{\partial {x_k}}}} \right| ^2\mathrm{d}x} \end{aligned}$$

Lemma 3

[32] Let ${g_1},{g_2},\ldots ,{g_N}:{{\mathbb {R}}^m} \rightarrow {{\mathbb {R}}^1}$ have positive values in an open subset E of ${{\mathbb {R}}^m}$. Then, the reciprocally convex combination of ${g_i}$ over E satisfies

$$\begin{aligned} & \left\{ {\nu _i}\left| {{\nu _i} > 0,\sum \limits _i {{\nu _i}} = 1} \right. \right\} \sum \limits _i {\frac{1}{{{\nu _i}}}{g_i}(t)}\\&= \sum \limits _i {{g_i}(t)} + \mathop {\max }\limits _{{f_{i,j}}(t)} \sum \limits _{i \ne j} {{f_{i,j}}(t)} \end{aligned}$$

subject to

$$\begin{aligned} \{ {f_{i,j}}:{{{\mathbb {R}}}^m} \rightarrow {{{\mathbb {R}}}^1},{f_{i,j}}(t) = {f_{j,i}}(t),\left[ {\begin{array}{*{20}{c}} {{g_i}(t)}&{}{{f_{i,j}}(t)}\\ {{f_{j,i}}(t)}&{}{{g_j}(t)} \end{array}} \right] \ge 0\} \end{aligned}$$

Lemma 4

[47] Given real matrices A, B and D with appropriate dimensions and a scalar $\varepsilon > 0$, moreover, ${D^\mathrm{T}}D \le I$, for any vectors $x,y \in {{\mathbb {R}}^n}$, the following inequation holds:

$$\begin{aligned} 2{x^\mathrm{T}}ADBy \le {\varepsilon ^{ - 1}}{x^\mathrm{T}}A{A^\mathrm{T}}x + \varepsilon {y^\mathrm{T}}{B^\mathrm{T}}By \end{aligned}$$

Lemma 5

[48] For any matrix $\mathcal{M} \in {{\mathbb {R}}^{n \times n}}$, $\mathcal{M} = {\mathcal{M}^\mathrm{T}} > 0$, the integrable function $\dot{\omega }(x)$ in $[a,b]\rightarrow {{\mathbb {R}}^n}$ satisfies:

$$\begin{aligned} \int _a^b {{{\dot{\omega }}^\mathrm{T}}(x)\mathcal{M}\dot{\omega }(x)\mathrm{d}x} \ge \frac{1}{{b - a}}\dot{r}_0^\mathrm{T}\mathcal{M}{\dot{r}_0} + \frac{3}{{b - a}}\dot{r}_1^\mathrm{T}\mathcal{M}{\dot{r}_1} \end{aligned}$$

where

$$\begin{aligned} {r_0} = \int _a^b {\omega (x)\mathrm{d}x} ,\ \ {\dot{r}_1} = \omega (b) + \omega (a) - \frac{2}{{b - a}}{r_0}. \end{aligned}$$

1.2 Appendix 2: Proof of Theorem 1

For the purpose of simplicity, the vector notations are denoted as follows:

$$\begin{aligned} &{\varpi _1} = \frac{1}{{\varsigma (t)}}\int _{t - \varsigma (t)}^t {{y_\mu }(z,x)} \mathrm{d}x,\\&{\varpi _2} = \frac{1}{{\varsigma (t)}}\int _{t - \varsigma (t) - \eta (t) }^{t - \eta (t) } {{y_\mu }(z,x)} \mathrm{d}x,\\&{\psi _1} = {y_\mu } - {y^\varsigma _\mu },\\&{\psi _2} = {y_\mu }+ {y^\varsigma _\mu } - 2{\varpi _1},\\&{\psi _3} = {y_{\mu \eta }}- {y^\varsigma _{\mu \eta } },\\&{\psi _4} = {y_{\mu \eta } } + {y^\varsigma _{\mu \eta }} - 2{\varpi _2},\ \ \chi _{1\mu }^\mathrm{T} = [y_\mu ^\mathrm{T}, {\tilde{f}^\mathrm{T}}({W_\alpha }{y_\mu })],\ \ \\&\chi _{2\mu }^\mathrm{T} = \{ {[\varsigma (t){\varpi _1}]^\mathrm{T}}, {[{y_\mu } - {y^\varsigma _\mu }]^\mathrm{T}}\},\ \ \\&\chi _{3\mu }^\mathrm{T}= \{ {[\varsigma (t){\varpi _2}]^\mathrm{T}},\ \ {[{y_{\mu \eta }} - {y^\varsigma _{\mu \eta }}]^\mathrm{T}}\}. \end{aligned}$$

We choose the following LKF candidate:

$$\begin{aligned} V({y_\mu },t) = \sum \limits _{\imath = 1}^9 {{V_\imath }({y_\mu },t)} \end{aligned}$$

(17)

where

$$\begin{aligned} {V_1}({y_\mu },t) =&\, \int _\Omega {\sum \limits _{\mu = 1}^n \left\{ y_\mu ^\mathrm{T}{\mathcal{P}_\alpha }{y_\mu } + {\gamma _2}\sum \limits _{k = 1}^q{{(\frac{{\partial {y_\mu }}}{{\partial {z_k}}})}^\mathrm{T}} {\mathcal{E}_k}\Gamma (\frac{{\partial {y_\mu }}}{{\partial {z_k}}}) \right\} } \mathrm{d}z\\ {V_2}({y_\mu },t) =&\, \int _\Omega \sum \limits _{\mu = 1}^n \left\{ \int _{t - h(t)}^t {\chi _{1\mu }^\mathrm{T}(z,x){\mathcal{Q}_1}{\chi _{1\mu }}(z,x)\mathrm{d}x}\right. \\&\left. + \int _{t - {h_1}}^t {\chi _{1\mu }^\mathrm{T}(z,x){\mathcal{Q}_2}{\chi _{1\mu }}(z,x)\mathrm{d}x} \right\} \mathrm{d}z \\&+ \int _\Omega {\sum \limits _{\mu = 1}^n \left\{ \int _{t - {h_2}}^t {\chi _{1\mu }^\mathrm{T}(z,x){\mathcal{Q}_3}{\chi _{1\mu }}(z,x)\mathrm{d}x}\right\} } \mathrm{d}z\\ {V_3}({y_\mu },t) =&\, \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ (\varsigma _m - \varsigma (t))\chi _{2\mu }^\mathrm{T}{\mathcal{W}_1}{\chi _{2\mu }}\right\} } } \mathrm{d}z\\ {V_4}({y_\mu },t) =&\, \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ (\varsigma { _m} - \varsigma (t))\chi _{3\mu }^\mathrm{T}{\mathcal{W}_2}{\chi _{3\mu }}\right\} } } \mathrm{d}z\\ {V_5}({y_\mu },t) =&\, \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ \int _{t - \eta (t) }^t {y_\mu ^\mathrm{T}(z,x){\mathcal{H}_1}{y_\mu }(z,x)\mathrm{d}x }\right\} } } \mathrm{d}z \\&+ \int _\Omega \sum \limits _{\mu = 1}^n {\left\{ \int _{t - \eta (t) }^t {\dot{y}_\mu ^\mathrm{T}(z,x){\mathcal{H}_2}{{\dot{y}}_\mu }(z,x)\mathrm{d}x }\right\} } \mathrm{d}z\\ {V_6}({y_\mu },t) =&\, \int _\Omega \sum \limits _{\mu = 1}^n \left\{ {\varsigma ^2}\int _{t - \varsigma (t)}^t \dot{y}_\mu ^\mathrm{T}(z,x){\mathcal{U}_1}{{\dot{y}}_\mu }(z,x)\mathrm{d}x \right. \\&\left. - \varsigma (t)\psi _1^\mathrm{T}{\mathcal{U}_1}{\psi _1} - 3\varsigma (t)\psi _2^\mathrm{T}{\mathcal{U}_1}{\psi _2} \right\} \mathrm{d}z\\ {V_7}({y_\mu },t) =&\, \int _\Omega \sum \limits _{\mu = 1}^n \left\{ {\varsigma ^2}\int _{t - \varsigma (t) - \eta (t) }^{t - \eta (t) } \dot{y}_\mu ^\mathrm{T}(z,x){\mathcal{U}_2}{{\dot{y}}_\mu }(z,x)\mathrm{d}x \right. \\&\left. - \varsigma (t)\psi _3^\mathrm{T}{\mathcal{U}_2}{\psi _3} { - 3\varsigma (t)\psi _4^\mathrm{T}{\mathcal{U}_2}{\psi _4}} \right\} \mathrm{d}z\\ {V_8}({y_\mu },t) =&\, \int _\Omega \sum \limits _{\mu = 1}^n \left. \left\{ ({h_2} - {h_1})\int _{ - {h_2}}^{ - {h_1}} \int _{t + \theta }^t {y_\mu ^\mathrm{T}(z,x){\mathcal{Z}_1}{y_\mu }(z,x)} \mathrm{d}x\mathrm{d}\theta \right. \right. \\&\left. + \varsigma \int _{ - \varsigma }^0 {\int _{t + \theta }^t {y_\mu ^\mathrm{T}(z,x){\mathcal{Z}_2}{y_\mu }(z,x)} \mathrm{d}x\mathrm{d}\theta } \right\} \mathrm{d}z\\ {V_9}({y_\mu },t) =&\, \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ ({\varsigma _m} - \varsigma (t))\varsigma (t)[\varpi _1^\mathrm{T},\varpi _2^\mathrm{T}]\mathcal{I}\left[ {\begin{array}{*{20}{c}} {{\varpi _1}}\\ {{\varpi _2}} \end{array}} \right] \right\} } } \mathrm{d}z \end{aligned}$$

Then, it can be deduced that for each $\alpha \in \mathcal{S}$,

$$\begin{aligned} \mathcal{L}V({y_\mu },t) = \sum \limits _{\imath = 1}^9 {\mathcal{L}{V_\imath }({y_\mu },t)} \end{aligned}$$

(18)

where

$$\begin{aligned}\mathcal{L}{V_1}({y_\mu },t) =& \int _\Omega \sum \limits _{\mu = 1}^n \left\{ 2y_\mu ^\mathrm{T}{\mathcal{P}_\alpha }{{\dot{y}}_\mu } + \sum \limits _{\beta \in \mathcal{S}} {y_\mu ^\mathrm{T}{\varphi _{\alpha \beta }}{\mathcal{P}_\beta }} {y_\mu } \right. \\&\quad \left. + 2 {\gamma _2}\sum \limits _{k = 1}^q {{{\left(\frac{{\partial {y_\mu }}}{{\partial {z_k}}}\right)}^\mathrm{T}}{\mathcal{E}_k}\Gamma \left(\frac{{\partial {{\dot{y}}_\mu }}}{{\partial {z_k}}}\right)} \right\} \mathrm{d}z\\ \mathcal{L}{V_2}({y_\mu },t) &\le \int _\Omega {\sum \limits _{\mu = 1}^n {\left. {\left\{ {\chi _{1\mu }^\mathrm{T}({\mathcal{Q}_1} + {\mathcal{Q}_2} + {\mathcal{Q}_3}){\chi _{1\mu }}} \right. } \right\} } \mathrm{d}z} \\&\quad - (1 - h)\int _\Omega {\sum \limits _{\mu = 1}^n {\left. {\left\{ {\chi _{1\mu h }^\mathrm{T}{\mathcal{Q}_1}{\chi _{1\mu h}}} \right. } \right\} } } \mathrm{d}z\\&\quad - \int _\Omega {\sum \limits _{\mu = 1}^n {\left. {\left\{ {\chi _{1\mu h_1 }^\mathrm{T}{\mathcal{Q}_2}{\chi _{1\mu h_1 }}} \right. } \right\} } \mathrm{d}z} \\&\quad - \int _\Omega {\sum \limits _{\mu = 1}^n {\left. {\left\{ {\chi _{1\mu h_2 }^\mathrm{T}{\mathcal{Q}_3}{\chi _{1\mu h_2}}} \right. } \right\} } \mathrm{d}z}\\ \mathcal{L}{V_3}({y_\mu },t) &= - \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ \chi _{2\mu }^\mathrm{T}{\mathcal{W}_1}{\chi _{2\mu }}\right\} } } \mathrm{d}z \\&\quad + 2\int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ (\varsigma { _m} - \varsigma (t))\chi _{2\mu }^\mathrm{T}{\mathcal{W}_1}\left[ \begin{array}{l} {y_\mu }\\ {{\dot{y}}_\mu } \end{array} \right] \right\} }} \mathrm{d}z\\ \mathcal{L}{V_4}({y_\mu },t) &= - \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ \chi _{3\mu }^\mathrm{T}{\mathcal{W}_2}{\chi _{3\mu }}\right\} } } \mathrm{d}z\\&\quad + 2\int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ (\varsigma { _m} - \varsigma (t))\chi _{3\mu }^\mathrm{T}{\mathcal{W}_2}\left[ \begin{array}{l} {y_{\mu \eta }}\\ {{\dot{y}}_{\mu \eta }} \end{array} \right] \right\} } } \mathrm{d}z\\ \mathcal{L}{V_5}({y_\mu },t) &= \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ y_\mu ^\mathrm{T}{\mathcal{H}_1}{y_\mu } - y_{\mu \eta } ^\mathrm{T}{\mathcal{H}_1}{y_\mu \eta }\right\} } } \mathrm{d}z\\&\quad + \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ \dot{y}_\mu ^\mathrm{T}{\mathcal{H}_2}{{\dot{y}}_\mu } - \dot{y}_{\mu \eta }^\mathrm{T}{\mathcal{H}_2}{{\dot{y}}_{\mu \eta }}\right\} } } \mathrm{d}z \\ \mathcal{L}{V_6}({y_\mu },t) &= \int _\Omega \sum \limits _{\mu = 1}^n \left\{ {\varsigma ^2}\dot{y}_\mu ^\mathrm{T}{\mathcal{U}_1}{{\dot{y}}_\mu } - \psi _1^\mathrm{T}{\mathcal{U}_1}{\psi _1} \right. \\&- 2\varsigma (t)\psi _1^\mathrm{T}{\mathcal{U}_1}{{\dot{y}}_\mu } - 3\psi _2^\mathrm{T}{\mathcal{U}_1}{\psi _2} \\&\left. - 6\psi _2^\mathrm{T}{\mathcal{U}_1}[\varsigma (t){{\dot{y}}_\mu } + 2{\varpi _1} - 2{y_\mu }]\right\} \mathrm{d}z\\ \mathcal{L}{V_7}({y_\mu },t) &= \int _\Omega \sum \limits _{\mu = 1}^n \left\{ {\varsigma ^2}\dot{y}_{\mu \eta } ^\mathrm{T}{\mathcal{U}_2}{{\dot{y}}_{\mu \eta } } \right. \\&\quad \left. - \psi _3^\mathrm{T}{\mathcal{U}_2}{\psi _3} - 2\varsigma (t)\psi _3^\mathrm{T}{\mathcal{U}_2}{{\dot{y}}_{\mu \eta } } - 3\psi _4^\mathrm{T}{\mathcal{U}_2}{\psi _4} \right. \\&\left. - 6\psi _4^\mathrm{T}{\mathcal{U}_2}[\varsigma (t){{\dot{y}}_{\mu \eta } } + 2{\varpi _2} - 2{y_{\mu \eta }}]\right\} \mathrm{d}z\\ \mathcal{L}{V_8}({y_\mu },t) &= \int _\Omega \sum \limits _{\mu = 1}^n \left\{ {{({h_2} - {h_1})}^2}y_\mu ^\mathrm{T}{\mathcal{Z}_1}{y_\mu } - ({h_2} - {h_1})\right. \\&\left. \int _{t - {h_2}}^{t - {h_1}} {y_\mu ^\mathrm{T}(z,x){\mathcal{Z}_1}{y_\mu }(z,x)\mathrm{d}x} \right. \\&\left. + {\varsigma ^2}y_\mu ^\mathrm{T}{\mathcal{Z}_2}{y_\mu } - \varsigma \int _{t - \varsigma }^t {y_\mu ^\mathrm{T}(z,x){\mathcal{Z}_2}{y_\mu }(z,x)\mathrm{d}x} \right\} \mathrm{d}z \end{aligned}$$

For ${h_1}< h(t) < {h_2}$, the following inequalities can be deduced by employing Lemmas 1 and 3:

$$\begin{aligned} &- ({h_2} - {h_1})\int _{t - {h_2}}^{t - {h_1}} {y_\mu ^\mathrm{T}(z,x){\mathcal{Z}_1}{y_\mu }(z,x)\mathrm{d}x}\\&\quad \le - \frac{{{h_2} - {h_1}}}{{{h_2} - h(t)}}{\left( {\int _{t - {h_2}}^{t - h(t)} {{y_\mu }(z,x)\mathrm{d}x} } \right) ^\mathrm{T}}{\mathcal{Z}_1}\left( {\int _{t - {h_2}}^{t - h(t)} {{y_\mu }(z,x)\mathrm{d}x} } \right) \\&\qquad - \frac{{{h_2} - {h_1}}}{{h(t) - {h_1}}}{\left( {\int _{t - h(t)}^{t - {h_1}} {{y_\mu }(z,x)\mathrm{d}x} } \right) ^\mathrm{T}}{\mathcal{Z}_1}\left( {\int _{t - h(t)}^{t - {h_1}} {{y_\mu }(z,x)\mathrm{d}x} } \right) \\&\quad \le - {\left[ \begin{array}{l} \int _{t - {h_2}}^{t - h(t)} {{y_\mu }(z,x)\mathrm{d}x} \\ \int _{t - h(t)}^{t - {h_1}} {{y_\mu }(z,x)\mathrm{d}x} \end{array} \right] ^\mathrm{T}}\left[ {\begin{array}{*{20}{c}} {{\mathcal{Z}_1}}&{}{{{\tilde{\mathcal{Z}}}_1}}\\ * &{}{{\mathcal{Z}_1}} \end{array}} \right] \left[ \begin{array}{l} \int _{t - {h_2}}^{t - h(t)} {{y_\mu }(z,x)\mathrm{d}x} \\ \int _{t - h(t)}^{t - {h_1}} {{y_\mu }(z,x)\mathrm{d}x} \end{array} \right] \end{aligned}$$

(19)

$$\begin{aligned} &- \varsigma \int _{t - \varsigma }^t {y_\mu ^\mathrm{T}(z,x){\mathcal{Z}_2}{y_\mu }(z,x)\mathrm{d}x} \\&\quad \le - \frac{\varsigma }{{\varsigma - \varsigma (t)}}{\left( {\int _{t - \varsigma }^{t - \varsigma (t)} {{y_\mu }(z,x)\mathrm{d}x} } \right) ^\mathrm{T}}\\&\quad {\mathcal{Z}_2}\left( {\int _{t - \varsigma }^{t - \varsigma (t)} {{y_\mu }(z,x)\mathrm{d}x} } \right) \\&\quad - \frac{\varsigma }{{\varsigma (t)}}{\left( {\int _{t - \varsigma (t)}^t {{y_\mu }(z,x)\mathrm{d}x} } \right) ^\mathrm{T}}{\mathcal{Z}_2}\left( {\int _{t - \varsigma (t)}^t {{y_\mu }(z,x)\mathrm{d}x} } \right) \end{aligned}$$

$$\begin{aligned} \le -&\left[ \begin{array}{l} \int _{t - \varsigma }^{t - \varsigma (t)} {{y_\mu }(z,x)\mathrm{d}x} \\ \int _{t - \varsigma (t)}^t {{y_\mu }(z,x)\mathrm{d}x} \end{array} \right] ^\mathrm{T}&\left[ {\begin{array}{c} {{\mathcal{Z}_2}}{{{\tilde{\mathcal{Z}}}_2}}\\ * {{\mathcal{Z}_2}} \end{array}} \right] \\&\left[ \begin{array}{l} \int _{t - \varsigma }^{t - \varsigma (t)} {{y_\mu }(z,x)\mathrm{d}x} \\ \int _{t - \varsigma (t)}^t {{y_\mu }(z,x)\mathrm{d}x} \end{array} \right] \end{aligned}$$

(20)

where

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\mathcal{Z}_1}}&{}{{{\tilde{\mathcal{Z}}}_1}}\\ * &{}{{\mathcal{Z}_1}} \end{array}} \right]> 0, \ \ \left[ {\begin{array}{*{20}{c}} {{\mathcal{Z}_2}}&{}{{{\tilde{\mathcal{Z}}}_2}}\\ * &{}{{\mathcal{Z}_2}} \end{array}} \right] > 0 \end{aligned}$$

In addition,

$$\begin{aligned} \mathcal{L}{V_9}({y_\mu },t) =&\, \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ ({\varsigma _m} - 2\varsigma (t))[\varpi _1^\mathrm{T},\varpi _2^\mathrm{T}]\mathcal{I}\left[ {\begin{array}{c} {{\varpi _1}}\\ {{\varpi _2}} \end{array}} \right] \right\} } }\mathrm{d}z\\&+ \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ 2({\varsigma _m} - \varsigma (t))[\varpi _1^\mathrm{T},\varpi _2^\mathrm{T}]\mathcal{I}\left[ {\begin{array}{c} { - {\varpi _1} + {y_\mu }}\\ { - {\varpi _2} + {y_{\mu \eta }}} \end{array}} \right] \right\} } } \mathrm{d}z \end{aligned}$$

From Assumption 1, we can obtain the following inequations for n-dimensional positive definite diagonal matrices ${\Theta _{o}}(o = 1,2,3)$:

$$\begin{aligned} 0\le & {} 2{[\tilde{f}({W_\alpha }{y_\mu }) - {V_1}{W_\alpha }{y_\mu }]^\mathrm{T}}{\Theta _1}[{V_2}{W_\alpha }{y_\mu }- \tilde{f}({W_\alpha }{y_\mu })] \end{aligned}$$

(21)

$$\begin{aligned} 0\le & {} 2{[\tilde{f}({W_\alpha }{y_{\mu h} }) - {V_1}{W_\alpha }{y_{\mu h} }]^\mathrm{T}}{\Theta _2}[{V_2}{W_\alpha }{y_{\mu h}}- \tilde{f}({W_\alpha }{y_{\mu h}})] \end{aligned}$$

(22)

$$\begin{aligned} 0\le & {} 2\{ \tilde{f}({W_\alpha }{y_\mu }) - \tilde{f}({W_\alpha }{y_{\mu h}}) \nonumber \\&- {V_1}[{W_\alpha }{y_\mu } - {W_\alpha }{y_{\mu h} }]\} ^\mathrm{T} {\Theta _3}\{ {V_2}[{W_\alpha }{y_\mu } - {W_\alpha }{y_{\mu h}}]\nonumber \\&\quad - \tilde{f}({W_\alpha }{y_\mu }) + \tilde{f}({W_\alpha }{y_{\mu h} })\} \end{aligned}$$

(23)

According to the error system (6), one has

$$\begin{aligned} 0&= 2\int _\Omega \sum \limits _{\mu \mathrm{{ = }}1}^n \left\{ \sum \limits _{i = 1}^r\sum \limits _{j = 1}^r {\theta _i}(\xi ){{\theta _j}(\xi ^\varsigma )} [{\gamma _1}y_\mu ^\mathrm{T}\Gamma \right. \nonumber \\&\quad \left. + {\gamma _2}\dot{y}_\mu ^\mathrm{T}\Gamma ] \left\{ - {{\dot{y}}_\mu } + \sum \limits _{k = 1}^q {\frac{\partial }{{\partial {z_k}}}} ({\mathcal{E}_k}\frac{{\partial {y_\mu }}}{{\partial {z_k}}}) - {\mathcal{B}_{i\alpha }}{y_\mu }+ {\mathcal{C}_{i\alpha }}\tilde{f}({W_\alpha }{y_\mu }) \right. \right. \nonumber \\&\quad \left. \left. +{\mathcal{D}_{i\alpha }}\tilde{f}({W_\alpha }{y_{\mu h}})\right. \right. \nonumber \\&\quad \left. \left. + [{K_{1j}} + \Delta {K_{1j}}( t)]{\mathcal{H}_i}_\alpha {y^\varsigma _\mu } + [{K_{2j}} + \Delta {K_{2j}}(t)]{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta } }\right\} \right\} \mathrm{d}z \end{aligned}$$

(24)

Then, using Lemma 4, we get

$$\begin{aligned}&2[{\gamma _1}y_\mu ^\mathrm{T}\Gamma + {\gamma _2}\dot{y}_\mu ^\mathrm{T}\Gamma ][\Delta {K_{1j}}(t){\mathcal{H}_i}_\alpha {y^\varsigma _\mu } + \Delta {K_{2j}}( t){\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta }} ]\\&= 2[{\gamma _1}y_\mu ^\mathrm{T}\Gamma + {\gamma _2}\dot{y}_\mu ^\mathrm{T}\Gamma ]{Q_j}{Y_j}(t)[{\mathcal{N}_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu }+ {\mathcal{N}_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta }} ]\\&\quad \le {\varepsilon ^{ - 1}}[{\gamma _1}y_\mu ^\mathrm{T}\Gamma + {\gamma _2}\dot{y}_\mu ^\mathrm{T}\Gamma ]{Q_j}Q_j^\mathrm{T}{[{\gamma _1}y_\mu ^\mathrm{T} \Gamma + {\gamma _2}\dot{y}_\mu ^\mathrm{T}\Gamma ]^\mathrm{T}} \\&\quad + \varepsilon [{\mathcal{N}_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu } + {\mathcal{N}_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta }} {]^\mathrm{T}}[{\mathcal{N}_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu } + {\mathcal{N}_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta }} ] \end{aligned}$$

Combining (24) and Lemma 2, one can easily derive that

$$\begin{aligned} \mathcal{L}{V_1}({y_\mu }&,t)\le 2\int _\Omega {\sum \limits _{\mu \mathrm{{ = }}1}^n {{\Upsilon _\mu }\mathrm{d}z} } \nonumber \\&+ \int _\Omega {\sum \limits _{\mu = 1}^n {\left\{ {\left. {\sum \limits _{\beta \in \mathcal{S}} {y_\mu ^\mathrm{T}{\varphi _{\alpha \beta }}{\mathcal{P}_\beta }} {y_\mu }} \right\} } \right. } } \mathrm{d}z \nonumber \\&+ \int _\Omega {\sum \limits _{\mu \mathrm{{ = }}1}^n {\left\{ {\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {{\theta _i}(\xi ){\theta _j}(\xi ^\varsigma )\varepsilon [{\mathcal{N}_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu }} } } \right. } }\nonumber \\&+ {\mathcal{N}_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta } } ]^\mathrm{T}\nonumber \\&\times [{\mathcal{N}_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu }\left. { + {\mathcal{N}_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta } } ]} \right\} \mathrm{d}z\nonumber \\&+ \int _\Omega \sum \limits _{\mu = 1}^n \left\{ {\sum \limits _{j = 1}^r {{\theta _j}(\xi ^\varsigma )} } [{\varepsilon ^{ - 1}}\left( {\gamma _1}y_\mu ^\mathrm{T}\Gamma \right. \right. \nonumber \\&\left. \left. + {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma \right) {Q_j}Q_j^\mathrm{T}{{({\gamma _1}y_\mu ^\mathrm{T} \Gamma + {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma )}^\mathrm{T}}] \right\} \mathrm{d}z \end{aligned}$$

(25)

where

$$\begin{aligned} {\Upsilon _\mu } =&\,\sum \limits _{i = 1}^r\sum \limits _{j = 1}^r{{\theta _i}(\xi ) {{\theta _j}(\xi ^\varsigma )} [y_\mu ^\mathrm{T}{\mathcal{P}_\alpha }{{\dot{y}}_\mu }} - {\gamma _1}y_\mu ^\mathrm{T}\Gamma {{\dot{y}}_\mu }- {\gamma _1}y_\mu ^\mathrm{T}\Gamma \tilde{\mathcal{E}}{y_\mu } \\&- {\gamma _1}y_\mu ^\mathrm{T}\Gamma {\mathcal{B}_{i\alpha }}{y_\mu } + {\gamma _1}y_\mu ^\mathrm{T}\Gamma {\mathcal{C}_{i\alpha }}\tilde{f}({W_\alpha }{y_\mu })\\&+ {\gamma _1}y_\mu ^\mathrm{T}\Gamma {\mathcal{D}_{i\alpha }}\tilde{f}({W_\alpha }{y_{\mu h}})\\&+ {\gamma _1}y_\mu ^\mathrm{T}\Gamma {K_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu }+ {\gamma _1}y_\mu ^\mathrm{T}\Gamma {K_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta }} \\&- {\gamma _2}\dot{y}_\mu ^\mathrm{T}\Gamma {{\dot{y}}_\mu }- {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma {\mathcal{B}_{i\alpha }}{y_\mu } + {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma {\mathcal{C}_{i\alpha }}\tilde{f}({W_\alpha }{y_\mu })\\&+ {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma {\mathcal{D}_{i\alpha }}\tilde{f}({W_\alpha }{y_{\mu h} }) \\&+ {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma {K_{1j}}{\mathcal{H}_i}_\alpha {y^\varsigma _\mu } + {\gamma _2}\dot{y}_\mu ^\mathrm{T} \Gamma {K_{2j}}{\mathcal{H}_i}_\alpha {y^\varsigma _{\mu \eta } }],\\ \tilde{\mathcal{E}} =&\, \mathrm{diag}\left\{ \sum \limits _{k = 1}^q {\frac{{{{\varepsilon }_{1k}}}}{{l_k^2}}} ,\sum \limits _{k = 1}^q {\frac{{{{\varepsilon }_{2k}}}}{{l_k^2}}} ,\ldots ,\sum \limits _{k = 1}^q {\frac{{{{\varepsilon }_{nk}}}}{{l_k^2}}} \right\} , \end{aligned}$$

and ${l_k} > 0$ are given scalars.

Let ${\hat{K}_{1j}} = \Gamma {K_{1j}}, {\hat{K}_{2j}} = \Gamma {K_{2j}}$, then, for ${t_m} \le t < {t_{m + 1}}$, by combining (18)–(25), we get

$$\begin{aligned} \mathcal{L}V({y_\mu },t)&\le \int _\Omega \sum \limits _{\mu = 1}^n \left\{ \sum \limits _{i = 1}^r\sum \limits _{j = 1}^r {{\theta _i}(\xi ){{\theta _j}(\xi ^\varsigma )} } {\nabla ^\mathrm{T}}\left[ \frac{{{\varsigma _m} - \varsigma (t)}}{{{\varsigma _m}}}{\mathcal{S}_{1ij}} \right. \right. \\&\quad\left. \left. + \frac{{\varsigma (t)}}{{{\varsigma _m}}}{\mathcal{S}_{2ij}} \right] \nabla \right\} \mathrm{d}z, \end{aligned}$$

where

$$\begin{aligned} {{\mathcal{S}}_{1ij}} =&\, {\bar{\Sigma }_{1ij}} + {\varsigma _m}{\Sigma _2},\ \ {\mathcal{S}_{2ij}} = {\bar{\Sigma }_{1ij}} + {\varsigma _m}{\Sigma _3},\\ {\bar{\Sigma }_{1ij}} =&\, {\Sigma _{1ij}} + {\varepsilon ^{ - 1}}({\gamma _1}\upsilon _1^\mathrm{T}\Gamma + {\gamma _2}\upsilon _2^\mathrm{T}\Gamma ){Q_j}Q_j^\mathrm{T}{({\gamma _1}\upsilon _1^\mathrm{T}\Gamma + {\gamma _2}\upsilon _2^\mathrm{T}\Gamma )^\mathrm{T}}, \end{aligned}$$

and ${\Sigma _{1ij}}$, ${\Sigma _2}$, ${\Sigma _3}$ have been defined in (8) and (9). It is obvious that if (8)–(11) hold, ${\mathcal{S}_{1ij}} = {\bar{\Sigma }_{1ij}} + {\varsigma _m}{\Sigma _2} < 0$ and ${\mathcal{S}_{2ij}} = {\bar{\Sigma }_{1ij}} + {\varsigma _m}{\Sigma _3} < 0$, then $\mathcal{L}V({y_\mu },t) < 0$. As a result, the error system (6) is asymptotically stable.

Additionally, ${K_{1j}} = {\Gamma ^{ - 1}}{\hat{K}_{1j}}, \, {K_{2j}} = {\Gamma ^{ - 1}}{\hat{K}_{2j}}$. This completes the proof. $\square$