1 Introduction

Microparticles with diameters below \(10\,\upmu \mathrm{{m}}\) and well-defined properties are increasingly used in e.g. the pharmaceutical and chemical industry or metallurgy (Baghban Taraghdari et al. 2019; Li et al. 2019; Kumar and Venkatesh 2019). Thus, multi-dimensional fractionation processes are essential to fabricate intermediate particle products with e.g. monodisperse size, shape or surface properties. Microfluidic systems allow to utilize particle migration effects in a laminar flow, driven by high local velocities and velocity gradients without suffering from undesirable transient flow effects. Therefore, microfluidic fractionation methods have the potential to address different particle properties, such as size or shape (Alfi and Park 2014; Jiang et al. 2015).

Microfluidic particle fractionation has been realized by means of active as well as passive approaches. While active approaches utilize external acoustic, magnetic or electrical force fields (Nilsson et al. 2004; Suwa and Watarai 2011; Podoynitsyn et al. 2019), passive approaches only rely on hydrodynamic forces. Specifically, inertial effects may be utilized to force particles on certain equilibrium trajectories, whose position depends on both the particle and fluid flow properties. Inertial effects include particle centrifugal forces, as well as inertial particle migration, which is present if the particle diameter is large compared to the channel dimensions (Di Carlo 2009). First experimental studies of the migration of \(D_\mathrm{{p}} = {\mathscr {O}}({1}\,\mathrm{{mm}})\) particles in a Poiseuille tube flow were performed by Segré and Silberberg and showed that particles focus at an annulus of approximately 0.6 times the tube radius (Segré and Silberberg 1962a, b). This inertial migration effect could later be explained to result from an equilibrium of shear gradient and wall lift forces (Ho and Leal 1974; Asmolov 1999). During the last decades, particle migration and underlying hydrodynamic drag and lift forces have been investigated. Maxey and Riley assumed infinitely small particles and derived a set of equations considering shear gradient and Stokes drag but also time-dependent contributions, i.e. virtual mass and history forces (Maxey and Riley 1983). Later studies aimed to extend the Maxey–Riley equations to develop a model that is also valid for finite particle sizes and Reynolds numbers, as well as for non-uniform, unsteady flow conditions (Loth and Dorgan 2009). Loth and Dorgan provide a model to calculate the net lift force on suspended particles if the detailed flow field around a particle is unknown. This is usually the case not only in experimental investigations, but also in numerical simulations, if the particle size is of similar order of magnitude as the numerical mesh. In the last years, direct numerical simulations have been performed where the flow field in the vicinity of submerged particles is fully resolved. In laminar and turbulent straight duct flow, such fully resolved simulations revealed that the particle migration dynamics strongly depends on the bulk Reynolds number (Kazerooni et al. 2017; Fornari et al. 2018).

Common passive microfluidic fractionation approaches that utilize inertial effects are e.g. the Multi-Orifice Fluid Fractionation (MOFF) and fractionation in a spiral or serpentine microchannel (Zhang et al. 2016). These approaches aim to enhance particle migration such that a decrease in particle focusing length is achieved. A geometrical key parameter for particle focusing is a cross-sectional change in streamwise direction (orifices), inducing strongly curved streamlines and thus centrifugal forces on suspended particles. Therefore, MOFF channels have been shown to achieve size fractionation performances of up to 100% (Park and Jung 2009; Sim et al. 2011; Fan et al. 2014). Studies, e.g. on hydrodynamic blood cell separation also show the practical use of MOFF channels (Kwak et al. 2018).

Spiral and serpentine microchannels have also been successfully utilized for particle fractionation (Bhagat et al. 2008; Zhang et al. 2015). In these channels, Dean vortices are induced due to the channel curvature. In combination with centrifugal forces and hydrodynamic shear forces, particles develop Reynolds number-dependent equilibrium trajectories (Di Carlo 2009; Zhang et al. 2014).

Previous experimental studies utilized fluorescence imaging to investigate the focusing behavior of particles in curved microchannels (Bhagat et al. 2008; Johnston et al. 2014). With that, it was shown that in asymmetrical serpentine channels, the number of equilibrium positions reduces in comparison to straight duct channel flows and that the width of the resulting focusing streak is particle Reynolds number dependent (Di Carlo et al. 2007, 2008). From studies of Di Carlo et al. (2008), it becomes evident that equilibrium trajectories narrow with increasing particle Reynolds number and start to blur again above a critical Reynolds number. This effect was assumed to result from an increased magnitude of the secondary flow enhancing the particle mixing. For investigations of mixing effects in curved microchannels an APTV approach could already be successfully applied by Rossi et al. (2011). Nevertheless, it should be noted that the mixing strength also depends on the microchannels cross-sectional aspect ratio (Zhang et al. 2014).

To obtain deeper insight into the development of particle equilibrium trajecories, Di Carlo et al. (2009) performed experimental and numerical studies to investigate the relation between particle size and microchannel dimensions. As a result, they showed that the location of particle equilibrium positions scales with the ratio of particle to channel dimensions, which emphasizes the need of models that go beyond point-particle descriptions. Further studies investigated the focusing behavior of single particles in a single turn of a curved microchannel (Gossett and Di Carlo 2009). There, fluorescence imaging was combined with high-speed particle tracking, indicating that out-of-plane particle motion is present during the development of equilibrium trajectories in a single turn microchannel. However, no detailed studies on the particles out-of-plane distribution and motion have been performed in their study.

Further experimental studies aimed to improve the focusing concept to make it usable for practical applications. Oakey et al. (2010) showed that a combination of straight duct and serpentine microchannel stages can lead to a single particle equilibrium trajectory over the channel cross-section at a particle Reynolds number determined in the straight channel section of \(\mathrm{{Re}}_\mathrm{{p}}=6\). Furthermore, it was experimentally shown that the focusing streak width decreases with increasing particle concentration, which is assumed to result from hydrodynamic particle–particle interactions (Oakey et al. 2010). A more recent investigation utilized a sharp corner serpentine microchannel to investigate the importance of particle centrifugal forces and, therefore, of the density difference between the fluid and particles on the development of equilibrium trajectories (Zhang et al. 2014). Zhang et al. (2014) provided also a scaling factor as a measure for the influence of the centrifugal force relatively to the Dean drag force on the development of particle equilibrium trajectories under the assumption of negligible inertial migration effects. As they also experimentally observed particle focusing for negligible inertial migration effects, this indicates that the density difference between particles and fluid, i.e. centrifugal forces play an important role for the development of particle equilibrium trajectories. Based on the knowledge that equilibrium trajectory locations are size and Reynolds number dependent in sharp corner serpentine microchannels, a spatial separation of particles with \(3\,\upmu \mathrm{{m}}\) and \(10\,\upmu \mathrm{{m}}\) diameter was reported by Zhang et al. (2015). Extending these investigations, it was recently shown that the usage of an elastic carrier fluid can further accelerate particle focusing and, thus, allows a reduction of the total amount of serpentine loops (Yuan et al. 2019).

Although it was already shown that sharp corner serpentine microchannels are able to focus particles below \(10\,\upmu \mathrm{{m}}\) diameter, detailed experimental investigations that are able to explain the lateral migration of particles in such a flow are still subject of ongoing research. That is also because previous studies were only able to determine in-plane particle trajectories using fluorescence imaging, where usually long exposure times are used during the recording of particle fluorescence signals (Gossett and Di Carlo 2009; Zhang et al. 2015). This makes it impossible to determine details of the three-dimensional particle dynamics that is essential to understand the particle migration and focusing behaviour, as was also assumed in previous studies (Gossett and Di Carlo 2009). Therefore, the present study is a first step to close this gap, by reconstructing three-dimensional particle trajectories, i.e. particle distributions not only in-plane but also over the channel height, utilizing an Astigmatism Particle Tracking Velocimetry (APTV) (Cierpka et al. 2010) approach. With this approach, we are testing a sharp corner serpentine microchannel to investigate not only size but also density fractionation at different Reynolds numbers.

2 Experimental set-up

To reconstruct three-dimensional particle distributions, an EPI-fluorescence microscope (Nikon Eclipse LV100) is used for measurements. For illumination, the beam of a double-pulsed, dual-cavity laser (Litron Nano S 65-15 PIV) is coupled into the system. Images are recorded with a dual-frame CCD camera (LaVision Imager pro SX) of \({2058}\,\mathrm{{px}} \times {2456}\,\mathrm{{px}}\) resolution. For APTV measurements, a cylindrical lens with a focal length of \(f = {200}\;\mathrm{{mm}}\) is positioned in front of the CCD camera. All images are magnified with an infinity corrected objective lens of \(M = 20\) and a numerical aperture of \(\mathrm{{NA}} = 0.4\) (20X Nikon CFI60 TU Plan Epi ELWD) resulting in a field of view of \({1.1}\,\mathrm{{mm}} \times {0.7}\,\mathrm{{mm}}\). The commercial software DaVis 8.4 (LaVision GmbH) is used for image acquisition.

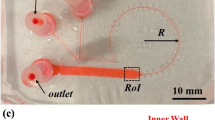
In the present study, a sharp corner serpentine channel with rectangular cross-sectional area is utilized that has been manufactured by Micronit GmbH. The channel assumes a height of \(h = 50\,\upmu \mathrm{{m}}\) and a width of \(w = 200\,\upmu \mathrm{{m}}\). A sketch of the channel geometry including the region of interest (marked red) is shown in Fig. 1a, b, respectively.

Fig. 1
figure 1

a Sharp corner serpentine microchannel and field of view at the end of the 24th serpentine, b enlarged detail at the end of the 24th serpentine (see a with field of view marked with a red rectangle) (color figure online)

Full size image

Measurements are performed inside the 24th serpentine loop, as depicted in Fig. 1a. As Zhang et al. (2014) showed in a similar sharp corner serpentine channel that equilibrium trajectories of PS particles with diameters in the order of magnitude of \(D_\mathrm{{p}} = {\mathscr {O}}(10\,\upmu \mathrm{{m}})\) already focus after six serpentine loops, fully developed particle equilibrium trajectories are expected here in the present investigation. To study size and density fractionation, polystyrene (PS) particles of \(3.55\pm 0.07\,\upmu \mathrm{{m}}\) diameter, as well as \(9.87\pm 0.28\,\upmu \mathrm{{m}}\) PS \(\left( \rho _{\mathrm{{PS}}} = {1.05}\,\mathrm{{g}}\,\mathrm{{cm}}^{-3} \right)\) and melamine \(\left( \text {MF}, \rho _{MF} = {1.51}\,\mathrm{{g}}\,\mathrm{{cm}}^{-3} \right)\) particles (microParticles GmbH) are suspended in distilled water.

3 Calibration procedure and experimental execution

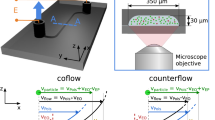
The presence of the cylindrical lens in the optical path of the microscope creates an astigmatism that allows to determine out-of-plane particle positions, i.e. their distribution over the channel height.

The astigmatism is characterized by the presence of two focal planes \(F_1\) and \(F_2\), which are spatially separated. This results in particle images, whose shape is rather circular near the middle plane between both focal planes. Please note that the particle is defocused at this location. In Fig. 2 the characteristic light path of the fluorescence signal of a particle is shown.

Fig. 2
figure 2

Light path of a fluorescent particle through a microscope with implemented cylindrical lens causing aberration that results in two spatially separated and perpendicularly aligned focal planes, leading to elliptical particle images

Full size image

The light emitted by the particle is first parallelized by an infinity corrected objective lens. Then, the parallelized beam passes a focusing and a cylindrical lens. Due to the presence of the cylindrical lens, the refracted light focuses on two spatially separated, perpendicularly aligned focal planes \(F_1\) and \(F_2\). This leads to an elliptical image shape, as shown in Fig. 2.

To reconstruct the out-of-plane position of a particle from its aberrated image, an in situ calibration has to be performed before each measurement. For this, images of sedimented particles are recorded in a scanning procedure with \({\delta z = 1\,\upmu \mathrm{{m}}}\) step size. Then, all recorded images are pre-processed before evaluation. Following Cierpka et al. (2010), a median filter with \({5}\,\mathrm{{px}}\) filter length is applied to spatially reduce image noise, in the first step. In the second step, a bandwidth filter is used to nearly completely eliminate background noise, while keeping structures between 3 and \({70}\,\mathrm{{px}}\) diameter. In the last step, images are dewarped on the basis of the recording of a calibration grid. All pre-processing steps are performed in the commercial software DaVis 8.4 (LaVision GmbH).

Separate calibration curves are generated for both camera frames individually to avoid systematic errors that may result from slightly differing illumination intensities between both frames. Seven to eight sedimented particles distributed over the field of view are used for each calibration curve. To quantify the aberration, the major and minor axis lengths of the auto-correlation peaks resulting from aberrated particle images are evaluated. For this, the major and minor axis lengths of the auto-correlation peak are taken at a certain contour level height, e.g. at \(R/R_{\mathrm{{max}}} = 0.2\) for \({3.55}\,\upmu \mathrm{{m}}\) PS particles. The axis length ratio is a measure for the particle’s out-of-plane position (Cierpka et al. 2011; Rossi and Kähler 2014). Exemplary auto-correlation maps for PS particles of \(D_\mathrm{{p}} = {3.55}\,\upmu \mathrm{{m}}\) diameter are given in Fig. 3a–c, where particles are located at distances \(\delta z={40}\,\upmu \mathrm{{m}}\), \(\delta z={0}\,\upmu \mathrm{{m}}\) and \(\delta z={-40}\,\upmu \mathrm{{m}}\) from the defined zero position. This zero position is defined where \(a_x/a_y \approx 1\). The corresponding calibration curve is shown in Fig. 3d. Here, the color coding indicates the position of the particle along the z axis, i.e. the out-of-plane position relatively to the zero position. Furthermore, red dots indicate data points which result from the auto-correlation maps shown in Fig. 3a–c. Black dots indicate measurement data of PS particles of \(D_\mathrm{{p}} = {3.55}\,\upmu \mathrm{{m}}\) diameter at \(\mathrm{{Re}}= 100\), resulting from 500 double-frame images. For data evaluation, an in-house code is developed based on the Euclidean method, as proposed by Cierpka et al. (2011).

Fig. 3
figure 3

Sample auto-correlation maps of a single \({3.55}\,\upmu \mathrm{{m}}\) PS particle at different out-of-plane positions \(\delta z\) relatively to the zero position. a\(\delta z=40\,\upmu \mathrm{{m}}\), b\(\delta z=0\,\upmu \mathrm{{m}}\), c\(\delta z=-40\,\upmu \mathrm{{m}}\). The axis lengths \(a_x\) and \(a_y\) of the auto-correlation peak \(R\) are taken at a correlation peak height of \(R/R_{\mathrm{{max}}} = 0.2\), d corresponding calibration curve. Red markers refer to the auto-correlation results shown in a–c. Measurement data of \({3.55}\,\upmu \mathrm{{m}}\) PS particles at \(\mathrm{{Re }}= 100\) are indicated with black dots (color figure online)

Full size image

To determine the measurement uncertainty with which the out-of-plane particle position can be reconstructed, absolute z-positions of the centers of sedimented particles are reconstructed from the calibration recordings and are compared to their theoretical position at \(z = D_\mathrm{{p}} / 2\). The resulting standard deviations between reconstructed and theoretical z-positions are smaller than \(2.7\,\upmu \mathrm{{m}}\) for all particle groups. Additional analyses also confirmed that particle z-positions can be reconstructed over the complete microchannel height with the pre-described procedure.

After the in situ calibration, measurements are performed inside the 24th serpentine loop at different Reynolds numbers of \(\mathrm{{Re}}=100,110,\ldots ,150\). Di Carlo et al. (2007) and Zhang et al. (2015) define this as \(\mathrm{{Re }}= \left( u_{\mathrm{{max}}} \cdot D_\mathrm{{h}}\right) /\upnu\). There, the maximum fluid velocity \(u_{\mathrm{{max}}}\) is calculated under the assumption of a plane Poiseuille flow as \(u_{\mathrm{{max}}} = 1.5 \cdot {\bar{u}}\), with \({\bar{u}}\) being the bulk velocity that can be calculated with the help of the volume flow rate \(Q = {\bar{u}} \cdot A\). As the flow profile inside the microchannel used in the present study differs from a plane Poiseuille profile due to finite aspect ratio and channel curvature, we provide corresponding bulk Reynolds numbers \(Re_\mathrm{{b}} = \left( {\bar{u}} \cdot D_\mathrm{{h}}\right) /\nu\) as well as volume flow rates in Table 1. However, it may be noted that further results are given as a function of the Reynolds number based on \(u_{\mathrm{{max}}}\) in order to ensure comparability with the studies mentioned above.

Table 1 Flow parameters at which measurements are performed
Full size table

For both, calibration and measurements, a mixture of \(3.55\,\upmu \mathrm{{m}}\) PS particles and either \(9.87\,\upmu \mathrm{{m}}\) PS or MF particles is injected into the serpentine microchannel. Small and large particles are distinguished during the evaluation, due to different astigmatism characteristics. These result in individual calibration curves for small and large particles. Thus, size fractionation results of \({3.55}\,\upmu \mathrm{{m}}\) and \({9.87}\,\upmu \mathrm{{m}}\) PS particles can be obtained simultaneously. Using an outlier criterion, particle images that exceed a certain Euclidean distance from the calibration curve are excluded from the evaluation. In a second measurement, particle distributions of \(9.87\,\upmu \mathrm{{m}}\) MF particles are obtained and are superimposed with results of \(9.87\,\upmu \mathrm{{m}}\) PS particles at the same Reynolds numbers. This is done as both, PS and MF particles, assume the same image diameter and are, therefore, not differentiable through image processing. As the particle volume concentration in all experiments is low, that is in the order of magnitude of \(\varphi = {\mathscr {O}}(10^{-4})\), no particle–particle interactions are expected in the experiments and the flow can be assumed to be unperturbed. Assuming negligible particle–particle interactions, particle locations of both measurement series are assumed to be independent from each other and representative for the hydrodynamical behavior of the individual particle group. Thus, a superposition of particle locations of both measurement series is done here.

During all measurements, 500 double-frame images are recorded at three reference plane positions, which are located \(\delta z = 20\,\upmu \mathrm{{m}}\) apart from each other. The time delay between the first and second frame is adjusted, depending on the Reynolds number to obtain similar particle image displacements throughout all measurements. Thus, each particle appears once in each frame. This measurement procedure results in a total number of evaluated particles of \({6899\pm 1658}\) (PS, \(D_\mathrm{{p}} = 3.55\,\upmu \mathrm{{m}}\)), \({2518\pm 615}\) (PS, \(D_\mathrm{{p}} = 9.87\,\upmu \mathrm{{m}}\)) and \({2461\pm 419}\) (MF, \(D_\mathrm{{p}} = 9.87\,\upmu \mathrm{{m}}\)), respectively, for measurements at a constant Reynolds number.

4 Results

To realize microparticle fractionation, each particle group has to assume equilibrium particle trajectories that are spatially separated across the flow such that each particle group may be separated through a flow branching downstream the fractionation channel. Thus, to validate the capability of the serpentine microchannel to fractionate particles according to size and density, three-dimensional particle distributions are determined in a first step. Afterwards, a virtual flow branching is performed, i.e. the serpentine channel is divided virtually into individual segments in the post-processing and fractionation efficiencies are analyzed with respect to varying virtual partitioning wall positions. Size fractionation results are analyzed in Sect. 4.1; a discussion with regard to density fractionation can be found in Sect. 4.2.

4.1 Size fractionation

An APTV approach is utilized to reconstruct 3D distributions of polystyrene (PS) particles with diameters of \(3.55\,\upmu \mathrm{{m}}\) and \(9.87\,\upmu \mathrm{{m}}\). Figure 4 shows exemplary distributions of both particle groups at a Reynolds number of \(\mathrm{{Re }}= 110\). The in- and out-flow direction is in negative x-direction and the channel walls are sketched with black dashed lines. The region of interest, for which the fractionation performance is investigated, is indicated with blue dashed lines. Please note, that Fig. 4 shows a superposition of both particle fractions including all reconstructed particle centroid positions of a time series of 1500 double-frame images. Both particle fractions were recorded simultaneously.

Fig. 4
figure 4

Measured particle centroid positions of polystyrene (PS) particles of \(D_\mathrm{{p}} = 3.55\,\upmu \mathrm{{m}}\) (red) and \(D_\mathrm{{p}} = 9.87\,\upmu \mathrm{{m}}\) (black) diameter at \(\mathrm{{Re }}= 110\). The particle distribution inside the flow volume between \(-200< x< 0\) and \(0<y<200\) (sketched in blue) is analyzed (color figure online)

Full size image

As shown in Fig. 4, each particle fraction forms spatially separated equilibrium trajectories. In contrast to Zhang et al. (2014, 2015) that used fluorescence imaging to detect in-plane particle trajectories in a similar sharp corner serpentine microchannel, the 3D reconstruction reveals that particle separation takes also place over the channel height (z-direction) leading to four and two equilibrium positions for \(3.55\,\upmu \mathrm{{m}}\) and \(9.87\,\upmu \mathrm{{m}}\) particles, respectively. Furthermore, a slight twist between in-plane equilibrium trajectories of \(3.55\,\upmu \mathrm{{m}}\) particles becomes visible.

The fractionation performance is analyzed in the region of interest that is sketched with blue dashed lines in Fig. 4. The spatial distribution of particles is given in Fig. 5a–f. An increase of the Reynolds number from \(\mathrm{{Re}} = 100\) to \(\mathrm{{Re}} = 150\) reduces the spread of the equilibrium trajectories of \(9.87\,\upmu \mathrm{{m}}\) PS particles in y-direction. In contrast to this, \(3.55\,\upmu \mathrm{{m}}\) particles stay in a four equilibrium trajectory configuration up to a Reynolds number of \(\mathrm{{Re}} = 130\) with centroid positions of \(y/w \approx 0.33\) and \(y/w \approx 0.8\), respectively. Therefore, they are located closer to the channel side walls compared to the larger particles. At \(\mathrm{{Re}}=150\), \(3.55\,\upmu \mathrm{{m}}\) and \(9.87\,\upmu \mathrm{{m}}\) particles are not spatially separated over the channel width any more as \({3.55}\,\upmu \mathrm{{m}}\) particle bands are merged, spanning a region of \(0.2< y/w < 0.8\). It may be noted that all equilibrium trajectories are displaced towards the bottom of the channel. We assume that this is due to particle sedimentation.

Fig. 5
figure 5

Projected view of particle positions of fractions with polystyrene (PS) particles of diameter \(D_\mathrm{{p}} = 3.55\,\upmu \mathrm{{m}}\) (red) and polystyrene (PS) particles of diameter \(D_\mathrm{{p}} = 9.87\,\upmu \mathrm{{m}}\) (black) inside the region of interest. The size fractionation performance is investigated for segments, which divide the test volume at \(y/w = \varDelta _y\), as well as \(y/w = 1-\varDelta _y\). Here \(\varDelta _y = 0.4\), which corresponds to the optimum size fractionation performance at \(\mathrm{{Re}} = 110\). Results are shown for Reynolds numbers of a\(\mathrm{{Re}}= 100\), b\(\mathrm{{Re}}= 110\), c\(\mathrm{{Re}} = 120\), d\(\mathrm{{Re}}= 130\), e\(\mathrm{{Re}}= 140\) and f\(\mathrm{{Re}}= 150\) (color figure online)

Full size image

To evaluate the fractionation performance, the cross-sectional particle distributions of Fig. 5a–f are virtually divided into three segments, indicated by two vertical black lines. These virtual partitioning walls are placed symmetrically around \(y/w=0.5\) at different distances \(\varDelta _y\) to the channel side walls, as denoted in Fig. 5a. Here, \(\varDelta _y\) is varied between \(0.05< \varDelta _y < 0.45\) in steps of 0.025. This corresponds to a step size of \({5}\,\upmu \mathrm{{m}}\). In each of these three segments, particle concentrations of both fractions are evaluated by means of a separation degree \(T = N_{9.87}^2/\left( N_{9.87}^2+N_{3.55}^2\right)\) (Stiess 2009). Here, \(N_i\) denotes the number of PS particles of diameter \(i\). \(T\) becomes zero in regions, where only \(3.55\,\upmu \mathrm{{m}}\) particles are located and one if only \(9.87\,\upmu \mathrm{{m}}\) particles are included in a segment. Thus, we obtain three values for \(T\), i.e. one for each segment. The difference in two neighbouring segments is defined as selectivity \(\kappa _y = \vert T_{i+1} - T_{i}\vert\). In the following, the selectivity for different \(\varDelta _y\) and \(\mathrm{{Re}}\) is evaluated. \(\kappa _{\text {y}}\) assumes one if both particle fractions are completely separated. Due to the fact that particles are almost symmetrically distributed around \(y/w = 0.5\), both values for \(\kappa _\mathrm{{y}}\) are averaged and mean values \({\bar{\kappa }}_\mathrm{{y}}\) are plotted as a function of the Reynolds number \(\mathrm{{Re}}\) and the partitioning wall position \(\varDelta _y\) in Fig. 6. Here, red crosses indicate \({\bar{\kappa }}_y\) values that are calculated for the particle distributions and partitioning wall positions shown in Fig. 5a–f.

Fig. 6
figure 6

Mean selectivities \({\bar{\kappa }}_y\) of \(3.55\,\upmu \mathrm{{m}}\) and \(9.87\,\upmu \mathrm{{m}}\) PS particles as a function of the Reynolds number \(\mathrm{{Re}}\) and the partitioning wall position \(\varDelta _y\). The maximum mean selectivity of \({\bar{\kappa }}_y = {0.981\pm 0.010}\) is reached at \(\mathrm{{Re}} = 110\) and \(\varDelta _y = 0.4\). Red crosses show the fractionation performances for the particle distributions and partitioning wall positions shown in Fig. 5a–f (color figure online)

Full size image

From this representation, a maximum mean selectivity of \({\bar{\kappa }}_y = {0.981\pm 0.010}\) is found for \(\mathrm{{Re}} = 110\) and \(\varDelta _y = 0.4\), as also indicated with a bold red cross in Fig. 6. This situation is displayed in Fig. 5b. Here, \(3.55\,\upmu \mathrm{{m}}\) particles are located in the lateral channel sections, i.e. at \(0 < y/w \le 0.4\) and \(0.6 < y/w \le 1\), respectively, while the majority of \(9.87\,\upmu \mathrm{{m}}\) particles is located in the channels middle section, i.e. at \(0.4 < y/w \le 0.6\). The corresponding values for \(T\) are shown in Fig. 7.

Fig. 7
figure 7

Separation degree \(T\) in three segments at a Reynolds number of \(\mathrm{{Re}} = 110\) and a partitioning wall position of \(\varDelta _y= 0.4\)

Full size image

As already expected from the corresponding particle distribution shown in Fig. 5b, \(T\) values switch from a low level of \(T_1 = 0.003\) at \(0 < y/w \le 0.4\) to a high value of \(T_2 = 0.994\) at \(0.4 < y/w \le 0.6\) and vice versa (\(T_3 = 0.023\) at \(0.6 < y/w \le 1\)). This corresponds to a nearly ideal separation situation.

Velocity measurements at this Reynolds number by means of APTV reveal that \({3.55}\,\upmu \mathrm{{m}}\) particles flow at a median speed of \(({1.25\pm 0.21})\;\mathrm{{ms}}^{-1}\). This is similar to the median velocity of \({9.87}\,\upmu \mathrm{{ms}}\) particles, which assumes \(({1.27\pm 0.10})\,\mathrm{{ms}}^{-1}\). Interestingly, both particle groups appear to be faster than the fluid bulk velocity of \({\bar{u}} = {0.92}\;\mathrm{{ms}}^{-1}\).

A further investigation of \({7.76\pm 0.12}\,\upmu \mathrm{{m}}\) and \({9.87\pm 0.28}\,\upmu \mathrm{{m}}\) PS particles revealed that if the Reynolds number, i.e. the volume flow rate in the experiment, can be controlled accurately enough, size fractionation can be realized even for a size difference as small as \(\approx {2}\,\upmu \mathrm{{m}}\). Specifically, a mean selectivity of \({\bar{\kappa }}_y \approx 0.9\) is obtained at a Reynolds number of \(\mathrm{{Re}}=102\) for the particle groups described above. Higher selectivities could not be reached here, because \({9.87}\,\upmu \mathrm{{m}}\) particles are still in a transition state while \({7.76}\,\upmu \mathrm{{m}}\) particles are located near the microchannel sidewalls. At higher Reynolds numbers, when \({9.87}\,\upmu \mathrm{{m}}\) particles have focused, \({7.76}\,\upmu \mathrm{{m}}\) particles are in return in a transition state.

4.2 Density fractionation

Up to date, the sharp corner serpentine channel has been only utilized for size fractionation of bidispers particle systems (Zhang et al. 2015). In the second part of this study, we use the serpentine microchannel to test its capability to separate particles with the same size and different densities. In particular, polystyrene (PS) and melamine resin (MF) particles with densities of \(\rho _{PS} = {1.05}\,\mathrm{{g}}\,\mathrm{{cm}}^{-3}\) and \(\rho _{MF} = {1.51}\,\mathrm{{g}}\,\mathrm{{cm}}^{-3}\) and equal diameters of \(D_{\mathrm{{p}}} = 9.87\,\upmu \mathrm{{m}}\) have been chosen. Particle trajectories of both particle groups were recorded sequentially, while in both recordings \(3.55\,\upmu \mathrm{{m}}\) PS particles were included as reference. Thus, resulting equilibrium trajectories of both measurements are superimposed for the same Reynolds number. Particle trajectories for \(\mathrm{{Re}}= 110\) are shown in Fig. 8.

Fig. 8
figure 8

Scatter plot of the three-dimensional distribution of polystyrene (PS, black) and melamine resin particles (MF, cyan) of diameter \(D_\mathrm{{p}} = {9.87}\,\upmu \mathrm{{m}}\) at a Reynolds number of \(\mathrm{{Re}}= 110\). The density fractionation performance is investigated inside the flow volume between \(-200< x < 0\) and \(0<y<200\) (sketched in blue)

Full size image

Obviously, both PS and MF particles are already in the transition process from four to two equilibrium trajectories. In contrast to the size fractionation results, where \({3.55}\,\upmu \mathrm{{m}}\) and \({9.87}\,\upmu \mathrm{{m}}\) PS particles assume spatially separated in-plane equilibrium trajectories, PS and MF particles seem to follow identical trajectories. Figure 9a–f display results for Reynolds numbers between \(100< \mathrm{{Re}}< 150\).

Fig. 9
figure 9

Projected view of polystyrene (PS, black) and melamine resin (MF, cyan) particles of diameter \(D_\mathrm{{p}} = 9.87\,\upmu \mathrm{{m}}\) inside a \(200\,\upmu \mathrm{{m}}\) volume as indicated in blue in Fig. 8. Results are shown for Reynolds numbers of a\(\mathrm{{Re}}= 100\), b\(\mathrm{{Re}}= 110\), c\(\mathrm{{Re}}= 120\), d\(\mathrm{{Re}}= 130\), e\(\mathrm{{Re}}= 140\) and f\(\mathrm{{Re}}= 150\) (color figure online)

Full size image

Here, both particle groups focus on two trajectories with increasing Reynolds number, located around \(y/w = 0.6\). Hence, only low separation degrees \(T = N_{\mathrm{{MF}}}^2/\left( N_{\mathrm{{MF}}}^2+N_{\mathrm{{PS}}}^2\right)\) and selectivities \(\kappa _y = \vert T_{i+1} - T_i\vert\) are reached for the Reynolds numbers investigated here. The resulting mean selectivities \({\bar{\kappa }}_\text {y}\) are shown in Fig. 10 as a function of the Reynolds number \(\mathrm{{Re}}\) and partitioning wall position \(\varDelta _y\).

Fig. 10
figure 10

Mean selectivities \({\bar{\kappa }}_y\) for density fractionation over the channel width as a function of the Reynolds number \(\mathrm{{Re}}\) and the partitioning wall position \(\varDelta _y\)

Full size image

Maximum values of \({\bar{\kappa }}_y \approx 0.5\) are reached, confirming that only poor density fractionation can be realized. From Fig. 8a–f, it becomes visible that this value is only reached due to a spread of single particles located closer to the side walls. From the present results, we conclude that a particle density increase of \(\rho _{\mathrm{{MF}}}/\rho _{\mathrm{{PS}}} = 1.44\) is not sufficient to force particles on spatially separated equilibrium trajectories after 24 serpentine loops at the investigated Reynolds numbers for the present serpentine channel. It is known that particle equilibrium trajectories develop due to inertial migration, i.e. at finite particle Reynolds numbers. If significant inertial migration effects are present, small deviations of the force balance will not lead to a significant shift of equilibrium positions. Such a deviation of the force balance can only be induced by centrifugal forces for particles of identical geometry but different density. In the present study, the particle to microchannel diameter ratio assumes \(D_\mathrm{{p}}/D_\mathrm{{h}} = 0.123 > 0.07\) (Di Carlo et al. 2007) and the particle Reynolds number can be estimated as \(\mathrm{{Re}}_\mathrm{{p}} = \mathrm{{Re}}\cdot \left( D_\mathrm{{p}}^2/D_\mathrm{{h}}^2\right) > 1\) for the whole investigated Reynolds number range. As no spatial separation of particle equilibrium trajectories can be observed in the present study, we assume that centrifugal forces play a negligible role compared to inertial migration effects.

5 Conclusion

In the present study, the size and density fractionation performance of a sharp corner serpentine channel was investigated for defined particle combinations. For this, particle trajectories in dilute suspension flows were recorded at different Reynolds numbers after 24 serpentine loops. An Astigmatism Particle Tracking Velocimetry (APTV) algorithm was utilized to reconstruct three-dimensional particle positions.

Distinct equilibrium trajectories were observed for all investigated particle fractions. While \(3.55\,\upmu \mathrm{{m}}\) PS particles undergo a transition from four equilibrium trajectories at \(\mathrm{{Re}}=100\) to two equilibrium trajectories that are spread over the channel width at \(\mathrm{{Re}}=150\), \({9.87}\,\upmu \mathrm{{m}}\) PS and MF particles stay in a two equilibrium trajectories configuration that narrows with increasing Reynolds number. Thus, size fractionation could be achieved, due to the spatial separation of differently sized polystyrene particles. Furthermore, in the present study, the capability for density fractionation in a serpentine microchannel was investigated. It was found that equilibrium trajectories of particles with equal size but different densities do not develop significantly spatially separated equilibrium trajectories within the investigated parameter range.

The fractionation performance was evaluated in terms of the separation degree and the selectivity, calculated over the channel width. For investigated particles of \(3.55\,\upmu \mathrm{{m}}\) and \(9.87\,\upmu \mathrm{{m}}\) diameter, a maximum mean selectivity of \({\bar{\kappa }}_y = {0.981\pm 0.010}\) was found at \(\mathrm{{Re}}= 110\) utilizing two vertical partitioning walls located at \(y/w = 0.4\) and \(y/w = 0.6\).

Overall, in the present study, the 3D distribution of microparticle equilibrium trajectories is investigated to perform for the first time a quantitative evaluation of the fractionation performance in a sharp corner serpentine microchannel. With this methodology, new means of size and density fractionation may be explored more easily in the future.