1 Introduction into nonlinear vehicle dynamics

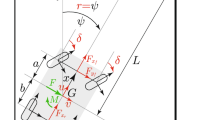
Figure 1 shows the applied quarter car model rolling on wavy roads with level z and slope u that effects coupled vibrations of vertical displacement y and horizontal travel velocity \(\mathrm {v}\) [1,2,3,4] described by

$$\begin{aligned}&\ddot{y}+2D\omega _{1}\left( \dot{y}-\dot{z} \right) +\omega _{1}^{2}\left( y-z \right) =0, \end{aligned}$$
(1)
$$\begin{aligned}&\dot{v}=\left[ \omega _{1}^{2}\left( y-z \right) +2D\omega _{1}\left( \dot{y}-\dot{z} \right) \right] \mathrm {tan}\alpha +f / m. \end{aligned}$$
(2)

Equations (1) and (2) are equations of motion where dots denote derivatives with respect to time t and \(\omega _{1}\) is the natural frequency of the vehicle given by \(\omega _{1}^{2}=c / {m}\). The parameter D determines the vehicle damping by \(2D\omega _{1}=b /{m}\), and m is the vehicle mass driven by the force f assumed to be constant. When \(\alpha \) is the slope angle in the frictionless contact point of road and vehicle, the vertical component \(\hbox {Ncos}\upalpha \) of the normal force N is determined by the linear forces of spring c and damper b so that the horizontal component \(\mathrm {Nsin}\upalpha \) enters through \(\tan {\upalpha }\) into the horizontal dynamic equilibrium, noted in Eq. (2). According to mass-point mechanics, the vehicle mass is assumed to be concentrated in the contact point. Consequently, there is no rotation, only two planar velocities: the horizontal travel velocity \(\mathrm {v}\) and the vertical vibration velocity \(\dot{y}\). The latter can be substituted by \(\dot{y}=\omega _{1}x\) what is later applied in order to rewrite the linear second-order equation (1) of motion into the state form of two first-order system equations.

Fig. 1
figure 1

Quarter car model rolling on wavy roads that is effecting vertical car vibrations and speed fluctuations

Full size image

Note that Eq. (2) is approximately investigated in [5, 6] by means of averaging methods which are only applicable when vibration displacements and velocity fluctuations of the vehicle are small. To obtain exact solutions, the one-dimensional road surface is modeled, e.g., by means of the sinusoidal forms [7, 8]

$$\begin{aligned} z\left( s \right) =z_{0}\cos \left( \Omega s \right) ,\quad u\left( s \right) =-\,z_{0}\mathrm {sin}\left( \Omega s \right) , \end{aligned}$$
(3)

where \(z_{0}\) is the amplitude of the road wave, \(s\left( t \right) \) determines the current position of the contact point of the vehicle moving with the horizontal velocity \(\dot{s}=\mathrm {v}\) and \(\Omega \) denotes the road frequency measurable by the wave length \(L={2\pi } /{\Omega }\). From Eq. (3), the slope angle \(\alpha (t)\) of the road is calculable by \({\mathrm{d}z} / {\mathrm{d}s}\) that leads to

$$\begin{aligned} \tan {\alpha ={\mathrm{d}z}/{\mathrm{d}s}=\, }\Omega u. \end{aligned}$$
(4)

After the insertion of \(\tan \alpha =\Omega u\) into Eq. (2), both equations of motion have to be solved under the condition that the geometrical equations (3) are satisfied. This is typical for DA equation systems where the sinusoidal functions (3) in the given problem take the role of algebraic terms in DA equations [9]. To eliminate the growing motion coordinate \(s\left( t \right) \), the geometrical conditions (3) are replaced by the dynamical relations

$$\begin{aligned} \dot{z}=\mathrm {v}\Omega u,\quad \dot{u}=-\,\mathrm {v}\Omega z, \end{aligned}$$
(5)

which are derived from Eq. (3) by means of \(\mathrm{d}z=-\,z_{0}\Omega \hbox {sin}{\left( \Omega s \right) \mathrm{d}s}\) and \(\mathrm{d}u=-\,z_{0}\Omega \hbox {cos}{\left( \Omega s \right) \mathrm{d}s}\) where \({-z}_{0}\hbox {sin}\left( \Omega s \right) \) is replaced by u and \(z_{0}\cos \left( \Omega s\right) \) by z and \({\mathrm{d}s}/{\mathrm{d}t}\) is substituted by \(\mathrm {v}\). Altogether, Eq. (1), (2) and (5) describe a five-dimensional problem with five unknowns: the horizontal velocity \(\mathrm {v}\left( \mathrm {t} \right) \) of the vehicle, its vertical vibration by \(y\left( t \right) \) and \(\dot{y}\left( t \right) =\omega _{1}x\left( t \right) \) and the road level \(z\left( t \right) \) and slope \(u\left( t \right) \) in the moving contact point. When \(\mathrm {v}\left( \mathrm {t} \right) \) is known, the moving contact coordinate \(s\left( t\right) \) can be calculated by the integration

$$\begin{aligned} s\left( t \right) =s_{0}+\int _{t_{0}}^{t} {\mathrm {v}\left( t_{1} \right) } \mathrm{d}t_{1} \end{aligned}$$

for any given initial position \(s_{0}\) at the time \(t_{0}\). In the special case that the velocity \(\mathrm {v}\) of the vehicle is constant with \(\dot{\hbox {v}}=0\), the nonlinear dynamical equation (2) degenerates to a static one. Furthermore, Eq. (5) becomes linear for \(\mathrm {v}=\mathrm {const}\). describing the motion of an oscillator with the constant time frequency \(\mathrm {v}\Omega \).

2 Limit cycles of travel speed and acceleration

For the control problem or inverse problem that the driving force is unknown and the vehicle is moved with given constant speed \(\mathrm {v}\), the road and vehicle equations (1) and (5) become linear and solvable by means of the sinusoidal solutions \(z\left( t \right) =z_{0}\mathrm {cos}\left( \mathrm {v}\Omega t \right) ,\, \, u\left( t \right) =-z_{0}\mathrm {sin}\left( \mathrm {v}\Omega t \right) \) and \(y\left( t \right) =V\mathrm {cos}\left( \mathrm {v}\Omega t-\varepsilon \right) \) where V and \(\varepsilon \) are amplitude and phase, respectively, to be calculated from the linear equation (1) of motion. The insertion of the calculated solutions \(z\left( t \right) , u\left( t \right) \) and \(y\left( t \right) \) into Eq. (2) gives the explicit form of the sinusoidal driving force \(f\left( t \right) \) necessary to maintain a constant travel speed. The time average of \(f\left( t \right) \) leads to the mean force

$$\begin{aligned}&\frac{\langle f\left( t \right) \rangle }{c/\Omega }=\frac{\left( z_{0}\Omega \right) ^{2}D{\upnu }^{5}}{\left( 1-\nu ^{2} \right) ^{2}+\left( 2D{\upnu } \right) ^{2}},\quad \nonumber \\&\quad \mathrm {with}\, \, \, \upnu = {\mathrm {v}\Omega } / \omega _{1}. \end{aligned}$$
(6)

In Fig. 2, the dimensionless mean force (6) is plotted versus the dimensionless speed \(\upnu ={\mathrm {v}}\Omega /\omega _{1}\) for the two dimensionless road factors \(z_{0}\Omega \) marked in red and cyan together with two typical motor characteristics in yellow. The first one is valid for a constant driving force. The second one holds for a more realistic driving force which decreases with growing speed. The two cutting points of driving characteristics and mean forces represent possible stationary velocities marked by circles before and after the related resonance velocity \(\upnu =1\). For the nonlinear case of fluctuating vehicle velocities, the simple result in Eq. (6) is confirmed in [5] by means of an averaging method. One finds the same result (6) in rotor dynamics [10,11,12,13] when the road factor \(z_{0}\Omega \) is replaced by the mass ratio of an elastically supported unbalanced rotor and the translation velocity \(\mathrm {v}\) is substituted by a rotation speed.

Fig. 2
figure 2

Two typical motor characteristics in yellow and two mean driving forces for \(z_{0}\Omega =1\) and \(z_{0}\Omega =0.6\)

Full size image
Fig. 3
figure 3

Limit cycles of zero mean accelerations versus travel speed for short time simulations

Full size image

In the following, numerical integration methods and nonlinear Fourier expansions are developed in order to extend the averaged solution in Eq. (6) to limit cycles of acceleration and travel velocity. First results are presented in Fig. 3 showing new limit cycles obtained by means of numerical integration of Eqs. (1), (2) and (5) applying Euler schemes for short dimensionless times \(\tau = \omega _{1}t\). The dimensionless acceleration \(\nu ^{'}=d\upnu /\hbox {d}\uptau \) is plotted against the velocity \(\upnu ={\mathrm {v}}\Omega /\omega _{1}\). The obtained results are shown in an appropriately scaled form where the dimensionless acceleration is divided by five and lifted by adding the dimensionless force value, applied. Therewith, all drawings of the limit cycles are more separated in Fig. 3 and degenerate to small circles around the driving force when the road factor decreases. This is due to the fact that the time mean value of the calculated acceleration is zero in the stationary case. The results in Fig. 3 are calculated for eight different parameters \({f\Omega } / c\) of the driving force marked by colored triangles on the red back bone curve of the driving force applied. The geometrical form of the road is chosen by the road factor \(z_{0}\Omega =1\). This indicates that the applied wave amplitude of the road is \(z_{0}={10} / \pi \,\mathrm {cm}\) for the wave length given by \(L=20\) cm. The selected damping is \(D=0.2\). The simulations are started with initial values marked by squares. Subsequent motions are plotted by thin dashed lines. After a sufficiently long transient period, the simulations end in limit cycles marked by colored thick lines. Limit cycles of travel speeds with mean speeds on negative slopes are unstable and therefore not realizable, physically.

To introduce averaging methods, the covariance equations of the four states \(\left\{ z,u,y,x \right\} \) are introduced by

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}\tau }\left[ \, {\begin{array}{*{20}c} {\overline{zy}}\\ {\overline{uy}}\\ {\begin{array}{*{20}c} {\overline{zx}}\\ {\overline{ux}}\\ \end{array} }\\ \end{array} }\, \right] +\left[ \, {\begin{array}{*{20}c} 0 &{}\quad -\nu &{}\quad {\begin{array}{*{20}c} -1 &{}\quad 0\\ \end{array} }\\ \nu &{}\quad 0 &{}\quad {\begin{array}{*{20}c} 0 &{}\quad -1\\ \end{array} }\\ {\begin{array}{*{20}c} 1\\ 0\\ \end{array} } &{} {\begin{array}{*{20}c} 0\\ 1\\ \end{array} } &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 2D &{}\quad -\nu \\ \end{array} }\\ {\begin{array}{*{20}c} \nu &{}\quad 2D\\ \end{array} }\\ \end{array} }\\ \end{array} }\, \right] \,\left[ \, {\begin{array}{*{20}c} \overline{zy}\\ \overline{uy}\\ {\begin{array}{*{20}c} \overline{zx}\\ \overline{ux}\\ \end{array} }\\ \end{array} }\, \right] \nonumber \\&\quad =z_{0}\Omega \left[ \, {\begin{array}{*{20}c} 0\\ 0\\ {\begin{array}{*{20}c} \bar{z}^{2}+2D\nu \overline{zu}\\ \overline{zu}+2D\nu \bar{u}^{2}\\ \end{array} }\\ \end{array} }\, \right] , \end{aligned}$$
(7)

They are derived from Eqs. (1) and (5) for the dimensionless time \(\tau =\omega _{1}t\) and the dimensionless coordinates \(\left( \bar{y},\bar{x} \right) =\Omega \left( y,x \right) \) of the vertical vehicle vibration and the coordinates \(\left( \bar{z},\, \bar{u} \right) =(zu)/z_{0}\) of the dimensionless road level and slope. Correspondingly, Eq. (2) takes the dimensionless form

$$\begin{aligned} \frac{d\nu }{d\tau }+2D\left( z_{0}\Omega \right) ^{2}\bar{u}^{2}\nu= & {} \frac{f}{c/\Omega }+z_{0}\Omega \left( \overline{uy}+2D\overline{ux} \right) \nonumber \\&-\left( z_{0}\Omega \right) ^{2}\overline{zu}. \end{aligned}$$
(8)

In Eqs. (7) and (8), level and slope are given by \(\bar{z}\left( \tau \right) =\cos \left( \nu \tau \right) \) and \(\bar{u}\left( \tau \right) =-\sin \left( \nu \tau \right) \), respectively. Both are calculable by means of Eq. (5) applying the associated dimensionless forms \(d\bar{z}/d\tau =\nu \bar{u}\) and \(d\bar{u}/d\tau =-\nu \bar{z}\).

3 Mean travel speed and stability in mean

Provided that the vehicle is moving with velocity \(\nu >0\), Eqs. (7) and (8) are averaged by taking the mean values \(\langle \bar{z}^{2}\rangle =\langle \bar{u}^{2}\rangle =1 / 2\) and \(\langle \overline{zu}\rangle =0\) that leads to the mean drift equation

$$\begin{aligned} \frac{\mathrm{d}m_{\nu }}{\mathrm{d}\tau }+D\left( z_{0}\Omega \right) ^{2}m_{\nu }= & {} \frac{f}{c/\Omega }\nonumber \\&+\,z_{0}\Omega \left( \langle \overline{uy}\rangle +2D\langle \overline{ux}\rangle \right) , \end{aligned}$$
(9)

for the mean velocity \(m_{\nu }=\langle v\rangle \) and to the averaged covariances matrix equation

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}\tau }\left[ {\begin{array}{*{20}c} \langle \overline{zy}\rangle \\ \langle \overline{uy}\rangle \\ {\begin{array}{*{20}c} \langle \overline{zx}\rangle \\ \langle \overline{ux}\rangle \\ \end{array} }\\ \end{array} }\, \, \right] \nonumber \\&\qquad +\left[ \, {\begin{array}{*{20}c} 0 &{}\quad -m_{\nu } &{} {\begin{array}{*{20}c} -1 &{}\quad \, \, \, 0\\ \end{array} }\\ m_{\nu } &{}\quad 0 &{}\quad {\begin{array}{*{20}c} 0 &{}\quad -1\\ \end{array} }\\ {\begin{array}{*{20}c} 1\\ 0\\ \end{array} } &{} {\begin{array}{*{20}c} 0\\ 1\\ \end{array} } &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 2D &{}\quad -m_{\nu }\\ \end{array} }\\ {\begin{array}{*{20}c} m_{\nu } &{}\quad 2D\\ \end{array} }\\ \end{array} }\\ \end{array} }\, \right] \,\left[ {\begin{array}{*{20}c} \langle \overline{zy}\rangle \\ \langle \overline{uy}\rangle \\ {\begin{array}{*{20}c} \langle \overline{zx}\rangle \\ \langle \overline{ux}\rangle \\ \end{array} }\\ \end{array} } \right] \nonumber \\&\quad =\left[ \, {\begin{array}{*{20}c} 0\\ 0\\ {\begin{array}{*{20}c} 1\\ 2Dm_{\nu }\\ \end{array} }\\ \end{array} }\, \right] \frac{1}{2}z_{0}\Omega \end{aligned}$$
(10)

for the covariances of the vehicle vibration \(y\left( t \right) , x\left( t \right) \) multiplied by the road level \(z\left( t \right) \) and slope \(u\left( t \right) \). Since the system matrix in Eq. (10) is skew-symmetric, the determinant of Eq. (10) is positive definite determining the mean values

$$\begin{aligned} \frac{\langle \overline{uy}_{0}\rangle }{z_{0}\Omega /2}= & {} \frac{-2Dm_{\nu }^{3}\, }{\left( 1-m_{\nu }^{2} \right) ^{2}+\left( 2Dm_{\nu } \right) ^{2}}\, \, ,\nonumber \\ \frac{\langle \overline{ux}_{0}\rangle }{z_{0}\Omega /2}= & {} \frac{m_{\nu }\left[ 1-m_{\nu }^{2}+\left( 2Dm_{\nu } \right) ^{2} \right] }{\left( 1-m_{\nu }^{2} \right) ^{2}+\left( 2Dm_{\nu } \right) ^{2}} \end{aligned}$$
(11)

and \({\langle \overline{zy}}_{0}\rangle =\langle \overline{ux}_{0}\rangle /m_{\nu }\) and \(\langle \overline{zx}_{0}\rangle =-\langle \overline{uy}_{0}\rangle m_{\nu }\). The insertion of Eq. (11) into Eq. (9) leads to

$$\begin{aligned} \frac{f}{c/\Omega }=\left( \Omega z_{0} \right) ^{2}\frac{{Dm}_{\nu }^{5}}{\left( 1-m_{\nu }^{2} \right) ^{2}+\left( 2Dm_{\nu } \right) ^{2}}, \end{aligned}$$
(12)

by which the travel velocity mean \(m_{\nu }\) can be calculated for given driving force \(f\Omega /c\), road factor \(\Omega z_{0}\) and damping D. The result (12) formally coincides with Eq. (6) of the inverse or control problem

Fig. 4
figure 4

Stability behavior of mean travel speed with squared initials and red end points on the driving force

Full size image

Figure 4 shows simulation results of Eqs. (9) and (10) where the acceleration is lifted by adding the applied driving force (6) and plotted versus the vehicle velocity for different initials marked by squares. After sufficiently long times, all simulated curves end in red circles on the thick red line calculated by Eq. (12). Note that stationary mean accelerations and travel speeds end in lower and upper force branch, only. End points, however, on the force characteristic with negative slope are unstable and therefore not realizable.

The stability of stationary mean velocities is investigated by means of the perturbations \(m_{\nu }=m_{0}+\Delta m_{\nu }\) and \(\langle \overline{\alpha \gamma }\rangle ={\langle \overline{\alpha \gamma }}_{0}\rangle +\Delta \overline{\alpha \gamma }\) for all state processes \((\alpha ,\,\gamma )\in \left\{ z,u,y,x \right\} \). Insertion of all perturbations into Eqs. (9) and (10) and linearization in \(\Delta \)-terms lead to the fifth-order stability equation

$$\begin{aligned}&\frac{d}{d\tau }\left[ \begin{array}{c} \Delta m_{\nu }\\ \Delta \overline{zy}\\ \Delta \overline{uy}\\ \Delta \overline{zx}\\ \Delta \overline{ux} \end{array} \right] \nonumber \\&\quad +\left[ \begin{array}{ccccc} D\left( z_{0}\Omega \right) ^{2} &{} 0 &{} -z_{0}\Omega &{} 0 &{} -{2Dz}_{0}\Omega \\ -{\langle \overline{uy}}_{0}\rangle &{}\quad 0 &{}\quad -m_{0} &{} -1&{} 0\\ \langle \overline{zy}_{0}\rangle &{}m_{0}&{} 0&{}0&{}-1\\ -\langle \overline{ux}_{0}\rangle &{}1&{}0&{}2D&{}-m_{0}\\ {\langle \overline{zx}}_{0}\rangle -z_{0}\Omega D&{}0&{}1&{}m_{0}&{}2D \end{array}\right] \, \nonumber \\&\qquad \left[ \begin{array}{c} \Delta m_{\nu }\\ \Delta \overline{zy}\\ \Delta \overline{uy}\\ \Delta \overline{zx}\\ \Delta \overline{ux}\\ \end{array} \right] =0. \end{aligned}$$
(13)

All stationary covariances calculated in Eq. (11) are inserted into Eq. (13) what leads to the characteristic equation \(\Delta \left( \lambda \right) =A_{0}\lambda ^{5}+A_{1}\lambda ^{4}+\cdots A_{4}\lambda +A_{5}=0\). The determinant of Eq. (13) yields

$$\begin{aligned} A_{5}=\frac{\left( z_{0}\Omega \right) ^{2}Dm_{0}^{4}[m_{0}^{4}-6\left( 1-2D^{2} \right) m_{0}^{2}+5]}{\left( 1-m_{0}^{2} \right) ^{2}+\left( 2Dm_{0} \right) ^{2}}\,. \end{aligned}$$
(14)

According to the Hurwitz Criterion, \(A_{5}<0\) determines divergence and gives the boundaries of monotonous instability. The new instability condition \(A_{5}<0\) determined by Eq. (14) coincides with the negative slope of the driving force calculable by differentiating Eq. (12) with respect to the mean travel speed \(m_{\nu }\). The coincidence of both, negative slope and instability in mean, is plausible and physically explainable: A perturbation of stable speed into the negative direction on the left side of the dynamic equilibrium generates acceleration since the applied force is bigger than that one of the new driving force of the perturbed speed. The vehicle, however, is braked if the speed perturbation goes into positive speed direction on the right side of the dynamical equilibrium since then the driving force is smaller than that one necessary to maintain the perturbed dynamic equilibrium. Vice versa, driving forces with negative slope lead to monotonous instability with the effect that speed leaves the unstable branch of the driving force, applied.

4 Stabilized integration by means of polar coordinates

For constant speeds, the road equations (5) possess two eigenvalues with vanishing real parts what causes numerical instability in integration routines. The resulting drift is avoided by means of the polar coordinates

$$\begin{aligned} \bar{z}=\bar{r}\,\mathrm { cos}\varphi \quad \bar{u}=\bar{r}\,\mathrm { sin}\varphi , \end{aligned}$$
(15)

The insertion of the coordinates (15) into the dimensionless forms \(\mathrm{d}\bar{z}=\nu \bar{u}\mathrm{d}\tau \) and \(\mathrm{d}\bar{u}=-\nu \bar{z}\mathrm{d}\tau \) of the road equations (5) gives the transformed road equations

$$\begin{aligned} \mathrm{d}\bar{r}=0,\quad \bar{r}=1,\quad \mathrm{d}\varphi =-\nu \mathrm{d}\tau . \end{aligned}$$
(16)

where the related polar radius is integrated to \(\bar{r}=1\) by which drift is eliminated and integration is stabilized.

Fig. 5
figure 5

Limit cycle of travel acceleration versus travel speed when vehicle gets stuck left of resonance

Full size image
Fig. 6
figure 6

Period-doubling effect in the phase portrait for long time simulations when car gets stuck before resonance

Full size image

Equations (15) and (16) are inserted into Eq. (7) that gives the new covariance matrix equation

$$\begin{aligned}&-\nu \frac{\mathrm{d}}{\mathrm{d}\varphi }\left[ {\begin{array}{*{20}c} \overline{zy}\\ \overline{uy}\\ {\begin{array}{*{20}c} \overline{zx}\\ \overline{ux}\\ \end{array} }\\ \end{array} } \right] +\left[ {\begin{array}{*{20}c} 0 &{}\quad -\nu &{}\quad {\begin{array}{*{20}c} -1 &{}\quad 0\\ \end{array} }\\ \nu &{}\quad 0 &{}\quad {\begin{array}{*{20}c} 0 &{}\quad -1\\ \end{array} }\\ {\begin{array}{*{20}c} 1\\ 0\\ \end{array} } &{} {\begin{array}{*{20}c} 0\\ 1\\ \end{array} } &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 2D &{}\quad -\nu \\ \end{array} }\\ {\begin{array}{*{20}c} \nu &{}\quad 2D\\ \end{array} }\\ \end{array} }\\ \end{array} } \right] \, \left[ {\begin{array}{*{20}c} \overline{zy}\\ \overline{uy}\\ {\begin{array}{*{20}c} \overline{zx}\\ \overline{ux}\\ \end{array} }\\ \end{array} } \right] \nonumber \\&\quad =\frac{z_{0}\Omega }{2}\left[ {\begin{array}{*{20}c} 0\\ 0\\ {\begin{array}{*{20}c} 1+\mathrm {cos}2\varphi +2D\nu \mathrm {sin}2\varphi \\ \mathrm {sin}2\varphi +2D\nu \left( 1-\mathrm {cos}2\varphi \right) \\ \end{array} }\\ \end{array} } \right] . \end{aligned}$$
(17)

Subsequently, Eqs. (15) and (16) are inserted into Eq. (8) in order to obtain the transformed drift equation

$$\begin{aligned}&-\,\nu \frac{\mathrm{d}\nu }{\mathrm{d}\varphi }+D\left( z_{0}\Omega \right) ^{2}\left( 1-\mathrm {cos}2\varphi \right) \nu =\frac{f}{c/\Omega }\nonumber \\&\quad +\,z_{0}\Omega \left( \overline{uy}+2D\overline{ux} \right) -\frac{1}{2}\left( \mathrm {z}_{\mathrm {0}}\Omega \right) ^{\mathrm {2}}\mathrm {sin}2\varphi . \end{aligned}$$
(18)

Note that in both Eqs. (17) and (18) the increment \(d\tau \) of the dimensionless time is replaced by the polar angle increment \(d\varphi \) given by Eq. (16). Consequently, the integration of both equations can be performed with respect to time or angle. In Fig. 5, the numerical integration of Eqs. (17) and (18) is performed by means of Euler schemes in the time domain applying the time step size \(\Delta \tau ={10}^{-4}\). The time integration is started in the blue square inside the limit cycle and ends in the yellow-black limit cycle around the yellow triangle on the driving force calculated by Eq. (6). The transient behavior from starting point up to the stationary limit cycle is marked by a blue dashed line. The applied road factor and driving force are \(z_{0}\Omega =0.7\) and \(f\Omega /c =0.3\), respectively. In addition, Fig. 5 shows results of a second simulation marked by a dashed green line which represents the moving average of the simulation results. This line starts in the green square outside the limit cycle and ends in the yellow triangle on the driving force calculated by Eq. (12). Moving average results are already shown in Fig. 4 where the averaged equations (9) and (10) are solved, numerically. Both curves, the black one in Fig. 4 and the green in Fig. 5, are slightly different because the order of averaging and integration is reversed in both figures. Finally, Fig. 6 shows the period-doubling effect obtained for the parameters \(z_{0}\Omega =0.9\), \(f\Omega /c =0.6\) and \(D=0.2\). Similar period-doubling effects are obtained when the travel velocity is plotted against the vibration velocity. The double-periodic limit cycle in Fig. 6 degenerates to the one-periodic limit cycle already shown in Fig. 5 when the road factor \(z_{0}\Omega \) and the driving force \(f\Omega /c\) are decreasing.

For analytical investigations, Eqs. (17) and (18) are solved by means of the Fourier expansions

$$\begin{aligned} \nu= & {} \sum \limits _{j=-\infty }^{j=+\infty } {\nu _{j}\mathrm {exp}\left( j2\varphi \right) ,} \quad \nonumber \\ \vec {k}= & {} \sum \limits _{j=-\infty }^{j=+\infty } {\vec {\kappa }_{\mathrm {j}}\mathrm {exp}\left( j2\varphi \right) ,} \end{aligned}$$
(19)

where \(\vec {k}\) is the vector of the covariances (\(\overline{zy},\, \overline{uy},\, \overline{zx},\,\overline{uz}\)). The insertion of the two Fourier series (19) into the drift equation (18) and covariances equation (17) gives the two first equations of expansion

$$\begin{aligned}&D\left( z_{0}\Omega \right) ^{2}\nu _{0}=\frac{f}{c/\Omega }+z_{0}\Omega \left( \overline{uy}_{0}+2D\overline{ux}_{0} \right) ,\\&\quad \left( A+\nu _{0}B \right) \vec {\kappa }_{0}=z_{0}\Omega (\vec {p}/2+D\vec {q}\nu _{0}), \end{aligned}$$

where the vectors \(\vec {p}\) and \(\vec {q}\) are determined by the right-hand side of Eq. (17) and the matrices A and B by its left-hand side. Both equations lead to the same velocity mean already calculated by averaging in Eq. (12) when higher terms of the Fourier expansion are neglected.

Summarizing it is noted that the longitudinal road vehicle problem is solved according to the theory of DA equations by eliminating the infinitely growing vehicle motion coordinate. This is possible when the geometrical road equations are replaced by means of corresponding dynamical ones. The calculated stationary solutions are evaluated in phase portraits plotting the horizontal acceleration versus the travel velocity. The numerical simulations show stable limit cycles before and after the resonance velocity, respectively. The middle limit cycles on negative slopes of the applied driving force are unstable and only detectable by means of analytical methods, e.g., by means of nonlinear Fourier expansions. For increasing driving forces needed for growing road factor, the one periodic limit cycle bifurcates into a double periodic one. For further growing driving forces, the limit cycles become one periodic, again.

5 Random road profiles in space and time

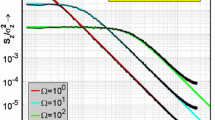
In order to characterize wave length \(L={2\pi } / w\) and way frequency w of level and slope of stochastic road processes, measurements [14] of one-dimensional profiles are evaluated by means of power spectral densities [15,16,17] plotted versus the road frequency w in double-logarithm scales. Random processes of road profiles are generated, e.g., by means of white way noise \(W_{s}^{'}\) with intensity \(\sigma \) applied to the oscillator equation

$$\begin{aligned}&Z_{s}^{''}+2\delta \Omega Z_{s}^{'}+\Omega ^{2}Z_{s}\nonumber \\&\quad =\Omega {\sigma W}_{s}^{'},\quad E\left( W_{s}^{'}W_{t}^{'} \right) =\delta \left( s-t \right) , \end{aligned}$$
(20)

where \(\delta >0\) denotes the bandwidth of the road process and the parameter \(\Omega \) denotes its center frequency. All processes in Eq. (20) are written in capital letters as set functions in dependence on the way coordinate s. Dashes denote derivatives with respect to s The input term in Eq. (20) is delta-correlated with zero mean. It is uniformly distributed in the frequency range [18] with the power spectrum \(S(w)=1.\)

The Fourier transform of Eq. (20) multiplied by its conjugate version gives the road power spectrum [19]

$$\begin{aligned}&S_{z}\left( w \right) =\frac{{(\Omega \sigma )}^{2}}{\left( \Omega ^{2}-w^{2} \right) ^{2}+\left( 2\delta \Omega w \right) ^{2}}\,,\quad \qquad \nonumber \\&\quad \mathrm { for}\quad \left| w \right| <\infty . \end{aligned}$$
(21)

It determines the frequency distribution of the vertical level of the road profile in way domain. In Figs. 7 and 8, evaluations of the above spectrum are marked by smooth red lines plotted in double-logarithmic scales for two sets of the parameters \(\Omega \, \mathrm {and}\, \delta \). The noise intensity in both figures is chosen to be \(\sigma =1\). Cyan lines belong to power spectra of the slope process \(U_{s}\).

Fig. 7
figure 7

Power spectra of the stochastic oscillator in double-logarithmic scales for two center frequencies

Full size image
Fig. 8
figure 8

Statistical and systematic errors in low- and high-frequency range obtained by stochastic FFT analysis

Full size image

The ordinary differential equation of the oscillator (20) is rewritten into Itô differential equations [20, 21]

$$\begin{aligned}&\mathrm{d}Z_{s}=\Omega U_{s}\mathrm{d}s,\quad E\left( \mathrm{d}W_{s}^{2} \right) =\mathrm{d}s, \end{aligned}$$
(22)
$$\begin{aligned}&\mathrm{d}U_{s}=-\Omega \left( 2\delta U_{s}+Z_{s} \right) \mathrm{d}s+\sigma \mathrm{d}W_{s}\, ,\quad \quad \nonumber \\&\Delta W_{s}=\sqrt{\Delta s} \, N_{n}, \end{aligned}$$
(23)

where the Wiener increment \(\mathrm{d}W_{s}\) is approximated [22] by the square root of the way increment \(\Delta s\) multiplied by normally distributed numbers \(N_{n}\) with zero mean \(E\left( N_{n} \right) =0\) and unit mean square \({E(N}_{n}^{2})=1\).

The application of the Maruyama scheme [23] to Eqs. (22) and (23) leads to M samples of finite signals with length \(L=N\Delta s\) and N simulated values \(Z_{k}\) to which the spectral analysis is numerically performed by means of the discrete Fourier transform \(\bar{u}_{nm}\) of all samples multiplied by its conjugate complex version \(\bar{u}_{nm}^{*}\). The product of both is averaged over all samples M in order to obtain the discrete power spectrum

$$\begin{aligned} \hat{S}_{z}\left( w_{n} \right)= & {} c_{z}\sum \nolimits _{m=1}^M {\bar{u}_{nm}\bar{u}_{nm}^{*}} ,\, \, \, \, \, \nonumber \\ \bar{u}_{nm}= & {} \sum \nolimits _{n=0}^{N-1} {\mathrm {Z}_{\mathrm {k}}\mathrm {exp}\left( -ink\,{2\pi } / N \right) } \,, \end{aligned}$$
(24)
$$\begin{aligned} \sigma _{z}^{2}= & {} \frac{1}{NM}\sum \nolimits _{k=1}^{NM} Z_{k}^{2} \nonumber \\= & {} \frac{1}{\pi }\sum \nolimits _{n=0}^{N/2} {\hat{S}_{z}\left( w_{n} \right) \Delta w_{L}} ,\quad \Delta w_{L}={2\pi } / L,\nonumber \\ \end{aligned}$$
(25)

where \(c_{z}\) is a scaling factor needed to satisfy Kolmogorov’s consistency condition. The scaling is carried out applying the mean square \(\sigma _{z}^{2}\) to be additionally measured from all \(Z_{k}\) and integrating over all frequencies \(w_{n}=n\Delta w_{L}\) with the step size \(\Delta w_{L}={2\pi } / L\) on the right side of Eq. (25). In Figs. 7 and 8, the FFT averages are plotted versus the frequency w. They are marked by rough black lines overlaying the smooth analytical results. The rough results become smoother for growing number M of all samples.

When vehicles roll on road with nonnegative velocity \(\bar{v}\ge 0\), the contact point between road and vehicle is moving with same velocity. Consequently, the road equations (22) and (23) must be transformed from way to time by means of the vehicle velocity \(\bar{v}\) applying the classical way-time relation \(\mathrm{d}s=\bar{v}\mathrm{d}t\). According to Itô’s calculus, the Wiener increments in way and time are scaled by \(\mathrm{d}W_{s}=\sqrt{{\bar{v}}} \, \mathrm{d}W_{t}\) [19] where \(E\left( \mathrm{d}W_{s}^{2} \right) =\mathrm{d}s\) and \(E\left( \mathrm{d}W_{t}^{2} \right) =\mathrm{d}t\). The introduction of both way-time relations into the road model (22) and (23) leads to transformed road processes \(Z_{t}\) and \(U_{t}\) described by the first order dynamical system

$$\begin{aligned} \mathrm{d}Z_{t}= & {} \bar{v}\Omega U_{t}\mathrm{d}t,\quad \nonumber \\ \mathrm{d}U_{t}= & {} -\left( 2\delta U_{t}+Z_{t} \right) \bar{v}\Omega \mathrm{d}t+\sigma \sqrt{{\bar{v}}} \mathrm{d}W_{t}, \end{aligned}$$
(26)

where the parameters \(\delta \) and \(\bar{v}\Omega \) denote the bandwidth of the road and its middle time frequency, respectively. The application of the two-dimensional Fokker-Planck equation [21] to Eq. (26) yields

$$\begin{aligned} \frac{\partial }{\partial t}p\left( z,u,t \right)= & {} -\bar{v}\Omega \frac{\partial }{\partial z}\left( up \right) \\&\quad +\,\bar{v}\Omega \frac{\partial }{\partial u}\left[ \left( 2\delta u+z \right) p \right] +\bar{v}\frac{\sigma ^{2}}{2}\frac{\partial ^{2}p}{\partial u^{2}}. \end{aligned}$$

This equation determines the joint density distribution of the two road processes in dependence on time. In the stationary case \(\, {\partial p} / {\partial t=0,}\) the velocity \(\bar{v}\) drops out with the consequence that the stationary density p(zu) is independent on velocity. Consequently, the road model (26) is applicable for all velocities \(\bar{v}\ge 0\). This is exactly the same situation as, e.g., in the deterministic case where the amplitude of the harmonic wave road remains unchanged when the vehicle speeds up or slows down.

6 Quarter car models rolling on random road surfaces

Quarter car models on random road are excited to vertical vibrations described by the equation of motion

$$\begin{aligned}&\ddot{Y}_{t}+2D\omega _{1}\left( \dot{Y}_{t}-\dot{Z}_{t} \right) \nonumber \\&\quad +\,{\upomega }_{\mathrm {1}}^{\mathrm {2}}\left( Y_{t}-Z_{t} \right) =0,\quad (\dot{Y}_{{{\varvec{t}}}}=\omega _{1}X_{t})\,, \end{aligned}$$
(27)

where \(2D\omega _{1}=b / m\) determines the car damping and \(\omega _{1}\) is the natural frequency of the vertical vibrations, given by \(\omega _{1}^{2}=c / {m\, .\, }\) In a first investigation, the velocity \(\bar{v}\) of the vehicle is assumed to be constant with the consequence that the road vehicle system (26) and (27) becomes linear and can be solved, e.g., by means of classical spectral methods [24]. Subsequently, the obtained car spectra are integrated over all spectral frequencies in order to calculate all mean squares and covariances needed in the drift equation

$$\begin{aligned} \dot{V}_{t}=[2D\omega _{1}^{2}{(\dot{Y}}_{t}-\dot{Z}_{t})+\omega _{1}^{2}\left( Y_{t}-Z_{t} \right) ]\, \Omega U_{t}+\, F_{t} / m.\nonumber \\ \end{aligned}$$
(28)

In the special case \({\dot{V}}_{t}=0\), the expectation \(E\left( F_{t} \right) \) of the driving force is subsequently calculated to the form

$$\begin{aligned} \frac{\mathrm {E(}\mathrm {F}_{\mathrm {t}}\mathrm {)}}{\mathrm {c\Omega }{\upsigma }_{\mathrm {u}}^{\mathrm {2}}}=2D\frac{\nu ^{2}\left[ \nu ^{3}+4\delta \nu \left( \delta +D\nu \right) +\delta / D \right] }{\left( 1-\nu ^{2} \right) ^{2}+4\nu \left( D+\delta \nu \right) \left( \delta +D\nu \right) },\nonumber \\ \end{aligned}$$
(29)

where \(\sigma _{z}=\sigma _{u}\) are the standard deviations of the road level and slope process. Both standard deviations are calculable to \(\sigma _{u}=\sigma /\sqrt{4\delta \Omega }\) by means of the linear filter equations, noted in Eq. (26).

In Fig. 9, the expected value (29) is plotted by a red line versus the related car velocity \(\nu =\bar{v}\Omega /\omega _{1}\) for the road intensity \(\Omega \sigma ^{2}=1\), the damping measure \(D=0.15\) and the bandwidth \(\delta =0.3\). The mean force is overlaid by green circles of measured values obtained by means of numerical simulations applying the Maruyama scheme with the step size \(\Delta \tau =\omega _{1}\Delta t=0.001\) for \(N={10}^{7}\) samples. Additionally, Fig. 9 shows probability distributions \(p\left( f \right) \) of the related driving process \(F_{t}\Omega /c\) marked by blue lines and plotted for four speeds of the vehicle. The obtained densities have the exponential form of Gaussian product processes with extremely wide distributions indicating that the assumption of constant speed is physically not realizable.

Fig. 9
figure 9

Force distributions simulated for constant speed and plotted together with the red force mean

Full size image

Hence, it is more realistic to investigate the inverse problem that the velocity is fluctuating meanwhile the driving force is assumed to be constant or given by any characteristic depending on speed. This dynamic problem is numerically investigated by means of the nonlinear first-order system

$$\begin{aligned} \mathrm{d}\bar{Y}_{\tau }= & {} \bar{X}_{\tau }\mathrm{d}\tau , \nonumber \\ \mathrm{d}\bar{X}_{\tau }= & {} -\left[ 2D\left( \bar{X}_{\tau }-\bar{V}_{\tau }\bar{U}_{\tau } \right) +\bar{Y}_{\tau }-\bar{Z}_{\tau } \right] \mathrm{d}\tau , \end{aligned}$$
(30)
$$\begin{aligned} \mathrm{d}\bar{Z}_{\tau }= & {} \bar{V}_{\tau }\bar{U}_{\tau }\mathrm{d}\tau , \nonumber \\ \mathrm{d}\bar{U}_{\tau }= & {} -\left[ \mathrm {2}\delta \left| \bar{V}_{\tau } \right| \bar{U}_{\tau }+\bar{V}_{\tau }\bar{Z}_{\tau } \right] \mathrm{d}\tau \mathrm {+2}\sqrt{\delta \left| \bar{V}_{\tau } \right| }\,\mathrm{d}W_{\tau }\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned} \mathrm{d}\bar{V}_{\tau }= & {} \left( {\Omega }\sigma _{z} \right) ^{\mathrm {2}}\left[ \mathrm {2}D\left( \bar{X}_{\tau }\mathrm {-}\bar{V}_{\tau }\bar{U}_{\tau } \right) \mathrm {+}\bar{Y}_{\tau }\mathrm {-}\bar{Z}_{\tau } \right] \,\bar{U}_{\tau }\mathrm{d}\tau \nonumber \\&+\,\bar{F}_{\tau }\mathrm{d}\tau , \end{aligned}$$
(32)
Fig. 10
figure 10

Velocity densities simulated for constant driving forces overlaid by red circles of mean speeds

Full size image

which is derived from Eq. (26), (27) and (28) introducing the dimensionless state processes \(\left( {{Z}}_{{{t}}},\,{{U}}_{{{t}}},\,{{Y}}_{{{t}}},\,{{X}}_{{{t}}} \right) ={{\upsigma }}_{{{u}}}\left( \bar{{Z}}_{{{t}}},\,\bar{{U}}_{{{t}}},\, \bar{{Y}}_{{{t}}},\,\bar{{X}}_{{{t}}} \right) \) and \(\bar{{{F}}}_{{t}}={{F}}_{{t}}{\Omega } / {{c}}\) and \(\bar{{{V}}}_{{{t}}}={{V}}_{{{t}}}{\Omega } / {{c}}\) as well as the dimensionless time and noise by means of \({{d}}{{\tau }} ={\omega }_{{1}}{{dt}}\) and \({{d}}{{W}}_{{\tau }}=\sqrt{{\omega }_{{1}}} {{dW}}_{{{t}}}\), respectively. Note that the road equation (31) is slightly modified in comparison with Eq. (26) through the introduction of the absolute value of the velocity in the excitation and damping term The latter don’t change the frequency behavior of the road process. However, taking the absolute velocity value is necessary in damping and excitation in order to ensure existence and stability in road simulations if the vehicle drives backwards where negative velocity occurs

In Fig. 10, probability density distributions of the vehicle velocity are plotted for given driving forces. The densities are obtained by means of numerical simulations performed with the time step \(\Delta \tau =0.01\) and \(N={10}^{8}\) samples. Red circles represent measured mean values of the simulated velocity process. The blue line represents the backbone curve of the mean driving force calculated by Eq. (29). For strong over-critical driving forces as shown in the upper right of Fig. 10, the calculated speeds are narrowly distributed with one peak, only. For decreasing driving force, however, the velocity distribution becomes broader and bifurcates into bi-modal probability density with two peaks when the driving force approaches its critical value \({f\Omega } / c=1\) where the vertical car vibrations become resonant. In this case, the global mean value is split into two separated mean values; i.e., the car velocity is fluctuating around two means. Simultaneously, the velocity is migrating from one mean to the next one and back again. For further decreasing driving forces into the under-critical range, the velocity regains its original distribution with one peak and one mean, only.

7 Probability bifurcation into turbulent travel speeds

The control problem, where the mean value of the driving force is calculated in Eq. (29), is now inverted in order to investigate the associated dynamic problem of fluctuating speeds when the driving force is constant. For these purposes, the velocity \({V}_{t}\) is centralized by means of \(V_{t}=\bar{V}_{t}+E(V_{t})\), that leads to \(E\left( \bar{V}_{t} \right) =0\). The insertion of the mean-free velocity into the drift equation (28) gives

$$\begin{aligned} d\left( \bar{V}_{t} \right)= & {} (f / m)\mathrm{d}t+\omega _{1}^{2}\Omega \{2DX_{t}U_{t}\\&-2D(\Omega / \omega _{1})\left[ \bar{V}_{t}+E\left( V_{t} \right) \right] U_{t}^{2}\\&+\left( Y_{t}-Z_{t} \right) U_{t}\}\mathrm{d}t. \end{aligned}$$

Taking into account that \(E\left( Z_{t}U_{t} \right) =0\) in the stationary case and that the velocity \(\bar{V}_{t}\) is uncorrelated to the road surface processes \(Z_{t}\) and \(U_{t}\), the above differential equation leads to the stationary mean equation

$$\begin{aligned}&{f\Omega } / c+2DE\left( X_{t}U_{t} \right) -2Dm_{v}E\left( U_{t}^{2} \right) \nonumber \\&\quad +\,E\left( Y_{t}U_{t} \right) =0, \end{aligned}$$
(33)

where \(E\left( U_{t}^{2} \right) =\sigma _{u}^{2}\) and the mean speed is introduced by \(m_{v}=E(V_{t})\Omega /\omega _{1}\). The stationary drift equation (33) coincides with Eq. (8) when the dimensionless processes \(\left( \bar{Y}_{t},\bar{X}_{t} \right) =\Omega \left( Y_{t},X_{t} \right) \) and \(\left( \bar{Z}_{t},\bar{U}_{t} \right) =(Z_{t}U_{t})/z_{0}\) are inserted. The covariances \(E\left( X_{t}U_{t} \right) \) and \(E\left( Y_{t}U_{t} \right) \) in Eq. (33) are determined by the vector equation

$$\begin{aligned} d\left( \vec {Q}_{t} \right)= & {} \omega _{1}\left[ -A\vec {Q}_{t}-\frac{\Omega }{\omega _{1}}B\bar{V}_{t}\vec {Q}_{t}+\vec {P}_{t} \right] \mathrm{d}t\nonumber \\&\quad +\,\sigma \sqrt{\bar{V}_{t}+E(V_{t})} \, \vec {S}_{t}\mathrm{d}W_{t}, \end{aligned}$$
(34)

where \(\vec {S}_{t}=\left( 0,Y_{t},0,X_{t} \right) ^{'}\) is the perturbation vector \(\vec {Q}_{t}=\left( Y_{t}Z_{t},\, Y_{t}U_{t},\, X_{t}Z_{t},\, X_{t}U_{t} \right) ^{'}\) is the system vector with four covariances and \(\vec {P}_{t}(m_{v})\) is the driving vector given by \((0,0, P_{3t}, P_{4t})'\) and the components

$$\begin{aligned} P_{3t}= & {} Z_{t}^{2}+2D[\bar{V}_{t}\Omega /\omega _{1}+m_{v}]Z_{t}U_{t}, \quad \\ P_{4t}= & {} Z_{t}U_{t}+2D[\bar{V}_{t}\Omega /\omega _{1}+m_{v}]U_{t}^{2}. \end{aligned}$$

The application of the expectation operator to Eq. (34) leads to the stationary covariances equation

$$\begin{aligned}&A\left( m_{v} \right) E\left( \vec {Q}_{t} \right) +\, BE\left( \bar{V}_{t}\vec {Q}_{t} \right) \Omega / \omega _{1}=\vec {P}_{t}\left( m_{v} \right) ,\quad \quad \nonumber \\&\quad \hbox { with }\vec {P}_{t}\left( m_{v} \right) =\sigma _{u}^{2}\left( 0,0, 1,\, 2Dm_{v} \right) , \end{aligned}$$
(35)

where the driving vector is calculated by means of \(E\left( Z_{t}U_{t} \right) =0\) and \(E\left( Z_{t}^{2} \right) =E\left( U_{t}^{2} \right) = \sigma _{u}^{2}.\) The system matrices A and B in Eq. (35) are skew-symmetric with \(4 \times 4\) elements. They are given, as follows:

$$\begin{aligned} A(m_{v})= & {} \left[ \, \, {\begin{array}{*{20}c} 0 &{} -m_{v} &{} {\begin{array}{*{20}c} -1 &{} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 0\\ \end{array} }\, \, \, \, \\ m_{v} &{} 2\delta m_{v} &{} {\begin{array}{*{20}c} 0 &{} \, \, \, \, \, \, \, \, \, \, \, \, \, \, -1\\ \end{array} }\\ {\begin{array}{*{20}c} 1\\ 0\\ \end{array} } &{} {\begin{array}{*{20}c} 0\\ 1\\ \end{array} } &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 2D &{} \, \, \, \, \, \, \, \, \, \, \, -m_{v}\\ \end{array} }\\ {\begin{array}{*{20}c} m_{v} &{} 2D+2\delta m_{v}\\ \end{array} }\\ \end{array} }\\ \end{array} }\, \, \right] \,, \quad \\ B= & {} \left[ \, \, {\begin{array}{*{20}c} 0 &{} -1 &{} {\begin{array}{*{20}c} 0 &{} 0\\ \end{array} }\\ 1 &{} 2\delta &{} {\begin{array}{*{20}c} 0 &{} 0\\ \end{array} }\\ {\begin{array}{*{20}c} 0\\ 0\\ \end{array} } &{} {\begin{array}{*{20}c} 0\\ 0\\ \end{array} } &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0\\ 1\\ \end{array} } &{} {\begin{array}{*{20}c} -1\\ 2\delta \\ \end{array} }\\ \end{array} }\\ \end{array} }\, \, \right] \,. \end{aligned}$$

Equation (35) couples the covariances vector \(\vec {Q}_{t}\) with higher potencies of speed \(\bar{V}_{t}\) so that a sequence of moment’s equations is obtained. It is approximately solved by means of the Gaussian closure [24] that \(E\left( \bar{V}_{t}\vec {Q}_{t} \right) =0\), when all zero mean processes are normally distributed Therewith, Eqs. (33) and (35) are solved by

$$\begin{aligned} \frac{f\Omega / c}{\left( {\upsigma }_{\mathrm {u}}{\Omega } \right) ^{\mathrm {2}}}=\frac{2Dm_{v}^{2}[m_{v}^{3}+4\delta m_{v}\left( \delta +Dm_{v} \right) +\delta / D]}{\left( 1-m_{v}^{2} \right) ^{2}+4m_{v}\left( D+\delta m_{v} \right) \left( \delta +Dm_{v} \right) }.\nonumber \\ \end{aligned}$$
(36)

This result is nonlinear with respect to the unknown mean value \(m_{v}=E(V_{t})\Omega / {\omega _{1}}\) of the travel velocity. Note that Eq. (36) coincides with Eq. (12) of the deterministic wavy road when the bandwidth of the stochastic road process tends to zero (\(\delta \rightarrow 0\)) and its standard deviation is replaced by \(\sigma _{u}=z_{0}/\sqrt{2}\).

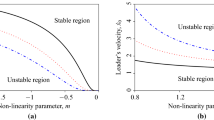
In Fig. 11, Eq. (36) is evaluated for the road bandwidth \(\delta =0.1\) and the intensity \(\upsigma _{\mathrm {u}}\Omega =1\). For driving forces \(f\Omega / c\) above or below the yellow range, Eq. (36) leads to one mean value \(m_{v}\) and to velocity distributions with one maximum, only. They are approximated, e.g., by the density

$$\begin{aligned}&p\left( v \right) =C\mathrm {exp}\left[ -{\frac{1}{2\sigma _{v}^{2}}\left( v-m_{\nu } \right) }^{n} \right] ,\quad \quad \nonumber \\&\quad \mathrm {for}\quad n=2,\, 4,\, 6 \end{aligned}$$
(37)

where C is the normalization constant and v is the density variable of the velocity process \(\bar{V}_{t}={V_{t}\Omega } /c\) with mean value \(m_{\nu }\) and standard deviation \(\sigma _{v}\) For \(n=2\), the density \(p\left( v \right) \) in Eq. (37) is Gaussian. For \(n>2\), the density is more concentrated with shorter distribution tales and gives a better fitting to the measured densities, shown in the upper part of Fig. 10. For driving forces inside the yellow range in Fig. 11, Eq. 36 leads to three different mean values indicating that the velocity distribution possesses three extreme values with two probability concentrations approximated, e.g., by the non-normal density

$$\begin{aligned} p\left( v \right) =C\mathrm {exp}\left[ -{\frac{1}{2\sigma _{v}^{2}}\left( v^{3}+av^{2}+bv+c \right) }^{2} \right] , \end{aligned}$$
(38)

where a, b, c are three parameters of the cubic exponent to be determined by means of the three mean values \(m_{\nu }\) such that the calculated distribution density possesses two maxima and one minimum. Subsequently, the standard deviation \(\sigma _{v}\) and the normalization C have to be determined. Since the stationary density is measurable applying the relative frequency and interval probability to all velocity trajectories realized in the whole speed range \(\vert {\bar{V}}_{t}\vert <\infty \), it is physically not possible to introduce three different distributions, as, e.g., in the deterministic case. Hence, there is only one density of one stationary velocity process distributed over the whole speed space.

The obtained distribution density has the consequence that there is a permanent migration from the lower mean velocity to the upper one and back. The superposition of noisy velocity fluctuations and systematic migrations of vehicle velocities is typical for turbulences similar as in fluid dynamics. The velocity range in yellow in Fig. 11 is extended to the much bigger one marked in green when the damping decreases from \(D=0.1\) to \(D=0.05\). For almost vanishing damping marked by blue dashed lines, turbulences practically are no longer avoidable. In contrast to that, the yellow range of turbulences completely vanishes for stronger damping, e.g., for \(D=0.4\) where the cyan-black curve is obtained instead of the red-black curve. This new force velocity curve rises steadily without resonance since there is no longer a horizontal gradient. In the case of highly damped vehicles, high energy loss occurs in the dampers and one needs growing driving forces to maintain higher speeds of vehicles.

Fig. 11
figure 11

Resonance and traveling speeds of vehicles for small road bandwidth and decreasing car damping

Full size image
Fig. 12
figure 12

Resonance and traveling speed of vehicles for small car damping and increasing road bandwidth

Full size image

Figure 12 shows resonance and travel velocities of vehicles for small car damping and growing road bandwidth. In this case, the resonance peak is lowered as well. However, the travel speed remains almost unchanged in the over-critical speed range. In the limiting case of white noise that the road bandwidth tends to infinity, the force–speed characteristic becomes linear marked by the thick black line in Fig. 12. This has the consequence that the turbulence speed region in yellow disappears, and Eq. 36 is simplified to the linear form \(({f{\Omega }/c)} / \left( {\upsigma }_{\mathrm {u}}{\Omega } \right) ^{\mathrm {2}}=2Dm_{v}\).

8 Conclusions

The paper investigates strong nonlinear systems in longitudinal road vehicle dynamics. When the assumption of constant speed is removed, nonlinearities are introduced by multiplicative state variables. They lead to the effect that vehicle get stuck before resonance when driving on wavy road surfaces. To overcome this blockade, one has to speed up if the driving motor is strong enough.

Experiences on non-fixed wavy roads, e.g., dessert roads show that resonance speeds of vehicles are about 40 km/h due to plastic deformations by heavy vehicles of road maintenance. Turbulences are avoided by speeding up to over-critical speeds or by increasing the car damping. Both leads to stronger driving forces which are necessary to balance the energy loss in dampers.

Bifurcations in probability are explained by the fact that stationary density distributions of interest possess three extreme values: two maxima and one minimum indicating that solution trajectories are seldom in the minimum and often in the maxima with a permanent change between both. This is completely different to the linear case where the trajectories are Gaussian and distributed with one maximum, only.