Abstract
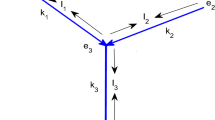
In this article, we study the dynamical behaviour of a new species spreading from a location in a river network where two or three branches meet, based on the widely used Fisher-KPP advection–diffusion equation. This local river system is represented by some simple graphs with every edge a half infinite line, meeting at a single vertex. We obtain a rather complete description of the long-time dynamical behaviour for every case under consideration, which can be classified into three different types (called a trichotomy), according to the water flow speeds in the river branches, which depend crucially on the topological structure of the graph representing the local river system and on the cross section areas of the branches. The trichotomy includes two different kinds of persistence states, and the state called “persistence below carrying capacity” here appears new.



Similar content being viewed by others
Notes
It is also well known that (1.1) has two positive steady-states \(\phi _\beta \) and 1 if \(\beta \ge c_*\), and 1 is the only positive steady-state if \(0<\beta <c_*\).
References
Aronson DG, Weinberger HF (1975) Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. In: Partial differential equations and related topics (Program, Tulane University, New Orleans, La., 1974). Lecture notes in mathematics, vol 446. Springer, Berlin, pp 5–49
Campbell Grant EH, Lowe WH, Fagan WF (2007) Living in the branches: population dynamics and ecological processes in dendritic networks. Ecol Lett 10:165–175
Corli A, di Ruvo L, Malaguti L, Rosini MD (2017) Traveling waves for degenerate diffusive equations on networks. Netw Heterog Media 12:339–370
Du Y, Lou B (2015) Spreading and vanishing in nonlinear diffusion problems with free boundaries. J Eur Math Soc 17:2673–2724
Fisher RA (1937) The wave of advance of advantageous genes. Ann Eugen 7:335–369
Hamel F, Nolen J, Roquejoffre J-M, Ryzhik L (2013) A short proof of the logarithmic Bramson correction in Fisher-KPP equations. Netw Heterog Media 8:275–289
Hilker FM, Lewis MA (2010) Predator–prey systems in streams and rivers. Theor Ecol 3:175–193
Huang Q-H, Jin Y, Lewis MA (2016) \(R_0\) analysis of a Benthic-drift model for a stream population. SIAM J Appl Dyn Syst 15:287–321
Jimbo S, Morita Y (2019) Entire solutions to reaction-diffusion equations in multiple half-lines with a junction. J. Differ. Equ. 267:1247–1276
Jin Y, Peng R, Shi J (2019) Population dynamics in river networks. J. Nonlinear Sci. 29(6):2501–2545
Kolmogorov AN, Petrovsky IG, Piskunov NS (1937) A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem. Bull Mosc Univ Math Mech 1:1–25
Lam K-Y, Lou Y, Lutscher F (2016) The emergence of range limits in advective environments. SIAM J Appl Math 76(2):641–662
Lutscher F, Pachepsky E, Lewis MA (2005) The effect of dispersal patterns on stream populations. SIAM Rev 47:749–772
Protter MH, Weinberger HF (1984) Maximum principles in differential equations. Springer, New York
Ramirez JM (2012) Population persistence under advection–diffusion in river networks. J Math Biol 65:919–942
Sarhad J, Carlson R, Anderson KE (2014) Population persistence in river networks. J Math Biol 69:401–448
Sarhad J, Manifold RS, Anderson KE (2017) Geometric indicators of population persistence in branching continuous-space networks. J Math Biol 74:981–1009
Speirs DC, Gurney WSC (2001) Population persistence in rivers and estuaries. Ecology 82:1219–1237
Vasilyeva O (2019) Population dynamics in river networks: analysis of steady states. J Math Biol 79:63–100
von Below J (1988) Classical solvability of linear parabolic equations on networks. J Differ Equ 72:316–337
Yanagida E (2001) Stability of nonconstant steady states in reaction-diffusion systems on graphs. Jpn J Ind Appl Math 18:25–42
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the two anonymous referees for their suggestions and comments which helped to improve the presentation of the paper. This research was partially supported by the Australian Research Council (No. DP190103757), the NSF of China (No. 11671262, 11671175, 11571200), the Priority Academic Program Development of Jiangsu Higher Education Institutions, Top-notch Academic Programs Project of Jiangsu Higher Education Institutions (No. PPZY2015A013) and Qing Lan Project of Jiangsu Province.
Rights and permissions
About this article
Cite this article
Du, Y., Lou, B., Peng, R. et al. The Fisher-KPP equation over simple graphs: varied persistence states in river networks. J. Math. Biol. 80, 1559–1616 (2020). https://doi.org/10.1007/s00285-020-01474-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-020-01474-1