Prediction of Electrolyte Distribution in Technical Gas Diffusion Electrodes: From Imaging to SPH Simulations

Abstract

The performance of the gas diffusion electrode (GDE) is crucial for technical processes like chlorine–alkali electrolysis. The function of the GDE is to provide an intimate contact between gaseous reactants, the solid catalyst, and the liquid electrolyte. To accomplish this, the GDE is composed of wetting and non-wetting materials to avoid electrolyte breakthrough. Knowledge of the spatial distribution of the electrolyte in the porous structure is a prerequisite for further improvement of GDE. Therefore, the ability of the electrolyte to imbibe into the porous electrode is studied by direct numeric simulations in a reconstructed porous electrode. The information on the geometry, including the information on silver and PTFE distribution of the technical GDE, is extracted from FIB/SEM imaging including a segmentation into the different phases. Modeling of wetting phenomena inside the GDE is challenging, since surface tension and wetting of the electrolyte on silver and PTFE surfaces must be included in a physically consistent manner. Recently, wetting was modeled from first principles on the continuum scale by introducing a contact line force. Here, the newly developed contact line force model is employed to simulate two-phase flow in the solid microstructures using the smoothed particle hydrodynamics (SPH) method. In this contribution, we present the complete workflow from imaging of the GDE to dynamic SPH simulations of the electrolyte intrusion process. The simulations are used to investigate the influence of addition of non-wetting PTFE as well as the application of external pressure differences between the electrolyte and the gas phase on the intrusion process.

1 Introduction

Gas diffusion electrodes (GDEs) are porous functional materials that are used in many electrochemical processes to convert chemical energy into electrical energy. Research currently focuses on metal–air batteries and the reverse process, electrolysis with gaseous and liquid reactants.

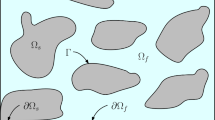
The GDE has the task of ensuring intimate contact between gaseous reactants, the solid catalyst, and liquid electrolyte. During operation, the GDE is supplied with oxygen from one side and electrolyte from the other. The electrolyte penetrates from one side into the GDE until a hydrodynamic equilibrium is reached. A breakthrough of the electrolyte to the gas side must be avoided (Fig. 1). Due to the low solubility of oxygen in the electrolyte, a spatially narrow reaction zone of silver particles, oxygen, and electrolyte forms inside the GDE at the three-phase boundary. At a given pressure and temperature, this depends on the structure of the pore space, the viscosity of the electrolyte, the surface tensions between electrolyte, gas phase, and solid, and the resulting wetting properties of the electrolyte on silver and the hydrophobic polymer. In addition to an extended three-phase boundary, electronic and ionic resistances in the GDE should be low and mass transport in the gas phase as high as possible for the electrochemical process. Further requirements for the GDE are sufficient chemical and mechanical stability.

Fig. 1

Schematic sketch of the different apparent phases in the gas diffusion electrode (GDE). Electrolyte (blue), gas (white), silver (black), and polytetrafluoroethylene (gray). In a uniform intrusion of electrolyte into the GDE is depicted whereas in b unwanted breakthrough of electrolyte happens

For chlorine–alkali electrolysis, the impact of the porous structure and wettability of the GDE on the overall performance of the oxygen reduction reaction (ORR) was shown experimentally by Moussallem et al. (2012). They added hydrophobic polytetrafluoroethylene (PTFE) in different concentrations to the hydrophilic silver electrode material during the electrode production and found that the addition of 2 wt.% of PTFE gave the highest half-cell potentials.

Knowledge of the in situ electrolyte distribution is crucial for further improvement of the ORR performance. Nevertheless, high resolution X-ray in situ measurements of a working electrode are hardly possible due to the high absorption potential of the silver backbone. Therefore, we took a two-step approach: First, pore morphology and PTFE distribution inside the GDE are reconstructed on the nanometer scale; then, direct numerical simulations of the spontaneous imbibition as well as a forced intrusion of the electrolyte are carried out using first principle models for the movement of the contact line. Using experimentally determined contact angles, the different wetting properties of electrolyte on silver and PTFE can be considered. Multiphase flow inside the porous structures is simulated using the smoothed particle hydrodynamics (SPH) method (Sivanesapillai et al. 2016; Tartakovsky and Panchenko 2016).

A prerequisite for such simulations is the proper description of a representative section of the GDE. Three-dimensional structures of electrodes on the nanometer scale can be determined by (ex situ) focused ion beam (FIB)/scanning electron microscopy (SEM) tomography with an accuracy of up to $10\;{\text{nm}}$ (Zils et al. 2010; Hutzenlaub et al. 2012; Ender et al. 2012). This allows a complete imaging of the entire inner pore-space structure as well as the distribution of different material phases (e.g., silver and PTFE) in a maximum volume of approximately $30 \times 30 \times 30\,\upmu{\text{m}}^{3}$.

An overview of the entire workflow from the FIB/SEM image acquisition to the SPH simulation is shown in Fig. 2. In this paper, all parts of the workflow are explained individually. In the last part, simulation results in a section of the GDE are presented for different applied external pressure differences between the electrolyte and gas phase to demonstrate the possibilities offered by this simulation method.

Fig. 2

Overview of the entire workflow from the FIB/SEM image acquisition to the SPH simulation

2 FIB/SEM Imaging and Pore-Space Segmentation

3D FIB/SEM tomography by means of serial sectioning on porous multiphase material is very challenging. For a successful and precise reconstruction of the material, a conducting fixation is needed that does not alter the sample itself. Due to low hardness of silver (Mohs hardness between 2.5 and 3 (Samsonov 1968) in combination with the porosity of the material, a mechanical fixation is not possible without a high probability of sample deformation. Carbon or copper adhesive disks do not provide the amount of fixation needed for the necessary mechanical preprocessing steps. The only option is an embedding of the sample. Unfortunately, it is not possible to gain enough material contrast inside the pores between the PTFE and the embedding material to reconstruct the pore space and the PTFE individually. Using different embedding materials (e.g., carbon or silicone-based materials) does not improve the material contrast sufficiently. Therefore, filling the sample pores is not possible.

For the FIB/SEM tomography presented in this work, we embedded the sample with partially cured adhesive to avoid pore filling.

First, a $3 \times 1\,{\text{mm}}^{2}$ segment was taken mechanically from the center of a pristine silver electrode. To allow for mechanical cross sectioning and for fixation that avoids sample alteration, the sample is then embedded in 3 h procured EpoThin™2 with a resin to hardener ratio of 20:9 (all at 25 °C). After complete curing, a cross section perpendicular to the sample surface was prepared by mechanically grounding with 1500 and 4000 SiC-paper under water. A polishing step is not useful because of silver smearing. To remove the uppermost silver layer of the cross section, the sample is polished with a Bal-Tec RES 101 argon ion mill for 2 h. The acceleration voltage was $3\,{\text{keV}}$ with a current of $1.5\,{\text{mA}}$ and a glancing angle of 5 degrees. The FIB/SEM tomography is performed by using a Zeiss Crossbeam 340 Gallium-FIB/SEM. An acceleration voltage of $30 {\text{keV}}$ and a current of $7 {\text{nA}}$ have been applied.

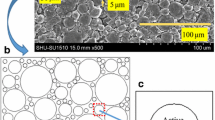
A total of 1300 slices have been scanned with an isotropic voxel size of 30 nm. The total measure time was 6 h with 5 h SEM image capture time and 1 h dwell time. The raw data were drift corrected and then denoised using a non-local means filter (Salzer et al. 2012, 2014). The vertical image intensity gradient was corrected using a maximum projection though a horizontal reslice of the 3D dataset resulting in a constant mean voxel value for the silver phase. The pore-space determination was done with a procedure based on the utilization of the shadow effects of the angled SE2 signal in dwelling direction proposed in Buades et al. (2005). All calculations of the derivatives of the first and second order in milling direction, the denoising and drift correction were done using the imaging software Fiji (Schindelin et al. 2012). After the determination of the pore space, the two phases silver and PTFE have been separated by means of histogram analysis using the Otsu threshold (Otsu 1979). The histogram in Fig. 3 shows the gray value distribution of silver (gray) and PTFE (green) phase.

Fig. 3

Schematic histogram of the gray values of the GDE’s phases

Figure 4 shows the first segmented slice of the tomography as example. The red-marked rectangle shows the area used for the SPH simulation.

Fig. 4

Segmented FIB/SEM tomography image, pore system (black), and PTFE depletion (green) at the silver grain (white) boundaries; red rectangle shows the area used for SPH simulation

To prove that the distribution of silver grains, PTFE, and also the form of the pore system is consistent in the GDE and that the FIB/SEM tomography of a smaller volume ($30 \times 30 \times 30\,\upmu{\text{m}}^{3}$) leads to reliable results, an extensive cut over the whole cross section of the GDE has been performed using an acceleration voltage of $30\,{\text{keV}}$ and a current of $80\,{\text{nA}}$ (Fig. 5). The SEM images of this cut have been composed and corrected using the imaging software Fiji (Schindelin et al. 2012). Due to the 2D characteristic of this cut, no reslices could be calculated, and therefore, the determination of the different phases cannot be realized without strong deviations. In this case, a manual labeling had to be performed to ensure a correct determination of the PTFE phase, which has been colored in green (Fig. 5) for a better clarity.

Fig. 5

SEM, FIB cut through the cross section of the GDE; pore system with PTFE depletion (in green) at the silver grain boundaries; red rectangles show higher magnification

Figure 5 shows the microstructure of the whole cross section of the GDE. Silver grains with typical twins and the pore system are visible. The PTFE is depleted at the silver grain boundaries. The red rectangles show higher magnification of the microstructure. Figure 4 shows clearly that the morphology and the distribution of the different phases are homogeneous over the whole cross section.

3 Multiphase Flow Model

Isothermal flow of immiscible and incompressible Newtonian fluids on the pore scale is described by the Navier–Stokes equations. With the extensions for surface tension effects between wetting, non-wetting, and solid phase, the governing equations in Lagrangian formulation read

$$\begin{aligned} \frac{{{\text{D}}\rho }}{{{\text{D}}t}} & = - \rho \left( {\nabla \cdot {\mathbf{v}}} \right) = 0 \\ \frac{{{\text{D}}{\mathbf{v}}}}{{{\text{D}}t}} & = - \frac{\nabla p}{\rho } + \frac{\mu }{\rho }\Delta {\mathbf{v}} + {\mathbf{g}} + \frac{1}{\rho }\left( {{\mathbf{f}}_{\text{eg}} + {\mathbf{f}}_{\text{egs}} } \right) \\ \frac{{{\text{d}}{\mathbf{x}}}}{{{\text{d}}t}} & = {\mathbf{v}}. \\ \end{aligned}$$

(1)

Here, $\rho ,\;{\mathbf{v}},\;p,\;\mu$, and ${\mathbf{g}}$ represent the density, velocity, pressure, dynamic viscosity, and any body force like gravity, respectively. The terms $- \left( {\nabla p/\rho } \right)$ and $\left( {\mu /\rho } \right)\Delta {\mathbf{v}}$ account for pressure and viscous forces per unit mass in the system. The effects of surface tension at the electrolyte–gas interface and solid–fluids contact line are described as volumetric forces ${\mathbf{f}}_{\text{eg}}$ and ${\mathbf{f}}_{\text{egs}}$ which represent the locally distributed forces acting in the vicinity of the electrolyte–gas interface and the solid–fluids contact line, respectively. The subscripts “e” (electrolyte), “g” (gas), and “s” (solid) denote the adjacent phases acting at the interface and contact line, respectively.

3.1 Surface Tension and Contact Line

The volumetric continuous surface force (CSF) at the electrolyte–gas interface is given as the surface force resulting from the momentum balance at the sharp interface and a volume reformulation term $\delta_{\text{eg}}$. Here, the volume reformulation converts the surface force into a volumetric force which acts in the direct vicinity of the boundary surface (Brackbill et al. 1992).

$${\mathbf{f}}_{\text{eg}} = \gamma_{\text{eg}} \kappa_{\text{eg}} {\hat{\mathbf{n}}}_{\text{eg}} \delta_{\text{eg}} ,$$

(2)

In Eq. (2), the product of the surface tension between electrolyte and gas phase $\gamma_{\text{eg}}$ and the local interface curvature $\kappa_{\text{eg}}$ defines the magnitude of the surface force, whereas the unit normal vector on the interface ${\hat{\mathbf{n}}}_{\text{eg}}$ defines the direction of the surface force. In a continuous field, the term ${\hat{\mathbf{n}}}_{\text{eg}} \delta_{\text{eg}}$ can be expressed as

$${\hat{\mathbf{n}}}_{\text{eg}} \delta_{\text{eg}} = \frac{\nabla c}{{\left| {c_{\text{e}} - c_{\text{g}} } \right|}}.$$

(3)

Here, $c_{\text{e}}$ and $c_{\text{g}}$ are the color (or indicator) function of the electrolyte and gas phase.

The approach of Brackbill et al. (1992) has been transferred recently by Huber et al. (2016) to the treatment of the contact line. From the momentum balance at the contact line between electrolyte, gas, and the solid wall, the volumetric contact line force (CLF) as introduced by Huber et al. (2016) is expressed as

$${\mathbf{f}}_{\text{egw}} = \left( {\gamma_{\text{gw}} - \gamma_{\text{ew}} + \gamma_{\text{eg}} \underbrace {{\left( {\hat{\varvec{\nu }}_{\text{gw}} \cdot \hat{\varvec{\nu }}_{\text{eg}} } \right)}}_{{ - { \cos }\theta_{\text{D}} }}} \right)\hat{\varvec{\nu }}_{\text{gw}} \delta_{\text{egw}} .$$

(4)

In Eq. (4), ${\hat{\mathbf{\nu }}}_{\text{gw}}$ is the unit vector tangential to the interface between non-wetting fluid and the solid phase pointing in normal direction to the contact line, whereas ${\hat{\mathbf{\nu }}}_{\text{eg}}$ is unit vector tangential to the fluid–fluid interface (Fig. 6). The volume reformulation term $\delta_{\text{egw}}$ distributes the line force as volume force near the contact line.

Fig. 6

Contact line at the connection point of the unit vectors $\hat{\nu }_{\text{eg}}$, $\hat{\nu }_{\text{ew}}$, and $\hat{\nu }_{\text{gw}}$, where each vector is located tangential on the corresponding interface and in normal direction with respect to the contact line

With Young’s equation for the equilibrium contact angle $\theta_{\text{E}}$

$$\cos \left( {\theta_{\text{E}} } \right) = \frac{{\gamma_{\text{gw}} - \gamma_{\text{ew}} }}{{\gamma_{\text{eg}} }} = \frac{{\Delta \gamma_{\text{w}} }}{{\gamma_{\text{eg}} }},$$

(5)

where $\Delta \gamma_{\text{w}} = \gamma_{\text{gw}} - \gamma_{\text{ew}}$ describes the difference in surface tension coefficients between gas/solid and electrolyte/solid. The momentum balance at the contact line in Eq. (4) can be expressed as

$${\mathbf{f}}_{\text{egw}} = \gamma_{\text{eg}} \left( {{ \cos }(\theta_{\text{E}} } \right) - { \cos }\left( {\theta_{\text{D}} } \right)) \hat{\varvec{\nu }}_{\text{gw}} \delta_{\text{egw}} .$$

(6)

In case of electrolyte intrusion into a GDE, the equilibrium contact angle is locally dependent on the type of the pore walls (silver or PTFE), which can be expressed by parameters of $\theta_{\text{E}} \;{\text{or}}\;\Delta \gamma_{\text{w}}$, respectively.

4 Numerical Method

Multiphase flow in porous media has been treated by a variety of methods. Besides the smoothed particle hydrodynamics method, which is used in this work, the most popular methods are the Lattice–Boltzmann (Ahrenholz et al. 2008; Hao and Cheng 2009; Mukherjee et al. 2009) and the volume of fluid (VOF) method (Raeini et al. 2015; Ferrari et al. 2015). Within the VOF method the continuous surface force (CSF) model of Brackbill is commonly used to describe surface tension at the fluid–fluid interface. An advantage of the SPH method compared to VOF is the Lagrangian movement of the fluid interface, what makes the reconstruction of the fluid–fluid interface obsolete. Without the necessity of the reconstruction, no boundary condition for the dynamic contact angle exists. In the SPH method, the dynamic wetting behavior is described from first principles with an extension to the Navier–Stokes equation by the contact line force (CLF) model which has been recently introduced by Huber et al. (2016). This allows to describe the movement of the contact line using the local surface tension coefficients. Compared with the SPH and the VOF method, most Lattice–Boltzmann methods require the determination of some fitting parameters.

The mesh-free Lagrangian smoothed particle hydrodynamics method (Gingold and Monaghan 1977; Lucy 1977) was introduced to solve astrophysical problems and was later adopted for problems in fluid dynamics by Morris et al. (1997). Especially, in the description of strong deformations of phase boundaries with the formation of new interfaces, Lagrangian methods offer advantages. A detailed introduction to the SPH method is given by Liu and Liu (2010).

In general, all field variables and their local derivatives in the smoothed particle hydrodynamics (SPH) method formulation are obtained by a convolution integral over the fluid domain $\Omega$

$$\left\langle {\psi \left( {\mathbf{x}} \right)} \right\rangle = \int_{\Omega } {\psi \left( x \right) W\left( {{\mathbf{x}} - {\mathbf{x^{\prime}}},h} \right){\text{d}}{\mathbf{x}}} .$$

(7)

Here, $W\left( {{\mathbf{x}} - {\mathbf{x^{\prime}}},h} \right)$ is the kernel (or weight) function, which has a compact support. The kernel function is defined by $h > 0$ in all practical applications. We chose the C2 spline kernel by Wendland (1995) for all our simulations

$$W\left( {r,h} \right) = \frac{21}{{16\pi h^{3} }}\left\{ {\begin{array}{*{20}l} {\left( {1 - \frac{q}{2}} \right)^{4} \left( {2q + 1} \right),\quad {\text{if}}\;q \le 2} \hfill \\ {0,\quad {\text{else}}} \hfill \\ \end{array} } \right.,$$

(8)

with $r = \left| {{\mathbf{x}} - {\mathbf{x}}'} \right|$ and $q = r/h$.

In the bulk of the fluid, where the compact support of the kernel function is completely inside of the simulation domain, the kernel function must fulfill the following conditions

$$\begin{aligned} & \int_{\Omega } {W\left( {{\mathbf{x}} - {\mathbf{x^{\prime}}},h} \right)} \,{\text{dx}} = 1 \\ & \int_{\Omega } {\nabla W\left( {{\mathbf{x}} - {\mathbf{x^{\prime}}},h} \right)} \,{\text{d}}{\mathbf{x}} = 0. \\ \end{aligned}$$

(9)

Nevertheless, at domain boundaries those conditions are not fulfilled (Colagrossi et al. 2009). Therefore, corrected gradients of the corrected kernels $\tilde{\nabla }\tilde{W}_{ij}$ (Bonet and Lok 1999) are applied in the whole simulation domain.

4.1 SPH Formulation of the Momentum Balance

In this work, a SPH discretization with particle averaged spatial derivatives according to the work of Hu and Adams (2006) is used. Here, density of particle $i$ is computed by

$$\rho_{i} = m_{i} \mathop \sum \limits_{j}^{{N_{i} }} W_{ij} .$$

(10)

According to the work of Morris et al. (1997), a separate treatment for interactions with other fluid and solid particles is necessary for the computation of the force per unit mass due to viscosity, which can be formulated as

$$\begin{aligned} \left( {\frac{\mu }{\rho }\Delta {\mathbf{v}}} \right)_{i} & = \frac{1}{{m_{i} }}\mathop \sum \limits_{j}^{{N_{{i,{\text{f}}}} }} \bar{\mu }_{ij} D_{ij} \frac{{{\mathbf{v}}_{ij} }}{{r_{ij} }}\frac{{\partial \tilde{W}_{ij} }}{{\partial r_{ij} }} \\ & \quad + \frac{1}{{m_{i} }}\mathop \sum \limits_{j}^{{N_{{i,{\text{w}}}} }} \mu_{i} D_{ij} \frac{{\beta_{ij} {\mathbf{v}}_{ij} }}{{r_{ij} }}\frac{{\partial \tilde{W}_{ij} }}{{\partial r_{ij} }} , \\ \end{aligned}$$

(11)

with ${\mathbf{v}}_{ij} = {\mathbf{v}}_{i} - {\mathbf{v}}_{j}$, $\bar{\mu }_{ij} = \left( {2\mu_{i} \mu_{j} } \right)/\left( {\mu_{i} + \mu_{j} } \right)$ and $D_{ij} = \left( {V_{i}^{2} + V_{j}^{2} } \right)$. The indices “f” and “w” in the particle numbers $N_{i}$ mark an exclusive summation of neighboring fluid or solid wall particles. In Eq. (11), the factor $\beta_{ij}$ is computed as

$$\beta_{ij} = 1 + \frac{{d_{j} }}{{d_{i} }}$$

(12)

and denotes the ratio of the wall distances $d_{i}$ of fluid particle $i$ and $d_{j}$ of solid particle $j$ in normal direction to the solid–fluid interface (Morris et al. 1997) which is shown in Fig. 7.

Fig. 7

Sketch of the distances of the fluid particle $d_{i}$ and the corresponding distance of the solid particle $d_{j}$ to the boundary of the solid wall

According to the discretization of Hu and Adams (2006), the pressure field gradient leads to the force per unit mass

$$- \left( {\frac{1}{\rho }\nabla p} \right)_{i} = - \frac{1}{{m_{i} }}\mathop \sum \limits_{j}^{{N_{i} }} \bar{p}_{ij} D_{ij} \tilde{\nabla }\tilde{W}_{ij} ,$$

(13)

with $\bar{p}_{ij} = \left( {\rho_{i} p_{j} + \rho_{j} p_{i} } \right)/\left( {\rho_{i} + \rho_{j} } \right).$

4.2 Implementation of Surface Tension and Contact Line in SPH

In this work, the continuous surface force (CSF) and the contact line force (CLF) model describe effects of surface tension. Both forces depend on the calculation of normal vectors at the fluid–fluid interface. According to Adami et al. (2010), the normal vector at the electrolyte–gas interface is computed by

$${\mathbf{n}}_{{{\text{eg}},i}} = - \frac{1}{{\left| {c_{\text{e}} - c_{\text{g}} } \right| V_{i} }}\mathop \sum \limits_{j}^{{N_{{i,{\text{f}}}} }} \bar{c}_{ij} D_{ij} \tilde{\nabla }\tilde{W}_{ij} ,$$

(14)

with $c_{ij} = \left( {\bar{\rho }_{j} c_{i} + \bar{\rho }_{i} c_{j} } \right)/\left( {\bar{\rho }_{j} + \bar{\rho }_{i} } \right)$ and an exclusive summation of fluid particles. The subscripts “e” and “g” correspond to electrolyte and gas phase, respectively.

The interface curvature $\kappa$ is computed as

$$\kappa_{{{\text{eg}},i}} = - \mathop \sum \limits_{j}^{{N_{i,\epsilon } }} V_{j} \left( {{\hat{\text{n}}}_{{{\text{eg}},j}} - {\hat{\text{n}}}_{{{\text{eg}},i}} } \right)\tilde{\nabla }\tilde{W}_{ij} ,$$

(15)

where $N_{i,\epsilon }$ denotes an exclusive summation of particles which fulfill the condition

$$\left| {{\mathbf{n}}_{{{\text{eg}},i}} } \right| > \epsilon = \frac{0.02}{h}\frac{{\rho_{i} }}{{\rho_{\text{e}} + \rho_{\text{g}} }}.$$

(16)

From Eqs. (14) and (15), the volumetric surface force is computed by

$${\mathbf{f}}_{{{\text{eg}},i}} = \gamma_{\text{eg}} \kappa_{{{\text{eg}},i}} {\mathbf{n}}_{{{\text{eg}},i}} .$$

(17)

According to Huber et al. (2016), the volume reformulation for the contact line force is computed by

$$\delta_{{{\text{egw}},i}} = - 2{\hat{\mathbf{d}}}_{i} \cdot \mathop \sum \limits_{j}^{{N_{i,\epsilon } }} \left( {\delta_{{{\text{egw}},j}}^{{\prime }} - \delta_{{{\text{egw}},i}}^{{\prime }} } \right)\tilde{\nabla }\tilde{W}_{ij} ,$$

(18)

where ${\hat{\mathbf{d}}}_{i}$ is the normalized distance vector pointing toward the closest solid wall, and $\delta_{{{\text{egw}},j}}^{{\prime }}$ is defined as

$$\delta_{{{\text{egw}},j}}^{{\prime }} = \left\{ {\begin{array}{*{20}l} {\delta_{{{\text{egw}},i}}^{{\prime }} ,\quad {\text{if}}\;j \in N_{{i,{\text{f}}}} } \hfill \\ {0,\qquad {\text{if}}\;j \in N_{{i,{\text{w}}}} } \hfill \\ \end{array} ,\quad {\text{with}}} \right.\quad\delta_{{{\text{egw}},i}}^{{\prime }} = {\hat{\mathbf{\nu }}}_{{{\text{gw}},i}} \cdot {\mathbf{n}}_{{{\text{eg}},i}} .$$

(19)

In Eq. (19), $\hat{\nu }_{{{\text{gw}},i}}$ is the unit normal vector tangential to the interface between non-wetting fluid and the solid phase pointing in normal direction to the contact line (Fig. 6) and is computed by

$$\varvec{\nu}_{{{\text{gw}},i}} = \left| {{\mathbf{d}}_{i} } \right|^{2} {\mathbf{n}}_{{{\text{eg}},i}} - \left( {{\mathbf{d}}_{i} \cdot {\mathbf{n}}_{{{\text{eg}},i}} } \right){\mathbf{d}}_{i} .$$

(20)

Different from the original formulation of Huber et al. (2016), for the calculation of the dynamic contact angle $\theta_{\text{D}}$ in Eq. (6), a weighted summation including the volume reformulation term $\delta_{{{\text{egw}},i}}$ is applied.

$$- \cos \theta_{D,i} = \mathop \sum \limits_{j}^{{N_{i,\epsilon } }} \frac{{V_{j} \delta_{{{\text{egw}},i}} {\hat{\mathbf{d}}}_{j} \cdot {\hat{\mathbf{n}}}_{{{\text{eg}},j}} }}{{V_{j} \delta_{{{\text{egw}},j}} }}$$

(21)

With this approach, the locally computed dynamic contact angles of the different particles $\theta_{{{\text{D}},i}}$ are more uniform.

In the application considered here, the equilibrium contact angle is not a constant for the system but is locally depend on the wettability of the solid wall, i.e., to what extend the pore wall consists of silver or PTFE. Finally, the local contribution to particle i of the contact line force can be computed by

$$\varvec{f}_{{{\text{egw}},i}} = \gamma_{\text{eg}} \left( {{ \cos }\theta_{{{\text{E}},i}} - { \cos }\theta_{{{\text{D}},i}} } \right) {\hat{\mathbf{\nu }}}_{{{\text{gw}},i}} \delta_{{{\text{egw}},i}} .$$

(22)

As already determined in Eq. (5), the equilibrium contact angle $\theta_{\text{E}}$ depends on the local substrate. To ensure a smooth transition of the wetting property, the local equilibrium contact angle for a fluid particle is calculated by

$$\cos \theta_{{{\text{E}},i}} = \frac{1}{{\gamma_{eg} }}\frac{{\mathop \sum \nolimits_{j}^{{N_{{i,{\text{w}}}} }} V_{j} \Delta \gamma_{w,j} W_{ij} }}{{\mathop \sum \nolimits_{j}^{{N_{{i,{\text{w}}}} }} V_{j} W_{ij} }},$$

(23)

where $N_{{i,{\text{w}}}}$ denotes an exclusive summation of wall particles, which belong either to the silver “s” or PTFE “p” phase. The difference in surface tension $\Delta \gamma_{w,j}$ is defined as

$$\Delta \gamma_{{{\text{w}},j}} = \left\{ {\begin{array}{*{20}l} {\Delta \gamma_{\text{s}} ,\quad {\text{if}}\;j \in {\text{silver}}\;{\text{phase}}\; \hbox{``}s\hbox{''}} \hfill \\ {\Delta \gamma_{\text{p}} , \quad {\text{if}}\;j \in {\text{PTFE}}\;{\text{phase}}\; \hbox{``}p\hbox{''}} \hfill \\ \end{array} } \right.,$$

(24)

In Eq. (24), the values of $\Delta \gamma_{\text{s}}$ and $\Delta \gamma_{\text{p}}$ are determined from equilibrium contact angle measurements which are presented in Sect. 7. Incompressibility of the fluids is obtained by the projection method, which was originally introduced by Cummins and Rudman (1999) and is generally referred as incompressible smoothed particle hydrodynamics. In this work, we use the time step algorithm of Hu and Adams (2007) to enforce both velocity-divergence-free and zero-density-variation conditions at each full time step. Inflow and outflow at the open domain boundaries are realized by Dirichlet boundary conditions for the projected pressure field (Kunz et al. 2016a).

The numerical approach has been validated by comparison to experiments in a flat microreactor, which allowed to visualize the displacement of a wetting by a non-wetting fluid. The comparison showed quantitative agreement of the phase distribution during the transition. Details are given by Kunz et al. (2016b).

The presented SPH models are implemented in SiPER.¹ SiPER is a free ISPH code under GNU General Public License developed at the University of Stuttgart. It is specialized on multiphase flow in complex porous media. It is an MPI parallel implementation in standard C language. The boomerAMG preconditioner from the HYPRE library with default configuration except for the number of iterations set to 5 instead of 1 and BiCGStab solver from the PETSc library (Balay et al. 2018) are used for solving the pressure Poisson equation.

5 Geometry Extraction for the SPH Simulation

In this section, the transition process from segmented voxel data to a geometry consisting of triangles adjoined to each other is presented. An overview of the individual necessary steps is shown in Fig. 8. In the following, the individual steps are briefly explained.

Fig. 8

Algorithm for the extraction of the geometry of the pore structure based on segmented voxel data. The steps in italic font are optional

5.1 Define 3D Data Arrays from Segmented Voxel Images

The original segmented voxel data of the FIB/SEM imaging are stored in a 3-dimensional array ${\mathbf{C}}$ with values $c_{jkl} = 0$ for pore space, $c_{jkl} = 1$ for silver and $c_{jkl} = 2$ for PTFE. For the geometry extraction, the original data array ${\mathbf{C}}$ is stored in two separate Boolean arrays.

Here, array ${\mathbf{A}}$ unites both solid phases, while array ${\mathbf{B}}$ considers only the PTFE phase.

5.2 Reduce to Percolating Pore Space

One mandatory condition to run a SPH simulation is the percolation of the simulation domain of the pore space. Therefore, the inverted Boolean array ${\mathbf{A}}^{*}$, with $a_{jkl}^{*} = 1 - a_{jkl}$, is defined and all connected clusters with values $a_{jkl}^{*} = 1$ are determined using the bwconncomp function from MATLAB (The Mathworks Inc. 2018). All values $a_{jkl}^{*}$ which belong to clusters which do not percolate between inlet and outlet zone are changed to zero. From the modified data, the new array ${\mathbf{D}}$, with $d_{jkl} = 1 - a_{jkl}^{*}$, is defined. Generally, multiple percolating clusters of pores can exist which connect the inlet and outlet zone. In the given example, only one percolating cluster exists, but the numerical method could also handle multiple clusters as well.

5.3 Erase Unphysical Solid Clusters in the Pore Space

The percolation of solids is a necessary property of a porous structure. Due to the cuts at the domain edges, there may be several connected clusters that contribute to the solid structure. However, small solid areas that have no connection with the domain boundary should be redefined as fluid. Therefore, connected clusters with value $d_{jkl} = 1$ are also searched for here using the bwconncomp function applied to array D. Values of the connected clusters, which have no connection to the domain boundary, are changed to zero. The updated array is stored in array E.

5.4 Erase Cavities Below Threshold Size

In array E, some narrow places and cavities, which are not possible to resolve with the final simulation, are erased in a coarsening stage of the voxel data prior to geometry extraction. Therefore, regions of the fluid phase, with thickness of one voxel ($30\,{\text{nm}}$), change the phase. This results in the final array of the pore space.

5.5 Extension of the Data Arrays by PTFE Wall in y- and z-direction and Inflow Section in x-direction

To limit the flow through the gas diffusion electrode in one direction, the segmented voxel data are extended in y- and z-direction by solid walls. The solid walls become the wetting property of PTFE to inhibit spontaneous imbibition in the pore spaces, which are connected to those artificial pore boundaries. In x-direction, the geometry is extended by ten voxels to ensure straight inflow channels at the open boundary for the SPH simulation.

5.6 Extract Geometries of Joint Solid and PTFE Phase

The pore-space geometry and the separated geometry of the PTFE phase are now extracted using MATLAB’s isosurface function (The Mathworks Inc. 2018) using standard options and an isovalue of 0.5. The result of this operation is a blocky geometry with edge length of the triangles according to the voxel sizes $l_{\text{v}}$, which is in this case $l_{\text{v}} = 30\,{\text{nm}}$.

5.7 Smoothing of the Geometries to Avoid Blocky Appearance

The extracted geometry has a blocky appearance according to the regular grid structure of the voxel data. The vertices of the triangulated surfaces are displaced in the direction normal to the surface, up to a limit of half the voxel size $l_{\text{v}}$ to keep the information of the geometry (Lalancette 2018).

5.8 Mesh Resampling to Reduce Number of Faces in Geometry

A possible simplification of the preprocessing step is the reduction of the number of faces, which define the full solid geometry as well as the PTFE sectors (Fang 2018). A reduction of the number of faces is helpful for a faster preprocessing since the performance of the ray tracing algorithm when placing the SPH particles in the geometry is linearly dependent on the total number of faces. In the presented study, a down sampling of the surface mesh is performed with the objective to reduce the number of faces by a factor of two.

6 Preprocessing of SPH Flow Simulations

To allocate SPH particles representing silver, PTFE, and fluid phase in the system, the user must specify the initial particle distance $l_{0}$. Then, a set of parallel straight lines are generated which run through the geometry with spacing $l_{0}$. Along these straight lines, particles are placed with spacing $l_{0}$. The intersection points of those straight lines with the faces are determined using the ray/triangle intersection MATLAB function by Tuszynski (2018). The SPH particles are then created on the rays with spacing $l_{0}$. SPH particles that are positioned in between of two intersection points are defined as solid particles, whereas all other particles become fluid particles. A sketch of this procedure is shown in Fig. 9. The same procedure is repeated with the PTFE geometry. Here, solid particles are defined as PTFE when they are placed inside the PTFE geometry.

Fig. 9

Allocation of the particles on a Cartesian grid. The top figure shows an excerpt of the overall structure. A set of parallel rays (blue lines) are arranged on a regular Cartesian grid with spacing $l_{0}$ is created which intersect with the faces of the solid geometry. In the bottom, SPH particles are defined on the rays with spacing $l_{0}$. The particles that lie between two faces that represent the solid become solid particles (black). All other particles are defined as fluid particles

7 Physical Properties

Most crucial for predictions of the electrolyte intrusion are precise knowledge of the wetting properties on the surfaces. Therefore, the contact angles of the electrolyte phase have been determined experimentally, using $32\,{\text{w}}\%$ sodium hydroxide solution (liquid electrolyte), silver, and PTFE, respectively. For the measurements of the equilibrium contact angles, the sessile drop method has been applied using the optical contact angle measuring system OCA 15EC of DataPhysics Instruments GmbH. The electrolyte is slightly wetting on silver with $\theta_{{{\text{E}},{\text{s}}}} = 80^{ \circ }$ and non-wetting on PTFE with $\theta_{{{\text{E}},{\text{p}}}} = 120^{ \circ }$. The surface tension between 32 w% sodium hydroxide solution and air was determined with the same system with a pendant drop as $\gamma_{\text{eg}} = 0.109 {\text{Nm}}^{ - 1}$, which is significantly higher than the one of pure water. From the values of the equilibrium contact angles, now $\Delta \gamma_{\text{s}} = 0.0189\,{\text{Nm}}^{ - 1}$ and $\Delta \gamma_{\text{p}} = - 0.0545\,{\text{Nm}}^{ - 1}$ can be derived from Eq. (5). In order to archive more robust and faster numerical calculations, some parameters have been modified. The density and viscosity of the electrolyte and the gas phase are chosen to be equal with $\rho = 1000\,{\text{kg}}\,{\text{m}}^{ - 3}$ and $\mu = 10^{ - 3} \,{\text{Pa}}\,{\text{s}}$. With the choice of equal fluid properties, spurious currents, a numerical artifact at the fluid–fluid interface, are reduced, and therefore, the simulation algorithm is more robust. Also, the actual viscosity of $32\,{\text{w}}\%$ sodium hydroxide is 19 times higher than pure water at room temperature (Merck KGaA 2019). The choice of a lower viscosity reduced the computational time of the intrusion process significantly from weeks to days in the chosen geometry. Those adjustments of fluid properties increase the absolute dynamics of the electrolyte intrusion process in the simulation. Since the viscosity ratio $\mu_{\text{e}} /\mu_{\text{g}}$ in the presented simulations is 1 instead of more than 1000, the effect of viscous fingering is stronger in simulation than in the real application. Nevertheless, the adjusted fluid properties have no effect on the accessibility of the individual pores, since this is only affected by the wetting properties.

8 Results and Discussion

From the segmented voxel images, a reduced domain with edge length of $6 \times 6 \times 6\,\upmu{\text{m}}^{3}$ is taken. The porosity of the chosen segment is $\epsilon_{\text{pore}} = 0.373$. As first case, single-phase flow of water is studied in the chosen domain (Configuration 1 in Table 1). The viscosity and density of water are $\rho = 1000\,{\text{kg}}\,{\text{m}}^{ - 3}$ and $\mu = 10^{ - 3} \,{\text{Pa}}\,{\text{s}}$, respectively. The flow is induced by an externally applied pressure difference of $\Delta p_{\text{ex}} = 100\,{\text{kPa}}$, where the pressure at the outlet (top) is set as $p_{{{\text{x}}\_{ \hbox{max} }}} = 10\,{\text{kPa}}$. In Fig. 10, the velocity and pressure fields are shown in steady state conditions. With the average flow velocity in x-direction of $\bar{v}_{x} = 0.197\,{\text{ms}}^{ - 1}$, the permeability of the domain can be computed as $k = \bar{v}_{x} \epsilon_{\text{pore}} \mu \Delta x\left( {\Delta p} \right)^{ - 1} = 4.85 \times 10^{ - 14} \,{\text{m}}^{2}$, where $\Delta x = 6.6\,\upmu{\text{m}}$ including the inlet/outlet section.

Table 1 Overview on specifications of all simulation runs

Fig. 10

Single-phase flow simulation of water through the domain. The flow is induced by an impressed external pressure difference of $\Delta p_{\text{ex}} = 100\,{\text{kPa}}$, where the pressure at the outlet (top) is set as $p_{{{\text{x}}\_{ \hbox{max} }}} = 10\,{\text{kPa}}$. In a, the resulting flow field is shown whereas in b the corresponding pressure field in the fluid is plotted. For the visualization of the simulation results, Paraview (Avila and Ayachit 2015) was used

In a second configuration, the electrolyte intrusion is simulated. Cases with different external pressure differences were studied. External pressure differences were chosen as 0, 50, 100 and 500 kPa (Configurations 2.1–2.4 in Table 1). Here, the case of $\Delta p_{\text{ex}} = 0\,{\text{kPa}}$ corresponds to a spontaneous imbibition process of the electrolyte.

Snapshots of the phase composition during the forced intrusion process of the electrolyte for the case of $\Delta p_{\text{ex}} = 500\,{\text{kPa}}$ are shown in Fig. 11. The electrolyte is shown in blue, the gas phase in red, and the PTFE geometry in green. The full solid geometry is shown in light gray. Initially, $0.9\,\upmu{\text{m}}$ of the domain is filled with electrolyte. From the time recordings in Fig. 11, it can be observed that primarily the large pores are filled with electrolyte when the process is mainly driven by the external pressure difference. After $3.5\,\upmu{\text{s}}$, the electrolyte has reached the opposite domain boundary. The main reason for this observation is that the entry pressure in the smaller pores is higher compared with the larger pores, and therefore, small pores are blocked due to the all in all non-wetting property of the silver–PTFE pore surfaces.

Fig. 11

Snapshots of the phase composition during the intrusion process for the case of $\Delta p_{\text{ex}} = 500\,{\text{kPA}}$. The electrolyte is shown in blue, the gas phase in red, and the PTFE geometry in green. The full solid geometry is shown in light gray. Initially a, $0.9\,\upmu{\text{m}}$ of the domain is filled with electrolyte. During the forced intrusion process (b, t = 1 μs, c, t = 2 μs and d, t = 3 μs) mainly the large pores are filled. At $t = 3\,\upmu{\text{s}}$d, the electrolyte in one pore has almost reached the opposite domain boundary

A great advantage of this type of simulation is the possibility to evaluate the individual interfaces between the phases and thus also to determine the total areas of the individual interfaces. With this information, the total Helmholtz free energy F for the considered system can be calculated by

$$F\left( t \right) = A_{\text{eg}} \left( t \right)\gamma_{\text{eg}} + A_{\text{es}} \left( t \right)\left( {\gamma_{\text{es}} - \gamma_{\text{gs}} } \right) + A_{\text{ep}} \left( t \right)\left( {\gamma_{\text{ep}} - \gamma_{\text{gp}} } \right),$$

(25)

where the total interfacial area between electrolyte and gas phase $A_{\text{eg}}$ can be calculated by

$$A_{\text{eg}} = V_{0} \mathop \sum \limits_{i}^{{N_{\text{tot}} }} \left| {{\mathbf{n}}_{{{\text{eg}},i}} } \right|,$$

(26)

In Eq. (26), $V_{0}$ is the volume represented by one SPH particle. All other interfacial areas can be calculated with the same approach. In the case of a spontaneous process, that is without external pressure difference, the configuration of the system changes in such a way that the free Helmholtz energy must be minimized.

In Fig. 12, the visualization of the electrolyte–gas, electrolyte–silver, and electrolyte–PTFE interfaces is shown for the forced intrusion process with $\Delta p_{\text{ex}} = 100\,{\text{kPa}}$ after $t = 2.5\,\upmu{\text{s}}$. The temporal evolution of the calculated area of the different interfaces and the Helmholtz free energy calculated from Eq. (25) are shown in Fig. 13. In the same way than computing the surface areas, the contact line length $L_{\text{CL}}$ between electrolyte, gas, and solid can be computed by

$$L_{\text{CL}} = V_{0} \mathop \sum \limits_{i}^{{N_{\text{tot}} }} \delta_{{{\text{egw}},i}} ,$$

(27)

where $\delta_{{{\text{egw}},i}}$ is calculated from Eq. (18). In Fig. 13, the temporal evolution of the contact line length and the saturation of the electrolyte in the pore space is shown.

Fig. 12

Visualization of the various interfaces is shown for the imbibition process with $\Delta p_{\text{ex}} = 100\,{\text{kPa}}$ after $t = 2.5\,\upmu{\text{s}}$. a Phase composition with electrolyte (blue) and gas phase (red). The PTFE geometry is shown in green and the full solid geometry transparent in light gray. Visualization of b$\left| {{\mathbf{n}}_{{{\text{eg}},i}} } \right|$, c$\left| {{\mathbf{n}}_{{{\text{es}},i}} } \right|$, and d$\left| {{\mathbf{n}}_{{{\text{ep}},i}} } \right|$ from which the total interfacial area can be calculated by Eq. (26)

Fig. 13

The temporal evolution of the calculated area of the electrolyte–gas interface (top left), electrolyte–silver interface (mid left), and electrolyte–PTFE (mid right). Additionally, the temporal evolution of the Helmholtz free energy stored in the interface (top right), the contact line length (bottom left), and the saturation of the electrolyte in the pore space (bottom right) is shown

In Fig. 13, significant difference in the temporal evolution exists for the forced intrusion with $\Delta p_{\text{ex}} = 500\,{\text{kPa}}$ and all other cases. This is because the overall non-wetting property of the pore space inhibits electrolyte intrusion for all other studied cases. For example, the increasing interface area between electrolyte and gas (top left) highlights the selective intrusion into the largest pore. Thereby additional surfaces are formed on the sides of the finger pore. The increase of interface area between electrolyte and silver (mid left) is a measure for the filling of the pore space and is very similar to the evolution of the electrolyte saturation (bottom right).

The temporal evolution of the areas of the interfaces gives an insight into the changing imbibition characteristic when going from spontaneous imbibition with $\Delta p_{\text{ex}} = 0\,{\text{kPa}}$ to an intrusion driven mainly by the external pressure difference. The most obvious point is the different behavior in the Helmholtz free energy between the case of $\Delta p_{\text{ex}} = 100\,{\text{kPa}}$ and $\Delta p_{\text{ex}} = 500\,{\text{kPa}}$. In the latter case, the Helmholtz free energy is mostly increasing as resulting from fast increasing electrolyte–gas and electrolyte–PTFE interfacial areas. In the case with reduced external pressure, an energetic more favorable flow path is chosen by the electrolyte resulting in reduced areas of the two interfaces. The difference in wetting of electrolyte on silver and PTFE can also be seen in the temporal change of the interfaces. While the wetted silver surface increase in all cases considered in the SPH simulations, an increase in the wetted PTFE surface only occurs above an external pressure difference of $\Delta p_{\text{ex}} = 100\,{\text{kPa}}$.

In a further case study, the effect of the addition of non-wetting PTFE is studied. Therefore, all PTFE in the system is assumed to have the same wetting behavior as silver (configuration 3 in Table 1). Then, the spontaneous electrolyte imbibition ($\Delta p_{\text{ex}} = 0\,{\text{kPa}}$) in this system is simulated. In Fig. 14, the temporal evolution of the electrolyte saturation and the Helmholtz free energy is shown for the modified case with a pure silver structure and the case already presented in Fig. 13 with the original PTFE content.

Fig. 14

Temporal evolution of the Helmholtz free energy (left) and the electrolyte saturation (right) for the modified case with a pure silver structure and the case already presented in Fig. 13 with the original PTFE content

9 Conclusion

We have developed a complete workflow from FIB/SEM imaging to SPH simulations of the imbibition process of electrolyte solution into the porous structure of a technical gas diffusion electrode. With the presented workflow, predictions on the final electrolyte distribution in the porous structure are possible. The SPH simulations are a useful tool for assessing the influence of the addition of PTFE during the manufacturing process of the technical gas diffusion electrodes. The presented procedure can be used in future developments to predict an optimal design of the gas diffusion electrode with the conflicting priorities of a maximum reactive three-phase boundary and shortest possible transport routes of the formed hydroxide out of the porous structure.