The Uniqueness of a Correction to Interaction Parameter Formalism in a Thermodynamically Consistent Manner

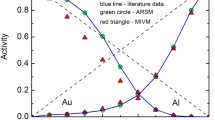
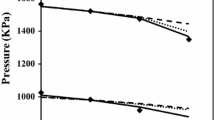
Abstract

Polynomial representation of partial excess Gibbs energy (i.e., activity coefficient) in multicomponent dilute solution has been widely used after Wagner. Although Wagner’s Interaction Parameter Formalism has been known to be only strictly valid at infinite dilute concentration, it has been used often, even at finite concentration, due to its mathematical simplicity. Nevertheless, several attempts have been made to correct the formalism to be thermodynamically consistent at finite concentration. Among those, Unified Interaction Parameter Formalism proposed by Pelton and Bale, which may be considered as an extension of Darken’s quadratic formalism, has obtained much attention. However, there have been much confusion and debate about the way of the correction. Recently, a thermodynamic analysis was reported that there are infinite numbers of ways to correct Wagner’s formalism to be thermodynamically consistent, which may prevent one from using the Unified Interaction Parameter Formalism with confidence. In the present article, the correction to the Wagner’s formalism is discussed by revisiting Darken’s condition of the thermodynamic consistency. It is shown that the correction to the Wagner’s formalism can be made uniquely. It is pointed out that to ensure the thermodynamic consistency among the activity coefficients of all components, Gibbs–Duhem relation and Maxwell relation among all components including solvent–solute, must be obeyed. Derived expressions for activity coefficients of all components by path-independent integration are also shown to be the same as those obtained by differentiating a corresponding integral excess partial Gibbs energy.

Appendices

Appendices

Appendix A

Extension of Darken’s Thermodynamic Consistency into Multicomponent Solution including Solvent

As Gibbs energy, G, is a state function, and its differential is exact, the Maxwell’s relation is obeyed:

$$\begin{aligned} \frac{\partial }{\partial n_i}\left( \frac{\partial G}{\partial n_j}\right) = \frac{\partial }{\partial n_j}\left( \frac{\partial G}{\partial n_i}\right) \end{aligned}$$

(A1)

where $n_i$, $n_j$ are the number of moles of components i and j, and

$$\begin{aligned} G = \sum _{i=1}^N n_ig_i^\circ + {{\text R}}T\left( \sum _{i=1}^N n_i\ln X_i + \sum _{i=1}^N n_i\ln \gamma _i\right) \end{aligned}$$

(A2)

and

$$\begin{aligned} X_i = \frac{n_i}{\sum _{j=1}^N n_j} = \frac{n_i}{n} \qquad \text {where } n=\sum _{j=1}^N n_j \qquad (i = 1, 2, \ldots , N) \end{aligned}$$

(A3)

By differentiating G with respect to $n_j$, while all other $n_i(i \ne j)$ are kept constant,

$$\begin{aligned} \frac{\partial G}{\partial n_j} = g_j^\circ + {\text R}T\left( \ln X_j + \ln \gamma _j + \sum _{k=1}^N n_k\frac{\partial \ln \gamma _k}{\partial n_j}\right) \end{aligned}$$

(A4)

The last term in the Eq. [A4] is zero due to the Gibbs–Duhem relation. From the above,

$$\begin{aligned} \frac{\partial }{\partial n_i}\left( \frac{\partial G}{\partial n_j}\right) = {\text R}T\left( \frac{\partial \ln \gamma _j}{\partial n_i} - \frac{1}{n}\right) \end{aligned}$$

(A5)

Similarly,

$$\begin{aligned} \frac{\partial }{\partial n_j}\left( \frac{\partial G}{\partial n_i}\right) = {\text R}T\left( \frac{\partial \ln \gamma _i}{\partial n_j} - \frac{1}{n}\right) \end{aligned}$$

(A6)

Therefore, the following relationship between activity coefficients of components i and j are obtained:

$$\begin{aligned} \frac{\partial \ln \gamma _j}{\partial n_i} = \frac{\partial \ln \gamma _i}{\partial n_j} \end{aligned}$$

(A7)

which is the same as the Eq. [14]. Taking all $X_i$’s except for $X_1$ as independent variables, and using the following derivatives of $X_k$ with respect to $n_i$,

$$\begin{aligned} \frac{\partial X_k}{\partial n_i} = \frac{\partial (n_k/n)}{\partial n_i} = \frac{\delta _{ik}n-n_k}{n^2}= \frac{\delta _{ik}-X_k}{n} \qquad (i,k = 1, 2, \ldots , N) \end{aligned}$$

(A8)

the above equation is expressed as:

$$\begin{aligned} \frac{\partial \ln \gamma _j}{\partial n_i}= & {} \sum _{k=2}^N \frac{\partial \ln \gamma _j}{\partial X_k} \left( \frac{\partial X_k}{\partial n_i}\right) \nonumber \\= & {} \sum _{k=2}^N \frac{\partial \ln \gamma _j}{\partial X_k} \left( \frac{\delta _{ik}-X_k}{n}\right) \end{aligned}$$

(A9)

Similarly,

$$\begin{aligned} \frac{\partial \ln \gamma _i}{\partial n_j} = \sum _{k=2}^N \frac{\partial \ln \gamma _i}{\partial X_k} \left( \frac{\delta _{jk}-X_k}{n}\right) \end{aligned}$$

(A10)

Therefore, the following equation is obtained which represents the conditions of thermodynamic consistency between two components (i and j) in N-component system, including solvent ($i=1$ or $j=1$) and solute ($i,j\ne 1$):

$$\begin{aligned} \sum _{k=2}^N (\delta _{ik}-X_k)\frac{\partial \ln \gamma _j}{\partial X_k} = \sum _{k=2}^N (\delta _{jk}-X_k)\frac{\partial \ln \gamma _i}{\partial X_k} \end{aligned}$$

(A11)

Appendix B

Derivation of $\ln \gamma _1$ in Multicomponent Solution

From the Eq. [57],

$$\begin{aligned} \frac{\partial \ln \gamma _1}{\partial X_i}= & {} 2a_{ii}X_i + 2\sum _{\begin{subarray}{c} k=2 \\ k\ne i \end{subarray}}^N b_{ik}X_k + c_i \end{aligned}$$

(B1)

$$\begin{aligned} \frac{\partial \ln \gamma _1}{\partial X_j}= & {} 2a_{jj}X_i + 2\sum _{\begin{subarray}{c} k=2 \\ k\ne j \end{subarray}}^N b_{jk}X_k + c_j \end{aligned}$$

(B2)

Then,

$$\begin{aligned}&\frac{\partial \ln \gamma _1}{\partial X_i} - \frac{\partial \ln \gamma _1}{\partial X_j} \nonumber \\&\quad = (2a_{ii}-2b_{ji})X_i + (2b_{ij}-2a_{jj})X_j + \sum _{\begin{subarray}{c} k=2 \\ k\ne i,j \end{subarray}} 2b_{ik}X_k \nonumber \\&\quad - \sum _{\begin{subarray}{c} k=2 \\ k\ne i,j \end{subarray}} 2b_{jk}X_k + c_i - c_j \end{aligned}$$

(B3)

$$\begin{aligned}&= \sum _{\begin{subarray}{c} k=2 \\ k\ne i,j \end{subarray}} (2b_{ik}-2b_{jk})X_k + (2a_{ii}-2b_{ji})X_i + (2b_{ij}-2a_{jj})X_j \nonumber \\&\quad + c_i - c_j \end{aligned}$$

(B4)

Therefore by comparison with the Eq. [56],

$$\begin{aligned} 2a_{ii} - 2b_{ji}= & {} \epsilon _{ji} - \epsilon _{ii} \end{aligned}$$

(B5)

$$\begin{aligned} 2b_{ij} - 2a_{jj}= & {} \epsilon _{jj} - \epsilon _{ij} \end{aligned}$$

(B6)

$$\begin{aligned} 2b_{ik} - 2b_{jk}= & {} \epsilon _{jk} - \epsilon _{ik} \end{aligned}$$

(B7)

$$\begin{aligned} c_i - c_j= & {} 0 \end{aligned}$$

(B8)

According to Raoult’s law ($\frac{\partial \ln \gamma _1}{\partial X_i} \rightarrow 0$ when $X_i,X_j \rightarrow 0$), it can be shown that $c_i = c_j = 0$. Furthermore, by inspection, $a_{ii}=-\frac{1}{2}\epsilon _{ii}$, $a_{jj}=-\frac{1}{2}\epsilon _{jj}$, $b_{ij} = b_{ji} = -\frac{1}{2}\epsilon _{ij}$, etc. Therefore,

$$\begin{aligned} \ln \gamma _1= & {} -\frac{1}{2}\sum _{k=2}^N \epsilon _{kk} X_k^2 - \frac{1}{2} \sum _{\begin{subarray}{c} k,l=2 \\ k \ne l \end{subarray}}^N\epsilon _{kl}X_kX_l \end{aligned}$$

(B9)

$$\begin{aligned}= & {} -\frac{1}{2}\sum _{j,k=2}^N \epsilon _{jk} X_jX_k \end{aligned}$$

(B10)