Skip to main content
SpringerLink
Log in

A sixth order optimal B-spline collocation method for solving Bratu’s problem

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

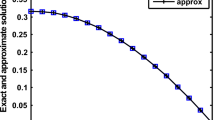
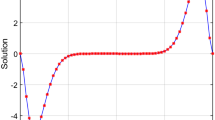
In this paper, we describe an optimal B-spline collocation method to solve one-dimensional non-linear Bratu problem. Convergence result of the method is established through Green’s function technique and it is proved that the method has sixth order convergence. The applicability and accuracy of the method are demonstrated through two numerical examples. It is shown that the computational result is consistent with theoretical prediction. Moreover, the numerical results obtained by the present method are compared with those obtained by two other B-spline collocation approaches reported in the literature. The computed results reveal that our method is accurate and easy to implement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. H. Caglar, N. Caglar, M. Ozer, A. Valarstos, A.N. Anagnostopoulos, B-spline method for solving Bratu’s problem. Int. J. Comput. Math. 87, 1885–1891 (2010)

    Article  Google Scholar 

  2. P. Roul, K. Thula, A fourth order B-spline collocation method and its error analysis for Bratu-type and Lane–Emden problems. Int. J. Comput. Math. 96, 85–104 (2019)

    Article  Google Scholar 

  3. D.A. Frank-Kamenetskii, Diffusion and Heat Exchange in Chemical Kinetics (Princeton University Press, Princeton, NJ, 1955)

    Book  Google Scholar 

  4. Y.Q. Wan, Q. Guo, N. Pan, Thermo-electro-hydro dynamic model for electro spinning process. Int. J. Nonlinear Sci. Numer. Simul. 5, 5–8 (2004)

    Google Scholar 

  5. N. Das, R. Singh, A.M. Wazwaz, J. Kumar, An algorithm based on the variational iteration technique for the Bratu-type and the Lane–Emden problems. J. Math. Chem. 54, 527–551 (2016)

    Article  CAS  Google Scholar 

  6. J.H. He, H.Y. Kong, R.X. Chen, M.S. Hu, Q.L. Chen, Variational iteration method for Bratu-like equation arising in electrospinning. Carbohydr. Polym. 105, 229–230 (2014)

    Article  CAS  Google Scholar 

  7. S. Chandrasekhar, Introduction to the Study of Stellar Structure (Dover, New York, 1967)

    Google Scholar 

  8. S. Li, S.J. Liao, An analytic approach to solve multiple solutions of a strongly nonlinear problem. Appl. Math. Comput. 169, 854–865 (2005)

    Google Scholar 

  9. A.M. Wazwaz, Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput. 166, 652–663 (2005)

    Google Scholar 

  10. J.H. He, Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 167, 57–68 (1998)

    Article  Google Scholar 

  11. J.H. He, Variational iteration method-A kind of non-linear analytical technique: some examples. Int. J. Nonlinear Mech. 34, 699–708 (1999)

    Article  Google Scholar 

  12. J.H. He, Some asymptotic methods for strongly non linear equations. Int. J. Mod. Phys. B 20, 1141–1199 (2006)

    Article  Google Scholar 

  13. J.H. He, Variational iteration method-some recent results and new interpretations. J. Comput. Appl. Math. 207, 3–17 (2007)

    Article  Google Scholar 

  14. J.H. He, An elementary introduction to recently developed asymptotic methods and nanomechanics in textile engineering. Int. J. Mod. Phys. B 22, 3487–3578 (2008)

    Article  Google Scholar 

  15. J.H. He, Asymptotic methods for solitary solutions and compactons. Abstr. Appl. Anal. Article ID 916793 (2012)

  16. J.H. He, X.H. Wu, Variational iteration method: new development and applications. Comput. Math. Appl. 54, 881–894 (2007)

    Article  Google Scholar 

  17. P. Roul, Numerical solutions of time fractional degenerate parabolic equations by variational iteration method with Jumarie-modified Riemann–Liouville derivative. Math. Methods Appl. Sci. 34, 1025–1035 (2011)

    Article  Google Scholar 

  18. P. Roul, H. Madduri, An optimal iterative algorithm for solving Bratu-type problems. J. Math. Chem. 57, 583–598 (2018)

    Article  Google Scholar 

  19. P. Roul, K. Thula, V.M.K.P. Goura, An optimal sixth-order quartic B-spline collocation method for solving Bratu-type and Lane–Emden type problems. Math. Methods Appl. Sci. 42, 2613–2630 (2019)

    Article  Google Scholar 

  20. P. Roul, V.M.K. Prasad Goura, B-spline collocation methods and their convergence for a class of nonlinear derivative dependent singular boundary value problems. Appl. Math. Comput. 341, 428–450 (2019)

    Google Scholar 

  21. K. Thula, P. Roul, A high-order B-spline collocation method for solving nonlinear singular boundary value problems arising in engineering and applied science. Mediterr. J. Math. 15, 176 (2018)

    Article  Google Scholar 

  22. P. Roul, K. Thula, A new high-order numerical method for solving singular two-point boundary value problems. J. Comput. Appl. Math. 343, 1–18 (2018)

    Article  Google Scholar 

  23. M.K. Kadalbajoo, P. Arora, B-spline collocation method for the singular-perturbation problem using artificial viscosity. Comput. Math. Appl. 57, 650–663 (2009)

    Article  Google Scholar 

  24. R.C. Mittal, R. Rohila, A fourth order cubic B-spline collocation method for the numerical study of the RLW and MRLW equations. Wave Motion 80, 47–68 (2018)

    Article  Google Scholar 

  25. P. Roul, A high accuracy numerical method and its convergence for time-fractional Black–Scholes equation governing European options. Appl. Numer. Math. (2019). https://doi.org/10.1016/j.apnum.2019.11.004

    Article  Google Scholar 

  26. P. Roul, V.M.K. Prasad Goura, R. Agarwal, A new high order numerical approach for a class of nonlinear derivative dependent singular boundary value problems. Appl. Numer. Math. 145, 315–341 (2019)

    Article  Google Scholar 

  27. P. Roul, V.M.K. Prasad Goura, A high order numerical method and its convergence for time-fractional fourth order partial differential equations. Appl. Math. Comput. 366, 124727 (2020)

    Google Scholar 

  28. C. De Boor, A Practical Guide to Splines (Springer, New York, 1978)

    Book  Google Scholar 

  29. D.J. Fyfe, Linear dependence relations connecting equal interval Nth degree splines and their derivatives. J. Inst. Math. Appl. 7, 398–406 (1971)

    Article  Google Scholar 

  30. T.R. Lucas, Error bound for interpolating cubic spline under various end conditions. SIAM. J. Numer. Anal. 3, 569–584 (1974)

    Article  Google Scholar 

  31. W.D. Hoskins, D.S. Meek, Linear dependence relations for polynomial splines at midknots. BIT 15, 272–276 (1975)

    Article  Google Scholar 

  32. R.D. Russell, L.F. Shampine, A collocation method for boundary value problems. Numer. Math. 19, 1–28 (1971)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to anonymous referees for their valuable suggestions and comments and thankfully acknowledge the financial support provided by the CSIR, India in the form of Project No. \(25(0286)/18/EMR-II\).

Author information

Authors and Affiliations

  1. Department of Mathematics, Visvesvaraya National Institute of Technology, Nagpur, 440010, India

    Pradip Roul & V. M. K. Prasad Goura

Authors
  1. Pradip Roul
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. M. K. Prasad Goura
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pradip Roul.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The elements of the coefficient matrix P are given as follows:

$$\begin{aligned} \begin{aligned} l_{1}&=717+36I_{0},\;\;l_{2}=1448+936I_{0},\;\;l_{3}=-4300+2376I_{0},\\ l_{4}&=1322+936I_{0},\;\;\\ l_{5}&=938+36I_{0},\;\;k_{1}=1475+18J_{1},\;\;k_{2}=30149+4266J_{1},\\ k_{3}&=-31918+30276J_{1},\;\;\\ k_{4}&=-30322+30276J_{1},\;\;k_{5}=27776+4266J_{1},\;\;k_{6}=3680+18J_{1},\\ q_{1}&=725+36I_{1},\;\;\\ q_{2}&=1454+936I_{1},\;\;q_{3}=-4396+2376I_{1},\;\;q_{4}=1574+936I_{1},\\ q_{5}&=602+36I_{1},\;\;\\ p_{i}&=728+36I_{i+1},\;\;s_{i}=1406+936I_{i+1},\;\;t_{i}=-4270+2376I_{i+1},\\ u_{i}&=1406+936I_{i+1},\;\;\\ v_{i}&=728+36I_{i+1},\;\;1\le i \le n-3,\;\;{\tilde{q}}_{1}=602+36I_{n-1},\\ {\tilde{q}}_{2}&=1574+936I_{n-1},\;\;\\ {\tilde{q}}_{3}&=-4396+2376I_{n-1},\;\;{\tilde{q}}_{4}=1454+936I_{n-1},\\ {\tilde{q}}_{5}&=725+36I_{n-1},\;\;{\tilde{k}}_{1}=3680+18J_{n},\;\;\\ {\tilde{k}}_{2}&=27776+4266J_{n},\;\;{\tilde{k}}_{3}=-30322+30276J_{n},\;\; {\tilde{k}}_{4}=-31918+30276J_{n},\;\;\\ {\tilde{k}}_{5}&=30149+4266J_{n},\;\;{\tilde{k}}_{6}=1475+18J_{n},\;\; {\tilde{l}}_{1}=938+36I_{n},\\ {\tilde{l}}_{2}&=1322+936I_{n},\;\;\\ {\tilde{l}}_{3}&=-4300+2376I_{n},\;\;{\tilde{l}}_{4}=1448+936I_{n},\;\; {\tilde{l}}_{5}=717+36I_{n},\;\;I_{i}=h^{2}{G}_{i},\\ 0&\le i \le n, J_{i}=h^{2}{G}(\tau _{i}),i=1,n. \end{aligned} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roul, P., Goura, V.M.K.P. A sixth order optimal B-spline collocation method for solving Bratu’s problem. J Math Chem 58, 967–988 (2020). https://doi.org/10.1007/s10910-020-01105-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-020-01105-6

Keywords

Search

Navigation