Soft and hard computation methods for estimation of the effective thermal conductivity of sands

Abstract

Thermal properties of sand are of importance in numerous engineering and scientific applications ranging from energy storage and transportation infrastructures to underground construction. All these applications require knowledge of the effective thermal parameters for proper operation. The traditional approaches for determination of the effective thermal property, such as the thermal conductivity are based on very costly, tedious and time-consuming experiments. The recent developments in computer science have allowed the use of soft and hard computational methods to compute the effective thermal conductivity (ETC). Here, two computation methods are presented based on soft and hard computing approaches, namely, the deep neural network (DNN) and the thermal lattice element method (TLEM), respectively, to compute the ETC of sands with varying porosity and moisture content values. The developed models are verified and validated with a small data set reported in the literature. The computation results are compared with the experiments, and the numerical results are found to be within reasonable error bounds. The deep learning method offers fast and robust implementation and computation, even with a small data set due to its superior backpropagation algorithm. However, the TLEM based on micro and meso physical laws outperforms it at accuracy.

1 Introduction

Thermal properties of sand, especially, the Effective Thermal Conductivity (ETC), is of importance in many engineering and scientific applications and investigations [1,2,3]. The ETC of sand is influenced by the environmental factors: water content, density, temperature, etc. the compositional elements: mineralogical composition, particle size, shape, gradation, inter-particle physical contact, etc. and the miscellaneous factors: properties of soil components, ions, salts, additives, and hysteresis effect, etc. [4,5,6]. The dominant factors controlling the changes are the environmental factors, such as the water content and porosity of the sand [7]. The effective parameter is either measured or computed following many different techniques available [8]. The measurement techniques are broadly classified into transient and steady-state method based on heat flow around a cylindrical heat source and the one-dimensional heat flow in the soil mass. Many different methods such as the guarded hot plate apparatus, pulse power technique, transient plane source method, parallel thermal conductance method, laser flash method and 3ω method are reported in the literature [9]. In the recent past, the ETC value determination has shifted from experimental to more computationally intensive. The shift in the approach finds its roots in groundbreaking discoveries in computer sciences and a cheaper hardware cost. Two distinct approaches based on the probabilistic and deterministic mathematical background has surfaced to compute the effective parameter. The soft computation finds its root in the recent breakthrough in Machine Learning (ML) and has converted the computer to an intelligent machine.

Intelligent machines have started developing as soon as computing power became significant and started by hardcoding rules enabling the device to perceive the environment and act based on control set instruction [10]. The ultimate purpose of Artificial Intelligence (AI) is to develop the Artificial General Intelligence (AGI) which surpasses human intelligence and hopefully be utilised to solve complex unheard problems with ease. However, at present, machine learning algorithms utilise linear regression, polynomial regression, K-Means clustering, classification, etc. for scenario forecasting and optimisation. In most of the neural networks, a single hidden layer is placed between the input and the output layer. The limitation of these methods is that they can only predict the scenarios for which they are trained [11]. Another approach to developing the neural network is to put two or more hidden layers generating a deep web or intricately connected layers. The term deep neural network (DNN) or deep learning (DL) finds the term from the multiple hidden layers. The profoundly relevant layers resemble the fundamental structure of the human brain. Each hidden layer is composed of many sets of nodes, also called the neurons. These neurons are connected to the neighbouring neurons. In a layer, as many neurons are placed as required. However, as a rule of thumb, which is not based on any scientific hypothesis or mathematical fundamental, an even number of neurons are added to an odd number of layers [12]. The deep neural network has shown superior prediction and optimisation ability with a small training data set [13]. The mostly employed neuron model is built on McCulloch and Pitts’s work [14], in which, the neuron comprises of two segments, including the net function and the activation function. During the training process, these connections are developed and strengthened. The neural network based on Multilayer Perceptron (MLP) has been applied in many engineering applications to study the thermal conductivity of Nanofluids, and a comprehensive review is given by Bahiraei et al. [15]. In another study, Zendehboudi et al. [16] compiled and compared different neural network applied to estimate the thermal conductivity of Nanofluids. However, very few studies have been undertaken for determining the effective thermal conductivity of granular solids [12, 17]. Go et al. have presented a mathematical model with two fitting parameters that can be calculated from the Artificial neural network (ANN) model. [18]

The hard computational methods are populated with theoretical, empirical, semi-empirical and numerical models. Theoretical models based on a cubic cell [19] and cylindrical cells [20, 21] are proposed and applied to predict the effective thermal conductivity of loose and cemented granular media with varying porosity and saturation degree. The empirical models are developed generally for a specific material type with specified boundary conditions and thus are limited. The empirical models which are widely used for geological and geotechnical engineering applications are from Johansen [22], Cote and Konrad [23], Lu et al. [24] and Chen [25]. The semi-empirical models offer a fast computation for the material and boundary conditions for which they are developed, such as Ballard and Arp [26] and Tarnawski et al. [27]. The most versatile computational method is the numerical method. Numerical methods are categorised as continuum-based methods, where the governing equations are formulated for the whole domain and later discretised with different meshing techniques. The variables are computed for each element. The predominantly used continuum-based methods are the Finite Element Method (FEM) [28] and the Boundary Element Method (BEM) [29]. The other approach to model the heat transfer in granular media is the Distinct Element Method (DEM) approach [30, 31]. Discontinuum-based modelling provides a better estimation of the ETC and particle level heat transfer characteristics [32]. However, the DEM method requires immense computational resources and has been unable to generate the representative model due to circular particle shape and packing algorithms. Hybrid approaches, which are developed with keeping the advantages of the continuum and discrete methods, offer a fast and robust solution for heat transport modelling and the ETC computation problem. Feng. et al. [33] proposed a DEM-BEM hybrid approach in which the contact area was computed based on mathematical abstract lacking any physical parameter. Also, the model was only implemented for the 2D scenario and required significant computational resources. In another hybrid approach, the checkerboard analogy [34] and the analytical homogenization based on Mori-Tanaka scheme [35] was applied to compute the effective thermal conductivity of two-phase and three-phase granular media, respectively. All these studies suggest the importance of inclusion of the microstructure and the distribution of pore spaces in the granular system. An alternative hybrid approach to model the heat transfer in a fast and realistic manner is the Lattice Element Method (LEM) [4, 36]. The domain is discretised with randomly generated seed points which are then partitioned into Voronoi cell to find the neighbouring seed points. Centres of the neighbouring cells are then connected following the Delaunay triangulation scheme. A mesh thus generated is termed as Poisson Random Lattice (PRL) [37]. The triangulated mesh is considered as the heat transport pathway. The pipe-network method has been used to model transient heat transfer in granular media. However, the model implements the contact conductance in an ad-hoc manner [38]. Here, we define the solid and fluid contact conductance by Hertz contact model considering the rough contact, fluid theory and gas theory to consider the effect of water and air in unsaturated soil [7, 39]. A detailed description is provided in section 3.

In this paper, we propose two soft computational approaches based on Thermal Lattice Element Method (TLEM) and Deep Learning Network (DLN). The Lattice Element Method is a mesoscale modelling technique applied generally to study the crack propagation in coalescing composites [40, 41]. Here, the method is extended to model heat transfer in the granular composite. The solid contacts are modelled with the modified Hertz contact model, and the microstructure of the porous media and the fluid phase is incorporated considering the fluid and gas theories, respectively. The deep learning is employed using in-house python scripting with MLP and backpropagation algorithms. A comprehensive study is performed to optimise the neural network with several hidden layers and the number of neurons in each layer. The standard errors are computed for each case and are reported. The TLEM and DLN predict the ETC with reasonable accuracy. The paper is divided into the following sections. After a general introduction, Section 2 outlines the DLN and its implementation. In Section 3, the TLEM is explained. In Section 4, the results from the TLEM along with DLN to predict the ETC are discussed in detail. Finally, in Section 5, the conclusions of the study are summarised.

2 Soft computational with deep neural network

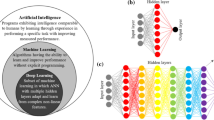
A Deep Neural Network (DNN) is a computing system composed of artificial neurons. They are made to mimic the structure of the biological brain. The most common form of deep network is the feed-forward Multilayer Perceptron (MLP). A Multilayer Perceptron is a neural network consisting of a minimum of 3 layers of neurons: the input layer, consisting of a neuron for every corresponding parameter, a hidden layer of neurons, and an output layer of neurons corresponding to the output of the neural network (Fig. 1). Neurons are connected through edges, each having a corresponding weight factor. Every neuron has a corresponding activation function. The output of the neuron is the activation function applied to the input of that neuron with the bais and the weight of the respective edge of the input. (Eq. 1).

Fig. 1

A Neural Network Structure with two inputs, porosity (n) and the degree of saturation (Sr) three hidden layers with six neurons in each layer and one output the ETC(k)

The research of neural network started as a single input layer where weights update giving out output in the output layer. The single hidden layer networks are applicable for short prediction range. But the introduction of the MLPs have changes the prediction ability and accuracy of the neural network [14]. These neural networks have hidden layers in between, and the ends are connected with the input layer and the output layer. When these hidden layers are more than one, it is called Deep Neural Network (DNN), as used in this study with different hidden layers and neurons. The feedforward MLP’s are applied as each layer acts as the input for the next layer, without loops.

As shown in Fig. 1, the neural network consists of several neurons arranged in layers, connected. As the inputs are passed on to the input layer; the neurons in subsequent layers are activated. The output of each neuron is calculated from the following formula

$$ {y}_j={\sum}_{i=0}^n{F}_i\left({w}_{ij}.{x}_i\right)+{b}_i $$

(1)

where w is the weight of the connecting edge to the neuron, x is the input of the neuron through that edge (which is the output of a neuron in the previous layer), b is the bias of the neuron, and F is activation function of the neuron. Every neuron performs this operation on the input given to that neuron. The result of the neural network is the output of the neuron in the output layer.

2.1 Neuron learning algorithm

At first, all the neurons are connected with random weights (random initialisation). The network is subsequently trained for a given set of training data. Initially, the predicted outputs are far away from the target outputs due to the random weight distribution. The weights are updated gradually to improve predictions. The process is termed as training. A loss value is calculated using the chosen loss function of the network and is the objective function of the neural network. The learning process aims to minimise this loss. While Mean Squared Error (MSE) is the most commonly used loss function, Cross-Entropy is also used for classification problems as it measures the distance between probability distributions. Backpropagation is a method used to optimise functions. All backpropagation algorithms are based on gradient descent. Gradient Descent (GD) is an iterative function optimisation algorithm. GD is used to optimise the loss function and minimise the cost function.

GD is used to minimise the cost function. There are two types of GD: Batch Gradient Descent (BGD) and Stochastic Gradient Descent (SGD). The BGD works to reduce the cost function by taking a step in the opposite direction of a cost gradient that is calculated from the whole training set. For a small data set, the method works well, but as the dataset becomes large, the computational cost rises exponentially, as the re-evaluation of the data set is necessary for each training step towards the global minimum. To circumvent this computational problem, the SGD, also called the iterative or online Gradient Descent is applied. Instead of updating the weights based on the sum of the accumulated errors overall samples, it updates the weights incrementally for each training sample. Although SGD can be considered as an approximation of GD, it typically reaches convergence much faster because of the more frequent weight updates. Since each gradient is calculated based on a single training example, the error surface is noisier than in BGD, which can also have the advantage that SGD can escape shallow local minima more readily with nonlinear cost functions. To obtain satisfying results via SGD, it is crucial to present its training data in random order. Also, the training set should be shuffled for every epoch to prevent cycles.

The standard method used by backpropagation to calculate weights is the SGD. The SGD draws out random samples of data through the network. The gradient, which is the derivative of a tensor operation, of the loss function, is calculated. This gradient is then used to update the weights. It works on the principle of finding the minimum of a function. The weights of the neurons are updated as.

$$ \mathrm{w}\left(\mathrm{t}+1\right)=\mathrm{w}\left(\mathrm{t}\right)+\upeta \frac{dL}{dw}+\upxi \left(\mathrm{t}\right) $$

(2)

where L is the loss function, η is the learning rate, and ξ(t) is the stochastic term. There are several variants of SGD that optimise the learning process by adding more parameters to the algorithm, such as momentum. These optimisers include Adagrad, RMSProp, Adam and several others.

In supervised learning, the complete dataset is divided into two sets, the training set and the testing set. The neural network is trained on the training data set, where the parameters are passed as input, and the loss is calculated from the predicted and actual outputs. The model is then validated on the testing dataset to calculate the error. The process allows for verification of the model (Fig. 2).

Fig. 2

The flowchart of the learning cycle for training the ANN

The neural network is trained over the training dataset several times called epochs. A common problem that plagues the learning process is overfitting. When a neural network is trained, after a certain number of epochs, the loss either starts to stagnate or increase. Many techniques are used to mitigate this, including adding L1, L2 regularisation, training the neural network for fewer epochs, adding dropout layers, or simply changing the hyperparameters of the neural network.

2.2 Model implementation

For designing a DNN for the prediction of the ETC, two physical input parameters which affect the ETC are chosen, namely, the porosity (n) and the degree of saturation (Sr). A single output layer predicts the ETC. The model is trained for four different sands with fifteen samples for training and five samples for validation. The samples input data had to be pre-processed before being fed into the network. Feature scaling was applied to every parameter so that the variance of the dataset is 1 and mean 0 [42].

$$ x=\frac{x-\overline{x}}{\sigma } $$

(3)

where$\overline{x}$ is the mean and σ is the standard deviation of the training data set. The backpropagation is very sensitive to data variance; hence, the input data is feature scaled to improve learning.

For the activation function, the hyperbolic tangent function (Fig. 3) is used as it improved the model and provided better results than the standard rectified linear unit function. To get a continuous-valued result, the output layer neuron has a linear activation function.

Fig. 3

The hyperbolic tangent activation function

The standard loss function used for regression problems is the Mean Square Error (MSE). It is the mean of the square of errors in prediction.

$$ MSE=\frac{1}{n}{\sum}_{i=0}^n{\left({Y}_i-\hat{Y_i}\right)}^2 $$

(4)

Also, the Mean Absolute Error (MAE) and the R² test are performed for statistical analysis.

$$ \mathrm{MAE}=\frac{1}{n}{\sum}_{i=0}^n\left|{Y}_i-\hat{Y_i}\right| $$

(5)

$$ {R}^2=1-\frac{\frac{1}{n}{\sum}_{i=0}^n{\left({Y}_i-\hat{Y_i}\right)}^2}{\sum_{i=0}^n{\left({Y}_i-{\overset{\bar{\mkern6mu} \bar{\mkern6mu} }{Y}}_i\right)}^2} $$

(6)

where Y_i is the actual measurement, ${\hat{Y}}_i$ is the predicted value, ${\overline{Y}}_i$ is the mean value of the measurement and n is the number of measurements.

For the implementation of the model, a high-level deep learning library for python named Keras is used. Keras provided a suite of activation, loss functions as well as many GD optimisation algorithms. We used Adam optimiser to improve the learning of the model. Adam is an algorithm for first-order gradient-based optimisation of stochastic objective functions [42]. The method calculates different adaptive learning rates for each parameter. It achieved the best results when running with a learning rate of 0.01, compared to RMSProp optimiser.

The neural network model has been trained for different number of epochs (Table 1). A total of four models are trained, one for each sample of sand, to predict the ETC against the degree of saturation and porosity.

3 Hard computational with thermal lattice element method

The Thermal Lattice Element Method (TLEM), which is derived from condensed matter physics, offers a solution to the complex problem of heat propagation in granular assembly [2, 4, 5]. In principle, the lattice-based models are working on atomic lattice models [36]. The TLEM model offers the best solution when the system could be represented with a discrete set of points connected with rod or beam elements of the same scale.

3.1 Generation of the granular media

The nodes are generated in a stochastic manner, and the Voronoi tessellation is used to find the nearest neighbouring points (Fig. 4). For the given set of nodes, the Voronoi tessellation of space consists of non-overlapping cells around each of the nucelli such that each cell contains the region of space closer to it than to any of the other sites. The Delaunay Triangulation (DT), the topological dual of Voronoi diagram is used to connect the neighbouring nodes to generate the lattice elements.

Fig. 4

The representation of the discrete system with a) Voronoi diagram with seed points b) Voronoi, seed points and Delaunay triangulation representing the conduction path

In 2D, the DT for a given set of nodes is a triangulation of the plane, where the nodes are the vertices of the triangles. Similarly, in three dimensions, the DT is formed by tetrahedral that are not allowed to contain any of the points inside their circumspheres [2]. The blue lines connecting the nodes are the 1D heat transfer rod called lattice elements. (Fig. 4b).

The advantageous feature of LEM is that it incorporates contact and intergranular conductance with ease. The two-body interactions are used to model many-body interactions. The critical factor in many-body interactions is that the chosen time step is such that any temperature disturbance is felt only to the neighbouring particle in one step [4, 5]. For this work, the constant contact among the elements is considered. However, a simple modification in contact laws based on fracture mechanics can also model crack initiation and propagation. Here, the TLEM [2, 4, 5] is extended to model the unsaturated loose granular media. The extension of TLEM to include the effect of stagnant interstitial fluid in TLEM is straight forward with the following assumptions. 1) All the phases are thermally stable and non-reactive. 2) The grain is nonporous. 3) the gas is insoluble in the liquid. 3) the gas phases don’t adsorb on the solid surface. 4) No jump in temperature across all interfaces. 5) the conductivity of the filler fluid is small relative to that of the grain. 6) Convection in the interstitial fluid is absent.

With the above assumptions, the heat transfer in the partially saturated media is the contribution of three mechanisms. 1) Inter and intragranular heat transfer in the grains 2) heat transfer in the fluid phase 3) heat transfer in the gas phase.

Following a similar approach as that of the dry granular media with fillers and voids, the unsaturated granular media is generated [4]. The two different schemes the segregated and the random are utilised for the narrowband grain size distributed sands and the broader dispersed grain size sands, respectively. For the random scheme, the percentage of each component is defined, and then each part is distributed in all particle size ranges randomly. In contrast to the random scheme, the segregated algorithm cluster the particle percentage based on the grain sizes. Figure 5 (a & b) give the pictorial representation of these two schemes with three different constituting particles. The random scheme holds its integrity for sands with a wide range of particles and similar distribution of pore shapes and sizes. For narrowband sand, the pore shapes and sizes are also uniform and small than the grains, thus fitting with the segregated scheme. A detail description of the algorithm is reported elsewhere. [4]

Fig. 5

Three-component granular system with particle percentage of 25% fine (blue), 15% medium (yellow) and 60% coarse (brown) particles. Two different schemes are shown with (a) Random distribution (b) Segregated distribution of the constituting particles

3.2 Phase equation of the unsaturated media

As in many particle-based methods, [30] the distribution of the temperature in a particle is the summation of all the contributions from all the contact conductions contributing to heat transfer. Considering the 0^th particle, the temperature T₀ depends on all the flux of all the particles entering and leaving (Fig. 6).

Fig. 6

The entering and leaving heat fluxes at the 0^th particle for a heterogeneous system consisting of Voronoi cells with different physical and thermal properties. The Solid Contact Conductance (SCC) with is the sum of the Boundary Contact Conductance (BCC) and the intragranular conductance. The contact boundary temperature (T_b) and the granular nodal temperatures are shown with T_x (x = 0, i,j…m)

Mathematically, for 0^th node (Fig. 6)

$$ \sum {Q}_{net}={Q}_i+{Q}_j+{Q}_m-{Q}_l-{Q}_k $$

(7)

Assuming that no heat is stored in the 0^th node,

$$ \sum {Q}_{net}=0 $$

(8)

The contribution of each flux entering and leaving could be decoupled. This contribution which accounts for the coupling effect is significantly small and thus contributes very little to the temperature field. Removing this contribution helps in two ways. 1) The system of equation is decoupled and could be solved linearly. 2) The resulting equation is represented by a simple lattice connecting the neighbouring particle nuclei. The Voronoi cells (grey), nucelli (red) and the lattice elements (black rod) are shown in Fig. 7 for a 3D representation. The conduction of heat in the 1D lattice element between nodes i and j is given by Eq. 9.

$$ {Q}_i={h}_{ij}\left({T}_i-{T}_j\right) $$

(9)

where Q_i is the entering heat flux and T_i and T_j are the nodal temperatures of the nodes i and j. The parameter h_ij is the total thermal conductance. For a fluid-saturated media, the total thermal conductance (TCC) is the sum of solid contact conductance (SCC) and Gap Fluid Conductance (GFC). For fluids with a relatively low thermal conductivity as that of constituting grains, the GFC contribution is negligible. However, GFC significantly alters the total thermal conductance at relative low contact pressure and when the GFC is of relatively high thermal conductivity. As the pore size is smaller than 6 mm and the temperature is lower than 375^oC, the effect of convection and radiation is negligible and not considered here. [2, 5]

Fig. 7

The modified the Hertz contact model between two grains. The material properties are transferred to Voronoi i and j, and the effect of external force on the grain is considered within the framework of Hertz contact theory

In this study, we use the equations developed by Yovanivich [43] for Boundary Contact Conductance (BCC) and GFC to calculate the TCC. Based on the equations, the contact conductance is assigned to the solid particle and the gap-filling fluid.

$$ {h}_{BCC}=C\tan \theta {\left(\frac{P}{H}\right)}^{0.94}\left(\frac{k_s}{\sigma}\right) $$

(10)

For a flat rough surface, the solid conductance is reported as

$$ {h}_{BCC}=0.113{\left(\frac{P}{H}\right)}^{0.94}\left(\frac{k_s}{\sigma}\right) $$

(11)

where σ = the RMS of surface roughness;k_s = particle thermal conductivity; P = applied load; H = the hardness number.

For a granular assembly with low thermal conductivity such as quartz, feldspar where phonons act as heat carriers (In case of the metals, only boundary contact conductance is sufficient as negligible resistance is offered by the vibrating electrons to heat transfer) the solid contact conductance, h_SCC is made up of two parts, the granular conductance, h_gr and the boundary contact conductance, h_BCC.

$$ {h}_{SCC}={h}_{BCC}+{h}_{gr} $$

(12)

the intragranular contact conductance is given by

$$ {h}_{gr}=\frac{K_s\left({T}_b-{T}_0\right)}{l_{b0}} $$

(13)

where h_SCC is the solid contact conductance, and h_BCC is the boundary contact conductance, and h_gr are the intragranular thermal contact conductance, T_b and T₀ are the boundaries, and nodal temperature and l_b0 is the length of the element from the periphery to 0^th node (Fig. 6).

Similarly, the gap fluid conductance (GFC) in case of the liquid is given by

$$ {h}_f=\frac{K_f}{3\sigma } $$

(14)

where h_f and K_f are the liquid contact conductance and the liquid thermal conductivity.

And for the gap fluid conductance (GFC) for the gaseous phase is expressed as

$$ {h}_g={k}_g^{\ast}\left[\frac{A_g}{l_g}\right] $$

(15)

where A_g, l_g and ${k}_g^{\ast }$ are representing the gas lattice element area, length and conductivity. ${k}_g^{\ast }$ the gas element thermal conductivity is calculated from k_g, the conductivity in an infinite gaseous medium as given by Kennard [44]

$$ {k}_g^{\ast }=\frac{k_g}{\left[1+\left(\frac{M}{l_g}\right)\right]} $$

(16)

Where l_g is the length of the lattice element representing the gas phase. The quantity M, the temperature jump distance, is estimated using Masamune and Smith [45] as

$$ M=\left[\frac{2-{ac}_1}{2-{ac}_1}+\frac{2-{ac}_2}{ac_2}\right]\frac{\gamma }{\gamma +1}\frac{1}{\mathit{\Pr}}\varLambda $$

(17)

where ac₁ and ac₂ are the thermal accommodation parameters of two surfaces and γ, Pr, and Λ are the ratio of the specific heats, the Prandtl number, and the molecular free mean path, respectively. The mean free path, Λ for gas molecules is given as

$$ \varLambda =\frac{k_bT}{\sqrt{2}\ \pi {d}_g^2P} $$

(18)

Where P is the gas pressure, k_b the Boltzmann constant, d_g the diameter of the gas molecules and T is the temperature. For two dissimilar Voronoi cells (solid-liquid, liquid-gas and gas-solid) 1 and 2 forming a lattice element, the average value of the conductance is assigned

$$ {h}_{ij}=\frac{{\left({h}_{ij}\right)}_1+{\left({h}_{ij}\right)}_2}{2} $$

(19)

In the TLEM model, T₀ has acted as the centre point for the calculation. Considering no heat storage in cells, the equilibrium of heat flux (flux entering and leaving) must be maintained. Mathematically, ΣQ_i = 0, which in turn simplifies the calculation of temperature at the centre T₀.

The temperature evolution of particle i is given as

$$ \frac{d{T}_0}{dt}=\frac{\sum_{i=1}^n Qi}{\rho_0{v}_0{c}_0} $$

(20)

Where ρ₀ is the density, v₀ is the volume and c₀ is the specific heat capacity. The term ρ₀v₀c₀ is also known as the thermal capacity of the 0^th particle. T₀ is the temperature and Q_i is the total amount of heat transported to the 0^th particle from its neighbour the i^th particle (Fig. 6).

The temperature of the 0^th particle T₀ at any instance t + Δ t is calculated using the following scheme

$$ {T}_0^{t+\Delta t}={T}_0^t+{\sum}_{i=1}^n\Delta {T}_{0i}^{t+\Delta t} $$

(21)

$$ ={T}_0^t+{\sum}_{i=1}^n\left({T}_i^t-{T}_0^t\right)\left(1-{e}^{\left[\frac{-{h}_{0i}}{\rho_0{v}_0{c}_0}\right]\Delta t}\right) $$

(22)

3.3 Effective thermal conductivity calculation

For a granular assembly attached to a heat source with 1D heat transport through the lattice elements, the average heat flux of k elements in volume V is defined as

$$ {Q}_i=\frac{1}{V}\ {\sum}_{k=1}^N{Q}_i^k{A}^k{l}^k $$

(23)

where A^kand l^k are the cross-section area and length of the element k, respectively.

The heat flux in the element Q_i is given by

$$ {Q}_n^k=-{h}_{ij}\frac{\Delta T{n}_m}{l^k{A}^k}\kern0.5em $$

(24)

where n_m the unit is normal outward vector, h_ij is the meso level conductance calculated from equation (19), ∆T is the temperature difference, l^k and A^k are the length and cross-sectional area of the element, respectively.

Applying the mean temperature gradient of ∂T/∂x_n in the material at the meso level in one element, the thermal gradient in each element is given by

$$ \varDelta T={l}^k{n}_n\frac{\partial T}{\partial {x}_n}\kern2.5em $$

(25)

Rearranging and substituting Eqs. (23), (24) and (25) gives the following equation

$$ {Q}_n=-\left[\frac{1}{V}{\sum}_{k=1}^N{h}_{ij}^k{l}^k{n}_n^k{n}_m^k\right]\frac{\partial T}{{\partial x}_n}\kern1.25em $$

(26)

Comparing the Eq. (23) with Fourier’s law of heat conduction given in terms of heat flux vector and the temperature gradient

$$ {Q}_n=-{\lambda}_n\frac{\partial T}{\partial {x}_n}\kern2.75em $$

(27)

yields the thermal conductivity tensor of the granular material as [4].

$$ {\lambda}_n^{eff}=\frac{1}{V}\sum {h}_{ij}^k{l}^k{n}_n^k{n}_m^k $$

(28)

4 Results and discussion

To validate the two mentioned computational techniques, we used the measurements reported by Chen [25]. Four different sand types are used to train and validate the neural network. The quartz content of these sands is exceeding 99%, and the air-dried moisture content is less than 0.1%. Figure 8 shows the particle size distribution of the four sands. Sand A is uniform medium sand, and sand B is a uniform coarse sand. The sand C is silty sand of uniform gradation while sand D is well-graded medium sand. These sands are saturated to a predetermined saturation, and the effective thermal conductivities have been reported for four different porosity values (Fig. 9).

Fig. 8

Grain size distribution of four different sands. (Chen 2008) [36]

Fig. 9

The ETC of four sands (A-D) using the transient needle method with the varying degrees of saturation [15]

For each neural network, the MSE, MAE and R² errors are calculated. Here, the Mean Squared Errors (MSE) of the training and the testing data sets is considered for the selection of the DNN. The lowest value to MSE corresponds to the best network. Although we have chosen here MSE for model selection which depends upon the model input and unexpected value elimination in the output, the other error score could be used. The results of the error calculations are tabulated in Table 1. The model with three hidden layers and eight neurons each is selected due to least error margin. It is also observed during the testing and training period that for same epoch training a marginal discrepancy could arise. Table 1 with three layers and eight neurons show such a result where for same epoch training a slight difference in the error values are observed.

Table 1 The performance of each neural network model with varying hidden layers and neurons in the layers on the training and testing data of the sands

Figure 10 shows the predicted results from the neural network model. A moderate range of 0.4 to 0.6 of the porosity values is chosen since most of the sand porosities are in the range. As the results suggest, the behaviour of the reduction of the ETC with the porosity is nonlinear. This justifies the fact that once the main heat conduction paths are formed, there is no noteworthy increase with addition conduction channels. The neural network model can capture the behaviour of sand of different particle sizes with minimal computation cost and decent accuracy. The trained model could be used to predict the ETC of the sands for any porosity value in the band range of (0.3–0.65) with the available dataset.

Fig. 10

The Neural Network prediction of the ETC for the four different sands (a–d) with porosity range between (0.4–0.6)

Figure 11 shows the modelling effort with the TLEM for the full range of saturation. Three different granular assemblies are generated mimicking the dry, unsaturated and fully saturated conditions with 3D Voronoi cells representing, solid (brown cells), liquid water (blue cells) and air (yellow cells). Figure 11a depicts a dry granular system with the solid quartz grains (brown cells) of different sizes and the voids filled with air (yellow cells). The heat transport mechanism in solids is modelled with the thermal Hertz contact model and for the air with gas theories as explained in Section 3.2. The dominant mode of heat transfer for the dry granular assembly is the grain to grain conduction, and thus a very haphazard temperature map is generated after an application of 1^oC temperature gradient from left to right. The left surface is kept at 1^oC (red), and the right at 0^oC(blue). The in-between temperature is shown with rainbow colours legend representing the different temperature of the grains. The method allows us to observe the complex heat transfer mechanism at the granular level with ease and could be used to study the fundamental behaviour of heat transfer at the mesoscale.

Fig. 11

A granular assembly with the wide range of particle sizes distribution captured with the random scheme (Fig. 11a-c) representing dry, unsaturated and saturated systems and temperature profiles (Fig. 11d-f) with 1oC temperature gradient at steady-state with various combinations. a 60% grain 40% air (the dry media) (b) (b) 60% grain 20% air 20% water (the unsaturated media) (d) 60% grain 40% water (the fully saturated media)

Figure 11 (b) shows a granular system having a porosity of 0.4 and the saturation level of 50%. The heat transfer and the temperature map become more irregular as the included water in the pores are of a higher thermal conductivity value compared to air and facilitates the flow of heat. The remaining air in the pores acts like pockets of an insulator. The high conductive filler material (water) further movement of heat in the granular assembly, but at the cost of the smoothness of the heat front. (Fig. 11e).

Figure 11 (c) shows a system with full saturation of the pores with all the pores filled with water. All the feasible heat conduction paths are formed. The corresponding temperature profile is shown in Fig. 11f. The temperature front doesn’t move further, but smoothening of the temperature front is visible as the pores filled with high conductive water, thermal conductivity 0.56 W/m.K compared to air, thermal conductivity 0.024 W/m.K facilitated heat movement in the granular assembly.

In all the above generated granular samples, a total of half a million Voronoi cells are used to create a representative volume element (RVE). The random distribution scheme is used to generate two or three phases of the granular system. The computations are performed on intel Xeon (3.6 GHz) 4 core processor and the mean computation time was about 2800 s.

In Fig. 12a the variation of the ETC with varying moisture content is shown. The experimental results are marked with green diamonds. The prediction from the neural network is shown with a blue line. The TLEM simulations are marked with black dots. For each saturation point, 20 simulations are performed with the TLEM. The variation is a result of the inability of the TLEM to control the porosity consistently and the saturation level as each simulation model produces a new granular assembly with slightly different conduction path [3]. A similar phenomenon is also observed during laboratory testing as each remoulding produces a somewhat different ETC result. As sand A is the uniform sand, the random distribution scheme is applied and can capture the particle generation and component assignment with relative ease. The precision of computed ETC value is scattered could be minimised with a higher number of Voronoi cells representing grains and voids as this will allow better control over porosity value and better partition of constituting phases. However, the process will exponentially increase the computation time.

Fig. 12

The changes in the ETC of four sand types (a–d). The green rhombus represents the experimental measurements from Chen [15]. The black cluster dots are from 20 simulations of each porosity value by the TLEM, and the solid black lines are the predictions from the neural network model

Figure 12b shows the prediction for the uniform coarse sand B. The neural network predicts the change in the ETC with varying saturation values at the lower saturation regime with accuracy. However, for the higher saturation regime, the accuracy depreciates. The trend is observable in all the predictions for each sand as there are fewer data sets to train the model at higher moisture content. The TLEM also shows a wider scatter in both the lower and higher saturation regime. The reduction in precision and accuracy of the model resulted from the inability of the model to precisely control the constituting phases as the pore and grain sizes are found in a very narrow band.

Figure 12c which shows the results of the ETC of a uniformly graded silty sand. The neural network predicts well the ETC value at lower moisture content, but at higher saturation, the results separate from the experimental results by a significant margin. The error arises from the training data set as two ETC values at 50% moisture content are almost similar for different porosity values (Fig. 8c). However, the TLEM based on physical laws can predict the ETC value with a certain accuracy even at higher saturation values.

Figure 12d depicts the behaviour of ETC of the well-graded medium sand. Here, the neural network method can predict the ETC to relative higher accuracy even in the high saturation regime. The TLEM method prediction for the sand shows increases in the precision and accuracy due to the uniform distribution of grain size, which is seldom observed during particle size generation with the Poisson Random Lattice (PRL). The availability of cells of all sizes allow better control in the distribution of the phases and also a more delicate regulation over the porosity value.

5 Conclusion

The paper presents two computational approaches, soft and hard to calculate the ETC of four different sands with varying porosity values and moisture contents. The experiment results are obtained from the literature reported by Chen [25]. The soft computational approach is implemented with a neural network based on the deep learning and Adam optimiser pertaining to its minimal data set requirement for training and validation. The trained network is in turn used to predict the ETC for various porosity values for all the sands. The hard computation approach is developed based on TLEM with particle generation schemes following the Voronoi tessellation and two different granular assembly generation schemes based on particle part partitioning. The random and the segregated granular assembly generation schemes are applied accordingly based on the variation in the particle size distribution of the granular assembly. The Hertz contact model, fluid and gas theories are used to model the conduction heat flow among the three phases present in the unsaturated granular assembly. The heat transfer calculations at mesoscale are done with the TLEM, and the temperature distribution at the granular level are plotted for dry, unsaturated and saturated scenarios. Finally, both of the computational methods are applied to calculate the variation of the ETC of four different sands for different porosity values and the results are compared with the experimental values reported in the literature. Both methods can predict the changes in the ETC with varying moisture and porosity values with certainty. However, the TLEM based on micro and mesoscale physical laws offers better precision and accuracy compared to the neural network model which is trained on a small database and requires significantly less computational time. The accuracy of the neural network method could be substantially improved with the introduction of more extensive training data set and other physical input parameters such as the mineralogical composition and grain-size distribution. A neural network model considering more input parameters as mentioned above will be reported elsewhere.