1 Introduction

Classical microfluidics is seen as a domain of viscous-dominated flows, where simple Ohm-like circuit analysis (analogical to electric circuits) can be applied with sufficient precision (Oh et al. 2012). That approach completely neglects inertia. However, there are loads of examples utilizing the inertial effects in microfluidics (Carlo 2009; Nunes et al. 2014; Amini et al. 2014; Zhang et al. 2015), showing that the impact of inertia can be significant. Thus, this arises vital questions: how we can recognize if the inertia can be neglected in a particular microfluidic system; what are the consequences of the unjustified omit of this inertia; what are the limitations for the applicability of the electric-like-circuit analysis in microfluidics?

The ratio of inertial and viscous interactions is described by the Reynolds number. For the flow through a long channel, the Reynolds number is defined as \({\text{Re}} = \rho UW/\mu\), where \(\rho\) and \(\mu\) are density and dynamic viscosity of the liquid, respectively, \(U\)—mean velocity of the fluid, \(W\)—the width of the channel. In the case of a circular pipe, experimentally obtained critical Reynolds number Re ≈ 2300 gives the upper limit for which the inertial effects can be neglected. In this range, the flow through a pipe is thought to be laminar. According to Hagen–Poiseuille’s law, stationary, viscous, laminar and incompressible flow satisfies the linear relation between the pressure drop and volumetric flow rate. Therefore, Hagen–Poiseuille’s law can be seen to be analogical to Ohm’s law, where the pressure drop is equivalent to the voltage drop, the volumetric flow rate is equivalent to the electric current and the so-called hydraulic resistance is equivalent to the electric resistance (Mortensen et al. 2005). This analogy provides a simplified description of the flow through a microfluidic channel, where the channel is treated as a one-dimensional wire, characterized by the constant resistance. The fact that the hydraulic resistance is proportional to the length of a channel and inversely proportional to the square of its cross-sectional area (the diameter to the power of 4) allows to obtain the required resistance of the channels during the process of design and fabrication. Moreover, if the electric circuit analogy is satisfied, the analytical solutions describing fluid flow in microfluidic networks can be derived from equivalent electric circuit equations which typically reduce to a system of linear algebraic equations (Oh et al. 2012).

Due to its convenience, this methodology is very commonly applied in microfluidics (Oh et al. 2012), e.g.: in the design of concentration-dependent microfluidic networks (Dertinger et al. 2001; Yamada et al. 2006; Lee et al. 2009, 2010), prediction of flow distribution in hierarchical networks (Hulme et al. 2007) design of systems built with combinations of discrete 3D modules (Bhargava et al. 2015), investigation of systems for filtering particles (Stiles et al. 2005), analysis of hydrodynamic trapping of droplets (Bithi and Vanapalli 2010; Korczyk et al. 2013; Zaremba et al. 2018), prediction of flow of droplets in microfluidics networks (Engl et al. 2005; Fuerstman et al. 2007; Cybulski et al. 2015, 2019; Zaremba et al. 2019), description of formation of droplets in microfluidic systems (van Steijn et al. 2013; Korczyk et al. 2019) and the generation of concentration gradation in droplets (Wegrzyn et al. 2012).

Despite numerous examples of successful and impressive applications of linear approximation in modelling of flows in microfluidics, this approach has significant limitations. Its reliability requires elimination from the design process any nonlinearity. However, inertial effects, even if negligible in straight, regular channels can appear for \({\text{Re}} \ll 2300\) in any non-regular element of the microfluidic network (Amini et al. 2014) where the flow is forced to submit to a sudden change of speed or direction (e.g. bends, branching point, contractions and expansions).

To minimize the impact of inertia, the microfluidic network can be built of only straight channels. However, the junctions linking the channels are unavoidable in the construction of non-trivial microfluidic networks. Commonly, the effect of branching points is assumed to be negligible in comparison with the resistance of channels. Although such a condition could be achieved by the use of appropriately long channels, it would cost the enlargements of the microfluidic architecture’s size. Moreover, such an increase in the size of the device is contrary to the idea of miniaturization—the vital advantage of microfluidics. Another way to damp inertial effects is to keep Reynolds number low (e.g. \({\text{Re}} < 1\)), what can be obtained simply by decreasing the rate of flow but with the cost of limiting the maximum throughput of the device. Microfluidics is a very rapidly developing discipline with an increasing area of applications including those which require high throughput (van Berkel et al. 2011). In this context, the expansion of microfluidics towards moderate Reynolds numbers (or even higher ones) seems to be the unavoidable process. The challenge which microfluidics faces now is to develop more complex, but still tractable, mathematical model(es) containing nonlinear effects, as there is no remedy to eliminate inertia. The main aim of this paper is to propose, verify and validate a new modelling approach concerning aforementioned issues.

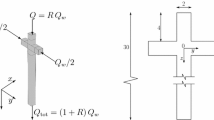
In this paper, we analyse a junction as a source of nonlinearity in microfluidic networks for moderate Reynolds numbers (\(1 < {\text{Re}} < 250\)). A junction, which connects at least three channels, is a ubiquitous element in microfluidic devices. As shown in Fig. 1a, this junction allows for dividing one inlet flow (\(Q_{\text{in}}\)) into two output flows \(Q_{1}\) and \(Q_{2}\), where \(Q_{\text{in}} = Q_{1} + Q_{2}\). In the reverse arrangement, it can be used to combine two input flows into one output flow.

Fig. 1
figure 1

The geometry of a junction and its electric representations. a The scheme of the microfluidic junction. b Electrical circuit diagram representing the junction in linear approximation—the flow depends only on linear resistances determined by the lengths of its arms. c The extended diagram, which includes dependence on the angle between arms of the junction. The influence of the angle between the arms on the local pressure loss is presented in the diagram as variable resistances \(\tilde{R}_{1}\) and \(\tilde{R}_{2}\) depended on Re. The highlighted red area in all graphs corresponds to the region of the junction or its representation in an equivalent circuit diagram

Full size image

The series of consecutive operations of splitting and merging of streams containing a sample and a buffer allow for the precise manipulation on concentrations of compounds. This approach is used to generate the desired distribution of concentration of reagents and for the generation of precisely defined gradients (Dertinger et al. 2001; Yamada et al. 2006; Lee et al. 2009, 2010). The final result of the cascade of splitting and merging of flows relies on the ratio of output flows \(\beta = Q_{1} /Q_{2}\) distributed in each splitting node. Hence, this distribution ratio needs to be determined at the design stage.

According to the linear approximation (as shown in the circuit diagram in Fig. 1b), the geometry of the junction is described by two parameters—the linear resistances of output arms \(R_{1}\), \(R_{2}\). Thus, the pressure drops in both output arms are: \(\Delta p_{1} = p_{\text{in}} - p_{0} = Q_{1} R_{1}\) and \(\Delta p_{2} = p_{\text{in}} - p_{0} = Q_{2} R_{2}\), respectively. If the channels have the same cross sections, the resistances depend only on the lengths of arms (\(L_{1}\) and \(L_{2}\)). Because \(\Delta p_{1} = \Delta p_{2}\), the ratio of flows after splitting is given by the inverted ratio of lengths of outlet arms: \(\beta = Q_{1} /Q_{2} = R_{2} /R_{1} = L_{2} /L_{1}\). Note that although the real geometry of the junction is also described by the angles between the channels: \(\phi_{1}\) and \(\phi_{2}\), these angles are not taken into account in the linear approximation. The consequence of such a reduced description is that the linear model predicts the output flows ratio \(\beta\) constant, regardless of the change of the magnitude of total incoming flow \(Q_{\text{in}}\). In other words, it does not account for any dependence of \(\beta\) on the Reynolds number. In the range of Re numbers in which this linear approximation is correct, the design of the microfluidic network enables the encoding of an arbitrary series of dilutions, where each dilution is hard-wired into the architecture by the ratio of lengths of channels behind each splitting point.

Although the linear approach has been commonly applied for a variety of microfluidic systems, there are examples in the literature, where the linear approximation for microfluidic junctions failed the proper prediction of the splitting ratio. Zeitoun et al. analysed the T-junction as an asymmetric splitter of incoming flow introduced through the inlet arm connecting with both outlet arms at a right angle (Zeitoun et al. 2013). The asymmetry was introduced by different lengths of outlet arms (different hydraulic resistances). They proved that the ratio of the output flows depends on the magnitude of the input flow. The higher the input flow \(Q_{\text{in}}\) (the higher Re), the higher the discrepancy from the prediction of \(\beta\) given by the linear resistance analysis. The authors have assumed that these nonlinearities are introduced by the start-up flow effect. This model, however, does not include any impact of the angle between the arms.

The experimental flow observations and CFD simulations in microfluidic junctions revealed that the first signs of secondary flows could appear for Re < 1 (S. Suteria et al. 2018). Other research disclosed formation of three-dimensional flow patterns with more complex morphology (even for Re < 200), such as standing recirculation zones with thin-layered spiral secondary flows (Karino et al. 1990; Vigolo et al. 2014; Ault et al. 2016; Oettinger et al. 2018) and even flow reversal zones (Karino et al. 1990). Due to the high dissipativity of such structures, they significantly contribute to the pressure drop driving the flow. The asymmetry of those structures in asymmetrical junctions can be problematic for the prediction of the splitting ratio of output flows.

Berkel et al. built a system for rapid blood cell analysis (van Berkel et al. 2011). They used this system containing a junction to divide the sample liquid into parts in required proportions, which then were being mixed with a buffer to finally obtain the required concentration of the sample. To circumvent the impact of the nonlinearity and make the device independent on the input flows, they investigated numerically different junction combinations. Finally, through a series of trials, they found the geometry which satisfied their requirements. This work has shown that inertial effects depend on the angles between the channels. However, the analysis of the impact of the angles has been limited only to the optimization of a single device.

Oh et al. in their review on electric circuit analogy in microfluidics noticed that nonlinearities in junctions can be problematic (Oh et al. 2012). They advised the use of slanted junctions instead of right-angle junctions to minimize these effects. This conclusion rightly suggests the impact of the angles on the inertial effects; however, it is rather an intuitive remark, which lacks deeper quantitative consideration.

The junctions in larger scales and for high Reynolds number have been investigated as a part of pipe systems (Matthew 1975; Hager 1984; Bassett et al. 2001) or as a part of vascular networks (Mynard and Valen-Sendstad 2015). In hydraulics, elements such as junctions or bends are considered to be a source of substantial pressure losses and described by the local pressure losses coefficients. These coefficients have been in general estimated experimentally for different geometries and are widely used in the practice of design of pipe systems (Idelchik 2005). While some concepts of hydraulics can be transferred into microfluidics, that cannot be done directly without appropriate adaptation. The reason is that the scope of hydraulics is the range of high Reynolds numbers, while microfluidics operates within small or moderate Reynolds numbers, where both viscous and inertial interactions are essential.

Therefore, the challenge is to describe pipe-like systems within the transitional range starting from low to moderate Reynolds number—in the range of the majority of microfluidics applications. The knowledge of this transition is vital to judge the applicability of the linear, electric-like circuit, analysis of microfluidic systems. The other goal is to find the description, which takes into account nonlinearities and allows for the proper analysis of nonlinear microfluidic systems.

In this paper, we developed an experimental approach, which allows for precise and effective investigation of the splitting ratio \(\beta\) in microfluidic junctions for moderate Re. We show measurements of \(\beta\) as a function of Reynolds number in a simple microfluidic system of junctions. Significant variations of \(\beta\) clearly prove the discrepancy from the linear model. We show that the magnitude of these variations strongly depends on the angles between channels of the junction and more importantly, that for some combinations of angles these variations can be damped.

Additionally, we propose a mathematical model of a junction accounting for the inertial effects and its dependence on angles. The knowledge about the role of geometry allows us to design a microfluidic junction, in which the sum of all nonlinear elements in the equations vanishes and the solution recovers its linear character and independence from the Reynolds number. This work provides a practical guide for minimization of the nonlinear effects by the optimization of the junction geometry.

2 Materials and methods

2.1 Fabrication of microfluidic devices

The microfluidic devices were fabricated by direct milling of the structure of channels in transparent, 5-mm-thick polycarbonate plates (Makrolon® GP, Bayer, Germany) using a CNC milling machine (MFG4025P, Ergwind, Poland) and a 2-flute fishtail milling bit with a diameter of 385 µm (FR208, InGraph, Poland). Engraved channels (grooves) were cleaned out with a high-pressure water washer (Karcher, K7 Premium, Germany), to remove turnings and loosely bound bulk material, formed during the milling process. Further, the milled chips were washed by hand with 1% water solution of Alconox detergent (Alconox, Alconox Inc., USA), washed with isopropanol and deionized water and finally dried out by compressed air. Then, to obtain closed microfluidic channels, the engraved plate was bounded to another flat slab of polycarbonate using a hot press (AW03, Argenta, Poland) at a temperature of 135 °C and with 0.1 bar/cm2 pressure. The chip was kept in the press at this high temperature for 10 min and then allowed to cool down remaining under pressure. No further channel modifications were applied.

2.2 Measurements of the dye’s concentration

In all presented experiments, we used as an indicator sodium pyruvate (Sigma-Aldrich, Germany) in aqueous solution with starting concentration \(C_{0}\) = 100 mM. As the buffer liquid, we used distilled water.

We used a Multiskan Go Microplate Spectrophotometer (Thermo Scientific) to measure the absorbance of the mixture collected in PMMA UV cuvettes (BRAND, Germany) with a minimum filling volume of 1.5 mL.

All absorbance measurements were taken at the wavelength of 316 nm, which corresponds to the local maximum in the spectrum of absorbance we took in the wavelength range from 200 to 500 nm.

As the principle of concentration estimation based on the measurements of absorbance, it is important to operate in the linear regime. Before all measurements of flow ratios, the calibration curve was determined to investigate relation between absorbance and concentration. The series of measurements for concentrations of sodium pyruvate up to 600 mM allowed us to estimate the maximum level for the linear regime—about 100 mM. We used this maximum value of concentration as a base starting value of concentration in our experiments.

2.3 Flow control

The chip was connected with the syringes via polyethylene tubing (PE60 Intramedic Tubing, Becton–Dickinson, USA), and the liquids were dispensed by syringe pumps (NE-1000, New Era Systems Inc.). 100 mM aqueous solution of sodium pyruvate was inducted into one of the microchannels, while for the other input we used distilled water. Both pumps operate with equal flow rates between: 5 and 350 mL/h. After flushing the channels for 3–5 min and eliminating the bubbles to stabilize the flow, 1.5 mL of the solutions was collected in two cuvettes from each of two outlets. In order to reduce evaporation and changes in the concentration of the liquids, the cuvettes were closed at the end of every experiment. Afterwards, the measurements of concentration from each cuvette were performed.

2.4 Numerical simulations

For the numerical analysis of the water flow through the investigated channel’s junctions, we used steady, isothermal, laminar model of incompressible, viscous liquid flow, implemented in ANSYS Fluent software. Therein, discretization of the liquid flow model governing equations is obtained using the finite volume method. Full, three-dimensional models of the analysed channel’s junctions were designed and created in Autodesk AutoCAD software and then transferred to ANSYS Meshing to generate the computational meshes representing the experimental devices. The boundary conditions (known from experiment) were set as velocity inlets at the inlets to the model, and as pressure outlets (pressure = 0) at the outlets. In the preliminary analysis, different meshes were tested until a mesh independent solution was obtained. As a compromise between accuracy and computational cost, we choose the mesh having 20 × 20 elements in the cross section of the channel. Further, mesh refining caused much higher consumption of the computer’s operating memory and little to none changes of velocity magnitude in the centre of the channel (less than 0.1%). Performed computations delivered accurate details about the flow structure in the analysed devices, including the flow rates in individual segments of the channel’s network.

3 Results and discussion

In the following, we show the experimental evidence of the angle’s impact on the flow distribution in a microfluidic junction, on the example of a specially designed microfluidic rectangular device. Afterwards, we extend the classical circuit analysis to provide the mathematical model accounting for the angles of the junctions. Next, using the new model we analyse numerically the microfluidic junctions to investigate the possibilities for the mitigation of inertial effects by the adjusting of angles. Finally, on the example of the rectangular device, we show the minimization of the inertia’s impact which can be achieved by using the optimization formula obtained in the course of this research.

3.1 Experimental and numerical evidence of the effect of inertia

3.1.1 Experiments

The experimental investigations of the single microfluidic junction (as shown in Fig. 1) may be problematic. They would require the use of direct measurements of the flow with the use of: flow-metres, pressure sensors (Kim et al. 2006); or indirect methods, e.g.: utilizing photobleaching (Cooksey et al. 2019), micro-PIV measurements (Santiago et al. 1998; Blonski et al. 2007) or weighting the output flows (Zeitoun et al. 2013).

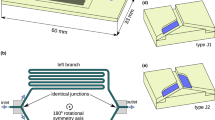
Here, we propose the concept of a symmetric, rectangular device for the precise estimation of the flow distribution via the measurement of the indicator’s concentration. The microfluidic device consists of two identical junctions (see Fig. 2a), which outputs are so connected that they ensure rotational symmetry on the whole device. Thus, the arms of the junctions form an internal rectangle. Two inputs of two independent inflows are placed in the opposite vertices of the rectangle. Two other opposite corners serve as outputs.

Fig. 2
figure 2

Schematic view of the experimental setup. a The idea of the experiment, b Configurations of inlets and outlets in the investigated microfluidic devices for all considered angles

Full size image

If two input flows are equal, the channel’s symmetry implies the symmetry of the flow in the device. Therefore, the flow rates on opposite sides of the rectangle are equal. Particularly, flow rates in both long sides (of the length \(L_{1}\)) are the same and equal \(Q_{1}\) and similarly, flow rates in both short arms (\(L_{2}\)) are identical and equal \(Q_{2}\) (see Fig. 2a).

Let us consider the addition of the optical indicator with a concentration \(C_{0}\) in the liquid injected to one of the inlets (as shown in Fig. 2a) while the clear buffer is injected into the opposite inlet. As illustrated in Fig. 2a, in our device the flow of indicator \(Q_{1}\) encounters the flow of a buffer \(Q_{2}\) at the outlet I, while the flow of indicator \(Q_{2}\) encounters the flow of buffer \(Q_{1}\) at outlet II. In result, we obtain different mixing ratios at each outlet. Thus, the resultant concentrations of the indicator are \(C_{\text{I}} = C_{0} Q_{1} /\left( {Q_{1} + Q_{2} } \right)\) and \(C_{\text{II}} = C_{0} Q_{2} /\left( {Q_{1} + Q_{2} } \right)\) for outputs I and II, respectively (see Fig. 2a). What is important for our investigations, is that the ratio of these concentrations equals the ratio of flows: \(C_{\text{I}} /C_{\text{II}} = Q_{1} /Q_{2} = \beta\).

As the concentration of the indicator is its quantity, which can be easily measured by the use of a spectrophotometer, the proposed design of the device provides a convenient method for the accurate and non-invasive measurement of the ratio of flows \(Q_{1} /Q_{2}\). In our experiments, the quantity we measured directly by the use of a spectrophotometer was the absorbance \(A\), which according to the Beer–Lambert law is proportional to the concentration. Thus, the ratio of flows was estimated directly as the ratio of absorbances: \(\beta = Q_{1} /Q_{2} = A_{\text{I}} /A_{\text{II}}\). This makes the estimation of \(\beta\) independent of possible fluctuations of starting concentration \(C_{0}\). The above-proposed approach ensures the high precision of measurements and a high reproducibility of results. The spectrophotometer is a very common and rather standard equipment available in most laboratories. Hence, this method may be very simply implemented in the investigation of flow distributions within microfluidic networks.

In order to investigate the impact of angles between channels on the flow distribution in junctions, we conducted a series of experiments in rectangular devices with different angles \(\phi_{1}\) and \(\phi_{2}\) (Fig. 2b). To focus solely on the impact of angles, we kept other geometric parameters constant, i.e. both lengths \(L_{1} = 16.67\,{\text{mm}}\) and \(L_{2} = 10\,{\text{mm}}\) with the constant \(\beta_{0} = L_{2} /L_{1} = 0.6\) and a constant sum of both angles \(\phi_{1} + \phi_{2} = 90^{ \circ }\), which sets the right angles between the output arms. All channels had a square cross section of the width \(W = 0.385\,{\text{mm}}\), and relative lengths of arms were: \(l_{1} = L_{1} /W = 43.29\) and \(l_{2} = L_{2} /W = 25.97\). The internal rectangle formed by the sides \(L_{1}\) and \(L_{2}\) was an element repeated in the architecture of each device used in this research. The only elements with varying configurations were two inlet channels and two output channels, which are connected to vertices of the rectangle at different angles \(\phi_{1}\) and \(\phi_{2}\) as shown in Fig. 2b. To minimize the number of varying parameters, the inlet and output channels were connected at the same angle ensuring the symmetry of the whole device. We have produced and tested devices characterized by the set of angles \(\phi_{1}\) with a step of \(22.5^{ \circ }\); however, investigations herein are limited only to cases where both values of angles \(\phi_{1}\) and \(\phi_{2}\) were not larger than \(135^{ \circ }\) and not smaller than \(- 135^{ \circ }\). The reason for that is, for the omitted values of angles, the input and output channels would partially overlap the channels of the internal rectangle, as, e.g. for angles \(180^{ \circ }\) or \(- 180^{ \circ }\) they would overlap completely. Taking this into account, we chose the following set of angles \(\phi_{1}\): − 135°, − 45°, − 22.5°, 0°, 22.5°, 45°, 67.5°, 90°, 112.5°, 135°.

In order to obtain identical flow symmetry of the flow, we ensured the same conditions at both inlets and the same conditions at both outlets (as shown in Fig. 2). The liquids flowing out from the outputs were directed into UV cuvettes via tubing of equal lengths. The collecting cuvettes were placed at the same level, which ensured equal pressures at both outlets.

3.1.2 Experimental results and numerical simulations of rectangular devices

Parallelly to the experiments, we investigated the same set of microfluidic geometries by the use of 3D numerical simulations. In order to simulate the conditions of the experiments, we applied the same conditions to the device, i.e. equal volumetric flow rates to both input channels and equal pressure to both output channel. Unlike in the experiments, where we used the chemical indicator and optical methods for indirect measurement of the flow ratio, in the numerical simulations, the flow rates in both channels-sides-of-rectangle were measured directly.

Figure 3 depicts the results of measurements of \(\beta\) normalized by \(\beta_{0}\) for different devices characterized by the specific angle \(\phi_{1}\) taken in a wide range of Re. Therein, we present the results of numerical simulations as well. Both numerical and experimental data are very similar to each other. The minimal quantitative differences between simulations and experiment could be explained as a discrepancy between the ideal in silico case and the real experiment, which may be influenced by a number of factors. In the particular case of our experiments, the main issue might be the fabrication precision of the microfluidic chip, which relies on a two-step process including micro-milling and bonding. However, despite some quantitative discrepancies, the qualitative similarity between both approaches is very good. Hence, we conclude, the numerical model can be used for the prediction of the flow distribution in microfluidic junctions.

Fig. 3
figure 3

Results of the experimental measurements (solid lines) and numerical simulations (dashed lines) for the rectangular devices with \(\beta_{0} = 0.6\) and with different angles of inlets and outlets. a The range of angles from − 22.5° to 112.5°. b The range of angles from 112.5° to − 22.5°

Full size image

Analysing data sets in Fig. 3, we can notice that for low Re all data for different angles converge to unity (\(\beta /\beta_{0} = 1\)), what proves for low Re the inertial effects vanish. So, in the regime of low Re there is no effect of the angle between the arms of the junction.

Observations of the data in Fig. 3 for higher values of Re implies that we can distinguish \({\text{Re}} = 10\)—an arbitrary transition threshold between the range of Re where inertial effects can be neglected, and the range of Re where the inertia significantly impacts on the distribution of flows (\({\text{Re}} > 10\)). In the latter regime, the larger the Re is the larger the deviation of \(\beta /\beta_{0}\) from unity. The rate of growth of this deviation depends on the angle \(\phi_{1}\) and—more importantly—for each geometry the slope of the curves in Fig. 3 depends on Re.

Extreme deviations of \(\beta /\beta_{0}\) unity in the case of our data sets are observed for \(\phi_{1} = - 22.5^{ \circ }\) and \(\phi_{1} = 112.5^{ \circ }\). Those observations directly prove that the angles between the arms of a junction can significantly influence the distribution of flow in junctions. Thus, the linear approximation may be completely inadequate for the mathematical description of flows in branching points for moderate Re.

The other interesting fact that we infer from the results in Fig. 3 is that the smallest deviations of \(\beta /\beta_{0}\) can be expected between \(\phi_{1} = 45^{ \circ }\) and \(\phi_{1} = 67.5^{ \circ }\). Notice that \(\beta /\beta_{0}\) rises with Re for \(\phi_{1} = 45^{ \circ }\) and decreases for \(\phi_{1} = 67.5^{ \circ }\). Thus, we can hypothesize that between these values of the angle \(\phi_{1}\), there exists an optimal value for which the dependence on Re vanishes.

3.2 Mathematical analysis

The classical circuit analysis commonly used in microfluidics does not account for any nonlinear effects and cannot explain the results of above-described experiments, where we observed the dependence of flows on both angle and Re. In this section, we propose a mathematical description which extends the linear circuit analogy. Here, we take into account the possible inertial effect that can occur in the junction. In this purpose, we adapt the hydraulic approach to the simplified description of a network of channels.

3.2.1 Description of the pressure losses in hydraulics

The pressure losses in the course of the motion of a fluid are due to the irreversible transformation of mechanical energy into heat. In classical hydraulics, two kinds of pressure losses are distinguished in principle: major losses (or frictional losses) \(\Delta p_{\text{F}}\) due to friction and minor losses (or local losses) \(\Delta p_{\text{L}}\) due to the change of velocity, e.g.: in bends, expansions, contractions, valves, etc. (Idelchik 2005).

The energy difference can be expressed in terms of the Bernoulli theorem, which results in the following equation commonly used in hydraulics:

$$\left( {p_{\text{start}} + \frac{1}{2}\rho U_{\text{start}}^{2} } \right) - \left( {p_{\text{end}} + \frac{1}{2}\rho U_{\text{end}}^{2} } \right) = \Delta p_{\text{F}} + \Delta p_{\text{L}}$$
(1)

Here, \(p_{\text{start}}\) and \(p_{\text{end}}\) are static pressures at the start point and the endpoint of the hydraulic conduit, respectively. \(\frac{1}{2}\rho U_{\text{start}}^{2}\) and \(\frac{1}{2}\rho U_{\text{end}}^{2}\) are dynamic pressures, which depend on the mean velocities \(U_{\text{start}}\) and \(U_{\text{end}}\) at selected points. The hydrostatic pressure is constant and is not relevant in this paper.

The major loss \(\Delta p_{\text{F}}\) is caused by a viscous friction during the flow of liquid in pipes and can be expressed by the use of the Darcy–Weisbach equation: \(\Delta p_{\text{F}} = \frac{1}{2}\lambda \rho U^{2} L/W\). Where \(\rho\) is the density of the liquid, \(L\)—channel length, \(W\)—hydraulic diameter (here equal the width of the channel), \(U = Q/S\)—the mean flow velocity calculated as the volumetric flow rate \(Q\) divided by the cross-sectional area of the channel \(S\).

The friction factor \(\lambda\) depends on the Reynolds number and the characteristics of the channel such as the shape of its cross section and roughness of walls. The friction factor in laminar flows depends on the \({\text{Re}}\) as: \(\lambda \propto {\text{Re}}^{ - 1}\). Thus, in the laminar regime, flow through the pipe can be expressed in terms of the modified Hagen–Poiseuille equation, which general form, applicable to any cross section of the channel is:

$$\Delta p_{\text{F}} = QR = Q\alpha L\mu S^{ - 2}$$
(2)

Here, \(R\) is the hydraulic resistance and \(\alpha\) is a non-dimensional coefficient of resistance depending only on the shape of the cross-section, e.g. \(\alpha = 28.6\) for square (Mortensen et al. 2005).

The minor losses (or local losses) appear at a disturbance of the flow in regions, where the flow encounters a sudden change of geometry. While viscous losses take place along the entire length of the microchannel (and depend on \(L\)), minor losses are taken into account only locally: \(\Delta p_{\text{L}} = \frac{1}{2}\zeta \rho U^{2}\), where \(\zeta\) is the local loss coefficient, specific for the geometry, in which the pressure loss takes place (Idelchik 2005).

In the case of the junction, we can expect that the local coefficients \(\zeta\) can display the impact of angles between the channels connected in the junction (Matthew 1975; Hager 1984; Bassett et al. 2001; Mynard and Valen-Sendstad 2015). Indeed, the angles determine the change of flow direction, but usually, they are neglected in the electric-like-analysis of microfluidic systems, where branching points are reduced to point nodes.

Here, we consider a junction connecting three channels of the same, square cross sections characterized with the width \(W\). At first, we consider only the case of a dividing junction which splits the incoming flow \(Q_{\text{in}}\) into two out-coming flows \(Q_{1}\) and \(Q_{2}\). We can expect that inertial effects can influence the splitting ratio \(\beta = Q_{1} /Q_{2} = U_{1} /U_{2}\).

Let us write the Bernoulli equations for both outflows in terms of local losses:

$$\left( {p_{\text{in}} + \rho \frac{{U_{\text{in}}^{2} }}{2}} \right) - \left( {p_{ 0} + \rho \frac{{U_{1}^{2} }}{2}} \right) = \zeta_{1} \rho \frac{{U_{1}^{2} }}{2} + Q_{1} \frac{\mu }{{W^{4} }}\alpha L_{1}$$
(3)
$$\left( {p_{\text{in}} + \rho \frac{{U_{\text{in}}^{2} }}{2}} \right) - \left( {p_{ 0} + \rho \frac{{U_{2}^{2} }}{2}} \right) = \zeta_{2} \rho \frac{{U_{2}^{2} }}{2} + Q_{2} \frac{\mu }{{W^{4} }}\alpha L_{2}$$
(4)

where \(\zeta_{1}\) and \(\zeta_{2}\) are coefficients of local pressure losses for both outputs. We assume that they can be expressed by the common function \(\zeta \left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right)\) of angles, \(\zeta_{1} = \zeta \left( {\phi_{1} ,\phi_{2} } \right)\) and \(\zeta_{2} = \zeta \left( {\phi_{2} ,\phi_{1} } \right)\), respectively.

The above set of equations can be expressed with the terms of pressure drop \(\Delta p = p_{\text{in}} - p_{0}\), hydraulic resistances \(R_{1}\) and \(R_{2}\) and ‘inertial’ resistances \(\tilde{R}_{1}\) and \(\tilde{R}_{2}\) (see Fig. 1c):

$$\Delta p = R_{1} Q_{1} + \tilde{R}_{1} Q_{1}$$
(5)
$$\Delta p = R_{2} Q_{2} + \tilde{R}_{2} Q_{2}$$
(6)

where the hydraulic resistances are:

$$R_{1} = \frac{\mu }{{W^{4} }}\alpha L_{1} = \frac{\mu }{{W^{3} }}\alpha l_{1}$$
(7)
$$R_{2} = \frac{\mu }{{W^{4} }}\alpha L_{2} = \frac{\mu }{{W^{3} }}\alpha l_{2}$$
(8)

and the inertial resistances are:

$$\tilde{R}_{1} = \text{Re} \frac{\beta }{\beta + 1}\left( {K_{1} \alpha - \frac{1}{2}\frac{{\left( {1 + \beta } \right)^{2} }}{{\beta^{2} }}} \right)\frac{\mu }{{W^{3} }}$$
(9)
$$\tilde{R}_{2} = \text{Re} \frac{1}{\beta + 1}\left( {K_{2} \alpha - \frac{1}{2}\left( {1 + \beta } \right)^{2} } \right)\frac{\mu }{{W^{3} }}$$
(10)

Here, the Reynolds number is taken for the inlet flow: \({\text{Re}} = \rho U_{\text{in}} W/\mu\). For the simplicity of further calculations, we introduced \(K_{1} = K\left( {\phi_{1} ,\phi_{2} } \right) = \frac{1}{2}\left( {\zeta_{1} + 1} \right)/\alpha\) and \(K_{2} = K\left( {\phi_{2} ,\phi_{1} } \right) = \frac{1}{2}\left( {\zeta_{2} + 1} \right)/\alpha\), where \(K\left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right)\) is a function of the angles \(\phi_{\text{i}}\) and \(\phi_{\text{j}}\) of the junction.

The set of Eqs. (5)–(6) leads to the following equation for \(\beta\):

$$\beta = \frac{{Q_{1} }}{{Q_{2} }} = \beta_{0} \frac{{1 + \tilde{R}_{2} /R_{2} }}{{1 + \tilde{R}_{1} /R_{1} }}$$
(11)

where \(\beta_{0}\) is a constant coefficient set by the ratio of the lengths of the arms—\(\beta_{0} = R_{2} /R_{1} = L_{2} /L_{1} = {\text{const}}\). In this equation, the inertial resistances introduce dependence on \({\text{Re}}\). Notice that if the numerator and the denominator in Eq. (11) are equal, it simplifies to the form:

$$\beta = \beta_{0} = \beta_{\text{opt}}$$
(12)

where \(\beta_{\text{opt}}\) is the optimal value of \(\beta_{0}\), ensuring the independence of \(\beta\) on \({\text{Re}}\). Finally, from Eqs. (7)–(12), we obtain the following relation:

$$\beta_{\text{opt}} \left( {\phi_{1} ,\phi_{2} } \right) = \sqrt {K_{2} /K_{1} } = \sqrt {K\left( {\phi_{2} ,\phi_{1} } \right)/K\left( {\phi_{1} ,\phi_{2} } \right)}$$
(13)

Here, the coefficient \(\beta_{\text{opt}} \left( {\phi_{1} ,\phi_{2} } \right)\) is the optimal ratio of arms \(\beta_{0} = L_{2} /L_{1}\) for which \(\beta \left( {\text{Re}} \right) = {\text{const}} = \beta_{0}\). The above implies that \(\beta_{\text{opt}}\) is solely a function of angles; hence, the condition \(\beta \left( {\text{Re}} \right) = \beta_{0}\) can be obtained by the proper adjustment of the lengths of the arms \(L_{1}\), \(L_{2}\) and angles \(\phi_{1}\) and \(\phi_{2}\). In the optimal configuration, \(\beta_{0} = L_{1} /L_{2} = \beta_{\text{opt}} \left( {\phi_{1} ,\phi_{2} } \right)\) and \(\beta\) does not depend on \({\text{Re}}\).

Although we do not know the exact form of the equation, defining \(\beta_{\text{opt}}\) as a function of angles, we can state here the hypothesis that optimal adjustment of the geometry of the junction can exist. We explore this hypothesis later.

The set of Eqs. (7)–(11) yields the following equation for \(\beta\):

$${\text{Re}}\frac{1}{{l_{1} }}\left( {K_{1} \beta^{2} - K_{2} } \right) = \left( {\beta_{0} - \beta } \right) \cdot \left( {1 + \beta } \right)$$
(14)

where \(l_{1} = L_{1} /W\).

Introducing \(\beta_{\text{opt}}^{2} = K_{2} /K_{1}\), Eq. (14) reads:

$${\text{Re}}\frac{{K_{1} }}{{l_{1} }}\left( {\beta^{2} - \beta_{\text{opt}}^{2} } \right) = \left( {\beta_{0} - \beta } \right) \cdot \left( {1 + \beta } \right)$$
(15)

The only non-negative solution of quadratic Eq. (15) is given by:

$$\beta = \frac{{\left( {\beta_{0} - 1} \right) + \sqrt {4\left( {\beta_{0} + \beta_{\text{opt}}^{2} {\text{Re}}\frac{{K_{1} }}{{l_{1} }}} \right)\left( {1 + {\text{Re}}\frac{{K_{1} }}{{l_{1} }}} \right) + \left( {\beta_{0} - 1} \right)^{2} } }}{{2 + 2{\text{Re}}\frac{{K_{1} }}{{l_{1} }}}}$$
(16)

Here, we still do not know the values of \(K_{1}\), \(K_{2}\) and so \(\beta_{\text{opt}}\), but we can assume all of them to be positive.

Investigating the limits of \(\beta\) for both vanishing and high values of \({\text{Re}}\), we obtain the limits:

$$\mathop { \lim }\limits_{{{\text{Re}} \to 0}} \beta = \beta_{0}$$
(17)

and

$$\mathop { \lim }\limits_{{{\text{Re}} \to \infty }} \beta = \beta_{\text{opt}}$$
(18)

Equation (17) is in line with our previous expectation and the data from the investigations of the rectangular device. This explains that \(\beta\) starts from \(\beta \left( {{\text{Re}} = 0} \right) = \beta_{0}\) so for low \({\text{Re}}\) it works analogically to electric circuits. Equation (18) implies that for large values of \({\text{Re}}\), value of \(\beta\) tends to \(\beta_{\text{opt}}\).

In other words, in the limit of low \({\text{Re}}\) [see Eq. (17)] the distribution of flows is determined only by the lengths of the arms of the junction (\(\beta_{0} = L_{2} /L_{1}\)), while for large \({\text{Re}}\) [see Eq. (18)] this distribution is determined by the angles (as \(\beta_{\text{opt}}\) is the function of angles only). Thus, we can expect that \(\beta \left( {\text{Re}} \right)\) is an increasing function if \(\beta_{0} < \beta_{\text{opt}}\) or a decreasing function if \(\beta_{0} > \beta_{\text{opt}}\). For \(\beta_{0} = \beta_{\text{opt}}\), the dependence on Re disappear. Thus, the above conclusions from the hydraulic description of the junction are in qualitative agreement with the previously obtained data.

In the following, we investigate separate junctions by the use of numerical simulations to show the difference between the splitting junctions and the merging ones. Afterwards, we show that even with the lack of the explicit form of \(K\left( {\phi_{1} ,\phi_{2} } \right)\) we can provide the approximate description of \(\beta_{\text{opt}}\) as a function of angles.

3.3 Numerical investigations of separate junctions

Once the numerical model had been verified on the base of experimental data, we performed a series of numerical investigations of single junctions. The great advantage of numerical simulations is that the boundary conditions can be easily and precisely defined, and all parameters can be measured without any disturbance of the system.

Particularly in the case of our research, thanks to numerical simulations, we could investigate separately, single junctions. The rectangular device used in experiments consists of four junctions, two splitting junctions and two merging ones. Measurements from that device yielded the evidence of the impact of angles, but the results are the combinations of effects from both junctions of different types.

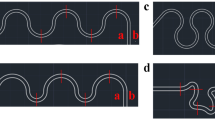
Although the general mathematical description can be applied to both kinds of junctions, due to the irreversibility of inertial flows, we can expect that local losses are different. To investigate these effects separately, we conducted a series of numerical experiments in single junctions of both types (see Fig. 4). In the case of simulating the single splitting junction, we set the same pressure on both outlets of the junction and a constant flow rate in the input channel. In the case of the simulation of the single merging junction, we set the same pressure on both inputs and the constant flow rate in the common output channel.

Fig. 4
figure 4

Two arrangements of the flow in junctions: a the splitting junction, b the merging junction

Full size image

In order to avoid uncertainties in the comparison of results from different separate junctions, in all considered cases we kept \(L_{1} = 10\,{\text{mm}}\) constant, changing \(\beta_{0} = L_{2} /L_{1}\) by adjusting \(L_{2}\).

3.3.1 Flow through a splitting junction

The example results of the simulations of the flow through the splitting junctions are presented in Fig. 5a where we compare data for junctions characterized by two different values of parameter \(\beta_{0}\) (0.5 and 4). We investigated different configurations of junctions changing angles \(\phi_{1}\) and \(\phi_{2}\), keeping the sum of these angles constant (\(\phi_{1} + \phi_{2} = 90^{ \circ }\)). Hence, two output arms form the right angle and only the angle of the input channel changes. The length of the first arm in both cases was the same and equal to \(L_{1} = 10\,{\text{mm}}\), what for the width of the channel \(W = 0.385\,{\text{mm}}\) results in a non-dimensional length \(l_{1} = L_{1} /W = 25.97\). For both values of \(\beta_{0}\), we used a set of angles of the inlet channel characterized by the angle \(\phi_{1}\) within the range from –45° to 135° with a step of 22.5°. For each geometry of the junction in numerical simulations, we estimated the ratio of flows \(\beta = Q_{1} /Q_{2}\) as a function of Reynolds number in the range from 3.85 to 269.5.

Fig. 5
figure 5

Numerical analysis of the dividing junction. a \(\beta = Q_{1} /Q_{2}\) as a function of Re for two examples of \(\beta_{0}\) (= 4,0.5) and for \(\phi_{1} + \phi_{2} = 90^{ \circ }\). Each data series corresponds to different angles between channels characterized by the specific values of \(\phi_{1}\) (see the legend and schematic presentations of the geometry of junctions on the side panels). b Non-dimensional deviation coefficient \(\varPsi\) [see Eq. (19)] as a function of angle \(\phi_{1}\) for the data series presented in a. The additional solid lines—the quadratic interpolation for three data points nearest the local minimum. The inset—optimal geometries of junctions, corresponding to estimations of \(\phi_{\text{opt}}\)

Full size image

The results, depicted in Fig. 5a, reveal the significant differences between junctions with different angles. Value of \(\beta = Q_{1} /Q_{2}\) is approximately equal \(\beta_{0}\) for small Re, while for larger Re, \(\beta\) depends significantly on Re. Depending on the value of \(\phi_{1}\), \(\beta\) can be a decreasing or increasing function of Re. In any case, the deviation of \(\beta\) from the value of \(\beta_{0}\) rises systematically with Re, with the rate of this deviation depending strongly on the angle \(\phi_{1}\). We can guess from the graph that the least deviation can be observed in the case for \(\beta_{0} = 0.5\) for the angle \(\phi_{1}\) between 45° and 67.5°, while for \(\beta_{0} = 4\) the optimal angle is less than 22.5° but more than 0°. These observations confirm our previous assumption that the optimal angles of the junctions are not universal, but they depend on \(\beta_{0}\). In order to compare the deviation rate of different curves from the characteristic value of \(\beta_{0}\), we quantified it by the use of a non-dimensional deviation coefficient \(\varPsi\) defined as follows:

$$\varPsi \left( {\beta_{0} ,\phi_{1} ,\phi_{2} } \right) = \sqrt {\frac{1}{{{\text{Re}}_{ \hbox{max} } }}\mathop \int \nolimits_{0}^{{{\text{Re}}_{ \hbox{max} } }} \left( {\frac{{\beta \left( {\text{Re}} \right)}}{{\beta_{0} }} - 1} \right)^{2} {\text{dRe}}}$$
(19)

where \({\text{Re}}_{ \hbox{max} }\) is the top limit of the range of Reynolds number used in the simulations. Figure 5b plots the values of the deviation coefficient \(\varPsi\) as a function of angle \(\phi_{1}\) calculated for the data sets from Fig. 5a.

This clearly shows the high variation of the deviation rate for different angles for a given junction. Dependence of the coefficient \(\varPsi\) on the angle can be used for the estimation of the optimal configuration by finding the minimum of \(\varPsi\). In this paper, for practical reasons, we limited ourselves only to the minimization of \(\varPsi\) for positive values of angles \(\phi_{1}\) and \(\phi_{2}\), however, as we can see in Fig. 5b the optimal conditions may exist for negative angles as well (see data for \(\beta_{0} = 4\), \(\phi_{1} = - 45^\circ\)). For better resolution of the optimal value estimation of the angle \(\phi_{opt}\), we used quadratic interpolation for three data points nearest to the local minimum.

We repeated the above-mentioned optimization procedure for more junction configurations changing the value of \(\beta_{0}\) within the range from 0.25 to 8 and for different sums of angles \(\phi_{1}\) and \(\phi_{2}\) (45°, 90°, 135°, 180°), keeping \(l_{1} = 25.97\) constant for all junctions. The optimal sets of angles for different values of \(\beta_{0}\) are plotted in Fig. 6.

Fig. 6
figure 6

Optimal values of angles \(\phi_{1}\) and \(\phi_{2}\) for different values of \(\beta_{0}\) estimated from numerical simulations. Markers—the data obtained from numerical optimization (see legend). The solid lines—plots of the optimization formula [see Eq. (21)] for different values of \(\beta_{\text{opt}}\), as indicated in the graph. The dashed lines—isolines of the constant sum of angles

Full size image

Looking for an effective and simplified optimization formula, we fitted the following equation to the obtained data points:

$$\beta_{0} = \frac{{a \cdot \phi_{2}^{2} + \phi_{2} + b}}{{a \cdot \phi_{1}^{2} + \phi_{1} + b}}$$
(20)

In result, we obtained the following values of fitting parameters: \(a = 0.5 \cdot 10^{ - 4} \pm 2.0 \cdot 10^{ - 4}\) and \(b = - 3.8^{^\circ } \pm 0.2^{^\circ }\). Neglecting the vanishing parameter \(a\), we rewrite the optimization formula in the following compact form:

$$\beta_{0} = \frac{{\phi_{2} - 3.8^{^\circ } }}{{\phi_{1} - 3.8^{^\circ } }}$$
(21)

To test this optimization formula, we plotted in Fig. 6 additional lines for constant values of \(\beta_{0}\), which very well agree with the data points obtained from numerical optimization.

3.3.2 Flow through a merging junction

We conducted numerical simulations for junctions, with reversed flow (see Fig. 4). In this case, two input flows meet in the junction and merge forming one output flow. In order to describe the flow, by analogy, we can use an equation similar to Eq. (14):

$${\text{Re}}\frac{1}{{l_{1} }}\left( {\hat{K}_{1} \beta^{2} - \hat{K}_{2} } \right) = \left( {\beta_{0} - \beta } \right) \cdot \left( {1 + \beta } \right)$$
(22)

where the additional coefficients \(\hat{K}_{1}\) and \(\hat{K}_{2}\) are introduced to distinguish them from the coefficients \(K_{1}\) and \(K_{2}\) for the splitting junction. Function \(\hat{K}\left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right)\) describes the dependence of the local loss coefficients on angles: \(\hat{K}_{1} = \hat{K}\left( {\phi_{1} ,\phi_{2} } \right)\) and \(\hat{K}_{2} = \hat{K}\left( {\phi_{2} ,\phi_{1} } \right)\).

In this case, the numerical results reveal that unlike in the case of a splitting junction, in the merging junction \(\beta\) does not depend significantly on the angles (compare Figs. 5a and 7). This is not surprising as the local reverse flow regions are not created. That suggests that in the case of the merging junction the main reason for the pressure loss is the change of the total cross section of the flow.

Fig. 7
figure 7

Numerical analysis of the merging junctions. \(\beta = Q_{1} /Q_{2}\) as a function of Re for four examples of \(\beta_{0}\) (= 4, 2, 1, 0.5) and for \(\phi_{1} + \phi_{2} = 90^{ \circ }\). Each data series corresponds to different angles between channels characterized by the specific values of \(\phi_{1}\) (see the legend)

Full size image

Let us assume that \(\hat{K}\left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right)\) can be expressed as a sum of a constant coefficient \(\varLambda\) and an angle-dependent part \(\kappa \left( {\phi_{i} ,\phi_{j} } \right)\): \(\hat{K}\left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right) = \varLambda + \kappa \left( {\phi_{i} ,\phi_{j} } \right)\). Because we observed that \(\beta\) weakly varies with the angle in the merging junction, we can assume that \(\varLambda \gg \kappa \left( {\phi_{i} ,\phi_{j} } \right)\). Applying the following substitution \(\hat{K}_{1} \approx \hat{K}_{2} \approx \varLambda\) in Eq. (22) and dividing both sides of the equation by \(\left( {1 + \beta } \right)\), we obtain:

$${\text{Re}}\frac{\varLambda }{{l_{1} }}\left( {\beta - 1} \right) = \left( {\beta_{0} - \beta } \right)$$
(23)

In the range of Re where \(\beta\) does not significantly differ from \(\beta_{0}\), we can use the following approximation—\(\left( {\beta - 1} \right) \approx \left( {\beta_{0} - 1} \right)\), which applied to Eq. (23) leads to the following linear relation for \(\beta \left( {\text{Re}} \right)\):

$$\beta \left( {\text{Re}} \right) = \beta_{0} + {\text{Re}}\frac{\varLambda }{{l_{1} }}\left( {1 - \beta_{0} } \right)$$
(24)

Via the fitting of Eq. (24) to the data sets obtained from numerical simulations, we estimated that parameter \(\varLambda = 0.01\).

The optimizing formula given by Eq. (13) is formally the same in the case of both type of junctions, so in case of the merging junction we can state:

$$\hat{\beta }_{\text{opt}} = \sqrt {\hat{K}_{2} /\hat{K}_{1} }$$
(25)

Here, we distinguish \(\hat{\beta }_{\text{opt}}\) as an optimum for the merging junction. As we mentioned above in the case of the merging junction \(\hat{K}_{1} \approx \hat{K}_{2}\), thus \(\hat{\beta }_{\text{opt}} \approx 1\). The conclusion is that unlike in the case of a splitting junction, the flows in merging junctions weakly depend on angles. So, practically this implies that the merging junction cannot be balanced for \(\beta_{0}\) other than 1 while adjusting the angle.

3.4 Optimization of the rectangular device

Above, we analysed the effect of inertia in both the splitting and the merging junctions, separately. Usually, microfluidic networks consist of both these types of junctions (e.g. our rectangular device). The effective minimization of inertial components in the mathematical models of such networks requires knowledge about the values of coefficients \(K\left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right)\) and \(\hat{K}\left( {\phi_{\text{i}} ,\phi_{\text{j}} } \right)\). However, this preliminary study does not provide the explicit formulas of angle-dependence of these important coefficients.

Despite the lacks mentioned above, the important and useful result of this work is the optimization formula for the splitting junction given by Eq. (21). Hence, that raises the question, if this formula can be used for the first attempt of inertial effect mitigation in microfluidic systems comprising both kinds of junctions. Comparing the results from the rectangular device (Fig. 3) and both types of junctions (Figs. 5 and 7), we can observe the qualitative similarity of the rectangular device and the splitting junction, consisting in the high dependence on the angle in both cases. That suggests that in the system consisting of both the splitting and the merging junctions the inertial effects occurring in the splitting junctions dominate in regards to the performance of the whole device.

These conclusions imply that the first attempt of microfluidic network optimization can be made by neglecting the merging junctions and by only accounting for the splitting junctions. We applied this approach in the case of our rectangular device using the optimization formula [Eq. (21)] for \(\beta_{0} = 0.6\), \(\phi_{2} = 90^{^\circ } - \phi_{1}\) and obtained \(\phi_{1} = 55^{^\circ }\). It is worth to notice the yielded value of \(\phi_{1}\) is between \(45^{^\circ }\) and \(67.5^{^\circ }\) as we predicted from the experimental analysis of the rectangular device.

In order to test the efficiency of this optimization, we performed both numerical and experimental analysis of the rectangle device with \(\phi_{1} = 55^{^\circ }\), as presented in Fig. 8. The results show that thanks to the application of the simplified optimization procedure, the impact of inertia in the microfluidic network can be effectively reduced. In the case of the presented data, the deviation caused by the inertia is less than 5%. Even, if the inertial effects do not vanish completely, it is still much better to use the proposed optimization than choose the angle randomly (compare Figs. 3 and 8).

Fig. 8
figure 8

Optimization of the rectangle device. The plot shows the comparison of numerical (dashed lines) and experimental (solid lines) results for rectangular device for the optimized geometry with \(\phi_{1} = 55^{ \circ }\). The results for the two nearest angles \(\phi_{1} = 45^{ \circ }\) and \(\phi_{1} = 67.5^{ \circ }\) from Fig. 3 are presented for the reference

Full size image

4 Conclusions

In this study, we show the experimental evidence of the impact of inertia on the distribution of flows in microfluidic networks in the range of moderate Re. To our knowledge, this is the first attempt to estimate the effect of angles between channels on the magnitude of inertial effects and assess the consequences of this effect for the flow distribution in microfluidic architectures. We show that the inertial effects, within the range of moderate Re, cannot be neglected; contrary, they may be critically affecting the flow.

The important outcome of this research is the optimization formula, which can be used for the effective mitigation of the nonlinear effects via the proper design of connections between channels. Thus, the output of this research is essential for the correct prediction of the operation of microfluidic networks and for its practical applications.

The presented study is a preliminary attempt to deal with nonlinearities in microfluidics. Some questions arose in the course of this work have been left without an answer and require further analysis. Although we provide guidelines, which can help in the finding of optimal angles for the mitigation of nonlinearities, we do not explain why a particular set of angles favours balancing the inertial effects in both arms of junctions. Our preliminary observations of flow patterns obtained from CFD revealed the spatial complexity of three-dimensional structures including secondary flows and flow reversal zones. The understanding of the role of these structures requires the analysis of their effect on the dissipation of energy and will be the focus of future works. This understanding of a variety of possible inertial phenomena that can occur in microfluidic systems is still the challenge and is a field for future exploration.