Synthesized magnetic field of a sawtooth superradiance lattice in Bose–Einstein condensates

Abstract

Ultracold atoms have become one of the most exciting platforms to synthesize novel condensed matter physics. Here we realize a sawtooth superradiance lattice in Bose–Einstein condensates and investigate its chiral edge currents. Based on one-dimensional superradiance lattice (SL) in standing wave-coupled electromagnetically induced transparency, a far-detuned standing-wave field is introduced to synthesize a magnetic field. The relative spatial phase between the two standing-wave coupling fields introduce a magnetic flux in the sawtooth loop transitions of the lattice. This flux determines the moving direction of excitations created in the SL and results in nonsymmetric reflectivities when the SL is probed in two opposite directions. Our work demonstrates an in situ technique to synthesize and detect artificial gauge field in cold atoms.

Introduction

Ultracold atoms have been a highly controllable system for investigating condensed matter physics,¹ quantum optics and quantum information processing.² In particular, optical lattices are widely used to manipulate ultracold atoms and simulate many-body quantum physics in solid state systems. Recently, ultracold atoms in optical lattices³ have been realized in honeycomb,⁴ checkerboard,⁶ Kagome geometries⁵ as well as in bichromatic superlattices, which are double-well lattices consisting of a fundamental lattice and a frequency-doubled lattice.^7,8 Incommensurate bichromatic lattice may generate a one-dimensional quasi-periodic lattice to study Anderson localization⁹ and effective magnetic fields.^10,11 To introduce boundaries in lattices and study topological physics on edges, artificial dimensions¹² have been synthesized by using the inner degrees of freedom of the atoms, such as spin,^13,14 momentum,^15,16 eigenstates in a harmonic trap.¹⁷ Chiral edge currents have been observed in ultracold^13,14,16,18 and hot atoms.¹⁹

Recently, one-dimensional superradiance lattice (1D SL)²⁰ of a Bose–Einstein condensate (BEC) based on standing wave-coupled electromagnetically induced transparency (EIT) was realized experimentally.²⁴ The band structure was investigated by measuring the directional emissions of one of the superradiant excited state in the 1D SL. Toward realizing higher dimensional SLs where topological phenomena can be studied,²⁵ in this paper, we investigate chiral edge dynamics of a quasi-1D sawtooth SL. The relative spatial phase between the two standing-wave coupling fields can be mapped to an Aharonov-Bohm (AB) phase in the sawtooth loop transitions of the lattice. This AB phase determines the moving direction of excitations created in the SL and induces nonsymmetric reflectivities when the SL is probed in two opposite directions. Compared with the lattices studied in previous work,^{13,14,16,18,19} the key difference of the edge states lies in the flatband. This work is promising to study the relevant effects, including the Bloch–Zener oscillation²¹ and compact localized states.²² Many-body physics of flatband²³ can also be explored when interaction is included. This work paves the way for simulating SL in higher dimensions and offers the possibility to in situ probe novel band structures.

Result

Artificial gauge field

We start with a brief description of our experimental method for generating the synthetic uniform magnetic field in a sawtooth SL (see details in “Methods” section). The original SL^20,24 involves with three atomic levels: a ground state $\left|g\right\rangle$, an excited state $\left|e\right\rangle$ and a metastable state $\left|m\right\rangle$. A set of timed-Dicke states²⁶ in the momentum space are coupled by a near-resonant standing wave, forming a 1D tight-binding lattice.²⁰ Based on that, we introduce a fourth atomic level $\left|d\right\rangle$ and couple it to $\left|m\right\rangle$ with a far-detuned standing-wave field, as shown in Fig. 1a. The key effect of this far-detuned standing-wave field is to induce second order transitions between timed-Dicke states that have a momentum difference of two light momenta, as shown by the effective Hamiltonian.¹⁵

$${H}_{f}=\sum _{{\bf{q}}}\kappa {e}^{2i\theta }{b}_{m}^{\dagger }({\bf{q}}-{{\bf{k}}}_{c1}+{{\bf{k}}}_{c2}){b}_{m}({\bf{q}})+h.c.,$$

(1)

where $\kappa ={\Omega }_{f}^{2}/\Delta$ with Ω_f being the Rabi frequency of each plane wave component of the far-detuned standing-wave coupling field, θ is the relative spatial phase between the far-detuned and the near-resonant standing-wave coupling fields, b_m(q) and ${b}_{m}^{\dagger }({\bf{q}})$ are the bosonic annihilation and creation operators of the atom in the state $\left|m\right\rangle$, and k_c1 and k_c2 are the wave vectors of the two counter-propagating plane waves in the near-resonant standing-wave coupling fields. In the theoretical analysis, we assume that the wave vectors of the near-resonant and far-detuned standing waves be the same. The variation of θ along the atomic ensemble is taken into account in fitting the experimental data (see “Flux average“ section).

Fig. 1: Schematics of the atomic levels and laser configuration in 1D SL.

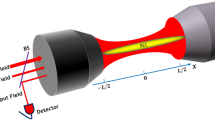
a Energy diagram of the 5²S_1∕2 − 5²P_1∕2 and 5²S_1∕2 − 5²P_3∕2 transitions of ⁸⁷Rb. A pair of strong coupling laser beams (around 795 nm) form a superradiance lattice and drive the transition between $\vert e\rangle =\vert F^{\prime} =1,{m}_{F}^{\prime}=1\rangle$, $\vert m\rangle =\vert F=1,{m}_{F}=1\rangle$. Another pair of strong laser beams (around 780 nm), which has a blue detuning of 200 MHz between $\vert m\rangle =\vert F=1,{m}_{F}=1\rangle$ and $\vert F^{\prime} =2 \rangle$ for 5²S_1∕2 − 5²P_3∕2 transition, provide the NNN transitions. The weak probe light drives the transition between the ground state $\vert g \rangle =\vert F=2,{m}_{F}=2 \rangle$ and the excited state $\vert e \rangle$. Atoms are initially prepared in $\vert g \rangle$. b The laser configuration for the experiment. Two probe lasers probe the BEC in two opposite directions.

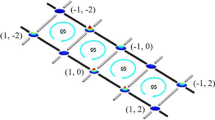
The phase 2θ carried by the next-nearest-neighbor (NNN) coupling introduces the effective magnetic flux Φ in the triangular transition loops in the lattice, as shown in Fig. 2a.^16,27 By tuning the relative spatial phase θ between the two standing waves, we can control the magnitude and sign of the synthetic magnetic field.

Fig. 2: Geometry and band structure of the 1D superradiance lattice.

a The lattice geometry of the 1D SL. b Chiral edge currents with phases θ = π∕4 (red) and 3π∕4 (blue). Coupling strengths κ = 0.15 (dotted) and 1 (solid). The currents with phases θ = 0, π∕2 are zero (not shown). c Energy bands of SLs with different phases θ = 0, π∕4, π∕2. Coupling strengths κ = 0.5. In all plots, Ω_r = 1 and Δ_c = 2κ.

The Hamiltonian

The total Hamiltonian of single excitations can be written in a tight-binding form

$$\begin{array}{ll}{H}_{I}=\displaystyle\sum _{l}\frac{{\Delta }_{c}}{2}(|{m}_{l}\rangle \langle {m}_{l}|-|{e}_{l}\rangle \langle {e}_{l}|)+\kappa {e}^{2i\theta }|{m}_{l}\rangle \langle {m}_{l+1}|\\ +\,({\Omega }_{r}|{m}_{l}\rangle \langle {e}_{l}|+{\Omega }_{r}|{e}_{l-1}\rangle \langle {m}_{l}|+h.c.),\end{array}$$

(2)

where Δ_c = δ + 2κ with δ = ν_r − ω_em being the detuning between near-resonant standing-wave frequency ν_r and the atomic transition frequency ω_em, Ω_r being the Rabi frequency of the near-resonant fields driving the transition between $\left|m\right\rangle$ and $\left|e\right\rangle$, $\left|{e}_{l}\right\rangle \equiv {\left|1,{{\bf{k}}}_{l}\right\rangle }_{e}{\left|N-1,0\right\rangle }_{g}$ denotes the state of N − 1 atoms with zero momentum in the ground state $\left|g\right\rangle$ and one atom with momentum ℏk_l in the excited state $\left|e\right\rangle$, $\left|{m}_{l}\right\rangle \equiv {\left|1,{{\bf{k}}}_{l}-{{\bf{k}}}_{c1}\right\rangle }_{m}{\left|N-1,0\right\rangle }_{g}$ is similarly defined as $\left|{e}_{l}\right\rangle$, and k_l = k_p − l(k_c1 − k_c2) with k_p being the wave vector of the probe field and l being an integer. In this lattice, the states $\left|{e}_{f}\right\rangle$ with ∣k_f∣ = ∣k_p∣ can be coupled to the ground state by a vacuum mode via a directional superradiant emission in k_f mode. A superradiant enhancement is absent when ∣k_f∣ ≠ ∣k_p∣, because the phase matching condition cannot be met. The kinetic energy due to the recoil can be neglected²⁴ (see “Methods” section). We arrange the lasers in such a way that we can probe the atomic ensembles in two opposite directions to measure the steady state populations on $\left|{e}_{+1}\right\rangle$ and $\left|{e}_{-1}\right\rangle$, as shown in Fig. 1b. If the ensemble is excited by the field Probe 1 (Probe 2), $\left|{e}_{-1}\right\rangle$ ($\left|{e}_{+1}\right\rangle$) is a superradiant state and emits light denoted by Scattering 1 (Scattering 2).

Without the far-detuned standing wave, the two probe fields and the corresponding supperradiant emissions are symmetric to each other. When the far-detuned standing-wave coupling field is added, the phase factor e^2iθ ≠ ±1 breaks the reflection symmetry between $\left|{e}_{\pm n}\right\rangle$. In the momentum-space lattice shown in Fig. 2a, each sawtooth loop transition encloses an AB phase Φ = 2θ. For this quasi-1D lattice, the direct consequence of the effective magnetic field is the unidirectional chiral edge currents along the $\left|e\right\rangle$ and $\left|m\right\rangle$ edges. The chiral edge currents result in nonequal population distribution on $\left|{e}_{+1}\right\rangle$ and $\left|{e}_{-1}\right\rangle$ in the steady state when the atoms are constantly pumped into state $\left|{e}_{0}\right\rangle$.

Band structure and chiral current

The Hamiltonian of the chiral superradiance lattice in real space can be written as

$$H=h{\bf{n}}\cdot {\boldsymbol{\sigma }}+{h}_{0}I,$$

(3)

where ${\boldsymbol{\sigma }}={\sum }_{j=x,y,z}{\sigma }_{j}\hat{j}$ is the vector of the Pauli matrices in the pseudo-spin basis $\left|e\right\rangle$ (spin-up) and $\left|m\right\rangle$ (spin-down), Bloch vector ${\bf{n}}=({h}_{x}\hat{x}+{h}_{z}\hat{z})/h$ with ${h}_{x}=2{\Omega }_{r}\cos ({k}_{x}x)$, ${h}_{z}=\kappa \cos (2{k}_{x}x+2\theta )+{\Delta }_{c}/2$, ${h}_{0}=\kappa \cos (2{k}_{x}x+2\theta )$, $h=\sqrt{{h}_{x}^{2}+{h}_{z}^{2}}$, and I is the 2 × 2 unit matrix. The dispersion relation (eigenenergies as functions of positions) of the two bands are E_± = ± h + h₀ with the eigenstates $\left|{\psi }_{+}\right\rangle =\cos \eta /2\left|e\right\rangle +\sin \eta /2\left|m\right\rangle$ and $\left|{\psi }_{-}\right\rangle =-\sin \eta /2\left|e\right\rangle +\cos \eta /2\left|m\right\rangle$, the η is the polar angle of n. The band structure is plotted in Fig. 2c, with the spin texture 〈σ_z〉 being denoted by the color. When the flux Φ equals to π∕2, we notice that the eigenstates that have large $\left|m\right\rangle$ state component have a positive dispersion. On the other hand, the eigenstates that have large $\left|e\right\rangle$ state component have a negative dispersion. When the flux equals to −π∕2, the dispersions are reversed (see more details about the n and h in “Methods“ section). In Fig. 2c, the non-zero Δ_c breaks the symmetry h_z(θ + π∕2) = −h_z(θ), leaving dispersionless band appears only for θ = π∕2.

The dispersion relation determines the direction of the edge currents, i.e., ∂p∕∂t = −∂E∕∂x with p the momentum of the excitation. The chiral current is defined as J_e = ∑_i=±∫dxδ(E_i − E)∣〈ψ_i∣e〉∣²∂E_i∕∂x.¹⁹ For positive dispersion of the $\left|e\right\rangle$ edge, i.e., red lines in Fig. 2b, the momentum decreases with time. In the steady state of the atoms being pumped into the state $\left|{e}_{0}\right\rangle$, the probability of state $\left|{e}_{-1}\right\rangle$ is larger than that of $\left|{e}_{+1}\right\rangle$. As a result, the superradiant emission of Scattering 1 when the atoms are pumped by Probe 1 is larger than the one of Scattering 2 when the atoms are pumped by Probe 2.

All the optical fields, including the coupling and probe lasers, illuminate atoms simultaneously for 80 μs. In order to obtain the direction of the chiral edge current, we measure the difference between Scattering 1 and 2 in Fig. 1b. Required by the phase matching of the superradiant emission, the angle between the probe light and the scattering light is 124°. The Scattering 1 and 2 are also in the opposite direction. In order to obtain the dark background and high signal-noise ratio for detecting the superradiant emission, the intersecting angle between the plane of the two coupling beams and the plane of the probe-scattering beams is 11°.²⁴ The superradiant emission is measured with EMCCD.

First we show the results with only the coupling fields that couple $\left|e\right\rangle$ and $\left|m\right\rangle$. In this case, an ordinary 1D SL is obtained.²⁴ The weak probe field pumps the ground state BEC into the state $\left|{e}_{0}\right\rangle$, which is further coupled to other states in the SL. We sweep the frequency of the probe field and keep the frequency of the coupling fields fixed. The spectrum is characterized by two narrow peaks, which is a feature of the density of states of the 1D tight-binding lattice, as shown in Fig. 3a. The spectra of Scattering 1 and 2 are the same when the BEC is probed in two opposite directions. The asymmetry of the two peaks is induced by the phase mismatch δk = ∣k_p − k_c1 + k_c2 − k_f∣ of the wave mixing process.³⁴

Fig. 3: Superradiance emission for the SL probed in two opposite directions as a function of the frequency detuning of the probe light.

a, b The results for SLs with only the on-resonant standing-wave coupling fields. (a1)–(a5) and (b1)–(b5) are experimental data and numerical simulations with both standing-wave coupling fields for different phases θ = −π∕2, −π∕4, 0, π∕4, π∕2, respectively. The red and blue colors are for the results in two opposite probe directions. The powers of the near-resonant and far-detuned coupling fields are 200 μW and 100 μW, respectively. In the numerical simulation, coupling strengths Ω_r = 2π × 15 MHz, κ = 2π × 2.25 MHz, detuning Δ_c = 2κ, and phase mismatch δk = 0.01k_p.

When both standing-wave coupling fields are applied to the BEC, the scattering spectra of Probe 1 and 2 are different depending on the spatial relative phases between the two standing waves. When the phase θ = −π∕2, the scattering spectra in the opposite directions have the same lineshape, as shown in Fig. 3a1, due to the zero chiral edge current. When θ = −π∕4, the superradiant emission Scattering 1 is larger than Scattering 2 (see Fig. 3a2), which indicates that the population on $\left|{e}_{-1}\right\rangle$ is larger than that of $\left|{e}_{+1}\right\rangle$ due to a negative chiral edge current, in particular near the zero detuning of the probe light. When θ = π, Scattering 1 equals to Scattering 2 again owing to the periodicity of the Hamiltonian in Eq. (3), i.e., H(π) = H(0), as shown in Fig. 3a3. When θ = π∕4, we obtain a larger Scattering 2 than Scattering 1, due to a positive chiral edge current (the red lines in Fig. 2b).

We further measure the two superradiant emissions as a function of the phase θ for the different powers of the far-detuned standing-wave laser. The power of the laser with wavelength 795 nm is fixed at 200 μW. The detuning of the probe light is set at zero. When the power of laser with wavelength 780 nm is low, the superradiance emission strength in two opposite directions are the same, as shown in Fig. 4a1. When we increase the power of the far-detuned laser, the difference between Scattering 1 and 2 appear, especially when ±π∕4, as shown in Fig. 4a6.

Fig. 4: Superradiance emission as a function of θ.

The laser power of the near-resonant coupling field is fixed at 200 μW and that of the far-detuned one is 10 μW (a1), 20 μW (a2), 40 μW (a3), 60 μW (a4), 80 μW (a5), and 100 μW (a6), respectively. The red and blue colors are the results for the two opposite probe directions. The frequency of the probe light is set at zero detuning. In the numerical simulation, coupling strengths Ω_r = 2π × 15 MHz, κ = 2π × (b1) 0.225, (b2) 0.45, (b3) 0.9, (b4) 1.35, (b5) 1.8, (b6) 2.25 MHz, detuning Δ_c = 2κ, and phase mismatch δk = 0.01k_p.

Discussion

In summary, we demonstrate the artificial magnetic field in a sawtooth lattice. Unlike previous study of the gauge field simulation in ultracold atoms,^10,11,13,14 the band structure is characterized by optical spectra.¹⁹ Our scheme offers the possibility to probe the band structure of SL in situ²⁸ without atomic time of flight (TOF) imaging. By using a short probe pulse, e.g., a π-pulse, instead of the long one in the current scheme to pump a single excitation to the SL, we can measure the dynamics of the single excitation. We can also prepare many excitations. They behave the same with the single excitation provided that interaction is absent. Each excitation emits a photon in a probabilistic way. The lattice is gradually destroyed until all the photons are emitted. The time-dependent signal (rather than the steady state response in this work) is expected to oscillate, which is similar with the signals in ref. ¹⁸

In the current work, the optical signals reveal the dynamics only on the sites $\left|{e}_{1}\right\rangle$ and $\left|{e}_{-1}\right\rangle$. However, it can be generalized to more complex lattice structure, as well as more superradiant sites. For instance, we can tune the far-detuned standing wave (lattice 2) on resonance. The corresponding diamond-shape SL is presented in Fig. 5. By pumping site $\left|{e}_{0}\right\rangle$, we can measure the emission from $\left|{e}_{-1}\right\rangle$ and $\left|{d}_{0}\right\rangle$ and distinguish them by the frequencies. The two signals indicate the dynamics along and perpendicular with the lattice, which may be used to characterize Hall-like effect.

Fig. 5: The diamond superradiance lattice.

The BEC is pumped to SL from ground level to $\vert{e}_{0}\rangle$. We can observe the superradiant emissions from $\vert{e}_{-1}\rangle$, $\vert{d}_{0}\rangle$, and $\vert{d}_{-1}\rangle$.

In addition, due to the inevitable spontaneous emission of atomic level $\left|e\right\rangle$, the Hamiltonian of SL is naturally non-Hermitian with different decay rates for $\left|e\right\rangle$ and $\left|m\right\rangle$ sites.^29,30 It can be used to study the topological physics in non-Hermitian systems.^31,32

Another remarkable feature is that one energy band becomes completely flat when Φ = π, as shown in Fig. 2b. The flatband is not observed in current scheme due to the flux averaging (see “Methods” section). In future, we can design a polarization dependent coupling scheme (see “Methods“ section) to make the two standing waves have comparable wavelengths and the synthetic magnetic flux is constant along the atomic ensemble. In that case, the optical signature of the flatband is a sharp peak without asymmetry for the signals in the two detectors. The flatband is preferred for a strong many-body interaction, which can be realized by introducing Rydberg interaction. It can be used to study the interplay between the many-body interactions and artificial gauge field in the SL.

Methods

Bloch vector

Bloch vectors n are plotted in Fig. 6. We notice that the Bloch vector is polarized in z-axis in the Bloch sphere on the positive (negative) slope of h when θ = π∕4 (3π∕4) (the gray areas). It results in a none-zero J_e in Fig. 2b.

Fig. 6: The Bloch vectors n and h.

The arrows indicate the Bloch vectors and the blue solid lines denote h with θ = (a) 0, (b) π∕4, (c) π∕2, and (d) 3π∕4.

Experimental setup

In our experiment, we prepared a pure BEC with typically 5 × 10^{5 87}Rb atoms in the $\left|g\right\rangle \equiv \left|F=2,{m}_{F}=2\right\rangle$ hyperfine ground state sublevel confined in a cross-beam dipole trap at a wavelength near 1064 nm. The geometric mean of trapping frequencies is $\overline{\omega }\simeq 2\pi \times 80$ Hz. The atomic size is estimated in the Thomas-Fermi regime to be 20 μm according to the scattering length for $\left|g\right\rangle$ state at zero magnetic field with about 100a₀. A homogeneous bias magnetic field along the z-axis (gravity direction) is provided with B₀ = 2 G by a pair of coils operating in the Helmholtz configuration. We choose the D₁ line (around 795 nm) of ⁸⁷Rb atom with a simple three-level Λ-type model as shown in Fig. 1a. The probe laser couples the transition between the ground state and $\left|e\right\rangle \equiv \left|F^{\prime} =1,{m}_{F}^{^{\prime} }=1\right\rangle$. A pair of strong laser beams with the intersecting angle φ = 56° couple the transition between $\left|m\right\rangle \equiv \left|F=1,{m}_{F}=1\right\rangle$ and $\left|e\right\rangle$, as shown in Fig. 1a. The coupling laser beams have the waist (1∕e² radius) about 280 μm at the BEC position. The weak probe light used to pump the atoms from $\left|g\right\rangle$ to $\left|e\right\rangle$ has a waist about 600 μm. The frequencies of the coupling and probe laser are locked, which is described in our previous work.²⁴ Another strong laser couples the D₂ transition (around 780 nm) between $\left|m\right\rangle$ and $\left|d\right\rangle \equiv \left|F^{\prime} =2\right\rangle$ with a blue detuning of 200 MHz. It induces a periodic dynamic Stark shift for the state $\left|m\right\rangle$, as shown in Fig. 1a. In the experiment, we simultaneously apply the standing waves and the probe field for 80 microseconds, at the same time the superradiant light is collected for the full 80 ms. The BEC is quickly heated once the superradiant process occurs. After each run, the BEC is depleted. Then we reload the BEC to repeat the experiment to collect the data of the spectra. The spatial coherence of the atoms in the ground state remains. In Fig. 7, we show the 45 ms TOF image of the level $\left|g\right\rangle$ with applying the lattices 1, 2 and probe field for 20 μs. We notice that Kapitza-Dirac scattering occurs owing to the standing waves, which is far-detuned for level $\left|g\right\rangle$. The TOF image indicates that the BEC in ground level $\left|g\right\rangle$ remains being condensate for the short time 20 μs. However, the number of the atoms being excited into the SL is much less than the total atom number of ⁸⁷Rb. Meanwhile, they are quickly heated owing to the dissipation. Therefore the atomic momentum distribution of the atoms in the SL is not obtained in the current scheme. Since all the relevant experimental parameters are in the order of MHz, the system quickly turns to steady in <1 μs. We only consider the response of steady state and neglect the stabilization process in the numerical simulation.

Fig. 7: TOF image.

45 ms TOF image of level $\vert g \rangle$ after applying lattices 1, 2 and probe fields for 20 μs with phase θ = π∕2. Each pair of nearest site is separated by 2ℏk_c1sin(φ∕2). The zeroth momentum state is indicated by the white circle.

Phase adjustment

The 780 nm lasers are combined with the 795 nm coupling laser beams by the beam splitters, and these laser beams are coupled simultaneously into the polarization maintaining single-mode fibers in order to obtain a perfect relative spatial overlap. The combined beams are split into two beams, and intersect at the position of the atoms to form standing waves. We change the displacement of the wedge to increase θ for seeing the response return to the same pattern. Thus, we obtain the periodic curves for two opposite direction scattering, then label the phase according to the symmetry of two opposite direction scattering. For example, there are equal scattering strength for θ = 0.

Kinetic energy

In the experiment, the ratio between the hopping strength and atomic decay rate Ω_r∕(γ₀∕2) ≈ 15 MHz∕3 MHz = 5. Within the life time of atoms in SL, the maximum momentum is about 10k_r, the corresponding maximum recoil energy is in the order of 100E_r ≈ 0.5 MHz, which is much smaller than relevant experimental parameters. k_r and E_r are the single photon recoil momentum, recoil energy of ⁸⁷Rb D1 line.

Flux average

The magnitudes of the wave vectors of the two coupling standing-wave laser fields are ${k}_{1}=2\pi \times \sin (\varphi /2)/{\lambda }_{1}$ and ${k}_{2}=2\pi \times \sin (\varphi /2)/{\lambda }_{2}$, where λ₁ = 795 nm, λ₂ = 780 nm, φ = 56⁰ is the intersecting angle between the two standing-wave laser beams. Due to the difference between λ₁ and λ₂, there is a long beating wavelength between the two standing waves, ${\lambda }_{D}={\lambda }_{1}{\lambda }_{2}/[2({\lambda }_{1}-{\lambda }_{2})\sin (\varphi /2)]$, In our experiment, λ_D ≃ 44 μm is larger than twice the length of the BEC in the trap. The relative phase θ varies for about π∕2 over the BEC and the mean phase can be controlled by adjusting the insertion depth of a wedge into one arm.

In order to take into account this variation in the numerical simulation, we split the atomic ensemble into many slices and each slice is much smaller than λ_D but includes large number of atoms. Since the relative phase θ in each slice is fixed, we treat each of them with independent atomic ensemble and calculate the transmission matrix M(θ).³³ The total reflection is obtained by M_t = Π_θM(θ). An interesting observation is that the asymmetry between the Scattering 1 and 2 is robust over the phase average, in Figs. 3 and 4.

To fix the phase, we propose a polarization dependent coupling scheme in Fig. 8. A bias magnetic filed is applied to split the spin states. BEC is prepared in the level $\left|g^{\prime} \right\rangle \equiv \left|{5}^{2}{S}_{1/2},F=1,m=1\right\rangle$. A σ polarized standing wave is used to couple level $\left|e^{\prime} \right\rangle \equiv \left|{5}^{2}{P}_{1/2},F=2,m=1\right\rangle$ and $\left|m^{\prime} \right\rangle \equiv \left|{5}^{2}{S}_{1/2},F=2,m=2\right\rangle$ resonantly, and a π polarized standing-wave couples level $\left|d^{\prime} \right\rangle \equiv \left|{5}^{2}{P}_{1/2},F=2,m=2\right\rangle$ and $\left|m^{\prime} \right\rangle$ with blue detuning. The beating wavelength between the two standing wave is in the order of centimeters, which is much larger than the typical length of the BEC. Therefore the phase can be regarded as constant.

Fig. 8

The schematic of atomic level to avoid the phase averaging.