Coordinated Variation of Contact Angles During Mobilization of Double Liquid–Gas Interfaces in a Microcapillary

Abstract

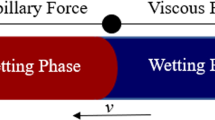
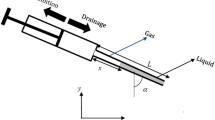
Effectively mobilizing displacement and predicting mobilization pressure in a porous-type reservoir filled with bubbles or blobs require the knowledge of variation of contact angles and capillary pressure. A bubble/blob has two interfaces and thus has two contact angles. It has been found that double interfaces cause resistance to displacement, and the resisting pressure rises while one contact angle increasing and the other decreasing during mobilization. To quantitatively explain how the resistance to flow builds up according to the contact angle variations during mobilization, it is assumed that (1) contact points remain unmoved; (2) the volume of a bubble or blob maintains constant; (3) once the interface starts moving at low capillary number, the contact angle remains to be the advancing or receding angle; (4) the viscous effect on pressure drop can be ignored; and (5) the two angles of two interfaces are equal to an equilibrium angle at the initiation of mobilization. A theoretical model is developed based on these assumptions, and the quantitative relationship of the two angles is expressed by an implicit function. Combining Young–Laplace equation, the capillary pressure induced by double interfaces is obtained. The model’s prediction is in good agreement with experiments in studies. The equilibrium angle has strong influence on the variation of the two angles. When the equilibrium angle is less than 90 degrees, a relatively greater change in the contact angle at the advancing interface leads to a smaller change in the other one. Otherwise, the opposite is true. The changes of the two angles are equal when the equilibrium angle is 90 degrees. Moreover, a linear trend proposed by a previous investigation is incorporated into the model, to predict the ending of mobilization stage and to predict the maximum mobilization pressure on a given solid surface.

Appendices

Appendix 1: The Volume Change Induced by Interface Deformation

As for the volume change in a circular tube, one has to calculate the volume of a spherical cap $v_{\text{SC}}$ first, depicted in Fig. 11. $v_{\text{SC}}$ is given by:

Fig. 11

Cross section of a circular tube, an interface and the contact angle $\alpha$

$$ v_{\text{SC}} = \left| {\frac{{\left( {1 - \sin \alpha } \right)^{2} \left( {2 + \sin \alpha } \right)}}{{\cos^{3} \alpha }}} \right|\frac{\pi R}{3}^{3} $$

(18)

However, Eq. (18) has been rearranged to calculate $v_{\text{SC}}$ as $\alpha$ approaches $\pi / 2$. Noting that x∈[0, π], one has:

$$ \mathop {\lim }\limits_{x \to \pi /2} \frac{{\left( {1 - \sin \alpha } \right)^{2} \left( {2 + \sin \alpha } \right)}}{{\cos^{3} \alpha }} = \left\{ \begin{aligned} &\mathop {\lim }\limits_{{x \to \pi /2^{ + } }} \frac{{\left( {1 - \sin \alpha } \right)^{1/2} \left( {2 + \sin \alpha } \right)}}{{\left( {1 + \sin \alpha } \right)^{3/2} }} = 0 \hfill \\ &\mathop {\lim }\limits_{{x \to \pi /2^{ - } }} - \frac{{\left( {1 - \sin \alpha } \right)^{1/2} \left( {2 + \sin \alpha } \right)}}{{\left( {1 + \sin \alpha } \right)^{3/2} }} = 0 \hfill \\ \end{aligned} \right. $$

(19)

Thus, Eq. (19) is continuous within the range of [0, π]. If the contact angle changes from $\alpha$ to $\beta$, then the volume change in a circular tube is given by:

$$ v\left( {\alpha ,\beta } \right) = \left[ {\frac{{\left( {1 - \sin \alpha } \right)^{2} \left( {2 + \sin \alpha } \right)}}{{\cos^{3} \alpha }} - \frac{{\left( {1 - \sin \beta } \right)^{2} \left( {2 + \sin \beta } \right)}}{{\cos^{3} \beta }}} \right]\frac{\pi R}{3}^{3} $$

(20)

Appendix 2: The Quadratic Approximation

We used a quadratic function $f_{t} \left( x \right) = \beta_{1} \left( {x - \beta_{2} } \right)\left( {x - \beta_{3} } \right)$ to approximate a sine function $f_{o} \left( x \right) = \alpha_{1} \sin \left( {\alpha_{2} x} \right)$ with $0 \le x \le \pi$, wherein $\beta_{1}$, $\beta_{2}$ and $\beta_{ 3}$ are undetermined parameters and $\alpha_{1}$ and $\alpha_{2}$ ($0 \le \alpha_{2} < 1$) are known parameters. $\beta_{1}$, $\beta_{2}$ and $\beta_{ 3}$ need to be expressed as functions of $\alpha_{1}$ and $\alpha_{2}$ for approximation. Within the range of $0 \le x \le \pi \Rightarrow 0 \le \alpha_{2} x < \pi$, the curve of $f_{o} \left( x \right) = \alpha_{1} \sin \left( {\alpha_{2} x} \right)$ resembles a downward parabola, which can be expressed by $f_{t} \left( x \right) = \beta_{1} \left( {x - \beta_{2} } \right)\left( {x - \beta_{2} } \right)$. At least three equations (three pairs of coordinates) are needed to determine $\beta_{1}$, $\beta_{2}$ and $\beta_{ 3}$. For $f_{o} \left( x \right) = \alpha_{1} \sin \left( {\alpha_{2} x} \right)$, three equations are already fixed when $x$ = 0, $\alpha_{2} x = \pi /2$ and $\alpha_{2} x = \pi$, and they are given by:

$$ \left\{ \begin{aligned} &f_{o} \left( 0 \right) = 0 \hfill \\ &f_{o} \left( {\frac{\pi }{{2\alpha_{2} }}} \right) = \alpha_{1} \hfill \\ & f_{o} \left( {\frac{\pi }{{\alpha_{2} }}} \right) = 0 \hfill \\ \end{aligned} \right. $$

(21)

These three equations are used to determine the unknown parameters:

$$ \left\{ \begin{aligned} &f_{t} \left( 0 \right) = f_{o} \left( 0 \right) \hfill \\ &f_{t} \left( {\frac{\pi }{{2\alpha_{2} }}} \right) = f_{o} \left( {\frac{\pi }{{2\alpha_{2} }}} \right) \hfill \\ &f_{t} \left( {\frac{\pi }{{\alpha_{2} }}} \right) = f_{o} \left( {\frac{\pi }{{\alpha_{2} }}} \right) \hfill \\ \end{aligned} \right. \Rightarrow \left\{ \begin{aligned} &\beta_{1} \beta_{2} \beta_{3} = 0 \hfill \\ &\beta_{1} \left( {\frac{\pi }{{2\alpha_{2} }} - \beta_{2} } \right)\left( {\frac{\pi }{{2\alpha_{2} }} - \beta_{3} } \right) = \alpha_{1} \hfill \\ &\beta_{1} \left( {\frac{\pi }{{\alpha_{2} }} - \beta_{2} } \right)\left( {\frac{\pi }{{\alpha_{2} }} - \beta_{3} } \right) = 0 \hfill \\ \end{aligned} \right. $$

(22)

Solving the above equations, we will have:

$$ \left\{ \begin{aligned} &\beta_{1} = \frac{{ - 4\alpha_{1} \alpha_{2}^{2} }}{{\pi^{2} }} \hfill \\ &\beta_{2} = 0 \hfill \\ &\beta_{3} = \frac{\pi }{{\alpha_{2} }} \hfill \\ \end{aligned} \right.\quad or\quad \left\{ \begin{aligned} &\beta_{1} = \frac{{ - 4\alpha_{1} \alpha_{2}^{2} }}{{\pi^{2} }} \hfill \\ &\beta_{2} = \frac{\pi }{{\alpha_{2} }} \hfill \\ &\beta_{3} = 0 \hfill \\ \end{aligned} \right. $$

(23)

Thus, to approximate the derivative of dimensionless mobilization pressure $\tilde{P}_{m}$, substituting the above results in the derivative, we obtain:

$$ \begin{aligned} \frac{{\partial \tilde{P}_{m} }}{{\partial \theta_{\text{adv}} }} & = - \left( {1 - k} \right)\sin \left[ {\left( {1 - k} \right)\theta_{\text{adv}} } \right] + \sin \theta_{\text{adv}} \\ & \approx \frac{{4\left( {1 - k} \right)^{3} }}{{\pi^{2} }}\theta_{\text{adv}} \left( {\theta_{\text{adv}} - \frac{\pi }{1 - k}} \right) - \frac{4}{{\pi^{2} }}\theta_{\text{adv}} \left( {\theta_{\text{adv}} - \pi } \right) \\ \end{aligned} $$

(24)

Rearranging Eq. (24), we will obtain the form of Eq. (15).