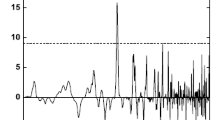Superfast Exoplanets and 9600 s

Abstract

Motion of a substantial part of the superfast exoplanets is found to be in the close resonance with the well-known “solar” timescale $P_{0} \approx 0.11$ days and/or the timescale 2$P_0$/$\pi \approx 0.07$ days (at 99.9% confidence for exoplanet periods $P < 2$ days). There is also a noticeable lack of the exoplanetary “unstable” orbits with $P \approx 3 \pi$$P_0$$\,\approx 1.05$ days, which copies the famous “period gap” of the cataclysmic variables at $P \approx 0.11$ days; strangely enough, the ratio of the central periods of these two gaps is equal to $\pi ^2$. The exoplanet phenomenon is supposed to be caused by a coherent, with the $P_0$ timescale, oscillation of gravity, operating within the extra-solar planetary systems.

1 Introduction

In 1974, pulsations of the Sun with a period of $P_0$$\,\approx 9600$ s, of unknown physical origin, were discovered (Brookes et al. 1976; Severny et al. 1976; Grec et al. 1980; Scherrer and Wilcox 1983; Kotov 2015). To get a reasonable explanation of this phenomenon, it seems worthy to pay attention to a time variability of other objects of Cosmos; in particular, to the new instrument of the investigation of the Universe—exoplanets (EP): recently it was pointed out that the $P_0$  timescale might be present, statistically, in the distribution of the EP superfast orbital rates (Kotov 2018a). If real, such phenomenon would be of a great interest for investigations of gravity.

Here we focus our attention again on the distribution of the shortest EP periods, leaving apart all odd properties of these new planetary objects (origin, peculiarities of migration, the closeness of many “hot jupiters” and “super-earths” to “parent” stars, etc.). Ignoring also the large dispersion of the EP masses and orbital eccentricities, masses and types of the parent stars, we shall be guided here by the facts, known from motion of planets and the largest asteroids of the solar system, and by the recent discovery of the $P_0$  timescale in the period distribution of the close binary stars (CBS), with a participation of the $\pi$ number as a factor of the orbital stability.

This work cannot be considered as a play in numerology: it points out significant correlations that are physically motivated, even not fully understood. Notice also that the “cosmic” $P_0$  oscillation, observed in the Sun for decades, was found in other objects of the Universe too (see Kotov 2018a, b, and references therein).

The resonances with a given period, or timescale, must have usually integer coefficients, by definition. Here, therefore, we mean resonances with the timescales $P_0$  and 2$P_0$/$\pi$, with the participation of integer coefficients also (see Sect. 4),—instead of the search for resonances with $P_0$  only. And we extend our previous work by the proper analysis of the maximal number of EP, discovered to 7 May, 2019, with the updated parameters.

2 Metrics of Motion, and $P_0$  $\approx 1/9$ days

Remarkable enough, a “mysterious” period $P_0 \approx 1 /9$ days of the Sun’s pulsations has been predicted long before its actual discovery in 1974. Namely, 73 years ago French amateur astronomer Sevin (1946) claimed that” la période propre de vibration du Soleil, c’est-á-dire la période de son infra-son (1/9 de jour), a joué un rôle essentiel dans la distribution des planètes supérieures.” Presumably, the Sevin’s “vibration period” of the Sun was merely an issue of his reflections about resonances and distances inside the solar system. Nevertheless, solar pulsations with exactly that period were discovered, after decades,—and independently of the Sevin’s paper,—by a few groups of astrophysicists, see Sect. 1. Soon the presence of the same period, or timescale, was found in other objects of Cosmos too (Gough 1983; Kotov and Koutchmy 1985; Kotov 2018a, b).

The most precise value of the “cosmic” timescale was determined by observations of the Sun: $P_0$  = 0.11111813(14) days, where the uncertainty in brackets approximates standard error (Kotov and Haneychuk 2016).

Below we take the solar system as a typical pattern of a periodic motion, and use the simple statistical method for the analysis of a given sample of periods, based on a computation of the so-called resonance spectrum $F (\nu )$ (RS, or “metrics of motion”; see Kotov 2018a): its maximum corresponds to a frequency which is the most commensurate with the total set of the object’s frequencies $\nu _i = P_i^{-1}$. Here $\nu > 0$ is the trial frequency, $P_i$ is the period under consideration, with $i = 1, 2, \ldots N$, the ordinal number of the sample periods, and N, the total amount of objects, or periods, in a given sample.

Fig. 1

The $F (\nu )$ spectrum, computed for $N = 15$ motions of the largest and fastest rotators of the solar system. On horizontal axis is logarithm of the frequency $\nu$ (in $\mu$Hz), the dashed line shows a 3$\sigma$ C.L., and the primary peak corresponds to a timescale of 9594(65) s (after Kotov 2018b)

Opponents emphasize often that $P_0$  is very close to 9th harmonic of the mean terrestrial day: the corresponding ratio—of the length of a day to the $P_0$  period—is equal to 8.99943(1),—and claim thus the $P_0$  oscillation of the Sun should be regarded as an artifact (see, e.g., Grec and Fossat 1979; Fossat et al. 2017). As a matter of fact, however, the $P_0$  period occurs to be the best commensurate timescale for spin rates of all the most massive and fast-rotating bodies of the solar system, in general.

To prove this intriguing fact, we present Fig. 1, where the best commensurability peak (of 15 motions of the total set of the largest and fastest rotators of the solar system,—of planets, asteroids and massive satellites, with the mean diameters $\ge \,500$ km and periods $P < 2$ days,—but excluding transneptunian objects) corresponds to a timescale of $P_P = 9594(65)$ s. The latter coincides, within the error limits, with $P_0$  at nearly $5.3 \sigma$ confidence level (C.L.); a probability that the two timescales, $P_P$ and $P_0$, coincide by chance, is about $10^{-7}$.

3 Close Binary Stars

On the other hand, motions of the “star–hot-jupiter” (or “star–super-earth”) binaries resemble those of CBS, where the resonance with the timescale 2$P_0$/$\pi$ appears to be the most prominent (see Kotov 2008, 2018a),—with the participation of the $\pi$ number as a factor of an absolute incommensurability of characteristic timescales, or that of the orbital stability (notice the $\pi$ number in geometry characterizes the “ideal” incommensurability of the length and diameter of a circle).

Fig. 2

Same as Fig. 1, for the spectrum $F_1 (\nu )$ of motion of $N = 839$ cataclysmic variables and related objects. The primary peak corresponds to a timescale of 9614(120) s

Fig. 3

Histogram of orbital periods of 839 cataclysmic variables and related objects. The horizontal axis gives logarithm of P (in days), the vertical one—the number n of periods within each data block of 0.1(logP) width. The numbers indicate the period gap ($P \approx 0.11$ days) and two peaks at $P \approx 0.07$ days and $\approx 0.14$ days

Figure 2, for example, shows the RS $F_1 (\nu ) \equiv F ( \pi \nu / 2 )$, computed for 839 cataclysmic variables (CV, including related binary objects; the data are taken from the CV catalogues and current literature), where one sees the best commensurability peak, corresponding to a timescale of 9614(120) s at nearly $12 \sigma$ formal C.L. (In the above expression for $F_1 (\nu )$, the factor 2 takes into account that one deals with a binary: one part of the orbit repeats the other one,—and the number $\pi$ characterizes geometry of space: the factor of an “ideal” incommensurability of a half binary period with the outer time-variable “agent”, or periodic perturbation of unknown physical nature.)

The CV period distribution is plotted in Fig. 3, where we see the so-called “period gap” at periods $P \approx P_0 \approx 0.11$ days (see, e.g., Spruit and Ritter 1983, and references therein), surrounded by the prominent excesses of binaries at $P \approx 2$$P_0$$/ \pi \approx 0.07$ days and $\approx 4$$P_0$/$\pi \approx 0.14$ days. Theoretically (Kotov 2008), the center of the CV “period gap” corresponds to a timescale

$$\begin{aligned} P_{CV} = \frac{3}{\pi } P_0 = 0.10610999(13) \ \mathrm{days}. \end{aligned}$$

(1)

4 Exoplanets

Among 4065 EP, discovered to 7 May, 2019 (see the Exoplanet.eu catalogue), 499 objects have $P < 3$ days. Their histogram, plotted in Fig. 4, did not show any peculiarity, significant for the RS calculations. The parabolic approximation shows a pseudo-smooth change of an orbital period “density”,—a reflection of the real, of yet unknown pattern, function $n_0 (P)$, distorted by observational selection effects (on the noticeable features of the EP amount n at periods from about 0.6 days to $\approx 1.5$ days see Sect. 5).

Fig. 4

Histogram of $N = 499$ periods of the ultra-fast EP. On the horizontal axis is period P in days, on the vertical one—number n of objects within each 0.2-day block of data. The solid line is the best-fitted parabolic approximation of the distribution, and the numbers indicate periods of the two plausible excesses ($P \approx 0.70$ days and $\approx 1.40$ days) and the gap ($P \approx 1.05$ days; see text)

To take into account both potential effects, we are looking for (i.e., the plausible excesses at periods $\approx Z_1$$P_0$  and $\approx 2 Z_2$$P_0$$/\pi$, with the small positive integers $Z_1$ and $Z_2$), we introduce the spectrum $F_2 (\nu )$, based on the calculation of the deviations $\delta _{i1}$ and $\delta _{i2}$ of the respective frequency ratios (see below) from the nearest integers:

$$\begin{aligned} F_2 (\nu ) = F_{02} (\nu ) \mid F_{02} (\nu ) \! \mid , \end{aligned}$$

(2)

where

$$\begin{aligned} F_{02} (\nu ) = A [ B - R_2 (\nu ) ] \end{aligned}$$

(3)

with

$$\begin{aligned} R_2 (\nu ) = \left[ \frac{\Sigma (\delta _{i1}^2 + \delta _{i2}^2 )}{2 N} \right] ^{1/2} . \end{aligned}$$

(4)

The summation in Eq. 4 is performed from $i = 1$ to N for periods $P_i$, while the values $\delta _{i1} = r_{i1} - Z_{i1}$ and $\delta _{i2} = r_{i2} - Z_{i2}$ are deviations of the frequency ratios $r_{i1}$ and $r_{i2}$ from their best approximations – integers $Z_{i1}$ and $Z_{i2}$, and those ratios themselves are: $r_{i1} = ( \nu _i / \nu )^p \ge 1$ and $r_{i2} = ( 2 \nu _i / \pi \nu )^q \ge 1$, where the powers p and q are equal to 1 or $-1$. The quantity $B = 12^{-1/2}$ in Eq. 3 presents the average value of $R_2 (\nu )$ for random ratios $r_{i1}$ and $r_{i2}$, and the value $A = ( 120 N )^{1/2}$ is the normalizing coefficient, reducing standard deviation of the differences $B - R_2 (\nu )$ to unity for a random set of $P_i$ (for other details see Kotov 2018a).

Fig. 5

Same as Fig. 1, for the $F_2 (\nu )$ spectrum of $N = 261$ exoplanets with periods $P < 2$ days. The highest peak of the composite commensurability corresponds to a period of 9603(60) s

The $F_2 (\nu )$ spectrum, calculated for 261 EP with periods $P_i < P_L = 2$ days, is shown in Fig. 5, where the highest peak of the compound resonance—with both timescales, $P_0$  and 2$P_0$/$\pi$, and with the overall C.L. of nearly $3.3 \sigma$,—corresponds to a timescale of 9603(60) s, which well agrees, within the error limits, with the a priori timescale $P_0$  = 9600.606(12) s.

Table 1 The $P_0$  effect for various cut-off boundaries $P_L$

To show this effect does not depend on the cut-off boundary $P_L$, the $F_2 (\nu )$ spectra were computed for $P_L$ values from 1.25 days to 3.00 days. The results are shown in Table 1: for any boundary one observes the prominent peak $P_m$ with a C.L. from 2.3$\sigma$ to 3.3$\sigma$.

5 Period Gap at 1.05 days

One must expect to observe the $P_0$  resonance at the EP half orbital periods, commensurate with $\pi$$P_0$  also (besides the above $P_i / 2$ resonance with the timescale $P_0$/$\pi$). It seems reasonable, therefore, to search for noticeable excesses of objects at periods $\approx 2 \pi$$P_0$$\,\approx 0.70$ days and $\approx 4 \pi$$P_0$$\,\approx 1.40$ days, accompanied by the orbital deficiency at $P \approx 3 \pi$$P_0$$\,\approx 1.05$ days.

(Notice the calculation of the respective RS, with the use of the $2 \pi$ factor instead of the factor $2 / \pi$, seems to be, however, a rather meaningless procedure for our limited EP sample due to the ad hoc presence of the cut-off boundary $P_L$, and also due to deviations of the observed distribution n(P) from the real, yet unknown for us, function $n_0 (P)$, which has presumably rather smooth profile; the main part of those deviations are caused presumably by observational selection effects.)

Such reasoning is strongly supported by the peculiar pattern of the EP period distribution, clearly observed in Fig. 4: the lack of the orbits with P around 1.05 days, surrounded by a pair of noticeable excess features at $P \approx 0.70$ days and $\approx 1.40$ days,—with nearly $3 \sigma$ C.L. of the whole pattern.

6 Conclusion

The $P_0$  resonance, with a participation of the factor $\pi$, appears to be a common property of the superfast EP. Its main point is that a substantial portion of these objects tends to revolve with periods (in days)

$$\begin{aligned} \approx Z_1 P_0 \ \mathrm{and} \ \approx 2 Z_2 P_0 / \pi \end{aligned}$$

(5)

around parent stars, avoiding a “period gap” at

$$\begin{aligned} P \approx 3 \pi P_0 \approx 1.05 \ \mathrm{days}, \end{aligned}$$

(6)

where $P_0$  $\approx 0.11$ days is the “cosmic” oscillation timescale of unknown nature. Namely, the portion of EP with periods (5) occurs to be much larger than that for randomly distributed orbital rates. The statistical significance of this overall effect is estimated to be nearly 99.9% for objects with $P < 2$ days.

The EP period deficiency (see Fig. 4 and Eq. 6), being a puzzling analogue of the famous CV “period gap” at $P_{CV} \approx 0.11$ days, corresponds to the central timescale

$$\begin{aligned} P_{EP} = 3 \pi P_0 = 1.0472637(13) \ \mathrm{days}, \end{aligned}$$

(7)

so that, remarkably enough, the ratio of the two “gap timescales”,

$$\begin{aligned} \frac{P_{EP}}{P_{CV}} = \pi ^2 . \end{aligned}$$

(8)

To make the problem more acute, we stress again that the $P_0$  timescale was discovered earlier in (a) global oscillations of the Sun, (b) in the period distribution of the most massive and rapidly spinning objects of the solar system, and (c) in other variable objects of the Universe (see Sects. 1, 2). Now the $P_0$  resonance is found in the EP orbital rates too, with the notable gap at $P_{EP}$. The apparent independence of this phenomena on the EP masses,—within the mass limits of the EP catalogue,—indicates that we meet here perhaps with some new, quite intriguing, property of gravity (plausibly, with a manifestation of the hypothetical $\varphi$-waves of “a scalar gravitational field”, proposed by R. Dicke decades ago, or with tiny periodic fluctuations of the gravitation constant G itself?).

True physics of the “fine tuning” of the EP motion to timescales (5), with the notable “period gap“ (6), is unknown, but the strong argument in favour of a cosmological origin of the $P_0$  phenomenon follows, for instance, from symmetry of energies of three fundamental physical interactions: electromagnetic, gravitational and weak,—which has led Sanchez et al. (2011) to the following, precise to 0.02%, expression for the observed 1/9-of-a-day “solar” timescale ${P_0}\,= 9600.606(12)$ s:

$$\begin{aligned} P_0 \approx \frac{\tau _e}{( \alpha _G \alpha _W)^{1/2}} = 9600.5(2) \ \mathrm{s} , \end{aligned}$$

(9)

in usual notations. Here $\tau _e \equiv \lambdabar _e / c \approx 1.288089 \times 10^{-21}$ s is electron timescale with the reduced Compton electron wavelength $\lambdabar _e \equiv \hbar / m_e c \approx 3.861593 \times 10^{-11}$ cm, the dimensionless value $\alpha _G \equiv G m_p m_H / \hbar c = 5.9105(2) \times 10^{-39}$ is the so-called “gravitational fine structure constant” (with a hydrogen atom mass $m_H$; see also Carr and Rees 1979), and $\alpha _W \equiv G_F c m_e^2 / \hbar ^3 = 3.045647(2) \times 10^{-12}$—“a weak fine structure constant” with the Fermi constant $G_F = 1.435851(1) \times 10^{-49}$ erg $\hbox {cm}^3$ (for the Newton constant we have taken the laboratory value of Quinn et al. (2014): $G = 6.67554(16) \times 10^{-8}\,\hbox {cm}^3\,\hbox {g}^{-1}\,\hbox {s}^{-2}$,—which is close to the Particle Data Group value 6.67408(31), in the same units, of Tanabashi et al. 2018).