Abstract
The behavior of a two-phase flow inside the inlet pipeline of a catalytic reactor is investigated. In addition to the classical approach using familiar flow diagrams, means of computational fluid dynamics are used for three-dimensional modeling of the spatial distribution of phases in the pipeline during operation. Results show a nonuniform distribution of the liquid phase over the over the pipeline outlet cross section surface, plus a mass flow of the liquid phase that is not stable over time. The maximum peak flow rates exceed the average values by ~300%. Compared to data from flow diagrams, CFD modeling shows that a change in the gas flow in the investigated range does not alter the nature of a two-phase flow, but an increase in the gas flow reduces the irregularity of the distribution of the liquid phase over the pipeline outlet cross section. Data on the behavior of a flow are needed to design catalytic reactor structures that ensure the uniform distribution of a two-phase flow to the catalyst bed for, e.g., hydrotreating reactors in the oil refining industry.









Similar content being viewed by others
REFERENCES
Wallis, G.B., One-Dimensional Two-Phase Flow, New York: McGraw-Hill, 1969.
Chisholm, D., Two-Phase Flows in Pipelines and Heat Exchangers, London: George Godwin, 1983.
Baker, O., Oil Gas J., 1954, vol. 53, no. 12, pp. 185–195.
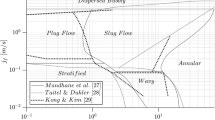
Mandhane, J.M., Gregory, G.A., and Aziz, K., Int. J. Multiphase Flow, 1974, vol. 1, no. 4, pp. 537–553.
Golan, L.P. and Stenning, A.H., Proc.—Inst. Mech. Eng., 1969, vol. 184, no. 3, pp. 110–116.
Lee, A.-H., Sun, J.-H., and Jepson, W.P., Abstract of Papers, Proc. 3rd Int. Offshore Polar Eng. Conf., Singapore, 1993, vol. 2, p 159.
Whalley, P.B., Boiling, Condensation, and Gas-Liquid Flow, Oxford: Clarendon Press, 1987.
Taitel, Y. and Dukler, A.E., AIChE J., 1976, vol. 22, no. 1, pp. 47–55.
Oshinowo, T. and Charles, M.E., Can. J. Chem. Eng., 1974, vol. 52, no. 1, pp. 25–35.
Pinto del Corral, N., Analysis of Two-Phase Flow Pattern Maps. http://www.energetickeforum.cz/ext/2pf/ maps/Documents/Analysis_of_maps.pdf. Cited October 15, 2018.
Vargaftik, N.B., Spravochnik po teplofizicheskim svoistvam gazov i zhidkostei (Handbook on the Thermophysical Properties of Gases and Liquids), Moscow: Nauka, 1972.
ANSYS Official Website, ANSYS FLUENT User’s Guide. https://www.pdfdrive.com/ansys-fluent-users-guide-e6036262.html. Cited July 7, 2019.
Funding
This work was performed as a part of the state task for the Boreskov Institute of Catalysis, project no. АААА-А17-117041710077-4.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by A. Bannov
Appendices
Calculation Model
To solve problems with multiphase flows (in our case, a two-phase gas–liquid system), Euler’s approachis used in computational fluid dynamics, which treats all phases as interpenetrating continua [12]. In each calculated cell there can be any phase, the amount of which is determined through the volume fraction of each phase, which varies in the range of 0 to 1.
To solve problems with stratified phases and the free surface of liquid, a version of the Euler approach is used that is labeled the Volume of Fluid (VOF) model in the literature [12].
The VOF model can simulate two or more phases, solving one set of momentum equations and tracking the volume fraction of each phase across the entire calculated domain. The VOF model is based on each control volume having a sum of the volume fractions of all phases that is equal to one. In other words, if the volume fraction of the qth fluid in a cell is denoted as αq, three conditions are possible:
• αq = 0: the cell is empty (for the qth liquid),
• αq = 1: the cell is filled (for the qth liquid),
• 0 < αq < 1: the cell contains a surface (interface) between qth liquid and one or more other liquids.
Based on the local value of the volume fraction αq, the corresponding properties of flow and individual phases and hydrodynamic variables are calculated in each control volume inside the calculated domain.
Continuity Equation
The surface between the phases is tracked by solving the continuity equation for the volume fraction of one phase (e.g., the liquid). For the qth phase, this equation generally has the form
where \({{\dot {m}}_{{qp}}}\) is the mass transfer from phase to phase and represents the mass transfer from the qth phase to the pth phase; \({{\vec {V}}_{q}}\) is the velocity of qth phase. In our case, the right part of the equation is equal to zero, since \({{S}_{{{{\alpha }_{q}}}}} = {{\dot {m}}_{{qp}}} = {{\dot {m}}_{{qp}}} = 0\).
The volume fraction of the other phase (e.g., gas) is determined using the relation
Preliminary analysis of the behavior of a two-phase flow in the considered pipeline showed that a nonstationary type of flow occurs. An explicit calculation scheme was therefore used in our calculations, i.e., a time step solution diagram:
where n + 1 is the index for a new (current) time step; n is the index for the previous time step; αq, f is the nominal value of volume fraction of the qth phase, calculated in the first or second order against the flow; v is the volume of control cell; and Uf is the volume of the flow through the face of control cell, calculated from the velocity normal to the face.
In an explicit approach, standard finite difference interpolation schemes are applied to volume fraction values that were calculated at the previous time step. This formulation does not require an iterative solution to the transport equation at each time step, as is required for an implicit scheme.
The flow properties used in the transport equations are determined by the presence of phases in each control volume. For example, in a two-phase system, if the phases are represented by subscripts g and l, and if the volume fraction of the second one is monitored, the density in each cell is determined using the relation
Equation for the Conservation of Momentum
The equation for the conservation of angular momentum is solved throughout the computational domain, and the resulting velocity field is distributed between the phases. The pulse equation given below depends on the volume fractions of all phases through the properties of ρ and μ:
where g is the acceleration of gravity, and \(\vec {F}\) is the external bulk forces. In our case, \(\vec {F}\) = 0.
Equation for the Conservation of Energy
The equation for the conservation of energy is also solved throughout the computational domain:
The VOF model considers energy E and temperature T to be average-weight variables:
where Eq for each qth phase is based on the specific thermal capacity of each phase and the total temperature.
External sources of energy are considered on the right-hand side of the equation by member Sh = 0, which can contain contributions from radiation and any other volumetric source of heat. In our case, Sh = 0.
Rights and permissions
About this article
Cite this article
Klenov, O.P., Noskov, A.S. Behavior of a Two-Phase Gas–Liquid Flow at the Inlet into a Catalytic Reactor. Catal. Ind. 11, 243–250 (2019). https://doi.org/10.1134/S2070050419030048
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S2070050419030048