Abstract
Physically Obfuscated Keys (POK) are used to embed in chips secret bit-strings to be used in cryptographic protocols. Usually a POK is built as an array of elementary 1-bit POKs (cells). In order to guarantee that the same secret bit-string is generated at every turn-on, stabilizer circuits are required, which are typically based on possibly expensive error-correction circuitry. In this paper we propose a stabilizer scheme that is not based on error-correction codes, but rather forces to zero the cells that are too unreliable and compensate for the disabled cells by means of a mixing stage.





Similar content being viewed by others
Notes
Note that with this definition the PO for \({\mathfrak p}_{1}=0.5\) is conventionally taken equal to 0. Since \({\mathfrak p}_{1}=0.5\) is a zero probability event, the actual definition of the PO for \({\mathfrak p}_{1}=0.5\) has no impact in practice.
Note that the fact that the probability of error is not larger than \(1-R\) holds in in any environment, because of the definition (4) of \(R\).
The common convention in error-correction code theory is that the codes are generated by the rows of the generator, therefore they are the image of the transpose.
Remember that
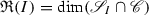 . If
. If 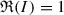 , then it must be
, then it must be  for some
for some  ;
;  cannot be a strict subset of
cannot be a strict subset of 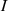 since it would be
since it would be  ; therefore,
; therefore,  is a code-word.
is a code-word.The codes have been extracted from the online code database www.codetables.de (that includes the codes with \(1 \le n\le 256\), \(1 \le \ell \le 256\)) by taking the codes whose distance \(d\) is exactly known.
Labels 0.5/0.5 and 1.5/5 are the same labels used in [19] and refer to two different variants.
References
Gassend, B., Clarke, D., van Dijk, M., Devadas, S.: Silicon physical random functions. In: Proceedings of the 9th ACM Conference on Computer and Communications Security, CCS ’02, (New York, NY, USA), pp. 148–160, ACM (2002)
Herkle, A., Becker, J., Ortmanns, M.: An arbiter PUF employing eye-opening oscillation for improved noise suppression. In: 2018 IEEE International Symposium on Circuits and Systems (ISCAS), pp. 1–5 (2018)
Lim, D., Lee, J., Gassend, B., Suh, G., van Dijk, M., Devadas, S.: Extracting secret keys from integrated circuits. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 13(10), 1200–1205 (2005)
Lim, D.: Extracting secret keys from integrated circuits. Master’s Thesis, MIT (2004)
Suh, G., Devadas, S.: Physical unclonable functions for device authentication and secret key generation. In: Design Automation Conference, 2007. DAC ’07. 44th ACM/IEEE, pp. 9–14 (2007)
Holcomb, D.E., Burleson, W.P., Fu, K.: Initial SRAM state as a fingerprint and source of true random numbers for RFID tags. In: In Proceedings of the Conference on RFID Security (2007)
Maes, R., Tuyls, P., Verbauwhede, I.: A soft decision helper data algorithm for SRAM PUFs. In: IEEE International Symposium on Information Theory, 2009. ISIT 2009, pp. 2101–2105 (2009)
Satpathy, S., Mathew, S., Suresh, V., Krishnamurthy, R.: Ultra-low energy security circuits for IoT applications. In: 2016 IEEE 34th International Conference on Computer Design (ICCD), pp. 682–685 (2016)
Satpathy, S., Mathew, S.K., Suresh, V., Anders, M.A., Kaul, H., Agarwal, A., Hsu, S.K., Chen, G., Krishnamurthy, R.K., De, V.K.: A 4-fJ/b delay-hardened physically unclonable function circuit with selective bit destabilization in 14-nm trigate CMOS. IEEE J. Solid-State Circuits 52, 940–949 (2017)
Alvarez, A., Alioto, M.: Security Down to the Hardware Level, pp. 247–270. Springer, Cham (2017)
Taneja, S., Alvarez, A., Sadagopan, G., Alioto, M.: A fully-synthesizable c-element based PUF featuring temperature variation compensation with native 2.8% ber, 1.02fj/b at 0.8–1.0v in 40nm. In: 2017 IEEE Asian Solid-State Circuits Conference (A-SSCC), pp. 301–304 (2017)
Bernardini, R., Rinaldo, R.: Making random permutations from physically unclonable constants. Int. J. Inf. Secur. 16, 249–261 (2016)
Dodis, Y., Reyzin, L., Smith, A.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. In: Cachin, C., Camenisch, J. (eds.) Advances in Cryptology—EUROCRYPT 2004, vol. 3027 of Lecture Notes in Computer Science, pp. 523–540. Springer, Berlin (2004)
Juels, A., Wattenberg, M.: A fuzzy commitment scheme. In: Proceedings of the 6th ACM Conference on Computer and Communications Security, CCS ’99, (New York, NY, USA), pp. 28–36. ACM (1999)
Skoric, B., de Vreede, N.: The spammed code offset method. IEEE Trans. Inf. Forensics Secur. 9, 875–884 (2014)
Škorić, B.: A trivial debiasing scheme for helper data systems. J. Cryptogr. Eng. 8, 341–349 (2018)
Hiller, M., Weiner, M., Rodrigues Lima, L., Birkner, M., Sigl, G.: Breaking through fixed PUF block limitations with differential sequence coding and convolutional codes. In: Proceedings of the 3rd International Workshop on Trustworthy Embedded Devices, TrustED ’13, (New York, NY, USA), pp. 43–54. ACM (2013)
Hiller, M., Yu, M., Sigl, G.: Cherry-picking reliable PUF bits with differential sequence coding. IEEE Trans. Inf. Forensics Secur. 11, 2065–2076 (2016)
Bernardini, R., Rinaldo, R.: Analytic and simulation results about a compact, reliable, and unbiased 1-bit physically unclonable constant. IEEE Trans. Inf. Forensics Secur. 11, 2804–2817 (2016)
Bernardini, R., Rinaldo, R.: Theoretical limits of helper-less stabilizers for physically unclonable constants. IEEE Trans. Emerg. Top. Comput. 4, 73–87 (2014). https://doi.org/10.1109/TETC.2014.2386137
Guajardo, J., Kumar, S.S., Schrijen, G.-J., Tuyls, P.: FPGA Intrinsic PUFs and Their Use for IP Protection, pp. 63–80. Springer, Berlin (2007)
Mathew, S.K., Satpathy, S.K., Anders, M.A., Kaul, H., Hsu, S.K., Agarwal, A., Chen, G.K., Parker, R.J., Krishnamurthy, R.K., De, V.: 16.2 a 0.19pj/b PVT-variation-tolerant hybrid physically unclonable function circuit for 100 stable secure key generation in 22nm cmos. In: 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), pp. 278–279 (2014)
Satpathy, S., Mathew, S., Li, J., Koeberl, P., Anders, M., Kaul, H., Chen, G.K., Agarwal, A., Hsu, S., Krishnamurthy, R.: 13fj/bit probing-resilient 250k PUF array with soft darkbit masking for 1.94% bit-error in 22nm tri-gate CMOS. In: ESSCIRC 2014—40th European Solid State Circuits Conference, Venice Lido, Italy, 22–26 September 2014, pp. 239–242 (2014)
Mathew, S., Satpathy, S., Suresh, V., Krishnamurthy, R.K.: Energy efficient and ultra low voltage security circuits for nanoscale cmos technologies. In: 2017 IEEE Custom Integrated Circuits Conference (CICC), pp. 1–4 (2017)
Van Herrewege, A., Katzenbeisser, S., Maes, R., Peeters, R., Sadeghi, A.-R., Verbauwhede, I., Wachsmann, C.: Reverse fuzzy extractors: enabling lightweight mutual authentication for PUF-enabled RFIDs. In: A. D. Keromytis (ed.) Financial Cryptography and Data Security , pp. 374–389. Springer, Berlin (2012)
Schaller, A., Stanko, T., Škorić, B., Katzenbeisser, S.: Eliminating leakage in reverse fuzzy extractors. IEEE Trans. Inf. Forensics Secur. 13, 954–964 (2018)
Yan, W., Tehranipoor, F., Chandy, J.A.: PUF-based fuzzy authentication without error correcting codes. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 36, 1445–1457 (2017)
Yan, W., Tehranipoor, F., Chandy, J.A.: A novel way to authenticate untrusted integrated circuits. In: 2015 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), pp. 132–138 (2015)
Herder, C., Ren, L., van Dijk, M., Yu, M., Devadas, S.: Trapdoor computational fuzzy extractors and stateless cryptographically-secure physical unclonable functions. IEEE Trans. Dependable Secure Comput. 14, 65–82 (2017)
Maes, R., Peeters, R., Van Herrewege, A., Wachsmann, C., Katzenbeisser, S., Sadeghi, A.-R., Verbauwhede, I.: Reverse fuzzy extractors: enabling lightweight mutual authentication for PUF-enabled RFIDs. In: International Conference on Financial Cryptography and Data Security, pp. 374–389, 01 (2012)
Holcomb, D.E., Burleson, W.P., Fu, K.: Power-up SRAM state as an identifying fingerprint and source of true random numbers. IEEE Trans. Comput. 58, 1198–1210 (2009)
Su, Y., Holleman, J., Otis, B.P.: A 1.6pj/bit 96% stable chip-id generating circuit using process variations. In: 2007 IEEE International Solid-State Circuits Conference, ISSCC 2007, Digest of Technical Papers, San Francisco, CA, USA, 11–15 February 2007, pp. 406–611 (2007)
Kumar, E.S., Guajardo, J., Maesyz, R., jan Schrijen, G., Tuyls, P.: Extended abstract: the butterfly PUF protecting IP on every FPGA. In: IEEE International Workshop on In Hardware-Oriented Security and Trust. HOST, 2008, pp. 67–70 (2008)
Su, Y., Holleman, J., Otis, B.: A digital 1.6 pJ/bit chip identification circuit using process variations. IEEE J. Solid-State Circuits 43, 69–77 (2008)
Xu, X., Rahmati, A., Holcomb, D., Fu, K., Burleson, W.: Reliable physical unclonable functions using data retention voltage of SRAM cells. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 34, 903–914 (2015)
Lee, J., Lim, D., Gassend, B., Suh, G., van Dijk, M., Devadas, S.: A technique to build a secret key in integrated circuits for identification and authentication applications. In: 2004 Symposium on VLSI Circuits, 2004. Digest of Technical Papers, pp. 176–179 (2004)
Bernardini, R., Rinaldo, R.: A very stable diode-based physically unclonable constant. Integr. VLSI J. 59, 179–189 (2017)
Cachin, C.: Entropy measures and unconditional security in cryptography. Ph.D. thesis, ETH Zurich, Institute of Theoretical Computer Science (1997)
Cover, T.M., Thomas, J.A.: Information Theory. Wiley, New York (1991)
Massey, J.L.: Guessing and entropy. In: Proc. 1994 IEEE International Symposium on Information Theory, p. 204 (1994)
Paral, Z., Devadas, S.: Reliable and efficient PUF-based key generation using pattern matching. In: 2011 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), pp. 128–133 (2011)
Yu, M.-D.M., Devadas, S.: Secure and robust error correction for physical unclonable functions. IEEE Des. Test Comput. 27(1), 48–65 (2010)
Van Zant, P.: Microchip Fabrication, 5th edn. McGraw-Hill Inc, New York (2004)
Chen, N., Yan, Z.: Complexity analysis of reed-solomon decoding over gf(\(2^{\wedge }\text{m}\)) without using syndromes. CoRR, vol. abs/0803.0731 (2008)
Funding
This study was not funded by any specific grant.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Both author declares that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Proofs
A Proofs
Lemma 4
Let  be any
be any  matrix in
matrix in  with
with  . If
. If  , then
, then  or, equivalently,
or, equivalently,

In particular, if  is full rank, then
is full rank, then  .
.
Proof
The case  is obvious. The other case follows from the fact that if
is obvious. The other case follows from the fact that if  the equation
the equation  has always
has always  solutions. \(\square \)
solutions. \(\square \)
Proof A.1
Proof of Lemma 1, page 9 Let  and let
and let  be the projection on
be the projection on  , that is,
, that is,

Step 1: Showing that  .
.
Let  . Since
. Since  it must exist
it must exist  such that
such that  . Since also
. Since also  , it must be
, it must be  , that is,
, that is,  . Therefore, we showed that
. Therefore, we showed that  . In order to show the other implication, let
. In order to show the other implication, let  . Of course,
. Of course,  and it remains to show that
and it remains to show that  , but in order to prove this it suffices to observe that
, but in order to prove this it suffices to observe that  since
since  .
.
Step 2: Prof of (14).
Since  is full-rank,
is full-rank,  and the following equality holds
and the following equality holds

where the last equality follows by observing that the null-rank theorem states that  and that \(\dim (\ker ({\mathbf M}^t))=0\). By exploiting the null-rank theorem, we can deduce
and that \(\dim (\ker ({\mathbf M}^t))=0\). By exploiting the null-rank theorem, we can deduce

Equation (14) follows at once from (41).
Step 3: Proof of (15) Call, for notational convenience,  and
and  and
and  .
.
The left-hand side inequality is obvious since  implies
implies  . In order to prove the right-hand side inequality, suppose
. In order to prove the right-hand side inequality, suppose  , that is,
, that is,  is strictly contained in
is strictly contained in  . Let \(\beta _1, \ldots , \beta _D\) be a basis of
. Let \(\beta _1, \ldots , \beta _D\) be a basis of  and let \(\alpha \) be a vector of
and let \(\alpha \) be a vector of  that does not belong to
that does not belong to  . At least one vector \(\alpha \) exists since we are supposing that
. At least one vector \(\alpha \) exists since we are supposing that  is strictly contained in
is strictly contained in  . Remember that
. Remember that  and observe that since
and observe that since  , the ath component of \(\alpha \) must be equal to 1, that is, \([\alpha ]_a =1\), otherwise \(\alpha \) would belong to
, the ath component of \(\alpha \) must be equal to 1, that is, \([\alpha ]_a =1\), otherwise \(\alpha \) would belong to  .
.
We want to show that every vector of  can be written as a linear combination of \(\beta _1, \ldots , \beta _D\) and \(\alpha \), that is, that \(\{\alpha , \beta _1, \ldots , \beta _D\}\) is a basis of
can be written as a linear combination of \(\beta _1, \ldots , \beta _D\) and \(\alpha \), that is, that \(\{\alpha , \beta _1, \ldots , \beta _D\}\) is a basis of  . This will imply
. This will imply  .
.
Let \(\xi \) be any vector of  .
.
-
if
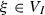 , \(\xi \) can obviously be written as linear combination of \(\beta _1, \ldots , \beta _D\);
, \(\xi \) can obviously be written as linear combination of \(\beta _1, \ldots , \beta _D\); -
if
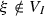 , then by repeating the reasoning done for \(\alpha \) we deduce \([\xi ]_a=1\). Therefore, \([\xi -\alpha ]_a=0\) and
, then by repeating the reasoning done for \(\alpha \) we deduce \([\xi ]_a=1\). Therefore, \([\xi -\alpha ]_a=0\) and  can be written as linear combination of \(\beta _1, \ldots , \beta _D\).
can be written as linear combination of \(\beta _1, \ldots , \beta _D\).
Step 4: Proof of (16) Equation (16a) follows at once from (14) since if  then
then  . Inequality (16b) is easily proved by induction by using any
. Inequality (16b) is easily proved by induction by using any  ,
,  as initial case and using (15) in the inductive step. \(\square \)
as initial case and using (15) in the inductive step. \(\square \)
Proof A.2
Proof of Theorem 1, page 9 In order to compute probabilities (17), we are going to condition over the set of zeroed cells. Let \({\mathfrak I}\) be a random subset of \(\{1, \ldots , n\}\) with the following probability

Note that the event \({\mathscr {A}}_{}\) is equivalent to \(|{{\mathfrak I}}|\le Z\). By conditioning over \({\mathfrak I}\) one obtains

where we used the fact that  is contained in \({\mathscr {A}}_{}\) (since
is contained in \({\mathscr {A}}_{}\) (since  ).
).
Since  is \(m\)-mixing with \(m\ge Z\),
is \(m\)-mixing with \(m\ge Z\),  is full rank for all
is full rank for all  . It follows from Lemma 4 that
. It follows from Lemma 4 that

Using (44) in (43) one obtains

where we used the fact that  since events
since events  are a partition of \({\mathscr {A}}_{}\). \(\square \)
are a partition of \({\mathscr {A}}_{}\). \(\square \)
Proof A.3
Proof of Theorem 2, page 9 Probability \( P[{{{\overline{{\mathbf x}}}_{}}={\mathbf x}_{}}|{{\mathscr {A}}_{\text {PUC}}}]\) can be computed by conditioning on  . Note that sets \({\mathscr {I}}_{ {c,s}}\) with \(c\le Z\) and \(s\le Z-m\) are a partition of \({\mathscr {I}}_{{\mathscr {A}}_{}}\) (note that some \({\mathscr {I}}_{ {c,s}}\) can be empty, but this does not invalidate the reasoning).
. Note that sets \({\mathscr {I}}_{ {c,s}}\) with \(c\le Z\) and \(s\le Z-m\) are a partition of \({\mathscr {I}}_{{\mathscr {A}}_{}}\) (note that some \({\mathscr {I}}_{ {c,s}}\) can be empty, but this does not invalidate the reasoning).
It follows

where we used definition (23) of \(q_{c}\) and the fact that event  is contained in \({{\mathscr {A}}_{\text {PUC}}}\). According to Lemma 4,
is contained in \({{\mathscr {A}}_{\text {PUC}}}\). According to Lemma 4,  is equal to
is equal to  if
if  and zero otherwise. It follows that in the last sum of (46), only the terms corresponding to
and zero otherwise. It follows that in the last sum of (46), only the terms corresponding to  such that
such that  survive. Remembering definition (22) of \({\mathscr {N}}_{c,s}\, {}\) one can write
survive. Remembering definition (22) of \({\mathscr {N}}_{c,s}\, {}\) one can write

\(\square \)
Proof A.4
Proof of Lemma 3, page 10 Step 1: Proof of (30) In order to prove (30), it is convenient first to isolate the values of \(c\) that are within the mixing limit \(m\) and use (19b) to obtain

As it will result clear later, the first addend in the last line of (48) can be written as ratio \({F_{{n},{p_{\text {u}}}} { {({m})}}} / {F_{{n},{p_{\text {u}}}} { {({Z})}}}\). Our aim is to extract from the second addend a term similar to the first one in order to combine them.

Observe that because of (19a), every  with
with  must belong to one (and only one) set \({\mathscr {I}}_{ {c,s}}\) with \(s\le c-m\). This implies that the sum in square brackets in (49) is equal to the number of the sets
must belong to one (and only one) set \({\mathscr {I}}_{ {c,s}}\) with \(s\le c-m\). This implies that the sum in square brackets in (49) is equal to the number of the sets  with
with  . Therefore, (49) can be rewritten as
. Therefore, (49) can be rewritten as
Equation (50) can now be used in (48) to obtain, using the definition of \(q_{c}\) and the fact that \(P[{{\mathscr {A}}_{\text {PUC}}}] = {F_{{n},{p_{\text {u}}}} { {({Z})}}}\),

where the last passage follows by observing that the sum at the numerator is the probability that a Binomial random variable is less or equal to \(Z\).
Step 2: Proof of bounds (31)
The lower bound in (31) is easily proved by limiting sum in (30) to only \(c=d\) (and, consequently, \(s=1\)) and remembering that \( |{{\mathscr {I}}_{ {d,1}}}| = W_{d}\) (see (19c)).
In order to prove the upper bound

where the last steps follow a reasoning similar to the one used for (51). More precisely, (*) is obtained by observing that every  belongs to one and only one \({\mathscr {I}}_{ {c,s}}\), while the last equality follows from the fact that the sum in (**) is the probability that a Binomial r.v. is not larger than \(Z\). \(\square \)
belongs to one and only one \({\mathscr {I}}_{ {c,s}}\), while the last equality follows from the fact that the sum in (**) is the probability that a Binomial r.v. is not larger than \(Z\). \(\square \)
Proof A.5
Proof of Theorem 4, page 11 First, let us compute the probability that the PO of a cell is 0 conditioned by \({{\mathscr {A}}_{\text {PUC}}}\).
Probability \(P[B_{i}=0|{{\mathscr {A}}_{\text {PUC}}}, U_{i}=0]\) is equal to 1 since if \(U_i=1\) the cell is zeroed, while probability \(P[B_{i}=0|{{\mathscr {A}}_{\text {PUC}}}, U_{i}=0]\) is equal to 1 / 2 since if \(U_i=0\) the cell is reliable and the PO is the “natural” one. Therefore,
Note that \(P[B_{i}=0|{{\mathscr {A}}_{\text {PUC}}}] \ge 1/2\), since \(B_i=0\) can be obtained with a reliable cell with PO equal to 0 or with an unreliable cell.
Proof of (34) First, we prove the equality in (34). Let \(U_i\), \(i=1,\ldots , L\) be the r.v. that assumes value 1 if the ith cell is unreliable and 0 otherwise. Suppose, without loss of generality, that we are considering the first cell, that is, we want to compute \({\mathfrak u}=P[U_1=1|{\mathscr {A}}_{}]\). Block acceptance event \({\mathscr {A}}_{}\) can clearly be written as \(\sum _{i=1}^{L} U_i \le Z\). Therefore,
Now, we need to prove the inequalities in (34). Left-hand side inequality \( {\mathfrak u}\ge 0\) is obvious. Moreover, it is easy to check that the extremes in (34) are reached for \(Z=0\) and \(Z=n\). It remains to show that \({F_{{n-1},{p_{\text {u}}}} { {({Z-1})}}} \le {F_{{n},{p_{\text {u}}}} { {({Z})}}}\). Suppose that \(A_i\), \(i=1, \ldots , n\) are iid Bernoulli r.v. with alphabet \(\{0,1\}\) and \(P[A_i =1]=p_{\text {u}}\). Since \(\sum _{i=1}^{n} A_i \sim {\mathscr {B}}( {n,} p_{\text {u}})\), it follows
Min-entropy (35) In order to compute min-entropy  observe that, for every cell, 0 is the most probable PO; therefore, the most likely outcome is the all-zero word. It follows that
observe that, for every cell, 0 is the most probable PO; therefore, the most likely outcome is the all-zero word. It follows that

\(\square \)
Rights and permissions
About this article
Cite this article
Bernardini, R., Rinaldo, R. Analysis of some simple stabilizers for physically obfuscated keys. Int. J. Inf. Secur. 19, 547–565 (2020). https://doi.org/10.1007/s10207-019-00473-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10207-019-00473-8





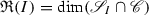 . If
. If 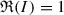 , then it must be
, then it must be  for some
for some  ;
;  cannot be a strict subset of
cannot be a strict subset of 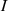 since it would be
since it would be  ; therefore,
; therefore,  is a code-word.
is a code-word.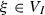 ,
, 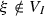 , then by repeating the reasoning done for
, then by repeating the reasoning done for  can be written as linear combination of
can be written as linear combination of