1 Introduction

The resonance of a bridge crossed by moving trains has arisen the interest of many researchers [1,2,3,4,5] because the resonant responses could affect the comfort of the passengers and stability of the tracks and even endanger the bridges and the trains. Simply supported beam models were generally adopted in former train-induced vibration analysis [1,2,3,4,5] when the tracks were usually laid on the deck near the webs of box girders or T-shaped girders. Yang and Yau [6] recently provided a complete investigation for both train-induced and bridge-induced resonances of the coupled train–bridge system, where simple beam model was still used in the study. Song et al. [7] proposed a nonconforming flat shell elements model for train–bridge interaction analysis, which allowed the analysis of local vibration of the bridge deck. Lee et al. [8] investigated the effect of the discrete support track on the resonance effect of the bridge using three-dimensional finite element models and found that the track model changed the dynamic responses of the bridge. Yang et al. [9] studied the vibration of a continuous plate crossed by a moving model car and found that the displacements of the plate obtained from the numerical model agreed well with the experimental ones. Yang and Hwang [10] recently presented a train-track-bridge model by combining the direct stiffness method for the track and the mode superposition method for the bridge to study the dynamic interaction problem of a railway steel arch bridge. The above research [7,8,9,10] could include the local vibration of the bridge deck, but the mechanism of resonance was not provided.

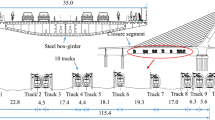
A continuous composite box girder bridge over Yangtze River in Shanghai China was designed to carry a three-lane highway and a single-track railway on the upper level of the bridge deck (see Fig. 1). The urban rail transit traffic must be arranged on the cantilever deck so that any one of the three highway lanes will not be isolated by the railway traffic. When the trains run on the cantilever deck of the box girder, they may generate excessive and repeated stresses on the root of the cantilever deck and affect the serviceability and durability of the prestressed concrete. The trains may also cause excessive vibration at the cantilever deck, which in turn affects the stability of the railway track laid on the cantilever deck and the comfort of the trains. To ensure the functionality of both bridge and trains, it is necessary to examine the resonance conditions of the cantilever deck and the dynamic responses of the railway train–bridge system considering local vibration of the cantilever deck.

Fig. 1
figure 1

Configuration of the continuous box girder bridge over Shanghai Yangtze River and the transportation layout (unit: cm): a cross section and b vertical view

Full size image

This paper first introduces a computer-aided general procedure for dynamic response analysis of coupled train–bridge systems. The finite element method coded in a commercial software package is used to establish the equations of motion of both vehicle subsystem and bridge subsystem. The connections between the two subsystems are considered through wheel-rail contact conditions, and the pseudo-force concept is used to handle contact forces and damping forces within the coupled system. The mode superposition method is then applied to the two subsystems and iterative computation schemes are utilized to find the dynamic solutions. The top plate, the bottom plate, the webs, the cantilever decks and even steel ribs of this continuous composite box girder bridge are all modeled by shell elements in this study to account for the local vibration. The DOFs of the finite element model of the 700-m-length continuous composite girder bridge are so large that component mode synthesis and Guyan reduction are used together with mode superposition method to reduce computation efforts.

The computed results indicate that the serviceability of the bridge and the ride quality of the railway vehicles are in good condition below certain critical speed. However, the resonance phenomenon is observed in the case of some high speeds, and the resonance speed predicted by the analytical method agrees well with the observation from the numerical results. Overall, it is generally feasible to arrange rail transit transportation with speed below 200 km/h on the cantilever deck of the Shanghai Yangtze River Bridge.

2 Train–Bridge Interaction Method

A numerical method has been proposed by Li et al. [11] to facilitate the refined analysis of coupled train–bridge system. This numerical method will be used in this study, and it is briefly introduced in this section for the sake of completion and easy understanding.

2.1 Train Model

A train usually comprises several locomotives, passenger coaches, freight cars, or their combination. Each vehicle is composed of wheel-sets, bogie frames, car body, primary suspension and secondary suspension systems (see Fig. 2). The car body, bogies and wheel-sets could be modeled by beam elements. The primary or secondary suspension systems could be modeled by spring elements and dashpot elements. Based on the established finite element model, the equation of motion of a vehicle can be expressed as:

$$\left[ {m_{\text{v}} } \right]\left\{ {\ddot{\delta }_{\text{v}} } \right\} + \left[ {c_{\text{v}} } \right]\left\{ {\dot{\delta }_{\text{v}} } \right\} + \left[ {k_{\text{v}} } \right]\left\{ {\delta_{\text{v}} } \right\} = \left\{ {f_{\text{v}} } \right\}$$
(1)

where \(\left[ {m_{\text{v}} } \right]\), \(\left[ {c_{\text{v}} } \right]\) and \(\left[ {k_{\text{v}} } \right]\) are, respectively, the mass, structural damping and linear elastic stiffness matrices of the vehicle; \(\left\{ {\delta_{\text{v}} } \right\}\), \(\left\{ {\dot{\delta }_{\text{v}} } \right\}\) and \(\left\{ {\ddot{\delta }_{\text{v}} } \right\}\) denote the displacement, velocity and acceleration vectors of the vehicle, respectively; and \(\left\{ {f_{\text{v}} } \right\}\) are the summation of the wheel-rail contact force vector \(\left\{ {f_{\text{vc}} } \right\}\) and the pseudo-force vector \(\left\{ {f_{\text{vn}} (\dot{\delta }_{\text{v}} ,\delta_{\text{v}} )} \right\}\) produced by all dashpots and nonlinear springs.

$$\left\{ {f_{\text{v}} } \right\} = \left\{ {f_{\text{vc}} } \right\} + \left\{ {f_{\text{vn}} (\dot{\delta }_{\text{v}} ,\delta_{\text{v}} )} \right\}$$
(2)

In this study, the wheel-rail creepage forces are omitted because the emphasis is put on the vertical vibration of the train–bridge system. The wheel-rail jump model [11] allowing for wheel-rail separation is employed to simulate the vertical contact force between the wheel and the rail based on the nonlinear Hertz contact theory.

Fig. 2
figure 2

Schematic model of a railway vehicle

Full size image

To apply the mode superposition method for the train–bridge system, the modal shape and the modal frequency of the vehicle shall be firstly obtained based on the eigenvalue analysis coded in the commercial software package.

$$\left( {\left[ {k_{\text{v}} } \right] - \omega_{\text{v}}^{ 2} \left[ {m_{\text{v}} } \right]} \right)\left\{ {\phi_{\text{v}} } \right\} = \left\{ 0 \right\}$$
(3)

Let us consider the first Nv vibration modes of the vehicle: the modal shape matrix of interest is \(\left[ {\varPhi_{\text{v}} } \right]\); and the corresponding modal frequency matrix is \(\left[ {\omega_{\text{v}} } \right]\). Then, by using the mode superposition method, Eq. (1) can be written as

$$\left\{ {\ddot{q}_{\text{v}} } \right\} + 2\left[ {\xi_{\text{v}} } \right]\left[ {\omega_{\text{v}} } \right]\left\{ {\dot{q}_{\text{v}} } \right\} + \left[ {\omega_{\text{v}}^{ 2} } \right]\left\{ {q_{\text{v}} } \right\} = \left[ {\varPhi_{\text{v}} } \right]^{\text{T}} \left\{ {f_{\text{v}} } \right\}$$
(4)

where \(\left\{ {q_{\text{v}} } \right\}\) and \(\left[ {\xi_{\text{v}} } \right]\) are the modal coordinate vector and the modal damping matrix, respectively; and the superscript T denotes the transpose operation of a matrix.

2.2 Bridge Model

A bridge of various types can be modeled by the finite element method using a series of beam elements, shell elements, volume elements and so on. The finite element method is utilized in this study to establish the equations of motion for the bridge subsystem.

$$\left[ {m_{\text{b}} } \right]\left\{ {\ddot{\delta }_{\text{b}} } \right\} + \left[ {c_{\text{b}} } \right]\left\{ {\dot{\delta }_{\text{b}} } \right\} + \left[ {k_{\text{b}} } \right]\left\{ {\delta_{\text{b}} } \right\} = \left\{ {f_{\text{b}} } \right\}$$
(5)

where \(\left[ {m_{\text{b}} } \right]\), \(\left[ {c_{\text{b}} } \right]\) and \(\left[ {k_{\text{b}} } \right]\) are, respectively, the mass, structural damping and stiffness matrices of the bridge subsystem; \(\left\{ {\delta_{\text{b}} } \right\}\), \(\left\{ {\dot{\delta }_{\text{b}} } \right\}\) and \(\left\{ {\ddot{\delta }_{\text{b}} } \right\}\) denote the displacement, velocity and acceleration vectors of the bridge subsystem, respectively; and \(\left\{ {f_{\text{b}} } \right\}\) is the force vector involving two parts:

$$\left\{ {f_{\text{b}} } \right\} = \left\{ {f_{\text{bc}} } \right\} + \left\{ {f_{\text{bn}} (\dot{\delta }_{\text{b}} ,\delta_{\text{b}} )} \right\}$$
(6)

where \(\left\{ {f_{\text{bc}} } \right\}\) denotes the wheel–rail contact forces exerted on the bridge subsystem; and \(\left\{ {f_{\text{bn}} (\dot{\delta }_{\text{b}} ,\delta_{\text{b}} )} \right\}\) is the pseudo-forces produced by dashpots and nonlinear springs in the bridge subsystem. By utilizing the mode superposition method, Eq. (5) can be changed to

$$\left\{ {\ddot{q}_{\text{b}} } \right\} + 2\left[ {\xi_{\text{b}} } \right]\left[ {\omega_{\text{b}} } \right]\left\{ {\dot{q}_{\text{b}} } \right\} + \left[ {\omega_{\text{b}}^{2} } \right]\left\{ {q_{\text{b}} } \right\} = \left[ {\varPhi_{\text{b}} } \right]^{\text{T}} \left\{ {f_{\text{b}} } \right\}$$
(7)

where \(\left[ {\xi_{\text{b}} } \right]\), \(\left[ {\omega_{\text{b}} } \right]\) and \(\left[ {\varPhi_{\text{b}} } \right]\) are, respectively, the modal damping, modal frequency, normalized modal shape matrices corresponding to the considered Nb modes of the bridge subsystem; and \(\left\{ {q_{\text{b}} } \right\}\) is the modal coordinate vector of the subsystem.

2.3 Numerical Solution

The coupled train–bridge system in this study is divided into two subsystems: the vehicle subsystem and the bridge subsystem. The equations of motion of the two subsystems are, respectively, expressed by Eqs. (4) and (7). The term on the right side of Eqs. (4) and (7) represents the pseudo-forces which are functions of the responses of both the vehicle and bridge subsystems. An iterative scheme [11] is generally required to solve Eqs. (4) and (7).

2.4 Stress Analysis

The generalized coordinates of the bridge are directly obtained from Eq. (7), and the dynamic stress vector \(\left\{ {\sigma_{{{\text{b,}}j}}^{\text{e}} } \right\}\) of the jth element can be obtained as follows:

$$\left\{ {\sigma_{{{\text{b,}}j}}^{\text{e}} } \right\} = \left[ {\varGamma_{{{\text{b,}}j}} } \right]\left\{ {q_{\text{b}} } \right\}$$
(8)

where \(\left[ {\varGamma_{{{\text{b,}}j}} } \right]\) denotes the modal stress matrix which can be determined as

$$\left[ {\varGamma_{{{\text{b,}}j}} } \right]{\mathbf{ = }}\left[ {D_{{{\text{b,}}j}} } \right]\left[ {L_{{{\text{b,}}j}} } \right]\left[ {N_{{{\text{b,}}j}} } \right]\left[ {\varPhi_{{{\text{b,}}j}} } \right]$$
(9)

where \(\left[ {\varPhi_{{{\text{b,}}j}} } \right]\) is the modal shape matrix corresponding to the nodes of the jth element; \(\left[ {N_{{{\text{b,}}j}} } \right]\) denotes the shape function that transforms node displacements to element displacement field; \(\left[ {L_{{{\text{b,}}j}} } \right]\) denotes the differential operator which transforms the element displacement field to the element strain field; and \(\left[ {D_{{{\text{b,}}j}} } \right]\) is the elastic matrix representing the material law.

3 Finite Element Model and Modal Analysis of the Continuous Bridge

In the train–bridge dynamic interaction computation, the finite model of the bridge of interest is required to be established first. It can be established in the commercial software as long as the modal results of the bridge can be then exported for the train–bridge interaction analysis.

The box girder bridge in question (see Fig. 1) is part of bridge approach of the Shanghai Yangtze River Bridge that connects the east of Shanghai and the Chongming Island in China. The bridge is a continuous bridge with an overall length of 700 m and constituted by 7 spans of 90 + 5 × 105 + 85 m. The two box girders in cross section are of 5 m height, separately supported on the two independent piers. The twin box girders are symmetric and independent, and thus only one of the two box girders is considered in this study for dynamic analysis.

3.1 Structural Details and Their Finite Element Models

The prestressed concrete deck is uniform in longitudinal direction of the box girder, while the thickness of the deck explicitly varies along the transverse direction of cross section. The thickness of the concrete deck is, respectively, 200 and 500 mm at the end and the root of the cantilever deck, and it varies to 280 mm at the center of the top plate. The four-node Shell63-Element is applied to model the prestressed concrete deck in commercial software ANSYS. Appropriate shell thickness at the four nodes of any shell element is allocated according to the design drawing. Depicted in Fig. 3 is a typical model detail of the continuous box girder.

Fig. 3
figure 3

Typical model details of the composite box girder bridge

Full size image

The steel webs are connected to the concrete deck through connecting plates and shear rods. The webs of the box girder are made of 28-mm steel plates in the vicinity of the piers and 18-mm steel plates for most of other locations of the girder. The steel bottom plates are of 28 mm in the vicinity of the piers and of 42 mm around the center of each span. The steel bottom plates in the vicinity of piers are also strengthened by 400-mm-thickness concrete to resist the shear force. Shell elements with proper thickness are also used to model these connecting plates, webs and bottom plates of the girder (see Fig. 3).

Longitudinal ribs, transverse ribs and stiffening steel pipes (see Fig. 3) are used to enforce the composite box girder. There are six longitudinal ribs on the bottom plate and generally two longitudinal ribs on each of the two webs. Transverse ribs are installed about every 1.67 m along the bridge span, and stiffening steel pipes are installed every 5 m. All of these ribs are modeled by shell elements of actual thickness, and the stiffening steel pipes are modeled by beam elements.

The bridge deck surfacing and railings are not considered as parts of the bridge structure, but their masses are included in the bridge deck. The sleepers, rail pads of track structures are not modeled in detail, and only the steel rails (see Fig. 3) are assumed to be connected to the cantilever deck directly.

This study focuses on the effect of vertical local vibration of the cantilever deck on the serviceability of the bridge and the ride quality of the railway vehicles, and thus the lateral vibration of piers is neglected and the continuous bridge is assumed to be supported on the ground.

3.2 Applying Component Mode Synthesis Method

The finite element model of the continuous bridge consists of 61,403 nodes and 69,342 elements, and it is quite difficult to find enough modes of vibration of this bridge with a common personal computer. Thus, this bridge is classified as 7 substructures shown as Fig. 4. The fixed-interface method is applied during the process of component mode synthesis. The nodes in the cross section of the supports and these nodes of the steel rail elements are selected as interface nodes for each substructure. For each of the 7 substructures, 100 normal modes are extracted and used to generate the corresponding super-element in ANSYS. The whole bridge model is rebuilt with the generated 7 super-elements.

Fig. 4
figure 4

Substructures and interface nodes of the composite box girder bridge: a vertical view and b plan view of substructure 4 with interface nodes

Full size image

3.3 Modal Analysis Based on Guyan Reduction

Guyan reduction is used to select bridge modes of vibration dominated by the cantilever deck, though modal analysis can be directly conducted based on the rebuilt bridge model with super-elements. It is assumed that details of such large bridge model are not very important for computing the dynamic responses of train bridge system with the exception of the cantilever deck on which railway vehicles must move. In addition, vertical vibration of the cantilever deck is focused in this study, and thus only vertical DOFs of the nodes of the rail elements are defined as master DOFs to facilitate the modal analysis on the basis of Guyan reduction.

A total of 500 modes of vibration ranging from 0.68 to 42.69 Hz are finally extracted using reduced method in ANSYS. Figure 5 shows couples of typical modal shapes of the fourth span of the bridge (substructure 4) and the corresponding frequencies. It can be seen that a few of low-frequency modes of vibration are dominated by global motion of the box girder, while quite a lot of high-frequency modes are dominated by local motion of the cantilever deck. It is noted that high-frequency modes of the cantilever deck are obtained with comparatively small number of modes. Therefore, the generalized DOFs of the bridge are dramatically reduced and the competing effort for train–bridge interaction analysis can be significantly saved.

Fig. 5
figure 5

Typical modal shapes and frequencies of substructure 4 of the composite box girder bridge

Full size image

4 Resonance Conditions of Cantilever Deck Under Moving Loads

The resonance conditions of a cantilever deck under moving loads will be analytically discussed in this section before numerical analyses of train–bridge interaction are conducted. The analytical formulas introduced in this section can be used to verify the followed numerical results, and they also provide a preliminary method for the design and check of the cantilever deck in view of suppressing obvious resonance responses of the plate.

4.1 Equation of Motion of the Cantilever Deck

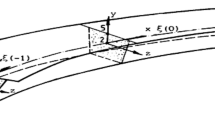
Depicted in Fig. 6 is a plate with sides \(L_{a}\), \(L_{b}\) and constant thickness h subjected to a sequence of moving loads with identical weight P and uniform interval \(d_{\text{v}}\) (\(d_{\text{v}}\) equal to vehicle length \(l_{\text{v}}\)). Suppose the moving loads travel on the plate from left to right at a constant speed V. The equation of motion of the plate subject to the moving loads can be written as

$$D\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2D\frac{{\partial^{4} w}}{{\partial x^{2} \partial z^{2} }} + D\frac{{\partial^{4} w}}{{\partial z^{4} }} + \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} = \sum\limits_{k = 0}^{N - 1} {\delta \left[ {x - V\left( {t - \frac{{k \cdot d_{\text{v}} }}{V}} \right),z - z_{\text{c}} } \right]} P$$
(10)

where w(x, z, t)is the deflection of the plate at position x, z and at time t; \(z_{\text{c}}\) is the lateral position of the center of the track on the plate; N is the total number of moving loads; δ is the two-dimensional Dirac delta function; ρ is density of the plate; and D is the bending stiffness of the plate

$$D = \frac{{Eh^{3} }}{{12(1 - \mu^{2} )}}$$
(11)

where E is the elastic modulus; and μ is the Poisson’s number.

Fig. 6
figure 6

Moving loads of train on the plate with constant thickness

Full size image

The solution of Eq. (10) relies on the boundary conditions for the four edges of the plate. The longitudinal length of a usual cantilever deck is generally much greater than the lateral length of the plate, i.e., \(L_{b} \gg L_{a}\). As a result, the boundary conditions for the two lateral edges of the plate are not essential for the mechanism behavior of the plate part far from these two edges, and these two edges are both assumed to be simply supported hereby. It is noticed that one of the longitudinal edges of the cantilever deck is elastically constrained by the web and top plate of the box girder and the other longitudinal edge is free.

According to the aforementioned boundary conditions, the mode shapes of the cantilever deck can be written as

$$W(x,z) = A^{\prime}_{n} f_{\text{a}} \left( {\frac{z}{{L_{\text{a}} }}} \right)\sin \left( {\frac{n\pi x}{{L_{\text{b}} }}} \right)\quad (n = 1,2,3, \ldots )$$
(12)

where n denotes mode number; \(A^{\prime}_{n}\) is the coefficient used to normalize the modes shapes to mass matrix of the plate; and \(f_{\text{a}} (\frac{z}{{L_{\text{a}} }})\) is the function satisfying the longitudinal boundary conditions, and it can be regarded as the representation of the fundamental lateral bending mode.

The mode shapes of the center of the track on the cantilever deck are obtained as

$$W(x,z_{\text{c}} ) = A_{n} \sin \left( {\frac{n\pi x}{{L_{\text{b}} }}} \right)\quad (n = 1,2,3, \ldots )$$
(13)

where

$$A_{n} = A^{\prime}_{n} f_{\text{a}} \left( {\frac{{z_{\text{c}} }}{{L_{\text{a}} }}} \right)$$
(14)

Using Eqs. (12) and (13), Eq. (10) can be expressed in terms of the generalized coordinates as [2, 5]

$$\left\{ {\begin{array}{*{20}l} {w(x,z,t) = \sum\limits_{n = 1}^{\infty } {A^{\prime}_{n} f_{\text{a}} \left( {\frac{z}{{L_{\text{a}} }}} \right)\sin \left( {\frac{n\pi x}{{L_{\text{b}} }}} \right)} q_{n} (t)} \hfill \\ {\ddot{q}_{n}^{ 2} (t) + \omega_{n}^{ 2} q_{n}^{ 2} (t) = PA_{n} \sum\limits_{k = 0}^{N - 1} {\sin \frac{n\pi V}{{L_{\text{b}} }}\left( {t - \frac{{k \cdot d_{\text{v}} }}{V}} \right)\varGamma_{\text{k}} ,\quad n = 1,2,3 \ldots } } \hfill \\ {\varGamma_{\text{k}} = H\left( {t - \frac{{k \cdot d_{\text{v}} }}{V}} \right) - H\left( {t - \frac{{k \cdot d_{\text{v}} }}{V} - \frac{{L_{\text{b}} }}{V}} \right)} \hfill \\ \end{array} } \right.$$
(15)

where \(\omega_{n}\) is the circular frequency of the cantilever deck; H is a unit step function; \(\varGamma_{\text{k}}\) is the function to determine whether the load is on the plate or not.

4.2 Analogous Resonance Condition as that of a Simply Supported Beam

It is noticed that dynamic solution of the plate subjected to moving loading series represented by Eq. (15) is similar to that of a simply supported beam under moving loading series [2, 5]. Therefore, the resonance conditions of the cantilever deck are introduced by analogy as those of the simply supported beam. According to literatures [2, 5], one of the most important resonance conditions can be expressed as

$$\frac{{\omega_{n} }}{2\pi } = \frac{V}{{d_{\text{v}} }}j\quad (j = 1,2,3 \cdots )$$
(16)

where number j can be explained as the production of the Fourier series expansion of generalized force induced by the moving loading series. This resonant phenomenon occurs when exciting frequency of the moving load series is consistent with one of the free vibration frequencies of the bridge.

The formula expressed as Eq. (16) is just a necessary condition when obvious resonance occurs, and the resonance responses also depend on the span of the simply supported bridge [2, 5]. For small to medium span simply supported bridge, the resonance responses that occur in the fundamental mode are usually the most significant compared with those in other higher modes. As to long-span bridge, the wavelength of the mode shape of the fundamental mode is much longer than the load interval, so remarkable periodical generalized exciting forces cannot be formed in the fundamental mode and the resonance responses are not obvious in such cases. Therefore, this resonance phenomenon is normally concerned in short and medium span bridges [2, 5], while the resonance phenomenon that occurs in long-span bridge is rarely discussed.

4.3 Effect of Modal Shapes of the Cantilever Deck on the Resonance Responses

According to the above knowledge, no obvious resonance responses will occur in the fundamental mode of a cantilever deck with long side \(L_{\text{b}}\), for example, \(L_{\text{b}}\) = 700 m for the girder bridge studied in Sect. 3, whereas this does not mean that resonance responses will not occur in higher modes of the cantilever deck. Actually, because the generalized force in certain mode of the plate depends on the characteristic of the mode shape, the effective span of the cantilever pate could not be measured as plate side \(L_{\text{b}}\) but the wavelength of the mode shape of the track. It is noted from Eq. (13) that the wavelength of the mode shape of the track deceases with the increase in mode number n. As a result, no matter how long the plate side \(L_{\text{b}}\) is, the effective span of the plate, namely the wavelength of the modal shape, will become small enough in higher modes of vibration. Thus, significant periodical generalized exciting forces and resonance responses may occur in some higher modes of vibration of the cantilever deck.

There are quite a lot of high-frequency modes for a cantilever deck, but obvious resonance responses will not occur in all of these high modes, and there shall be a most significant resonance phenomenon occurring in certain critical mode. This critical mode of vibration can be found based on the wavelength of the mode shape. As seen from the second term of Eq. (15), in the case when all of the N moving loads are on the plate, the generalized force in mode n reaches its extreme form and all the loads produce the same generalized force at any time when the following condition is satisfied

$$2L_{\text{b}} /n = d_{\text{v}} /j\quad (j = 1,2,3 \ldots )$$
(17)

The wavelength of the nth mode shape of a simple beam or the track on the deck is \(2L_{\text{b}} /n\). Thus, the condition expressed by Eq. (17) is satisfied when the wavelength of a particular mode shape equal the nominal load interval \(d_{\text{v}} /j\) (see Fig. 7). If the wavelength of mode shape of certain mode equals the load interval \(d_{\text{v}}\) and the frequency of this mode satisfies Eq. (16), this mode shall be the critical mode in which significant resonance responses will occur.

Fig. 7
figure 7

Sketch map of the condition when generalized force of a simply supported beam reaches its extreme form

Full size image

To demonstrate the influence of wavelength of modal shape on the generalized force, a numerical example is used herein. Consider 11 equidistance moving loads with interval 25 m moving on a simply supported beam with span 100 m or a cantilever deck with long side 100 m. The moving speed is set as 305 km/h. Suppose the wavelengths of modal shapes of the beam or the track on the plate vary from 10 to 100 m. The magnitude of any normalized modal shape of the simply supported beam is irrespective of the modal frequency or the wavelength, whereas the maximum generalized force in every mode may be different owing to the difference of the wavelength. On the basis of spectrum analysis of the time-history of the generalized force, the dominant frequency of the generalized force and its magnitude can be obtained. The spectrum of generalized force against various assumed wavelengths of the mode shapes is depicted in Fig. 8. The generalized forces are normalized to 1.0 in Fig. 8. It is observed that the maximum generalized force is obtained when the wavelength of the modal shape equals the load interval 25 m or half the load interval 12.5 m. Therefore, the formula represented by Eq. (17) is proved to be true. It is also seen from Fig. 8 that the dominant frequency can be calculated as the right term of Eq. (16).

Fig. 8
figure 8

Spectra of relative generalized forces against various assumed wavelengths of the mode shapes

Full size image

Overall, if the frequency of certain mode of the cantilever deck equals to the dominant exciting frequency of the moving loads, i.e., Eq. (16) is satisfied for j = 1, and the wavelength of the mode shape of this mode equals to the load interval, i.e., Eq. (17) is satisfied for j = 1, significant resonant responses of the cantilever deck will be produced by the moving loads.

5 Numerical Results and Discussion

5.1 Relevant Parameters for Train–Bridge Interaction Analysis

To illustrate the resonant responses at high speeds, the geometry, stiffness, damping and mass parameters of the high-speed train provided by Wu and Yang [12] is used in this section to investigate dynamic responses of train and the coupled bridge. The car body, wheel-sets and bogies of the vehicle are regarded as rigid bodies, and 10 identical vehicles with vehicle length 25 m are used to compose a train of 250 m. Track irregularities are important excitation sources for railway train–bridge systems. The track irregularities are generated by computer simulation from the power spectrum density function used in German for low disturbance track [13]. The bridge model introduced in Sect. 3 is used for the train–bridge dynamic interaction analysis in this section.

5.2 Responses of the Cantilever Deck

To investigate the influence of train speed on the dynamic responses of the train–bridge system, a total of 15 values of train speed ranging from 125 km/h and 405 km/h are considered in the train–bridge dynamic interaction analyses. Figure 9 shows the maximum deflection, acceleration at the outer rail and the maximum stress at the root of the cantilever deck under various train speeds. It can be seen from Fig. 9 that the defection, acceleration and stress responses of the cantilever deck reach their peak values at the speed of 305 km/h. The cantilever deck is undergoing obvious resonant responses at the speed 305 km/h, as seen from the response time-histories plotted in Fig. 10. Depicted in Fig. 11 is the spectrum of the acceleration responses at the outer rail under various train speeds. One can observe that the acceleration peak with frequency 3.354 Hz occurs at train speed 305 km/h. The dominant exciting frequency \(f_{\text{v}}\) induced by the moving train at speed 305 km/h can be calculated as the right term of Eq. (16)

$$f_{\text{v}} = \frac{V}{{d_{\text{v}} }}j = \frac{305/3.6}{25} \times 1 = 3.389\;{\text{Hz}} .$$
(18)

Figure 12 shows wavelengths of dominant mode shapes of the cantilever of the fourth span at the center of the track. The wavelengths of the modal shapes are determined using spectrum analysis method based on the computed modal shapes of the cantilever deck. It is observed that the wavelengths of the modal shapes generally decrease with the modal frequencies of the cantilever deck, and the wavelength of the mode shape with modal frequency 3.373 Hz just equals the vehicle length of 25 m. The occurrence of these peak responses in Fig. 9 can be explained as a resonance phenomenon when the dominant exciting frequency of the moving train is coincident with the one of the free vibration frequencies of the cantilever deck, and meanwhile the wavelength of the modal shape of this mode equals to the vehicle length.

Fig. 9
figure 9

Maximum responses of the cantilever deck at the center of the fourth span of the composite box girder bridge: a deflection at the outer rail; b acceleration at the outer rail; and c stress at the root of the cantilever deck

Full size image
Fig. 10
figure 10

Response time-histories of the cantilever deck at the center of the fourth span of the continuous girder bridge at train speed 305 km/h: a deflection at the outer rail; b acceleration at the outer rail and c stress at the root of the cantilever deck

Full size image
Fig. 11
figure 11

Spectra of the acceleration responses at the outer rail under various train speeds

Full size image
Fig. 12
figure 12

Wavelengths of dominant mode shapes of the cantilever of the fourth span at the center of the track: a modal frequency 0–40 Hz and b modal frequency 1.5–4 Hz

Full size image

Generally, the dynamic responses of the cantilever at the speeds vicinity to the resonant speed 305 km/h are also quite obvious as seen from Fig. 9, which is a typical phenomenon of resonance. Therefore, to avoid excessive responses of the cantilever deck, the maximum train speed allowed on this cantilever deck, namely the critical speed, should be much less than the resonant speed 305 km/h to sustain sufficient safety margin.

The determination of the critical train speed depends on the threshold values of dynamic responses of the bridge and the train regulated in related codes. The threshold value of maximum bridge acceleration under 30 Hz proposed in European code [14] for the stability of tracks is 3.5 m/s2 for bridges with ballasted tracks and 5.0 m/s2 for other bridges. If ballasted track is applied on the cantilever deck, the train speed should not exceed 225 km/h so that the bridge acceleration will not exceed 3.5 m/s2. In addition, to avoid excessive tensile stress at the root of the concrete cantilever deck and to keep the dynamic impact factor of the tensile stress below the design value 0.3, the train speed should not be higher than 200 km/h.

All in all, it is realized that the analytical formula derived in Sect. 4 predicted the resonance phenomenon and the resonance speed very well compared to the numerical result provided in this section. However, the analytical formula could not give the exact allowable train speed on the cantilever, and the safety margin is neither clear if the maximum train speed is not determined. Compared with the analytical method, the train–bridge dynamic interaction analysis provides a much more reliable method for the design and examination of the dynamic performance of the cantilever deck. For the safety of the cantilever deck of the composite girder bridge concerned in this study and the stability of the track structures on the cantilever deck, it is feasible to arrange train under speed 200 km/h on the cantilever deck while a much higher train speed is not allowed unless the cantilever deck is reinforced or redesigned.

5.3 Responses of the Railway Vehicles

The comfort and safety of the operating vehicles running on the bridge are very important parameters for the design and examination of the bridge. The maximum acceleration of the car body is a usual index used to measure the comfort a vehicle and the unloading factor is often utilized to weigh the safety of the vehicle.

The unloading factor ΔP/P0 is defined as the ratio of the reduction in the vertical force of a wheel to the static wheel load

$$\Delta P/P_{0} = \frac{{P_{0} - P}}{{P_{0} }}$$
(19)

where P0 is the static wheel load and \(P\) is the minimum dynamic vertical force in the wheel of a wheel-set.

Figure 13 shows the car-body maximum vertical accelerations and the maximum unloading factors of the train at various train speed. As seen from the figure, the car-body vertical accelerations do not exceed the threshold value 1.3 m/s2 regulated by the Chinese code [13]. To keep the unloading factor less than the threshold value 0.6 required by the Chinese code [13], the train speed should not exceed 245 km/h.

Fig. 13
figure 13

Maximum responses of the train at various speeds: a car-body vertical acceleration and b unloading factor

Full size image

In summary, the train speed is one of the critical parameters that governs the comfort and safety of the train running on the cantilever deck. The train speed should be less than the speed 245 km/h to guarantee the safety of the train.

6 Conclusion

The feasibility of arranging the running train on the cantilever deck of a continuous girder bridge has been analyzed by the train–bridge dynamic interaction analysis method. It was concluded that the train speed should not be higher than certain critical value to guarantee the safety of the bridge, the stability of the track and the comfort and the safety of the moving train. The obvious resonance phenomenon occurs in the cantilever deck concerned in this study at a resonance speed of 305 km/h, which is predicted exactly with both analytical method and numerical analysis. To keep the train speed under some critical value is the fundamental method to suppress the resonance responses. The analytical method can be used to predict the resonance speed but not the critical speed because it could not give the dynamic responses of the bridges and the coupled trains. Nevertheless, the numerical analysis of train–bridge interaction system provides a more reliable method to determine the critical train speed by comparing the computed responses with those threshold values regulated by related codes. On the basis of numerical analysis, the critical train speed is determined to be 200 km/h for the cantilever deck of the continuous composite box girder bridge over Yangtze River in Shanghai. That’s to say, it is feasible to arrange the train with speed below the critical speed 200 km/h on the cantilever deck of the continuous bridge in this study, but a much higher train speed is not permitted unless the cantilever deck is reinforced or redesigned.

This study only focused on the vertical dynamic performance of the cantilever deck of the box girder bridge under the railway traffic, the local dynamic performance of the top plate and the webs of the box girder are worthy of further study considering both the effects of the railway traffic and the highway traffic in the future. The comparison of the numerical results with the filed measured results is anticipated after the operation of the bridge.