Estimation of abundance from presence–absence maps using cluster models

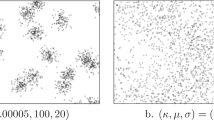
Abstract

A presence–absence map consists of indicators of the occurrence or nonoccurrence of a given species in each cell over a grid, without counting the number of individuals in a cell once it is known it is occupied. They are commonly used to estimate the distribution of a species, but our interest is in using these data to estimate the abundance of the species. In practice, certain types of species (in particular flora types) may be spatially clustered. For example, some plant communities will naturally group together according to similar environmental characteristics within a given area. To estimate abundance, we develop an approach based on clustered negative binomial models with unknown cluster sizes. Our approach uses working clusters of cells to construct an estimator which we show is consistent. We also introduce a new concept called super-clustering used to estimate components of the standard errors and interval estimators. A simulation study is conducted to examine the performance of the estimators and they are applied to real data.

Appendices

Appendix A: Elementary calculations

1.1 A.1 One Cluster

We establish some probabilities associated with a single cluster. Consider a single cell. Let $\lambda \sim \mathrm{Gamma}(\kappa ,\beta )$, which has density

$$\begin{aligned} g(\lambda ;\kappa ,\beta )=\frac{\lambda ^{\kappa -1}}{\Gamma (\kappa )\beta ^\kappa } \exp (-\lambda /\beta ), \end{aligned}$$

where $\lambda >0$ and $\Gamma (\cdot )$ is the usual gamma function. We suppose that given $\lambda$, the number of a species in a grid cell X satisfies $X \sim \mathrm{Poisson}(\lambda )$ so that if $Z=I(X=0)$ we have $p(\lambda )=P(Z=1\mid \lambda )=P(X=0 \mid \lambda )=\exp (-\lambda )$.

Consider a cluster of c random variables $X_1,\ldots ,X_{c}$ that have the same value of $\lambda$, and given $\lambda$, $X_1,\ldots ,X_c$ are independent $\mathrm{Poisson}(\lambda )$ distributed. Hence, $X_1,\ldots , X_{c}$ are exchangeable. Then, with $s=x_1+\cdots +x_{c}$, it yields the following joint distribution

$$\begin{aligned} P(X_1=x_1,\ldots ,X_{c}=x_{c})=\frac{\Gamma (\kappa +s)}{\Gamma (\kappa )x_1! \cdots x_{c}!}\frac{\beta ^s}{(1+c \beta )^{\kappa +s}}. \end{aligned}$$

Clearly the marginal distributions of the $X_\ell$ are negative binomial:

$$\begin{aligned} P(X_\ell =m)=\frac{\Gamma (\kappa +m)}{\Gamma (\kappa )m!}\left( \frac{1}{1+\beta }\right) ^\kappa \left( \frac{\beta }{1+\beta }\right) ^m, m=0,1,\ldots , \end{aligned}$$

so that $E(X_\ell )=\beta \kappa$, $\mathrm{Var}(X_\ell )=\kappa \beta (1+\beta )$ and $\mathrm{Cov}(X_1,X_2)=\kappa \beta ^2$. A direct calculation leads to $\mathrm{Var}\left( \sum _{\ell =1}^{c} X_\ell \right) =\kappa (\beta ^2c^2+\beta c)$.

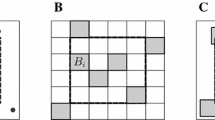
Now, let $F_k$ be the number of nonempty cells in the kth working cluster, $k=1,\ldots ,M/c'$, let $\theta =(\beta ,\kappa )$, and let $p_{c'}(\ell ;\theta )= P(Z_{k}=\ell )$, $\ell =0,1,\ldots ,c'$. Then, with $\theta =(\beta ,\kappa )^\intercal$,

$$\begin{aligned} p_{c'}(j;\theta )=P(F_k=j)&={c' \atopwithdelims ()j} \int _0^\infty (1-e^{-\lambda })^je^{-(c'-j)\lambda }g(\lambda ;\beta ,\kappa ) \mathrm{d}\lambda \nonumber \\&={c' \atopwithdelims ()j} \sum _{\ell =0}^j (-1)^\ell {j \atopwithdelims ()\ell } \int _0^\infty e^{-(c'-j+\ell )\lambda }g(\lambda ;\beta ,\kappa )\mathrm{d} \lambda \nonumber \\&= {c'\atopwithdelims ()j} \sum _{\ell =0}^j{j \atopwithdelims ()\ell } \frac{(-1)^\ell }{\{1+(c'-j+\ell )\beta \}^\kappa }. \end{aligned}$$

(11)

1.2 A.2 Multiple Clusters

Lemma 1

Under the c-cluster model,

$$\begin{aligned}&E(f_0)=\frac{M}{(1+\beta )^\kappa },\quad E(f_0^{c'})=\frac{M}{c'(1+c'\beta )^\kappa }, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{c'}{M} f_0^{c'} \buildrel {a.s.} \over \longrightarrow \frac{1}{(1+c'\beta )^\kappa }, ~ \text{ and } ~\frac{1}{M} f_0 \buildrel {a.s.} \over \longrightarrow \frac{1}{(1+\beta )^\kappa }. \end{aligned}$$

(13)

Proof

First, from (11) we have

$$\begin{aligned} p(0)=p_1(0;\theta )=\frac{1}{(1+\beta )^\kappa }, \text{ and } p_{c'}(0;\theta )=\frac{1}{(1+c'\beta )^\kappa }, \end{aligned}$$

which yields (12). The law of large numbers yields

$$\begin{aligned} T^{-1} \sum _{t=1}^T \sum _{j=1}^K Z_{tj}\buildrel {a.s.} \over \longrightarrow \frac{K}{(1+c'\beta )^\kappa }, \text{ and } T^{-1} \sum _{t=1}^T \sum _{j=1}^K \sum _{k=1}^{c'} Z_{tjk} \buildrel {a.s.} \over \longrightarrow \frac{Kc'}{(1+\beta )^\kappa }, \end{aligned}$$

and (13) follows. $\square$

Lemma 2

$$\begin{aligned} \frac{\partial g(\theta )}{\partial \theta ^\intercal }= M D(\theta ). \end{aligned}$$

Proof

First, $T=M/c$, $K=c/c'$ and

$$\begin{aligned} \frac{\partial g_t(\theta )}{\partial \theta ^\intercal }= \left[ \begin{array}{cc} \frac{\kappa c' K}{(1+c'\beta )^{\kappa +1}}&{}\frac{K \log (1+c'\beta )}{(1+c'\beta )^{\kappa }}\\ \frac{\kappa K c'}{(1+\beta )^{\kappa +1}}&{}\frac{K c'\log (1+\beta )}{(1+\beta )^\kappa } \end{array} \right] . \end{aligned}$$

so that $T{\partial g_t(\theta )}/{\partial \theta ^\intercal }=M D(\theta )$. $\square$

Lemma 3

$\mathrm{Cov}(g_t(\theta ))=K \Sigma (\theta ,K)$.

Proof

Elementary calculations show that for $j \ne \ell$, we have

$$\begin{aligned} E(Z_{tj})&= \mu =\frac{1}{(1+c'\beta )^\kappa },\quad \mathrm{Var}(Z_{tj})=\sigma ^2=\frac{1}{(1+c'\beta )^\kappa }-\frac{1}{(1+c'\beta )^{2\kappa }},\\ \mathrm{Cov}(Z_{tj},Z_{t\ell })&=\sigma _{12}=\frac{1}{(1+2c'\beta )^\kappa }-\frac{1}{(1+c'\beta )^{2\kappa }}, \end{aligned}$$

and

$$\begin{aligned} E(Z_{tjk})&= \mu ^0=\frac{1}{(1+\beta )^\kappa },\quad \mathrm{Var}(Z_{tjk})=\sigma ^{02}=\frac{1}{(1+\beta )^\kappa }-\frac{1}{(1+\beta )^{2\kappa }},\\ \mathrm{Cov}(Z_{tjk},Z_{t \ell m})&=\sigma ^0_{12}=\frac{1}{(1+2\beta )^\kappa }-\frac{1}{(1+\beta )^{2\kappa }}. \end{aligned}$$

Also, note that

$$\begin{aligned} \mathrm{Cov}(Z_{tjk},Z_{tj})&=P(Z_{tj}=1)-P(Z_{tj}=1)P(Z_{tjk}=1)\\&=\frac{1}{(1+c'\beta )^\kappa }\left\{ 1-\frac{1}{(1+\beta )^\kappa }\right\} = s_1 \end{aligned}$$

and

$$\begin{aligned} \mathrm{Cov}(Z_{tj},Z_{t\ell k})&=P(Z_{tj}=1,Z_{t\ell k}=1)-P(Z_{tj}=1)P(Z_{t\ell k}=1)\\&= \frac{1}{\left\{ 1+(c'+1)\beta \right\} ^\kappa }-\frac{1}{(1+c'\beta )^\kappa }\frac{1}{(1+\beta )^\kappa }=s_2. \end{aligned}$$

$\square$

Note that $\Sigma (\theta ,K)$ depends on the true cluster size c through K.

Lemma 4

Let $\theta ^0$ denote the true value of $\theta$. Then

$$\begin{aligned} \widetilde{\Sigma }(\theta ^0) \buildrel {a.s.} \over \longrightarrow \Sigma (\theta ^0,K) \end{aligned}$$

(14)

and hence,

$$\begin{aligned} \widetilde{\Sigma }(\tilde{\theta }_{c'}) \buildrel {a.s.} \over \longrightarrow \Sigma (\theta ^0,K) \end{aligned}$$

(15)

Proof

First, note that if the pair of random variables (W, X) are independent of the pair (Y, Z) and w.l.o.g. all have zero means then

$$\begin{aligned} E\left\{ (W+X+Y+Z)^2\right\}&= E\left\{ (W+X)^2\right\} +E\left\{ (Y+Z)^2\right\} \\&\quad +2E\left\{ (W+X) (Y+Z)\right\} \\&= E\left\{ (W+X)^2\right\} +E\left\{ (Y+Z)^2\right\} . \end{aligned}$$

so that $(W+X)^2+(Y+Z)^2$ and $(W+X+Y+Z)^2$ have the same mean. Now, using (6), $g_t^*(\theta )$, $t=1,\ldots ,T^*$ are independently and identically distributed with zero means and arguing as in Lemma 3, have the common covariance matrix $s^*K\Sigma (\theta ^0,K)=K^*\Sigma (\theta ^0,K)$. Hence

$$\begin{aligned} \left( T^*\right) ^{-1}\sum _{t=1}^{T^*} g^*_t(\theta ) g^*_t(\theta )^\intercal \buildrel {a.s.} \over \longrightarrow K^*\Sigma (\theta ^0,K^0) \end{aligned}$$

and noting that $T^*K^*=M/c'$ yields (14). Next,

$$\begin{aligned} \frac{1}{T^*} \sum _{t=1}^{T^*} g^*_t(\tilde{\theta }_{c'}) g^*_t(\tilde{\theta }_{c'})^\intercal= & {} \frac{1}{T^*} \sum _{t=1}^{T^*} \left[ g^*_t(\tilde{\theta }_{c'})\{ g^*_t(\tilde{\theta }_{c'})^\intercal -g^*_t(\theta ^0)^\intercal \}\right. \\&\left. +\{g^*_t(\tilde{\theta }_{c'})-g^*_t(\theta ^0)\} g^*_t(\theta ^0)^\intercal \right] \end{aligned}$$

and (15) follows from the Toeplitz lemma. $\square$

Lemma 5

Recall $X_t=\sum _{j=1}^K\sum _{k=1}^{c'} X_{tjk}$. Then $\mathrm{Cov}\{g_t(\theta ), X_t\}=K C(\theta ,K)$ where $C(\theta ,K)$ is given by (9), i.e.,

$$\begin{aligned} C(\theta ,K)=\left[ \begin{array}{c}\frac{- c'\kappa \beta }{(1+c'\beta )^\kappa }+(K-1)\left\{ \frac{c'\kappa \beta }{(1+c'\beta )^{\kappa +1}} -\frac{c'\kappa \beta }{(1+c'\beta )^\kappa }\right\} \\ \frac{-c'\kappa \beta }{(1+\beta )^\kappa } - c'(Kc'-1)\frac{\kappa \beta ^2}{(1+\beta )^{\kappa +1}}\end{array}\right] . \end{aligned}$$

Proof

First, $Z_{tj} X_{tj}=0$ and as $E(X_{tj})=c'\kappa \beta$, it is easily seen that

$$\begin{aligned} E\left\{ \left( Z_{tj}-\frac{1}{(1+c'\beta )^\kappa }\right) (X_{tj}-c'\kappa \beta )\right\} =\frac{-c'\kappa \beta }{(1+c'\beta )^\kappa }. \end{aligned}$$

Next,

$$\begin{aligned}&E\left\{ \left( Z_{tj}-\frac{1}{(1+c'\beta )^\kappa }\right) (X_{t\ell }-c' \kappa \beta ) \right\} \\&\quad = E\left\{ Z_{tj}(X_{t\ell }-c'\kappa \beta ) \right\} \\&\quad = E(Z_{tj} X_{t\ell }) -\frac{c'\kappa \beta }{(1+c'\beta )^\kappa } \end{aligned}$$

Now, as $X_{t\ell } \mid \lambda _t \sim \mathrm{Poisson}(c' \lambda _t)$ and for $\ell \ne j$ given $\lambda _t$, $X_{t\ell }$ and $Z_{tj}$ are independent, then for $\ell \ne j$ and $s>0$,

$$\begin{aligned} P(X_{t\ell }Z_{tj}=s)&= P(X_{t\ell }=s,Z_{tj}=1)\\&= \int _0^\infty \frac{\exp (-\lambda c') (\lambda c')^s}{s!} \exp (-\lambda c') \frac{\lambda ^{\kappa -1}}{\Gamma (\kappa )\beta ^\kappa } \exp (-\lambda /\beta ) \mathrm{d} \lambda \\&=\frac{\Gamma (\kappa +s)}{\Gamma (\kappa )s!} \left( \frac{1}{1+2c'\beta }\right) ^\kappa \frac{(c'\beta )^s}{(1+2c'\beta )^{s}}, \end{aligned}$$

so that

$$\begin{aligned} E\left( Z_{tj} X_{t\ell }\right) =\sum _{s=1}^\infty s \frac{\Gamma (\kappa +s)}{\Gamma (\kappa )s!}\left( \frac{1}{1+2c'\beta }\right) ^\kappa \frac{(c'\beta )^s}{(1+2c' \beta )^{s}}= \frac{c'\kappa \beta }{(1+c'\beta )^{\kappa +1}}, \end{aligned}$$

and hence

$$\begin{aligned} E\left\{ \left( Z_{tj}-\frac{1}{(1+c'\beta )^\kappa }\right) (X_{t\ell }-c'\kappa \beta )\right\} =\frac{c'\kappa \beta }{(1+c'\beta )^{\kappa +1}} -\frac{c'\kappa \beta }{(1+c'\beta )^\kappa }. \end{aligned}$$

Thus, the first term in $C(\theta ,K)$ is

$$\begin{aligned} \frac{- c'\kappa \beta }{(1+c'\beta )^\kappa }+(K-1) \left\{ c'\kappa \beta -\frac{c'\kappa \beta }{(1+c'\beta )^\kappa }\right\} . \end{aligned}$$

Similarly,

$$\begin{aligned}&E\left\{ \sum _{j=1}^K \sum _{k=1}^{c'}\left( Z_{tjk}-\frac{1}{(1+\beta )^\kappa }\right) \sum _{j=1}^K\sum _{k=1}^{c'}\left( X_{tjk}- \kappa \beta \right) \right\} \\&\quad = Kc' E\left\{ \left( Z_{tjk}-\frac{1}{(1+\beta )^\kappa }\right) \left( X_{tjk}-\kappa \beta \right) \right\} \\&\qquad + Kc'(Kc'-1) E\left\{ \left( Z_{tjk}-\frac{1}{(1+\beta )^\kappa }\right) \left( X_{tj\ell }-\kappa \beta \right) \right\} \\&\quad = \frac{-Kc'\kappa \beta }{(1+\beta )^\kappa } - Kc'(Kc'-1)\frac{\kappa \beta ^2}{(1+\beta )^{\kappa +1}}. \end{aligned}$$

$\square$

Appendix B: Proofs of Theorems 2, 3, and 5

1.1 B.1 Proof of Theorem 2

Now $g(\theta )$ is the sum of the i.i.d. vectors $g_t(\theta )$, $t=1,\ldots ,T$. These have zero means and, from Lemma 3, the covariance matrix $K\Sigma (\theta ^0)$. The central limit theorem for independent random vectors yields $T^{-1/2}g(\theta ^0) \buildrel D \over \longrightarrow N(0,K\Sigma (\theta ,K))$. Also, ${\partial g(\theta )}/{\partial \theta ^\intercal }=MD(\theta )$ and $\tilde{\theta }_{c'} -\theta \approx -M^{-1} D(\theta ^0) ^{-1}g(\theta ^0)$ so that

$$\begin{aligned} \left( \frac{M}{c}\right) ^{1/2}\left( \tilde{\theta }_{c'}-\theta \right)&\approx -\left( \frac{M}{c}\right) ^{1/2} D(\theta ^0) ^{-1} \frac{1}{M} g(\theta ^0)\\&= -\frac{1}{c} D(\theta ^0) ^{-1} T^{-1/2} g(\theta ^0). \end{aligned}$$

As a consequence, this implies that

$$\begin{aligned} \left( \frac{M}{c}\right) ^{1/2}\left( \tilde{\theta }_{c'} -\theta ^0\right) \buildrel D \over \longrightarrow N\left( 0,\frac{K}{c^2}D(\theta ^0) ^{-1}\Sigma (\theta ^0,K)D(\theta ^0) ^{-\intercal } \right) , \end{aligned}$$

where $D(\theta ^0)^{-\intercal }=\{D(\theta ^0) ^{-1}\}^\intercal$.

1.2 B.2 Proof of Theorem 3

Note that under the c-cluster model, the $X_t(\theta )$ are independent. Then,

$$\begin{aligned} \tilde{N}_{c'} - N&=\tilde{N}_{c'}-M\kappa \beta -\sum _{t=1}^T (X_{t}-Kc'\kappa \beta )\\&\approx M \eta ^\intercal (\tilde{\theta }_{c'}-\theta )-\sum _{t=1}^T (X_{t}-Kc'\kappa \beta )\\&\approx -\eta ^\intercal D(\theta )^{-1}\sum _{t=1}^Tg_t(\theta )-\sum _{t=1}^T (X_t-Kc'\kappa \beta )\\&= -\sum _{t=1}^T \left\{ \eta ^\intercal D(\theta )^{-1} g_t(\theta )+(X_t-c\kappa \beta )\right\} . \end{aligned}$$

As a consequence, we have

$$\begin{aligned} T^{-1/2} \left( \tilde{N}_{c'}-N\right) \buildrel D \over \longrightarrow N(0,w^2(\theta ^0)). \end{aligned}$$

1.3 B.3 Proof of Theorem 5

Without loss of generality, suppose that $c=n_1\times 1$ and $c'=n_2 \times 1$. The proof is complete by considering four cases as follows:

• 1.  $n_1=\phi n_2$, where $\phi \in Z^+$.

  This is the so-called proper case and the estimator is asymptotically unbiased.

• 2.  $n_1=\phi n_2+j$, where $\phi , j\in Z^+$.

  Let $\ell$ be the least common multiple of $n_1$ and $n_2$ and let $\ell /n_1=m_1$ and $\ell /n_2=m_2$. Consider the case where each of the $\ell \times 1$ cells consists of $m_1$ independent $n_1$-clusters. In contrast, the $\ell \times 1$ cells are also divided into $m_2's$ $n_2$-clusters, however, some of these are dependent.

  In regards to the $m_2$ clusters, we find some of them are included in a single $n_1$-cluster but some are from two $n_1$-cluster. Specifically, there may be $[m_2/2]+1$ types of the working clusters, denoted by Type$_s$, where $s=0,1,\ldots ,S$ and $S=[m_2/2]$. A working cluster belongs to the Type$_s$ if it has s cells from another $n_1$-cluster. (Type$_0$ represents that all $n_2$ cells are from a single $n_1$-cluster).

  It is then easy to see that the empty (absence) probability of the Type$_s$ cluster is $\{(1+s\beta )^\kappa (1+(n_2- s)\beta )^\kappa \}^{-1}$. Let $t_s$ be the frequency of Type$_s$, so that $\sum _{s=0}^S t_s= m_2$. Consequently,

  $$\begin{aligned} E\left( \frac{n_2f_0^{n_2}}{M}\right) = \sum _{s=0}^S \frac{t_s}{m_2}\frac{1}{(1+s\beta )^\kappa \left\{ 1+(n_2- s)\beta \right\} ^\kappa } <\frac{1}{(1+n_2\beta )^{\kappa }} \end{aligned}$$

  as $t_0< m_2$.

• 3.  $n_2=\phi n_1$, where $\phi \in Z^+$.

  $E(n_2f_0^{n_2}/M )=\frac{1}{(1+n_1\beta )^{\kappa \phi }}< \frac{1}{(1+n_2\beta )^{\kappa }}$ as $(1+n_1 \beta )^\phi > 1+\phi n_1 \beta = 1+n_2 \beta$.

• 4.  $n_2=\phi n_1+j$, where $\phi , j \in Z^+$.

  Similar to the case 2 and 3.