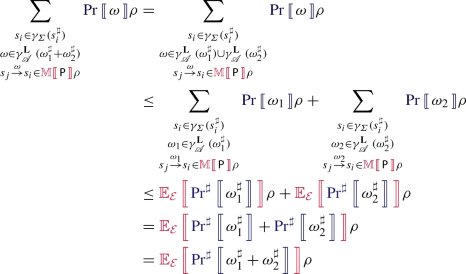Abstract
In this paper we present a static analysis of probabilistic programs to quantify their performance properties by taking into account both the stochastic aspects of the language and those related to the execution environment. More particularly, we are interested in the analysis of communication protocols in lossy networks and we aim at inferring statically parametric bounds of some important metrics such as the expectation of the throughput or the energy consumption. Our analysis is formalized within the theory of abstract interpretation and soundly takes all possible executions into account. We model the concrete executions as a set of Markov chains and we introduce a novel notion of abstract Markov chains that provides a finite and symbolic representation to over-approximate the (possibly unbounded) set of concrete behaviors. We show that our proposed formalism is expressive enough to handle both probabilistic and pure non-deterministic choices within the same semantics. Our analysis operates in two steps. The first step is a classic abstract interpretation of the source code, using stock numerical abstract domains and a specific automata domain, in order to extract the abstract Markov chain of the program. The second step extracts from this chain particular invariants about the stationary distribution and computes its symbolic bounds using a parametric Fourier–Motzkin elimination algorithm. We present a prototype implementation of the analysis and we discuss some preliminary experiments on a number of communication protocols. We compare our prototype to the state-of-the-art probabilistic model checker Prism and we highlight the advantages and shortcomings of both approaches.
















Similar content being viewed by others
Notes
Note that the hardware model of the function
 employs the
employs the  primitive since it emulates the physical delay of wireless transmissions, which is not affected by the drifts of the system clock.
primitive since it emulates the physical delay of wireless transmissions, which is not affected by the drifts of the system clock.
References
Abate A, Katoen J-P, Lygeros J, Prandini M (2010) Approximate model checking of stochastic hybrid systems. Eur J Control 16(6):624–641
Anand S, Păsăreanu, CS, Visser W (2007) JPF-SE: a symbolic execution extension to Java Path Finder. In: TACAS’07, volume 4424 of LNCS. Springer, pp 134–138
Barthe G, Espitau T, Ferrer Fioriti L, Hsu J (2016) Synthesizing probabilistic invariants via Doob’s decomposition. In: CAV ’16, volume 9779 of LNCS. Springer, pp 43–61
Bouissou O, Goubault E, Goubault-Larrecq J, Putot S (2012) A generalization of p-boxes to affine arithmetic. Computing 94(2):189–201
Bouissou, O, Goubault E, Putot S, Chakarov A, Sankaranarayanan S (2016) Uncertainty propagation using probabilistic affine forms and concentration of measure inequalities. In: TACAS ’16, volume 9636 of LNCS. Springer, pp 225–243
Buchholz P (1994) Exact and ordinary lumpability in finite Markov chains. J Appl Probab 31(1):59–75
Chakarov A, Sankaranarayanan S (2013) Probabilistic program analysis with martingales. In: CAV ’13, volume 8044 of LNCS. Springer, pp 511–526
Chakarov A, Sankaranarayanan S (2014) Expectation invariants for probabilistic program loops as fixed points. In: SAS ’14, volume 8723 of LNCS. Springer, pp 85–100
Cousot P, Cousot R (1977) Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: POPL ’77. ACM, pp 238–252
Cousot P, Halbwachs N (1978) Automatic discovery of linear restraints among variables of a program. In: POPL ’78. ACM, pp 84–97
Cousot P, Monerau M (2012) Probabilistic abstract interpretation. In: ESOP ’12, volume 7211 of LNCS. Springer, pp 169–193
Cousot R (1985) Fondements des méthodes de preuve d’invariance et de fatalité de programmes parallèles. Thèse d’État ès sciences mathématiques, Institut National Polytechnique de Lorraine, Nancy, France
Dattatreya GR (2008) Performance analysis of queuing and computer networks. Chapman and Hall/CRC, Boca Raton
Daws C (2004) Symbolic and parametric model checking of discrete-time Markov chains. In: ICTAC ’04, volume 3407 of LNCS. Springer, pp 280–294
De Loera JA, Hemmecke R, Tauzer J, Yoshida R (2004) Effective lattice point counting in rational convex polytopes. J Symb Comput 38(4):1273–1302
Dehnert C, Junges S, Jansen N, Corzilius F, Volk M, Bruintjes H, Katoen J.-P, Ábrahám E (2015) PROPhESY: a PRObabilistic ParamEter SYnthesis tool. In: CAV ’15, volume 9206 of LNCS. Springer, pp 214–231
Dubhashi DP, Panconesi A (2009) Concentration of measure for the analysis of randomized algorithms. Cambridge University Press, Cambridge
Feret J (2001) Abstract interpretation-based static analysis of mobile ambients. In: SAS ’01, volume 2126 of LNCS. Springer, pp 412–430
Ferson S, Kreinovick V, Ginzburg L, Sentz F (2003) Constructing probability boxes and Dempster-Shafer structures. Technical report, SAND2002-4015
Filieri A, Păsăreanu CS, Visser W (2013) Reliability analysis in symbolic pathfinder. In: ICSE ’13. IEEE Press, pp 622–631
Filieri A, Păsăreanu CS, Visser W, Geldenhuys J (2014) Statistical symbolic execution with informed sampling. In: FSE ’14. ACM, pp 437–448
Geldenhuys J, Dwyer MB, Visser W (2012) Probabilistic symbolic execution. In: ISSTA ’12. ACM, pp 166–176
Grimmett G, Stirzaker D (2001) Probability and random processes. Oxford University Press, Oxford
Grïßlinger A (2003) Extending the polyhedron model to inequality systems with non-linear parameters using quantifier elimination. Master thesis, University of Passau
Hahn E, Hermanns H, Zhang L (2011) Probabilistic reachability for parametric Markov models. Int J Softw Tools Technol Transf 13(1):3–19
Jeannet B, Miné A (2009) Apron: a library of numerical abstract domains for static analysis. In: CAV ’09, volume 5643 of LNCS. Springer, pp 661–667
Kemeney JG, Snell JL (1976) Finite Markov chains. Springer, Berlin
Kozen D (1985) A probabilistic PDL. J Comput Syst Sci 30(2):162–178
Kwiatkowska M, Norman G, Parker D (2011) PRISM 4.0: verification of probabilistic real-time systems. In: CAV ’11, volume 6806 of LNCS. Springer, pp 585–591
Le Gall T, Jeannet B (2007) Lattice automata: a representation for languages on infinite alphabets, and some applications to verification. In: SAS ’07, volume 4634 of LNCS. Springer, pp 52–68
Lesens D, Halbwachs N, Raymond P (2001) Automatic verification of parameterized networks of processes. Theor Comput Sci 256(1–2):113–144
Luckow K, Păsăreanu CS, Dwyer MB, Filieri A, Visser W (2014) Exact and approximate probabilistic symbolic execution for nondeterministic programs. In: ASE ’14. ACM, pp 575–586
McIver A, Morgan C (2004) Abstraction, refinement and proof for probabilistic systems. Monographs in Computer Science. Springer, Berlin
Miné A (2006) The octagon abstract domain. Higher Ord Symb Comput (HOSC) 19(1):31–100
Monniaux D (2000) Abstract interpretation of probabilistic semantics. In: SAS ’00, volume 1824 of LNCS. Springer, pp 322–339
Monniaux D (2001) Backwards abstract interpretation of probabilistic programs. In: ESOP ’01, volume 2028 of LNCS. Springer, pp 367–382
Monniaux D (2005) Abstract interpretation of programs as Markov decision processes. Sci Comput Program 58:179–205
Necula G, McPeak S, Rahul S, Weimer W (2002) CIL: intermediate language and tools for analysis and transformation of C programs. In: CC ’02, pp 213–228
Ouadjaout A, Miné A (2017) Quantitative static analysis of communication protocols using abstract Markov chains. In: SAS ’17, volume 10422 of LNCS. Springer, pp 277–229
Parikh R (1966) On context-free languages. J ACM 13(4):570–581
Puterman ML (1994) Markov decision processes: discrete stochastic dynamic programming. Wiley Series in Probability and Statistics. Wiley, Hoboken
Ross S (1996) Stochastic processes. Wiley, Hoboken
Sankaranarayanan S, Chakarov A, Gulwani S (2013) Static analysis for probabilistic programs: inferring whole program properties from finitely many paths. In: PLDI ’13. ACM, pp 447–458
Shafer G (1976) A mathematical theory of evidence. Princeton University Press, Princeton
Soudjani SEZ, Abate A (2014) Precise approximations of the probability distribution of a Markov process in time: an application to probabilistic invariance. In: TACAS ’14, volume 8413 of LNCS. Springer, pp 547–561 (2014)
Suriana P (2016) Fourier–Motzkin with non-linear symbolic constant coefficients. Master thesis, Massachusetts Institute of Technology
Van Hentenryck P, Cortesi A, Le Charlier B (1995) Type analysis of Prolog using type graphs. J Log Program 22(3):179–209
Venet A (1999) Automatic analysis of pointer aliasing for untyped programs. Sci Comput Program 35(2):223–248
Villemot S (2002) Automates finis et intérpretation abstraite: application à l’analyse statique de protocoles de communication. Rapport de DEA, École normale supérieure
Wang D, Hoffmann J, Reps T (2018) PMAF: an algebraic framework for static analysis of probabilistic programs. In: PLDI ’18. ACM, pp 513–528
Wolfram Research, Inc. (2017) Mathematica, Version 11.2, Champaign, IL
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is partially supported by the European Research Council under Consolidator Grant Agreement 681393 – MOPSA.
Appendices
A Proof of Theorem 2
Let \(\rho \in \{\,\rho \;|\;(-,\rho ,-) \in \gamma (I^\sharp )\,\}\) be a concrete initial environment. We divide the proof into two parts.
1.1 A.1 Proof of the weak Markov property
First, we want to prove that:

Let \(s^\sharp _i \in \varSigma ^\sharp \) be an abstract state of the final abstract Markov chain  . We start by linking the evaluation of the abstract distribution
. We start by linking the evaluation of the abstract distribution  to the value of the concrete one
to the value of the concrete one  :
:

where \(\nu _i\) and \(\nu _j\) are the sojourn times at states \(s_i\) and \(s_j\) respectively.
By exploiting the over-approximation of these sojourn times provided by the abstract numeric domain, we can infer the following:

Using the soundness condition guaranteed by Theorem 1 we can derive:

For the next step, we need to over-approximate the concrete transition probabilities  , which is done using the following lemma:
, which is done using the following lemma:
Lemma 1
Let \(s_j \in \varSigma \) a concrete state and \(\omega ^\sharp \in \varOmega ^\sharp \) an abstract scenario. We have:

Proof
We proceed by induction on the structure of \(\omega ^\sharp \) using Definition 12 of abstract scenarios probabilities. An important notice that allows building this proof is that, starting from a concrete state \(s_j\), outgoing transitions could be labeled only by outcomes of the same distribution. Indeed, because we are dealing with transitions from only one discrete time Markov chain  , we can have only a pure probabilistic behavior with no non-determinism and with a single distribution at each state. So, we have the following cases:
, we can have only a pure probabilistic behavior with no non-determinism and with a single distribution at each state. So, we have the following cases:
-
Case \(\omega ^\sharp = \varepsilon ^\sharp \):

-
Case \(\omega ^\sharp = \mathbf {b}_{l}\):

-
Case \(\omega ^\sharp = \overline{\mathbf {b}}_{l}\):

-
Case \(\omega ^\sharp = \mathbf {u}^{i}_{l}\):
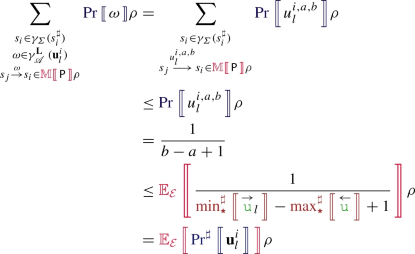
-
Case
 :
: 
-
Case \(\omega ^\sharp = \omega ^\sharp _0 \xi ^\sharp \):

-
Case \(\omega ^\sharp = {\omega ^\sharp }_1 + {\omega ^\sharp }_2\):
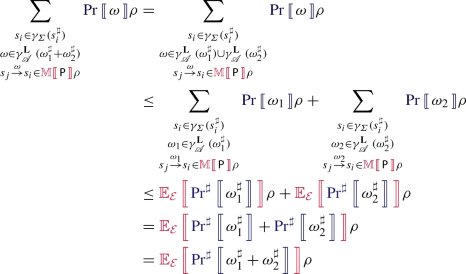
\(\square \)
Finally, using this lemma as an over-approximation of concrete scenario probabilities, we can derive from (4) the following:

\(\square \)
1.2 A.2 Normalization constraint
The second part of the theorem is the normalization constraint:

We have:

\(\square \)
B Benchmarks programs
See Fig. 17.
Rights and permissions
About this article
Cite this article
Ouadjaout, A., Miné, A. Quantitative static analysis of communication protocols using abstract Markov chains. Form Methods Syst Des 54, 64–109 (2019). https://doi.org/10.1007/s10703-019-00331-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10703-019-00331-2





 employs the
employs the  primitive since it emulates the physical delay of wireless transmissions, which is not affected by the drifts of the system clock.
primitive since it emulates the physical delay of wireless transmissions, which is not affected by the drifts of the system clock.


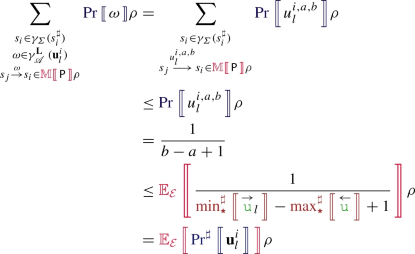
 :
: