Leveraging multiple channels in ad hoc networks

Abstract

We examine the utility of multiple channels of communication in wireless networks under the SINR model of interference. The central question is whether the use of multiple channels can result in linear speedup, up to some fundamental limit. We answer this question affirmatively for the data aggregation problem, perhaps the most fundamental problem in sensor networks. To achieve this, we form a hierarchical structure of independent interest, and illustrate its versatility by obtaining a new algorithm with linear speedup for the node coloring problem.

Appendices

Appendix A: Proof of Lemma 3

Proof

(Proof of Lemma 3) We divide the proof into two parts: we first compute the interference experienced by every node $u\in Q_F\cap E_v^{R}$ caused by nodes outside the region $E_v^{\rho R}$, where $\rho \ge 1$ is a constant that will be determined later; and we then consider the probability that there are no other transmitters in $Q_F\cap E_v^{\rho R}$.

We first compute the interference experienced by u that is caused by nodes outside $E_v^{\rho R}$. Let $C_t$ be the ring with distance from v in the range $[t\rho R,(t+1)\rho R)$ for $t\ge 1$. Without confusion, $C_t$ is also used to denote the set of nodes in $C_t$ that operate on F. Let $M_t$ be maximal R-independent set in $C_t$. Hence, any pair of nodes in $M_t$ are separated by a distance at least R. Because disks $E_w^{R/2}$ for $w\in M_t$ are disjoint, an area argument implies that $|M_t|\le 4(2t+1)\rho (\rho +1)$.

Denote by T the set of nodes outside $E_v^{\rho R}$ that select the same channel and transmit simultaneously with v. Then, we bound the expected interference $I_u$ experienced by u caused by nodes in T as follows.

$$\begin{aligned} \begin{aligned} E[I_u]&=\sum _{w\in T}\frac{P}{d_{wu}^\alpha }\cdot p_w\\&\le \sum _{t=1}^\infty \frac{N\beta R_T^{\alpha }}{((t\rho -1)R)^\alpha }\sum _{y\in M_t}\sum _{w\in E_y^{R}}p_w\\&\le \sum _{t=1}^\infty \frac{N\beta R_T^{\alpha }}{((t\rho -1) R)^\alpha }\cdot 4(2t+1)\rho (\rho +1)\cdot \psi \\&\le \frac{24\cdot 2^\alpha N\beta R_T^{\alpha }\psi }{R^\alpha }\cdot \rho ^{2-\alpha }\sum _{t=1}^\infty t^{-\alpha +1}\\&\le \frac{24\cdot 2^\alpha N\beta R_T^{\alpha }\psi }{R^\alpha }\cdot \rho ^{2-\alpha }\cdot \frac{\alpha -1}{\alpha -2}\\&\le \frac{1}{2}(\frac{P}{\beta R^{\alpha }}-N) \end{aligned} \end{aligned}$$

(4)

The last inequality holds by setting $\rho \ge \left( \frac{48\cdot 2^\alpha N\beta R_T^{\alpha }\psi }{R^\alpha }\cdot \frac{\alpha -1}{\alpha -2}\right) ^{\frac{1}{\alpha -2}}\cdot (\frac{P}{\beta R^{\alpha }}-N)^{-1/(\alpha -2)}$. Using Markov inequality, with probability at least $\frac{1}{2}$, $I_u$ is at most $\frac{P}{\beta R^{\alpha }}-N$.

We next compute the probability that there are no other transmitters in $E_v^{\rho R}$. By standard argument, $E_v^{\rho R}$ can be covered with at most $(2\rho +1)^2$ disks of radius R. Since by assumption, the sum of the transmission probabilities in each disk is at most $\psi$, the sum of transmission probabilities in $E_v^{\rho R}$ is at most $(2\rho +1)^2 \psi$. The probability of the event A that there are no other transmitters in $Q_F\cap E_v^{\rho R}$ can then be bounded below by:

$$\begin{aligned} \begin{aligned} Pr[A]&\ge \prod _{y\in M}\prod _{w\in Q_F\cap E_y^{\rho R}}(1-p_w) \\&\ge (1/4)^{\sum _{w\in Q_F\cap E_y^{\rho R} }p_w} \ge (1/4)^{(2\rho +1)^2\psi }. \end{aligned} \end{aligned}$$

(5)

Setting $\kappa =\frac{1}{2}\cdot (1/4)^{(2\rho +1)^2\psi }\in \varOmega (1)$, we get that with probability $\kappa$, the interference at every node $u\in Q_F\cap E_v^{\rho R}$ is at most $\frac{P}{\beta R^{\alpha }}-N$. By the SINR condition, u will then receive the message of v. $\square$

Appendix B: Dominating set algorithm

For completeness, we introduce the dominating set algorithm, the TWIN protocol, given by Scheideler et al. [25].

In the TWIN protocol, a node can either be inactive or active, and active nodes are either singles or twins, as will be explained later. The active nodes eventually converge to a dominating set. Each round of the TWIN protocol consists of three stages. In Stage 1, the active twins send out an ACTIVE signal with a certain probability so that inactive nodes or active singles can learn about active twins in their vicinity. In Stage 2, those nodes v that have not yet found an active twin in their vicinity probe the wireless medium and adjust their probabilities $p_v$ so that in most rounds the contention within the transmission range of any node is constant bounded. In Stage 3, the non-twin nodes that were able to receive each other’s signal in Stage 2 acknowledge this to each other to be sure to form active twins. In order to become an active single, each node v maintains a counter $acc(v)\ge 0$. Each time $p_v=\hat{p}$, the maximum transmission probability a node can have, it sets $acc(v) :=acc(v) + 4$, and each time $p_v <\hat{p}$, it sets $acc(v) := \max \{acc(v)-1,0\}$. A node is an active single as long as $acc(v) > 0$. The details of each stage is given as follows. Initially, all nodes are inactive and $acc(v) = 0$ for every node v. The probability $p_v$ may be set to any value x with $0 < x\le \hat{p}$. Let $T'_s=(P/\rho ' R_T^\alpha )$, where P is the transmission power of nodes, $\rho '$ is a small constant in (0,1), and $R_T$ is the transmission range of nodes.

• Stage 1: Announcing active twins

  This stage consists of one time slot. In that time slot, each active twin v decides with probability 1/D to send out an ACTIVE signal, where the constant D is an upper bound on the maximum density of twins determined in the analysis. Each inactive node or active single v that receives an ACTIVE signal from a r-neighbor stops executing the protocol (since it is covered) and sets $acc(v) := 0$ (i.e., becomes inactive).

• Stage 2: Guessing the right density

  This stage consists of two time slots. Each inactive node or active single v still participating in the protocol chooses one of the two time slots of this stage uniformly at random, say, slot s. For slot s, v decides with probability $p_v$ to send a PING signal. If v sends a PING signal, it senses the wireless channel with threshold $T'_s$ in the alternative slot, $\bar{s}$. Otherwise, it senses the wireless channel with threshold $T'_s$ in both slots. If it does not sense anything in either case, it sets $p_v := \min \{(1 + \gamma )p_v, \hat{p}\}$, and otherwise it sets $p_v := (1 + \gamma )^{-1}p_v$ for some constants $\hat{p}<1$ and $0< \gamma <1$. Whereas $\gamma$ may be set to any constant value, the analysis requires that $\hat{p}$ to be a small enough constant. If $p_v =\hat{p}$, then $acc(v) :=acc(v)+4$, (i.e., v becomes or remains an active single) and otherwise $acc(v) := \max \{acc(v)-1,0\}$.

• Stage 3: Forming new twins

  This stage consists of two time slots. Every inactive node or active single v that sent a PING signal in some slot s and received a PING signal in the alternative slot $\bar{s}$ does the following. It sends an ACK signal in slot s of this stage and listens to the wireless channel in slot $\bar{s}$ of this stage. If it receives an ACK signal in slot $\bar{s}$, it becomes an active twin.

With the above algorithm, it is shown that in any interval of $\varTheta (\log n)$ rounds, for each node v, the contention in the vicinity and the interference from faraway nodes are bounded in most rounds. In this case, there will be a constant probability ensuring that an active twin appears in its vicinity in each of these rounds. Hence, at the end of the interval, either v joins an active twin or an active twin makes it inactive, with a high probability guarantee. Because each active twin can make all nodes within the transmission range stop executing the algorithm, the conclusion of constant density then follows. Formally, the following result was obtained in [25].

Theorem 4

The TWIN protocol can compute a dominating set of constant density in $O(\log n)$ rounds with high probability.

Appendix C: Cluster size approximation with small ${{\hat{\varvec{\varDelta }}}}$

When the contention is known to be small relative to the number of channels, we can reduce the time complexity for computing the cluster size. Here we consider the case that ${{\hat{\varDelta }}}\le \mathcal {F}\log ^{c}n$ for some constant $c\ge 1$.

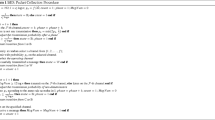
Algorithm For each cluster $C_v$, the algorithm consists of four procedures:

1. Initially, each dominatee in $C_v$ selects a channel from $\mathcal {F}$ uniformly at random. On each channel, the nodes selecting the channel elect a leader by executing the ruling-set algorithm given in Sect. 4. This procedure consists of $\gamma _3\ln n$ rounds, where $\gamma _3$ is set to be a sufficiently large constant such that there are enough rounds for the execution of the algorithm in Sect. 4.

2. On each channel, nodes execute the CSA Algorithm with ${{\hat{\varDelta }}} = \gamma _3\ln ^cn$, where the leader functions as the dominator on the channel.

3. The leaders aggregate the number of nodes that selected the channels they dominate. This procedure consists of $O(\log \mathcal {F})$ rounds. In particular, denote by $U_v=\{x_1,\ldots ,x_\mathcal {F}\}$ the set of leaders in cluster $C_v$. Note that there may be some channels without nodes selecting it and thus without leaders elected on them. Hence, there may be some nodes $x_i$ missing. For each channel that does not have nodes, we add an auxiliary node, and it will be introduced how to deal with these auxiliary nodes in the aggregation process.

We first construct a binary tree on these $\mathcal {F}$ nodes rooted at the dominator using the same manner as the reporter tree construction in Sect. 5.2. Then we use the data aggregation algorithm on the reporter tree given in Sect. 6 to aggregate the number of nodes to the dominator. Specifically, we need to handle here the auxiliary nodes. The solution is to divide each slot in each round into two sub-slots (recall that there are two slots in each round for the data aggregation on reporter trees), and make a parent send the ack message when it receives a message from its children. For each node $x_j$ transmits, if it does not receive the ack message from its parent, which means that its parent is an auxiliary node, $x_j$ will function as its parent in the subsequent aggregation process.

4. Finally, in a single round, v broadcasts the estimate of the cluster size to its dominatees on the first channel.

Analysis

Proof of Lemma 11 Consider a cluster $C_v$. We analyze the four procedures one by one. We first bound the number of nodes operating on each channel in the first procedure.

Claim

For a cluster $C_v$, in the first procedure, there are at most $2\ln ^c n$ nodes on each channel with probability $1-n^{-2}$.

Proof

Because dominatees select channels uniformly at random, the expected number of dominatees selecting each channel is at most $\ln ^cn$. Consider a channel F. Using Chernoff bound (3), we get that the number of dominatees selecting F is at most twice the expectation, with probability $1-n^{-3}$. By the union bound on all channels, the result follows. $\square$

A channel F is nonempty with respect to a cluster $C_v$ if there are dominatees in $C_v$ selecting it in the first procedure. Using a similar argument for proving Lemma 13, we have the following result for the first procedure.

Claim

For each cluster and each nonempty channel F, exactly one leader is elected on F in $O(\log n)$ rounds, with probability $1-n^{-2}$.

Using a similar argument for proving Lemma 10, we have the following result for the second procedure.

Claim

Each leader in each cluster can get an absolute constant approximation of the number of dominatees selecting its channel in $O(\log n\log \log n)$ rounds, with probability $1-n^{-2}$.

By Lemma 8, a node will receive an ack message after it sends a message to its parent if its parent is not an auxiliary node. Hence, the auxiliary nodes will not affect the aggregation process in the third procedure. Hence, we have the following result.

Claim

For a cluster $C_v$, the estimates of leaders will be aggregated to the dominator v in $O(\log \mathcal {F})$ rounds.

After the estimates of leaders are aggregated to the dominator, the dominator v will get a constant approximation of the cluster size by Claim 1. Then in the fourth procedure, v can send the estimate of the cluster size to all dominatees by Lemma 8. Adding the time used in each procedure, each node in cluster $C_v$ will get a constant approximation of the cluster size in $O(\log n\log \log n)$ rounds with probability $1-O(n^{-2})$. The result is then proved by the union bound. $\square$