1 Introduction

Current trends in international markets such as competition and globalization are forcing all organisations across supply chains to reduce their costs including logistics expenditures (related to travel distance, travel time, holding cost, etc.) through more efficient decision making. Routing and loading are important parts of such decisions. In the case of frozen and perishable items in particular, tackling the Vehicle Routing Problem (VRP) and vehicle loading simultaneously can enhance a logistics system (Schmid et al. 2013).

The well-known VRP is a combinatorial optimisation problem which is usually formulated as an integer programming model. The VRP aims to generate a number of vehicle routes. Each vehicle will be loaded at a single depot and be routed to service a group of customers then return to the depot. Each customer will be serviced once and only once, and the demands of all customers must be met. The objectives associated with the VRP vary across the literature. The two most frequent objectives are minimising the number of vehicles used and minimising the total travel distance. In practice, the capacity of a vehicle is limited. The VRPs that take the vehicle capacity into consideration are termed Capacitated VRPs (CVRPs). Further, deliveries are often subject to time constraints (time windows), leading to the Capacitated Vehicle Routing Problem with Time Windows (CVRPTW). A detailed survey of the exact algorithms on CVRP and different methodologies on VRPTW can be found in Baldacci et al. (2010) and EI-Sherbeny (2010) respectively.

The Vehicle Loading Problem (VLP) is also a challenging combinatorial optimisation problem. The goal is to optimally load/pack a set of pallets/items into a set of vehicles/bins of predefined dimensions, which is also a form of Bin-Packing problem (Wäscher et al. 2007). Several versions of the problem exist depending on the number of pallet dimensions (one-, two- or multi-dimensional) and the characteristics of the items they are carrying (guillotine, fragility, stability, etc.). A detailed survey on constraints in container loading can be found in Bortfeldt and Wäscher (2013). Although there are many research papers in the area of loading problems, there remain many unexplored topics in this field when it comes to practical aspects of the problem (Schmid et al. 2013).

This paper analyses a Multi-Objective Vehicle Routing and Loading Problem with Time Window constraints (MO-VRLPTW). This research is motivated by a real-life application in the food services industry, delivering a mixture of Ambient, Produce, Chilled and Frozen food together with basic kitchen cleaning Chemical products. The deliveries are loaded onto three types of containers: pallets, and small and big roll-cages. The frozen food needs to be palletised and loaded into the front compartment of the vehicle and is separated with a bulkhead from the rest of the products. The chilled food is also palletised, whereas the ambient food is packed onto big roll-cages and the chemical cleaning materials are kept on separate big roll-cages. Finally, the produce is packed onto small roll-cages. The vehicles are multi-temperature, rigid trucks with two unloading doors. A main rear door with tail-lift is used for unloading chilled, chemical, produce and ambient products. A side door near the front left of the truck is used for unloading frozen products only. The bulkhead separating the main compartment from the frozen compartment is moveable to allow variation in quantity of frozen food loaded (and is raised to allow faster loading of frozen goods).

For simplicity of exposition, the term pallet is used to refer to both types of pallet, big and small roll-cages. Figure 1 provides a loading diagram.

Fig. 1
figure 1

A loading diagram

Full size image

From Fig. 1, it can be seen that a number of rectangular pallets of different lengths and widths and of the same height need to be loaded onto the vehicle in a feasible way. However, before loading the pallets onto the vehicle, the 3D items ordered by the customers need to be loaded onto the pallets. Since the decision maker assumes that if the total volume and the total weight of the items do not exceed the volume and weight limit of the pallet, then the items can be physically loaded onto the pallet. The 3D items can be treated as 1D items. Thus the items of same type ordered by the same customer are recorded by their weights, volumes and numbers rather than their weights, lengths, widths and heights, following the ontology of the Pallet-Packing Vehicle Routing Problem (PPVRP) (Zachariadis et al. 2012). Note that in Fig. 1, the shapes representing items in each pallet do not reflect the actual sizes (volumes, weights and numbers) of the items. The shapes only carry the information of the customer indices. Apart from the weight and volume limits for pallets of different sizes, there are also weight and volume limits for the vehicles as a whole. So this MO-VRLPTW is actually a MO-VRLPTW with 1D pallet loading and 2D vehicle loading constraints.

The mathematical description of the above problem is as follows:

  • Customers We are given a complete undirected graph \(G=(V,E)\), in which V defines the set of \(n+2\) vertices corresponding to the depot (vertex 0 and n+1) and to the customers (vertices \(1, \ldots , n\)). Each edge (i, j) of the graph has an associated travel distance \(d_{ij}\), which is the distance of travelling from customer i to customer j. In addition, there is a time window \([e_i, l_i]\) related to each customer \(i \in V\) that specifies that customer i cannot be serviced before \(e_i\) or visited later than \(l_i\). However, waiting times are permitted. That is, a customer i can be reached before the start of their time window \(e_i\) but the truck has to wait there until \(e_i\) to start servicing the customer.

  • Items Each customer \(i\in V \backslash \{0, n+1\}\) requires a supply of \(m_{is}\) items of type \(s\in S\), where \(S =\,\){1—ambient; 2—chemical; 3—chilled; 4—frozen; 5—produce} is the product type set. The total weight and volume of these items are \(w_{is}\) and \(v_{is}\), ordered by the customers. The \(m_{is}\)items are of the same weight and volume and can be treated as 1D objects.

  • Orders The items of different product types ordered by the same customer \(i\in V \backslash \{0, n+1\}\) is called order \(i\in V \backslash \{0, n+1\}\).

  • Pallets There are in total five types of pallets of width \(\omega _s\) and length \(l_s\), where \(s \in S = \{1,2,3,4,5\}\). The items of product type s will be loaded in pallet type s. In addition, each pallet has weight capacity \(DW_{s}\) and volume capacity \(DV_{s}\) limits, for \(s \in S\).

  • Vehicles The delivery of orders is performed by a fleet \(F=\{1, 2, \ldots , K\}\) of identical vehicles, each one with weight capacity D. The two dimensional loading area has width W and length L. So the total loading area available for each vehicle is \(A = W\cdot L\).

In addition, the following loading constraints must be satisfied:

  • The delivered orders are directly unloaded from the vehicle-loading space, without it being necessary to reposition any of the orders that are going to be delivered later on the route. In the literature, the last-in-first-out (LIFO) constraint was defined, where only the straight movements parallel to the length dimension of the vehicle surface are allowed when unloading items (Gendreau and Martello 2006; Iori et al. 2007; Wei et al. 2015). In this paper, we define the adapted LIFO constraint, which allows the combination of the straight movements parallel to both the length dimension and the width dimension of the vehicle surface. An assumption is also made that, after unloading the customer orders, the empty roll-cages can be collapsed and empty pallets can be strapped to the side so they do not interfere with unloading.

  • All pallets need to be loaded onto this vehicle in a feasible way. The feasibility of the way of loading a set of pallets onto the vehicle is defined as follows.

    • The pallets must not overlap.

    • The pallets cannot be rotated 90\(^{\circ }\) about the vertical axis.

    • All ambient and chemical items need to be loaded on pallet type \(s=1\) and \(s=2\). All chilled and frozen items need to be loaded on pallet type \(s=3\) and \(s=4\). All produce items need to be loaded on pallet type \(s=5\).

    • The frozen products must be loaded at the front of the truck with a handling area (of width \(\omega _h\) and length \(l_h\)) for unloading and be separated from the rest of the products with a bulkhead of fixed width \(\omega _b\) and length \(l_b\). From Fig. 1, it can be seen that \(\omega _h = \omega _b = W\).

  • The capacities (weight and loadable area) of pallets of different types need to be respected.

  • The capacities (weight and volume) of vehicles need to be respected.

  • Order splitting is not allowed. That is, an order must be loaded on the same vehicle. Note that the problem assumes that a vehicle is always sufficient for accommodating the order of a single customer.

Fig. 2
figure 2

Illustration of a feasible loading of the vehicles

Full size image

Figure 2 presents the loading of the vehicle graphically, which illustrates an example solution for an MO-VRLPTW instance of two vehicles with 10 customers, requiring in total 1 pallet for frozen products, 3 pallets for chilled products, 15 pallets for ambient products, 2 pallets for chemical products and 3 pallets for produce products. From Fig. 2, it can be seen that the adapted LIFO constraint is necessary. For example, in route A, after unloading the pallets carrying order 1 and 2, the next pallet carrying item 3 needs to be moved down first then to the right of the vehicle to avoid repositioning the chilled pallet next to the right door of the vehicle.

Finally, there are three objectives in the problem that we are examining. The first two objectives are to minimise the total travel distance and the number of routes, which are frequently found in the CVRPTW literature. The third objective is to minimise the total number of mixed orders in the same pallet. Consulting our industrial partner, they favour putting the same orders in the same pallets with as minimum mixture as possible (that is, the same pallet should contain the items from the same customer of same product type). This is because when unloading a dedicated pallet (a pallet that contains the items from the same customer of same product type), the driver can work quicker as he/she does not have to check the items as would be the case for a mixed order pallet. In addition, the likelihood of expensive mis-delivery is reduced. For each current order, there are two loading strategies. One is to start loading the current order in an empty pallet and the other is to start loading the current order in the pallet loaded with the previous order from a different customer. The pallet with mixture of orders comes from the second strategy only. Thus, to minimise the total number of mixed orders in the same pallet, we need to apply the second loading strategy as few times as possible, that is, to minimise the total number of loading strategies that start loading the current order in the pallet loaded with the previous order from a different customer. A graphical explanation of these two loading strategies can be found in Sect. 3.

For real-world problems, the sequence of the customers to be visited by the vehicle routes and the sequence of the products to be loaded onto the pallets and vehicles should be efficiently designed to avoid unnecessary unloading and repacking operations. Solving these loading and routing problems separately may lead to suboptimal decisions, which means optimal solutions can be found for these two problems independently. However, neither of these optimal solutions is likely to be optimal for the integrated problem. The purpose of this paper is to propose a Mixed Integer Linear Programming (MILP) model for the MO-VRLPTW, capturing the interdependencies of these two problems. To achieve a solution with no preferential information known in advance from the decision maker, the MILP model is constructed with one objective function, minimising the total cost, where the three original objective functions are incorporated as parts of the total cost function. The MILP can be solved to optimality for small-sized problems. A Generalised Variable Neighbourhood Search (GVNS) algorithm is also proposed to find solutions for a real-life large-sized problem.

The remainder of the paper is organised as follows: Sect. 2 provides a literature review. Section 3 provides a MILP mathematical formulation for the MO-VRLPTW. Section 4 presents a detailed solution methodology. Section 5 introduces new MO-VRLPTW instances. It also evaluates the performance of the proposed method, providing various experimental results. Finally, Sect. 6 concludes the paper and offers some possible future research directions.

2 Literature review

The proposed MO-VRLPTW in this paper is a variant of the CVRPTW with two/three-dimensional loading constraints (2/3L-CVRP) (Iori and Martello 2010).

The 2/3L-CVRP problems and their variants have only been studied recently; for example the first paper on 2L-CVRP was published by Iori et al. (2007). The 2L-CVRP deals with an extension of the CVRP problem where the total weight of the demand of a customer is determined by several items ordered by the customer. Items have different widths and lengths and are of the same height as the vehicle, while the loading floor of each vehicle is a rectangle with fixed width and length. In addition to the classical CVRP capacity constraint, a solution requires a feasible non-overlapping loading of all items into the loading area of the vehicles. Additional operational constraints are introduced for easy unloading at each customer site. This is sequential loading or Last-In First-Out (LIFO). The authors Iori et al. (2007) solved the underlying problem to optimality with a branch-and-cut method for instances involving up to 30 customers and 90 boxes. Lately, Côté et al. (2014) and Hokama et al. (2016) presented improved branch-and-cut methods for the first 60 instances of the 180 created 2L-CVRP instances reported in Gendreau et al. (2007). Most of the 2L-CVRP instances were tackled with heuristic, meta-heuristic and evolutionary methods. For example, Tabu Search (TS) (Gendreau et al. 2007; Zachariadis et al. 2009; Leung et al. 2011), Ant Colony Optimisation (ACO) (Fuellerer et al. 2009) are the two most popular ones. Other heuristic and meta-heuristic algorithms used are Simulated Annealing (SA) (Leung et al. 2013; Wei et al. 2018), Greedy Randomized Adaptive Search Procedure (GRASP) (Duhamel et al. 2011), VNS (Wei et al. 2015), Iterated Local Search (ILS) (Pollaris et al. 2017), Elitist Non-dominated Sorting Local Search (ENSLS) (Alinaghian et al. 2017) and column generation based heuristics (Pinto et al. 2018). Considering the relevant classic variants of 2L-CVRP, the following papers have been found in the literature: Khebbache-Hadji et al. (2013) considered a 2L-CVRP with time window constraints. That is, customer services must be performed within predetermined time windows. This type of problem is called 2L-CVRPTW. The authors provided some heuristics and GA algorithms to tackle the 2L-CVRPTW. In Leung et al. (2013), the vehicles are not identical. The SA algorithm was presented combined with a heuristic local search to improve the solutions found. In Martínez (2013), the transported items are circular in shape. Most recently, in Zachariadis et al. (2016), a memorisation technique is designed to solve a VRP with Simultaneous Pick-ups and Deliveries and Two-Dimensional Loading Constraints (2L-SPD). Dominguez et al. (2016) examined a two-dimensional loading capacitated vehicle routing problem (2L-CVRP) with a heterogeneous fleet (2L-HFVRP) using a biased randomization technique. Côté et al. (2017) considered the 2L-CVRP in an integrated manner and compared the solutions with those obtained from three non integrated approaches based on addressing separately the routing and the loading problems. Bódis and Botzheim (2018) applied Bacterial Memetic Algorithms for a order picking routing Problem with pallet loading constraints, which is also a variant 2L-CVRP.

The first research on 3L-CVRP was developed by Gendreau and Martello (2006). Unlike 2L-CVRP, the 3L-CVRP considers customer demand to be composed of orthogonal three-dimensional boxes of different widths, lengths and heights. These boxes must be loaded into the rectangular vehicle containers. Additional operational constraints are introduced to ensure the stability of stacked boxes, the secure transportation of fragile boxes and the easy unloading of boxes at customers’ sites (LIFO). The authors proposed TS to tackle problem instances involving up to 100 customers and 199 boxes. Junqueira et al. (2011) applied an MIP-based approach for the container loading problem with multi-drop constraints, which is a simplified 3L-CVRP. Metaheuristic approaches for the 3L-CVRP can be classified as: TS (Gendreau and Martello 2006; Tarantilis et al. 2009; Bortfeldt 2012; Zhu et al. 2012; Ruan et al. 2013; Tao and Wang 2015; Reil et al. 2018), ACO (Fuellerer et al. 2010), Genetic Algorithm (GA) (Moura 2008; Moura and Oliveira 2009), VNS (Wei et al. 2014) and Evolutionary Local Search (ELS) (Zhang et al. 2015). Most recently Vega-Mejia et al. (2019) have extended an existing vehicle routing problem with loading constraints (VRPLC) optimization model to a nonlinear optimization model that considers weight-bearing strength of three-dimensional items, vehicle weight capacity, weight distribution inside vehicles, delivery time windows, and a balanced fleet of vehicles. The model was solved with an optimisation software. Some efforts on setting up a mathematical model for the 3L-CVRP can also be found in Moura (2019), in which the problem was defined as an integration of a VRPTW and a 3D-CLP (Container Loading Problem).

In particular, one of the recent publications on Pallet-Packing Vehicle Routing Problem (PPVRP) (Zachariadis et al. 2012) is mostly related to the MO-VRLPTW as illustrated in Sect. 1. In the PPVRP, a number of three-dimensional rectangular boxes (items) need to be feasibly stacked into pallets that are then loaded onto the vehicles before initiating their tours. A 3L-CVRP can be viewed as a PPVRP instance that involves vehicles carrying only one pallet.

Although all of the above mentioned literature addresses 2/3L-CVRPTW problems and their variants, the objective functions of the studies are rather simple. Furthermore, the objectives only consider economic rather than logistical aspects of the problem. To our best knowledge, there is only one paper in the literature, addressing three objectives when dealing with 2/3L-CVRPTW (Moura, 2008). However, most real-world problems involve multiple objectives. From the above literature review, no formal mathematical model is available for the MO-VRLPTW in the literature. The MILP model built in this paper is hence novel.

From methodological point of view, a number of publications applied VNS to solve VRPTW or TSPTW problems. The most recent works are Armas et al. (2015), Bortfeldt et al. (2015), Dhahri et al. (2015), Kalayci and Kaya (2016), Karabulut and Tasgetiren (2014), Mladenović et al. (2012), Silva and Urrutia (2010), Sze et al. (2016), Tricoire et al. (2011), Wei et al. (2015), in which three most relevant papers are Bortfeldt et al. (2015), Tricoire et al. (2011) and Wei et al. (2015), who solved VRPs with loading constraints. The VNS has also been applied to solve the multi-objective optimisation (MOO) successfully, like Janssens et al. (2015) and Duarte et al. (2015). However, to our best knowledge, no paper in the literature has solved the MO-VRLPTW problem proposed in this paper. Thus the model and methodology developed are novel.

3 Mathematical modelling

The mathematical model is constructed in a way that the orders of the same route are loaded onto the same vehicle physically, thus satisfying the constraints described in Sect. 1. The following notations are defined for our MO-VRLPTW.

3.1 Sets

  • \(V = \{0,1,\ldots , n, n+1\}\)—Node set, where \(i = 0\) and \(i = n+1\) represents the depot and \(i=1,\ldots ,n\) represent customers;

  • \(S =\,\) {1—ambient; 2—chemical; 3—chilled; 4—frozen; 5—produce}—Product type set and pallet type set, where \(s\in S\) represents both the sth type of product and the pallet type s.

  • \(F = \{1,2, \ldots , K\}\)—Vehicle set and \(k\in F\) represents the kth vehicle.

3.2 Parameters

3.2.1 Input parameters

The following are input parameters provided by the customers of our industrial partner:

  • P—The fuel cost per kilometre.

  • H—The cost of hiring one vehicle.

  • I—The cost of inconvenience incurred by unloading one mixed order from a pallet.

  • \(d_{ij}\)—The distance of travelling from node i to node j, (\(i,j \in V\)).

  • \([e_i, l_i]\)—The time window of customer \(i, i \in V \backslash \{0, n+1\}\) indicating that customer i cannot be serviced before \(e_i\) or visited later than \(l_i\).

  • \(\tau _{ij}\)—The travel time between nodes i and j, \(i, j \in V \).

  • \(T_{i}\)—Service time at customer i, \(i \in V \backslash \{0, n+1\}\).

  • \(m_{is}\)—The number of items of product type \(s\in S\) requested by customer i, \(i \in V\backslash \{0, n+1\}\), \(s\in S\).

  • \(w_{is}\)—The total weight of the items of type \(s\in S\) requested by customer i. The weight of one item of product type s needed by customer i is \( \frac{w_{is}}{m_{is} }\). The total weight of the customer order i is \(\sum _{s=1}^5 w_{is}\), \(i \in V\backslash \{0, n+1\}\), \(s\in S\).

  • \(v_{is}\)—The total volume of the items of type \(s\in S\) requested by customer i. The volume of one item of product type s needed by customer i is \(\frac{v_{is}}{m_{is}}\). The total volume of customer order i is \(\sum _{s=1}^5 v_{is}\), \(i \in V\backslash \{0, n+1\}\), \(s\in S\).

  • \(\omega _s\)—The width of the pallet s, \(s \in S\).

  • \(l_s\)—The length of the pallet s, \(s \in S\).

  • \(\omega _b\)—The width of the bulkhead.

  • \(l_b\)—The length of the bulkhead.

  • \(\omega _h\)—The width of the handling area when the bulkhead is needed.

  • \(l_h\)—The length of the handling area when the bulkhead is needed.

  • \(DW_{s}\)—The weight capacity of pallet s, \(s \in S\).

  • \(DV_{s}\)—The volume capacity of pallet s, \(s \in S\).

  • W—The width of the loading area in the vehicle k, \(k \in F\).

  • L—The length of the loading area of the vehicle k, \(k \in F\). The total loading area available for each vehicle is \(A = W\cdot L\).

  • D—Weight capacity of the vehicle k, \(k \in F\).

3.2.2 Calculated parameters

The following parameters are defined in order to simplify the formulation:

  • \(uw_{is}\)—The weight of one item of type \(s\in S\) requested by customer i. \(uw_{is}=\frac{w_{is}}{m_{is}}\).

  • \(uv_{is}\)—The volume of one item of type \(s\in S\) requested by customer i. \(uv_{is}=\frac{v_{is}}{m_{is}}\).

  • \(maxM_{is}\)—The maximum number of items of type \(s\in S\) requested by customer i, which can be loaded in pallet s. \(maxM_{is} =min(\lfloor \frac{DW_s}{uw_{is}} \rfloor ,\lfloor \frac{DV_s}{uv_{is}}\rfloor )\).

  • \(minX_{is}\)—The minimum number of pallets required to load items of type \(s\in S\) requested by customer i on pallet type s. \(minX_{is} = \lceil m_{is}/maxM_{is} \rceil \).

3.3 Decision variables

  • \(y_{ijk}\)—A binary variable, which equals 1, if customer j is served immediately after customer i by vehicle k; 0, otherwise. \(i \in V\backslash \{n+1\}\), \(j \in V \backslash \{0\}\) and \(i\ne j\).

  • \(z_k\)—A binary variable, which equals 1, if vehicle k is used; 0, otherwise. \(k \in F\).

  • \(t_{ik}\)—Arrival time of vehicle k at node i. \(i \in V \backslash \{0\}\).

  • \(Z_{js}\)—A binary variable, which is equal to 1, if items of type \(s\in S\) requested by customer j starts in an empty pallet of type s; 0, otherwise.

  • \(B_{js}\)—A binary variable, which equals 1, if items of type \(s\in S\) requested by customer j can be completely loaded in the same pallet with the previous order by another customer; 0, otherwise.

  • \(qV_{js}\)—Cumulated volume in the last pallet of type s for items of type \(s\in S\) requested by customer j.

  • \(qW_{js}\)—Cumulated weight in the last pallet of type s for items of type \(s\in S\) requested by customer j.

  • \(X_{js}\)—Number of pallets used for loading items of type \(s\in S\) requested by customer j.

  • \(nP_{js}\)—Number of extra pallets needed for loading items of type \(s\in S\) requested by customer j (Compared with \(X_{js}\), the pallet with the mixture of the items requested by customer j and items requested by previous customers do not count in \(nP_{js}\). A graphical explanation of \(X_{js}\) and \(nP_{js}\) can be found in Sect. 3.4).

  • \(nPallet_{jsk}\)—Number of extra pallets of type s needed to load order j in vehicle k excluding the pallets used for loading the previous orders.

  • \(XV_{k}\)—x coordinate of the reference point of the vehicle k.

  • \(YV_{k}\)—y coordinate of the reference point of the vehicle k.

  • \(XP_{ksu}\)—x coordinate of the reference point of the uth pallet of type s on vehicle k.

  • \(YP_{ksu}\)—y coordinate of the reference point of the uth pallet of type s on vehicle k.

  • \(maxL_{k}\)—maximum x-coordinate of all the pallets loaded on the vehicle k.

3.4 The MILP model

In this paper, the MO-VRLPTW is modelled in two stages. In Stage One, the routing and 1D pallet loading problem will be tackled simultaneously, whereas the 2D vehicle loading will be tackled in Stage Two. This is due to the complexity of the 2D vehicle loading problem.

To avoid the sub-optimality discussed in Sect. 1, a constraint is added to the Stage One modelling to guarantee that the total areas of the pallets to be loaded onto the vehicle will not exceed the loadable area of the vehicle \(\alpha \cdot L\cdot W\), where \(\alpha \) is a percentage to indicate the required level of the usage of the vehicle. The lower \(\alpha \) will lead to unnecessary wastage. The higher \(\alpha \) might lead to an infeasible solution in Stage Two. A set of discrete \(\alpha \) values were used to run the Stage One and Stage Two models in an iterative way. The procedure starts with running the Stage One model with the highest \(\alpha \) value and then running the Stage Two model to check if the solution of Stage One model can lead to a feasible 2D loading in Stage Two. The \(\alpha \) value is decreased to run Stage One model again if no feasible solution exists in Stage Two in the last iteration. Following some experimental analysis, the set of discrete \(\alpha \) values are chosen as 0.92, 0.87 and 0.82.

It should be noted that the Stage One model is already very complicated and that no comparable model exists in the literature to our best knowledge. Furthermore, the combination of the Stage One and Stage Two models will lead to a model too complicated to be currently solved by standard optimisation software. The aim of the paper is to derive high quality solutions for industry usage. Thus the compromising between optimality and solvability is necessary.

Fig. 3
figure 3

Three loading scenarios: Scenario One—Start loading the current order j onto an empty pallet. Scenario Two—Start loading the current order j onto the same pallet as the previous order i (order j can be completely loaded.). Scenario Three—Start loading the current order j onto the same pallet as the previous order i (order j can be partially loaded)

Full size image

3.4.1 Stage one routing with 1D pallet loading

The challenge of this Stage One modelling is that the number of pallets of each type s to be loaded onto the vehicle is unknown in advance (it is not known in advance which orders will be delivered on the same vehicle). In addition, the total number of mixed orders in the same pallet will be influenced by the choice of loading strategy. As mentioned in Sect. 1, the first loading strategy is to start loading the current order onto an empty pallet and the second loading strategy is to start loading the current order onto the pallet loaded with the previous orders already. Note that in the second loading strategy, a small current order can be loaded completely onto the same pallet with the previous order and a large current order can be loaded partially on the same pallet with the previous order. Figure 3 gives three examples for the above three scenarios, where the first and second digits in the bracket on the pallets give the total volume and the total weight of the items of the same product type in an order.

In Fig. 3, the values of decision variables \(Z_{js}\) and \(B_{js}\) are provided to reflect the above three scenarios. Correspondingly, the values of the decision variables \(qV_{js}\) and \(qW_{js}\) are provided to indicate the accumulated volumes and weights that the order j incurs in the final pallet of type s (For example, in Scenario Two \(qV_{js}=144+412=556\)). Further, the values of decision variables \(X_{js}\) and \(nP_{js}\) are provided to indicate the number of pallets used for loading order j of pallet type s and number of extra pallets needed for loading order j of pallet type s. Note that if \(Z_{js}=1\), we have \(X_{js}=nP_{js}\); otherwise, \(nP_{js}=X_{js}-1\)

In scenario one, \(Z_{js}=1\),

$$\begin{aligned} \begin{array}{lll} qV_{js}&{} =&{}[m_{js}-(minX_{js}-1)\cdot maxM_{js}]\cdot uv_{js} \\ qW_{js}&{} = &{}[m_{js}-(minX_{js}-1)\cdot maxM_{js}]\cdot uw_{js} \\ X_{js}&{}= &{}minX_{js} \\ nP_{js}&{}=&{} X_{js} \\ \end{array} \end{aligned}$$
(1)

In scenario two, \(Z_{js}=0\), \(B_{js}=1\) and \(\sum _{k\in F} y_{ijk}=1\)

$$\begin{aligned} \begin{array}{lll} qV_{js} &{}=&{}qV_{is} +v_{js} \\ qW_{js} &{}=&{}qW_{is}+w_{js} \\ X_{js}&{}=&{} 1 \\ nP_{js}&{}=&{} 0 \end{array} \end{aligned}$$
(2)

In scenario three, \(Z_{js}=0\), \(B_{js}=0\) and \(\sum _{k\in F} y_{ijk}=1\)

If the order j cannot be completely loaded in the same pallet with the previous order i due to the pallet volume capacity, we have.

$$\begin{aligned} \begin{array}{cll} v_{js}-(X_{js}-2)\cdot (maxM_{js}\cdot uv_{js})-qV_{js}+qV_{is} &{}\le &{}DV_{s} \\ v_{js}-(X_{js}-2)\cdot (maxM_{js}\cdot uv_{js})-qV_{js}+qV_{is}+uv_{js}-1 &{}\ge &{}DV_{s} \\ qV_{js}&{}=&{} qV_{js}\cdot \frac{uw_{js}}{uv_{js}} \\ X_{js}&{}\ge &{} 2 \\ nP_{js}&{}=&{} X_{js}-1 \end{array} \end{aligned}$$
(3)

The first constraint in (3) guarantees that the total volume of the first pallet in Fig. 3 to load order j does not exceed the volume capacity of the pallet of type s. The second constraint in (3) guarantees that the total volume of the first pallet in Fig. 3 to load order j is used to its maximum. That is, given one more unit of order j, the volume of the first pallet to load order j will be exceeded. And the third constraint in (3) makes sure that \(qW_{js}\) is in ratio to \(qV_{js}\).

On the other hand, if the order j cannot be completely loaded in the same pallet with the previous order i due to the pallet weight or volume capacity, the first three constraints in (3) need to be replaced by the following constraints (4).

$$\begin{aligned} \begin{array}{cll} w_{js}-(X_{js}-2)\cdot (maxM_{js}\cdot uw_{js})-qW_{js}+qW_{is} &{}\le &{}DW_{s} \\ w_{js}-(X_{js}-2)\cdot (maxM_{js}\cdot uw_{js})-qW_{js}+qW_{is}+uw_{js}-1 &{}\ge &{}DW_{s} \\ qV_{js}&{}=&{} qW_{js}\cdot \frac{uv_{js}}{uw_{js}} \end{array} \end{aligned}$$
(4)

From the above analysis, two extra decision variables \(B_{1_{js}}\) and \(B_{2_{js}}\) are needed to identify if order j cannot be completely loaded in the same pallet with the previous order i due to the pallet volume capacity or weight capacity, where \(B_{1_{js}}=0\) if the volume capacity is exceeded, 1, otherwise. The definition of \(B_{2_{js}}\) is similar to that of \(B_{1_{js}}\).

$$\begin{aligned} \begin{array}{lll} qV_{is}+v_{js}-DV_{s}&{}\le &{}M_1\cdot (1-B_{1_{js}}) \\ DV_{s}-qV_{is}-v_{js}&{}\le &{}M_1\cdot B_{1_{js}}-1\\ qW_{is}+w_{js}-DW_{s}&{}\le &{} M_2\cdot (1-B_{2_{js}})\\ DW_{s}-qW_{is}- w_{js}&{}\le &{}M_2\cdot B_{2_{js}}-1 \\ \end{array} \end{aligned}$$
(5)

where \(M_1\) and \(M_2\) are large positive constants. The explanation of \(M_1\) and \(M_2\) are given in the next Section.

With the definition of \(B_{1_{js}}\) and \(B_{2_{js}}\), the definition of \(B_{js}\) can be realised using the following constraints. That is, only when \(B_{1_{js}}=1\) and \(B_{2_{js}}=1\), the order j can be completely loaded in the same pallet with the previous order i and \(B_{js}=1\), otherwise, \(B_{js}=0\).

$$\begin{aligned} \begin{array}{lll} B_{1_{js}}+B_{2_{js}}&{}\le &{}1+2\cdot B_{js} \\ B_{1_{js}}+B_{2_{js}}&{}\ge &{}2-2\cdot (1-B_{js})\\ \end{array} \end{aligned}$$
(6)

With the above analysis, the MILP model for Stage One is given as follows:

$$\begin{aligned} Min Z=\sum _{k\in F} \sum _{j\in V}\sum _{i\in V} P\cdot d_{ij}\cdot y_{ijk} + H\cdot \sum _{k\in F} z_{k} + I\cdot \sum _{j \in V\backslash \{0, n+1\}} \sum _{s \in S} (1-Z_{js}) \end{aligned}$$
(7)

Subject to

$$\begin{aligned}&\sum _{k\in F} \sum _{j \in V\backslash \{0, n+1\}} y_{ijk} = 1, \quad i \in V\backslash \{0\} \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{j \in V\backslash \{0, n+1\}} y_{0jk} = z_k,\quad k\in F \end{aligned}$$
(9)
$$\begin{aligned}&\sum _{i \in V\backslash \{0, n+1\}} y_{i(n+1)k} = z_k, \quad k\in F \end{aligned}$$
(10)
$$\begin{aligned}&\sum _{i \in V\backslash \{0\}} y_{ipk} = \sum _{j \in V\backslash \{n+1\}} y_{pjk}, \quad p \in V\backslash \{0, n+1\} \end{aligned}$$
(11)
$$\begin{aligned}&t_{ik} \ge e_{i} \cdot z_k,\quad i \in V\backslash \{0, n+1\}, \quad k\in F \end{aligned}$$
(12)
$$\begin{aligned}&t_{ik} \le l_{i} \cdot z_k, \quad i \in V\backslash \{0, n+1\}, \quad k\in F \end{aligned}$$
(13)
$$\begin{aligned}&t_{ik} + T_{i} + \tau _{ij}\le t_{jk}+M\cdot (1-y_{ijk}), \quad i \in V\backslash \{n+1\}, \quad j \in V\backslash \{0\}, \quad k\in F \end{aligned}$$
(14)
$$\begin{aligned}&qV_{js} \ge [m_{js}-(minX_{js}-1)\cdot maxM_{js}]\cdot uv_{js}-M_1\cdot (1-Z_{js}),\nonumber \\&\quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(15)
$$\begin{aligned}&qV_{js} \le [m_{js}-(minX_{js}-1)\cdot maxM_{js}]\cdot uv_{js}+M_1\cdot (1-Z_{js}),\nonumber \\&\quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(16)
$$\begin{aligned}&qW_{js} \ge [m_{js}-(minX_{js}-1)\cdot maxM_{js}]\cdot uw_{js}-M_2\cdot (1-Z_{js}), \nonumber \\&\quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(17)
$$\begin{aligned}&qW_{js} \le [m_{js}-(minX_{js}-1)\cdot maxM_{js}]\cdot uw_{js}+M_2\cdot (1-Z_{js}), \nonumber \\&\quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(18)
$$\begin{aligned}&X_{js} \ge minX_{js}-M_3\cdot (1-Z_{js}), \quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(19)
$$\begin{aligned}&X_{js} \le minX_{js}+M_3\cdot (1-Z_{js}), \quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(20)
$$\begin{aligned}&nP_{js} \ge X_{js}-M_3\cdot (1-Z_{js}), \quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(21)
$$\begin{aligned}&nP_{js} \le X_{js}+M_3\cdot (1-Z_{js}), \quad j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(22)
$$\begin{aligned}&qV_{js} \ge qV_{is} +v_{js}-M_1\cdot (1-B_{js})\nonumber \\&\quad -M_1\cdot Z_{js}-M_1\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) , \quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(23)
$$\begin{aligned}&qV_{js} \le qV_{is} +v_{js}+M_1\cdot (1-B_{js})+M_1\cdot Z_{js}\nonumber \\&\quad +M_1\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) , \quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(24)
$$\begin{aligned}&qW_{js} \ge qW_{is}+w_{js}-M_2\cdot (1-B_{js})-M_2\cdot Z_{js}\nonumber \\&\quad -M_2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) , \quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(25)
$$\begin{aligned}&qW_{js} \le qW_{is}+w_{js}+M_2\cdot (1-B_{js})\nonumber \\&\quad +M_2\cdot Z_{js}+M_2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) , \quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(26)
$$\begin{aligned}&X_{js} \ge 1-M_3\cdot (1-B_{js})-M_3\cdot Z_{js}\nonumber \\&\quad -M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(27)
$$\begin{aligned}&X_{js} \le 1+M_3\cdot (1-B_{js})+M_3\cdot Z_{js}\nonumber \\&\quad +M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(28)
$$\begin{aligned}&nP_{js} \ge 0-M_3\cdot (1-B_{js})-M_3\cdot Z_{js}\nonumber \\&\quad -M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) , \quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(29)
$$\begin{aligned}&nP_{js} \le 0+M_3\cdot (1-B_{js})+M_3\cdot Z_{js}\nonumber \\&\quad +M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) , \quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(30)
$$\begin{aligned}&v_{js}-(X_{js}-2)\cdot \left( maxM_{js}\cdot uv_{js}\right) -qV_{js}+qV_{is}+uv_{js}-1 \ge DV_{s}-M_1\cdot B_{js} \nonumber \\&-M_1\cdot Z_{js}-M_1\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(31)
$$\begin{aligned}&v_{js}-(X_{js}-2)\cdot (maxM_{js}\cdot uv_{js})-qV_{js}+qV_{is} \le DV_{s}+M_1\cdot B_{js} \nonumber \\&+M_1\cdot Z_{js}+M_1\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(32)
$$\begin{aligned}&qW_{js} \ge qV_{js}\cdot \frac{uw_{js}}{uv_{js}}-M_2\cdot B_{js}-M_2\cdot Z_{js}\nonumber \\&\quad -M_2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(33)
$$\begin{aligned}&qW_{js} \le qV_{js}\cdot \frac{uw_{js}}{uv_{js}}+M_2\cdot B_{js}+M_2\cdot Z_{js}\nonumber \\&\quad +M_2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(34)
$$\begin{aligned}&X_{js} \ge 2-M_3\cdot B_{js}-M_3\cdot Z_{js}\nonumber \\&\quad -M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(35)
$$\begin{aligned}&nP_{js} \ge X_{js}-1-M_3\cdot B_{js}-M_3\cdot (1-B_{js})\nonumber \\&\quad -M_3\cdot Z_{js}-M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) \nonumber \\&i,j \in V\backslash \{0,n+1\}, \quad s\in S \end{aligned}$$
(36)
$$\begin{aligned}&nP_{js} \le X_{js}-1 + M_3\cdot B_{js}+M_3\cdot (1-B_{js})\nonumber \\&\quad +M_3\cdot Z_{js}+M_3\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) \nonumber \\&i,j \in V\backslash \{0,n+1\},\quad s\in S \end{aligned}$$
(37)
$$\begin{aligned}&qV_{is}+v_{js}-DV_{s} \le M_1\cdot (1-B_{1_{js}})+ M_1\cdot Z_{js}\nonumber \\&\quad +M_1\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(38)
$$\begin{aligned}&DV_{s}-qV_{is}-v_{js} \le M_1\cdot B_{1_{js}}-1+ M_1\cdot Z_{js}\nonumber \\&\quad +M_1\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(39)
$$\begin{aligned}&qW_{is}+w_{js}-DW_{s} \le M_2\cdot (1-B_{2_{js}})+ M_2\cdot Z_{js}\nonumber \\&\quad +M_2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(40)
$$\begin{aligned}&DW_{s}-qW_{is}- w_{js} \le M_2\cdot B_{2_{js}}-1 + M_2\cdot Z_{js}\nonumber \\&\quad +M_2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(41)
$$\begin{aligned}&B_{1_{js}}+B_{2_{js}} \le 1+2\cdot B_{js}+ 2\cdot Z_{js}\nonumber \\&\quad +2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(42)
$$\begin{aligned}&B_{1_{js}}+B_{2_{js}} \ge 2-2\cdot (1-B_{js})-2\cdot Z_{js}\nonumber \\&\quad -2\cdot \left( 1-\sum _{k\in F} y_{ijk}\right) ,\quad i,j \in V\backslash \{0,n+1\}, s\in S \end{aligned}$$
(43)
$$\begin{aligned}&nPallet_{jsk} \ge nP_{js}-M_3\cdot \left( 1-\sum _{i \in V \backslash \{n+1\}}y_{ijk}\right) ,\quad j \in V\backslash \{0,n+1\}, k\in K, s\in S \end{aligned}$$
(44)
$$\begin{aligned}&nPallet_{jsk} \le nP_{js} ,\quad j \in V\backslash \{0,n+1\}, k \in K, s\in S \end{aligned}$$
(45)
$$\begin{aligned}&\sum _{s \in S} \sum _{j \in V \backslash \{0,n+1\}} \omega _{s} \cdot l_{s} \cdot nPallet_{jsk}+B_{EXTRA_k}\cdot \omega _{4}\cdot l_{4} \nonumber \\&\quad + B_{BULK_k}\cdot \omega _b\cdot (l_b+l_h) \le \alpha \cdot L\cdot W, \quad k\in K \end{aligned}$$
(46)

Objective function (7) minimises the total cost.

Constraint set (8) guarantees that following on from a customer location, only one customer can be immediately visited.

Constraint set (9) states that each used vehicle starts its tour from the depot.

Constraint set (10) imposes that each used vehicle ends its tour at the depot.

Constraint set (11) is a flow conservation constraint; it ensures each vehicle entering a customer location will leave it.

Constraint sets (12) and (13) set the time window constraints for customer visits.

Constraint set (14) ensures that each customer will be served only when a vehicle arrives at its location.

Constraints set (15)–(22) corresponds to Scenario One in Fig. 3.

Constraints set (23)–(30) corresponds to Scenario Two in Fig. 3.

Constraints set (31)–(37) corresponds to the situation that the current order j cannot be completely loaded in the same pallet with the previous order i due to the pallet volume capacity in Scenario Three in Fig. 3. The constraints set which corresponds to the situation that the current order j cannot be completely loaded in the same pallet with the previous order i due to the pallet weight capacity in Scenario Three in Fig. 3, is not listed here for simplicity.

Constraints set (38)–(43) justify the definition of the decision variable \(B_{js}\).

Constraints (44)–(46) put an upper limit on the total area of the pallets on each vehicle. The upper limit is \(\alpha \cdot L\cdot W\) as explained at the beginning of Sect. 3. The decision variable \(nPallet_{jsk}\) is defined to keep the number of the extra pallets needed to load order j of type s completely in vehicle k. The binary variable \(B_{BULK_k}=1\) if there is any frozen product \((s=4)\) loaded on vehicle k, 0, otherwise. The binary variable \(B_{EXTRA_k}=1\) if the number of frozen pallets is odd on vehicle k, where an extra empty area of one frozen pallet size (\(s=4\)) is needed in the vehicle loading diagram (See Fig. 1), 0, otherwise. For simplicity, the constraints defining \(B_{BULK_k}\) and \(B_{EXTRA_k}\) are not given here.

In the constraints (15)–(46), \(M_1, M_2, M_3\) are large positive constants, which can be set as the upper limit for the corresponding decision variables: \(M_1=max_{s\in S}(DV_{s})\), \(M_2=max_{s\in S}(DW_{s})\) and \(M_3=\sum _{s \in S, j \in j \in V \backslash \{0, n+1\}} minX_{js}\)

3.4.2 Stage two 2D vehicle loading

With the decision variable values from Stage One modelling, the following information can be specified for any given vehicle k as input data for the Stage Two.

  • nV—tal number of routes.

  • \(nVP_{ks}\)—Total number of pallets of type s on Vehicle k, \(k=1,\ldots , nV; s \in S\).

  • \(nVPI_{ksu}\)—Total number of orders on the uth pallet of type s on vehicle k, \(k=1,\ldots , nY; s \in S; u=1, \ldots , nVP_{ks}\).

  • \(I_{ksuv}\)—Customer index of the vth order on the uth pallet of type s loaded on vehicle k, \(k=1,\ldots , nV; s \in S\); \(u= 1, \ldots , nPV_{ks}\); \(v=1, \ldots , nVPI_{ksu}\). The orders are allocated in a way that an order from the customer to be visited earlier will be allocated in the pallet with lower index u and lower index v to help with the adapted LIFO constraint modelling.

Since the allocation of the pallets on vehicles can be realised one by one, it is not necessary to allocate all the nV vehicles at the same time. We hence set up the mathematical model for only one vehicle, thus the index k in all input data and decision variables in Stage Two modelling can be dropped.

Objective The Stage Two modelling is a decision problem, that is, to decide if a feasible packing exists. We define the objective of the Stage Two problem as to minimise the maximum x-coordinate of all the pallets loaded on the vehicle k. With this objective, the pallets are loaded to the left-most position on the vehicle and the loading layout of the vehicle will be as compact as possible. From a realistic point of view, the pallets will be loaded as close to each other as possible, this can improve the stability of the pallets inside the vehicle.

$$\begin{aligned} ZZ=min ~~ maxL \end{aligned}$$
(47)

Constraints Let the reference points of both pallets and vehicles be at the bottom left corners of the pallets and vehicles. Also let the x and y coordinates originate from the bottom-left corner of the vehicle and x-coordinate will increase to the right and y-coordinate will increase upwards respectively.

The first constraint set ensures that the pallets are allocated within the vehicle:

$$\begin{aligned} \omega _{s}+YP_{su}\le & {} W+YV,\quad s\in S, u=1, \ldots , nVP_{s} \end{aligned}$$
(48)
$$\begin{aligned} YP_{su}\ge & {} YV, \quad s\in S, u=1, \ldots , nVP_{s} \end{aligned}$$
(49)
$$\begin{aligned} l_{s}+XP_{su}\le & {} maxL, \quad s\in S, u=1, \ldots , nVP_{s} \end{aligned}$$
(50)

If \(B_{BULK}\) = 0, that is, there is no frozen product loaded on the current vehicle, we have

$$\begin{aligned} l_{s}+XP_{su}\le & {} L+XV + M_4\cdot B_{BULK} \quad s\in S, u=1, \ldots , nVP_{s} \end{aligned}$$
(51)
$$\begin{aligned} XP_{su}\ge & {} XV - M_4 \cdot B_{BULK} \quad s\in S, u=1, \ldots , nVP_{s} \end{aligned}$$
(52)

Otherwise, let \(W_{frozen}\) be the width of the vehicle area to load the frozen product, which is also a decision variable.

$$\begin{aligned} l_{s}+XP_{su}\le & {} L+XV + M_4\cdot (1- B_{BULK}), \quad s= 1,2,3,5, u=1, \ldots , nVP_{s} \end{aligned}$$
(53)
$$\begin{aligned} XP_{su}\ge & {} XV+ W_{frozen} - M_4\cdot (1- B_{BULK}), \quad s=1,2,3,5, u=1, \ldots , nVP_{s} \end{aligned}$$
(54)
$$\begin{aligned} l_{s}+XP_{su}\le & {} W_{frozen} + XV + M_4 \cdot (1- B_{BULK}), \quad s=4, u=1, \ldots , nVP_{s} \end{aligned}$$
(55)
$$\begin{aligned} XP_{su}\ge & {} XV - M_4\cdot (1- B_{BULK}), \quad s=4, u=1, \ldots , nVP_{s} \end{aligned}$$
(56)

The following set of constraints guarantee the non-overlapping among the pallets of the same type s. To realise the adapted LIFO constraint, the binary variables \(B_{3_{su'}}\) and \(B_{4_{su'}}\) are defined as 0 if the pallet with higher index \(u'\) (orders to be unloaded later) is loaded on the left or above the pallet with lower index u (orders to be unloaded earlier); 1, otherwise. In addition, for ease of unloading, the rightmost edge of the pallets of higher index should not exceed the rightmost edge of the pallets of lower index. The constraints for the frozen products are not given here for simplicity. Bear in mind that the door for the frozen products is at the front bottom of the vehicle.

$$\begin{aligned} XP_{su'}+l_{s}\le & {} XP_{su}-M_4\cdot B_{3_{su}}, \quad s = 1,2,3,5, u=1, \ldots , nVP_{s}, u'>u \end{aligned}$$
(57)
$$\begin{aligned} YP_{su}+\omega _{s}\le & {} YP_{su'}-M_4\cdot B_{4_{su}}, \quad s= 1,2,3,5, u=1, \ldots , nVP_{s}, u'>u \end{aligned}$$
(58)
$$\begin{aligned} B_{3_{su}}+B_{4_{su}}= & {} 1 \quad s= 1,2,3,5, u=1, \ldots , nVP_{s} \end{aligned}$$
(59)
$$\begin{aligned} XP_{su'}&leq&XP_{su}, \quad u, u'=1, \ldots , nVP_{s}, u'>u \end{aligned}$$
(60)

The following set of constraints guarantee the non-overlapping among the pallets of different type s. To realise the adapted LIFO, binary variables \(B_{5_{s'u'}}\) and \(B_{6_{s'u'}}\) are defined as 0 if the pallet \(u'\) of type \(s'\) to be unloaded later is loaded on the left or above the pallet u of type s to be unloaded earlier, 1, otherwise. In addition, to realise the adapted LIFO, the rightmost edge of the pallet to be unloaded later should not exceed the rightmost edge of the pallet to be unloaded earlier. This is the an extra constraint compared with the traditional LIFO constraint.

$$\begin{aligned} XP_{s'u'}+l_{s'}\le & {} XP_{su}-M_4\cdot B_{5_{s'u'}}, \quad s, s' = 1,2,3,5,u=1, \ldots , nVP_{s}, u'=1, \ldots , nVP_{s'}\nonumber \\ \end{aligned}$$
(61)
$$\begin{aligned} YP_{su}+\omega _{s}\le & {} YP_{s'u'}-M_4\cdot B_{6_{s'u'}} \quad s, s'= 1,2,3,5, u=1, \ldots , nVP_{s}, u'=1, \ldots , nVP_{s'} \nonumber \\ \end{aligned}$$
(62)
$$\begin{aligned} B_{5_{s'u'}}+B_{6_{s'u'}}= & {} 1 \quad s, s' = 1,2,3,5, u=1, \ldots , nVP_{s}, u'=1, \ldots , nVP_{s'} \end{aligned}$$
(63)
$$\begin{aligned} XP_{s'u'}+l_{s'}\le & {} XP_{su}+l_{s} \quad s, s' = 1,2,3,5, u=1, \ldots , nVP_{s}, u'=1, \ldots , nVP_{s'} \nonumber \\ \end{aligned}$$
(64)

In the Stage Two modelling, \(M_4\) is defined as a large positive constant. The bound for \(M_4\) could be \(M_4=max(L, W)\).

4 GVNS for large sized MO-VRLPTW problems

Due to the complexity of the MO-VRLPTW problem, optimisation software can be applied to solve a small sized Stage One routing with 1D pallet loading model and a Stage Two 2D vehicle loading model as proposed in Sect. 3.

It is noted that most of the computational effort in solving the Stage One model to optimality is to cope with the challenge that the loading has to be considered when there is no clear idea about which orders are to be delivered in the same vehicle and in which sequence are the orders to be delivered. Thus a GVNS algorithm is proposed to route the customers’ orders first, then the feasible loading for each vehicle is considered by solving a simplified Stage One model and Stage Two model in an iterated way with optimisation software.

Let \(V_k\) be the customer set for vehicle k. The objective of the simplified Stage One model for vehicle k is defined as follows:

$$\begin{aligned} \text{ Min } \quad Z_k=\sum _{j \in V_k} \sum _{s \in S} (1-Z_{js}) \end{aligned}$$

The constraints of the simplified Stage One model are the same as constraints (15)–(46). The main framework of the GVNS algorithm for the MO-VRLPTW is described in Sect. 4.1. The subroutines of the algorithm will be provided in Sects. 4.2–4.5.

4.1 The framework of the GVNS algorithm for the MO-VRLPTW

The basic idea of this Generalised VNS Algorithm for the MO-VRLPTW, provided in Table 1, is to start from an initial solution \(s^0\) using a Sweep Line procedure to be illustrated in Sect. 4.2. This is followed by a Two Route Exchange procedure to achieve the local optimal solution \(s^L\) (see Sect. 4.3). The Two Route Exchange procedure is run for up to \(l_{max}\) number of neighbours and the best solution is kept in \(s^B\). Whenever an improvement is found, the neighbour index is set to \(l=1\). The feasibility of the loading and the third objective have not been considered in the Two Route Exchange procedure. This is due to the fact that it takes a significant computational time to run the simplified Stage One model and Stage Two model in an iterative way using optimisation software.

Once the local optimum solution \(s^B\) is found with the Two Route Exchange procedure, the Make Feasible procedure is applied to update the solution \(s^B\) to a solution \(s^P\) considering feasible loading constraints. Meanwhile, the inconvenience cost of unloading the mixed orders \(I\cdot \sum _{j \in V_k} \sum _{s \in S} (1-Z_{js})\) for each vehicle k is calculated in the Make Feasible procedure through running the simplified Stage One model.

To further improve the solution \(s^P\), a Shaking procedure (see Sect. 4.5) is applied to generate a random solution \(s^R\) by r kicks of \(s^P\), which generates a new local random solution \(s_L\). Then the \(s^L\) is improved with the TwoRouteExchange procedure again. The Shaking procedure repeats until no further improvement on \(s^P\) is found. Whenever the \(s^P\) is improved, the kick size is reset to 1. The algorithm is halted when r exceeds the maximum kick size up to \(r_{max}\). The solution \(s^P\) is defined to keep the solution with the lowest total cost as the final choice.

Table 1 Basic steps of the GVNS algorithm for the MO-VRLPTW
Full size table

4.2 Initial solution

The procedure Sweep Line() follows the traditional sweep algorithm for VRP (Gillett and Millet 1974). That is: choose an unused vehicle and rotate a straight line in a circle with the centre point at the depot. Whenever it touches a customer, this customer’s order is loaded onto the selected vehicle. This procedure continues until all the customer orders are loaded. When loading a vehicle, the time window constraint and weight limit of the vehicle constraint need to be satisfied.

4.3 Local search

Given any solution s, the basic structure of procedure Two Route Exchange (s) is an extension to the variable iterated greedy algorithm for a TSPTW in Karabulut and Tasgetiren (2014). That is, given each pair of different routes in the solution s, a Two Route Destruct Construct (\(k_1\),\(k_2\)) procedure similar to the Destruct Construct () in Karabulut and Tasgetiren (2014) is applied to exchange \(k_1\) number of customers from route one with the \(k_2\) number of customers from route two in order to generate two new routes. The two new routes are treated as independent TSPTW problems and are optimised using the VNS_1_Opt local search of Karabulut and Tasgetiren (2014). The original two routes will be replaced by the two new routes if the resulting new solution \(s_{new}\) has smaller value of total fuel cost and total vehicle hiring cost, as defined in (7) \(\sum _{k\in F} \sum _{j\in V}\sum _{i\in V} P\cdot d_{ij}\cdot y_{ijk} + H\cdot \sum _{k\in F} z_{k}\) than that of the original solution s.

One new feature of this Two Route Exchange (s) is that the Destruct Construct() in Karabulut and Tasgetiren (2014) destroys ONE original route and constructs ONE new route (The problem they dealt with is the TSPTW problem), whereas the Two Route Destruct Construct (\(k_1\),\(k_2\)) procedure in this paper destroys TWO original routes into parts and construct TWO new routes by exchanging the parts from the original routes.

The other feature of this Two Route Exchange (s) is that the best improve strategy is adopted. That is, given one fixed route, choose the route to exchange, which will lead to the best improved result among all unchanged routes. Mark these two routes as exchanged routes. We repeatedly search all unchanged routes for the next pair to exchange using the best improve strategy until all routes are considered.

The third feature is that different neighbourhoods are used in the Two Route Exchange (s) by exchanging different numbers of customers in the two routes. The number of customers chosen in each route to be exchanged is generated randomly in the range [1, 4].

We adapted the Variable Iterated Greedy Algorithm from Karabulut and Tasgetiren (2014) because this is a well performing method from the literature.

4.4 Make feasible procedure

The MakeFeasible(\(s_1, s_2\)) is used to update the solution \(s_1\) from a solution without the loading feasibility check to a feasible solution \(s_2\) with the loading feasibility check. The basic steps of the function MakeFeasible(\(s_1, s_2\)) is provided in Table 2.

For each route k in solution \(s_1\), the procedure starts with running the simplified Stage One model with the highest \(\alpha \) value in constraint (48) and then run the Stage Two model to check if the solution of Stage One model can lead to a feasible 2D vehicle loading solution in Stage Two. The \(\alpha \) value is decreased to run the simplified Stage One model again if no feasible solution exists in the Stage Two in the last iteration. With some experimental analysis, the set of discrete \(\alpha \) values are chosen as 0.92, 0.87 and 0.82.

If after all the three iterations, a route k in solution \(s_1\) cannot be made feasible, then the route will be split up into two smaller routes with equal number of orders in each route. Thus the load feasibility can be easily achieved with less loads for the two new smaller routes.

Table 2 Basic steps of the function MakeFeasible(\(s_1, s_2\))
Full size table

When solving the simplified Stage One model, the value of the \(min \quad Z_k=\sum _{j \in V_k} \sum _{s \in S} (1-Z_{js})\) can be achieved. And with the known value \(Z_k\), the selection criterion in the GVNS becomes to choose the solutions with the lowest total cost defined in Eq. (7).

4.5 Shaking

The Shake() procedure generates a random solution by kicking the original solution randomly r times. This is done by exchanging min (number of customers in the route-1, r) number of customers for each pair of selected routes. Once a pair of routes is exchanged, they will not be considered for other route exchanges. This exchange procedure will be applied repeatedly until all routes are exchanged.

5 Experimental analysis

To assess the effectiveness of the MO-VRLPTW models, a small sized data set with 5 customers was used as our case study and the Xpress-IVE 1.23.02 software used to solve the model. The data input and the parametric analyses are provided in Sect. 5.1. Then in Sect. 5.2, a real industrial case study based on real geographic data and simulated customers’ data is generated and solved by both the GVNS algorithm and the software provided by our industrial partner—Optrak. The effectiveness of the GVNS algorithm is also discussed in Sect. 5.2.

5.1 A small sized case study for assessing the stage one and stage two models

In this case study, the fuel cost per kilometre is \(P = \pounds 0.12/km\), cost of hiring a vehicle is \(H= \pounds 50/vehicle\). There is no clear definition about the cost of inconvenience of unloading one mixed order. Thus a set of values are set to represent this cost \(I=\pounds 1, \pounds 5\), and \(\pounds 10\) to assess the influence of this inconvenience on the final solution. The detailed parametric analysis is given in Sect. 5.1.2. Section 5.1.1 gives detailed data input information.

5.1.1 Data inputs

The distance and time matrix of the five customers are given in Tables 3 and 4. Table 5 gives the customers’ demand on volume, number and weight of items of different product types. Table 6 gives the sizes and capacities of the vehicle and the pallets. Table 7 gives the service time and time window for each customer.

Table 3 Distance matrix (km)
Full size table
Table 4 Time matrix (minutes)
Full size table
Table 5 Customers’ demand on volume, number and weight of pallets of different product types
Full size table
Table 6 Sizes and capacities of the vehicle and the pallets
Full size table
Table 7 Service time and time window for each customer (minutes)
Full size table

5.1.2 Parametric analysis

The \(\alpha \) value is set to be \(\alpha =0.92\), which can lead to feasible solutions for all vehicles for all sets of parameters.

Let \(Z'=\sum _{k\in F} \sum _{j\in V}\sum _{i\in V} d_{ij}\cdot y_{ijk}\) be the total travel distance, \(Z''=\sum _{k\in F} z_{k}\) be the total number of vehicles used and \(Z'''=\sum _{j \in V\backslash \{0, n+1\}} \sum _{s \in S} (1-Z_{js})\) be the total number of mixed orders to be unloaded. The results and a parametric analysis of parameters are summarised in Table 8. Columns 2 in Table 8 details the set of values of the inconvenience cost I of unloading one mixed order. Columns 3–5 give the total travel distance, total number of vehicles used and total number of mixed orders to be unloaded. Columns 6–9 give the total fuel cost, total cost of hiring a vehicle, total inconvenience cost and total cost Z. The final column gives the computational time for each analysis.

Table 8 Solutions produced by the sensitivity analysis
Full size table

All the solutions are optimal and found within the given computational time in Table 8. It can be seen from Table 8 that along with the increase of the unit inconvenience cost I, the number of the mixed orders to be unloaded is reduced from 11 to 10. On the other hand, the total travel distance has increased from 455.94 to 481.00 km. If a decision maker prefers a solution with the least fuel cost, then the value of the unit inconvenience cost I needs to be set as small as possible.

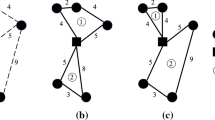
The loading graph for unit inconvenience cost \(I=\pounds 1\) and the corresponding routing strategy is given by Fig. 4. In Fig. 4, the number i in a circle represents the ith pallet of the same type. The number on the left-bottom corner represents which order has been loaded. The first number in the bracket represents the volume of the order loaded in the pallet; the second number in the bracket represents the weight of the order loaded in the pallet. The “Visit Seq.” gives the visiting sequence of the orders, where “0” represents the depot. The “Visit Time” gives the time that the order is delivered to the customer.

Fig. 4
figure 4

The loading graph for unit inconvenient cost \(I=\pounds 1\) and the corresponding routing strategy

Full size image

5.2 Large sized case studies for assessing the generalized GVNS algorithm

Similar to the parametric analysis for the small sized problem, the set of values of the inconvenience cost of unloading one mixed order I are chosen for evaluating how sensitive the GVNS algorithm is to the different values of I for the large scale MO-VRLPTW problems. The algorithm is coded with Microsoft Visual Studio C++ 2012 on a laptop of Window 7 x64, with the processor Intel(R) core(TM) CPU 2.40 GHz. The installed memory (RAM) is 8.00GB.

One new instance based on real geographic data and simulated customers’ data is generated with a total of 489 customers. The information of the data input is exactly the same as that is provided in Sect. 5.1. The only difference is that the size of the problem is much larger. Thus we upload all the data information to the website https://sites.google.com/a/port.ac.uk/song-2016-mo-vrltw-data-site/ for researchers who wish to make future investigations.

In addition, the solution from the Industrial Software Optrak is also provided in Table 9.

Table 9 Solutions produced by the Optrak Software
Full size table

An explanation of the algorithm of the Optrak Software Company is that various local search techniques, which are well known in the literature, have been implemented. The best result is used as their final solution. The algorithm was designed to achieve a good solution in an acceptable customer time. Thus the parameters are usually set to small values. However, to compare this with this paper’s result, the software parameters are set to its upper limit. For example, in 2-opt search algorithm, the number of the nearest neighbours considered is set to 489. So the computational time is somewhat slow (320 s). Another reason for the longer computational time is that the Optrak software is designed to take into account additional constraints such as driver break regulations and rush-hour travel speeds, which although omitted from our problem definition and data sets still impact computational times.

A small deviation from the model presented in this paper is that the company allow a driver to carry out two routes on the same day. That is, if one order is too small, the driver might return to the depot too early. They will send that driver off again on the same day to deliver another order. In that case, their number of routes used is a bit more than necessary, because some routes were actually run by the same vehicle. Thus, we don’t compare the second objective—minimising the total number of routes used in the following experiments, since the problem solving strategies of this GVNS algorithm and OPTRAK software are slightly different as explained above.

The results in Table 10 follow the same basic format as in Table 8. In addition to Table 8, the Z value of the GVNS algorithm is defined as \(Z_{GVNS}\). The corresponding objective Z value of the Software is also provided, which is defined as \(Z_{optrak}\). The upper limit of computational time is set to 300 s, which is assumed to be acceptable in industry and recommended by Optrak as a typical user expectation. The key parameter values in the GVNS are set as \(l_{max}=4, r_{max}=30\).

Table 10 Solutions produced by the GVNS
Full size table

From Table 10, it can be seen that the GVNS algorithm provides solutions with a better overall z-value than those of the OPTRAK software company. And also the GVNS algorithm is sensitive to the different values of I. The tendency is clear that the total travel distance will increase along with a larger I value and the number of mixed orders loaded on the same pallet will decrease on the vice versa.

6 Conclusions and future work

In this paper, a MILP model for the multi-objective vehicle routing and loading with time window constraints is formulated. In addition to the classic time window constraints, the 1D pallet loading and 2D vehicle loading constraints are also taken into consideration. The problem consists of routing a number of routes to serve a set of customers, and determining the best way for loading the goods ordered by the customers on the vehicles used for transportation. The three objective functions pertaining to minimisation of total travel distance, number of routes to use and total number of mixed orders in the same pallet are, more often than not, conflicting. In the formulated MILP model, the problem is converted to one objective - minimising the total cost, where the three original objectives are incorporated as parts of the total cost function.

The Xpress-IVE 1.23.02 software is used to solve the MILP models. The real data is provided by our industrial collaborator and the results and sensitivity has been provided for different scenarios. Due to the complexity of the problem, it takes a long time for the computer to find optimal solutions to the different combinations of the weights for large sized problems. Thus, a case study with only 5 customers was solved to optimality. The individual execution times are acceptable for this small-sized case study.

To solve the practical industrial case study with up to 489 customers, we have proposed a GVNS algorithm, which provides a set of distinct solutions to this optimisation problem with different unit inconvenience costs for unloading one mixed order. In addition, the local search function is novel compared to other published algorithms in the VRPTW domain. The algorithm was coded with C++ and the results show that it can provide overall efficient solutions as compared with the Optrak software.

In the future, shift rules and patterns for drivers (legal limits for drivers’ shifts correspond to the HGV and van regulations like the hours of the night or day shifts, start time of the work and the amount of time working) as well as work limits (non-legal shift limits) can been considered for incorporation in the mathematical model and algorithm as a future research work.