A regime switching model for temperature modeling and applications to weather derivatives pricing

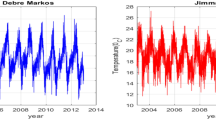
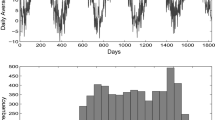
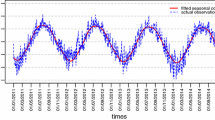
Abstract

In this study, we propose a regime-switching model for temperature dynamics, where the parameters depend on a Markov chain. We improve upon the traditional models by modeling jumps in temperature dynamics via the chain itself. Moreover, we compare the performance of the proposed model with the existing models. The results indicate that the proposed model outperforms in the short time forecast horizon while the forecast performance of the proposed model is in line with the existing models for the long time horizon. It is shown that the proposed model is a relatively better representation of temperature dynamics compared to the existing models. Furthermore, we derive prices of weather derivatives written on several temperature indices.

Appendix

Threshold Autoregressive (TAR) model. Consider the 2-state version of the threshold autoregressive (TAR) model proposed by [42] given by

$$\begin{aligned} y_{t} = (1-I_{t})(\alpha _{1}+ \phi _{1}y_{t-1}) + I_{t}(\alpha _{2}+ \phi _{2}y_{t-1}) + \epsilon _{t}, \end{aligned}$$

with

$$\begin{aligned} I_{t}={\left\{ \begin{array}{ll}1,\quad \text {if} \ y_{t-1}\ge \tau ,\\ 0, \quad \text {if} \ y_{t-1}< \tau , \end{array}\right. } \end{aligned}$$

where $\tau$ is the value of the threshold, see [21]. The estimation results of the 2-state TAR model for the deseasonalized temperature process are presented in Table 18, where the standard errors are given in parenthesis. Figure 16 shows the deseasonalized temperature data together with the TAR model threshold obtained from the estimation of the TAR model.

Table 18 Estimation of the TAR model for the deseasonalized temperature process

Fig. 16

The TAR model for the deseasonalized temperature data together with the TAR model threshold

Proof of Lemma 2. Remember that, by Eq. (16), under $\mathbb {P},$

$$\begin{aligned} dY_{t}=\kappa \left( Y_{t}-S_{t}\right) dt+\sigma _{t}dW_{t}+\sum _{j=1}^{N}\beta ^{j}_{t}d\mathcal {N}^{j}_{t}. \end{aligned}$$

By Lemma 1,

$$\begin{aligned} dW^{\theta }_{t} = dW_{t}-\theta _{t}\sigma _{t}dt \end{aligned}$$

(57)

and

$$\begin{aligned} d\mathcal {M}^{\theta j}_{t} = d\mathcal {N}^{j}_{t}- e^{\theta _{t}\beta _{t}^{j}}a_{t}^{j}dt. \end{aligned}$$

(58)

Hence, under $\mathbb {Q}^{\theta }$ we can write

$$\begin{aligned} dY_{t}&=\kappa \left( Y_{t}-S_{t}\right) dt + \left( \theta _{t}\sigma _{t}^{2} + \sum _{j=1}^{N}e^{\theta _{t}\beta _{t}^{j}}\beta ^{j}_{t}a_{t}^{j}\right) dt +\sigma _{t}dW^{\theta }_{t} +\sum _{j=1}^{N}\beta ^{j}_{t}d\mathcal {M}^{\theta j}_{t} \\&=\kappa \left( Y_{t}-S_{t}\right) dt + R_{t}dt +\sigma _{t}dW^{\theta }_{t} +\sum _{j=1}^{N}\beta ^{j}_{t}d\mathcal {M}^{\theta j}_{t}, \end{aligned}$$

and by applying Itô’s Formula, the result follows. $\square$

Proof of Lemma 3. By Eq. (13), we have

$$\begin{aligned} \int _{\tau _{1}}^{\tau _{2}}T_{t}dt = \int _{\tau _{1}}^{\tau _{2}} \varLambda _{u}du + \int _{\tau _{1}}^{\tau _{2}} Y_{u}du. \end{aligned}$$

(59)

From Eq. (46), we can write

$$\begin{aligned} Y_{\tau _{2}}&=Y_{\tau _{1}} + \kappa \int _{\tau _{1}}^{\tau _{2}}Y_{u}du - \kappa \int _{\tau _{1}}^{\tau _{2}}S_{u}du + \int _{\tau _{1}}^{\tau _{2}}R_{u}du \\&\quad + \int _{\tau _{1}}^{\tau _{2}} \sigma _{u}dW^{\theta }_{u} + \int _{\tau _{1}}^{\tau _{2}} \sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u} \end{aligned}$$

and, thus,

$$\begin{aligned} \int _{\tau _{1}}^{\tau _{2}}Y_{u}du&=\kappa ^{-1}\left( Y_{\tau _{2}}-Y_{\tau _{1}}\right) + \int _{\tau _{1}}^{\tau _{2}}S_{u}du -\kappa ^{-1} \int _{\tau _{1}}^{\tau _{2}}R_{u}du \nonumber \\&\quad -\kappa ^{-1} \int _{\tau _{1}}^{\tau _{2}} \sigma _{u}dW^{\theta }_{u} -\kappa ^{-1}\int _{\tau _{1}}^{\tau _{2}} \sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u}. \end{aligned}$$

(60)

Now, by Eq. (47), we have

$$\begin{aligned} \kappa ^{-1}\left( Y_{\tau _{2}}-Y_{\tau _{1}}\right)&= \kappa ^{-1}\left( e^{\kappa (\tau _{2}-s)}-e^{\kappa (\tau _{1}-s)}\right) {Y}_{s} \nonumber \\&\quad - \int _s^{\tau _{2}} e^{\kappa (\tau _{2}-u)}S_{u}du + \int _s^{\tau _{1}} e^{\kappa (\tau _{1}-u)}S_{u}du \nonumber \\&\quad +\kappa ^{-1} \int _s^{\tau _{2}} e^{\kappa (\tau _{2}-u)}R_{u}du - \kappa ^{-1} \int _s^{\tau _{1}}e^{\kappa (\tau _{1}-u)} R_{u}du \nonumber \\&\quad + \kappa ^{-1} \int _s^{\tau _{2}}e^{\kappa (\tau _{2}-u)}\sigma _{u}dW^{\theta }_{u} - \kappa ^{-1} \int _s^{\tau _{1}}e^{\kappa (\tau _{1}-u)}\sigma _{u} dW^{\theta }_{u} \nonumber \\&\quad + \kappa ^{-1} \int _s^{\tau _{2}}e^{\kappa (\tau _{2}-u)}\sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u} - \kappa ^{-1} \int _s^{\tau _{1}} e^{\kappa (\tau _{1}-u)}\sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u}. \end{aligned}$$

(61)

Hence, by Eq. (61), we can write Eq. (60) as

$$\begin{aligned} \int _{\tau _{1}}^{\tau _{2}}Y_{u}du&= \kappa ^{-1}\left( e^{\kappa (\tau _{2}-s)}-e^{\kappa (\tau _{1}-s)}\right) {Y}_{s} \nonumber \\&\quad - \int _s^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) S_{u}du + \int _s^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) S_{u}du \nonumber \\&\quad +\kappa ^{-1} \int _s^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) R_{u}du - \kappa ^{-1} \int _s^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) R_{u}du \nonumber \\&\quad + \kappa ^{-1} \int _s^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) \sigma _{u}dW^{\theta }_{u} - \kappa ^{-1} \int _s^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) \sigma _{u} dW^{\theta }_{u} \nonumber \\&\quad + \kappa ^{-1} \int _s^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) \sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u} \nonumber \\&\quad - \kappa ^{-1} \int _s^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) \sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u}. \end{aligned}$$

(62)

Therefore, by putting Eq. (62) into Eq. (59), the result follows. $\square$

Proof of Theorem 1. Remember that by Eq. (4)

$$\begin{aligned} F_{\mathrm{CAT}}(s,\tau _{1},\tau _{2}; T)= \mathbb {E}^{\theta } \left[ \int _{\tau _{1}}^{\tau _{2}} T_{t}dt | \mathcal {G}_{s}\right] . \end{aligned}$$

(63)

By Eq. (48) and Fubini’s Theorem, we have

$$\begin{aligned} \mathbb {E}^{\theta } \left[ \int _{\tau _{1}}^{\tau _{2}} T_{t}dt | \mathcal {G}_{s}\right]&= \int _{\tau _{1}}^{\tau _{2}} \varLambda _{u}du + \kappa ^{-1}\left( e^{\kappa (\tau _{2}-s)}-e^{\kappa (\tau _{1}-s)}\right) Y_{s} \nonumber \\&\quad - \int _{s}^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) \mathbb {E}^{\theta }\left[ S_{u} | \mathcal {G}_{s}\right] du \nonumber \\&\quad + \int _{s}^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) \mathbb {E}^{\theta }\left[ S_{u} | \mathcal {G}_{s}\right] du \nonumber \\&\quad +\kappa ^{-1} \int _{s}^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) \mathbb {E}^{\theta }\left[ R_{u} | \mathcal {G}_{s}\right] du \nonumber \\&\quad - \kappa ^{-1} \int _{s}^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) \mathbb {E}^{\theta }\left[ R_{u} | \mathcal {G}_{s}\right] du, \end{aligned}$$

(64)

since by the martingale property

$$\begin{aligned}&\mathbb {E}^{\theta } \left[ \int _{s}^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) \sigma _{u}dW^{\theta }_{u} | \mathcal {G}_{s}\right] =0,\\&\mathbb {E}^{\theta } \left[ \int _{s}^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) \sigma _{u}dW^{\theta }_{u} | \mathcal {G}_{s}\right] =0,\\&\mathbb {E}^{\theta } \left[ \int _{s}^{\tau _{2}} \left( e^{\kappa (\tau _{2}-u)} - 1\right) \sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u} | \mathcal {G}_{s}\right] =0,\\&\mathbb {E}^{\theta } \left[ \int _{s}^{\tau _{1}} \left( e^{\kappa (\tau _{1}-u)} - 1\right) \sum _{j=1}^{N} \beta ^{j}_{u}d\mathcal {M}^{\theta j}_{u} | \mathcal {G}_{s}\right] =0. \end{aligned}$$

It can be easily shown that

$$\begin{aligned} \mathbb {E}^{\theta }\left[ \zeta _{u}| \mathcal {G}_{s}\right] = e^{\mathbf {A}^{\theta }(u-s)} \zeta _{s}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \mathbb {E}^{\theta }\left[ S_{u} | \mathcal {G}_{s}\right]&= \mathbb {E}^{\theta }\left[ \langle \bar{S}, \zeta _{u} \rangle | \mathcal {G}_{s}\right] \nonumber \\&= \langle \bar{S}, \mathbb {E}^{\theta }\left[ \zeta _{u}| \mathcal {G}_{s}\right] \rangle \nonumber \\&= \langle \bar{S}, e^{\mathbf {A}^{\theta }(u-s)} \zeta _{s} \rangle \end{aligned}$$

(65)

and

$$\begin{aligned} \mathbb {E}^{\theta }\left[ R_{u} | \mathcal {G}_{s}\right]&= \mathbb {E}^{\theta }\left[ \langle \bar{R}, \zeta _{u} \rangle | \mathcal {G}_{s}\right] \nonumber \\&= \langle \bar{R}, \mathbb {E}^{\theta }\left[ \zeta _{u}| \mathcal {G}_{s}\right] \rangle \nonumber \\&= \langle \bar{R}, e^{\mathbf {A}^{\theta }(u-s)} \zeta _{s} \rangle . \end{aligned}$$

(66)

Therefore, by inserting Eqs. (65) and (66) into Eq. (64), the result follows. $\square$

Proof of Lemma 4. Let be

$$\begin{aligned} Z_{t} :=e^{-\kappa t}Y_{t} \end{aligned}$$

and apply Itô’s Formula to $e^{iuZ_{t}}$. Then,

$$\begin{aligned} e^{iuZ_{t}}&= e^{iuZ_{s}} + \int _{s}^{t} e^{iuZ_{r}}\left( iue^{-\kappa r}(-\kappa S_{r}+ R_{r}) - \dfrac{1}{2}u^{2}e^{-2 \kappa r}\sigma _{r}^{2} \right) dr \\&+ \int _{s}^{t} e^{iuZ_{r}} \sum _{j=1}^{N} e^{\theta _{r}\beta _{r}^{j}} (e^{iue^{-\kappa r }\beta _{r}^{j}} -1 -iue^{- \kappa r}\beta _{r}^{j} )a_{r}^{j}dr \\&+ \int _{s}^{t} e^{iuZ_{r}} iue^{- \kappa r} \sigma _{r}dW_{r}^{\theta } + \int _{s}^{t} e^{iuZ_{r-}} \sum _{j=1}^{N} (e^{iue^{-\kappa r }\beta _{r}^{j}} -1 ) d \mathcal {M}^{\theta j}_{r} \\&= e^{iuZ_{s}} + \int _{s}^{t} e^{iuZ_{r}} \langle g(r, u), \zeta _{r}\rangle dr \\&+ \int _{s}^{t} e^{iuZ_{r}} iue^{- \kappa r} \sigma _{r}dW_{r}^{\theta } + \int _{s}^{t} e^{iuZ_{r-}} \sum _{j=1}^{N} (e^{iue^{-\kappa r }\beta _{r}^{j}} -1 ) d \mathcal {M}^{\theta j}_{r}. \end{aligned}$$

We define for each $s \le t \in [0, \mathsf {T}],$$\mathcal {\bar{G}}_{s, t}:= \mathcal {F}_{s}\vee \mathcal {F}^{\zeta }_{t},$ which represents the enlarged $\sigma$-field generated by $\mathcal {F}_{s}$ and $\mathcal {F}^{\zeta }_{t}$. Moreover, write ${\bar{\mathbf {G}}}:= ( \mathcal {\bar{G}}_{s, t}: \ s, t \in [0, \mathsf {T}] )$ for the corresponding complete enlarged filtration. Let $\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u)$ denote the characteristic function of $Z_{t}$ conditional on $\mathcal {\bar{G}}_{s, t};$ that is,

$$\begin{aligned} \varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u) := \mathbb {E}^{\theta } \left[ e^{iuZ_{t}} | \mathcal {\bar{G}}_{s, t} \right] . \end{aligned}$$

(67)

Then, from above we obtain

$$\begin{aligned} d\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u)= \varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u) \left( \langle g(t, u), \zeta _{t} \rangle dt + \sum _{j=1}^{N} (e^{iue^{-\kappa t }\beta _{t}^{j}} -1 ) d \mathcal {M}^{\theta j}_{t}\right) . \end{aligned}$$

(68)

For notational convenience, we simply write $\mathbf {B}^{\theta }(t)=\mathbf {B}^{\theta }(t,u).$ Let $\mathbf {D}^{\theta }(t) := (d_{jl}^{\theta }(t))_{j,l=1, \ldots , N},$ where

$$\begin{aligned} d_{jl}^{\theta }(t) = \left\{ \begin{array}{ll} e^{iue^{-\kappa t }\beta _{jl}},&{}\quad \text {for} \ l \ne j, \\ \dfrac{\sum _{j=1, j \ne l}^{N} e^{iue^{-\kappa t }\beta _{jl}}a_{jl}^{\theta }}{\sum _{j=1, j \ne l}^{N} a_{jl}^{\theta }},&{}\quad \text {for} \ l=j. \end{array} \right. \end{aligned}$$

Notice that $d_{jl}^{\theta }(t) = b_{jl}^{\theta }(t)/a_{jl}^{\theta },$ for each $j, l= 1, \ldots , N$. Define $\mathbf {D}_{0}^{\theta }(t) := \mathbf {D}^{\theta }(t) - diag[d^{\theta }(t)],$ where $d^{\theta }(t) = (d_{11}^{\theta }(t), \ldots , d_{NN}^{\theta }(t))' \in \mathbb {R}^{N}$. Then, we can write

$$\begin{aligned} \sum _{j=1}^{N} (e^{iue^{-\kappa t }\beta _{t}^{j}} -1 ) d\mathcal {M}^{\theta j}_{t} = \left( \mathbf {D}_{0}^{\theta }(t) \zeta _{t-} + \zeta _{t-} -\mathbf {1} \right) ' d\mathcal {M}^{\theta }_{t}, \end{aligned}$$

(69)

where $\mathcal {M}^{\theta }_{t}=(\mathcal {M}^{\theta 1}_{t}, \ldots , \mathcal {M}^{\theta N}_{t})' \in \mathbb {R}^{N}$. It can be easily shown that, by Remark 1, we can write

$$\begin{aligned} \zeta _{t} = \zeta _{0}+\int _{0}^{t} (\mathbf {I}-\zeta _{s-}\mathbf {1}')d\mathcal {N}_{s} \end{aligned}$$

with

$$\begin{aligned} \mathcal {M}^{\theta }_{t} = \mathcal {N}_{t} - \int _{0}^{t} \mathbf {A}^{\theta }_{0}\zeta _{s-}ds. \end{aligned}$$

Therefore, Eq. (68) can be written as

$$\begin{aligned} d\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u)= \varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u) \left( \langle g(t, u), \zeta _{t} \rangle dt + \left( \mathbf {D}_{0}^{\theta }(t) \zeta _{t-} + \zeta _{t-} -\mathbf {1} \right) ' d\mathcal {M}^{\theta }_{t}\right) . \end{aligned}$$

(70)

We define

$$\begin{aligned} h(t, u) := \zeta _{t}\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u), \qquad t \in [0, \mathsf {T}]. \end{aligned}$$

(71)

By Itô’s Formula we obtain

$$\begin{aligned} h(t, u)&= h(s, u) + \int _{s}^{t}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u)\left( \mathbf {A}^{\theta } \zeta _{r-}dr + dV_{r}^{\theta }\right) \nonumber \\&\quad + \int _{s}^{t}\zeta _{r-}d\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) + \sum _{s< r \le t } \varDelta \zeta _{r} \varDelta \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u)\nonumber \\&= h(s, u) + \int _{s}^{t}\left( diag[g(r, u)] + \mathbf {A}^{\theta } \right) h(r, u)dr \nonumber \\&\quad + \int _{s}^{t}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) dV_{r}^{\theta } \nonumber \\&\quad + \int _{s}^{t} h(r-, u) \left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} + \zeta _{r-} -\mathbf {1} \right) ' d\mathcal {M}^{\theta }_{r} \nonumber \\&\quad + \sum _{s < r \le t } \varDelta \zeta _{r} \varDelta \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u). \end{aligned}$$

(72)

Here, we used $\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u) \zeta _{t} \langle g(t, u), \zeta _{t} \rangle = diag[ g(t, u)] \zeta _{t}\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u)$.

Now, by using

$$\begin{aligned} (\mathbf {I}-\zeta _{t}\mathbf {1}')diag[\varDelta \mathcal {N}_{t}]\zeta _{t}= \mathbf {0}, \end{aligned}$$

we can write

$$\begin{aligned}&\sum _{s< r \le t } \varDelta \zeta _{r} \varDelta \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) \nonumber \\&= \sum _{s< r \le t} (\mathbf {I}-\zeta _{r-}\mathbf {1}')\varDelta \mathcal {N}_{r}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u)\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} + \zeta _{r-} -\mathbf {1} \right) ' \varDelta \mathcal {N}_{r} \nonumber \\&= \sum _{s< r \le t} \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[\varDelta \mathcal {N}_{r}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} + \zeta _{r-} -\mathbf {1} \right) \nonumber \\&= \sum _{s < r \le t} \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[\varDelta \mathcal {N}_{r}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} -\mathbf {1} \right) \nonumber \\&= \int _{s}^{t}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[\mathbf {A}_{0}^{\theta }\zeta _{r-}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} -\mathbf {1} \right) dr \nonumber \\&\quad + \int _{s}^{t} \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[d\mathcal {M}^{\theta }_{r}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} -\mathbf {1} \right) . \end{aligned}$$

(73)

It can be easily shown that

$$\begin{aligned} diag[\mathbf {A}_{0}^{\theta }\zeta _{t}]\left( \mathbf {D}_{0}^{\theta }(t) \zeta _{t} -\mathbf {1} \right) = \left( \mathbf {B}^{\theta }_{0}(t) - \mathbf {A}^{\theta }_{0}\right) \zeta _{t}. \end{aligned}$$

Hence, we can write

$$\begin{aligned}&\int _{s}^{t}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[\mathbf {A}_{0}^{\theta }\zeta _{r-}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} -\mathbf {1} \right) dr \nonumber \\&\quad = \int _{s}^{t}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')\left( \mathbf {B}^{\theta }_{0}(r) - \mathbf {A}^{\theta }_{0}\right) \zeta _{r-}dr \nonumber \\&\quad = \int _{s}^{t} \left( \mathbf {B}^{\theta }(r)-\mathbf {A}^{\theta }\right) h(r, u)dr, \end{aligned}$$

(74)

since

$$\begin{aligned} (\mathbf {I}-\zeta _{t}\mathbf {1}')\mathbf {B}^{\theta }_{0}(t)\zeta _{t} = \mathbf {B}^{\theta }(t)\zeta _{t} \end{aligned}$$

and

$$\begin{aligned} (\mathbf {I}-\zeta _{t}\mathbf {1}')\mathbf {A}^{\theta }_{0}\zeta _{t}= \mathbf {A}^{\theta }\zeta _{t}. \end{aligned}$$

Thus, by combining Eqs. (73) and (74), we get

$$\begin{aligned}&\sum _{s < r \le t } \varDelta \zeta _{r} \varDelta \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) \nonumber \\&\quad = \int _{s}^{t} \left( \mathbf {B}^{\theta }(r)-\mathbf {A}^{\theta }\right) h(r, u)dr \nonumber \\&\qquad + \int _{s}^{t} \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[d\mathcal {M}^{\theta }_{r}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} -\mathbf {1} \right) . \end{aligned}$$

(75)

Thus, by Eqs. (75), (72) becomes

$$\begin{aligned} h(t, u)&= h(s, u) + \int _{s}^{t}\left( diag[g(r, u)] + \mathbf {B}^{\theta }(r) \right) h(r, u)dr \nonumber \\&\quad + \int _{s}^{t}\varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) dV_{r}^{\theta } \nonumber \\&\quad + \int _{s}^{t} h(r-, u) \left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} + \zeta _{r-} -\mathbf {1} \right) ' d\mathcal {M}^{\theta }_{r} \nonumber \\&\quad + \int _{s}^{t} \varPhi _{Z_{r}|\mathcal {\bar{G}}_{s, r}} (u) (\mathbf {I}-\zeta _{r-}\mathbf {1}')diag[d\mathcal {M}^{\theta }_{r}]\left( \mathbf {D}_{0}^{\theta }(r) \zeta _{r-} -\mathbf {1} \right) . \end{aligned}$$

(76)

Therefore, by Fubini’s Theorem and using the martingale property, we have

$$\begin{aligned} \mathbb {E}^{\theta } \left[ h(t, u) | \mathcal {G}_{s}\right] = h(s, u) + \int _{s}^{t}\left( diag[g(r, u)] + \mathbf {B}^{\theta }(r) \right) \mathbb {E}^{\theta } \left[ h(r, u)| \mathcal {G}_{s}\right] dr. \end{aligned}$$

Thus, we get

$$\begin{aligned} d\mathbb {E}^{\theta } \left[ h(t, u) | \mathcal {G}_{s}\right] = \left( diag[g(t, u)] + \mathbf {B}^{\theta }(t) \right) \mathbb {E}^{\theta } \left[ h(t, u) | \mathcal {G}_{s}\right] dt \end{aligned}$$

and after solving we have

$$\begin{aligned} \mathbb {E}^{\theta } \left[ h(t, u) | \mathcal {G}_{s}\right] = e^{iuZ_{s}}\zeta _{s}\exp \left( \int _{s}^{t}\left( diag[g(r, u)] + \mathbf {B}^{\theta }(r) \right) dr\right) . \end{aligned}$$

(77)

Notice that

$$\begin{aligned} \varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u)&= \langle \zeta _{t}\varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (u), \mathbf {1} \rangle \nonumber \\&= \langle h(t, u), \mathbf {1} \rangle , \end{aligned}$$

(78)

since $\langle \zeta _{t}, \mathbf {1} \rangle = 1$.

Now, by the tower property and Eq. (78), we have

$$\begin{aligned} \mathbb {E}^{\theta } \left[ e^{iuY_{t}} | \mathcal {G}_{s}\right]&= \mathbb {E}^{\theta } \left[ \mathbb {E}^{\theta } \left[ e^{iuY_{t}} | \mathcal {\bar{G}}_{s, t}\right] | \mathcal {G}_{s}\right] \\&= \mathbb {E}^{\theta } \left[ \mathbb {E}^{\theta } \left[ e^{iue^{kt}Z_{t}} | \mathcal {\bar{G}}_{s, t}\right] | \mathcal {G}_{s}\right] \\&= \mathbb {E}^{\theta } \left[ \varPhi _{Z_{t}|\mathcal {\bar{G}}_{s, t}} (ue^{\kappa t}) | \mathcal {G}_{s}\right] \\&= \mathbb {E}^{\theta } \left[ \langle h(t, ue^{\kappa t}), \mathbf {1} \rangle | \mathcal {G}_{s}\right] \\&= \langle \mathbb {E}^{\theta } \left[ h(t, ue^{\kappa t}) | \mathcal {G}_{s}\right] , \mathbf {1} \rangle . \end{aligned}$$

Therefore the result follows by Eq. (77). $\square$

Proof of Theorem 2. Remember that by Eq. (5)

$$\begin{aligned} F_{\mathrm{CDD}}(s,\tau _{1},\tau _{2}; T) = \mathbb {E}^{\theta } \left[ \int _{\tau _{1}}^{\tau _{2}}\max ( T_{t}-c, 0)dt | \mathcal {G}_{s}\right] . \end{aligned}$$

Now by Lemma 5, we can write

$$\begin{aligned} \max ( T_{t}-c, 0) = \dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \exp \left( (\epsilon + iu)T_{t}\right) du. \end{aligned}$$

(79)

Thus, by Eq. (79) and Fubini’s Theorem,

$$\begin{aligned}&\mathbb {E}^{{\theta }} \left[ \max ( T_{t}-c, 0) | \mathcal {G}_{s}\right] \nonumber \\&\quad = \dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \mathbb {E}^{{\theta }} \left[ \exp \left( (\epsilon + iu) T_{t} \right) | \mathcal {G}_{s}\right] du \nonumber \\&\quad = \dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \exp \left( (\epsilon + iu)\varLambda _{t}\right) \mathbb {E}^{{\theta }} \left[ \exp \left( (\epsilon + iu) Y_{t}\right) | \mathcal {G}_{s}\right] du \nonumber \\&\quad = \dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \exp \left( (\epsilon + iu)\varLambda _{t}\right) \mathbb {E}^{{\theta }} \left[ \exp \left( i (u - i\epsilon ) Y_{t}\right) | \mathcal {G}_{s}\right] du \nonumber \\&\quad = \dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \exp \left( (\epsilon + iu)\varLambda _{t}\right) \varPhi _{Y_{t}|\mathcal {G}_{s}} (u - i\epsilon ) du, \end{aligned}$$

(80)

where $\varPhi _{Y_{t}|\mathcal {G}_{s}} (u) = \mathbb {E}^{\theta } \left[ e^{iuY_{t}} | \mathcal {G}_{s}\right]$ is given by Eq. (54).

Therefore, by Fubini’s Theorem and Eq. (80), we obtain

$$\begin{aligned}&\mathbb {E}^{\theta } \left[ \int _{\tau _{1}}^{\tau _{2}}\max ( T_{t}-c, 0)dt | \mathcal {G}_{s}\right] \\&\quad = \int _{\tau _{1}}^{\tau _{2}}\mathbb {E}^{{\theta }} \left[ \max ( T_{t}-c, 0) | \mathcal {G}_{s}\right] dt \\&\quad = \int _{\tau _{1}}^{\tau _{2}}\dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \exp \left( (\epsilon + iu) \varLambda _{t}\right) \varPhi _{Y_{t}|\mathcal {G}_{s}} (u - i\epsilon )dudt \\&\quad = \dfrac{1}{2 \pi } \int _{\mathbb {R}} \hat{f}_{\epsilon }(u) \int _{\tau _{1}}^{\tau _{2}}\exp \left( (\epsilon + iu) \varLambda _{t}\right) \varPhi _{Y_{t}|\mathcal {G}_{s}} (u - i\epsilon )dtdu. \end{aligned}$$

We notice that, by Lemma 4,

$$\begin{aligned}&\varPhi _{Y_{t}|\mathcal {G}_{s}} (u-i\epsilon ) \\&\quad = \left\langle \zeta _{s}\exp \left( (\epsilon + iu) e^{\kappa (t-s)}Y_{s} + \int _{s}^{t} \left( diag [g(r, (u-i\epsilon )e^{kt})] \right. \right. \right. \\&\qquad \left. \left. \left. +\, \mathbf {B}^{\theta }(r,(u-i\epsilon )e^{kt}) \right) dr \right) , \mathbf {1} \right\rangle . \end{aligned}$$

Therefore, the result follows. $\square$