Sparsity in max-plus algebra and systems

Abstract

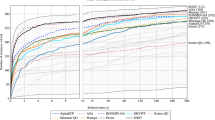
We study sparsity in the max-plus algebraic setting. We seek both exact and approximate solutions of the max-plus linear equation with minimum cardinality of support. In the former case, the sparsest solution problem is shown to be equivalent to the minimum set cover problem and, thus, NP-complete. In the latter one, the approximation is quantified by the ℓ₁ residual error norm, which is shown to have supermodular properties under some convex constraints, called lateness constraints. Thus, greedy approximation algorithms of polynomial complexity can be employed for both problems with guaranteed bounds of approximation. We also study the sparse recovery problem and present conditions, under which, the sparsest exact solution solves it. Through multi-machine interactive processes, we describe how the present framework could be applied to two practical discrete event systems problems: resource optimization and structure-seeking system identification. We also show how sparsity is related to the pruning problem. Finally, we present a numerical example of the structure-seeking system identification problem and we study the performance of the greedy algorithm via simulations.

Appendices

Appendix A: Previous results

The result below was originally proved in Vorobyev (1967) and Zimmermann (1976). A reference in English can be found in Butkovič (2003).

Theorem 7 (Covering theorem)

An element$\boldsymbol {x}\in \mathbb {R}_{\max }^{n}$isa solution to Eq. 1orx ∈ S(A,b) if and only if:

$$ \begin{array}{@{}rcl@{}} &&\text{a) } \boldsymbol{x}\le \bar{\boldsymbol{x}}\\ &&\text{b) }\bigcup_{j\in J_{x}} I_{j}=I, \end{array} $$

where$\bar {\boldsymbol {x}}$is the principal solutiondefined in Eq. 3, setJ_xisdefined in Eq. 8, and setsI_jare defined in Eq. 9.

Theorem 8 (Cuninghame-Green 1979)

Let$\bar {\boldsymbol {x}}$bethe principal solution defined in Eq. 3. The following equivalence holds:

$$ \boldsymbol{A} {\boxplus} \boldsymbol{x}\le \boldsymbol{b} \Leftrightarrow \boldsymbol{x}\le \bar{\boldsymbol{x}}. $$

(25)

Moreover, $\bar {\boldsymbol {x}}$is an optimal solution to problem (5).

Appendix B: Proofs

Proof of Theorem 1

First, we prove i). Suppose that x^∗ is an optimal solution to Eq. 6. Since it is a solution of the equation $\boldsymbol {A} {\boxplus } \boldsymbol {x}=\boldsymbol {b}$, by Theorem 7, the subcollection $\{I_{j}:j\in J_{{x}^{*}}\}$, determined by the agreement set $J_{{x}^{*}}=\{j\in J: x^{*}_{j}=\bar {x}_{j}\}$, is a set cover of I. We will show that the size $\left |J_{{x}^{*}}\right |$ of the set cover is minimum. By optimality of x^∗, we necessarily have $x^{*}_{j}=-\infty$, for $j\in J\setminus J_{{x}^{*}}$ and the support of x^∗ is the same as the agreement set; otherwise, we could create a sparser solution by forcing the elements outside of the agreement set to be −∞. So, $\left |\text {supp}({\boldsymbol {x}}^{\boldsymbol {*}})\right |=\left |J_{{x}^{*}}\right |$. Now, take any set cover {I_j : j ∈ K ⊆ J} of I and define element x(K) as:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{x}(K)_{j}&=&\bar{x}_{j}, j\in K\\ \boldsymbol{x}(K)_{j}&=&-\infty, j\in J\setminus K \end{array} $$

(26)

Notice that |supp(x(K))| = |K| and by Theorem 7, x(K) is also a solution to the max-plus equation $\boldsymbol {A} {\boxplus } \boldsymbol {x}=\boldsymbol {b}$. By optimality, x^∗ has the smallest support, or |supp(x^∗)|≤ |supp(x(K))|. But this implies that $\left |J_{{x}^{*}}\right |\le |{K}|$, which shows that $\{I_{j}:j\in J_{{x}^{*}}\}$ is a minimum set cover of I.

Conversely, suppose the collection {I_j : j ∈ K^∗⊆ J} is a minimum set cover of I. Then, we can define the solution $\hat {\boldsymbol {x}}$ as in Eq. 10. We will show that $\hat {\boldsymbol {x}}$ is an optimal solution to Eq. 6. Suppose x^∗ is one optimal solution to Eq. 6. Then, the collection $\{I_{j}:j\in J_{{x}^{*}}\}$ is a set cover with $J_{{x}^{*}}=\{j\in J: x^{*}_{j}=\bar {x}_{j}\}$. Since x^∗ is the sparsest solution, we can only have $\left |\text {supp}(\boldsymbol {x}^{\boldsymbol {*}})\right |=\left |J_{{x}^{*}}\right |$. Meanwhile, by optimality of the set cover we have

$$ \left|\text{supp}({\hat{\boldsymbol{x}}})\right|=\left|K^{*}\right|\le \left|J_{{x}^{*}}\right|=\left|\text{supp}({\boldsymbol{x}}^{\boldsymbol{*}})\right|. $$

Hence, $\hat {\boldsymbol {x}}$ is also an optimal solution to Eq. 6.

Second, we prove ii). This part is adapted from Butkovič (2003). Suppose we are given an arbitrary collection of nonempty subsets

$$ S_{j}\subseteq\{1,\dots,m\}=I, j\in\{1,\dots,n\}=J, $$

for some $m, n\in \mathbb {N}$, such that $\bigcup _{j\in J}S_{j}=I$. Define $A_{ij}={\mathbbm {1}}(i\in S_{j})$ for all i ∈ I,j ∈ J, where $\mathbbm {1}$ is the indicator function, and b_i = 1, for all i ∈ I. By Eqs. 3, 9, it follows that the principal solution is $\bar {\boldsymbol {x}}=[1 \ldots 1]^{\intercal }$, while the sets S_j are equal to the sets I_j. But following the analysis of i), finding the minimum set cover of I using S_j = I_j is equivalent to finding the solution to problem (6) with the above selection of A,b. This completes the proof of part ii).

□

Proof of Lemma 2

By construction, the agreement set and the support are equal to T or

$$ \begin{array}{@{}rcl@{}} z_{j}&=&\bar{x}_{j},\text{ for }j\in T\\ z_{j}&=&-\infty,\text{ for }j\in J\setminus T \end{array} $$

Thus, $\boldsymbol {z}\le \bar {\boldsymbol {x}}$ and by Theorem 8, also $\boldsymbol {A} {\boxplus } \boldsymbol {z}\le \boldsymbol {b}$, which proves that z ∈ X_T.

To prove the second part, again from Theorem 8, if x ∈ X_T then

$$ \begin{array}{@{}rcl@{}} x_{j}&\le& \bar{x}_{j}=z_{j}, \text{ for }j\in T\\ x_{j}&=&z_{j}=-\infty, \text{ for }j\in J\setminus T \end{array} $$

As a result, x ≤z for any x ∈ X_T. Now, since $\boldsymbol {A}{\boxplus } \cdot$ is increasing (Cuninghame-Green 1979) we obtain the inequality:

$$ \boldsymbol{b} -\boldsymbol{A} {\boxplus} \boldsymbol{z}\le \boldsymbol{b} -\boldsymbol{A} {\boxplus} \boldsymbol{x}, $$

for any x ∈ X_T. Since both x,z satisfy the lateness constraint (4), we finally have

$$ \|\boldsymbol{b}-\boldsymbol{A}\boxplus\boldsymbol{x}\|_{1}=\mathbf{1}^{\intercal}(\boldsymbol{b} -\boldsymbol{A}\boxplus\boldsymbol{x})\ge \mathbf{1}^{\intercal}(\boldsymbol{b} -\boldsymbol{A}\boxplus\boldsymbol{z})=\|\boldsymbol{b}-\boldsymbol{A} \boxplus \boldsymbol{z}\|_{1} $$

for any x ∈ X_T, where $\mathbf {1}=[1 \cdots 1]^{\intercal }$. □

Proof of Corollary 1

Let x^∗, $\hat {T}$ be the optimal solutions of problems (7), (16) respectively. Denote by T^⋆ = supp(x^∗) the support of x^∗. Then construct a new vector z^∗ such that $z^{*}_{j}=\bar {x}_{j}, j\in T^{*}$ and $z^{*}_{j}=-\infty , i\in J\setminus T^{*}$. By Lemma 2,

$$ E({T^{*}})=\left\|\boldsymbol{b}-\boldsymbol{A} {\boxplus} \boldsymbol{z}^{*}\right\|_{1}\le \left\|\boldsymbol{b}-\boldsymbol{A} {\boxplus} \boldsymbol{x}^{*}\right\|_{1}\le \epsilon. $$

Thus, T^∗ = supp(x^∗) is a feasible point of problem (16), implying $|\hat {T}|\le \left |{T^{*}}\right |$.

Conversely, define $\hat {\boldsymbol {x}}$ as in Eq. 17. By construction and the feasibility of $\hat {T}$ and Lemma 2, we have:

$$ \begin{array}{@{}rcl@{}} \left\|\boldsymbol{b}-\boldsymbol{A} {\boxplus} \hat{\boldsymbol{x}}\right\|_{1}&=&E(\hat{T})\le \epsilon.\\ \boldsymbol{A} {\boxplus} \hat{\boldsymbol{x}}&\le& \boldsymbol{b} \end{array} $$

Thus, $\hat {\boldsymbol {x}}$ is a feasible point of problem (7), which implies $\left |{T^{*}}\right |\le |\hat {T}|$. From the above inequalities we obtain $\left |{T^{*}}\right |= |\hat {T}|$, which also proves that $\hat {\boldsymbol {x}}$ is an optimal solution to problem (7).

□

Proof of Theorem 3

Notice that we have:

$$ \bigvee\limits_{j\in T}(\boldsymbol{A}_{j}+\bar{x}_{j})\le \bigvee\limits_{j\in J}(\boldsymbol{A}_{j}+\bar{x}_{j})=\boldsymbol{A} {\boxplus} \bar{\boldsymbol{x}}\le \boldsymbol{b} $$

Thus, we get by construction that the error vector e(T) has only positive components, for every T ⊆ J, which implies:

$$ E(T)=\|\boldsymbol{e}(T)\|=\mathbf{1}^{\intercal}\boldsymbol{e}(T), $$

(27)

where $1^{\intercal }=[1 \ldots 1]^{\intercal }$. For convenience, define matrix $\boldsymbol {\hat {A}}\in \mathbb {R}_{\max }^{m\times n}$ as $\hat {A}_{ij}=A_{ij}+\bar {x}_{j}$. Then, by the definition (14) of error vector:

$$ \bigvee\limits_{j\in T}\boldsymbol{\hat{A}}_{\boldsymbol{j}}=\boldsymbol{b}-\boldsymbol{e}(T). $$

First, we show that E(T) is decreasing. Let B, C be two nonempty subsets of J with C ⊆ B ⊂ J. Then, $\bigvee \limits _{j\in C}\boldsymbol {\hat {A}}_{\boldsymbol {j}}\le \bigvee \limits _{j\in B}\boldsymbol {\hat {A}}_{\boldsymbol {j}}$. Consequently, e(B) ≤ e(C). Now if C is empty and B is non-empty, then by construction $e(\emptyset )\ge \bigvee \limits _{k\in J}e(\{k\})\ge e(B)$ (if C, B are both empty we trivially have e(C) = e(B)). In any case, by Eq. 27, we obtain E(C) ≥ E(B).

Second, we show that E(T) is supermodular. Let C ⊆ B ⊆ J and k ∈ J ∖ B. It is sufficient to prove that:

$$ \boldsymbol{e}(C\cup\{k\})-\boldsymbol{e}(C)\le \boldsymbol{e}(B\cup\{k\})-\boldsymbol{e}(B). $$

(28)

For C≠∅ define:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{u}&=&\bigvee\limits_{j\in C}\boldsymbol{\hat{A}}_{j},\quad\quad\quad\quad \boldsymbol{v}=\bigvee\limits_{j\in C\cup \{k\}}\boldsymbol{\hat{A}}_{j}\\ \boldsymbol{z}&=&\bigvee\limits_{j\in B}\boldsymbol{\hat{A}}_{j},\quad\quad\quad\quad \boldsymbol{w}=\bigvee\limits_{j\in B\cup \{k\}}\boldsymbol{\hat{A}}_{j}. \end{array} $$

By this definition, $v_{i}=u_{i}{\vee } \hat {A}_{ik}$, $w_{i}=z_{i}{\vee } \hat {A}_{ik}$ for every i ∈ I. Also, by monotonicity u ≤z, v ≤w. There are three possibilities:

• i) If $u_{i}>\hat {A}_{ik}$ then v_i = u_i. But also w_i = z_i, since by monotonicity z ≥u and $z_{i}\ge u_{i}> \hat {A}_{ik}$. In this case, v_i − u_i = w_i − z_i = 0.

• ii) If $u_{i}\le \hat {A}_{ik}$ and $z_{i}>\hat {A}_{ik}$ then $v_{i}-u_{i}=\hat {A}_{ik}-u_{i}\ge 0$ and w_i − z_i = 0 ≤ v_i − u_i.

• iii) If both $u_{i}\le \hat {A}_{ik}$ and $z_{i}\le \hat {A}_{ik}$ then $v_{i}-u_{i}=\hat {A}_{ik}-u_{i}\ge \hat {A}_{ik}-z_{i}=w_{i}-z_{i}$, since by monotonicity z_i ≥ u_i.

If C is the empty set, we define u = b −e(∅) and v,z,w are defined as before. Since by construction e(∅) ≤e(k) for all k ∈ J, we also have u ≤v and u ≤z. Thus, either case ii) or case iii) applies.

In any case, v −u ≥w −z which is equivalent to Eq. 28. Finally, multiplying both sides of Eq. 28 from the left by $\mathbf {1}^{\intercal }$ gives the desired result: E(C ∪{k}) − E(C) ≤ E(B ∪{k}) − E(B). □

Proof of Theorem 4

Define the truncated error set function

$$ \bar{E}(T)=\max(E(T),\epsilon). $$

By Theorem 3, the error set function E(T) is supermodular and decreasing. Thus, so is the truncated error function (Krause and Golovin 2012). This enables as to express the constraint E(T) ≤ 𝜖 as $\bar {E}(T)=\bar {E}(J)$. Then, the lines 6 − 11 of Algorithm 2 are a version of Algorithm 1. Hence, Theorem 2 readily applies giving the bounds

$$ \frac{\left|{T_{k}}\right|}{|\hat{T}|}\le 1+\log\left( \frac{\bar{E}(\emptyset)-\bar{E}(J)}{\bar{E}(T_{k-1})-\bar{E}(J)}\right), $$

where $\hat {T}$ is the optimal solution of problem (16). From Corollary 1 we can replace $\hat {T}$ with T^∗. By the assumption E(∅) > 𝜖 and the definition of the ℓ₁-error set function at ∅:

$$ \bar{E}(\emptyset)=E(\emptyset)=\sum\limits_{i\in I}\bigvee\limits_{j\in J}(b_{i}-A_{ij}-\bar{x}_{j})\le m{\Delta}. $$

Meanwhile, we have $\bar {E}(J)\ge 0$ and the result for the nominator in the logarithm follows. For the denominator, notice that k is such that E(T_k− 1) > 𝜖 and E(T_k) ≤ 𝜖. Such k exists since E(J) ≤ 𝜖 and in the worst case, Algorithm2 halts at k = |J| with T_k = J. Thus, we have $\bar {E}(T_{k-1})=E(T_{k-1})$ and $\bar {E}(J)=\epsilon$. □

Proof of Lemma 3

It is sufficient to prove that the feasible regions of both problems are identical. First, we prove that:

$$ \boldsymbol{A} {\boxplus} \boldsymbol{x}\le \boldsymbol{b} \Leftrightarrow \boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x}\le \boldsymbol{b} $$

(29)

But from Theorem 8, it is equivalent to show that $\bar {\boldsymbol {x}}=\hat {\bar {\boldsymbol {x}}}$, where $\bar {\boldsymbol {x}}$ is the original principal solution defined in Eq. 3 and $\hat {\bar {\boldsymbol {x}}}$ is the new principal solution with $\boldsymbol {\hat {A}}(M)$ instead of A:

$$ \hat{\bar{x}}_{j}=\bigwedge\limits_{i=1}^{m}\left( b_{i}-\hat{A}_{ij}(M)\right), \forall j\in J. $$

(30)

By construction, $A_{ij}\le \hat {A}_{ij}(M)$, which by Eqs. 3, 30, implies $\hat {\bar {\boldsymbol {x}}}\le \bar {\boldsymbol {x}}$. To show the other direction, we have

$$ \hat{\bar{x}}_{j}=b_{k}-\hat{A}_{kj}(M), \text{ for some }k\in I. $$

There are two cases:

• i) $\hat {A}_{kj}(M)=A_{kj}$. Then, $\hat {\bar {x}}_{j}=b_{k}-A_{kj}\ge \bigwedge \limits _{i\in I}b_{i}-A_{ij}= \bar {x}_{j}$.

• ii) $\hat {A}_{kj}(M)=b_{k}-M-\bar {x}_{j}$. Then, $\hat {\bar {x}}_{j}=M+\bar {x}_{j}> \bar {x}_{j}$, since M > 0.

Thus, we also have $\hat {\bar {\boldsymbol {x}}}\ge \bar {\boldsymbol {x}}$. This proves $\bar {\boldsymbol {x}}=\hat {\bar {\boldsymbol {x}}}$.

Second, we prove that under the constraint $\boldsymbol {A} {\boxplus } \boldsymbol {x}\le \boldsymbol {b}$ (which we showed is equivalent to $\boldsymbol {\hat {A}}(M) {\boxplus } \boldsymbol {x}\le \boldsymbol {b}$) we have:

$$ \|\boldsymbol{b}-\boldsymbol{A} {\boxplus} \boldsymbol{x}\|_{1}\le \epsilon \Leftrightarrow \|\boldsymbol{b}-\boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x}\|_{1}\le \epsilon $$

(31)

“⇒” direction. Since $A_{ij}\le \hat {A}_{ij}(M)$, we obtain

$$ \boldsymbol{A} {\boxplus} \boldsymbol{x}\le \boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x} . $$

But we have $\boldsymbol {A} {\boxplus } \boldsymbol {x}\le \boldsymbol {b}, \boldsymbol {\hat {A}}(M) {\boxplus } \boldsymbol {x}\le \boldsymbol {b}.$ Thus,

$$ \|\boldsymbol{b}-\boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x}\|_{1} \le \|\boldsymbol{b}-\boldsymbol{A} {\boxplus} \boldsymbol{x}\|_{1}\le \epsilon. $$

“⇐” direction. For every i ∈ I, there exists an index j_i ∈ J such that:

$$ \|\boldsymbol{b}-\boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x}\|_{1} ={\sum}_{i=1}^{m}(b_{i}-\hat{A}_{ij_{i}}(M)-x_{j_{i}}) $$

Now assume that some element $\hat {A}_{kj_{k}}(M)$ is equal to $-M+b_{i}-\bar {x}_{j_{i}}$, for some k ∈ I. Then, this implies

$$ \begin{array}{@{}rcl@{}} \epsilon&\ge& \|\boldsymbol{b}-\boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x}\|_{1}={\sum}_{i=1}^{m}(b_{i}-\hat{A}_{ij_{i}}(M)-x_{j_{i}})\\ &\ge& b_{k}-\hat{A}_{kj_{k}}(M)-\bar{x}_{j_{k}}=M, \end{array} $$

where the second inequality follows from $\boldsymbol {\hat {A}}(\boldsymbol {M}) {\boxplus } \boldsymbol {x}\le \boldsymbol {b}$ and the equivalent fact $\boldsymbol {x}\le \bar {\boldsymbol {x}}$ (see Theorem 8). But since M > 𝜖, this is a contradiction and the only possible case is $\hat {A}_{ij_{k}}(M)=A_{ij_{i}}$, for all i ∈ I. Finally,

$$ \begin{array}{@{}rcl@{}} \epsilon&\ge&\|\boldsymbol{b}-\boldsymbol{\hat{A}}(M) {\boxplus} \boldsymbol{x}\|_{1}={\sum}_{i=1}^{m}(b_{i}-A_{ij_{i}}-x_{j_{i}})\\ &\ge& {\sum}_{i=1}^{m}\left( b_{i}-\bigvee\limits_{j\in J}(A_{ij}+x_{j})\right)=\|\boldsymbol{b}-\boldsymbol{A} {\boxplus} \boldsymbol{x}\|_{1}. \end{array} $$

This completes the proof. □

Proof of Theorem 6

Define $\boldsymbol {b}=\boldsymbol {A} {\boxplus } \boldsymbol {z}$. It is sufficient to show that for any solution $\boldsymbol {x}\in \mathbb {R}_{\max }^{n}$ of equation $\boldsymbol {A} {\boxplus } \boldsymbol {x}=\boldsymbol {b}$, we have:

$$ x_{j}=z_{j},\text{ for all }j\in \text{supp}({\boldsymbol{z}}). $$

(32)

Then, since x^∗ is also a solution we have $x^{*}_{j}=z_{j}$, for j ∈supp(z). But x^∗ is the sparsest solution. Thus, we necessarily have $x^{*}_{j}=-\infty$ for j∉supp(z); otherwise, z would be a sparser solution contradicting the assumptions. This implies that z = x^∗.

We now prove (32). Given a j ∈supp(z), let i = i(j) ∈ I be the row index such that the condition of the theorem holds. Consider the row index sets I_j ⊆ I, j ∈ J defined in Eq. 9. Part b) of the condition implies that

$$ \bar{x}_{l}=\bigwedge\limits_{t\in I}b_{t}-A_{tl}\le b_{s}-A_{sl} <b_{i}-A_{il},\text{ for all }l\in J\setminus\text{supp}({\boldsymbol{z}}). $$

This implies that the above minimum is not attained at i or:

$$ i\not\in I_{l},\text{ for all } l\in J\setminus\text{supp}({\boldsymbol{z}}). $$

(33)

Part a) of the condition implies that

$$ b_{i}=\bigvee\limits_{p\in J}(A_{ip}+z_{p})=A_{ij}+z_{j}. $$

Moreover, by the definition (3) of the principal solution:

$$ \bar{x}_{j}=\bigwedge\limits_{q\in I}(b_{q}-A_{qj})\le b_{i}-A_{ij}= z_{j}. $$

But by Theorem 7, only $\bar {x}_{j}=z_{j}$ is possible since the principal solution dominates every other solution. Let k ∈supp(z), k≠j be another index in the support of z. We can similarly show that $\bar {x}_{k}=z_{k}$. Now, we claim that i∉I_k. If we had i ∈ I_k, then $z_{k}=\bar {x}_{k}=b_{i}-A_{ik}$ or by replacing b_i = A_ij + z_j:

$$ A_{ij}+z_{j}= A_{ik}+z_{k}, $$

which contradicts the theorem hypothesis A_ij + z_j > A_ik + z_k. Thus:

$$ i\not\in I_{k},\text{ for all } k\in \text{supp}({\boldsymbol{z}})\setminus\{j\}. $$

(34)

Since the system $\boldsymbol {A} {\boxplus } \boldsymbol {x}=\boldsymbol {b}$ is solvable, from Eqs. 33, 34j is the unique index such that i ∈ I_j. Hence, set I cannot be covered without including set I_j in the covering. By Theorem 7, any solution $\boldsymbol {x}\in \mathbb {R}_{\max }^{n}$ must necessarily have $x_{j}=\bar {x}_{j}=z_{j}$. □