Abstract
SAT solvers decide the satisfiability of Boolean formulas in conjunctive normal form. They are commonly used for software and hardware verification. Modern SAT solvers are highly complex and optimized programs. As a single bug in the solver may invalidate the verification of many systems, SAT solvers output certificates for their answer, which are then checked independently. However, even certificate checking requires highly optimized non-trivial programs. This paper presents the first SAT solver certificate checker that is formally verified down to the integer sequence representing the formula. Our tool supports the full DRAT standard, and is even faster than the unverified state-of-the-art tool drat-trim, on a realistic set of benchmarks drawn from the 2016 and 2017 SAT competitions. An optional multi-threaded mode further reduces the runtime, in particular for big certificates.
Similar content being viewed by others
1 Introduction
Modern SAT solvers are highly optimized and use complex algorithms and heuristics. This makes them prone to bugs. Given that SAT solvers are used in software and hardware verification, a single bug in a SAT solver may invalidate the verification of many systems. One measure to increase the trust in SAT solvers is to make them output a certificate, which is used to check the result of the solver by a simpler algorithm. Most SAT solvers support the output of a satisfying valuation of the variables as an easily checkable certificate for satisfiability. Certificates for unsatisfiability are more complicated, and different formats have been proposed (e. g. [44,45,46]). Since 2013, the SAT competition [40] requires solvers to output unsat certificates. Since 2014, only certificates in the DRAT format [46] are accepted [41].
The standard tool to check DRAT certificates is drat-trim [9, 46]. It is a highly optimized C program with many features, including forward and backward checking modes, a satisfiability certificate checking mode, and a feature to output reduced (trimmed) certificates. However, the high degree of optimization and the wealth of features come at the price of code complexity, increasing the likelihood of bugs. And indeed, during our formalization of DRAT certificates, we realized that drat-trim was missing a crucial check, thus accepting (maliciously engineered) unsat certificates for satisfiable formulas. This bug has been confirmed by the authors, and is now fixed. Moreover, we discovered several numeric and buffer overflow issues in the parser [10], which could lead to misinterpretation of the formula. Thus, although being less complex than SAT solvers, efficient DRAT checkers are still complex enough to easily overlook bugs.
One method to ensure correctness of software is to conduct a machine-checked correctness proof. A common approach is to prove correct a specification in the logic of an interactive theorem prover, and then generate executable code from the specification. Here, code generation is merely a syntax transformation from the executable fragment of the theorem prover’s logic to the target language. Following the LCF approach [14], modern theorem provers like Isabelle [38] and Coq [3] are explicitly designed to maximize their trustworthiness. Unfortunately, the algorithms and low-level optimizations required for efficient unsat certificate checking are hard to verify and existing approaches (e. g. [8, 45]) do not scale to large problems.
While working on the verification of an efficient DRAT checker, the author learned about GRIT, proposed by Cruz-Filipe et al. [7]: They use a modified version of drat-trim to generate an enriched certificate from the original DRAT certificate. The crucial idea is to record the required unit propagations, such that the checker of the enriched certificate only needs to implement a check whether a clause is unit, instead of a fully fledged unit propagation algorithm.
Cruz-Filipe et al. formalize a checker for their enriched certificates in the Coq theorem prover [3], and generate OCaml code from the formalization. However, their approach still has some deficits: GRIT only supports the less powerful DRUP fragment [45] of DRAT, making it unsuitable for SAT solvers that output full DRAT. Also, their checker does not consider the original formula but assumes that the certificate correctly mirrors the formula. Moreover, they use unverified code to parse the certificate into the internal data structures of the checker. Finally, their verified checker is quite slow: Checking a certificate requires roughly the same time as generating it, which effectively doubles the verification time. In contrast, an unverified implementation of their checker in C is two orders of magnitude faster.
Independently of us, Cruz-Filipe et al. also extended their tool to DRAT [6], and optimized their verified checker [18]. Their tool is called LRAT.
In this paper we present the GRAT toolchain: An enriched certificate format for full DRAT, a highly optimized certificate generator, and a certificate checker whose correctness is formally verified down to the integer array representing the formula. The simple unverified parser that reads a formula into an integer array is written in Standard ML [34], which guarantees that numeric and buffer overflows will not go unnoticed. On the same basis, we also implement and verify a sat certificate checker, obtaining a complete and formally verified SAT solver certification tool.
We use stepwise refinement techniques to obtain an efficient verified checker, and implement aggressive optimizations in the generator. A distinguishing feature is a multi-threaded mode for the generator, which allows us to trade computing resources for additional speedup.
We benchmark our tool against drat-trim and LRAT on a realistic benchmark suite drawn from the 2016 and 2017 SAT competitions: Already in single-threaded mode, our tool is faster than LRAT on every single problem, and, on most problems, even faster than the (unverified) drat-trim. In multi-threaded mode with 8 threads, we get an average speedup of 2.2.
This paper is an extended version of our conference papers [28, 29]. It provides a unified description of both the certificate generator and checker, and extends the benchmark set to include problems from the 2017 SAT competition. Our tools, formalizations, and benchmark results are available online [23].
The rest of this paper is organized as follows: After briefly recalling the theory of DRAT certificates (Sect. 2), we introduce our enriched certificate format (Sect. 3). We then give a short overview of the Isabelle Refinement Framework (Sect. 4) and describe its application to verifying our certificate checker (Sect. 5). Next, we describe our certificate generator (Sect. 6) and report on the experimental evaluation of our tools (Sect. 7). Finally, we discuss future work (Sect. 8) and give a conclusion (Sect. 9).
2 Unsatisfiability Certificates
We briefly recall the theory of DRAT unsatisfiability certificates. Let V be a set of variable names. The set of literals is defined as \(L := V \dot{\cup }\{\lnot v \mid v\in V \}\). We identify v and \(\lnot \lnot v\). Let \(F = C_1 \wedge \cdots \wedge C_n\) for \(C_i \in 2^L\) be a formula in conjunctive normal form (CNF). F is satisfied by an assignment\(A : V \Rightarrow \text {bool}\) iff instantiating the variables in F with A yields a true (ground) formula. We call Fsatisfiable iff there exists an assignment that satisfies F.
A clause C is called a tautology iff there is a variable v with \(\{v,\lnot v\} \subseteq C\). Removing a tautology from a formula yields an equivalent formula. In the following we assume that formulas do not contain tautologies. The empty clause is called a conflict. A formula that contains a conflict is unsatisfiable. A singleton clause \(\{l\} \in F\) is called a unit clause. Removing all clauses that contain l, and all literals \(\lnot l\) from F yields an equisatisfiable formula. Repeating this exhaustively for all unit clauses is called unit propagation. We name the result of unit propagation \(F^{\text {u}}\), defining \(F^{\text {u}} = \{\emptyset \}\) if unit propagation yields a conflict.Footnote 1
A DRAT certificate \(\chi = \chi _1\cdots \chi _n\) with \(\chi _i \in 2^L \mathbin {\dot{\cup }} \{ \text {d} C \mid C\in 2^L \}\) is a list of clause addition and deletion items. The effect of a (prefix of) a DRAT certificate is to add/delete the specified clauses to/from the original formula \(F_0\), and apply unit propagation:
where \(F {\setminus } C\) removes one occurrence of clause C from F. We call the clause addition items of a DRAT certificate lemmas.
A DRAT certificate \(\chi = \chi _1\ldots \chi _n\) is valid iff \(\text {eff}(\chi ) = \{\emptyset \}\) and each lemma has the RAT property wrt. the effect of the previous items:
A clause C has the RAT (resolution asymmetric tautology) property wrt. formula F (we write \(\text {RAT}(F,C)\)) iff either C is empty and \(F^{\text {u}}=\{\emptyset \}\), or if there is a pivot literal\(l\in C\), such that for all RAT candidates\(D\in F\) with \(\lnot l \in D\), we have \((F \wedge \lnot (C \cup D{\setminus }\{\lnot l\}))^{\text {u}} = \{\emptyset \}\). Adding a lemma with the RAT property to a satisfiable formula preserves satisfiability [45], and so do unit propagation and deletion of clauses. Thus, existence of a valid DRAT certificate implies unsatisfiability of the original formula.
A more restrictive property than RAT is RUP (reverse unit propagation): A lemma C has the RUP property wrt. formula F iff \((F \wedge \lnot C)^{\text {u}} = \{\emptyset \}\). Adding a lemma with the RUP property yields an equivalent formula. The predecessor of DRAT is DRUP [19], which admits only lemmas with the RUP property.
Checking a lemma for RAT is much more expensive than checking for RUP, as the clause database must be searched for candidate clauses, performing a unit propagation for each of them. Thus, practical DRAT certificate checkers first perform a RUP check on a lemma, and only if this fails they resort to a full RAT check. Exploiting that \((F\wedge \lnot (C\cup D))^\text {u}\) is equivalent to \(((F \wedge \lnot C)^\text {u} \wedge \lnot D)^\text {u}\), the result of the initial unit propagation from the RUP check can even be reused. Another important optimization is backward checking [13, 19]: The lemmas are processed in reverse order, marking the lemmas that are actually needed in unit propagations during RUP and RAT checks. Lemmas that remain unmarked need not be processed at all. To further reduce the number of marked lemmas, core-first unit propagation [46] prefers marked unit clauses over unmarked ones.
In practice, DRAT certificate checkers spend most time on unit propagation,Footnote 2 for which highly optimized implementations of rather complex algorithms are used (e. g. drat-trim uses a two-watched-literals algorithm [36]). Unfortunately, verifying such highly optimized code in a proof assistant is a major endeavor. Thus, a crucial idea is to implement an unverified tool that enriches the certificate with additional information that can be used for simpler and more efficient verification. For DRUP, the GRIT format has been proposed recently [7]. It stores, for each lemma, a list of unit clauses in the order they become unit, followed by a conflict clause. Thus, finding the next unit or conflict clause is replaced by simply checking whether a clause is unit or conflict. A modified version of drat-trim can be used to generate a GRIT certificate from the original DRAT certificate.
3 The GRAT Format
The first contribution of this paper is to extend the ideas of GRIT from DRUP to DRAT. To this end, we define the GRAT format. Like for GRIT, each clause is identified by a unique positive ID. The clauses of the original formula implicitly get the IDs \(1\ldots N\). The lemma IDs explicitly occur in the certificate.
For memory efficiency reasons, we store the certificate in two parts: The lemma file contains the lemmas, and is stored in DIMACS format. During certificate checking, this part is entirely loaded into memory. The proof file contains the hints and instructions for the certificate checker. It is not completely loaded into memory but only streamed during checking.
The proof file is a binary file, containing a sequence (stored in reverse order) of 32 bit signed integers in 2’s complement little endian format. The sequence is interpreted according to the following grammar:

The checker maintains a clause map that maps IDs to clauses, and a partial assignment that maps variables to true, false, or undecided. Partial assignments are extended to literals in the natural way. Initially, the clause map contains the clauses of the original formula, and the partial assignment maps all variables to undecided. Then, the checker iterates over the items of the proof, processing each item as follows:
- rat-counts:
This item contains a list of pairs of literals and the count how often they are used in RAT proofs. This map allows the checker to maintain lists of RAT candidates for the relevant literals, instead of gathering the possible RAT candidates by iterating over the whole clause database for each RAT proof, which is expensive. Literals that are not used in RAT proofs at all do not occur in the list. This item is the first item of the proof.
- unit-prop:
For each listed clause ID, the corresponding clause is checked to be unit, and the unit literal is assigned to true. Here, a clause is unit if the unit literal is undecided, and all other literals are assigned to false.
- deletion:
The specified IDs are removed from the clause map.
- rup-lemma:
The item specifies the ID for the new lemma, which is the next unprocessed lemma from the lemma file, a list of unit clause IDs, and a conflict clause ID. First, the literals of the lemma are assigned to false. The lemma must not be blocked, i. e. none of its literals may be already assigned to true.Footnote 3 Note that assigning the literals of a clause C to false is equivalent to adding the conjunct \(\lnot C\) to the formula. Second, the unit clauses are checked and the corresponding unit literals are assigned to true. Third, it is checked that the conflict clause ID actually identifies a conflict clause, i. e. that all its literals are assigned to false. Finally, the lemma is added to the clause-map and the assignment is rolled back to the state before checking of the item started.
- rat-lemma:
The item specifies a pivot literal l, an ID f or the lemma, an initial list of unit clause IDs, and a list of candidate proofs. First, as for
 , the literals of the lemma are assigned to false and the initial unit propagations are performed. Second, it is checked that the provided RAT candidates are exhaustive, and then the corresponding
, the literals of the lemma are assigned to false and the initial unit propagations are performed. Second, it is checked that the provided RAT candidates are exhaustive, and then the corresponding
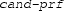 items are processed: A
items are processed: A
 item consists of the ID of the candidate clause D, a list of unit clause IDs, and a conflict clause ID. To check a candidate proof, the literals of \(D{\setminus }\{\lnot l\}\) are assigned to false, the listed unit propagations are performed, and the conflict clause is checked to be actually conflict. Afterwards, the assignment is rolled back to the state before checking the candidate proof. Third, when all candidate proofs have been checked, the lemma is added to the clause map and the assignment is rolled back. To simplify certificate generation in backward mode, we allow candidate proofs referring to arbitrary, even invalid, clause IDs. Those proofs must be ignored by the checker.
item consists of the ID of the candidate clause D, a list of unit clause IDs, and a conflict clause ID. To check a candidate proof, the literals of \(D{\setminus }\{\lnot l\}\) are assigned to false, the listed unit propagations are performed, and the conflict clause is checked to be actually conflict. Afterwards, the assignment is rolled back to the state before checking the candidate proof. Third, when all candidate proofs have been checked, the lemma is added to the clause map and the assignment is rolled back. To simplify certificate generation in backward mode, we allow candidate proofs referring to arbitrary, even invalid, clause IDs. Those proofs must be ignored by the checker.- conflict:
This is the last item of the certificate. It specifies the ID of the conflict clause found by unit propagation after adding the last lemma of the certificate (root conflict). It is checked that the ID actually refers to a conflict clause.
4 Program Verification with Isabelle/HOL
Isabelle/HOL [38] is an interactive theorem prover for higher order logic. Its design features the LCF approach [14], where a small logical inference kernel is the only code that can produce theorems. Bugs in the non-kernel part may result in failure to prove a theorem but never in a false proposition being accepted as a theorem. Isabelle/HOL includes a code generator [15,16,17] that translates the executable fragment of HOL to various functional programming languages, currently OCaml, Standard ML, Scala, and Haskell. Via Imperative HOL [5], the code generator also supports imperative code, modeled by a heap monad inside the logic.
A common problem when verifying efficient implementations of algorithms is that implementation details tend to obfuscate the proof and increase its complexity. Hence, efficiency of the implementation is often traded for simplicity of the proof. A well-known approach to this problem is stepwise refinement [1, 2, 48], where an abstract version of the algorithm is refined towards an efficient implementation in multiple correctness preserving steps. The abstract version focuses on the algorithmic ideas, leaving open the exact implementation, while the refinement steps focus on more and more concrete implementation aspects. This modularizes the correctness proof, and makes verification of complex algorithms manageable in the first place.
For Isabelle/HOL, the Isabelle Refinement Framework [24, 26, 27, 32] provides a powerful stepwise refinement tool chain, featuring a nondeterministic shallowly embedded programming language [32], a library of efficient collection data structures and generic algorithms [26, 27, 30], and convenience tools to simplify canonical refinement steps [24, 26]. It has been used for various software verification projects (e. g. [25, 31, 47]), including a fully fledged verified LTL model checker [4, 11].
5 A Verified GRAT Certificate Checker
We give an overview of our Isabelle/HOL formalization of a GRAT certificate checker (cf. Sect. 3). We use the stepwise refinement techniques provided by the Isabelle Refinement Framework to verify an efficient implementation at manageable proof complexity.
Note that we display only slightly edited Isabelle/HOL source text, and try to explain its syntax as far as needed to get a basic understanding. Isabelle/HOL uses a mixture of common mathematical notations and Standard ML [34] syntax (e. g. there are algebraic data types, function application is written as
 , functions are usually curried, e. g.
, functions are usually curried, e. g.
 , and abstraction is written as
, and abstraction is written as
 ).
).
5.1 Syntax and Semantics of Formulas
For the abstract syntax of CNF formulas, we represent variables by natural numbers, use an algebraic data type to specify positive and negative literals, model clauses as sets of literals, and a CNF formula as a set of clauses:

The concrete syntax that our tool accepts is a list (array) of integers, representing a formula in the well-known DIMACS format. Variables are positive natural numbers. Literals are non-zero integers of the form v or \(-v\), representing positive and negative literals on variable v. A clause is a list of literals, and a formula is the concatenation of its clauses, separated and terminated by nulls. The following definitions specify the restrictions on the concrete syntax (
 ) and the translation from concrete to abstract syntax (
) and the translation from concrete to abstract syntax (
 ):
):

where
 converts an integer to a natural number,
converts an integer to a natural number,
 converts a list to the set of its elements, and
converts a list to the set of its elements, and
 splits the concatenation of null-terminated lists into a list of lists. Note that every list that ends with a null represents a valid formula.
splits the concatenation of null-terminated lists into a list of lists. Note that every list that ends with a null represents a valid formula.
We define the semantics of literals, clauses, and formulas wrt. a valuation, which is a function from variables to Booleans. A positive literal is true if its variable is assigned to true, a negative literal is true if its variable is false, a clause is true if it contains a true literal, and a formula is true if all its clauses are true:

Note that type specifications on constant definitions are optional in Isabelle/HOL, and if they are omitted, the most general type is inferred automatically.
We define the models of a formula to be the set of all valuations that make the formula true, and we define a formula to be satisfiable if it has a model:

While unit propagation can be presented by modifying the formula (removing false literals and true clauses), practical implementations use a partial assignment (where variables can be true, false, or undecided) and do not change the formula on unit propagation. At this point, we have the design choice to either formalize unit-propagation by modifying the formula, and then refine this model to partial assignments, or to formalize unit propagation on partial assignments directly. We decided for the latter, as we found it to be convenient, and it saves the overhead of one refinement step.
A partial assignment has type
 , which is abbreviated as
, which is abbreviated as
 . It maps a variable to
. It maps a variable to
 for undecided, or to
for undecided, or to
 or
or
 . We specify the semantics of literals and clauses as follows:
. We specify the semantics of literals and clauses as follows:

For a fixed formula F, we define the models induced by a partial assignment A to be all total extensions that satisfy the formula, and a predicate
 which holds iff such a model exists:
which holds iff such a model exists:

Obviously, a formula is satisfiable wrt. the empty partial assignment if, and only if, it is satisfiable:

Two assignments
 and
and
 are equivalent iff they induce the same models:
are equivalent iff they induce the same models:

5.2 Unit Propagation and RAT
We define a predicate to state that, wrt. a partial assignment A, a clause C is unit, with unit literal l:

Assigning a unit literal to true yields an equivalent assignment:

For a fixed formula F and assignment A, a clause C is implied if adding it to F does not change the models, and redundant if it does not change satisfiability:

Recall that DRAT proofs work by deleting clauses, adding redundant clauses, and applying unit propagations, until the formula becomes trivially unsatisfiable (cf. Sect. 2). A clause is accepted as redundant if it has the RAT property. Abstractly, the RAT property is justified by the following lemma:

To test whether a clause is implied, we use the RUP property:

where the assignment
 will be computed by unit propagation.
will be computed by unit propagation.
5.3 Abstract Checker Algorithm
Having formalized the basic theory of CNF formulas, unit propagation, and RAT, we can specify an abstract version of the certificate checker algorithm. Our specifications live in an exception monad stacked onto the nondeterminism monad of the Isabelle Refinement Framework. Exceptions are used to indicate failure of the checker, and are never caught. We only prove soundness of our checker, i. e. that it does not accept satisfiable formulas. Our checker actually accepted all certificates in our benchmark set (cf. Sect. 7), yielding an empirical argument that it is sufficiently complete.
At the abstract level, we model the proof as a stream of integers. On this, we define functions
 and
and
 that fetch an element from the stream, try to interpret it as an ID or literal, and fail if this is not possible. The state of the checker is a tuple
that fetch an element from the stream, try to interpret it as an ID or literal, and fail if this is not possible. The state of the checker is a tuple
 . The clause map
. The clause map contains the current formula as a mapping from IDs to clauses, and also maintains the RAT candidate database. The assignment
contains the current formula as a mapping from IDs to clauses, and also maintains the RAT candidate database. The assignment is the current partial assignment.
is the current partial assignment.
As first example, we present the abstract algorithm that is invoked after reading the item-type of a
 item (cf. Sect. 3), i. e. we expect a sequence of the form
item (cf. Sect. 3), i. e. we expect a sequence of the form
 (lemma, unit-clauses, conflict-clause).
(lemma, unit-clauses, conflict-clause).

We use do-notation to conveniently express monadic programs. First, the ID for the new lemma is pulled from the proof stream (line 2) and checked to be available (3). The
 function throws an exception unless the first argument evaluates to true. Next,
function throws an exception unless the first argument evaluates to true. Next,
 (4) parses the next lemma from the lemma file, checks that it is not blocked, and assigns its literals to false. Then, the function
(4) parses the next lemma from the lemma file, checks that it is not blocked, and assigns its literals to false. Then, the function
 (5) pulls the unit clause IDs from the proof stream, checks that they are actually unit, and assigns the unit literals to true. Finally, we pull the ID of the conflict clause (6), obtain the corresponding clause from the clause map (7), check that it is actually conflict (8), and add the lemma to the clause map (9). We return (10) the new clause map and the old assignment, as the changes to the assignment are local and must be backtracked before checking the next clause. Additionally, we return the new position in the lemma file (
(5) pulls the unit clause IDs from the proof stream, checks that they are actually unit, and assigns the unit literals to true. Finally, we pull the ID of the conflict clause (6), obtain the corresponding clause from the clause map (7), check that it is actually conflict (8), and add the lemma to the clause map (9). We return (10) the new clause map and the old assignment, as the changes to the assignment are local and must be backtracked before checking the next clause. Additionally, we return the new position in the lemma file (
 ) and the new proof stream (
) and the new proof stream (
 ). Note that this abstract specification contains non-algorithmic parts: For example, in line 8, we check for the semantics of the conflict clause to be
). Note that this abstract specification contains non-algorithmic parts: For example, in line 8, we check for the semantics of the conflict clause to be
 , without specifying how to implement this check. We prove the following lemma for
, without specifying how to implement this check. We prove the following lemma for
 :
:

Here,
 describes the postcondition
describes the postcondition
 in case of an exception, and the postcondition
in case of an exception, and the postcondition
 for a normal result. As we only prove soundness of the checker, we use
for a normal result. As we only prove soundness of the checker, we use
 as postcondition for exceptions. For normal results, we show that an invariant on the state is preserved,Footnote 4 and that the resulting formula and partial assignment is satisfiable if the original formula and partial assignment was.
as postcondition for exceptions. For normal results, we show that an invariant on the state is preserved,Footnote 4 and that the resulting formula and partial assignment is satisfiable if the original formula and partial assignment was.
Finally, we present the definition of the checker’s main function:

The parameters
 and
and
 indicate the range that holds the representation of the formula,
indicate the range that holds the representation of the formula,
 points to the first lemma, and
points to the first lemma, and
 is the proof stream. First, the RAT literal counts are read (2) and the formula is parsed into the clause map (3). Then, the assignment is initialized to everything undecided (4). The function then iterates over the proof stream and checks each item (5–9), until the formula has been certified (or an exception terminates the program). Here, the checker’s state is wrapped into an option type, where
is the proof stream. First, the RAT literal counts are read (2) and the formula is parsed into the clause map (3). Then, the assignment is initialized to everything undecided (4). The function then iterates over the proof stream and checks each item (5–9), until the formula has been certified (or an exception terminates the program). Here, the checker’s state is wrapped into an option type, where
 indicates that the formula has been certified. The function
indicates that the formula has been certified. The function
 extracts the value from an option. Correctness of the abstract checker is expressed by the following lemma:
extracts the value from an option. Correctness of the abstract checker is expressed by the following lemma:

Intuitively, if the range from
 to
to
 is valid and contains the sequence
is valid and contains the sequence
 , and if
, and if
 returns a normal value, then
returns a normal value, then
 represents a valid CNF formula (
represents a valid CNF formula (
 ) that is unsatisfiable (
) that is unsatisfiable (
 ). Note that the correctness statement does not depend on the lemmas (
). Note that the correctness statement does not depend on the lemmas (
 ) or the proof stream (
) or the proof stream (
 ). This will later allow us to use an optimized (unverified) implementation for streaming the proof, without impairing the formal correctness statement.
). This will later allow us to use an optimized (unverified) implementation for streaming the proof, without impairing the formal correctness statement.
5.4 Refinement Towards an Efficient Implementation
The abstract checker algorithm that we described so far contains non-algorithmic parts and uses abstract types like sets. Even if we could extract executable code, its performance would be poor. For example, we model assignments as functions. Translating this directly to a functional language results in assignments to be stored as long chains of function updates with worst-case linear time lookup.
We now refine the abstract checker to an efficient implementation, replacing the specifications by actual algorithms, and the abstract types by efficient data structures. The refinement is done in multiple steps, where each step focuses on different aspects of the implementation. Formally, we use a refinement relation that relates objects of the refined type (e. g. a hash table) to objects of the abstract type (e. g. a set). In our framework, refinement is expressed by propositions of the form
 : if the concrete argument
: if the concrete argument
 is related to the abstract argument
is related to the abstract argument
 by
by
 , then the result of the concrete algorithm
, then the result of the concrete algorithm
 is related to the result of the abstract algorithm
is related to the result of the abstract algorithm
 by
by
 . Moreover, if the concrete algorithm throws an exception, the abstract algorithm must also throw an exception.
. Moreover, if the concrete algorithm throws an exception, the abstract algorithm must also throw an exception.
In the first refinement step, we record the set of variables assigned while checking a lemma, and use this set to reconstruct the original assignment from the current assignment after the check. This saves us from copying the whole original assignment before each check. Formally, we define an \(A_0\)-backtrackable assignment to be an assignment A together with a set of assigned variables T, such that unassigning the variables in T yields \(A_0\). The relation
 relates \(A_0\)-backtrackable assignments to plain assignments:
relates \(A_0\)-backtrackable assignments to plain assignments:

where
 restricts a partial assignment
restricts a partial assignment
 to the variables not in
to the variables not in
 .
.
We define
 , which operates on \(A_0\)-backtrackable assignments. If applied to assignments
, which operates on \(A_0\)-backtrackable assignments. If applied to assignments
 and
and
 related by
related by
 , and to the same proof stream
, and to the same proof stream
 , then the results of
, then the results of
 and
and
 are related by
are related by
 , i. e. the returned assignments are again related by
, i. e. the returned assignments are again related by
 , and the new proof streams are the same (related by
, and the new proof streams are the same (related by
 ):
):

In the next refinement step, we implement clauses by iterators pointing to the start of a null-terminated sequence of integers. Thus, the clause map will only store iterators instead of (replicated) clauses. Now, we can specify algorithms for functions on clauses. For example, we define:

i. e. we iterate over the clause, checking each literal to be false. We show:

where the relation
 relates iterators to clauses.
relates iterators to clauses.
In the next refinement step, we introduce efficient data structures. For example, we implement the iterators by indexes into an array of integers that stores both the formula and the lemmas. For many of the abstract types, we use general purpose data structures from the Isabelle Refinement Framework [26, 27]. For example, we refine assignments to arrays, using the
 data structure, which implements functions of type
data structure, which implements functions of type
 by arrays of type
by arrays of type
 . It is parameterized by a relation
. It is parameterized by a relation
 and a default concrete element
and a default concrete element
 that does not correspond to any abstract element (
that does not correspond to any abstract element (
 ). The implementation uses
). The implementation uses
 to represent the abstract value
to represent the abstract value
 . We define:
. We define:

i. e. we implement
 by 1,
by 1,
 by 2, and
by 2, and
 by 0. Here,
by 0. Here,
 is the relation of the
is the relation of the
 data structure.Footnote 5 The refined programs and refinement theorems in this step are automatically generated by the Sepref tool [26]. For example, the command
data structure.Footnote 5 The refined programs and refinement theorems in this step are automatically generated by the Sepref tool [26]. For example, the command

takes the definition of
 , generates a refined version, and proves the corresponding refinement theorem. The first parameter is refined wrt.
, generates a refined version, and proves the corresponding refinement theorem. The first parameter is refined wrt.
 (refining the set of clauses into an array), the second parameter is refined wrt.
(refining the set of clauses into an array), the second parameter is refined wrt.
 (refining the clause map and the assignment into arrays), the third parameter is refined wrt.
(refining the clause map and the assignment into arrays), the third parameter is refined wrt.
 (refining the iterator into an array index), and the fourth parameter is refined wrt.
(refining the iterator into an array index), and the fourth parameter is refined wrt.
 (refining the stream position). Exception results are refined wrt.
(refining the stream position). Exception results are refined wrt.
 (basically the identity relation), and normal results are refined wrt.
(basically the identity relation), and normal results are refined wrt.
 ,
,
 , and
, and
 . The \(x^d\) and \(x^k\) annotations indicate whether the generated function may overwrite a parameter (d like destroy) or not (k like keep).
. The \(x^d\) and \(x^k\) annotations indicate whether the generated function may overwrite a parameter (d like destroy) or not (k like keep).
By combining all the refinement steps and unfolding some definitions, we prove the following correctness theorem for the implementation of our checker:

This Hoare triple states that if
 points to an array holding the elements
points to an array holding the elements
 , and we run
, and we run
 , the array will be unchanged, and if the return value is no exception, the range
, the array will be unchanged, and if the return value is no exception, the range
 in the arrayFootnote 6 represents a valid unsatisfiable formula in DIMACS format:
in the arrayFootnote 6 represents a valid unsatisfiable formula in DIMACS format:

We also define a checker for satisfiability certificates, which are null-terminated lists of non-contradictory literals starting at index
 , and prove:
, and prove:

Finally, to obtain our verified sat and unsat checker gratchk, Isabelle/HOL’s code generator is used to extract Standard ML code for
 . We add a command line interface and a small (40 LOC) parser to read the formula into an array. Moreover, we implement a buffered reader for the proof file. This, however, does not affect the correctness statement, which is valid for all proof stream implementations. The resulting program is compiled with MLton [35].
. We add a command line interface and a small (40 LOC) parser to read the formula into an array. Moreover, we implement a buffered reader for the proof file. This, however, does not affect the correctness statement, which is valid for all proof stream implementations. The resulting program is compiled with MLton [35].
5.5 Concise Correctness Statement
We have shown that our checker only accepts arrays containing (un)satisfiable formulas in DIMACS format. To describe a satisfiable input (cf. Sect. 5.1), we have first mapped the array to a formula (constants
 ,
,
 ,
,
 ,
,
 ). Then, we defined a semantics to describe satisfiability of a formula (
). Then, we defined a semantics to describe satisfiability of a formula (
 ,
,
 ,
,
 ,
,
 ,
,
 ). In this section, we outline a more direct specification, which only uses elementary list and set operations of Isabelle/HOL, and show that it is equivalent to our original specification. This can be seen as a sanity check for our semantics.
). In this section, we outline a more direct specification, which only uses elementary list and set operations of Isabelle/HOL, and show that it is equivalent to our original specification. This can be seen as a sanity check for our semantics.
We again use tokenization to convert the input into a list of lists. We further justify tokenization by showing that it is the unique inverse of concatenation:

where
 is the definite description operator. Next, we define an assignment from integers to Booleans to be consistent iff a negative value is mapped to the opposite of its absolute value:
is the definite description operator. Next, we define an assignment from integers to Booleans to be consistent iff a negative value is mapped to the opposite of its absolute value:

Finally, we characterize an (un)satisfiable input by the (non)existence of a consistent assignment that assigns at least one literal of each clause to true:

In the case of unsatisfiability, the bounds have been adjusted to exclude the empty formula, which is trivially satisfiable.
6 Multithreaded Generation of Enriched Certificates
In order to generate GRAT certificates, we extend a DRAT checker algorithm to record the unit clauses that lead to a conflict when checking each lemma. As the certificate generator is not part of the trusted code base, we can afford aggressive optimizations. Our generator gratgen started as a reimplementation of the backward mode of drat-trim [9, 45] in C++, to which we added certificate generation. Later, we implemented multithreading and some additional optimizations. The multithreading mode allows us to trade computing resources for faster response time. It makes sense in settings where parallelization on the granularity of whole problems does not exhaust the available computing resources, e. g. when one is interested in a quick answer for a single problem.
The following displays high-level pseudocode of our certificate generator:

The initial forward phase starts with the original formula (line 2), and performs unit propagation (3). If this already yields a conflict, the formula is unsatisfiable. Otherwise, we iterate over the certificate (4). Each item of the certificate either deletes (6) or adds (8) a clause. After adding, we perform unit propagation (9), and if this yields a conflict, we mark all clauses required for the conflict (11), discard the remaining items in the certificate if any (12), and finish the forward phase.
Next, the backward phase iterates over the certificate in reverse order (line 16), undoes the effects of the items (18 and 20), verifies the lemmas, and marks all lemmas required for verification (22). Unmarked lemmas are skipped (21). The enriched certificate is generated during the backwards phase, while undoing unit propagations and verifying lemmas. For better readability, we have omitted certificate generation from the above listing.
The backwards phase is parallelized: Each thread maintains its own copy of the clause database. Before proving a lemma, a thread needs to acquire it (21), thus ensuring that each lemma is only proved by a single thread. The information about marked lemmas is periodically synchronized between the threads (23), such that a thread can generate work for other threads. Interestingly, there is no synchronization apart from lemma acquisition and sharing of marked clauses between the threads. In theory, one thread could prove most of the lemmas, while the other threads quickly run to the beginning of the certificate, seeing only very few marked lemmas. However, we have not observed such behavior in practice, and thus did not implement any further synchronization between the threads.
In the remainder of this section, we describe the most important optimizations that we have implemented in gratgen: RAT-run heuristics and separate watchlists.
6.1 RAT-Run Heuristics
To verify that a lemma has the RAT property (cf. Sect. 5.2), one has to collect all RAT candidate lemmas, i. e. those clauses in the database that contain the negated pivot literal. As it is not known in advance which of the lemmas will actually be marked and require a full RAT proof (most lemmas are proved by a RUP-proof), maintaining a database of candidate lemmas for each literal would be inefficient. Thus, drat-trim iterates over the whole clause database on each RAT proof. Our profiling indicated that a significant amount of the runtime may be spent on searching candidate lemmas. However, we observed that certificates usually contain runs of multiple RAT lemmas with the same pivot. Thus, we store the result of the last search through the database, and reuse it if we should encounter a RAT lemma over the same pivot. Moreover, in multi-threaded mode, we always allocate a run of lemmas with the same pivot to the same thread, as the stored search result is maintained thread-locally. Our benchmarks (Sect. 7) indicate that this optimization is very efficient if actual RAT lemmas are present. If there are no RAT lemmas, the heuristics’ overhead is effectively a single check in the outer loop of the backwards phase, and, as expected, we observed no decrease in performance.
6.2 Separate Watchlists
Another important heuristics, which is already implemented in drat-trim, is core-first unit propagation. On unit propagation, marked lemmas are preferred over unmarked ones. This way, the unit clauses used for a proof are more likely to be already marked, thus reducing the overall number of marked lemmas.
Unit propagation is done by a two-watched-literals data structure [36], where, for each clause, two distinct literals are marked as watched. As long as the clause is not blocked or conflict, the two watched literals must be undecided. When assigning a new variable, this invariant may be broken, and is then restored by the unit propagation algorithm: For each clause watching a literal that has been assigned to false, a new watched literal is searched. If no new watched literal can be found, the clause is unit or conflict, in which case the unit literal is assigned to true or unit propagation stops with a conflict. To efficiently iterate over the clauses watching a literal, they are stored in a watchlist for each literal.
In drat-trim, core first unit propagation is implemented by two iterators over the watchlists of the newly assigned literals. The first iterator ignores unmarked clauses, while the second iterator processes unmarked clauses. The second iterator is only advanced when the first iterator cannot be advanced further. By advancing the second iterator, new literals may be assigned, which makes advancing the first iterator possible again. However, skipping the iterators over irrelevant clauses may yield considerable overhead in the performance sensitive inner loop of unit propagation. Thus, for gratgen, we have implemented two watchlists for each literal, one for the marked and one for the unmarked lemmas. This way, the iterators during unit propagation never have to skip over irrelevant clauses. On the other hand, when marking a clause, we have to spend additional time to move it from the unmarked to the marked watchlists.Footnote 7 In practice, we found this optimization to be effective.
7 Benchmarks
We have benchmarked GRAT with one and eight threads against drat-trim and LRAT [18] on problems taken from the main tracks of the 2016 and 2017 SAT competitions [42, 43]. We consider the problems solved by 2017 gold medalist Maple, and the problems solved by 2016 silver medalist Riss6. We chose the silver medalist for 2016, as the gold medalist is, again, Maple. Moreover, we consider the problems solved by CryptoMiniSat in 2016. Although not among the Top 3 solvers, we included CryptoMiniSat because it seems to be the only prover that produces a significant amount of RAT lemmas. For the 2017 competition, only abcdSAT seems to produce RAT lemmas, and we did not include it in our benchmarks.Footnote 8
All tested tools verified all but four unsatisfiability certificates: On two certificates, drat-trim timed out (using the default timeout of 20.000 s), and it segfaulted on a third one. A fourth certificate led to an out-of-memory error of multithreaded gratgen. Table 1 displays the results for these certificates.
Figure 1 shows the results for the other unsatisfiability certificates. The first three scatter plots compare the wall-clock time of LRAT against GRAT with one and eight threads. Here, already single-threaded GRAT is faster than LRAT on every problem. As expected, the difference is more significant on problems that contain RAT lemmas: for the problems that actually contain RAT lemmas, single-threaded GRAT is about 3 times faster than LRAT, while, for the other problems, it is only 1.7 times faster.
Except for small problems, multithreading yields a significant speedup: Considering only problems where single-threaded gratgen needs longer than 100 s, the average speedup with eight threads is 2.1, the average speedup of the backwards checking phase of gratgen, which is the only parallelized part, is 3.3.
Finally, the last scatter plot in Fig. 1 compares GRAT against drat-trim. Although we compare a verified tool against an unverified one, GRAT wins this comparison: Except for a few certificates, it is faster than drat-trim, and there is only a single outlier where GRAT is significantly slower than drat-trim.
We also compare the memory consumption: In single threaded mode, gratgen needs roughly three times more memory than drat-trim, with eight threads, this figure increases to roughly nine times more memory. Due to the garbage collection in Standard ML, we could not measure meaningful memory consumptions for gratchk. The extra memory in single-threaded mode is mostly due to the proof being stored in memory, the extra memory in multithreaded mode is due to the duplication of data for each thread.
Finally, Table 2 shows the runtimes of the verified second phase only. Here, gratchk is significantly faster than LRAT’s verified phase lrat-check. In particular, due to the RAT-counts field that is available in GRAT, but not in LRAT (cf. Sect. 3), true RAT lemmas are handled more efficiently. This explains the large discrepancy for the CryptoMiniSat prover.
For completeness, we also report on the satisfiable problems in our benchmark set: The 241 sat certificates in our benchmark set have a size of 566MiB and could be checked in roughly 100 s.
8 Discussion and Future Work
Currently, the formal proof of our verified checker goes down to the representation of the formula as integer array, thus requiring a (small) unverified parser. A next step would be to verify the parser, too. Moreover, verification stops at the Isabelle/HOL code generator, whose correctness is only proved on paper [16, 17]. There is work on the mechanical verification of code generators [37], and even the subsequent compilers [22]. This technology became available for Isabelle/HOL only recently [20] but does not yet support the imperative arrays required for our application.
If the memory consumption of gratgen should become a problem, we could easily write out the proof to disk instead of storing it in RAM. We expect that this would yield a memory consumption similar to drat-trim. For multi-threaded mode, we plan to share more (read-only) data between the threads.
An interesting research topic would be to integrate enriched certificate generation directly into SAT solvers. The performance decrease in the solver could be weighed against the cost of generating an enriched certificate. A main challenge would be to manage the size of the enriched certificates, which, without reductions as done by, e. g. backward checking, may become prohibitively large. Moreover, such modifications are probably SAT-solver specific, whereas DRAT certificates are designed to be easily integrated into virtually any CDCL based SAT solver.
An alternative to certification would be to verify the SAT solver itself. While this has been attempted several times (e. g. [33, 39]), including our own work [12], we do not expect that verified SAT solvers will become competitive to unverified solvers in the near future.
Finally, we chose a benchmark set which is realistic but can be run in a few weeks on the available hardware. We plan to run our tools on larger benchmark suites, once we have access to sufficient (supercomputing) hardware.
9 Conclusions
We have presented a formally verified SAT solver certification tool. Already in single threaded mode, it is significantly faster than the unverified standard tool drat-trim, on a benchmark suite taken from the 2017 and 2016 SAT competitions. Additionally, we implemented a multi-threaded mode, which allows us to trade computing resources for significantly smaller response times. The formal proof covers the actual implementation of the checker and the semantics of the formula down to the sequence of integers by which it is represented.
Our approach involves two phases: The first phase generates an enriched certificate, which is then checked against the original formula by the second phase. While the main computational work is done by the first phase, soundness of the approach only depends on the second phase, which is also algorithmically less complex, making it more amenable to formal verification. Using stepwise refinement techniques, we were able to formally verify a rather efficient implementation of the second phase. Together with novel optimizations in the first phase, this makes our tool faster than the unverified drat-trim. Although most computational work is done in the first phase, optimizing the second phase is important: While gratchk was quite efficient from the beginning, the LRAT checker has seen several improvements over time [18]. The initial version was purely functional, and often dominated the runtime of the whole certification process [6].
We conclude with some statistics: The formalization of the certificate checker is roughly 5k lines of code. In order to realize this formalization, several general purpose libraries (e. g. the exception monad and some imperative data structures) had to be developed. These sum up to additional 3.5k lines. The time spent on the formalization was roughly three man-months. The multi-threaded certificate generator has roughly 3k lines of code, and took two man-months to develop.
Notes
This is well-defined as unit-propagation is strongly normalizing up to conflicts.
Our profiling data indicates that, depending on the problem, up to 93% of the time is spent for unit propagation.
Blocked lemmas are useless for unsat proofs, such that there is no point to include them in the certificate.
The invariant states that there are no syntactic tautologies, i. e. clauses that contain both a positive and negative literal over the same variable, and that the RAT candidate database, which is used to quickly identify RAT candidates (cf. Sect. 3), is accurate.
The name suffix
 instead of
instead of
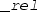 indicates that the data structure may be stored on the heap.
indicates that the data structure may be stored on the heap.Element 0 is used as a guard in our implementation.
We have also experimented with lazily moving marked clauses if they are encountered in the unmarked list during unit propagation but this turned out to be less efficient.
Due to constraints on available computation time. Note that this shifts the benchmark results in favor of drat-trim, as our tool has optimizations specifically tailored to handle RAT lemmas.
References
Back, R.-J.: On the correctness of refinement steps in program development. Ph.D. thesis, Department of Computer Science, University of Helsinki (1978)
Back, R.-J., von Wright, J.: Refinement Calculus—A Systematic Introduction. Springer, Berlin (1998)
Bertot, Y., Castran, P.: Interactive Theorem Proving and Program Development: Coq’Art: The Calculus of Inductive Constructions, 1st edn. Springer, Berlin (2010)
Brunner, J., Lammich, P.: Formal verification of an executable LTL model checker with partial order reduction. In: Proceedings of NFM, pp. 307–321. Springer (2016)
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: TPHOL, volume 5170 of LNCS, pp. 134–149. Springer (2008)
Cruz-Filipe, L., Heule, M., Hunt, W., Kaufmann, M., Schneider-Kamp, P.: Efficient certified RAT verification. In: Proceedings of CADE. Springer (2017)
Cruz-Filipe, L., Marques-Silva, J., Schneider-Kamp, P.: Efficient certified resolution proof checking. In: Proceedings of TACAS, pp. 118–135. Springer (2017)
Darbari, A., Fischer, B., Marques-Silva, J.: Industrial-strength certified SAT solving through verified SAT proof checking. In: Proceedings of ICTAC, pp. 260–274. Springer (2010)
DRAT-trim homepage. https://www.cs.utexas.edu/~marijn/drat-trim/
DRAT-trim issue tracker. https://github.com/marijnheule/drat-trim/issues
Esparza, J., Lammich, P., Neumann, R., Nipkow, T., Schimpf, A., Smaus, J.-G.: A fully verified executable LTL model checker. In: CAV, volume 8044 of LNCS, pp. 463–478. Springer (2013)
Fleury, M., Blanchette, J. C., Lammich, P.: A verified SAT solver with watched literals using imperative HOL. In: Proceedings of CPP, pp. 158–171 (2018)
Goldberg, E., Novikov, Y.: Verification of proofs of unsatisfiability for CNF formulas. In: Proceedings of DATE, IEEE (2003)
Gordon, M.: From LCF to HOL: a short history. In: Plotkin, G., Stirling, C.P., Tofte, M. (eds.) Proof, Language, and Interaction, pp. 169–185. MIT Press, Cambridge (2000)
Haftmann, F.: Code generation from specifications in higher order logic. Ph.D. Thesis, Technische Universität München (2009)
Haftmann, F., Krauss, A., Kunčar, O., Nipkow, T.: Data refinement in Isabelle/HOL. In: Proceedings of ITP, pp. 100–115. Springer (2013)
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: FLOPS 2010, LNCS. Springer (2010)
Heule, M., Hunt, W., Kaufmann, M., Wetzler, N.: Efficient, verified checking of propositional proofs. In: Proceedings of ITP. Springer (2017)
Heule, M., Hunt, W., Wetzler, N.: Trimming while checking clausal proofs. In: 2013 Formal Methods in Computer-Aided Design, FMCAD 2013, pp. 181–188. IEEE (2013)
Hupel L., Nipkow T.: A verified compiler from Isabelle/HOL to CakeML. In: Ahmed, A. (ed.) Programming Languages and Systems. ESOP 2018. volume 10801 of LNCS, pp. 999–1026. Springer, Cham (2018)
Kirchmeier, M.: Functional implementation of an optimized UNSAT proof-checker. Bachelor’s Thesis, Technische Universität München (2017)
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: a verified implementation of ML. In: Proceedings of POPL, pp. 179–192. ACM (2014)
Lammich, P.: Grat tool chain homepage. http://www21.in.tum.de/~lammich/grat/
Lammich, P.: Automatic data refinement. In: ITP, volume 7998 of LNCS, pp. 84–99. Springer (2013)
Lammich, P.: Verified efficient implementation of Gabow’s strongly connected component algorithm. In: ITP, volume 8558 of LNCS, pp. 325–340. Springer (2014)
Lammich, P.: Refinement to imperative/HOL. In: ITP, volume 9236 of LNCS, pp. 253–269. Springer (2015)
Lammich, P.: Refinement based verification of imperative data structures. In: CPP, pp. 27–36. ACM (2016)
Lammich, P.: Efficient verified (UN)SAT certificate checking. In: Proceedings of CADE. Springer (2017)
Lammich, P.: The GRAT tool chain—efficient (UN)SAT certificate checking with formal correctness guarantees. In: SAT, pp. 457–463 (2017)
Lammich, P., Lochbihler, A.: The Isabelle collections framework. In: Proceedings of ITP, volume 6172 of LNCS, pp. 339–354. Springer (2010)
Lammich, P., Sefidgar, S.R.: Formalizing the Edmonds–Karp algorithm. In: Proceedings of ITP, pp. 219–234 (2016)
Lammich, P., Tuerk, T.: Applying data refinement for monadic programs to Hopcroft’s algorithm. In: Proceedings of ITP, volume 7406 of LNCS, pp. 166–182. Springer (2012)
Marić, F.: Formal verification of a modern SAT solver by shallow embedding into Isabelle/HOL. Theor. Comput. Sci. 411(50), 4333–4356 (2010)
Milner, R., Harper, R., MacQueen, D., Tofte, M.: The Definition of Standard ML. The MIT Press, Cambridge (1997)
MLton Standard ML compiler. http://mlton.org/
Moskewicz, M. W., Madigan, C. F., Zhao, Y., Zhang, L., Malik, S.: Chaff: Engineering an efficient SAT solver. In: Proceedings of DAC, pp. 530–535. ACM (2001)
Myreen, M.O., Owens, S.: Proof-producing translation of higher-order logic into pure and stateful ML. J. Funct. Program. 24(2–3), 284–315 (2014)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL—A Proof Assistant for Higher-Order Logic, volume 2283 of LNCS. Springer, Berlin (2002)
Oe, D., Stump, A., Oliver, C., Clancy, K.: versat: a verified modern SAT solver. In: VMCAI, volume 7148 of LNCS, pp. 363–378. Springer (2012)
SAT competition, 2013. http://satcompetition.org/2013/
SAT competition, 2014. http://satcompetition.org/2014/
SAT competition, 2016. http://baldur.iti.kit.edu/sat-competition-2016/
SAT competition, 2017. https://baldur.iti.kit.edu/sat-competition-2017/
Sinz, C., Biere, A.: Extended resolution proofs for conjoining BDDs. In Proceedings of CSR, pp. 600–611. Springer (2006)
Wetzler, N., Heule, M. J. H., Hunt, W. A.: Mechanical verification of SAT refutations with extended resolution. In: Proceedings of ITP, pp. 229–244. Springer (2013)
Wetzler, N., Heule, M. J. H., Hunt, W. A.: Drat-trim: efficient checking and trimming using expressive clausal proofs. In: Proceedings of SAT 2014, pp. 422–429. Springer (2014)
Wimmer, S., Lammich, P.: Verified model checking of timed automata. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. volume 10805 of LNCS, pp. 61–78. Springer, Cham (2018)
Wirth, N.: Program development by stepwise refinement. Commun. ACM 14(4), 221–227 (1971)
Acknowledgements
We thank Maximilian Kirchmeier for proposing and evaluating optimizations for gratgen [21]. Moreover, we thank Mathias Fleury and Simon Wimmer for very useful comments on the draft version of this paper, and Lars Hupel for instant help on any problems related to the benchmark server. Finally, we thank the anonymous reviewers for their useful comments. This work has been supported by the DFG Grant LA 3292/1 “Verifizierte Model Checker” and the VeTSS Grant “Formal Verification of Information Flow Security for Relational Databases”.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lammich, P. Efficient Verified (UN)SAT Certificate Checking. J Autom Reasoning 64, 513–532 (2020). https://doi.org/10.1007/s10817-019-09525-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-019-09525-z





 , the literals of the lemma are assigned to false and the initial unit propagations are performed. Second, it is checked that the provided RAT candidates are exhaustive, and then the corresponding
, the literals of the lemma are assigned to false and the initial unit propagations are performed. Second, it is checked that the provided RAT candidates are exhaustive, and then the corresponding
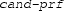 items are processed: A
items are processed: A
 item consists of the ID of the candidate clause D, a list of unit clause IDs, and a conflict clause ID. To check a candidate proof, the literals of
item consists of the ID of the candidate clause D, a list of unit clause IDs, and a conflict clause ID. To check a candidate proof, the literals of 
 instead of
instead of
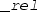 indicates that the data structure may be stored on the heap.
indicates that the data structure may be stored on the heap.