Effect of compressibility factor on the hydrodynamics of naphtha catalytic-reforming reactors

Abstract

A detailed steady-state catalytic-reforming unit (CRU) reactor process model is simulated in this work, and for the first time, different compressibility Z factor correlations have been applied using gPROMS software. The CRU has been modeled and simulated with the assumption that the gas phase behaves like an ideal gas. This is assumed for the four reactors in series and for different conditions of hydrogen–hydrocarbon ratio (HHR), operating temperature, and pressure. The results show that the Z factor varies at every point along the height of the reactors depending on reaction operating pressure, temperature, and HHR ratio. It also shows that the magnitude of deviation from ideal gas behaviour can be measured over the reactor height. The Z factor correlation of Mahmoud (J Energy Resour Technol Trans ASME 136:012903, 2014) is found to be suitable for predicting the Z factor distribution in the reactors.

Introduction

The catalytic-reforming unit is an important integral part of the refinery operations. It is used to improve the quality of low-to-high-octane naphtha in a series of reactors (three or four, depending on the design of the refinery). The system can either be a semi regenerative (fixed bed) where the reaction proceeds for a particular period and the catalyst is regenerated, or a continuous one where the catalyst is continuously regenerated in a regenerator. The continuous process has the advantage of using a lower pressure and lower hydrogen usage. However, there is the need for more technical monitoring for the mechanisms of engagement and disengagement of the catalyst from the last reactor through the regenerator and back to the first reactor in continuous flow. To improve the quality and the yield of the reformate, one important aspect is the hydrodynamics study of the reaction which helps to improve the efficiency of the system by maintaining an effective pressure gradient across the reactors. The low octane naphtha meets recycled hydrogen from the recycle gas compressor and enters the first heater that precedes the reactor, a process that continues for the other four reactors and heaters in series. The hydrodynamics is important, since the variations of temperature and pressure of the reaction affect the rate of reactions, which in turn affect the entire system responses. Increase in reaction pressure decreases the reformate yield, the hydrogen yield, and the research octane number, RON [10]. The Ergun equation, as a function of density, viscosity, bed void, particle diameter, and mass flux, is used to model the behaviour of pressure in these reactors. Since these reactions’ parameters such as enthalpy, density, viscosity, and pressure change with reactor height, there is need to study the effect of the compressibility factor which affects these parameters [13]. In the past, all the CRU was modeled with compressibility factor Z as unity, implying an ideal gas system, which may not always be the case. Real systems tend to vary from ideal system. The Z factor of a fluid catalytic cracking (FCC) riser has been modeled as unity until John et al. [13] simulated the riser with different Z factor correlations and found that the riser can be modeled with Heidaryan et al. [11] correlation. Hence, the need to find the actual Z factor for the CRU and consequently investigate the response of the CRU under real system conditions.

In characterizing fluid flow behaviour in the oil and gas, it is very important to study the effect of Z factor, both upstream and downstream [12]. The fluid can be said to be compressible or incompressible depending on the type of process which it undergoes [11]. Variation in density of the gas during reaction, as in the case with catalytic-reforming, may bring about change in compressibility factor. Therefore, assuming a changing gas density system as ideal may not be always true especially when there is velocity variation as the gas density varies and the fluid could be compressible [5]. Transport and physical properties like density, viscosity, and fraction of void of the treated naphtha during reaction could change when reaction conditions [temperature, pressure, feed rate, and hydrogen–hydrocarbon ratio (HHR)] are altered. Since there is significant variation of these properties with operating conditions, there is a need to study the compressibility factor effect. An important variable in the process conditions is the HHR which preserves the catalyst activity by sweeping off amorphous carbon deposit on the catalyst, but has little effect on the aromatics and reformate yield. This variable has an effect on the reactor pressure, since it increases the partial pressure of the vapor by increasing the number of moles of hydrogen; hence, it will have effect on the reaction hydrodynamics. To have optimum and precise condition of the catalyst, the reactor bed and other equipment should adhere to professional design of the catalytic-reforming plant. In this paper, the effect of compressibility factor on reaction pressure, which is a major hydrodynamic parameter, is studied. This will help in determining an appropriate gas compressibility factor to be applied in plant design and when any modifications of the design are required such as scale up or scale down, the assumption of ideal case may not always hold. The precise compressibility factor can assist to predict accurately the hydrodynamic behaviour of operational variables like pressure drop across the reactors to ensure effective process plant design.

In this work, the effect of compressibility factor on four commercial catalytic naphtha reactors in series is investigated for the first time, by applying various correlations to model the behaviour of the reaction using gPROMS software. Hence, the Z factor variation across the reactors heights will be determined for different Z factors and a suitable correlation model for the CRU will be determined.

Compressibility factor Z

The compressibility factor of gases (Z factor) from principle of corresponding of state is defined based on the pseudo-reduced temperature (T_pr) and pseudo-reduced pressure (P_pr), which are important thermodynamic variables when determining the behaviour of gases and liquids both in upstream and downstream computations [11]. These are described in Eqs. (2) and (3):

$${\text{PV}} = ZnRT,$$

(1)

$$T_{\text{pr}} = \frac{T}{{T_{\text{c}} }},$$

(2)

$$P_{\text{pr}} = \frac{P}{{P_{\text{c}} }}.$$

(3)

The three equations are applied to both real and ideal gases where the Z factor is unity for ideal cases which in reality is non-existent. It is thus of paramount importance to predict the compressibility effect in gaseous phase reactions when dealing with changes of physical and transport properties. The simple definition is the ratio of actual gas volume to the gas volume of ideal gas implying a measure and extent of deviation from ideal behaviour [12].

According to Fayazi et al. [9], this parameter can be determined experimentally or from equations of state or using semi-empirical correlations. The use of experimental data seems more expensive and takes a lot of time and energy and that could be so tedious considering the number of gases in petroleum to account for Ahmed [1], whilst the use of semi-empirical correlations has proved accurate and simpler than even the use of equations of state EoS [8]. Whenever the pseudo-reduced pressure and pseudo-reduced temperature of the gas is known, the Z factor of the vapor of the hydrocarbon could be predicted and estimated [9].

In this work, T_pr and P_pr are computed using Eqs. (2) and (3). The T_pr and P_pr are shown in Fig. 1 with variation along the reactor heights. The P_pr obtained is in the range $1.218066 \le P_{\text{pr}} \le 1.023427$ and its T_pr is within the range $0.528144 \le T_{\text{pr}} \le 0.348992$. The values of the T_pr and P_pr may change based on the conditions of operations of the reaction. This implies that, as the variables of the process which affect the temperature and pressure of the CRU vary during plant run, the T_pr and P_pr will also vary. Conversely, the compressibility, a function of T_pr and P_pr will as well not remain constant but change.

Fig. 1

Variation of P_pr and T_pr along reactor heights

There are some common empirical correlations [6, 14] that are not suitable when T_pr ≤ 0.92. Some of the correlations applied in this research accept T_pr above 0.92 [11, 17]. In the quest to determine the most accurate and precise Z factor for the vapor state of the reactions, a number of different empirical correlations are used. Each of the Z factors determined is compared with both the plant data and that of the literature and ascertain which of the compressibility factors predicts closely. The computed pseudo-reduced temperature here is outside the boundary of some of the empirical correlations used, but the P_pr is within the range $0.364 \le P_{\text{pr}} \le 0.375$ which lies within the boundaries of the P_pr in the used empirical correlations in this work which are given below.

• 1. Azizi et al. [3] Z factor:

Azizi et al. [3] established their Z factor empirical correlation by applying standing Katz chart with about 3038 points with a range of P_pr of $0.2 \le P_{\text{pr}} \le 11$ and T_pr range of $1.1 \le T_{\text{pr}} \le 2$. This is presented in Eq. (4):

$$Z = A + \frac{B + C}{D + E}.$$

(4)

The variables in Eq. (4) are presented in Eqs. (5–9):

$$A = aT_{\text{pr}}^{2.16} + bP_{\text{pr}}^{1.028} + cP_{\text{pr}}^{1.58} T_{\text{pr}}^{ - 2.1} + d\ln T_{\text{pr}}^{ - 0.5} ,$$

(5)

$$B = e + fT_{\text{pr}}^{2.4} + gP_{\text{pr}}^{1.56} + hP_{\text{pr}}^{0.124} T_{\text{pr}}^{3.033} ,$$

(6)

$$C = i\ln T_{\text{pr}}^{ - 1.28} + j\ln T_{\text{pr}}^{1.37} + k\ln (P_{\text{pr}} ) + l\ln (P_{\text{pr}} )^{2} + m\ln (P_{\text{pr}} )\ln (T_{\text{pr}} ),$$

(7)

$$D = 1 + nT_{\text{pr}}^{5.55} + oP_{\text{pr}}^{0.68} T_{\text{pr}}^{0.33} ,$$

(8)

$$E = p\ln T_{\text{pr}}^{1.18} + q\ln T_{\text{pr}}^{2.1} + r\ln (P_{\text{pr}} ) + s\ln (P_{\text{pr}} )^{2} + t\ln (P_{\text{pr}} )\ln (T_{\text{pr}} ).$$

(9)

The tuned coefficients for Eqs. (5–9) are presented in Appendix Table 14.

• 2. Bahadori et al. [4] compressibility factor:

Compressibility factor of Bahadori et al. [4] is given in Eq. (10) and its coefficients are presented in Eqs. (10–14) [4]. The range is $0.2 \le P_{\text{pr}} \le 16$ and $1.05 \le T_{\text{pr}} \le 2.4$:

$$Z = a - bP_{\text{pr}} + cP_{\text{pr}}^{2} + dP_{\text{pr}}^{3} ,$$

(10)

$$a = Aa + BaT_{\text{pr}} + CaT_{\text{pr}}^{2} + DaT_{\text{pr}}^{3} ,$$

(11)

$$b = Ab + BbT_{\text{pr}} + CbT_{\text{pr}}^{2} + DbT_{\text{pr}}^{3} ,$$

(12)

$$c = Ac + BcT_{\text{pr}} + CcT_{\text{pr}}^{2} + DcT_{\text{pr}}^{3} ,$$

(13)

$$d = Ad + BdT_{\text{pr}} + CdT_{\text{pr}}^{2} + DdT_{\text{pr}}^{3} .$$

(14)

The tuned coefficients for Eqs. (10–14) are presented in Appendix Table 15.

• 3. Compressibilty factor Heidaryan et al. [11]:

The compressibility factor for Heidaryan et al. [11] is defined as in Eq. (15) and the fine-tuned coefficients are given in Appendix Table 16. The P_pr is within $0.2 \le P_{\text{pr}} \le 3$ and this is within the range of that of Heidaryan et al. [12]:

$$Z = \ln \left[ {\frac{{A_{1} + A_{3} \ln (P_{\text{pr}} ) + \frac{{A_{5} }}{{T_{\text{pr}} }} + A_{7} (\ln P_{\text{pr}} )^{2} + \frac{{A_{9} }}{{T_{\text{pr}}^{2} }} + \frac{{A_{11} }}{{T_{\text{pr}} }}\ln (P_{\text{pr}} )}}{{1 + A_{2} \ln (P_{\text{pr}} ) + \frac{{A_{4} }}{{T_{\text{pr}} }} + A_{6} (\ln P_{\text{pr}} )^{2} + \frac{{A_{8} }}{{T_{\text{pr}}^{2} }} + \frac{{A_{10} }}{{T_{\text{pr}} }}\ln (P_{\text{pr}} )}}} \right] .$$

(15)

• 4. Heidaryan et al. [12] compressibility factor:

The compressibility factor of Heidaryan et al. [11, 12] is defined in Eq. (16) with the tuned coefficients reported in Appendix Table 17. The boundaries of the P_pr and T_pr are $0.20 \le P_{\text{pr}} \le 15.0$ and $1.20 \le T_{\text{pr}} \le 3.0$ (Heidaryan et al. 2010c). The boundary of the P_pr here in this research is concurrent as that of Heidaryan et al. [11]:

$$Z = \frac{{A_{1} + A_{2} \ln (P_{\text{pr}} ) + A_{3} (\ln P_{\text{pr}} )^{2} + A_{4} (\ln P_{\text{pr}} )^{3} + \frac{{A_{5} }}{{T_{\text{pr}} }} + \frac{{A_{6} }}{{T_{\text{pr}}^{2} }}}}{{1 + A_{7} \ln (P_{\text{pr}} ) + A_{8} (\ln P_{\text{pr}} )^{2} + \frac{{A_{9} }}{{T_{\text{pr}} }} + \frac{{A_{10} }}{{T_{\text{pr}}^{2} }}}}.$$

(16)

• 5. Mahmoud [16] compressibility Z factor:

The compressibility Z factor for Mahmoud [16] is defined by Eq. (17). The correlation was derived from measurements taken of 300 Z factors [16]:

$$Z = (0.702{\text{e}}^{{( - 2.5T_{\text{pr}} )}} )P_{\text{pr}}^{2} - (5.524{\text{e}}^{{( - 2.5T_{\text{pr}} )}} )P_{\text{pr}} + (0.044T_{\text{pr}}^{2} + 1.15).$$

(17)

• 6. Papay [17] compressibility factor:

The compressibility factor Z of Papay [17] is defined by Eq. (18) [15]:

$$Z = 1 - \frac{{P_{\text{pr}} }}{{T_{\text{pr}} }} \left[ {0.3648758 - 0.04188423 \left( {\frac{{P_{\text{pr}} }}{{T_{\text{pr}} }}} \right)} \right].$$

(18)

• 7. Z factor correlation of Sanjari and Lay [20]:

Sanjari and Lay [17] got their compressibility factor correlation from 5844 experimental data points of different compressibility factors within the boundary of 0.010 ≤ P_pr ≤ 15.0 and 1.0 ≤ T_pr ≤ 3.0. It is reported in Eq. (19) with the fine-tuned coefficients given from Appendix Table 18:

$$Z = 1.0 + A_{1} P_{\text{pr}} + A_{2} (P_{\text{pr}} )^{2} + \frac{{A_{3} P_{\text{pr}}^{{A_{4} }} }}{{T_{\text{pr}}^{{A_{5} }} }} + \frac{{A_{6} P_{\text{pr}}^{{(A_{4} + 1)}} }}{{T_{\text{pr}}^{{A_{7} }} }} + \frac{{A_{8} P_{\text{pr}}^{{(A_{4} + 2)}} }}{{T_{\text{pr}}^{{(A_{7} + 1)}} }}.$$

(19)

• 8. Shokir et al. [21] Z factor:

The Shokir et al. [21] compressibility factor is defined by Eq. (20), with its parameters given in Eqs. (21–25) [21]:

$$Z = A + B + C + D + E,$$

(20)

$$A = 2.679562 \frac{{(2T_{\text{pr}} - P_{\text{pr}} - 1)}}{{[(P_{\text{pr}}^{2} + T_{\text{pr}}^{3} )/P_{\text{pr}} ]}},$$

(21)

$$B = - 7.686825 \left[ {\frac{{(P_{\text{pr}} T_{\text{pr}} + P_{\text{pr}}^{2} )}}{{[(P_{\text{pr}} T_{\text{pr}} + 2T_{\text{pr}}^{2} + T_{\text{pr}}^{3} )]}}} \right],$$

(22)

$$C = - 0.000624 (P_{\text{pr}} T_{\text{pr}}^{2} - T_{\text{pr}} P_{\text{pr}}^{2} + T_{\text{pr}} P_{\text{pr}}^{3} + 2P_{\text{pr}} T_{\text{pr}} - 2P_{\text{pr}}^{2} + 2P_{\text{pr}}^{3} ),$$

(23)

$$D = 3.067747 \frac{{(T_{\text{pr}} - P_{\text{pr}} )}}{{[(P_{\text{pr}}^{2} + T_{\text{pr}} + P_{\text{pr}} )]}},$$

(24)

$$\begin{aligned} E &= \frac{0.068059}{{P_{\text{pr}} T_{\text{pr}} }} + 0.139489T_{\text{pr}}^{2} - 0.081873P_{\text{pr}}^{2} - \left[ {\frac{{0.041098T_{\text{pr}} }}{{P_{\text{pr}} }}} \right] \\ & \quad+\, \left[ {\frac{{8.152325P_{\text{pr}} }}{{T_{\text{pr}} }}} \right] - 1.63028P_{\text{pr}} + 0.24287T_{\text{pr}} - 2.64988. \end{aligned}$$

(25)

Kinetic models

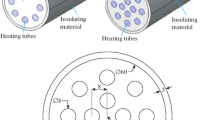
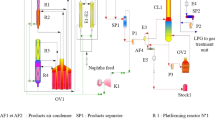
The assumptions made, model equations used, and the method and procedures are presented in this section. The reactors are in series, as shown in Fig. 2. The first reactor is 5.632 m in height, 5.83 m for the second, 6.51 m for the third, and 7.26 m for the fourth reactors. The total height of the reactors in series is 25.232 m.

Fig. 2

Catalytic-reforming process with four reactors in series

Some of the assumptions made are as follows:

• The reactors are modeled as adiabatic processes, i.e., no heat escapes or enters the reactors due to sufficient lagging.

• The reactors are modeled as plug flow, because naphtha flows as gas through the reactor at the pressure and temperature of reaction. Due to the reactor length, dispersion of matter is negligible as supported by a criterion reported elsewhere [10].

• The reaction is considered as first order, because the reforming reaction uses HHR higher than the hydrocarbon concentration. Hence, its concentration is grouped with reaction coefficient.

• Pseudo-homogeneous reactor model is assumed, since the vapor phase reaction is too complex to solve heterogeneously and the diffusion along the radius is negligible with the height of the reactor much greater than the radius.

Various models have been developed for both steady-state and dynamic processes of the catalytic-reforming reaction with different lumps to investigate the behaviour of the reaction and product distribution. The reaction steps and equations of the model are shown in Table 1 (a zero value is registered when the data are not available).

Table 1 Table of reaction steps and rate constants of the model

The kinetic rate equations for the components are given in Eqs. (26–50) where SV is space velocity and $\frac{1}{\text{SV}}$ is residence time:

$$\begin{aligned} \frac{{{\text{d}}P_{1} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = & \,K_{2} P_{11 } + K_{8} P_{10} + K_{14} P_{9} + K_{19} P_{8} + K_{24} P_{7} \\ & +\, K_{29} P_{6} + K_{32} P_{5} + K_{36} N_{11} \\ & + \,K_{41} N_{10} + K_{45} N_{9} + K_{50} N_{8} + K_{50} A_{11} + K_{62} A_{10} \\ &+\, K_{66} A_{9} + K_{99} A_{8} , \\ \end{aligned}$$

(26)

$$\begin{aligned} \frac{{{\text{d}}P_{2} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = & \,K_{3} P_{11 } + K_{9} P_{10} + K_{15} P_{9} + K_{20} P_{8} + K_{25} P_{7} + K_{30} P_{6} \\ & + \,K_{33} P_{5} + K_{37} N_{11} + K_{42} N_{30} + K_{47} N_{9} \\& +\, K_{60} A_{11} + K_{62} A_{10} + K_{67} A_{9} , \\ \end{aligned}$$

(27)

$$\begin{aligned} \frac{{{\text{d}}P_{3} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} &= K_{4} P_{11 } + K_{10} P_{10} + K_{16} P_{9} + K_{21} P_{8} + K_{26} P_{7} + 2K_{31} P_{6}\\& +\, K_{33} P_{5} + K_{38} N_{11} + K_{43} N_{10} + K_{64} A_{10} , \end{aligned}$$

(28)

$$\begin{aligned}\frac{{{\text{d}}P_{4} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}}& = K_{5} P_{11 } + K_{11} P_{10} + K_{17} P_{9} + 2K_{22} P_{8} + K_{25} P_{7} \\&+\, K_{10} P_{6} + K_{32} P_{5} , \end{aligned}$$

(29)

$$\begin{aligned} \frac{{{\text{d}}P_{5} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}}& = K_{6} P_{11 } + 2K_{12} P_{10} + K_{17} P_{19} + K_{21} P_{8} + K_{24} P_{7} + K_{29} P_{6} \\&+ \,(K_{32} + K_{33} )P_{5} , \end{aligned}$$

(30)

$$\begin{aligned} \frac{{{\text{d}}P_{6} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}}& = K_{6} P_{11 } + K_{11} P_{10} + K_{16} P_{9} + K_{20} P_{8} + K_{25} P_{7} + K_{53} N_{6} + K_{96} {\text{MPC}} \\& -\, (K_{27} + K_{28} + K_{29} + K_{30} + K_{31} )P_{6} ,\end{aligned}$$

(31)

$$\begin{aligned} \frac{{{\text{d}}P_{7} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} &= K_{5} P_{11 } + K_{10} P_{10} + K_{15} P_{9} + K_{19} P_{8} + K_{51} N_{7} + K_{70} A_{7} \\&-\, (K_{23} + K_{24} + K_{25} + K_{26} + K_{27} )P_{7} ,\end{aligned}$$

(32)

$$\begin{aligned} \frac{{{\text{d}}P_{8} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}}& = K_{4} P_{11 } + K_{9} P_{10} + K_{14} P_{9} + K_{48} N_{8} + K_{68} A_{8}\\& - \,(K_{18} + K_{19} + K_{20} + K_{21} + K_{22} )P_{8} , \end{aligned}$$

(33)

$$\begin{aligned} \frac{{{\text{d}}P_{9} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} &= K_{3} P_{11 } + K_{8} P_{10} + K_{44} N_{9} + K_{66} A_{9} \\&-\, (K_{13} + K_{14} + K_{15} + K_{16} + K_{17} )P_{9} ,\end{aligned}$$

(34)

$$\begin{aligned}\frac{{{\text{d}}P_{10} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} &= K_{2} P_{11 } + K_{39} N_{10} + K_{61} A_{10}\\& -\, (K_{7} + K_{8} + K_{9} + K_{10} + K_{11} + K_{12} )P_{10} , \end{aligned}$$

(35)

$$\frac{{{\text{d}}P_{11} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{34} N_{11 } + K_{58} A_{11} - (K_{1} + K_{2} + K_{3} + K_{4} + K_{5} + K_{6} )P_{1} ,$$

(36)

$$\frac{\text{dMCP}}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{28} P_{6 } + K_{55} N_{6} - (K_{56} + K_{57} ),$$

(37)

$$\frac{{{\text{d}}N_{6} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{27} P_{6 } + K_{57} {\text{MCP}} + K_{71} A_{6} - (K_{53} + K_{54} + K_{55} )N_{6} ,$$

(38)

$$\frac{{{\text{d}}N_{7} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{23} P_{7 } + K_{43} N_{10} + K_{47} N_{10} + K_{50} N_{9} - (K_{51} + K_{52} )N_{7} ,$$

(39)

$$\frac{{{\text{d}}N_{8} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{18} P_{8 } + K_{38} N_{11} + K_{42} N_{10} + K_{46} N_{9} - (K_{48} + K_{49} + K_{50} )N_{8} ,$$

(40)

$$\frac{{{\text{d}}N_{9} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{13} P_{9 } + K_{37} N_{11} + K_{41} N_{10} - (K_{44} + K_{45} + K_{46} + K_{47} )N_{9} ,$$

(41)

$$\frac{{{\text{d}}N_{10} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{7} P_{10 } + K_{36} N_{11 } - (K_{39} + K_{40} + K_{41} + K_{42} + K_{43} )N_{10} ,$$

(42)

$$\frac{{{\text{d}}N_{11} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{1} P_{11 } - (K_{34} + K_{35} + K_{36} + K_{37} + K_{38} )N_{11} , .$$

(43)

$$\frac{{{\text{d}}A_{6} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{49} N_{8} + K_{63} A_{10} + K_{66} A_{10} - (K_{68} + K_{69} )A_{8} ,$$

(44)

$$\frac{{{\text{d}}A_{7} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{49} N_{8} + K_{63} A_{10} + K_{66} A_{10} - (K_{68} + K_{69} )A_{8} ,$$

(45)

$$\frac{{{\text{d}}A_{8} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{49} N_{8} + K_{63} A_{10} + K_{66} A_{10} - (K_{68} + K_{69} )A_{8} ,$$

(46)

$$\frac{{{\text{d}}A_{9} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{45} N_{9} + K_{60} A_{11} + K_{62} A_{10} - (K_{65} + K_{66} + K_{67} )A_{9} ,$$

(47)

$$\frac{{{\text{d}}A_{10} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{40} N_{10} + K_{59} A_{11} - (K_{61} + K_{62} + K_{63} + K_{64} )A_{10} ,$$

(48)

$$\frac{{{\text{d}}A_{11} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = K_{35} N_{11 } - (K_{58} + K_{59} + K_{60} )A_{11} ,$$

(49)

$$\begin{aligned} \frac{{{\text{dH}}_{2} }}{{{\text{d}}\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{SV}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{SV}}$}}} \right)}} = & \,a_{1} P_{11 } + a_{2} P_{10} + a_{3} P_{9} + a_{4} P_{8} + a_{5} P_{7} + a_{6} P_{6} + a_{7} P_{5} + b_{1} N_{11} + b_{2} N_{10} + b_{3} N_{9} \\ & + \,b_{4} N_{8} + b_{5} N_{7} + b_{6} N_{6} + c_{1} A_{11} + c_{2} A_{10} + c_{3} A_{9} + c_{4} A_{8} + c_{5} A_{7} + c_{6} A_{6} , \\ \end{aligned}$$

(50)

$$K_{i} = K_{i}^{0} \left[ {\frac{{E_{\text{Ai}} }}{R}\left( {\frac{1}{{T_{0} }} - \frac{1}{T}} \right)} \right]\left( {\frac{P}{{P_{0} }}} \right)^{{a_{k} }} ,$$

(51)

where K_i is the kinetic constants for the reactions, T₀ and P₀ are the reference temperatures and pressures, E_Ai the activation energy, and w is an exponential effect of pressure, as given in Tables 2 and 3, respectively. k_i, E_Ai, w, T₀, and P₀ are values obtained from Elizalde and Ancheyta [7].

Table 2 Activation energies for the reactions

Table 3 Exponential values of pressure (adapted from Elizalde and Ancheyta [7]

Mathematical model

Modeling the behaviour of the reactions is done by solving the model equations describing the system. The equations describing the mass balance and heat balance are solved simultaneously on gPROMS as represented in Eqs. (52–57):

$$- \frac{{{\text{d}}F}}{{{\text{d}}W}} + \mathop \sum \limits_{j = 1}^{Nr} (r_{j} \gamma_{i} ) = \frac{{\varepsilon {\text{d}}(ci)}}{{\rho b{\text{d}}t}},$$

(52)

$$\frac{{{\text{d}}T}}{{{\text{d}}t}} = \frac{{ - \left( {\mathop \sum \nolimits_{i = 1}^{\text{NC}} F_{i} CP_{i} } \right)+\frac{{{\text{d}}T}}{{{\text{d}}W}}\mathop \sum \nolimits_{j = 1}^{Nr} (r_{j} \gamma_{i} )( - \Delta H_{Rj} )}}{{{\text{Cp}}_{\text{cat}} + \frac{\varepsilon }{\rho b} \mathop \sum \nolimits_{i = 1}^{\text{NC}} C_{i} CP_{i} }},$$

(53)

$$\frac{{{\text{d}}P}}{{{\text{d}}w}} = \left[ {1.75 \times 10^{ - 5} \frac{(1 - \varepsilon )}{{\varepsilon^{3} }}\frac{{G^{2} }}{{\rho d_{\text{P}} g_{\text{C}} }} + 1.5 \times 10^{ - 5} \frac{(1 - \varepsilon )}{{\varepsilon^{3} }}\frac{G\mu }{{\rho d_{\text{P}}^{2} g_{\text{C}} }}} \right] \times \rho A,$$

(54)

$$\Delta H_{\text{R}} = \sum v_{\text{P}} H_{\text{fP}} - \sum v_{\text{r}} H_{\text{fr}} ,$$

(55)

$$H_{ri} = H_{ri}^{0} + \mathop \smallint \limits_{{298{\text{K}}}}^{T} C_{\text{p}} {\text{d}}T,$$

(56)

$$C_{\text{p}} = A1 + B1T + C1T^{2} + D1T^{3} .$$

(57)

Equations (26–50) are the rate equations for all the components, while Eq. (51) is the kinetic rate constant applied to all the rate equations.

Equation (52) is the material balance equation where $\rho b$ is the bulk density and $\varepsilon$ the bed voidage. Equation (53) is the heat balance of the reaction to determine the temperature behaviour where $- \Delta H_{Rj}$ is the heat of the reaction of the jth component and C_pcat is the heat capacity of the catalyst. Equation (54) gives the pressure profile of the reaction where D_p is particle diameter, G the mass flux, $\varepsilon$ the bed voidage, $\rho$ the gas density, and A the reactor area. $H_{ri}^{0}$, the standard heat of formation of the components and the constants of A1, B1, C1, and D1 for the C_p, heat capacity, in Eqs. (56, 57), are taken from Riazi [18]. These equations are solved simultaneously using gPROMS to determine the behaviour of the system. gPROMS is a robust mathematical software that could solve all the four reactors in series dynamically given the behaviour of the paraffins, naphthenes and aromatics as well as the dynamics of the temperature in the reactors. All the components’ behaviour was determined.

RON model

The estimation of the RON of hydrocarbons for the feed and products can be done using different methods of prediction. RON can be calculated for each pure component using a polynomial equation that correlates to the normal boiling point [18] as shown by Eq. (58):

$${\text{RON}} = Aa + BbT + CcT^{2} + DdT^{3} + EeT^{4} ,$$

(58)

where $T = {\text{TBP}} \times 0.01$, TBP represents the normal boiling point (°C), and Aa, Bb, Cc, Dd, and Ee, are coefficients. The RON of a hydrocarbon mixture is calculated by assuming that the mixture consists of paraffins, naphthenic hydrocarbons, and aromatics. The equation is expressed as the sum of the RON for each pure component multiplied by the volume fractions of the components.

Model validation

The model validation was carried out by modeling and simulating the commercial data of Ancheyta et al. [2] and Rodríguez and Ancheyta [19] on gPROMS to ascertain the capability and ruggedness of the mathematical software in complex modeling. The modeling of Ancheyta et al. [2] was performed using MATLAB software and the result is compared with that obtained with gPROMS. The configuration of the commercial reformer and feed properties are given in Tables 4 and 5, respectively.

Table 4 Configuration of commercial catalytic reformer [2]

Table 5 Feed stock properties of commercial catalytic reformer [2]

Model validation results

The commercial reformer Ancheyta et al. [2] were simulated with the properties of Tables 4 and 5, respectively, with four semi regenerative reactors in series. The reformer’s throughput is 30 MBPD at inlet temperature of 495 °C and pressure of 10.5 kg/cm² using MATLAB mathematical tool on ODE45. The simulation was performed on gPROMS software to validate its capability in modeling this problem. The result obtained from gPROMS is compared with that obtained with MATLAB from Ancheyta et al. [2], and presented in Table 6.

Table 6 Comparison between results from MATLAB [2] and gPROMS

From the modeling and simulation results, the Ancheyta et al.’s [2] result and that of gPROMS were compared and analyzed. The result showed a good and comparable result between the actual and that simulated with gPRMOs. This is an indication of the capability of the mathematical tool in solving complex model equations

Results and discussion

Simulation analysis

The model was validated with commercial data from Ancheyta et al. [2] and Rodríguez and Ancheyta [19] and Kaduna refinery and petrochemical company (KRPC), and shows good agreement with data from both sources. The commercial plant modeling and simulation results are in good agreement, as shown in Fig. 3 and Table 7. Tables 8 and 9 show the configuration and feed properties of KRPC commercial catalytic reformer.

Fig. 3

Comparison between model simulation and industrial plant data

Table 7 Relative errors between industrial and simulated results of KRPC plant

Table 8 Configuration of KRPC commercial catalytic reformer (Chiyoda, 1980 #293)

Table 9 Feed properties of KRPC commercial catalytic reformer

Figure 4 shows the concentration profile of paraffins along the reactor height. P₅, P₆, P₇, P₈, P₉, and P₁₀ are paraffins with hydrocarbon numbers 5, 6, 7, 8, 9, and 10, respectively. Normal paraffin components basically undergo three major reactions during naphtha reforming. Firstly, they undergo hydrocracking to lighter paraffins, i.e., methane, ethane, propane, and butane, as shown in reactions 8–33 in Table 1. Secondly, the isomerization reaction to form isoparaffins. This is a slow reaction with slow reaction rate, hence, it is not considered in this work. Thirdly, the dehydrocyclization to naphthenes, a very slow reaction, leads to a decrease in the paraffins. These reactions are reactions 1–7 from Table 1. Dehydrocyclization reaction becomes easier as the molecular weight of the paraffins increases as in P₈, P₉, and P₁₀, while P₇ shows little increase. P₅ and P₆ increase due to hydrocracking. The main effects of hydrocracking are decrease of paraffins (C5⁺) in the reformate, decrease in hydrogen production, and increase in LPG production and hydrogenolysis. The isomerization reactions are fast, slightly exothermic and do not affect the number of carbon atoms. The thermodynamic equilibrium of isoparaffins to paraffins depends mainly on the temperature and pressure which has no effect. The paraffins isomerization results in a slight increase of the octane number. These reactions are promoted by the acidic function of the catalyst support. The paraffin dehydrocyclization step becomes easier as the molecular weight of the paraffin increases. From Table 1, the rates increase from 0.00, 0.58, 1.33, 1.81, and 2.54 for P₆–P₁₁. However, the tendency of paraffins to hydrocrack increases concurrently. Kinetically, the rate of dehydrocyclization increases with low pressure and high temperature. To sum up, the dehydrocyclization of P₆ paraffins to benzene is more difficult than that of C₇ paraffin to toluene, which itself is more difficult than that of C₈ paraffin to xylenes. Accordingly, the most suitable fraction to feed a reforming process is the C₇–C₁₀ fraction.

Fig. 4

Concentration profile of paraffins with changing reactor height

Figure 5 shows the behaviour of the naphthenes along the reactor height. N₆, N₇, N₈, N₉, and N₁₀ are naphthenes with hydrocarbon number 6, 7, 8, 9, and 10, respectively. The fastest reaction is aromatization, i.e., dehydrogenation of naphthenes, resulting in the large temperature drop due to its highly endothermic nature. The drastic reduction is due to the aromatization to aromatics. Thermodynamically, the reaction is highly endothermic and is favored by high temperature and low pressure. In addition, the higher the number of carbon atoms, the higher the aromatics production at equilibrium from N₈, N₉, and N₁₀. This can be seen from Table 1 in Eqs. (34–39) where the reaction rates increase from 4.02, 9.03, 21.5, 24.5, and 24.5, respectively, for N₆, N₇, N₈, N₉, and N₁₀. From a kinetic point of view, the rate of reaction increases with temperature. The naphthenes also undergo hydrocracking to lighter hydrocarbons leading to their decrease as shown in reactions (49–57) in Table 1.

Fig. 5

Concentration profile of naphthenes with changing reactor height

Figure 6 shows the behaviour of aromatics along the reactor height. A₆, A₇, A₈, A₉, and A₁₀ are paraffins with hydrocarbon numbers 5, 6, 7, 8, 9, and 10, respectively. The dehydrogenation of naphthenes, as shown in Fig. 5, increases the aromatics, as shown in Fig. 6. The sharp increase is because of drastic aromatization of the naphthenes favored by the metallic sites of the catalyst. The rate of benzene formation is lower due to lower carbon number of N₆, while A₇, A₈, and A₉ increase rapidly due to higher carbon number of N₇, N₈, and N₉.

Fig. 6

Concentration profile of aromatics with changing reactor height

Figure 7 shows the temperature profile of the reactions along the reactor height and the sharp drop in first and second reactors is due to the more endothermic dehydrogenation reaction of naphthenes to aromatics. Typically, dehydrogenation and isomerization reactions take place in the first reactor, dehydrogenation, isomerization, dehydrogenation, and cracking in the second followed by dehydrogenation and cracking in the third and fourth reactors.

Fig. 7

Temperature profile with changing reactor height

Figures 8 and 9 show how the increase in hydrogen yield and RON varies, respectively, along the height of the reactor. This is due to the increase in the aromatics along the reactor height. The RON increases from reactor one to four due to increase in aromatization reaction, which gives a higher research octane number, a parameter for antiknock in the gasoline engine. Treated naphtha has low RON and cannot be used as gasoline, hence the reforming reaction of the components to give a gasoline with higher research octane number.

Fig. 8

H₂ yield along the four reactors height

Fig. 9

RON along the reactor height

Analysis of compressibility factor

In this study, initially, the compressibility factors of different empirical correlations were added to catalytic-reforming reactor model using HHR of 6.4. The pressure profile of the four reactors in series is given in Fig. 10. The pressure decreases continually from the first reactor and decreases from 18.65 to 12.6 kPa at the exit of the last reactor. In Fig. 11, the profile of the gas densities behaves in similar way due to the drop and decrease in the reactors pressure, but the last reactor exhibits a slightly different behaviour due to the larger pressure drop in the last reactor.

Fig. 10

Pressure profile with changing reactor height

Fig. 11

Gas density profile with changing reactor height

Figure 12 shows the compressibility factor profiles along the reactor heights of the different correlations used. The correlation of Shokir et al. [21] gave a non-zero Z factor along the reactor heights, because the range of P_pr and T_pr is wider than others. The Heidaryan et al.’s [12] compressibility factor was negative and thus would not give meaningful data and so it is not reported. The Z factor changes along the reactor heights due to the variation of operational conditions and transport properties aforementioned. The Z factor at each height of reactor is not the same, and it is obvious that if these variables change with the Z factors as in Fig. 12, the Z factor cannot be a constant value of unity as always assumed. The Mahmoud [16] Z factor is the closest to the ideal compared to others, although this does not signify that it is the true representation of the Z factors, but further analysis will be carried out on how it correlates or deviates from other process variables in the reactors. Factors such as the yield of reformate, hydrogen, and aromatics yield for each compressibility correlation, and the temperature and pressure profiles along the reactors’ heights will need to be considered as well.

Fig. 12

Compressibility Z factor profiles

ZB represents Bahadori et al. [4], ZH1 represents Heidaryan et al. [11], ZM represents Mahmoud [16], ZP represents Papay [17], ZS represents Sanjari and Lay [20], and ZSH represents Shokir et al. [21].

Figure 13 shows the profiles of the density of the gas phase along the reactor heights. Gas density is a function of pressure and temperature as well as feed flow rate. The pressure model equation is also a function of gas density as in Eq. (54). Therefore, the density is significant in determining the Z compressibility factors and the pressure profiles. The density profile decreases along the reactor height due to the drop in temperature across the various reactors. The behaviour is true for all the correlations and Fig. 12 shows that the Z factors have different profiles of gas densities. However, in Fig. 13, the profile of gas density for Papay [17] is the closest to that of the density for ideal vapor unlike Fig. 12 where the compressibility factor correlation of Mahmoud [16] is the closest. This implies that further analysis needs to be carried out.

Fig. 13

Density profile along the reactors

The temperature variation with Z factor, as shown in Fig. 14, has effect on the product quality and yield generally as a result of the effect of the kinetic equations which are dependent on reaction temperature. Therefore, enthalpy of various compressibility factors correlations could also vary simultaneously, but the effect is obvious in the last reactor temperature decrease, as shown in Fig. 14. Figure 15 shows reformate yield along the reactors’ heights of various Z factor correlations. As with the case of temperature, where the enthalpy of reactions has a pronounced effect, the pressure, HHR, the reformate yield, and hydrogen yield also change due to the variation of the different Z factors as shown in Figs. 15 and 16. For the reformate and hydrogen yields, Table 10 gives the different exit values of the RMT and hydrogen yields with the values from the Mahmoud [16] being the closest.

Fig. 14

Temperature profile along the reactors

Fig. 15

RMT profile along the reactors

Fig. 16

Hydrogen profile along the reactors

Table 10 RMT and hydrogen yields at the outlet of the fourth reactor

Table 11 Pressure drop (Pa) across the four reactors for various Z factor correlations at HHR 6.0

For an accurate prediction of a suitable compressibility factor correlation for the CRU modeling, a study of the hydrogen-to-hydrocarbon ratio, which is a major dynamic variable that influences the reaction hydrodynamics, is performed. The variation of reaction pressure is investigated also for the compressibility empirical correlations and a comparison with the pressure values of the model results and that of the ideal case is depicted in Fig. 15

The various pressures vary along the reactor height with some above the ideal gas correlations and some below are shown in Fig. 17. The closest to ideal behaviour is the Mahmoud Z factor correlation [16].

Fig. 17

Pressure profile along the reactors for different compressibility correlations. The decrease in pressure for the various empirical correlations for different HHR ratios is given in Table 11. The closest among them to the ideal is Mahmoud [16]. It has 0.65% deviation at the exit of the first reactor, 1.58% at the exit of the second reactor, 2.78% at the exit of the third reactor, and 3.814% at the exit of the fourth reactor

Since the Mahmoud’s [16] compressibility factor correlation is the closest to that of the ideal case, a further analysis is performed between the two by varying the pressure of the reaction and the HHR. This will give the extent of closeness of the product distribution. Tables 7 and 8 show the pressure drops with variation in HHR, while Fig. 16 shows the effects of variation of the pressure using the Mahmoud correlation with Z equal to one. For HHR of 6.4, it has a 0.709% deviation at the exit of the first reactor, 1.734% at the exit of the second reactor, 3.118% at the exit of the third reactor, and 4.343% at the exit of the fourth reactor.

For HHR of 7.0, it has a 0.796% deviation at the exit of the first reactor, 2.00% at the exit of the second reactor, 3.720% at the exit of the third reactor, and 5.319% at the exit of the fourth reactor. The decrease in pressure for the various empirical correlations for different HHR ratios of 6.4 and 7.0 is given in Tables 12 and 13.

Table 12 Pressure drop (Pa) across the four reactors for various Z factor correlations at HHR 6.4

Table 13 Pressure drop (Pa) across the four reactors for various Z factor correlations at HHR 7.0

The increase in pressure shows a match between the Mahmoud’s [16] correlation and the ideal, as shown in Fig. 18. At the different exit of the reactor, the temperatures are different due to fall in temperature. The Z compressibility factors are different which are functions of the gas densities which are functions of pressure. The Mahmoud [16] correlation becomes more suitable and applicable at a higher pressure and lower HHR.

Fig. 18

Effects of variation of the pressure with Mahmoud’s [16] correlation with ideal at different height

Conclusion

A detailed steady-state model of catalytic-reforming unit (CRU) of four reactors in series is modeled in this work and a simulation with various compressibility factors is performed using gPROMS, a mathematical and modeling software. The conclusions are:

• 1. The simulated results from this study are compared with data from the KRPC industrial plant. The parameters of both kinetic and thermodynamic are obtained from the open literature [7]. Good agreement between the simulated and plant data shows the robust strength and capability of the gPROMS model builder in modeling and simulating four reactors in series. Therefore, gPROMS can be recommended for modeling complex processes such as simulation of the CRU unit.

• 2. Mahmoud’s [16] compressibility Z factor is found to be a more suitable correlation in predicting the Z factor across the four reactors.

• 3. Different yields of profiles for process variables such as density, reaction pressure, and enthalpy of reaction are obtained with corresponding different compressibility factors in the simulation of the CRU using the same process conditions. These profiles are as a result of varying temperature profiles and varying RMT yield as well as hydrogen yield.

• 4. The pressure in each reactor is not the same for different HHR ratios. The reaction pressure is also not the same in each of the reactors when the Mahmoud [16] compressibility Z factor correlation is applied rather than assuming and treating the vapor as an ideal gas.

• 5. The pressure drops across the four reactors are similar and comparable when Mahmoud’s [16] correlation is applied and gives almost the same result at an inlet pressure of 2265 kPa. Hence, Mahmoud’s [16] correlation can be used in modeling the pressures in CRU.

Appendix A

Tables 14, 15, 16, 17 and 18 are parameters adopted from the literature

Table 14 Tuned coefficients for Z factor [3]

Table 15 Tuned coefficients for Z factor [4]

Table 16 Tuned coefficients for $0.2 \le P_{\text{pr}} \le 3$ [11]

Table 17 Tuned coefficients for Z factor [12]

Table 18 Tuned coefficients for Z factor [20]