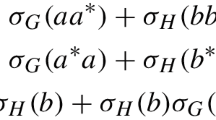Double bordered constructions of self-dual codes from group rings over Frobenius rings

Abstract

In this work, we describe a double bordered construction of self-dual codes from group rings. We show that this construction is effective for groups of order 2p where p is odd, over the rings $\mathbb {F}_{2}+u\mathbb {F}_{2}$ and $\mathbb {F}_{4}+u\mathbb {F}_{4}$. We demonstrate the importance of this new construction by finding many new binary self-dual codes of lengths 64, 68 and 80; the new codes and their corresponding weight enumerators are listed in several tables.

1 Introduction

Group rings and algebraic coding theory have been extensively studied as a result of their numerous theoretical and practical applications in cryptography, error correction and lattices to name a few. This strong connection between group rings and coding theory is frequently endorsed in the successful search for extremal binary self-dual codes. This has been an area of great research since the pure double-circulant construction was introduced in the 1960s [3, 24].

As the theory surrounding extremal binary self-dual codes is established, one remaining constraint is the size of the search field. A common technique in order to reduce the search field is to use special construction methods and apply certain restrictions; this frequently includes the use of group rings [23]. Fundamentally, Hurley [22] introduced a map from any group ring element, to a matrix, A, over the ring of coefficients. The matrix, A, has been used in numerous construction methods to describe a linear code, [28]. This theory was well established with the realization of the [48,24,12] extended QR code as a group ring code for the dihedral group, [27]. Notably, in 1990 [1], the extended Golay codes were constructed from ideals in group rings. A popular technique, which has resulted in countless self-dual codes, has been to consider the generator matrix (I_n|A) where A satisfies AA^T = −I_n, [18,19,20, 29, 30]. Initially applied over the binary field, these constructions can be extended over finite commutative rings. Recently, the theory surrounding group ring elements to construct codes has progressed to any group [9]. This has led to stronger connections between certain group ring elements called unitary units and self-dual codes [16].

The common double-circulant and four-circulant construction methods have been adjusted and modified numerous times in order to reduce the search field, in the hope of finding new extremal self-dual codes [8, 10, 17]. One particular modification of interest is the bordered double-circulant construction [2]. This construction method has shown considerable results, where the generator matrix is in the form:

A natural extension of this work is to consider the following generator matrix where the identity matrix also has a border:

Here, A is a matrix generated from a group ring element. In this paper, we put restrictions on the values of α and β in order to relax restrictions on the type of element chosen from the group ring.

This paper is organised as follows: Section 2 discusses the preliminaries, including definitions and notation, essential to the understanding and interpretation of results in this paper. In Section 3, we consider the new double bordered construction and look at the theory surrounding its effectiveness. We specify conditions on the construction in order to maximise its practicality and effectiveness. The following sections are allocated to the results, computed using MAGMA [25], and proving the efficiency of the theory. The new extremal binary self-dual codes are listed in numerous tables and summarised in the final section. Notably, this research includes new self-dual codes of length 64, 68 and 80.

2 Preliminaries

In this section, we will define extremal self-dual codes over Frobenius rings. We refer to certain types of these rings, of characteristic 2, throughout this paper. Here, we define the notation used in this paper in order to condense the results.

Frobenius rings can be characterised as follows. Denoting the character module of R by $\widehat {R}$, for a finite ring R the following are equivalent:

• R is a Frobenius ring.

• As a left module, $\widehat {R} \cong { }_{R}R.$

• As a right module, $\widehat {R} \cong R_{R}$.

The first commutative ring that we consider is $\mathbb {F}_{2}+u\mathbb {F}_{2} := \mathbb {F}_{2} [X]/(X^{2})$, where u satisfies u² = 0. The elements of the ring may be written as 0,1, u and 1 + u, where 1 and 1 + u are the units of $\mathbb {F}_{2}+u\mathbb {F}_{2}$. We also consider $\mathbb {F}_{4}+u\mathbb {F}_{4}$; the commutative binary ring of size 16. $\mathbb {F}_{4}+u\mathbb {F}_{4}$ can be viewed as an extension of $\mathbb {F}_{2}+u\mathbb {F}_{2}$. Therefore, we can express any element of $\mathbb {F}_{4} +u\mathbb {F}_{4}$ in the form ωa + (1 + ω)b, where $a, b\in \mathbb {F}_{2} + u\mathbb {F}_{2}$. These rings are generalised in [13] and [14]. In the upcoming results, we use the hexadecimal number system in order to represent the elements of $\mathbb {F}_{4}+u\mathbb {F}_{4}$. This is achieved by use of the ordered basis {uω, ω, u,1}.

$$ \begin{array}{@{}rcl@{}} 0 &\leftrightarrow &0000,\ 1\leftrightarrow 0001,\ 2\leftrightarrow 0010,\ 3\leftrightarrow 0011, \\ 4 &\leftrightarrow &0100,\ 5\leftrightarrow 0101,\ 6\leftrightarrow 0110,\ 7\leftrightarrow 0111, \\ 8 &\leftrightarrow &1000,\ 9\leftrightarrow 1001,\ A\leftrightarrow 1010,\ B\leftrightarrow 1011, \\ C &\leftrightarrow &1100,\ D\leftrightarrow 1101,\ E\leftrightarrow 1110,\ F\leftrightarrow 1111. \end{array} $$

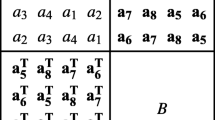
For example, the element 1 + u + uω in $\mathbb {F}_{4} +u\mathbb {F}_{4}$ is expressed as 1011 from the ordered basis, which we refer to as B from the hexadecimal system.

Now, we will look at some definitions and notation regarding coding theory; the following is required for full understanding of the successive results. A code over a finite commutative ring R is defined as any subset C of Rⁿ. An element of C is called a codeword. If a code satisfies C = C^⊥ then the code C is said to be self-dual, alternatively if $C \subseteq C^{\perp }$ then the code is said to be self-orthogonal. The Hamming weight enumerator of a code is defined as:

$$ W_{C}(x,y) = \sum\limits_{\mathbf{c} \in C} x^{n-wt(\mathbf{c})} y^{wt(\mathbf{c})}. $$

(1)

For binary codes, a self-dual code where all weights are congruent to 0 (mod 4) is said to be Type II and the code is said to be Type I otherwise. If a code satisfies $W_{C}(x,y) = W_{C^{\perp }}(x,y)$ then the code is said to be formally self-dual. The bounds on the minimum distances, d(n) for Type I and Type II codes respectively, are

$$ d(n) \leq 4 \lfloor \frac{n}{24} \rfloor +4 $$

and

$$ d(n) \leq \left\{\begin{array}{ll} 4 \lfloor \frac{n}{24} \rfloor +4 ~\text{if}~ n \not \equiv 22\pmod{24} \\ 4 \lfloor \frac{n}{24} \rfloor +6 ~\text{if}~ n \equiv 22\pmod{24} \end{array}\right. $$

If these bounds are met for self-dual codes, they are called extremal. Extremal binary self-dual codes are of great interest for their numerous applications.

We also define the Gray maps $\phi ^{\prime }$ from $\mathbb {F}_{2}+u\mathbb {F}_{2}$ to ${\mathbb {F}_{2}^{2}}$ given by $\phi ^{\prime }(a+bu)=(b,a+b)$ where $a,b \in \mathbb {F}_{2}$, and ϕ from $\mathbb {F}_{4}+u\mathbb {F}_{4}$ to ${\mathbb {F}_{4}^{2}}$ given by ϕ(a + bu) = (b, a + b) where $a,b \in \mathbb {F}_{4}$. Introduced in [7], ϕ is a distance preserving linear isometry which preserves orthogonality in the corresponding alphabets. We also consider the Gray maps $\psi ^{\prime }$ from $\mathbb {F}_{4}$ to ${\mathbb {F}_{2}^{2}}$ given by $\psi ^{\prime }(a\omega +b\bar {\omega })=(a,b)$ where $a,b \in \mathbb {F}_{2}$, and ψ from $\mathbb {F}_{4}+u\mathbb {F}_{4}$ to $(\mathbb {F}_{2}+u\mathbb {F}_{2})^{2}$ given by $\psi (a\omega +b\bar {\omega })=(a,b)$ where $a,b \in {\mathbb {F}_{4}^{2}}$. Initially introduced in [15], these maps were generalised in [26].

Next, we define a group ring and summarise its properties and notation; group rings are frequently used in various construction methods ([31]). Let G be a finite group or order n, then the group ring RG consists of ${\sum }_{i=1}^{n} \alpha _{i} g_{i}$, α_i ∈ R, g_i ∈ G. Addition in the group ring is done by coordinate addition, namely

$$ \sum\limits_{i=1}^{n} \alpha_{i} g_{i} + \sum\limits_{i=1}^{n} \beta_{i} g_{i} = \sum\limits_{i=1}^{n} (\alpha_{i} + \beta_{i} ) g_{i}. $$

(2)

The product of two elements in a group ring is given by

$$ \left( \sum\limits_{i=1}^{n} \alpha_{i} g_{i} \right) \left( \sum\limits_{j=1}^{n} \beta_{j} g_{j}\right) = \sum\limits_{i,j} \alpha_{i} \beta_{j} g_{i} g_{j}. $$

(3)

It follows that the coefficient of g_i in the product is ${\sum }_{g_{i} g_{j} = g_{k} } \alpha _{i} \beta _{j}$. Throughout this work, e_G denotes the identity element of any group G.

The following construction of a matrix was first given for codes over fields by Hurley in [22] and extended to rings in [9]. Let R be a finite commutative Frobenius ring and let $G = \{ g_{1},g_{2},\dots ,g_{n} \}$ be the elements of a group of order n in a given listing. Let $v = {\sum }_{i=1}^{n} \alpha _{g_{i}} \in RG$. Define the matrix σ(v) ∈ M_n(R) to be $\sigma (v)=(\alpha _{g_{i}^{-1} g_{j}})$ where i, j ∈{1,2,⋯ , n}.

Two groups that are often considered when applying the theory are cyclic and dihedral groups. For these groups, we consider circulant n × n matrices denoted cir(α₁, α₂,⋯ , α_n), where each row vector is rotated one element to the right relative to the preceding row vector [5]. Furthermore, the notation CIR(A₁, A₂,⋯ , A_m) denotes the nm × nm circulant matrix constructed of m smaller n × n circulant matrices, A_i. We will now look at the structure of the matrix σ(v) where v is an element of the cyclic or dihedral group of order 2p.

Firstly, let $C_{2p}^{\prime }= \langle x~|~x^{2p}=1 \rangle$ and

$$ v=\sum\limits_{i=0}^{p-1} {\sum}_{j=0}^{1} \alpha_{i+pj+1} x^{2i+j} \in RC_{2p}^{\prime} $$

then,

$$ \sigma(v)=\left( \begin{array}{ll} A_{1} & A_{2} \\ A_{2}^{\prime} & A_{1} \end{array}\right) $$

where $A_{j}=cir(\alpha _{(j-1)p+1}, \alpha _{(j-1)p+2}, \dots , \alpha _{jp})$ and $A^{\prime }_{j}=cir(\alpha _{jp}, \alpha _{(j-1)p+1}, \dots , \alpha _{jp-1})$.

Alternatively, let D_2p = 〈x, y | x^p = y² = 1, x^y = y^− 1〉 and

$$ v=\sum\limits_{i=0}^{p-1} \sum\limits_{j=0}^{1} \alpha_{i+pj+1} x^{i} y^{j} \in RD_{2p} $$

then,

$$ \sigma(v)=\left( \begin{array}{ll} A_{1} & A_{2} \\ {A_{2}^{T}} & {A_{1}^{T}} \end{array}\right) $$

where $A_{j}=cir(\alpha _{(j-1)p+1}, \alpha _{(j-1)p+2}, \dots , \alpha _{jp})$.

We can use an effective technique in order to extend the length of a given code by 2. The following result, introduced in [12], will be utilised frequently in this work.

Theorem 2.1

Let Cbe a self-dual code over$\mathbb {F}_{2}+u\mathbb {F}_{2}$of length nand G = (r_i) be a j × ngenerator matrix for C, where r_iis the i −th row of G, 1 ≤ i ≤ k. Let cbe a unit in$\mathbb {F}_{2}+u\mathbb {F}_{2}$and Xbe a vector in$(\mathbb {F}_{2}+u\mathbb {F}_{2})^{n}$with 〈X, X〉 = 1 and y_i = 〈r_i, X〉. Then the following matrix

generates a self-dual codes$C^{\prime }$over$\mathbb {F}_{2}+u\mathbb {F}_{2}$of length n + 2.

3 Construction

Let v ∈ RG where R is a finite Frobenius ring of characteristic 2 and G is a finite group of order 2p where p is odd. Define the following matrix:

where α_i ∈ R. Let C_σ be a code that is generated by the matrix M(σ). Then, the code C_σ has length 4p + 4. Throughout this paper, we assume that G is a group of order 2p that contains a subgroup of order p where p is odd. If we fix a listing of G where the first p elements of G are the elements of H, then σ(v) takes a certain form. The next result states the form that σ(v) takes in this case. It also provides an important property that enables us to prove our main result.

Lemma 3.1

Let Rbe a commutative ring. If H = {g₁, g₂,…, g_p} is a subgroup of the finite group G = {g₁, g₂,…, g_p, g_p+ 1,…, g_2p} of order 2 p (pis odd), then

where M₁, M₂are p × pmatrices, $M_{1}^{\prime }$is permutation similar to M₁and$M_{2}^{\prime }$is permutation to M₂. Moreover

$$ M_{k} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= {M_{k}^{T}} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= M^{\prime}_{k} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= {M^{\prime}_{k}}^{T} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= \left( \begin{array}{c}\mu_{k}\\\vdots\\\mu_{k} \end{array}\right) (k=1,2), $$

where$\mu _{1}=\sum \limits _{g\in H} \alpha _{g}$, $\mu _{2}=\sum \limits _{g\in G\backslash H} \alpha _{g}$.

Proof

Clearly, $M_{1}= (\alpha _{g_{i}^{-1}g_{j}})_{i,j=1,\ldots ,p}$, $M_{2}= (\alpha _{g_{i}^{-1}g_{p+j}})_{i,j=1,\ldots ,p}$$M^{\prime }_{2}= (\alpha _{g_{p+i}^{-1}g_{j}})_{i,j=1,\ldots ,p}$ and $M^{\prime }_{1}= (\alpha _{g_{p+i}^{-1}g_{p+j}})_{i,j=1,\ldots ,p}$. Let a ∈ G∖H. Then, for any 1 ≤ i ≤ p, g_p+i ∈ aH and g_p+i = ag_δ(i) for some 1 ≤ δ(i) ≤ p. Moreover δ : i → δ(i) is a permutation of degree p and

$$ M^{\prime}_{1}= (\alpha_{g_{p+i}^{-1}g_{p+j}})_{i,j=1,\ldots,p}= (\alpha_{(ag_{\delta(i)})^{-1}ag_{\delta(j)}})_{i,j=1,\ldots,p}= $$

$$ (\alpha_{g_{\delta(i)}^{-1}a^{-1}ag_{\delta(j)}})_{i,j=1,\ldots,p}= (\alpha_{g_{\delta(i)}^{-1}g_{\delta(j)}})_{i,j=1,\ldots,p}. $$

If we rearrange the rows and columns of the matrix $M_{1}=(\alpha _{g_{i}^{-1}g_{j}})_{i,j=1,\ldots ,p}$ in the order δ(1),…δ(p) we will obtain $M^{\prime }_{1}$. So, M₁ is permutation similar to $M^{\prime }_{1}$.

It is well known that group G of order 2p contains a subgroup of order 2. So there is a ∈ Ga≠e_G, a² = e_G. Thus |H| = p, a∉H. Again, let g_p+i = ag_δ(i) for some 1 ≤ δ(i) ≤ p. Moreover, δ : i → δ(i) is a permutation of degree p and

$$ M_{2}= (\alpha_{g_{i}^{-1}g_{p+j}})_{i,j=1,\ldots,p}= (\alpha_{g_{i}^{-1}ag_{\delta(j)}})_{i,j=1,\ldots,p}, $$

$$ M^{\prime}_{2} = (\alpha_{g_{p+i}^{-1}g_{j}})_{i,j=1,\ldots,p}= (\alpha_{(ag_{\delta(i)})^{-1}g_{j}})_{i,j=1,\ldots,p}= (\alpha_{g_{\delta(i)}^{-1}a^{-1}g_{j}})_{i,j=1,\ldots,p} = (\alpha_{g_{\delta(i)}^{-1}ag_{j}})_{i,j=1,\ldots,p}. $$

Now, if we rearrange the rows of the matrix $M_{2}=(\alpha _{g_{i}^{-1}ag_{\delta (j)}})_{i,j=1,\ldots ,p}$ in the order δ(1),…δ(p) and if we rearrange the its columns in the order δ^− 1(1),…δ^− 1(p) we will obtain

$$ (\alpha_{g_{\delta(i)}^{-1}ag_{\delta(\delta^{-1}(j))}})_{i,j=1,\ldots,p}=(\alpha_{g_{\delta(i)}^{-1}ag_{j}})_{i,j=1,\ldots,p}=M^{\prime}_{2}. $$

This implies that $SM_{2}S=M^{\prime }_{2}$ for a permutation matrix S, which contains ones in positions (i, δ(i)) (i = 1,…, p) or, which is the same, in positions (δ^− 1(j), j) (j = 1,…, p).

Now, the i-th element of column $M_{1}\left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )$ is

$$ \sum\limits_{j=1}^{p} \alpha_{g^{-1}_{i}g_{j}}= \sum\limits_{g\in H} \alpha_{g^{-1}_{i} g}= \sum\limits_{g\in H} \alpha_ g=\mu_{1}, ~~ g_{i} \in H, ~g_{i}^{-1} \in H, $$

and the i-th element of column ${M_{1}^{T}}\left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )$ is

$$ \sum\limits_{j=1}^{p} \alpha_{g^{-1}_{j}g_{i}}= \sum\limits_{g\in H} \alpha_{g^{-1}g_{i}}= \sum\limits_{g\in H} \alpha_{gg_{i}}= \sum\limits_{g\in H} \alpha_ g=\mu_{1}, ~~ g_{i} \in H. $$

Thus,

$$ M_{1} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= {M_{1}^{T}} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= \left( \begin{array}{c}\mu_{1}\\\vdots\\\mu_{1} \end{array}\right), $$

since we have $S\left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )= \left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )$ for any permutation matrix S, and M₁ is permutation similar to $M^{\prime }_{1}$. Furthermore,

$$ M^{\prime}_{1} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= {M^{\prime}_{1}}^{T} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= \left( \begin{array}{c}\mu_{1}\\\vdots\\\mu_{1} \end{array}\right). $$

Now, the i-th elements of columns $M_{2}\left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )$ and ${M_{2}^{T}}\left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )$ respectively, are

$$ \sum\limits_{j=1}^{p} \alpha_{g^{-1}_{i}g_{p+j}}= \sum\limits_{g\in G\backslash H} \alpha_{g^{-1}_{i} g}= \sum\limits_{g\in G\backslash H} \alpha_ g=\mu_{2}, $$

$$ \sum\limits_{j=1}^{p} \alpha_{g^{-1}_{p+j}g_{i}}= \sum\limits_{g\in G\backslash H} \alpha_{g^{-1}g_{i}}= \sum\limits_{g\in G\backslash H} \alpha_{gg_{i}}= \sum\limits_{g\in G\backslash H} \alpha_ g=\mu_{2}, $$

where g_i ∈ H and $g_{i}^{-1} \in H$.

Thus,

$$ M_{2} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= {M_{2}^{T}} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= \left( \begin{array}{c}\mu_{2}\\\vdots\\\mu_{2} \end{array}\right) $$

Therefore, we have $SM_{1}S=M^{\prime }_{1}$ for some permutation matrix S, $S\left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right )= \left (\begin {array}{c} 1\\\vdots \\1 \end {array}\right ),$ and

$$ M^{\prime}_{2} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= {M^{\prime}_{2}}^{T} \left( \begin{array}{c}1\\\vdots\\1 \end{array}\right)= \left( \begin{array}{c}\mu_{2}\\\vdots\\\mu_{2} \end{array}\right). $$

□

We can now state and prove our main result.

Theorem 3.2

Let Rbe a finite commutative Frobenius ring of characteristic 2, G = {g₁, g₂,…, g_p, g_p+ 1,…, g_2p} be a finite group of order 2pand H = {g₁, g₂,…, g_p} be a subgroup of group G. Then, C_σis a self-dual code of length 4p + 4 if and only if

• ${\sum }_{i=1}^{8} \alpha _{i}=0$,

• $vv^{*} = 1+{\sum }_{i=1}^{2}(\alpha _{i+2}^{2} +\alpha _{i+6}^{2})\widehat {g},$

• (α₁ + 1)α₃ + α₂α₄ + (α₅ + μ₁)α₇ + (α₆ + μ₂)α₈ = 0,

• (α₁ + 1)α₄ + α₂α₃ + (α₅ + μ₁)α₈ + (α₆ + μ₂)α₇ = 0 and

• 7.19.6$\left (\begin {array}{llllll} \alpha _{1}+{\alpha _{3}^{2}}+{\alpha _{4}^{2}}\!\!&\alpha _{2}&\alpha _{5}+\alpha _{3}\alpha _{7}+\alpha _{4}\alpha _{8}&\alpha _{6}+\alpha _{3}\alpha _{8}+\alpha _{4}\alpha _{7}&\alpha _{7}+\mu _{1}\alpha _{3}+\mu _{2}\alpha _{4}&\alpha _{8}+\mu _{1}\alpha _{4}+\mu _{2}\alpha _{3}\\ \alpha _{2}&\!\!\alpha _{1}+{\alpha _{3}^{2}}+{\alpha _{4}^{2}}&\alpha _{6}+\alpha _{3}\alpha _{8}+\alpha _{4}\alpha _{7}&\alpha _{5}+\alpha _{3}\alpha _{7}+\alpha _{4}\alpha _{8}&\alpha _{8}+\mu _{1}\alpha _{4}+\mu _{2}\alpha _{3}&\alpha _{7}+\mu _{1}\alpha _{3}+\mu _{2}\alpha _{4} \end {array} \right )$has free rank 2

where$\widehat {g}={\sum }_{i=1}^{p}g_{i}$, $\mu _{1}=\sum \limits _{g\in H} \alpha _{g}$ and $\mu _{2}=\sum \limits _{g\in G\backslash H} \alpha _{g}$.

Proof

Let $M(\sigma )=\left (\begin {array}{cccc}A_{1}&A_{2}&A_{3}&A_{4}\\A_{2}^{T}&I_{2p} & {A_{4}^{T}} & \sigma (v) \end {array}\right )$ where A₁ = circ(α₁, α₂), A₂ = CIRC(B₁, B₂), A₃ = circ(α₁, α₂), A₄ = CIRC(B₃, B₄), B₁ = (α₃,…, α₃) ∈ R^p, B₂ = (α₄,…, α₄) ∈ R^p, B₃ = (α₇,…, α₇) ∈ R^p and B₄ = (α₈,…, α₈) ∈ R^p. Then

$$ \begin{array}{ll} M(\sigma) M(\sigma)^{T} &=\left( \begin{array}{cc} A_{1}{A_{1}^{T}}+A_{2} {A_{2}^{T}}+A_{3}{A_{3}^{T}}+A_{4}{A_{4}^{T}} & A_{1}A_{2}+A_{2}+A_{3}A_{4}+A_{4}\sigma(v)^{T}\\ {A_{2}^{T}} {A_{1}^{T}}+{A_{2}^{T}}+{A_{4}^{T}}{A_{3}^{T}}+\sigma(v){A_{4}^{T}} & {A_{2}^{T}}A_{2}+I_{2p}+{A_{4}^{T}}A_{4}+\sigma(v)\sigma(v)^{T} \end{array}\right). \end{array} $$

Now,

$$ A_{1}{A_{1}^{T}}+A_{2} {A_{2}^{T}}+A_{3}{A_{3}^{T}}+A_{4}{A_{4}^{T}}=\text{circ}\left( {\sum}_{i=1}^{2}({\alpha_{i}^{2}}+p\alpha_{i+2}^{2}+\alpha_{i+4}^{2}+p\alpha_{i+6}^{2}),0 \right)=\text{circ}\left( {\sum}_{i=1}^{8}{\alpha_{i}^{2}},0 \right) $$

and

$$ \begin{array}{ll} {A_{2}^{T}}A_{2}+I_{2p}+{A_{4}^{T}}A_{4}+\sigma(v)\sigma(v)^{T}&=\sum\limits_{i=1}^{2}(\alpha_{i+2}^{2} +\alpha_{i+6}^{2})\text{CIRC}(\mathbf{A},\mathbf{0}) +I_{2p}+\sigma(vv^{*}) \end{array} $$

where $\mathbf {A}= \text {circ}(\underbrace {1,\ldots ,1}_{p-\text {times}})$ and $\mathbf {0}= \text {circ}(\underbrace {0,\ldots ,0}_{p-\text {times}})$. It follows from Lemma 3.1 that

$$ \sigma(v){A_{4}^{T}}= \left( \begin{array}{cc} M_{1} & M_{2} \\ M^{\prime}_{2} & M^{\prime}_{1} \end{array} \right) \left( \begin{array}{cc} \alpha_{7} & \alpha_{8} \\ {\vdots} & {\vdots} \\ \alpha_{7} & \alpha_{8} \\ \alpha_{8} & \alpha_{7} \\ {\vdots} & {\vdots} \\ \alpha_{8} & \alpha_{7} \end{array} \right)= \left( \begin{array}{cc} \mu_{1}\alpha_{7}+\mu_{2}\alpha_{8} & \mu_{1}\alpha_{8}+\mu_{2}\alpha_{7} \\ {\vdots} & {\vdots} \\ \mu_{1}\alpha_{7}+\mu_{2}\alpha_{8} & \mu_{1}\alpha_{8}+\mu_{2}\alpha_{7} \\ \mu_{1}\alpha_{8}+\mu_{2}\alpha_{7} & \mu_{1}\alpha_{7}+\mu_{2}\alpha_{8} \\ {\vdots} & {\vdots} \\ \mu_{1}\alpha_{8}+\mu_{2}\alpha_{7} & \mu_{1}\alpha_{7}+\mu_{2}\alpha_{8} \end{array} \right)=\text{CIRC}((\mu_{1}\alpha_{7}+\mu_{2}\alpha_{8})c, (\mu_{1}\alpha_{8}+\mu_{2}\alpha_{7})c) $$

where $c=\begin {pmatrix}1\\\vdots \\1\end {pmatrix}$. Additionally,

$$ \begin{array}{ll} {A_{2}^{T}} {A_{1}^{T}}+{A_{2}^{T}}+{A_{4}^{T}}{A_{3}^{T}}+\sigma(v){A_{4}^{T}}=& \text{CIRC}((\alpha_{1}\alpha_{3}+\alpha_{2}\alpha_{4})c, (\alpha_{1}\alpha_{4}+\alpha_{2}\alpha_{3})c)+\text{CIRC}(\alpha_{3}c, \alpha_{4}c)\\& +\text{CIRC}((\alpha_{5}\alpha_{7}+\alpha_{6}\alpha_{8})c, (\alpha_{5}\alpha_{8}+\alpha_{6}\alpha_{7})c)\\& +\text{CIRC}((\mu_{1}\alpha_{7}+\mu_{2}\alpha_{8})c, (\mu_{1}\alpha_{8}+\mu_{2}\alpha_{7})c)\\& \end{array} $$

$$ \begin{array}{ll} =\text{CIRC}(&((\alpha_{1}+1)\alpha_{3}+\alpha_{2}\alpha_{4}+(\alpha_{5}+\mu_{1})\alpha_{7}+(\alpha_{6}+\mu_{2})\alpha_{8})c,((\alpha_{1}+1)\alpha_{4}+\alpha_{2}\alpha_{3}+(\alpha_{5}+\mu_{1})\alpha_{8}+(\alpha_{6}+\mu_{2})\alpha_{7})c)\\& . \end{array} $$

Clearly, M(σ)M(σ)^T is a symmetric matrix and C_σ is self orthogonal if ${\sum }_{i=1}^{8} {\alpha _{i}^{2}}=0$, $vv^{*} = 1+{\sum }_{i=1}^{2}(\alpha _{i+2}^{2} +\alpha _{i+6}^{2})\widehat {g}$,

$$ \begin{array}{ll} (\alpha_{1}+1)\alpha_{3}+\alpha_{2}\alpha_{4}+(\alpha_{5}+\mu_{1})\alpha_{7}+(\alpha_{6}+\mu_{2})\alpha_{8}= &0 \text{and}\\ (\alpha_{1}+1)\alpha_{4}+\alpha_{2}\alpha_{3}+(\alpha_{5}+\mu_{1})\alpha_{8}+(\alpha_{6}+\mu_{2})\alpha_{7}= &0. \end{array} $$

Moreover,

where γ₁ = α₇ + μ₁α₃ + μ₂α₄ and γ₂ = α₈ + μ₁α₄ + μ₂α₃. Therefore M(σ) has free rank 2p + 2 if and only if:

$$ \left( \begin{array}{cccccccccccc} \alpha_{1}+{\alpha_{3}^{2}}+{\alpha_{4}^{2}}\!\!&\alpha_{2}&\alpha_{5}+\alpha_{3}\alpha_{7}+\alpha_{4}\alpha_{8}&\alpha_{6}+\alpha_{3}\alpha_{8}+\alpha_{4}\alpha_{7}&\alpha_{7}+\mu_{1}\alpha_{3}+\mu_{2}\alpha_{4}&\alpha_{8}+\mu_{1}\alpha_{4}+\mu_{2}\alpha_{3}\\ \alpha_{2}&\!\!\alpha_{1}+{\alpha_{3}^{2}}+{\alpha_{4}^{2}}&\alpha_{6}+\alpha_{3}\alpha_{8}+\alpha_{4}\alpha_{7}&\alpha_{5}+\alpha_{3}\alpha_{7}+\alpha_{4}\alpha_{8}&\alpha_{8}+\mu_{1}\alpha_{4}+\mu_{2}\alpha_{3}&\alpha_{7}+\mu_{1}\alpha_{3}+\mu_{2}\alpha_{4} \end{array} \right) $$

has free rank 2. □

The next two results provide conditions when units/non units in RG can be used to be used to yield self-dual codes using the above construction.

Corollary 3.3

Let Rbe a finite commutative Frobenius ring of characteristic 2, let Gbe a finite group of order 2pwhere pis odd, and let C_σbe a self-dual code. If${\sum }_{i=1}^{2}(\alpha _{i+2} +\alpha _{i+6})=0$then v ∈ RGis a unit.

Proof

If ${\sum }_{i=1}^{2}(\alpha _{i+2} +\alpha _{i+6})=0$, then σ(vv^∗) = I_2p and vv^∗ = 1. Therefore v is unitary. □

Corollary 3.4

Let Rbe a finite commutative Frobenius ring of characteristic 2, let Gbe a finite group of order 2pwhere pis odd, and let C_σbe a self-dual code. If${\sum }_{i=1}^{2}(\alpha _{i+2} +\alpha _{i+6})=1$then v ∈ RGis a non-unit.

Proof

If ${\sum }_{i=1}^{2}(\alpha _{i+2} +\alpha _{i+6})=1$, then

$$ {\sum}_{i=1}^{2}(\alpha_{i+2}^{2} +\alpha_{i+6}^{2})\text{CIRC}(\mathbf{A},\mathbf{0}) +I_{2p}+\sigma(vv^{*})=\text{CIRC}(\mathbf{A},\mathbf{0})+\sigma(vv^{*})=0 $$

where $\mathbf {A}= \text {circ}(0,\underbrace {1,\ldots ,1}_{(p-1)-\text {times}})$ and $\mathbf {0}= \text {circ}(\underbrace {0,\ldots ,0}_{p-\text {times}})$. Now det(CIRC(A, 0)) = det(A)² and

$$ det(A)=det\left( \begin{array}{ccccc} 0 & 1 & 1 & {\dots} & 1 \\ 1 & 0 & 1 & {\cdots} & 1 \\ 1 & 1 & 0 & {\cdots} & 1 \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 1 & 1 & 1 & {\dots} & 0 \end{array}\right)=(p-1)det\left( \begin{array}{ccccc} 1 & 1 & 1 & {\dots} & 1 \\ 0 & 1 & 0 & {\cdots} & 0 \\ 0 & 0 & 1 & {\cdots} & 0 \\ {\vdots} & {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 0 & 0 & 0 & {\dots} & 1 \end{array}\right)=0. $$

Therefore, det(σ(vv^∗)) = 0 and vv^∗ is a non-unit by Corollary 3 in [22]. Hence, v ∈ RG is a non-unit. □

4 Computational results

Now, we will construct self-dual codes of various lengths (64, 68, 80) using groups of order 6, 14, 18, 30 and 38.

4.1 Constructions coming from D₆

In this section, we implement the above construction using G = D₆. We construct self-dual codes of length 64 by considering this construction over $\mathbb {F}_{4}+u\mathbb {F}_{4}$. Using this construction, we were able to construct one new code of length 64.

The possible weight enumerators for a self-dual Type I $\left [ 64,32,12 \right ]$-code is given in [4, 11] as:

$$ \begin{array}{@{}rcl@{}} W_{64,1} &=&1+\left( 1312 + 16\beta \right) y^{12}+\left( 22016-64\beta \right) y^{14}+{\cdots} ,14\leq \beta \leq 284, \\ W_{64,2} &=&1+\left( 1312 + 16\beta \right) y^{12}+\left( 23040-64\beta \right) y^{14}+{\cdots} ,0\leq \beta \leq 277. \end{array} $$

With the most updated information, the existence of codes is known for β = 14, 18, 22, 25, 29, 32, 35, 36, 39, 44, 46, 53, 59, 60, 64 and 74 in W_64,1 and for β = 0, 1, 2, 4, 5, 6, 8, 9, 10, 12, 13, 14, 16,…, 25, 28, 19, 30, 32, 33, 34, 36, 37, 38, 40, 41, 42, 44, 45, 48, 50, 51, 52, 56, 58, 64, 72, 80, 88, 96, 104, 108, 112, 114, 118, 120 and 184 in W_64,2.The new code that we have constructed is β = 57 in W_64,2.

4.2 Constructions coming from groups of order 14

Here we present the results for the above construction using G ∈{D₁₄, C₁₄}. We construct self-dual codes of length 64 by considering this construction over $\mathbb {F}_{2}+u\mathbb {F}_{2}$.

4.3 Constructions coming from a groups of order 18

Now, we implement the above construction using G ∈{D₁₈, C₁₈}. We construct self-dual codes of length 80 by considering this construction over $\mathbb {F}_{2}+u\mathbb {F}_{2}$. In [32], the possible weight enumerators for a self-dual Type I $\left [80,40,14\right ]$-code is given in as:

$$ W_{80,2} =1+\left( 3200+4 \alpha \right) y^{14}+\left( 47645-8 \alpha+256 \beta \right) y^{16}+{\cdots} , $$

where α and β are integers. A [80,40,14] was constructed in [6], however its weight enumerator was not stated. A [80,40,14] code was constructed in [21] with α = − 280, β = 10 and [80,40,14] codes were constructed for β = 0 and α = − 17k where k ∈{2,…,25,27} in [32]. None of the codes presented here have been previously constructed.

4.4 Constructions coming from D₃₈

In this section, we implement the construction on G = D₃₈. We construct self-dual codes of length 80 by considering this construction over $\mathbb {F}_{2}$.

5 New codes of length 68

In this section, we implement Theorem 2.1 to construct new extremal self-dual codes. We extend the codes previously constructed in Tables 1, 2 and 3.

Table 1 Self-dual code of length 64 from D₆ over $\mathbb {F}_{4}+u\mathbb {F}_{4}$

Table 2 Self-dual codes of length 64 from D₁₄ over $\mathbb {F}_{2}+u\mathbb {F}_{2}$

Table 3 Self-dual codes of length 64 from $C_{14}^{\prime }$ over R₁

Table 4 Self-dual codes of length 80 from D₁₈ over $\mathbb {F}_{2}+u\mathbb {F}_{2}$ where (α₁,…, α₈) = (u,1, u, u,0,0, u,1)

The known weight enumerators of a self-dual [68,34,12]_I-code are as follows:

$$ \begin{array}{@{}rcl@{}} W_{68,1}&=&1+(442+4\beta)y^{12}+(10864-8\beta)y^{14}+ {\dots} \\ W_{68,2}&=&1+(442+4\beta)y^{12}+(14960-8\beta-256\gamma)y^{14} +\dots \end{array} $$

where 0 ≤ γ ≤ 9. Codes have been obtained for W_68,2 when

$$ \begin{array}{@{}rcl@{}} \gamma &=&2,\ \beta \in \left\{ 2m\left\vert m=29,\ldots ,100,103,104\right. \right\} \text{ or }\beta \in \left\{ 2m+1\left\vert m=32,34,{\ldots} ,79\right. \right\} ;\\ \gamma &=&3,\ \beta \in \left\{ 2m\left\vert m=40,{\ldots} ,98,101,102\right. \right\} \text{ or} \\ \beta &\in &\left\{ 2m+1|m=41,43,{\ldots} ,77,79,80,83,96\right\} ; \\ \gamma &=&4\text{, }\beta \in \left\{ 2m\left\vert m=43,44,48,\ldots ,92,97,98\right. \right\} \text{ or } \\ \beta &\in &\left\{ 2m+1\left\vert m=48,{\ldots} ,55,58,60,\ldots ,78,80,83,84,85\right. \right\} ;\text{ } \\ \gamma &=&5\text{ with }\beta \in \left\{ m|m=113,116,{\ldots} ,181\right\}; \end{array} $$

Recall that the codes constructed in Tables 1, 2 and 3 are codes over $\mathbb {F}_{4}+u\mathbb {F}_{4}$. Consequently, we converted these codes to codes over $\mathbb {F}_{2}+u\mathbb {F}_{2}$ (using the Gray map $\psi _{{\mathbb {F}}_{4}+u{\mathbb {F}}_{4}}$) before applying Theorem 2.1. The following table displays the newly constructed extremal codes of length 68. We replace u + 1 with 3 to save space (Tables 4 and 5).

Table 5 Self-dual codes of length 80 from D₃₈ over $\mathbb {F}_{2}$ where (α₁,…, α₈) = (0,1,0,0,1,1,0,1)

Two self-dual binary codes of dimension k are said to be neighbors if their intersection has dimension k − 1. We consider the standard form of the generator matrix of C to reduce down the search field. Let $x\in {\mathbb {F}}_{2}^{n}-C$ then $D=\left \langle \left \langle x\right \rangle ^{\bot }\cap C,x\right \rangle$ is a neighbor of C (Table 6). Without loss of generality, the first 34 entries of x are set to be 0, the rest of the vectors are listed in Table 7. As neighbors of codes in Table 5 we obtain 12 new codes with weight enumerators in W_68,2. All the codes have an automorphism group of order 2.

Table 6 Self-dual codes of length 68 from extending [64,32,12]_I

Table 7 New codes of length 68 as neighbors of $\mathcal {C}_{68,6}$

6 Conclusion

In this work, we have introduced a new construction for constructing self-dual codes using group rings. We provided certain conditions when this construction produces self-dual codes and we established a link between units/non-units and self-dual codes. We demonstrated the relevance of this new construction by constructing many binary self-dual codes, including new self-dual codes of length 64, 68 and 80.

• Code of length 64: We were to able to construct the following [64,32,12] codes with new weight enumerator in W_64,2:

  $$ \beta=\{57\}. $$

• Codes of length 68: We were able to construct the following extremal binary self-dual codes with new weight enumerators in W_68,2:

  $$ \begin{array}{ll} (\gamma=2, &\quad \beta=\{161,163,169,171,173\}),\\ (\gamma=3, &\quad \beta=\{163,175,177\}),\\ (\gamma=4, &\quad \beta=\{159,175,186,191,200\}),\\ (\gamma=5, &\quad \beta=\{182,187,189,191,193\}), \end{array} $$

• Codes of length 80: We were to able to construct the following [80,40,14] codes with new weight enumerators in W_80,2:

  $$ \begin{array}{ll} (\beta=18, &\quad \alpha=\{-211,-229,-249,-256,-274,-287,-306,-310,-325,-355,-363,-401\}). \end{array} $$