Abstract
We establish the rectifiability of measures satisfying a linear PDE constraint. The obtained rectifiability dimensions are optimal for many usual PDE operators, including all first-order systems and all second-order scalar operators. In particular, our general theorem provides a new proof of the rectifiability results for functions of bounded variations (BV) and functions of bounded deformation (BD). For divergence-free tensors we obtain refinements and new proofs of several known results on the rectifiability of varifolds and defect measures.
Similar content being viewed by others
1 Introduction
Let \(\mathcal {A}\) be a \(k{\text {th}}\)-order linear constant-coefficient PDE operator acting on \({\mathbb {R}}^m\)-valued functions on \(\mathbb {R}^d\) via
where \(A_{\alpha }\in {\mathbb {R}}^{n}\otimes \mathbb {R}^m \) (\(\cong \mathbb {R}^{n \times m}\)) are (constant) matrices, \(\alpha =(\alpha _1,\dots ,\alpha _d)\in ({\mathbb {N}} \cup \{0\})^d\) is a multi-index and \(\partial ^\alpha :=\partial _1^{\alpha _1}\ldots \partial _d^{\alpha _d}\). We also assume that at least one \(A_\alpha \) with \(|\alpha | = k\) is non-zero.
An \(\mathbb {R}^m\)-valued Radon measure \(\mu \in {\mathcal {M}}(U;\mathbb {R}^m)\) defined on an open set \(U\subset \mathbb {R}^d \) is said to be \(\mathcal {A}\)-free if
The Lebesgue–Radon–Nikodým theorem implies that
where \(g\in \mathrm {L}^1(U;\mathbb {R}^m)\), \(|\mu |^s\) is the singular part of the total variation measure \(|\mu |\) with respect to the d-dimensional Lebesgue measure \(\mathcal {L}^d\), and
is the polar of \(\mu \), which exists and belongs to \({\mathbb {S}}^{m-1}\) for \(|\mu |\)-almost every \(x \in U\).
In [DR16] it was shown that for any \(\mathcal {A}\)-free measure there is a strong constraint on the directions of the polar at singular points:
Theorem 1.1
([DR16, Theorem 1.1]). Let \(U\subset \mathbb {R}^d\) be an open set, let \(\mathcal {A}\) be a \(k{\text {th}}\)-order linear constant-coefficient differential operator as above, and let \(\mu \in {\mathcal {M}}(U;\mathbb {R}^m)\) be an \(\mathcal {A}\)-free Radon measure on U with values in \(\mathbb {R}^m\). Then,
where \(\Lambda _\mathcal {A}\) is the wave cone associated to \(\mathcal {A}\), namely
It has been shown in [DR16], see also [D16, DR18] for recent surveys and [Rin18, Chapter 10] for further explanation, that by suitably choosing the operator \(\mathcal {A}\), the study of the singular part of \(\mathcal {A}\)-free measures has several consequences in the calculus of variations and in geometric measure theory. In particular, we recall the following:
-
If \(\mathcal {A}=\mathrm{curl}\), the above theorem gives a new proof of Alberti’s rank-one theorem [Alb93] (see also [MV16] for a different proof based on a geometrical argument).
-
If \(\mathcal {A}={{\,\mathrm{div}\,}}\), combining Theorem 1.1 with the result of [AM16], one obtains the weak converse of Rademacher’s theorem (see [DMR17, GP16, KM18] for other consequences in metric geometry).
The main results of this paper is to show how Theorem 1.1 can be improved by further constraining the direction of the polars on “lower dimensional parts” of the measure \(\mu \) and to establish some consequences of this fact concerning dimensional estimates and rectifiability of \(\mathcal {A}\)-free measures. To this end let us define a hierarchy of wave cones as follows:
Definition 1.2
(\(\ell \)-wave cone) Let \(\mathrm {Gr}(\ell ,d)\) be the Grassmannian of \(\ell \)-planes in \(\mathbb {R}^d\). For \(\ell =1,\ldots ,d\) we define the \(\ell \)-dimensional wave cone as
where \(\mathbb {A}^k(\xi )\) is defined as in (1.2).
Equivalently, \(\Lambda ^\ell _{\mathcal {A}}\) can be defined by the following analytical property:

where  is the partial differential operator
is the partial differential operator

with \(\varvec{p}_{\pi }\) the orthogonal projection onto \(\pi \).
Note that, by the very definition of \(\Lambda ^{\ell }_\mathcal {A}\), we have the following inclusions:
To state our main theorem, we also recall the definition of the integral-geometric measure, see [Mat95, Section 5.14]: Let \(\ell \in \{0,\ldots ,d\}\). For a Borel set \(E\subset \mathbb {R}^d\), the \(\ell \)-dimensional integral-geometric (outer) measure is
where \(\gamma _{\ell ,d}\) is the unique \(\mathrm {O}(d)\)-invariant probability measure on \(\mathrm {Gr}(\ell ,d)\) and \(\mathcal {H}^\ell \) is the \(\ell \)-dimensional Hausdorff measure (normalized as in [Mat95] such that \(\mathcal {H}^\ell (B^\ell _1) = 2^\ell \), where \(B^\ell _1\) is the \(\ell \)-dimensional unit ball).
Our main result establishes that the polar of an \(\mathcal {A}\)-free measure is constrained to lie in a smaller cone on \(\mathcal {I}^\ell \)-null sets:
Theorem 1.3
Let \(U \subset \mathbb {R}^d\) be open, let \(\mathcal {A}\) be as in (1.1), and let \(\mu \in \mathcal {M}(U;\mathbb {R}^m)\) be an \(\mathcal {A}\)-free measure on U. If \(E \subset U\) is a Borel set with \({\mathcal {I}}^{\ell }(E) = 0\) for some \(\ell \in \{0,\ldots ,d\}\), then
Note that, by taking \(\ell =d\), Theorem 1.3 recovers Theorem 1.1. As a corollary we obtain the following dimensional estimates on \(\mathcal {A}\)-free measures; see also [Arr18] for a different proof of (1.4) in the case of first-order systems.
Corollary 1.4
(Dimensional estimate). Let \(\mathcal {A}\) and \(\mu \) be as in Theorem 1.3 and assume that \(\Lambda ^\ell _{\mathcal {A}}=\{0\}\) for some \(\ell \in \{0,\ldots ,d\}\). Then,
In particular,
and thus
where
The results above and (1.3) entail that the smaller the dimension of an \(\mathcal {A}\)-free measure \(\mu \) is, the more its polar is constrained at singular points. Let us also remark that the 1-dimensional wave cone \(\Lambda ^{1}_{\mathcal {A}}\) has been implicitly introduced by van Schaftigen in [Van13]. There, the author calls a (homogeneous) oparator \(\mathcal {A}\)cocanceling provided that \(\Lambda _\mathcal {A}^1 = \{0\}\). Moreover, it is shown that the cocanceling condition is equivalent to the property
Thus, the conclusion of Theorem 1.3 improves upon the dimensional estimates for \(\mathcal {A}\)-free measures with \(\mathcal {A}\) cocanceling.
The use of the integral-geometric measure, besides being natural in the proof, allows one to use the Besicovitch–Federer rectifiability criterion to deduce the following rectifiability result. Recall that for a positive measure \(\sigma \in {\mathcal {M}}_{+}(U)\) the upper\(\ell \)-dimensional density is defined as
Theorem 1.5
(Rectifiability). Let \(\mathcal {A}\) and \(\mu \) be as in Theorem 1.3, and assume that \(\Lambda ^{\ell }_{\mathcal {A}}=\{0\}\). Then, the set \(\{\theta ^*_\ell (|\mu |) = +\infty \}\) is \(|\mu |\)-negligible. Moreover,  is concentrated on an \(\ell \)-rectifiable set R and
is concentrated on an \(\ell \)-rectifiable set R and

where \(\lambda :R \rightarrow {\mathbb {S}}^{m-1}\) is \(\mathcal {H}^\ell \)-measurable; for \(\mathcal {H}^\ell \)-almost every \(x_0\in R\) (or, equivalently, for \(|\mu |\)-almost every \(x_0\in R\)),

and
Here \(T^{x_0,r}(x):=(x-x_0)/r\) and \(T_{x_0} R\) is the the approximate tangent plane to R at \(x_0\).
Theorem 1.5 contains the classical rectfiability result for the jump part of the gradient of a \(\mathrm{BV}\) function, see [AFP00], and the analogous result for \(\text {BD}\), see [Koh79, ACD97]. By choosing \(\mathcal {A}={{\,\mathrm{div}\,}}\) we also recover and (in some cases slightly generalize) several known rectifiability criteria, such as Allard’s rectifiability theorem for varifolds [All72], its recent extensions to anisotropic energies [DDG18], the rectifiability of generalized varifolds established in [AS97], and the rectifiability of various defect measures in the spirit of [Lin99], see also [Mos03]. We refer the reader to Sect. 3 for some of these statements.
It is worth noting that, with the exception of the \(\text {BD}\)-rectifiability result in [ACD97, Proposition 3.5], none of the above rectifiability criteria rely on the Besicovitch–Federer theorem and their proofs are based on more standard blow-up techniques. However, in the generality of Theorem 1.5 a blow-up proof seems hard to obtain. Indeed, roughly, a blow-up argument follows two steps:
-
By some measure-theoretic arguments one shows that, up to a subsequence,
$$\begin{aligned} r^{-\ell } T^{x_0,r}\mu \overset{*}{\rightharpoonup }\lambda \sigma \end{aligned}$$for some positive measure \(\sigma \) and some fixed vector \(\lambda \).
-
One exploits this information together with the \(\mathcal {A}^k\)-freeness of \(\lambda \sigma \), where \(\mathcal {A}^k\) is the principal part of \(\mathcal {A}\), to deduce that \(\sigma \) is translation-invariant along the directions in an \(\ell \)-dimensional plane \(\pi \) and thus
 . In this step one usually uses that \(\pi \) is uniquely determined by \(\lambda \) and \(\mathcal {A}\).
. In this step one usually uses that \(\pi \) is uniquely determined by \(\lambda \) and \(\mathcal {A}\).
However, assuming that  , the only information one can get is
, the only information one can get is
see Lemma 2.3, and this does not uniquely determine \(\pi \) in general.
Let us now briefly discuss the optimality of our results. First note that (1.6) and (1.7) are true whenever an \(\mathcal {A}\)-free measure \(\mu \) has a non-trivial part concentrated on an \(\ell \)-rectifiable set R, see Lemma 2.3 below.
In particular, defining for \(\ell = 0,\ldots ,d-1\) the cone
we have that
and
Hence, setting
the above discussion yields that if \(\mu \) has a non-trivial \(\ell \)-rectifiable part, then necessarily
and this bound is sharp for homogeneous operators since if \(\lambda \in \bigcap _{\xi \in \pi ^\perp } \ker \mathbb {A}^k(\xi )\setminus \{0\}\) for some \(\ell \)-plane \(\pi \), then  is an \(\mathcal {A}^k\)-free measure.
is an \(\mathcal {A}^k\)-free measure.
Recalling the definition of \(\ell _\mathcal {A}\) in (1.5), this discussion together with Corollary 1.4 and (1.8) can then be summarized for homogeneous operators \(\mathcal {A}\) as
For first-order operators it is not hard to check that \(\ell _\mathcal {A}=\ell _\mathcal {A}^*\) (by the linearity of \(\xi \mapsto \mathbb {A}^k(\xi )\)). The same is true for second-order scalar operators (\(n=1\)) by reducing the polynomial to canonical form (which makes \(\mathbb {A}^k(\xi )\) linear in \(\xi _1^2,\ldots ,\xi _d^2\)). Hence, the above inequality for such homogeneous operators becomes an equality and our theorem is sharp.
On the other hand, it is easy to build examples where \(\ell _\mathcal {A}<\ell _\mathcal {A}^*\). For instance, one can easily check that for the \(3\text {{rd}}\)-order scalar operator defined on \(\mathrm {C}^{\infty }(\mathbb {R}^{3})\) by
we have \(\ell _\mathcal {A}= 1 < 2 = \ell ^{*}_\mathcal {A}\) since its characteristic set \(\{\, \xi \in \mathbb {R}^3 \ \ \mathbf : \ \ \xi _1^3 + \xi _2^3 + \xi _3^3=0 \,\}\) is a ruled surface (and hence it contains lines) but it does not contain planes. Moreover, let \({\widetilde{\mathcal {A}}}\) be the \(6^\text {{th}}\)-order operator acting on maps from \(\mathbb {R}^3\) to \(\mathbb {R}^2\) with symbol
For this operator we still have \(\ell _{{\widetilde{\mathcal {A}}}} = 1 < 2 = \ell ^{*}_{{\widetilde{\mathcal {A}}}}\), but \({\widetilde{A}}\) additionally satisfies Murat’s constant rank condition [Mur81].
Let us remark that in the case \(\ell _\mathcal {A}<\ell _\mathcal {A}^*\), Theorem 1.5 implies that if \(\mu \) is an \(\mathcal {A}\)-free measure, then
Hence \(\mu \) is “more diffuse” than an \(\ell _\mathcal {A}\)-dimensional measure. Furthermore, \(\mu \) cannot sit on rectifiable sets of any (integer) dimension \(\ell \in [\ell _\mathcal {A},\ell _\mathcal {A}^*)\). It seems thus reasonable to expect that its dimension should be larger than \(\ell _\mathcal {A}\). In particular, one might conjecture the following improvement of Corollary 1.4:
Conjecture 1.6
Let \(\mu \) be \(\mathcal {A}\)-free and let \(\ell _\mathcal {A}^*\) be the rectifiability dimension defined in (1.8). Then,
We note that the same conjecture has also been advanced by Raita in [Rai18, Question 5.11]; also see [AW17, Conjecture 1.5].
Further, if one extends van Schaftigen’s terminology [Van13] by saying that \(\mathcal {A}\) is “\(\ell \)-cocanceling” provided that \(\mathcal {N}^{\ell -1}_\mathcal {A}= \{0\}\) (classical cocanceling then being 1-cocanceling while ellipticity is d-cocancelling), the above conjecture reads as
Recently, a related (dual) notion of “\(\ell \)-canceling” operators has been introduced in [SV18].
We conclude this introduction by remarking that the above results can be used to provide dimensional estimates and rectifiability results for measures whose decomposability bundle, defined in [AM16], has dimension at least \(\ell \). Namely, in this case the measure is absolutely continuous with respect to \(\mathcal {I}^{\ell }\) and the set where the upper \(\ell \)-dimensional density is positive, is rectifiable, compare with [Bat17, Theorem 2.19] and with [AMS]. However, since by its very definition the dimension of the decomposability bundle is stable under projections, in this setting one can directly rely on [DR16, Corollary 1.12]. This is essentially the strategy followed in the cited references.
2 Proofs
The proof of Theorem 1.3 is a combination of ideas from [DR16] and [DDG18]. We start with the following lemma.
Lemma 2.1
Let \(\mathcal {B}\) be a homogeneous \(k\text {{th}}\)-order linear constant-coefficient operator on \(\mathbb {R}^\ell \),
Let \(\{\nu _j\}\subset \mathcal {M}(B_1^\ell ;\mathbb {R}^m)\), where \(B_1^\ell \subset \mathbb {R}^\ell \) is the unit ball in \(\mathbb {R}^\ell \), be a uniformly norm-bounded sequence of Radon measures satisfying the following assumptions:
-
(a1)
\(\mathcal {B}\lambda \) is elliptic for some \(\lambda \in \mathbb {R}^m\), that is,
$$\begin{aligned} \lambda \notin \ker \mathbb {B}(\xi ) \quad \text {for all }\xi \in \mathbb {R}^\ell \setminus \{0\}, \end{aligned}$$where \(\mathbb {B}(\xi ):=\sum _{|\beta |=k} A_{\beta } \xi ^\beta \in \mathbb {R}^n \otimes \mathbb {R}^m\);
-
(a2)
\(\{({{\,\mathrm{\mathrm {Id}}\,}}-\Delta )^{-\frac{s}{2}}\mathcal {B}\nu _j\}_j\) is pre-compact in \(\mathrm {L}^1(B_1^\ell ;\mathbb {R}^n)\) for some \(s<k\);
-
(a3)
\(\displaystyle \lim _{j\rightarrow \infty } \int _{B^\ell _1} \biggl | \frac{\mathrm{d}\nu _j}{\mathrm{d}|\nu _j|} - \lambda \biggr | \;\mathrm {d}|\nu _j|= 0\).
Then, up to taking a subsequence, there exists \(\theta \in \mathrm {L}^1(B^\ell _1)\) such that
Proof
The proof is a straightforward modification of the main step of the proof of [DR16, Theorem 1.1], see also [All86] and [Rin18, Chapter 10]. We give it here in terse form for the sake of completeness.
Passing to a subsequence we may assume that \(|\nu _j| \overset{*}{\rightharpoonup } \sigma \) in \( \mathrm {C}^\infty _c(B_1^\ell )^*\) for some positive measure \(\sigma \in \mathcal {M}^+(B_1^\ell )\). We must show that \(\sigma = \theta \mathcal {L}^d\) and that (2.1) holds. Fix \(t<1\) and two smooth cut-off functions \(0 \le \chi \le \tilde{\chi } \le 1\) with \(\chi =1\) on \(B_t\), \(\tilde{\chi }=1\) on \({{\,\mathrm{spt}\,}}(\chi )\), and \({{\,\mathrm{spt}\,}}(\chi )\subset {{\,\mathrm{spt}\,}}(\tilde{\chi }) \subset B_1\). Let \((\varphi _{\varepsilon })_{\varepsilon > 0}\) be a family of smooth approximations of the identity. Choose \(\epsilon _j \downarrow 0\) with \(0< \epsilon _j < 1-t\) for all j, such that
We will show that the sequence
is pre-compact in \(\mathrm {L}^1(B_1)\), which proves the lemma.
For every j we set \(f_j := \mathcal {B}\nu _j\) and compute
Note that the commutator \([\mathcal {B},\chi ] := \mathcal {B} \circ \chi - \chi \circ \mathcal {B}\) is a differential operator of order at most \(k-1\) with smooth coefficients. Taking the Fourier transform (which we denote by \(\mathcal {F}\) or by the hat “\(\widehat{\phantom {w}}\)”), multiplying by \([\mathbb {B}(\xi )\lambda ]^*\), and adding \({\widehat{u}}_j(\xi )\), we obtain
Hence,
with the pseudo-differential operators \(T_0,\ldots ,T_3\) defined as follows:
We see that, in the language of pseudo-differential operators (see for instance [Ste93, Chapter VI]):
-
(i)
the symbol for \(T_0\) is a Hörmander–Mihlin multiplier (i.e. a pseudo-differential operator with smooth symbol of order 0) since, due to (a1), \(|{\mathbb {B}}(\xi )\lambda | \ge c|\xi |^k\) for some \(c > 0\) and all \(\xi \in \mathbb {R}^\ell \);
-
(ii)
\(T_1\) is a pseudo-differential operator with smooth symbol of order \(-k\);
-
(iii)
\(T_2\) is a pseudo-differential operator with smooth symbol of order \(-1\);
-
(iv)
\(T_3\) is a pseudo-differential operator with smooth symbol of order \(-2k\).
By the classical theory of Fourier multipliers and pseudo-differential operators we then get the following:
-
(I)
\(T_0\) is bounded from \(\mathrm {L}^1\) to \(\mathrm {L}^{1, \infty }\) (weak-\(\mathrm {L}^1\)), see e.g. [Gra14, Theorem 6.2.7]. Owing to (a3), it follows that for \(j \rightarrow \infty \) we obtain
$$\begin{aligned} \int |V_j| \;\mathrm {d}x&\le \int \chi \, \varphi _{\epsilon _j}\!\star \!\left( \biggl | \frac{\mathrm {d}\nu _j}{\mathrm {d}|\nu _j|} - \lambda \biggr | \, |\nu _j|\right) \;\mathrm {d}x \\&\le \int _{B_1}\biggl | \frac{\mathrm {d}\nu _j}{\mathrm {d}|\nu _j|} - \lambda \biggr | \;\mathrm {d}|\nu _j| \\&\rightarrow 0. \end{aligned}$$Thus,
$$\begin{aligned} \sup _{t \ge 0} t \, \mathcal {L}^d(\{ |T_0[V_j]|>t\}) \le C \int |V_j| \;\mathrm {d}x \rightarrow 0 \qquad \text {as }j \rightarrow \infty . \end{aligned}$$That is, \(T_0[V_j] \rightarrow 0\) in measure.
-
(II)
Due to (a2), \(T_1[f_j]\) is pre-compact in \(\mathrm {L}^1\) (this follows directly by the symbolic calculus [Ste93, Section VI.3] or direct manipulation of Fourier multipliers).
-
(III)
\(T_2\) and \(T_3\) are compact operators from \(\mathrm {L}^1_c\) to \(\mathrm {L}^1_{\text {loc}}\) (see for instance [Ste93, Propositions VI.4, VI.5] in conjunction with Lemma 10.1 in [DR16] or Lemma 10.11 in [Rin18]) and thus the families \(\{T_2[W_j]\}\), \(\{T_3[u_j]\}\) are pre-compact in \(\mathrm {L}^1\).
Hence, passing to a subsequence, we may assume that \( T_1[f_j] + T_2[W_j] +T_3[u_j]\rightarrow \theta \) in \(\mathrm {L}^1_{\text {loc}}\) and \(T_0[V_j] \rightarrow 0\) in measure. Since furthermore \(u_j \ge 0\), we can apply Lemma 2.2 below and deduce that \(T_0[V_j] \rightarrow 0\) strongly in \(\mathrm {L}^1\). This concludes the proof. \(\square \)
The following is Lemma 2.2 in [DR16], we report here its straightforward proof for the sake of completeness.
Lemma 2.2
Let \(\{f_j\} \subset \mathrm {L}^1(B_1)\) be such that
-
(i)
\(f_j\overset{*}{\rightharpoonup }0\) in \( \mathrm {C}^\infty _c(B_1)^*\);
-
(ii)
the negative parts \(f_j^- := \max \{-f_j,0\}\) of the \(f_j\)’s converge to zero in measure, i.e.,
$$\begin{aligned} \lim _{j\rightarrow \infty }\, \bigl |\bigl \{\, x \in B_1 \ \ \mathbf : \ \ f_j^-(x)> \delta \,\bigr \}\bigr | = 0 \qquad \text {for every }\delta >0; \end{aligned}$$ -
(iii)
the family of negative parts \(\{f_j^{-}\}\) is equiintegrable.
Then, \(f_j \rightarrow 0\) in \(\mathrm {L}^1_\mathrm {loc}(B_1)\).
Proof
Let \(\varphi \in \mathrm {C}^\infty _c(B_1;[0,1])\). Then,
The first term on the right-hand side vanishes as \(j\rightarrow \infty \) by assumption (i). Vitali’s convergence theorem in conjunction with assumptions (ii) and (iii) further gives that the second term also tends to zero in the limit. \(\square \)
Proof of Theorem 1.3
Let E be such that \(\mathcal {I}^\ell (E)=0\) and let us define
By contradiction, let us suppose that \(|\mu |(F)>0\). Note that, by the very definition of F, for all \(x\in F\) there exists an \(\ell \)-dimensional plane \(\tilde{\pi }_x\subset \mathbb {R}^d\) such that it holds that
By continuity, the same is true for all planes \(\pi '\) in a neighbourhood of \(\tilde{\pi }_x\). In particular, since by assumption \({\mathcal {I}}^\ell (F)=0\), for every \(x\in E\) there is an \(\ell \)-dimensional plane \(\pi _{x}\) such that
Since we assume \(|\mu |(F)>0\), by standard measure-theoretic arguments (see the proof of [DR16, Theorem 1.1] for details), we can find a point \(x_0 \in F\), an \(\ell \)-dimensional plane \(\pi _0\), and a sequence of radii \(r_j \downarrow 0\) with the following properties:
-
(b1)
\(\lambda :=\dfrac{\mathrm{d}\mu }{\mathrm{d}|\mu |}(x_0)\) exists, belongs to \({\mathbb {S}}^{m-1}\), and satisfies
$$\begin{aligned} \mathbb {A}^k(\xi )\lambda \ne 0 \qquad \text {for all }\xi \in \pi _0\setminus \{0\}; \end{aligned}$$(2.3) -
(b2)
setting
 ,
, 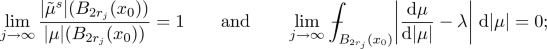
-
(b3)
for
$$\begin{aligned} \mu _j:=\frac{T^{x_0,r_j}_\#\mu }{|\mu |(B_{2r_j}(x_0))} \end{aligned}$$the following convergence holds:
$$\begin{aligned} |\mu _j|:=\frac{T^{x_0,r_j}_\#|\mu |}{|\mu |(B_{2r_j}(x_0))}\overset{*}{\rightharpoonup } \sigma \end{aligned}$$for some \(\sigma \in \mathcal {M}^+(B_2)\) with
 . Here, \(T^{x_0,r_j}(x):=\dfrac{x-x_0}{r_j}\).
. Here, \(T^{x_0,r_j}(x):=\dfrac{x-x_0}{r_j}\).
After a rotation we may assume that \(\pi _{0}=\mathbb {R}^\ell \times \{0\}\). We shall use the coordinates \((y,z) \in \mathbb {R}^\ell \times \mathbb {R}^{d-\ell }\) and we will denote by \(\varvec{p}\) the orthogonal projection onto \(\mathbb {R}^\ell \). Note that
where \(\mathcal {A}^k\) is the \(k\text {{th}}\)-order homogeneous part of \(\mathcal {A}\), i.e.,
and \(R_j\) contains all derivatives of \(\mu _j\) of order at most \(k-1\). Thus,
where \( \mathrm {W}_\mathrm{loc}^{-k,q}(\mathbb {R}^{d})\) is the local version of the dual of the Sobolev space \(\mathrm {W}^{k,q'}(\mathbb {R}^{d})\), \(q'=q/(q-1)\).
Define

Note that \(\mathcal {B}\) is a homogeneous constant-coefficient linear differential operator such that for any \(\psi \in \mathrm {C}^\infty (\mathbb {R}^\ell )\),
and, by (2.3),
Moreover, the measure
is concentrated on the the set \(F_j:=T^{x_0,r_j}(F)\), which by (2.2) satisfies
We consider the (localized) sequence of measures
where \(\chi (y,z)={\tilde{\chi }}(z)\) for some cut-off function \({\tilde{\chi }} \in \mathrm {C}^\infty _c (B_1^{d-\ell };[0,1])\) satisfying \(\chi \equiv 1\) on \(B^{d-\ell }_{1/2}\). Our goal is to apply Lemma 2.1 to the sequence \(\{\nu _j\}\subset \mathcal {M}(B_1^\ell ;\mathbb {R}^m)\), from where we will reach a contradiction. We must first check that \(\{\nu _j\}\) satisfies the assumptions of Lemma 2.1. Since
the sequence is equi-bounded. We further claim that (b2) implies that
Consequently, assumption (a3) in Lemma 2.1 is then satisfied for \(\{\nu _j\}\).
Concerning the assumption (a2), we argue as follows. Let \(\psi \in \mathrm {C}^\infty _c(B^\ell _1;\mathbb {R}^n)\). Then, for the adjoint
equation (2.5) gives
where \([(\mathcal {A}^k)^*,\chi ] = (\mathcal {A}^k)^* \circ \chi - \chi \circ (\mathcal {A}^k)^*\) is the commutator of \((\mathcal {A}^k)^*\) and \(\chi \), as well as \(C_\beta \in \mathrm {C}^\infty _c(B_1^{d-\ell }) \). Hence, in the sense of distributions,
Note that \(\chi R_j\) is compactly supported in the z-direction and thus the push-forward under \(\varvec{p}\) is well defined. Exactly as in the proof of [DR16, Theorem 1.1] we infer the following: since for each \(\beta \) we have \(\varvec{p}_\# (C_\beta \mu _j) \in \mathcal {M}(B_1^\ell ;\mathbb {R}^m)\) and \(|\beta |<k\), the family \(\{({{\,\mathrm{\mathrm {Id}}\,}}-\Delta )^{-\frac{s}{2}}\partial ^\beta \varvec{p}_\# (C_\beta \mu _j)\}_j\) is pre-compact in \(\mathrm {L}^1_\mathrm{loc}(\mathbb {R}^\ell )\) for every \(s\in (k-1,k)\), and by (2.4) the same holds for \(\{({{\,\mathrm{\mathrm {Id}}\,}}-\Delta )^{-\frac{s}{2}}\varvec{p}_\# (\chi R_j)\}_j\).
Thus, we can apply Lemma 2.1 to deduce (up to taking a subsequence) that
for some \(\theta \in \mathrm {L}^1(B^\ell _1)\). Consequently,
However, \(\sigma (B_{1/2}) = 0\) is a contradiction to (b3).
It remains to show the claim (2.7). By disintegration, see for instance [AFP00, Theorem 2.28], for every \(j\in \mathbb {N}\),
Here, each \(\nu _y^j\) is a probability measure supported in \(B_{1}^{d-\ell }\). Let
Then,
In particular, \(|g_j| \le 1\). Furthermore, since \(|\lambda |=1\),
Since \(|\nu _j|= |g_j| \kappa _j\), this proves the first part of (2.7). The second part follows from this estimate and (b2) because
This concludes the proof. \(\square \)
Before proving Theorem 1.5, let us start with the following elementary lemma:
Lemma 2.3
Let \(\mu \) be an \(\mathcal {A}\)-free measure and assume that there exists an \(\ell \)-rectifiable set R such that

Then,

where \(\lambda :R \rightarrow {\mathbb {S}}^{m-1}\) is \(\mathcal {H}^\ell \)-measurable. Moreover for \(\mathcal {H}^\ell \)-almost every \(x_0\in R\),

and
where \(T_{x_0} R\) is the the approximate tangent plane to R at \(x_0\).
Proof
By [Mat95, Theorem 6.9],
Hence, by (2.8), we can assume that \(R\subset \{\theta _{\ell }^*(|\mu |)<+\infty \}\). In particular, by [Mat95, Theorem 6.9] again,  is \(\sigma \)-finite and the Radon–Nikodým theorem implies
is \(\sigma \)-finite and the Radon–Nikodým theorem implies

with \(f\in \mathrm {L}^1(R,\mathcal {H}^\ell ;\mathbb {R}^m)\) such that \(|f|>0\) -almost everywhere. A standard blow-up argument then gives (2.9) and (2.10). Choosing a point such that the conclusion of (2.10) holds true and blowing up around that point, one deduces that the measure
-almost everywhere. A standard blow-up argument then gives (2.9) and (2.10). Choosing a point such that the conclusion of (2.10) holds true and blowing up around that point, one deduces that the measure

is \(\mathcal {A}^k\)-free, where \(\mathcal {A}^k\) is the k-homogeneous part of \(\mathcal {A}\). Since  is a tempered distribution, by taking the Fourier transform of the equation \(\mathcal {A}^k{\bar{\mu }}=0\), we obtain
is a tempered distribution, by taking the Fourier transform of the equation \(\mathcal {A}^k{\bar{\mu }}=0\), we obtain

which implies that \(\mathbb {A}^k(\xi ) \lambda (x_0)=0\) for all \(\xi \in (T_{x_0} R)^\perp \). This concludes the proof.
\(\square \)
Proof of Theorem 1.5
By classical measure theory, see [Mat95, Theorem 6.9],
Hence, the assumption \(\Lambda _{\mathcal {A}}^\ell =\{0\}\) and Corollary 1.4 together imply that
By [Mat95, Theorem 6.9], the set
is \(\mathcal {H}^\ell \)\(\sigma \)-finite and

According to [Mat95, Theorem 15.6] we may write
where R is \(\mathcal {H}^\ell \)-rectifiable, S is purely unrectifiable and \(\mathcal {H}^\ell (R\cap S)=0\). By the Besicovitch–Federer rectifiability theorem, see [Fed69, Section 3.3.13], [Mat95, Chapter 18] or [Whi98],
Hence, since \(\Lambda _{A}^\ell =\{0\}\), Corollary 1.4 implies that \(|\mu |(S)=0\). Therefore,

Owing to this and to (2.11) we can apply Lemma 2.3 and thus conclude the proof. \(\square \)
3 Applications
In this section we sketch applications of the abstract results to several common differential operators \(\mathcal {A}\). In this way we recover and improve several known results.
3.1 Rectifiability of \(\text {BV}\)-gradients.
Let \(\mu =Du\in {\mathcal {M}}(U;\mathbb {R}^p\otimes \mathbb {R}^d)\), where \(u\in \text {BV}(U; \mathbb {R}^p)\), \(U \subset \mathbb {R}^d\) open; see [AFP00] for details on this space of functions of bounded variation. Then \(\mu \) is \({{\,\mathrm{curl}\,}}\)-free. By a direct computation,
hence \(\Lambda ^{d-1}_{{{\,\mathrm{curl}\,}}}=\{0\}\) and Corollary 1.4 in conjunction with Theorem 1.5 implies the well-known fact that \(|Du|\ll \mathcal {H}^{d-1}\) and

for some \((d-1)\)-rectifiable set \(R \subset U\) and where \( n_R : R \rightarrow \mathbb {S}^{d-1}\) is a measurable map with the property that \( n_R(x)\) is orthogonal to \(T_xR\) at \(\mathcal {H}^{d-1}\)-almost every x. This is the well-known rectifiability result of \(\text {BV}\)-maps (see [AFP00]).
3.2 Rectifiability of symmetrized gradients.
Let \(U \subset \mathbb {R}^d\) be an open set and let \(\mu =Eu\in {\mathcal {M}}(U, (\mathbb {R}^d\otimes \mathbb {R}^d)_\mathrm{sym})\), where \(u\in \text {BD}(U; \mathbb {R}^d)\) is a function of bounded deformation and
is the symmetric part of the distributional derivative of u. Then \(\mu \) is \({{\,\mathrm{curl}\,}}{{\,\mathrm{curl}\,}}\)-free (see [FM99, Example 3.10(e)]), where
In this case,
where \(a\odot \xi := (a \otimes \xi + \xi \otimes a)/2\). Hence, \(\Lambda ^{d-1}_{{{\,\mathrm{curl}\,}}{{\,\mathrm{curl}\,}}}=\{0\}\). Corollary 1.4 and Theorem 1.5 yield that \(|Eu| \ll \mathcal {H}^{d-1}\) and

for some \((d-1)\)-rectifiable set \(R \subset U\) and \( n_R(x)\) is orthogonal to \(T_xR\) at \(\mathcal {H}^{d-1}\) almost every x. This comprises the dimensional estimates and rectifiability of \(\text {BD}\)-functions from [Koh79, ACD97] (see in particular [ACD97, Proposition 3.5]).
3.3 Rectifiability of varifolds and defect measures.
Let \(U \subset \mathbb {R}^d\) be an open set and let us assume that \(\varvec{\mu } \in {\mathcal {M}}(U;\mathbb {R}^d\otimes \mathbb {R}^d)\) is a matrix-valued measure satisfying
where “\({{\,\mathrm{div}\,}}\)” is the row-wise divergence.
Proposition 3.1
Let \(\varvec{\mu } \in {\mathcal {M}}(U;\mathbb {R}^d\otimes \mathbb {R}^d)\) be as above. Assume that for \(|\varvec{\mu }|\)-almost every \(x \in U\),
Then, \(|\varvec{\mu }|\ll \mathcal {I}^\ell \ll \mathcal {H}^{\ell }\) and there exists an \(\ell \)-rectifiable set \(R\subset U\) and a \(\mathcal {H}^\ell \)-measurable map \(\lambda :R \rightarrow \mathbb {R}^d \otimes \mathbb {R}^d\) satisfying
such that

Proof
Let \(\widetilde{\varvec{\mu }}:=(\varvec{\mu },\sigma )\in {\mathcal {M}}(U;(\mathbb {R}^d\otimes \mathbb {R}^d)\times \mathbb {R}^d) \) and let us define the (non-homogeneous) operator \(\mathcal {A}\) via
so that \(\ker \mathbb {A}^1(\xi )= \ker ({{\,\mathrm{div}\,}}) (\xi )\times \mathbb {R}^d\). Since
we see that
Since \(|\varvec{\mu }|\ll |\widetilde{\varvec{\mu }}|\), for \(|\varvec{\mu }|\)-almost every x there exists a scalar \(\tau (x)\ne 0\) such that
and hence by Theorem 1.3,
In particular, by the assumption on the lower bound of the rank, we deduce that \(|\varvec{\mu }|\ll \mathcal {I}^\ell \ll \mathcal {H}^\ell \) and that there exists a rectifiable set R such that

The last part of the theorem then easily follows from Lemma 2.3. \(\square \)
The above proposition allows, for instance, to reprove the results of [All72] and to slightly improve the one in [DDG18]. To see this, recall that an \(\ell \)-dimensional varifold can be seen as a measure V on \(\mathbb {R}^d\times \mathrm {Gr}(\ell ,d)\) and that the condition of having bounded first variation with respect to an integrand F can be written as
where \(\Vert V\Vert \) is the projection of V on \(\mathbb {R}^d\) (the first factor), \(V(\mathrm{d}x,\mathrm{d}T)=V_{x}(\mathrm{d}T)\otimes \Vert V\Vert (\mathrm{d}x)\) is the disintegration of V with respect to this projection,
and \(B_F :\mathbb {R}^d\times \mathrm {Gr}(\ell ,d)\rightarrow \mathbb {R}^d\otimes \mathbb {R}^d\) is a matrix-valued map that depends on the specific integrand F, see the introduction of [DDG18] for details.
The (AC)-condition in [DDG18, Definition 1.1] exactly implies that the assumptions of Proposition 3.1 are satisfied. We remark that in fact Proposition 3.1 allows to slightly improve [DDG18, Theorem 1.2] in the following respects:
-
(a)
One obtains that
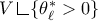 is rectifiable while in [DDG18] only the rectifiability of
is rectifiable while in [DDG18] only the rectifiability of 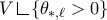 is shown (here, \(\theta _{*,\ell }\) is the lower \(\ell \)-dimensional Hausdorff density map).
is shown (here, \(\theta _{*,\ell }\) is the lower \(\ell \)-dimensional Hausdorff density map). -
(b)
If one only wants to get the rectifiability of the measure
 , then condition (i) in [DDG18, Definition 1.1] is enough. This allows, in the case \(\ell =d-1\), to work with convex but not necessarily strictly convex integrands.
, then condition (i) in [DDG18, Definition 1.1] is enough. This allows, in the case \(\ell =d-1\), to work with convex but not necessarily strictly convex integrands.
By similar arguments one recovers the results of Ambrosio & Soner [AS97], and of Lin [Lin99] and Moser [Mos03]; we omit the details.
References
G. Alberti. Rank one property for derivatives of functions with bounded variation. Proc. R. Soc. Edinb. Sect. A, 123 (1993), 239–274.
G. Alberti and A. Marchese. On the differentiability of Lipschitz functions with respect to measures in the Euclidean space. Geom. Funct. Anal., 26 (2016), 1–66.
G. Alberti, A. Massaccesi, and E. Stepanov. On the geometric structure of normal and integral currents, II. In preparation.
W.K. Allard. On the first variation of a varifold. Ann. Math., 95 (1972), 417–491.
W.K. Allard. An integrality theorem and a regularity theorem for surfaces whose first variation with respect to a parametric elliptic integrand is controlled, in Geometric Measure Theory and the Calculus of Variations, W.K. Allard and F.J. Almgren Jr., eds., Vol. 44 of Proceedings of Symposia in Pure Mathematics. Amer. Math. Soc. (1986).
L. Ambrosio, A. Coscia, G. Dal Maso. Fine properties of functions with bounded deformation. Arch. Ration. Mech. Anal., 139 (1997), 201–238.
L. Ambrosio, N. Fusco, and D. Pallara. Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs. Oxford University Press (2000).
L. Ambrosio and H.M. Soner. A measure-theoretic approach to higher codimension mean curvature flows. Ann. Scuola Norm. Sup. Pisa Cl. Sci., 25 (1997), 27–49 (1998).
A. Arroyo-Rabasa. An elementary approach to the dimension of measures satisfying a first-order linear PDE constraint. arXiv:1812.07629, (2018).
R. Ayoush and M. Wojciechowski. On dimension and regularity of bundle measures. arXiv:1708.01458, (2017).
D. Bate. Purely unrectifiable metric spaces and perturbations of Lipschitz functions. arXiv:1712.07139, (2017).
G. De Philippis. On the singular part of measures constrained by linear PDEs and applications, in Proceedings of the Seventh European Congress of Mathematics (Berlin 2016), (2016).
G. De Philippis, A. De Rosa, and F. Ghiraldin. Rectifiability of varifolds with locally bounded first variation with respect to anisotropic surface energies. Comm. Pure Appl. Math., 71 (2018), 1123–1148.
G. De Philippis, A. Marchese, and F. Rindler. On a conjecture of Cheeger, in Measure Theory in Non-Smooth Spaces, N. Gigli, ed., De Gruyter, (2017), pp. 145–155.
G. De Philippis and F.Rindler. On the structure of measures constrained by linear PDEs, in Proceedings of the International Congress of Mathematicians 2018 (Rio de Janeiro 2018).
G. De Philippis and F. Rindler. On the structure of \(\cal{A}\)-free measures and applications. Ann. Math., 184 (2016), 1017–1039.
H. Federer. Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, Band 153, Springer, (1969).
I. Fonseca and S. Müller. \(\cal{A}\)-quasiconvexity, lowersemicontinuity, and Young measures. SIAM J. Math. Anal., 30 (1999), 1355–1390.
N. Gigli and E. Pasqualetto. Behaviour of the reference measure on \({\sf RCD}\) spaces under charts. arXiv:1607.05188, (2016).
L. Grafakos. Classical Fourier Analysis, Vol. 249 of Graduate Texts in Mathematics, Springer, New York, 3rd ed., (2014).
M. Kell and A. Mondino. On the volume measure of non-smooth spaces with Ricci curvature bounded below. Ann. Sc. Norm. Super. Pisa Cl. Sci., 18 (2018), 593–610.
R.V. Kohn. New estimates for deformations in terms of their strains, PhD thesis, Princeton University, (1979).
F.-H. Lin. Gradient estimates and blow-up analysis for stationary harmonic maps. Ann. Math., 149 (1999), 785–829.
A. Massaccesi and D. Vittone. An elementary proof of the rank-one theorem for BV functions. J. Eur. Math. Soc. arXiv:1607.05188, (2016)
P. Mattila. Geometry of Sets and Measures in Euclidean Spaces. Fractals and Rectifiability, Vol. 44 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, (1995).
R. Moser. Stationary measures and rectifiability. Calc. Var. Partial Differ. Equ., 17 (2003), 357–368.
F. Murat. Compacité par compensation: condition nécessaire et suffisante de continuité faible sous une hypothèse de rang constant. Ann. Sc. Norm. Sup. Pisa Cl. Sci., 8 (1981), 69–102.
B. Raita. \(L^1\)-estimates and \(\mathbb{A}\)-weakly differentiable functions, Technical Report OxPDE-18/01, University of Oxford, (2018).
F. Rindler. Calculus of Variations, Universitext, Springer, (2018).
D. Spector and J.Van Schaftingen. Optimal embeddings into Lorentz spaces for some vector differential operators via Gagliardo’s lemma. arXiv:1811.02691, (2018).
E.M. Stein. Harmonic Analysis, (1993).
J. Van Schaftingen. Limiting Sobolev inequalities for vector fields and canceling linear differential operators. J. Eur. Math. Soc., 15 (2013), 877–921.
B. White. A new proof of Federer’s structure theorem for \(k\)-dimensional subsets of \({\mathbf{R}}^N\). J. Am. Math. Soc., 11 (1998), 693–701.
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, Grant Agreement No. 757254 (SINGULARITY), and from the INDAM-grant “Geometric Variational Problems”. We thank the anonymous referee for various comments that improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Arroyo-Rabasa, A., De Philippis, G., Hirsch, J. et al. Dimensional estimates and rectifiability for measures satisfying linear PDE constraints. Geom. Funct. Anal. 29, 639–658 (2019). https://doi.org/10.1007/s00039-019-00497-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-019-00497-1



 . In this step one usually uses that
. In this step one usually uses that  ,
, 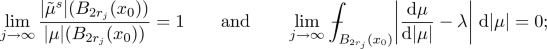
 . Here,
. Here, 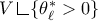 is rectifiable while in [
is rectifiable while in [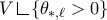 is shown (here,
is shown (here,  , then condition (i) in [
, then condition (i) in [