Clustering of Thrombin Generation Test Data Using a Reduced Mathematical Model of Blood Coagulation

Abstract

Correct interpretation of the data from integral laboratory tests, including Thrombin Generation Test (TGT), requires biochemistry-based mathematical models of blood coagulation. The purpose of this study is to describe the experimental TGT data from healthy donors and hemophilia A (HA) and B (HB) patients. We derive a simplified ODE model and apply it to analyze the TGT data from healthy donors and HA/HB patients with in vitro added tissue factor pathway inhibitor (TFPI) antibody. This model allows the characterization of hemophilia patients in the space of three most important model parameters. The proposed approach may provide a new quantitative tool for the analysis of experimental TGT. Also, it gives a reduced model of coagulation verified against clinical data to be used in future theoretical large-scale modeling of thrombosis in flow.

Appendix

1.1 From the Simulating to the Reduced Model

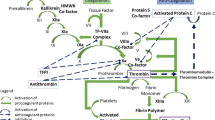
The coagulation cascade explained in Sect. 2.1 can be described using Fig. 5. The equations corresponding to this model give the system (1–17).

Fig. 5

Biochemical reactions of the blood coagulation cascade, (Hemker and Béguin 1995; Panteleev et al. 2006; Orfeo et al. 2005)

In the following approximations, we will explicitly refer to one of the Hypothesis of Sect. 2.2. The new constants will not always be explicitly expressed from the previous ones, since we do not use this expressions.

The first Hypothesis A1 leads to the equality: $u_i+v_i=v_i^0$. Hence, $v_i=v_i^0-u_i$. In order to describe the action of anticoagulant factors, we only apply this approximation to the inactive factors V, VIII, IX, X and XI.

Equations (3, 5, 7, 9) and (11), respectively, become as follows:

$$\begin{array}{ll} \frac{d u_5}{dt} = k_5T(v_5^0-u_5)- \sigma _5 u_5 - \kappa _3 u_5u_{10} + \alpha _3 c_3 , \end{array}$$

(25)

$$\frac{{du_{8} }}{{{\text{dt}}}} = k_{8} T(v_{8}^{0} - u_{8} ) - \sigma _{8} u_{8} - \kappa _{2} u_{9} u_{8} + \alpha _{2} c_{2} ,{\text{ }}$$

(26)

$$\begin{aligned} \frac{du_9}{dt} = (k_9^1 u_{11}+ k_9^2 c_1) (v_9^0-u_9) - \sigma _9 u_9 A - \kappa _2 u_9 u_8 + \alpha _2 c_2 , \end{aligned}$$

(27)

$$\begin{aligned} \frac{du_{10}}{dt}= (k_{10}^1 c_1+k_{10}^2 u_9 +k_{10}^3 c_2) (v_{10}^0-u_{10}) - \sigma _{10} u_{10}A - \kappa _3 u_5 u_{10} -k_TTFPIu_{10} + \alpha _3 c_3 , \end{aligned}$$

(28)

$$\begin{aligned} \frac{du_{11}}{dt}= k_{11}T (v_{11}^0-u_{11}) - \sigma _{11} u_{11}A. \end{aligned}$$

(29)

We will now use the fact that some reactions have high kinetics rates, and rapidly reach their equilibrium. Following assumption A2, we set the time derivative equal to zero. We first proceed with Eq. (17) and we get the equality:

$$\begin{aligned} TFPI_{10}=\frac{\sigma _5 TFPI u_{10}}{\sigma _4 c_1}. \end{aligned}$$

(30)

It is applied to (14), and using, as before, the Hypothesis A2 of high kinetic rates, we obtain:

$$\begin{aligned} c_1 = \frac{\kappa _1 TF v_7-\sigma _5 TFPI u_{10}}{\sigma _3 A}. \end{aligned}$$

(31)

Similarly, we have from Eqs. (15) and (16):

$$\begin{aligned} c_2= \frac{\kappa _2 u_8u_9}{\alpha _2}=\gamma _2u_8u_9, \end{aligned}$$

(32)

$$\begin{aligned} c_3= \frac{\kappa _3 u_5u_{10}}{\alpha _3}=\gamma _3u_5u_{10}. \end{aligned}$$

(33)

These two approximations lead to some simplifications: (32) simplifies equations (26) and (27) for activated factors VIIIa and IXa, while (33) simplifies (25) for activated factor Va. Using Hypothesis A2 we have the following expressions for activated factors Va, VIIIa, IXa and XIa:

$$\begin{aligned} u_5= \frac{k_5Tv^0_5}{k_5T+\sigma _5}, \end{aligned}$$

(34)

$$\begin{aligned} u_8= \frac{k_8Tv^0_8}{k_8T+\sigma _8}, \end{aligned}$$

(35)

$$\begin{aligned} u_9= \frac{(k_9^1u_{11}+k_9^2c_1)v^0_9}{k_9^1u_{11}+k_9^2c_1+\sigma _9A}, \end{aligned}$$

(36)

$$\begin{aligned} u_{11}= \frac{k_{11}Tv^0_{11}}{k_{11}T+\sigma _{11}A}. \end{aligned}$$

(37)

Let us now simplify these four equations using the third Hypothesis A3 according to which anticoagulating factors are in excess and their concentrations are higher than the concentrations of other factors. Thus, the denominators of (34–37) can be approximated by constants. Moreover, since $\kappa _1 \gg \sigma _5$ Chelle et al. (2018), it can be assumed that $\kappa _1 TF v_7 \gg \sigma _5 TFPI u_{10}$. Therefore, we can write (31) in the following form:

$$\begin{aligned} c_1=\gamma _1TFv_7. \end{aligned}$$

(38)

Hence, we have the following equalities:

$$\begin{array} {ll}u_5= &\gamma _5v_5^0T, \end{array}$$

(39)

$$\begin{array}{ll} u_8= \gamma _8v_8^0T, \end{array}$$

(40)

$$\begin{array}{ll} u_9= \gamma _9v_9^0v_{11}^0T, \end{array}$$

(41)

$$\begin{array}{ll} u_{11}= \gamma _{11}v_{11}^0T. \end{array}$$

(42)

Let us now focus our attention on Eq. (28) for activated factor Xa. Considering Eqs. (32, 33, 38, 40) and (41), we obtain:

$$\begin{aligned} \begin{aligned} \frac{du_{10}}{dt} =\,\, (\gamma _1^{10}TFv_7+\gamma _{10}^2v_9^0v_{11}^0T +\gamma _{10}^3v_8^0v_9^0v_{11}^0T^2) (v_{10}^0-u_{10}) \\&- (\sigma _{10} A +k_TTFPI)u_{10}. \end{aligned} \end{aligned}$$

(43)

Equation (43) can be considered as always valid in our approximation, but once the initiation phase is over, this expression can be simplified assuming two hypothesis: the reaction has reached its equilibrium (Hypothesis A2) and the concentration of anticoagulant factors is high (Hypothesis A3). In this case we have the following expression for activated factor Xa:

$$\begin{aligned} u_{10} = (\gamma _1^{10}TFv_7+\gamma _{10}^2v_9^0v_{11}^0T +\gamma _{10}^3v_8^0v_9^0v_{11}^0T^2) \gamma _{10}^4v_{10}^0. \end{aligned}$$

(44)

Finally, we deal with Eqs. (1) and (2) for thrombin and prothrombin. In this reaction, the activation of thrombin happens through the terms $k_2^1u_{10}P$ and $k_2^2c_3P$. The first one is due to the quantity of activated factor Xa produced after the initiation while the second one is the impact of the positive feedback loop in the amplification phase. Thus, it is possible to approximate the value of $c_3$ using Eqs. (33, 39) and (44). We obtain the following equations:

$$\begin{array} {ll} \frac{dT}{dt}= (\gamma _2^1 u_{10} + v_{10}^0v_5^0(\gamma _2^2TFv_7T+\gamma _2^3v_9^0v_{11}^0T^2 +\gamma _2^4v_8^0v_9^0v_{11}^0T^3 ))P - \sigma _2 A T, \end{array}$$

(45)

$$\begin{aligned} \frac{dP}{dt}= - (\gamma _2^1 u_{10} + v_{10}^0v_5^0(\gamma _2^2TFv_7T+\gamma _2^3v_9^0v_{11}^0T^2 +\gamma _2^4v_8^0v_9^0v_{11}^0T^3 ))P . \end{aligned}$$

(46)

Under Hypothesis A3, we assume that the concentrations of anticoagulating factors are in excess, and for further simplification we assume that the concentration of antithrombin is constant. To find this constant, we use the approximation of $c_1$ given by (31). In this case we obtain:

$$\begin{aligned} \frac{d A}{dt}=(-\sigma _2 T -\sigma _9u_9-\sigma _{10}u_{10} -\sigma _{11}u_{11})A - \kappa _1 TF v_7+\sigma _5 TFPI u_{10}. \end{aligned}$$

(47)

The concentration of antithrombin is very large and the coagulation only uses some part of it (from 3400 nM/L at the beginning to 2100 nM/L at the end). Furthermore, this anticoagulation effect only appears after the amplification phase where the concentration of activated factor Xa is stabilized and remains constant. Since we are expressing the anticoagulating factor, we preserve the dependence on TFPI, IX and XI, so we obtain:

$$\begin{aligned} A=A^0+kTFPI-k_A^1v_9^0-k_A^2v_{11}^0. \end{aligned}$$

(48)

Finally, we apply the equality (48) to the three remaining ODEs (43, 45, 46), and we obtain:

$$\begin{aligned}&\begin{aligned} \frac{du_{10}}{dt} =\,\,(\gamma _1^{10}TFv_7+\gamma _{10}^2v_9^0v_{11}^0T +\gamma _{10}^3v_8^0v_9^0v_{11}^0T^2) (v_{10}^0-u_{10}) \\&- (\sigma _{10}^1 A +\sigma _{10}^2TFPI -k_A^1v_9^0-k_A^2v_{11}^0)u_{10}. \end{aligned} \end{aligned}$$

(49)

$$\frac{{dT}}{{dt}} = \left( {\gamma _{2}^{1} u_{{10}} + v_{{10}}^{0} v_{5}^{0} \left( {\gamma _{2}^{2} TFv_{7} T + \gamma _{2}^{3} v_{9}^{0} v_{{11}}^{0} T^{2} + \gamma _{2}^{4} v_{8}^{0} v_{9}^{0} v_{{11}}^{0} T^{3} } \right)} \right)P - \left( {\sigma _{2}^{1} A + \sigma _{2}^{2} TFPI - k_{A}^{1} v_{9}^{0} - k_{A}^{2} v_{{11}}^{0} } \right)T,$$

(50)

$$\begin{aligned}&\frac{dP}{dt} = - (\gamma _2^1 u_{10} + v_{10}^0v_5^0(\gamma _2^2TFv_7T+\gamma _2^3v_9^0v_{11}^0T^2 +\gamma _2^4v_8^0v_9^0v_{11}^0T^3 ))P . \end{aligned}$$

(51)

Using the notation

$$\begin{array}{ll} \begin{array}{ll} K_1=\gamma _1^{10}TFv_7,&{}K_6=v_{10}^0v_5^0\gamma _2^2TFv_7,\\ K_2=\gamma _{10}^2v_9^0v_{11}^0,&{}K_7=v_{10}^0v_5^0\gamma _2^3v_9^0v_{11}^0,\\ K_3=\gamma _{10}^3v_8^0v_9^0v_{11}^0,&{}K_8=v_{10}^0v_5^0\gamma _2^4v_8^0v_9^0v_{11}^0,\\ K_4=\sigma _{10}^1 A +\sigma _{10}^2TFPI-k_A^1v_9^0-k_A^2v_{11}^0,&{}K_9=\sigma _2^1 A+\sigma _2^2 TFPI-k_A^1v_9^0-k_A^2v_{11}^0,\\ K_5=\gamma _2^1,&{} \end{array} \end{array}$$

we obtain the Reduced model in the following form:

$$\begin{array}{ll} \frac{du_{10}}{dt}= (K_1+K_2T +K_3T^2) (v_{10}^0-u_{10})- K_4u_{10}, \end{array}$$

(52)

$$\begin{array}{ll} \frac{dT}{dt}= (K_5u_{10}+K_6T+K_7T^2+K_8T^3))P - K_9T, \end{array}$$

(53)

$$\begin{aligned} \frac{dP}{dt}= - (K_5u_{10}+K_6T+K_7T^2+K_8T^3))P. \end{aligned}$$

(54)

We note that coefficients $K_i$ depend on the combinations of parameters leading to possible correlations between them. For example, the correlation of the coefficients $K_2$, $K_3$, $K_7$, and $K_8$ can be observed under the variation of $v_9^0$ for all other parameters are fixed. This is the case of hemophilia patients for whom the value of $v_9^0$ is less than for normal subjects.

1.2 Table of the Features Values

Table presents the characterization of TGC for healthy and hemophilia subjects. The data are obtained with added TFPI antibodies (set 1) or factors VIII, IX (set 2).

	Mean	Min	Max
Healthy
ETP	584.0292	281.365	1009.341
Max	42.3619	16.7496	84.5972
TtP	13.8375	9.39	19.67
Lag	5.899	3.38	12
Tt0	37.448	32.33	49.79
Hemophilia, set 1
ETP	317.0233	89.6358	788.2092
Max	18.6827	3.6511	82.1361
TtP	11.7627	6	25.33
Lag	2.5818	0.59	5.98
Tt0	37.4717	24.67	49.67
Hemophilia, set 2
ETP	249.9358	45.1653	645.3389
Max	10.9127	1.8174	33.965
TtP	29.4	13.33	58.67
Lag	9.6667	1.33	26.33
Tt0	48.844	41	58.67

1.3 Smoothing Algorithm

The exponential smoothing algorithm for the sequence $(x_n)_{n\ge 0}$ is defined by the formula:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_0=x_0, \\ y_{n+1}=\alpha x_{n+1} +(1-\alpha )x_n, \end{array}\right. } \end{aligned}$$

(55)

where $\alpha \in [0,1]$. We write: $(y_n)=S((x_n))$. The new sequence $(y_n)_{n\ge 0}$ contains the smoothing of the sequence $(x_n)_{n\ge 0}$. The value of $\alpha$ can depends on n. In our case, $x_n$ is the measure of thrombin concentration at time n. We write N, the number of measures. For our database we mostly preserve the peak of thrombin, and mainly smooth the tail of the TGC. Hence, $\alpha$ is close to 1 until the tail start, and then $\alpha$ decreases. We choose two different values for $\alpha$. Considering a data with N measures, we have $\alpha =0.9$ for $n=0$ to N / 3 (the beginning of the tail), and $\alpha = 0.2$ afterwards. These values where chosen empirically in order to always have a positive concentration of thrombin, which was not always the case in the initial experiment data. The smoothing algorithm is applied twice on the data: the final data used is given by $S(S(x_n))$.

1.4 Fitting for Hemophilia Patients

A typical case of fitting of the data with model (21–23) is shown in Fig. 6

Fig. 6

Example of a fitting of TGC curve with the Reduced model for Hemophilia patients. Left: Hemophilia A, Right: Hemophilia B. Data are shown with crosses, solid lines represent simulations with model (21–23)

1.5 Validation of the Reduced model

The three models are plotted in Fig. 7, and the relative errors for ETP, maximum of thrombin, lag time and time to maximum, for models (1–17) and (21–23) compared to the Hockin model, are under 10%. Figure 8 shows how the main features of TGC evolve as the concentration of TFPI varies. It can be seen that these dependencies are similar for all three models, though the time to maximum for model (21–23) increases faster than for the other two models. Parameters of the Hockin model for Fig. 8 are chosen using the values in Chelle et al. (2018). They correspond to a virtual healthy subject. Then, parameters for models (1–17) and (21–23) are found fitting their respective TGC to the TGC obtained with the Hockin model.

Fig. 7

Thrombin Generation curves for Hockin model (solid), model (1–17) (dashed), and Reduced model (dot dashed)

Fig. 8

Characterization of thrombin generation curves obtained by the Hockin model (solid), model given by system (1–17) (dashed), and Reduced model (dot dashed). The curves represent average values for 10 virtual patients chosen randomly

1.6 The Hill Equation (Goutelle et al. 2008; Hill 1910)

We use the Hill equation to determine the concentration of TFPI when TFPI antibodies are added. More generally, the Hill equation is used to represent the binding of ligands (here, the antibodies) to macromolecules (here, the TFPI). The chemical reactions writes:

(56)

where P is the macromolecule, L the ligand, $PL_n$ the product and n the coefficient of Hill. Considering the affinity constant, $K_a$:

$$\begin{aligned} (K_a)^n=\frac{k_d}{k_a}, \end{aligned}$$

(57)

and $\theta$ the fraction of the bounded protein, the Hill equation writes:

$$\begin{aligned} \theta =\frac{K_a[L]^n}{1+K_a[L]^n}. \end{aligned}$$

(58)

The coefficient of the Hill equation represents the cooperativity between different subunits of a ligand. Here, this coefficient is chosen equal to 1 since there is no cooperativity between the several subunits of a TFPI antibody. It means that the affinity of TFPI for a antibody does not depend on whether or not other TFPI molecules are already bound to that antibody.

Hence, the Hill equation provides the following equation for the evolution of TFPI:

$$\begin{aligned} {[TFPI]}=[TFPI]_0\left( 1-\frac{K_a[TFPI_{AB}]}{1+K_a[TFPI_{AB}]}\right) , \end{aligned}$$

(59)

where $[TFPI]_0$ is the initial concentration of TFPI while $[TFPI_{AB}]$ is the concentration of TFPI antibodies.

In the model, the variation of TFPI impacts the coefficient $k_9$, which corresponds to the anticoagulant part. Constant $K_a$ was first determined for several patients, then the median value was chosen since $K_a$ should not dependent on the subject.

1.7 Correlation Between ETP and Maximum of Thrombin

Figure 9 shows that there is a linear correlation between ETP and the maximum of thrombin for healthy and hemophilia patients in the experimental thrombin generation curves.

Fig. 9

Linear correlation between ETP and the maximum of thrombin for healthy patients (cross), hemophilia A (circles), hemophilia B patients (triangles). Tendencies for healthy patients (line), and for hemophilia patients (dash line) are shown