An application of generalised simulated annealing towards the simultaneous modelling and clustering of glaucoma

Abstract

Optimisation methods are widely used in complex data analysis, and as such, there is a need to develop techniques that can explore huge search spaces in an efficient and effective manner. Generalised simulated annealing is a continuous optimisation method which is an advanced version of the commonly used simulated annealing technique. The method is designed to search for the global optimum solution and avoid being trapped in local optima. This paper presents an application of a specially adapted generalised simulated annealing algorithm applied to a discrete problem, namely simultaneous modelling and clustering of visual field data. Visual field data is commonly used in managing glaucoma, a disease which is the second largest cause of blindness in the developing world. The simultaneous modelling and clustering is a model based clustering technique aimed at finding the best grouping of visual field data based upon prediction accuracy. The results using our tailored optimisation method show improvements in prediction accuracy and our proposed method appears to have an efficient search in terms of convergence point compared to traditional techniques. Our method is also tested on synthetic data and the results verify that generalised simulated annealing locates the optimal clusters efficiently as well as improving prediction accuracy.

1 Introduction

In recent years data has been collected at a vastly increasing rate. This data is typically complex in nature and high in both dimensionality and size. To cope with this data explosion there is a need for efficient algorithms that can effectively “keep up”.

Generalised simulated annealing (GSA) is an improved version of the simulated annealing (SA) algorithm, proposed by Tsallis and Stariolo (1996) and Xiang et al. (2017). The algorithm generalises both types of SA, i.e. classical simulated annealing (CSA) and fast simulated annealing (FSA). This family of stochastic algorithms was inspired by the metallurgy process for making a molten metal reach its crystalline state by employing an artificial temperature (Xiang et al. 1997). Unlike hill climbing (HC) (Selman and Gomes 2006; Tovey 1985), SA and GSA methods are able to avoid local optimum in the search due to the inherent statistical nature of the method (Bohachevsky et al. 1986). Worse solutions found in the search are accepted when certain probabilistic criteria are met, thus enabling the methods to escape local optima.

CSA is likely to find a global optimum solution in the search. However, the convergence is fairly slow (Xiang et al. 1997). This is attributed to the nature of the visiting distribution which uses a Gaussian distribution (local search distribution). Thus in 1987, Szu and Hartley (1987) proposed FSA which uses a Cauchy-Lorentz visiting distribution (semi-local search distribution). The FSA method is quicker at finding the optimum solution compared to the CSA since the jumps are frequently local, but can occasionally be quite long. The cooling of temperature in the method is much faster which makes the search more efficient.

Later in 1988, a generalisation of Boltzmann–Gibb statistics was introduced (Tsallis 1988). GSA was invented for generalising both CSA and FSA methods according to the Tsallis statistics. GSA uses a distorted Cauchy–Lorentz visiting distribution where the distribution is controlled by the visiting index parameter (${q_{v}}$). This method (GSA) was believed to be more efficient in terms of convergence and global optimum in nonconvex problems (multiple extrema) compared to the precedence methods of annealing. Because of these advantages, there are many studies have applied the method in many fields.

Application of GSA in the field of biology, chemistry, physic and mathematics (Andricioaei and Straub 1996; Brooks and Verdini 1988; dos R Correia et al. 2005; Sutter et al. 1995; Xiang et al. 2017) have often the determination of the global optimum of multidimensional continuous functions (Xiang et al. 2013). The GSA approach was proven faster than the other simulated annealing algorithms (CSA and FSA) in the study of mapping minima points of molecular conformational energy surfaces (Moret et al. 1998). Xiang and Gong (2000) have shown that the GSA algorithms are relatively efficient in Thomsons model and nickel clusters compared to CSA and FSA. It was also claimed that the more complex the system, the more efficient the GSA method. A recent study Mojica and Bassrei (2015) on the simulation of 2D gravity inversion of basement relief with synthetic data has found that the GSA method produces better results with the calibrated parameters. Another recent study by Menin and Bauch (2017) have used GSA in finding the source of an outbreak (patient zero). They found that GSA is able to identify the location and time of infection of patient zero with good accuracy. Meanwhile Feng et al. (2018) presented a case study of dynamic land using cellular automata simulation with GSA. Their GSA algorithm in the problem took the least time in the optimisation process compared to other heauristics search methods (particle swam optimisation and genetic algorithm).

The positive findings from the previous studies on GSA have inspired this study to further investigate the compatibility of GSA algorithm with SMC to efficiently (with high accuracy and fast convergence) cluster and classify high dimensional data such as visual fields. Our work is an extension of the work done by Jilani et al. (2016) where SMC was experimented on visual field data using simple optimisation methods such as hill climbing to predict glaucoma progression. Since there is very little work has been done in this problem, taking advantage of GSA that has been proven an efficient method in literature, it is an open research opportunity.

We note that most of the studies have applied GSA towards solving continuous problems (Advanced Glaucoma Intervention Study Investigators 1994); hence within this paper we present a GSA algorithm for discrete optimisation. Our hypothesis underpinning this research is that the GSA method finds the optimum solution more efficiently than SA. Efficiency is measured in two ways, firstly we use prediction accuracy and secondly we look at algorithmic convergence, i.e. the speed an algorithm locates a high quality solution.

This paper is organised into the following sections: Sect. 2 details the background of the data used in this study. Section 3 describes the application of GSA algorithm towards simultaneous modelling and clustering. In Sect. 4, details regarding the experimental setup are discussed. Section 5 describes the results of our experiments and results are tabulated for comparison. The results are discussed in Sect. 6 and conclusion and future work are presented in Sect. 7.

2 Background

2.1 Glaucoma

Glaucoma is the second leading cause of blindness disease in the world (Quigley and Broman 2006) and is an irreversible disease that can seriously affect a sufferers quality of life (McKean-Cowdin et al. 2007). The disease is typically caused by a build-up of intraocular pressure in the eye that causes damage to the optic nerve, which delivers image signals to the brain (Quigley 2011). In clinical practice, glaucoma is commonly managed by performing a visual field test which captures the sensitivity of the eye to light (Kristie Draskovic 2016; Westcott et al. 1997).

Fig. 1

The 54 locations of the visual field test for the right eye

Much research has been done to study glaucoma deterioration such as statistical analysis and data modelling using visual field data as presented by Pavlidis et al. (2013), Swift and Liu (2002) and Ceccon et al. (2014). However, there is less work on analysing and modelling visual field data using significant clustering arrangements of the data.

Since there is no gold standard established in analysing glaucoma data (Schulzer et al. 1994), applying machine learning techniques to find patterns of glaucoma deterioration in visual field data helps medical practitioners to provide appropriate treatments, i.e. the prediction of potential future visual field loss (Swift and Liu 2002; Tucker and Garway-Heath 2010). Additionally, this piece of work is a novel approach of high-dimensional data analysis in which a continuous optimisation method is applied in a discrete problem finding the best clustering arrangement of visual field locations.

2.2 Visual field data

Visual field data is commonly used in glaucoma management. It is collected via a non-invasive clinical procedure by means of computerised automated perimetry (Heijl and Patella 2002). Typically 54 or 76 points (including the blind spot) are tested to determine a patients eye sensitivity to light (Fig. 1). A diagnosis of glaucoma using VF data is often quantified by the Advance Glaucoma Intervention Studies (AGIS) score (Advanced Glaucoma Intervention Study Investigators 1994). This metric is used to classify the severity of a glaucoma patients condition. In this study we aim to predict future values of this AGIS metric from previously recorded VF data observations, i.e. VF data recorded at a time T is used to predict the AGIS score of the next visit ($T+1$) (Advanced Glaucoma Intervention Study Investigators 1994; Sacchi et al. 2013). In addition to envisage the level of glaucoma deterioration in the next VF test, predicting AGIS with high accuracy prediction could equip physician to prepare an appropriate treatment for patient. Table 1 shows the AGIS score used in this study that have been classified into 3 categories for an efficient classification (Jilani et al. 2016; Sacchi et al. 2013). In clinical practices, the AGIS score is computed to determine patient glaucoma stage and most analyses in research use six nerve fibre bundle (6NFB), which was established by Garway-Heath et al. (2000), for data modelling and prediction.

Table 1 AGIS score classification

2.3 Simultaneous modelling and clustering of visual field data

Data clustering (Ghahramani 2004) techniques commonly use the data point structure to group data based on similarity such as distance between object in data. However, clustering technique such as those introduced by Banfield and Raftery (1993) have introduced methods based on modelling the data. Datasets are clustered based on object shape and structure rather than on proximity between data points. Likewise, the introduced approach that is SMC a model-based clustering method that finding clusters within data based on the best modelling result using an optimisation search method. In this paper presents the extension on the approach using GSA method in VF data. The SMC approach was used by Jilani et al. (2016) predicting the stages of glaucoma progression using VF data. The best clusters, which represent the collections of visual field locations, are searched in the data to improve prediction of glaucomatous progression as well as understanding the clusters arrangement. The motivation behind SMC is that a search for the best clustering arrangement is made, where the worth of such an arrangement is based on using the clusters to create compound variables that in turn can be used to classify accurately and predict the AGIS score. The clusters discovered in the search are hypothesised to be better than the six nerve fibre bundles (6NFB) in terms of prediction accuracy. These nerve fibre bundles are effectively a clustering arrangement that has been clinically determined through observing the physiological layout of the retina and optic nerves. Currently there is no conclusive evidence that this layout provides the best predictive accuracy, although there is some work on modelling the data using them (Sacchi et al. 2013).

3 Method

3.1 Data pre-processing

The VF data consists of 13,739 records of 1580 patients obtained from Moorfields Eye Hospital London (United Kingdom). The AGIS score was provided with the data and the data were prepared into a time series record which each record has the next visit AGIS ($T+1$) score. As such, the cleaning dataset after excluded the most recent record and consists of 12,159 records of VF data¹.

3.2 Clustering

Clustering, which is also known as unsupervised learning (Duda et al. 2000), is a data analysis technique for finding similarity amongst objects and grouping similar objects into the same cluster. The objects in the cluster share the common feature, function, shape, and attribute. In classical data clustering, the distance between objects (e.g. Euclidean) is commonly used (Jain and Dubes 1988). However, this study applies model-based technique to cluster data based on classification performance.

3.3 Data modelling

Data modelling is a key process involved in SMC. This process is also known as supervised learning where the data are classified to a set of categories it belongs. In this study, VF data is modelled by classifying the target variable (AGIS) which indicates the stage of glaucoma disease. The VF data is classified into $T+1$ of AGIS which is the time series record. Since the target variable value is $T+1$ of the AGIS, the classification is a prediction of the patient glaucoma progression. The Naive Bayes Multinomial Updateable (NBU) classifier is used in the modelling process owing to the most efficient method in terms of runtime and has good accuracy when applied to a number of different problem domains (Jilani et al. 2016; Rennie et al. 2003; Sundar 2013; Tao and Wei-hua 2010).

3.4 Simultaneous modelling and clustering

The approach used in the SMC comprises of these two main analysis techniques that is clustering and modelling. The 52 VF locations are grouped into clusters randomly then the clusters are used for data modelling as the validation to the clusters. The clusters validation is measured as prediction accuracy. The SMC process uses optimisation methods searching the best cluster with prediction accuracy as the fitness function. The hypothesis underpinning this approach is that the higher prediction accuracy, the better the quality of the associated clustering arrangement. This heuristic process iterates for suitable number of iterations and searches for the best clusters using an optimisation method. The final clusters arrangements (resulting bundles) of the VF locations are captured. This SMC process is schematically illustrated in Fig. 2.

The final clusters obtained in the search using SMC are recorded and analysed using the Weighted Kappa statistic. The Weighted Kappa statistic (Table 2) (Viera and Garrett 2005) between the clustering arrangement of SMC and the 6NFB (Garway-Heath et al. 2000) (depicted in Fig. 3) is computed to measure the similarity of resulting clusters with the 6NFB. The resulting clusters are also mapped on the VF to visualise the association between VF location and bundles in order to comprehend the glaucomatous progression. By looking at the bundles of VF points discovered by the method, patterns of glaucoma progression can be understood.

Fig. 2

High level process of simultaneous modelling and clustering

Table 2 Weighted kappa statistic metric

Fig. 3

The 54 locations of the visual field data mapped to the six nerve fibre bundles

3.5 Generalised simulated annealing algorithm

The GSA method is distinct from SA in determining the temperature, the acceptance probability value and the selection of a neighbouring point in the search space. These parameter values regulate the methods behaviour such as convergence and cooling rate. The acceptance probability (Eq. 1) and artificial temperature (Eq. 2) use an acceptance index (${q_{a}}$) and visiting index (${q_{v}}$) as parameters (Tsallis and Stariolo 1996). Furthermore, the visiting index (${q_{v}}$) is used in the visiting distribution equation (Eq. 4) (Tsallis and Stariolo 1996) to determine the size of change (in this study this is the number of VF locations to be re-arranged between clusters) for the next potential solution in the GSA search. The size of change (small change) in Algorithm 1 is defined as a number of moves, i.e. exchanging two variables from two different clusters. Each new better (in terms of fitness function) solution found in the search is accepted. However, if the new solution is worse, a criterion of acceptance the solution is derived by computing the acceptance probability according to Eq. 1. Then the acceptance probability (p) value is compared with a random number (r) which obtained from a uniform distribution (0,1). The new worse solution is accepted if p >r. This process continues until a number of iterations are complete. The detailed procedure of the GSA method is described in Algorithm 1.

$$\begin{aligned} p_{q^A} (x_{t}\rightarrow x_{t+1}) = \frac{1}{[1+(q_{A}-1)(E(x_{t+1})-E(x_{t}))/T_{q_{A}}^{A}]^{1/(q_{A}-1)}} \end{aligned}$$

(1)

where $x_t$ is the current solution (VF clusters) of the current iteration, while $x_{t+1}$ is the new solution for next iteration. E($x_{t}$) is defined as the fitness value of solution x. $T_{qa}^{A}$ is the acceptance temperature at time t that decreasing from initial value to zero.

$$\begin{aligned} T_{qv}^{V} (t) = T_{qv}(1) \frac{2^{q_{v}-1}-1}{(1+t)^{q_{v}-1}-1} \end{aligned}$$

(2)

where $T_{q_{V}}^{V}$ is the visiting temperature at time t.

$$\begin{aligned} a = \frac{[T_{q_{v}}^{V}(t)]^{-D/(3-q_{v})}}{\left\{ 1+ (q-1)\frac{(\triangle x_{t})^{2}}{[T_{q_{v}}^{V}(t)]^{2/(3-q_{v})}} \right\} ^{1/(q_{v}-1)+(D-1)/2}} \end{aligned}$$

(3)

As suggested by Advanced Glaucoma Intervention Study Investigators (1994) D is set to 1.

$$\begin{aligned} g_{q_{v}}(\triangle x_{t}) = \Big (\frac{q_{v}-1}{\pi } \Big )^{D/2} \frac{\varGamma \Big (\frac{1}{q_{v}-1} +\frac{D-1}{2}\Big )}{\varGamma \Big (\frac{1}{q_{v}-1}-\frac{1}{2} \Big )}\times a \end{aligned}$$

(4)

According to Tsallis and Stariolo (1996), parameter $q_{a}$ and $q_{v}$ are calibrated depending upon the nature of the problem where the best value range for $q_{v}$ is between 1.66 to 2.70. However, they also presented that the GSA was found having faster convergence when $q_{a}<1$. Therefore in our study, the region of exploration for the $q_{a}$ variable is between 0 and 1. Our new visit value ($q_{v}$) is represented by the number of VF locations (totalling 52 locations) to be re-arranged between the VF bundles in the next iteration of the search.

4 Experiment setup

4.1 GSA parameter exploration

Many studies have devised GSA algorithms and calibrate the parameters in the GSA to suit the nature of the problem at hand. Determination of the best parameters value ($q_{a}$ and $q_{v}$) is the crucial part in developing the GSA algorithm. A study applied GSA to protein folding (Agostini et al. 2006) has explored the best parameters values range and discovered the best values ranges are between 1.10 to 2.60 and 1.50 to 2.60 for $q_{a}$ and $q_{v}$ respectively. The study also introduced a new parameter ($q_{t}$) for the cooling function to better control the temperature decreasing in the GSA system. Whereas in this paper we use the Newton Raphson mathematical technique to compute the suitable parameters values ($q_{v}$ and $T_{0}$). The equations, which have three parameters values to be determined, are simplified to a single parameter. With the knowledge of the $q_{a}$ value and a few assumptions e.g. fitness value is between 0 to 1, equations are manipulated using Newton Raphson method to get the $q_{v}$. As such, Eqs. 1 and 2 are simplified to derive $T_{0}$, and thus $q_{v}$ is obtained.

4.2 Newton Raphson

The Newton Raphson technique (Akram and Ann 2015; Kelley 2003) is a powerful mathematical technique to solve numeric equations. It involves finding a value for the root of a function. Finding a root in an equation is an iterative process by guessing the initial value of x from the function (f(x)) and the derivative of the function (tangent line - f(x)) is used to obtain the intercept of the tangent line. The x-intercept will be the enhanced approximation to the functions root. This iterates until $x: f(x) = 0$. The Newton Raphson method is as follows,

Let f(x) be a continuous function.

$x_{1} = x_{0} - \frac{f(x_{0})}{f^{'}(x_{0})}$ geometrically $(x_{1},0)$ is the intersection with the x-axis of the tangent to the f(x) of $(x_{0},f(x_{0}))$. This process iteratively repeats as $x_{n+1} = x_{n} - \frac{f(x_{n})}{f^{'}(x_{n})}$ until a sufficient accurate value $(f(x)\approx 0)$ is reached.

This method is used to solve the GSA equations in order to get the appropriate value of parameter $q_{v}$ and $T_{0}$ . This study manipulates the acceptance probability equation (Equation 1) and temperature equation (Eq. 2) to derive the parameters values. We define the acceptance probability at iteration zero as

$$\begin{aligned} P_{0} = \frac{1}{[1+(q_{a}-1)(\triangle f)/T_{0}]^{1/q_{a}-1}} \end{aligned}$$

(5)

In order to get the initial temperature ($T_{0}$) from this equation, some assumptions have been made. We assume that the acceptance probability is 0.4 at iteration 1 in the search. This is possible when the worst random solution obtain at iteration 1 would have different of fitness 0.5 (50% deviates from the initial fitness value). This means that when $P_0$ is set to 0.4, there is a 40% chance of accepting a worse solution when the prediction accuracy is 0.5 (50%) worse than the current accuracy. Thus Eq. 5 is simplified as follows,

Assumptions	$(1+q(\triangle f / T_{0}))^{1/q_{a}-1} = \frac{1}{P_{0}}$	$\frac{q\triangle f}{T_{0}} = \big (\frac{1}{P_{0}} \big )^q -1$
$q = q_{a}-1$	$(1+q(\triangle f/T_{0}))= \big (\frac{1}{P_{0}} \big )^q$	$\frac{q}{2.5T_{0}} = 5^{q}-1$
$\triangle f=0.5$	$q(\triangle f/T_{0}) = \big ( \frac{1}{P_{0}} \big )^q -1$
$P_{0} = 0.4$
$P_{0} = \frac{1}{(1+q(\triangle f / T_{0}))^{1/q_{a}-1}}$

	$T_{N}(1+N)^s - T_{0}2^s = T_{N}-T_{0}$
where $s = q_{v}-1$, N is number of iteration
$T_{N} \big ( (1+N)^s -1\big ) = T_{0}(2^s -1)$
$T_{N}(1+N)^s -T_{N} = T_{0}2^s - T_{0}$

Within Eq. 11, the $T_{0}$ value is obtained from Eq. 9 by selecting the $q_{a}$ (values ranged between − 0.5 to 1.6). With $T_{0}$ and N (number of iterations, 100,000) in hand, the Eq. 11 is used to derive the correspondent value of $q_{v}$ where $T_{N}$ is the final temperature set as 0.001. Equation 11 is solved by means the Newton Raphson method. We know that $ab^x + cd^x = 1$ is non-linear. Therefore, Eq. 11 is written as $a(1+N)^s + c2^s = 1$ , where $a = \frac{T_{n}}{T_{n}-T_{0}}$ and $\frac{-T_{0}}{T_{n}-T_{0}}$. Thus, the non-linear function of Eq. 11 is,

$$\begin{aligned} f(x)= & {} a(1+N)^s + c2^s - 1 \end{aligned}$$

(9)

$$\begin{aligned} f(x)= & {} ab^x +cd^x -1 \end{aligned}$$

(10)

and the derivative of the function f(x) is,

$$\begin{aligned} f'(x) = ab^x ln(b) + cd^x ln(d) \end{aligned}$$

(11)

Thus with $x_{1} = x_{0} - \frac{f(x_{0})}{f'(x_{0})}$ iteratively repeats until $f(x) \approx 0$ the value of x is obtained to derived the value of $q_{v}$.

4.3 Experiment strategy

The experiments were run on both VF and synthetic data [multivariate normal (MVN) generated data] which consists of 12,159 and 1500 records respectively. However, in order to avoid bias in the VF experiments, the data is resampled every iteration resulting in 1580 records.

A synthetic dataset was constructed as a verification tool for the SMC approach. Three samples (2500 in length) are generated from three multivariate normal distributions (15 variables each). Each distribution has a different mean vector and different positive semi definite covariance matrix. The samples are then concatenated to form a single 45 variable dataset of 2500 samples in length. Each row in the dataset is given a class label defined by which 15 variables (from the original datasets) have the highest average. For example, if the first 15 variables of a given row have a larger average than the second or third set of 15 variables, then the class label is “1”. That is, if the first 15 variables of a given row have a larger average than the second or third set of 15 variables, then the class label is “1”, if the second 15 variable average is the largest then the class label is “2”, for the third 15 variables “3” (as depicted in Figure 4). The process (data generation) is repeated until the distribution of the three classes are approximately equal. The expectation is that the SMC approach will be able to reverse engineer the original structure of the underlying data generation process, i.e. three clusters of 15 variables each.

Fig. 4

Visualisation of synthetic dataset for defining target variable class

The GSA and SA algorithms were used in the experiments presented in this paper. The experiments were modelled using three modelling strategies that is 10 folds cross validation (10FCV) (Zhang 1993), 2 folds cross validation (2FCV) with 10 repeats and no fold cross validation (NoCV). The classifier used in modelling is NBU. Each of the experiment strategies was run for 25 times. Statistical values such as mean, maximum, minimum of the prediction accuracy and convergence point of the search are observed. These results are tabulated and compared between the optimisation methods and the modelling strategies.

4.4 Simulated annealing

The SA algorithm has been selected as a comparison method with GSA since previous work (Jilani et al. 2016; Vincent et al. 2017) have shown that SA is a very competitive search method and can outperform a number of standard methods (random mutation hill climbing and random restart hill climbing). We have also used the same strategy for determining the SA algorithms parameters (initial temperature and cooling rate) from previous work (Swift et al. 2004). Within our formal experiment on SA, the initial temperature (Eq. 15) obtained from a simulation in which the summation of different fitness function evaluations (Eq. 13) is computed from a number of iterations. The simulation was run for 5000 iterations and upon obtaining the initial temperature, the formal experiment of SA resumes for another 95,000 iterations to complete 100,000 iterations as per the GSA experiment. The cooling rate of SA is then computed using Eq. 14.

$$\begin{aligned} T_{0} = \frac{f}{n} \end{aligned}$$

(12)

where n is 5% from the formal experiment of SA.

$$\begin{aligned} f= & {} \sum _{i=1}^{n}\triangle f_{i}=\sum _{i=1}^{n}|f'-f| \end{aligned}$$

(13)

$$\begin{aligned} T_{iter}= & {} \lambda ^{iter}T_{0} \end{aligned}$$

(14)

4.5 Generalised simulated annealing parameters

In the GSA optimisation method, preliminary experiments were conducted to find the suitable value for the $q_{a}$ and $q_{v}$ index. Experiments were run for 10,000 iterations (10 repeats) on both VF and synthetic data with 10-fold cross validation. Values range between 0.1 and 0.5 (Tsallis and Stariolo 1996) were applied in exploration experiments to determine the $q_{a}$. Tables 3 and 4 show the corresponding fitness value (predictive accuracy) and convergence point of the search to the $q_{a}$ for VF and synthetic data respectively.

Table 3 VF data parameter fitness value

Table 4 Synthetic data parameter fitness value

Our hypothesis is that the GSA method will converge earlier than SA, thus as tabulated in Table 3 and 4, $q_{a}$ values with the minimum averaged convergence were chosen for GSA experiments. Therefore, $q_{a} = 0.010$ and $q_{a} = 0.009$ were used in our experiments for VF data and synthetic data respectively. Thereafter, the correspondent values of $q_{v}$ for VF data and synthetic data were calculated using the Newton Raphson.

5 Results

This section presents initial experiments and the main result of this work. The main results include the model prediction accuracy, Weighted Kappa statistic (WK), convergence point and resultant clusters. Statistical values of the results for each modelling strategy are tabulated for comparison.

5.1 Initial experiment

Initial experiments (25 samples) were conducted to evaluate the classification performance on visual field data using 6NFB clustering arrangement. In this set of experiment, the data are prepared in the 6NFB clustering arrangement for classification. Additionally, another experiment (25 samples) was conducted with the same purpose, which the data were clustered first using K-Means before classification. Both experiments used Multinomial Naive Bayes Updatable classifier. The results from these experiments are obtained to be the benchmark for our study. The results are presented in following sub-sections:

6NFB experiment From Table 5, the average predictive accuracies of visual field data using the 6NFB are 83.27%, 83.90% and 83.65% for 10FCV, 2FCV and NoFCV respectively. On average result, 2FCV is slightly higher than the other two modelling strategies. However, the experiment recorded maximum accuracy of 85.31% with 10FCV.

K-Means clustering experiment Meanwhile, predictive accuracies from K-Means clustering arrangement experiment are consistently higher (slightly) than the 6NFB. On average, the predictive accuracies are 84.30%—10FCV, 84.22%—2FCV and 84.47%—NoFCV as shown in Table 6. The NoFCV modelling strategy recorded the highest predictive accuracy in the experiment with 86.27%.

Table 5 Prediction accuracy of visual field data using 6NFB (sampled data)

Table 6 Prediction accuracy of visual field data using K-Means resultants clusters (sampled data)

5.2 Predictive accuracy: visual field data

Both methods predict the VF data better using the 10FCV strategy with 88.48 % (Table 7) and 88.54% (Table 8) than 2FCV. The results of VF experiments show that the GSA method improves the prediction accuracy better than SA in all modelling strategies where the highest accuracy is 87.89% (average) in 10-fold cross validation (Table 8). From the result we note that the average accuracy of 2FCV is slightly lower than 10FCV and NoFCV. The WK values (average) in all experiments present poor agreement with the 6NFB that is less than 0.005. The best average WK value is recorded by the GSA method in 2FCV with 10 repeats (0.004 - Table 8). We compute the confidence intervals (95%) of the accuracy in these 25 experiments, Tables 9 and Table 10 show the confidence intervals for SA and GSA respectively. The 10FCV strategy has a higher accuracy range (upper and lower limits) in both methods. With the 10FCV modelling strategy, the GSA experiments show with a 95% confidence that prediction accuracy is between 88.002% and 87.765%.

Table 7 Prediction accuracy of SA for VF data

Table 8 Prediction accuracy of GSA for VF data

Table 9 Confidence interval of SA for VF data

Table 10 Confidence interval of GSA for VF data

Table 11 Prediction accuracy of SA for synthetic data

Table 12 Prediction accuracy of GSA for synthetic data

Table 13 Confidence interval of SA for synthetic data

Table 14 Confidence interval of GSA for synthetic data

5.3 Predictive accuracy: synthetic data

Tables 11 and 12 show the prediction accuracy of the synthetic data by modelling strategy for the SA and GSA method respectively. Prediction accuracy results in the synthetic data experiments were found higher in both methods and modelling strategies compared to visual field data (98.55%—SA and 98.59%—GSA). The synthetic results do not show any pattern in prediction accuracy in both methods and modelling strategies. However, the SA 10FCV outperforms the GSA 10FCV. Whilst with 2FCV and NoFCV, the GSA method accuracies are higher than the SA method. The significant difference between these 2 methods on synthetic data can be seen in the WK values. It can be concluded that the GSA recorded almost perfect WK (near 1.0) which agrees with the expected synthetic clusters of the 45 variables. Table 13 (SA) and Table 14 (GSA) show the 95% confidence intervals of the accuracy for the synthetic dataset. Confidence interval in the synthetic dataset was found has higher range in NoCV strategy in both methods (SA and GSA).

5.4 Convergence point

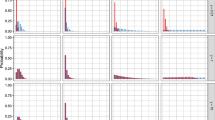
GSA methods are often described as having a very fast convergence in literature (Bohachevsky et al. 1986; Penna 1995; Tsallis and Stariolo 1996). Thus, the iteration point that the search has converged was captured. Since the fitness function of both datasets is noisy (as depicted in Fig. 5), we established a rule to determine the convergence point by calculating a noisy fitness tolerance. We define a noisy fitness function as one that returns different fitness values each time it is evaluated on the same solution. This will occur in this work due to both cross validation (different cross validation folds) and to sampling (a random pair of VF records is selected for each patient for each fitness evaluation). This is not uncommon and other noisy fitness functions can arise due to measurement limitations or the nature of training datasets used in modelling (Rattray and Shapiro 1998). From the graph shown in Fig. 5, the search has converged before reaching the 10,000th iteration, however within the convergence line, the fitness value (prediction accuracy) varies. This shows that with the GSA rule (acceptance probability) for searching for the best solution, poorer solutions with a certain degree of change are still being accepted. In order to cater for the inherent noisy nature of the fitness function an investigation into tolerance limits was conducted. We first ensure the fitness values in both data are normally distributed. We have shown that the fitness values are normal distributed (with p-value 0.49) and Table 15 shows the standard deviation of the data by methods and strategies.

Fig. 5

Convergence point of the synthetic data with the GSA method (10FCV)

Table 15 Standard deviation of the data

From Table 15, we found that the standard deviation of the fitness within the 10-fold experiments is very high. This strongly indicates that the fitness for this strategy is highly noisy. Using these standard deviation values, standard score (z-score) for each of the modelling strategy were calculated in order to derive a noisy fitness tolerance limit. The noisy fitness tolerance limits were calculated with z-score value 1.98 (Weiss 2013) which equivalent to 97.61% of the data lies under the defined limits (Table 16). The noisy fitness tolerance limits tabulated in Table reftab:14 are used to determine whether the change of fitness value is a significant change or not. At any point of the search that has change in the fitness value ($\triangle F$) within the limit are considered has no significant change. The different of fitness values is calculated using Eq. 15.

$$\begin{aligned} \triangle F = F_{t+1} - F_{t} \end{aligned}$$

(15)

Table 16 Noisy fitness tolerance

Table 17 tabulates the average of convergence point of the individual experiments for visual field data. It shows that the GSA method has converged fastest in 10FCV that is in average at iteration 2839. This also can be shown in Fig. 6 for the 25 experiment repeats convergence point in comparison with the SA method. However, for 2FCV modelling strategy, the SA method is far outperformed the GSA method with average 19,938 (GSA: 34,889). The synthetic data convergence point results (Table 18) are found consistent with the VF data. The best convergence point for the synthetic data was the GSA method in 10FCV (7328).

To support these convergence point results, we run simulations (25 samples) on the algorithms for SA and GSA on visual field data. The simulations comprised of the same experiments property as the main experiments including 100,000 iterations and Naive Bayes Multinomial Updatable classifier with 10FCV. The simulations were conducted to capture the runtime (in s) for the algorithms. In these simulations, the total effort of the experiments (entire SMC) and the effort for classification were captured. Classification effort includes data preparation within the iteration loops of the experiment. The algorithm effort in terms of runtime is obtained by subtracting the total effort and classification effort. The reason being is that based on our observation, classification effort in SMC is not part of the algorithm (SA and GSA) process and classification effort is dependent with number of moves which is more complex with high number of moves. From Table 19, our simulation experiments reveal that algorithmic computation time is taken by the fitness function where the GSA algorithm only took 1.67% (meanwhile SA took 6.40%) from the total effort of SMC. This figure indicates that GSA is 4.74% more efficient than SA.

Table 17 Average convergence point of VF data

Fig. 6

Convergence point of VF data For 10FCV

Table 18 Average convergence point of synthetic data

Table 19 Algorithm effort runtime

5.5 Resultant clusters

The clusters size of each experiment was captured to see the range of clusters size searched by the algorithms. We note that VF data experiments with the SA method tend to get lower clusters size when the number of fold cross validation is decreasing. There are 12–18 (minimum–maximum), 7–17, and 6–15 clusters sizes with the mode 15, 12 and 10 for 10FCV, 2FCV and NoFCV respectively. However the GSA method has range between 3–12 (minimum–maximum) clusters size for both 10FCV and 2FCV with 10 repeats, and 3–14 clusters size for NoFCV. All modelling strategies of the GSA method have the same mode value of clusters size that is 7 clusters.

For the synthetic data, the range clusters size are 4–6 (minimum–maximum), 3–4, and 4–7 in SA method for 10FCV, 2FCV with 10 repeats, and NoFCV respectively. Knowing that the correct cluster size for the synthetic data is 3 clusters, we found that the GSA method searches the clusters better than the SA method with the range of clusters size are 4–5, (minimum–maximum), 3–4, and 4–4 for 10FCV, 2FCV with 10 repeats, and NoFCV respectively (with mode: 4, 3, and 4). Also, 2FCV strategy is the efficient strategy finding the right cluster in the synthetic data when the WK value is very near to 1.0.

6 Discussion

Empirical observation on the experiments found that GSA appears to be an effective algorithm to find good solutions (with high WK) in the synthetic data with 2FCV modelling strategy as far as the reverse-engineer is concerned. In terms of prediction accuracy (synthetic dataset), there was less significant difference (with only 0.04%) between SA and GSA, where NoFCV and 10FCV have better prediction than 2FCV. Having slightly higher accuracy in 10FCV and NoFCV can be due to a bias element and overfitting (Varma and Simon 2006).

Fig. 7

Convergence point of VF data For 10FCV

However, in the real data experiments, WK statistics indicate poor agreement between the resultant clusters and the 6NFB. WK metric is not the main criteria to indicate a quality solution (clustering arrangement) because the 6NFB is just a common practice being used in clinical. Furthermore, the motivation of this research is to find any other clustering arrangements in visual field data that can highly predicts the AGIS score using an advanced optimisation method in SMC. Our finding is that 10FCV appears to be the best modelling strategy in SMC as this strategy consistently produced higher accuracy in both methods, where GSA slightly outperformed SA. This finding corresponds to Kohavi (1995).

Additionally, from our initial experiments results for K-Means and the 6NFB classification, SMC with GSA has improved 3.90% and 3.42% prediction accuracy (average results) from the 6NFB and K-Means respectively.

In terms of algorithm efficiency for SMC, GSA has proven in our experiments to be more efficient than SA as the convergence points are best recorded in GSA with 10FCV (both datasets). The GSA method was 8.80% faster than the SA in visual field data, while it was 12.25% faster in the synthetic data. In contrast, the SA method is faster than the GSA in 2FCV in both data (14.95% and 14.88% visual field and synthetic respectively). Whilst, our analysis results on algorithms effort runtime have shown that GSA only took 1.67% from the total effort of the SMC process (meanwhile SA used up 6.40% from the total SMCs runtime). This shows that GSA is 4.74% more efficient than SA in terms of SMCs runtime.

Apart from the analysis of the experiments results on prediction, convergence and resultant clusters size, we extended our analysis to visualise the resultant clusters by mapping the VF locations on the VF grid map. Mapping the VF locations on the grid is to comprehend the pattern of visual loss suggested by our algorithms. The highest prediction accuracy of the GSA was selected for this analysis. Therefore, the resultant clusters from the GSA method in 10FCV (88.54% accurate with 8 clusters) are visualised in the 54 locations VF grid map (Fig. 7). From the visualisation of the clusters, we found that the larger clusters size appears on the periphery of vision. This can be seen from the Fig. 7 that clusters 2 and 4 are on the periphery of the VF grid. Also, it exhibits that cluster 2 locations are near to the blind spot as well as cluster 5 which only in the center of the grid. These findings positively correspond to the clinical evidence that glaucoma first starts at the periphery and near to the blind spot.

7 Conclusion

In this paper we have presented SMC that has been tailored with the GSA algorithm to solve discrete optimisation problems. The method is arguably more efficient in solving problems that have multiple local optima, in that it is less likely to get trapped near a sub-optimal point in the search space (Tsallis and Stariolo 1996). Our proposed algorithm in SMC for the problem has shown improvement in predictive accuracy by 3.90% and 3.42% compared to the 6NFB and K-Means respectively. Furthermore, GSA appears to be compatible with SMC in terms of efficacy where our evaluation on convergence points have shown significantly faster (with 10FCV) than SA. Also, we have discovered that GSA uses little effort in the SMC process compared to SA (evaluated in algorithms runtime).

The visiting distribution ($q_{v}$) in the GSA method makes it distinct from the other annealing methods. This parameter is responsible for controlling how the search space is explored, allowing the method to locate high quality clustering arrangements of the VF data in an efficient manner. The findings conclude that the GSA algorithm outperforms the SA method in terms of convergence point, which the algorithm effectively locates the best clusters of VF as well as improving the predictive accuracy and an efficient method in the search.

The effectiveness of the algorithm is also proven in our synthetic data experiments where the correct clusters underlying the data were found in 24 out of the 25 experiments (with a WK of 1.0) with 2FCV modelling strategy. Furthermore, the WK results of the other 2 strategies (10FCV and NoFCV) of GSA also outperformed SA in the synthetic data.

Based on the positive finding from our study, a number of research opportunities can be considered in future work. Application of SMC using an advanced optimisation method and datasets manipulation can be further explored to reduce noisy fitness found in this work. This includes applying an operator for solution selection in the algorithm that could possibly reduce noisy fitness and by segmenting the data according to early, moderate and advance glaucoma. Secondly more extensive experiments are needed to explore the visiting index and probability index of the GSA algorithm. We note that the exploration of these parameters could be delegated to an automatic configuration algorithm, for example Lpez-Ibez et al. (2016) and Hoos (2012). The range of parameters for GSA can be established for a certain domain of problems based on a dataset’s nature and the choice of fitness function as a reference. Furthermore, improving algorithmic performance and developing a tool for clinicians would help in providing better treatments for glaucoma patients and help in understanding the nature of visual deterioration of the disease.