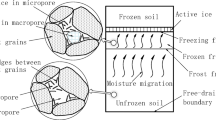
Abstract
The transversely isotropic (TISO) constitutive and frost heave models for the freezing of fine-grained soils are more accurate than the isotropic model and simpler than the orthotropic models. First, in combination with the mesoscopic composition of freezing soils, a mechanical model for the interaction between the equivalent ice lens and the soil in frozen soils is established based on the series and parallel models in the theory of composite mechanics. Second, the TISO constitutive model together with the analytic expression of five elastic constants is provided for analysis of the freezing soils. Third, a preliminary elastoplastic model for TISO freezing soil is established based on the Hill plastic model. Fourth, the heat–moisture–deformation coupling TISO model and the hydrodynamic frost heave model are derived according to a thermodynamics equation, a soil water motion equation, and generalized Hooke’s law. Synchronization and uniformity of the TISO constitutive model and the TISO frost heave model are realized for analyzing the interaction between permafrost soils and buildings. Finally, an indoor standard frost heave test and the frost heave of a prototype canal are simulated based on the above models. The numerical results indicated that the models presented in this paper accurately described the frost heave and revealed the interaction between permafrost and buildings.
Similar content being viewed by others
1 Introduction
Approximately 17% of the northern hemisphere is permanently frozen ground (permafrost) and another 34% are seasonally frozen soils [42]. In China, seasonal frozen soils occupy an area of 513.7 km2, which is 53.5% of the total area of the 13 related provinces’ municipalities and autonomous regions. The areas underlain by permafrost and seasonally frozen soils experience serious engineering problems. Statistics indicate that 83% of the canals in the highly irrigated district of Heilongjiang have suffered frost damage due to inappropriate anti-frost heaving measures. In Jilin and northern Xinjiang, more than half of the concrete trunk and branch canals exhibit different degrees of frost heave damage. In the Hetao region of Inner Mongolia, approximately 70% of the hydraulic buildings exhibit various degrees of freezing and thawing damage. In the Shule area of the Gansu Province, before repair operations, 54% of the canals had serious frost heave damage and lost their anti-seepage properties. Therefore, safe operation of the canals cannot be guaranteed. Both construction and safe operations of these systems in cold areas are severely restricted by permafrost foundations. For example, before 2015, frost-induced uplifting of foundation piles resulted in the Harbin–Dalian and Panjin–Yingkou high-speed railways reducing their operating speeds to 200 km/h in winter, which is considerably lower than the standard speed of 300–350 km/h. The physical and mechanical properties of frozen soil and frost heave models must be thoroughly understood for construction projects in cold regions.
There are two main reasons that cause damage of structures in seasonally frozen ground: the heaving and thawing settlement of the foundation soil. Owing to wider capillary water migration under the same temperature and moisture conditions, fine-grained soil has a higher frost heave sensitivity than other soil types. In addition, a recent study [25] has demonstrated that with a sufficient water supply, significant frost heave can also occur in gravel with a limited amount of fine material. Frost heaving and freezing in soils are complex physical processes. Frost damage appears during repeated freezing and thawing cycles of the soil throughout the engineering life cycle. In particular, frost damage is the result of long-term repeated interactions between the soil and a superstructure. In this process, soil heaving is caused by phase transitions of the water in the soil from fluid to solid, but settlement is due to reverse phase transition. For an accurate analysis of the interaction between permafrost and buildings, accurate models of permafrost constitutive and frost heave are required. A frost heave model considers various factors, such as soil hydrodynamics, the physics of frozen soils, frozen soil mechanics, thermodynamics, and engineering mechanics. For example, the rigid ice model [28, 32] and the segregation potential model [12, 13, 27] can accurately explain the formation of an ice lens. However, these models are primarily used to simulate one-dimensional freezing of saturated homogeneous soils. The dissipation of an ice lens in the rigid ice model has been rarely reported. In addition, the interaction between frozen soils and building has rarely been considered. The HFHM [5, 6, 8, 21, 23, 34], also known as the thermal–moisture–deformation coupled model or physical field model, cannot adequately describe the characteristics of the generation and elimination of the ice lens, but they have an advantage in the determination of the macro-characteristics of the temperature distribution, water migration, frost heave, and thaw settlement. Numerous indoor and field monitoring results [8, 9, 11, 16, 31] have shown that HFHM is suitable to describe the energy and mass transfers during the freezing and thawing processes. In addition, the physical field model also can be used to describe the coupled process in the frozen fringe. A separate-ice frost heave model, proposed by Zhou et al. [44], can describe the growth of a single ice lens by extending the thermal–moisture model and the formation of a new ice lens using Gilpin’s theory. Furthermore, HFHM is highly compatible both with the nonlinear dynamics model [15, 40] and with the contact model [20, 36, 43] for permafrost. A centrifuge model and numerical modeling of a cold-region canal were conducted by Li et al. [19]. The models indicated that the HFHM-computed temperature perfectly agreed with the measured results, but had less accurate results regarding deformation along the lining. This was likely due to complicated multidirectional freezing.
Generally, the HFHM assumes that frost heave occurs when the total water content (ice content plus unfrozen water content) of the feature unit is larger than the critical pore volume [5, 10, 18]. Deformation of the unit is then assumed to be evenly distributed in all of the dimensions and independent of the temperature gradient. The constitutive and frost heave models are considered to be ISO models. The empirical formula for the elastic constants of the frozen soils can be obtained according to the composition of the physical components using the mixed law [24]. The aforementioned two assumptions imply that the models ignore the directionality and distribution of the growth of the ice lens under a temperature gradient, which conflicts with the freezing and frosting evolution and microstructure of the frozen soil. Therefore, a realistic coupled thermal–moisture–deformation model is required to accurately reflect the composition, mesoscopic structure, and frost heave evolution. Additionally, the model should be able to describe the orthogonality of the frost heave and the microstructure of the frozen soil in the direction of the temperature gradient and frozen fronts. An appropriate coupled thermal–moisture–deformation model needs to contain a constitutive model and a model for frost heave in frozen soils.
The ISO constitutive model has been widely used. However, it is inconsistent with the profile of layered ice lenses. The orthotropic constitutive model is more realistic than the ISO constitutive model. However, it is complicated by having nine elastic constants, which cannot be easily determined using tests. Transversely isotropic (TISO) constitutive models combine the advantages of the aforementioned two models. TISO models have been widely used. Studies have indicated that fine-grained frozen soils belong to TISO materials. Most frozen soil tests involve triaxial tests with a constant temperature and overburden without water supply, creep tests, and frost heave tests. Up to now, there has been no feasible method or device that can directly determine the TISO elastic constants for frozen soils. Although a few mechanical parameters can be obtained using tests, the testing process is too complicated to effectively utilize in multiphysical coupled simulations. Therefore, a TISO constitutive model has been proposed for the theoretical calculation of the elastic constants of frozen soils [38]. However, the constitutive model does not consider the static balance between the ice and soil and does not take into account their deformation compatibility. Furthermore, the TISO constitutive models are seldom built for frozen soils. Even though plastic or creep models for ISO frozen soils have been studied since the 1970s [14], related models for TISO frozen soils have not been reported.
In this study, the serial model and parallel model are proposed on the basis of both the mesoscopic profile of fine-grained frozen soils and the theory of composite mechanics. This is done by assuming an ideal bond between the ice layers and soil layers. The elastic constants of TISO frozen soils with ice lenses are derived by combining the primary equations of Hooke’s law, equilibrium equations, and strain compatibility equations. In addition, in terms of the strength index of frozen soil at the principle directions, an elastoplastic model for TISO frozen soils is proposed based on the Hill orthotropic plasticity theory. Furthermore, a modified HFHM for freezing soils is presented that considers the evolution of the thermal–moisture–deformation interaction and the TISO characteristics of freezing soil.
2 Frost heave characteristics of freezing fine-grained soils
The results of the indoor unidirectional freezing test [33] indicated that when the freezing front is irregularly developing during freezing, the ice lenses and the dehydrated soil layers form laminated structures in the frozen zone on the mesoscale (Fig. 1). Furthermore, soil particles, unfrozen water, crystal ice, air, and small serial cracks were present in the frozen zone because of the complex formation process of the fine-grained soils. Therefore, obvious macroscopic differences were observed in the linear and nonlinear mechanical performances of the frozen soils along their principal directions. Arenson et al. [1] considered that fine-grained soils had a clear stratification in the frozen zone when the ice content was between 10 and 90%. Results from a series of unconfined unidirectional freezing tests and an expanded foundation model test [37] indicated that the frozen silt could be modeled as TISO under natural freezing conditions. Correspondingly, the nine elastic constants of the orthotropic constitutive model can be reduced to five in the TISO constitutive model. Moreover, Wang et al. [39] developed an empirically nonlinear constitutive model for TISO frozen silt on the basis of the axial and lateral deformations observed in unconfined uniaxial compression tests, which were performed at temperatures ranging from −9 to −5 °C.
Snapshots of a cylinder sample of frozen clay in a freezing test by Taber [33], indicating that the ice lenses and dehydrated soil layers formed alternately laminated structures during freezing. a Clay frozen without overburden. b Clay frozen under pressure of 15 kilograms per square centimeter
The physical properties of a frozen soil depend on the freezing process. Uniaxial freezing tests of frost-susceptible soils indicate that migration of the moisture in fine-grained soils exhibits directional dependence during freezing. Initially, due to a high temperature gradient near the cold boundary, the frozen fringe advances quickly from the cool side to the warm side. Rapid cooling causes in situ freezing of the water in soil. Heaving results in water migration being impeded by a dispersive ice crystal. As the temperature gradually decreases, the frozen front acts as a sink. Water migrates continuously if a temperature gradient exists and an external water supply is available. If the sum of the unfrozen water and accumulated ice exceeds the pore volume in the soil, layers of clear ice may form parallel to the surface due to considerable frost heaving. Moreover, unconfined uniaxial frost heave tests of fine-grained soil indicate that thermal expansion along the temperature gradient direction is larger than that along the perpendicular direction. Thus, the frozen fine-grained soil deforms in a TISO manner rather than in an ISO manner, which determines different macroscopically mechanical properties and frost heave. Therefore, the TISO constitutive model is more reasonable than the ISO constitutive model for describing both frost heaving and the interaction between frozen soil and a foundation.
To predict the mechanical behavior of a TISO frozen soil in a construction project, the material constants must be first obtained. However, few laboratory tests have been conducted on the mechanics of an ice-embedded frozen soil due to such reasons as inhomogeneous distribution, environmental sensitivity, and large uncertainties of the basic material properties. An analytical method for determining the elastic constants of frozen soil with a lenticular structure is presented in this paper.
3 Transversely isotropic elastic constants for frozen soils with ice lenses
The elastic moduli and Poisson’s ratios can be used to determine the characteristic features of the freezing processes of frost-susceptible soils. Ice provides mechanical bonds on the interface between a soil particle and the bedding planes. The ice lenses and soil layers in the representative volume element (RVE) are assumed to possess deformability. Furthermore, the soil with lenticular structure can be considered as a single-layered composite when the REV is suitably large. In the local Cartesian coordinate system, anisotropy of material occurs in the 2-direction, that is, the direction of the heat flow lines (Fig. 2). The principal material axes are aligned with the coordinate axes, respectively. Material in planes 1–3 shows isotropic (ISO) behavior. The strain vector is defined as ε = [ε11, ε22, ε33, γ12, γ23, γ31]T, and the stress vector is defined as σ = [σ1, σ2, σ3, σ11, τ12, τ23, τ31]T. εii and σi represent the normal strain and stress along the i-direction, respectively. γij and τij represent the shear strain and stress, respectively.
3.1 Anisotropic character of frost heave
The frost heave of frozen fine-grained soil exhibited temperature dependence due to the formation of the ice lens [22, 37]. Hence, a dimensionless quantity, ξ (the frost heave partition coefficient), is used to illustrate the anisotropy of the volumetric growth. The plastic strain increment can be defined as follows:
where εvh,123 is the plastic strain tensor for the entire frozen composite due to volumetric growth in the local system. The volumetric contents of unfrozen water and ice and the initial porosity are represented as θw, θi, and θ0, respectively. The value of ξ ranges from 0.33 to 1.0 for the ISO growth and unidirectional growth of ice lenses.
3.2 Stiffness matrix of frozen soil
Conventionally, the five independent elastic constants in the TISO constitutive model are the Young’s modulus and Poisson’s ratio in planes 1–3 (E1 and υ13, respectively), Young’s modulus and Poisson’s ratio in the 2-direction (E2 and υ12, respectively), and the shear modulus in the 2-direction (G12). The stiffness matrix reads:
where
By assuming deformability, the serial model and the parallel model [45] can be used to estimate the elastic constants and unbalanced shear force between the ice and soil layers due to different Poisson’s ratios of contents. The elastic modulus and Poisson’s ratio for the ice and soil matrix are represented as Ei, υi, Em, and υm, respectively. The volume of the ice lenses and soil in an RVE are represented as θi and θm = 1 − θi, respectively. The stresses at the interface are represented as σji and σjm (j = 1, 2, 3 are the principal material axes in Fig. 2).
3.2.1 Serial model
A modified serial model that considers the deformability and the interlayer interaction is used to estimate the elastic constants of the frozen soil along the 2-direction (Fig. 2a). The RVE is assumed to be subjected to an axial load, σ2, along the 2-direction. The equilibrium along the 2-direction suggests σ2i = σ2m. The frictional force between the layers is absent if the deformation of an individual layer is either independent or the layers have the same Young’s modulus and Poisson’s ratio. Then, the effective elastic constants of the RVE can be obtained using the general rule of mixtures. For consistent lateral deformation of the two layers, the interactions parallel to the interface (σ1i, σ3i, σ1m, and σ3m) are nonzero because of the interfacial adhesion and the differences between the Poisson’s ratios for ice and soil. Considering symmetry in the planes 1–3, then:
The equilibrium equations and deformability along the principal axes yield:
Hence,
For a cubic element within the calculated domain, Hooke’s law reads:
By substituting Eqs. 6 and 7 into Eqs. 5 and 8, the strain components of the RVE along the principal axes can be represented using the elastic constants of soil and ice. Hence:
and the two elastic constants of the element, E2 and υ21, can be obtained. They are:
3.2.2 Parallel model
The parallel model accounts for deformability and is suitable for predicting the linear elasticity of frozen soil in the symmetric plane (planes 1–3 in Fig. 2b). The RVE is assumed to be subjected to an axial load, σ1, along the 1-direction. The equilibrium equations and deformability along the principal axes satisfy the following:
Hooke’s law can be expressed as:
By combining Eqs. 13–15, we have:
By substituting Eqs. 16–19 into Eqs. 14 and 15, we have:
The three elastic constants, E1, υ12, and υ13, can be also obtained.
3.2.3 Shear modulus
It is assumed that the layers do not separate under shear deformation if an ideal bond exists between them. Thus, the two layers have the same shear strain. Therefore, the equilibrium equation and Hooke’s law can be written as:
where τ12, γ12, and G12 are the shear stress, engineering shear strain, and effective shear modulus, respectively, in the planes 1–2. Substituting γi = γm = γ12 into Eqs. 26 and 27, G12 reads:
In most analyses of frozen ground engineering, the plane strain model is adopted. The computation will be performed in an arbitrary global coordinate system x–y. The strain increments due to frost heave and the stiffness matrix can be transformed to the x, y coordinate system using the following transformation rule:
where \(\beta\) is the angle between axis y and the local 2-direction (heat flow direction). It will be synchronously updated as the temperature field changes.
3.3 Ideal plastic model for transversely isotropic frozen soil
In this study, the Hill orthotropic plasticity was applied for describing the elastoplastic behavior of transversely ISO frozen soil. In a complex stress state, the plastic strain rate is generally expressed as [29]:
A quadratic yield function, Fy (and associated plastic potential, Fy = Qp), in a local coordinate system is given by the orthogonal principal axes [7]:
The six parameters F, G, H, L, M, and N are related to the state of anisotropy and can be expressed as:
Here, σysi represents the tensile yield stress in the principle direction and τysij represents the yield shear stress on the planes i–j.
For transversely ISO material, F = H and L = N. Hence, the yield function can be rewritten as:
For ISO plasticity, the elastic region satisfies Qp < 0, and the yield surface is defined by Qp = 0.
4 Frost heave modeling with the coupled heat–moisture–deformation model
4.1 Thermal field
The principles of energy, mass, and energy dissipation can be formalized within a multiphase media. Similarly, considering water migration and phase change, the energy conservation principle can be written as:
By neglecting the volumetric heat capacity of air, the semiempirical formulas are used to estimate Cv and λ [4]:
where T is the temperature; Cv is the effective volumetric heat capacity; λ is the thermal conductivity; θ is the volume of the soil; Lf is the latent heat of fusion of water per unit mass; and t is time. The subscripts p, w, i, and a represent the soil particles, water, ice, and air, respectively. Equation 34 does not contain the terms with respect to the heat transport through water flow and the mechanical work.
4.2 Hydraulic field
Recently published research that used molecular dynamics [41] indicated that the unfreezable threshold corresponds to pore diameter and the adsorption of the soil. This is further evidence for the analogy of the freezing and drying processes [2]. Therefore, Richard’s equation can be used to describe the fluid movement with a source term related to ice formation [3]:
The simplified van Genuchten [35] equation for the soil–water characteristic curve (SWCC) can be extended to describe the relationships among the unfrozen water content, matric potential, and hydraulic conductivity:
where h is the matric potential (negative water suction); C = dθw/dh is the specific moisture capacity; k and ks are the hydraulic conductivities for unsaturated and saturated soils, respectively; Se is the effective saturation; and θs and θr are the volumes of the saturated and residual water, respectively. Water density ρw = 1000 kg/m3 and ice density ρi = 931 kg/m3. i is the unit vector in the direction of gravity. α and m are the empirical parameters of the SWCC.
Assuming thermodynamic equilibrium at the ice–pore–water interface is maintained in an infinitesimal time interval, the rate of ice content can be derived using the chains rule with the generalized Clapeyron equation, as follows:
where T0 = 273.15 K is the nominal freezing temperature and Tf is the freezing temperature for unsaturated soil.
4.3 The stress–strain field
The governing equation for the stress field is the Navier equation, which incorporates the equation of motion, strain–displacement correlation, and constitutive relationship. For a static problem, the equation of motion can be written in the general tensor format as:
where u is the displacement vector; D is the fourth-order tensor of material stiffness; and F is the body force vector.
The strain–displacement equation is:
The constitutive equation is:
where σ is the Cauchy stress tensor and ε, εel, εvh, and εp are the infinitesimal strain tensor, elastic strain tensor, volumetric plastic strain tensor by frost heave, and plastic strain tensor by stress, respectively.
4.4 General boundary condition
The general boundary conditions, which include one or more of the Dirichlet, Neumann, and Robin boundary conditions, are expressed as:
where n is the outward normal unit vector of a boundary; u is the dependent variable of the individual field; c is a conductivity term; ζ is the conservative flux convection coefficient; γ is the source in the subdomain; q is the boundary absorption coefficient; δ is the boundary source; hT is a matrix representing the flexibility of the constraint type; and μ is the matrix of the Lagrange multiplier.
5 Model implementation
Equations 1 and 34–40 express the variables and the governed equations that frame heat–moisture–deformation coupling in frozen soil. A frost heave model that accounts for the lenticular structure of the fine-grained soil can be developed by combining Eqs. 2, 11, 12, 23–25, and 28–33. The equations must be solved numerically because of the high nonlinearity of the variables and the immediate updating of the local coordinate system for each element with respect to the temperature gradient. The coupled multiphysical model was solved by using COMSOL for the cross-platform finite element analysis of the coupled systems of partial differential equations.
6 Validation of the transversely isotropic frost heave model
A standard laboratory uniaxial frost heave test and field measurements of canals were performed to validate the TISO model for frozen soil. Moreover, a generalized ISO frost heave model was applied for comparison. For the ISO constitutive model, the dimensionless quantity, ξ, was set as 1/3, and the elastic constants were given by the general rule of mixtures:
For ISO plasticity, yield stresses satisfied σys1 = σys2 = σys3 = σys0 and τy23 = τys31 = τys12 = τys0.
6.1 Simulation case I: standard uniaxial frost heave test and simulation
First, two of the experimental results presented by Penner [30] were repeated using numerical simulations. Both the length and the diameter of the soil column were 10 cm. The level of the external water supply was controlled to be aligned with the top of the cell. The temperature ramp rate was − 0.50 °C/day, and the temperature gradient was 0.33 °C/m in Test 1. In Test 2, the temperature ramp rate was − 0.50 °C/day with a temperature gradient of 0.12 °C/m. The initial temperature of the cold end was set at 0 °C. The sides of the samples were thermally insulated. Moreover, an axial load of 50 kPa was applied. The simulation parameters listed in Table 1 were set according to the experimental data and the relevant literature [26]. The dimensionless quantity, ξ, was 0.9 for anisotropic deformation in the TISO model [22]. Under such a small axial load, the plastic behavior of the soil was not considered.
Comparisons of the experimental and simulated results are shown in Fig. 3. The TISO and ISO models indicated that the total frost heaving increases approximately linearly with time. Obviously, the TISO model agreed more accurately in both tests. The absolute errors for the TISO model were 0.64 mm in Test 1 and 0.57 mm in Test 2, whereas those for the ISO model were − 2.90 mm in Test 1 and − 1.29 mm in Test 2.
6.2 Simulation case II: monitoring and simulation of prototype canal frost heave
Li [17] observed a prototype of frost heave in a large U-shaped concrete canal. The test was conducted at the loess terrace on the east coast of the Qianhe River in the Fengjia mountain irrigation area in Baoji, China. The test canal flows from west by south to east by north, where sunny and shady slopes are clearly distinguished. The designed discharge is 58 m3/s. The canal depth is 5.1 m, with a 7.1-m-wide opening. The arc radius of the canal bottom is 3.2 m, and the canal is inclined against a wall at 10°. The canal featured a 10-cm thickness of shotcrete lining. Eleven points of measurement, N1–S1, were symmetrically deployed in the canal basin for observing and measuring the frozen depth and frost heave. Figure 4a illustrates the cross section of the canal and the distribution of the measurement points.
Four rows of water inlets with an 8-cm-diameter and 1.5–4-m-deep opening were established on both sides of the test canal to supply water and soak the soil in the canal with water for two months before freezing occurred in the canal. The perched water table was observed 3.5–4 m beneath the canal after water was supplied. Observation started from November 14 to March 28 of the subsequent year when the daily average temperature was higher than 0 °C. Maximum frost depth and frost heave were observed on January 24.
The observed soil was silty clay containing 6.8–12.8% gravel, 55.2–62.6% fine particles, and 27.0–38.0% clay, indicating frost-susceptibility. The following properties were also experimentally determined: specific gravity = 2.71; liquid limit = 29.2–31.6%; plastic limit = 17.7–19.0%; cohesive force = 11–68 kPa; and the internal friction angle = 24.5°–31.5°. Regarding thermodynamic parameters, Cp = 3.09 × 106 J m3/K and λp = 1.85 W/(m K). In terms of hydraulic parameters, θs = 0.41, θr = 0.03, α = 0.21 m−1, m = 0.22, and ks = 3 × 10−6 m/s. Em = 10.2 MPa and υm = 0.44. The dimensionless quantity of frost heave for loess was ξ = 0.7 [39]. Other fundamental physical constants are listed in Table 1. The basic material parameters of concrete are: density ρc = 2300 kg/m3, thermal conductivity λc = 1.8 W/(m·K), volumetric heat capacity Cc = 2 × 106 J·m3/K, elastic modulus Ec = 25 GPa, and Poisson’s ratio υc = 0.33.
For the TISO plasticity of the frozen soil, σys1 = 0.2877 |T| + 0.5, σys2 = 0.2549 |T| + 0.5, τys12 = 0.18 |T| + 0.10, and τys31 = 0.425 |T| + 0.10. The unit of yield stress is MPa, and if the soil temperature is greater than 0 °C, only constant terms are used. It is noted that the slope terms of the yield shear stresses, τys12 and τys31, were determined from the adfreeze bond strength test and shear test, respectively. For the ISO model, the yield stresses are conventionally taken as σys0 = σys2, τys0 = τys31.
A two-dimensional thermal–moisture–deformation coupled finite element model of the test canal was developed. Analysis was performed for 72 days, which began on November 14 to January 24 of the subsequent year. Figure 4b shows the mesh and boundary condition control of the finite element model.
The origin of the global Cartesian coordinate system of the model was consistent with the circle in the bottom arc of the canal. The dimensions of the model are of 20 m in length and 13.38 m in width. According to Saint–Venant’s Principle and numerical analysis experience, uneven distribution of hydraulic, thermal, and stress fields in the canal only occurred within one to two times the area of canal sections. The left and right boundaries of the model were kept to be thermally insulated (∂T/∂n = 0) and impermeable (∂h/∂n = 0), and the left and right and bottom boundaries were set as a directional hinged constraint (∂u/∂n = 0). It was assumed that the underground water level was located 3.2 m from the bottom of the canal (y = − 7 m) and, before calculation, the water content of soil had reached equilibrium under gravity. Therefore, Richards’ equation for a steady-state solution was used to obtain the initial hydraulic field of the base soil. It was assumed that the soil had completed consolidation before testing. Therefore, the initial stress field of the model could be determined by using the gravity static analysis method. Boundaries of the initial soil temperature and bottom constant temperature were consistent with the temperature of the supplied water, that is, 13 °C. Ambient temperature was described in terms of a trigonometric function based on the measurement results of the three groups of daily average temperature as follows:
where Tamb (°C) denotes the daily average ambient temperature of the upper surface of the model and t(d) denotes the number of days in a cycle starting from January 1. Combined with the observation date, the equation yields t = 318 days when the observation commences and t = 389 days when frost depth and frost heave reach peak values.
Under the influence of solar radiation and a local winter monsoon, the canal test exhibited distinctive characteristics of sunny and shady slopes. To eliminate the effects of the two aspects on the hydraulic, thermal, and stress fields, the convective heat transfer coefficient (hc) along the upper surfaces was determined using an inversion thermal–moisture–deformation coupled finite element analysis through the observed frost depth data at t = 389 days. The obtained convective heat transfer coefficients (unit: W/m2 K) for each measurement point are as follows: hcN1 = 0.45, hcN2 = 0.30, hcN3 = 0.60, hcN4 = 1.10, hcN5 = 1.40, hc0 = 1.85, hcS5 = 1.50, hcS4 = 1.60, hcS3 = 1.28, hcS2 = 0.95, hcS1 = 1.45. The convective heat transfer coefficients of the ground surfaces in the north and south coast of the canal are hcNW = 0.55 and hcSE = 0.99, respectively. The inversion results, displayed in Fig. 5, indicate that the calculated frost depth and the observed results are basically consistent, with an absolute error ranging from − 3.38 cm to 2.63 cm.
Similar to the comparative analysis method adopted in Case I, the ISO model and TISO model of frozen soils were compared. The numerical results of the normal frost heave in the lining of the canal and the normal stress at the bottom of the lining at t = 389 days are shown in Fig. 6. The numerical results demonstrate that the normal frost heave deformation and the normal stress distribution considering TISO are both fundamentally consistent with actual measurements. The normal frost heave of the canal lining increased with frost depth, and the frost heave of the shady (north-facing) slope was greater than that of the sunny (south-facing) slope. Maximum frost heave appeared along the top of the canal because of a lesser lining constraint and its double-direction freezing of the lining surface and ground surface. The bottom of the canal exhibited relatively distinctive frost heave deformation because of the frost depth and water supply. At measurement point 0, the absolute error of the normal frost heave and normal stress were 0.64 mm and − 25 kPa. The normal frost heave and normal stress were 8.96 mm and − 104 kPa with respect to the actual measurement 8.32 mm and − 129 kPa, respectively.
Simulation results along the lining at t = 389 days when the frost heave reaches a maximum, and the variation in normal displacement of the measurement points with elapsed time. a Frost heave comparisons. A positive value indicates that the lining deformed toward the inner portion of the canal; otherwise, it occurred toward the base. b Normal stress comparisons at the bottom of the canal lining. A positive value indicates that the bottom of the canal lining suffered tension; otherwise, it suffered compression. c Normal displacement with respect to the TISO model versus elapsed time. TISO transversely isotropic
The frost heave analysis result using the ISO model showed a nonpositive correlation between frost heave and frost depth at the measurement points. The U-shaped lining was subjected to symmetrical extrusion, which caused the bottom of the canal to deform toward the base soil. The normal frost heave at measurement point 0 at the bottom of the canal was − 3.52 mm, and the actual measurement was 8.32 mm, indicating an absolute error of − 11.84 mm.
As shown in Fig. 6c, the amount of frost heave was positive and was primarily related to the depth of freezing. However, due to asymmetric frost heaving of the shady slope and sunny slope, the canal lining tended to tilt toward the sunny slope. At the beginning of the frost heave (t = 357–373 days), N4 showed a distinct normal displacement toward the foundation because of the hysteresis of freezing at the sunny slope. After that, the lining played a certain role of constraint in the frost heaving process of the foundation soil, especially at the canal bottom. Also, the normal displacements of the measured points at shady slope (N5–S2) exhibited a stepped increase with freezing time.
The effective plastic strain distribution calculated with the elastoplastic model at t = 389 days is shown in Fig. 7. It can be seen that the ground frost within a 70 cm depth received various degrees of yielding due to the lining confining. The effective plastic strain occurred in the range of N3–S2. The maximum of the effective plastic strain was approximately 0.019 and occurred at approximately point S5.
7 Discussion
7.1 Equivalence of micro-ice lenses and soil
In the derivation of TISO elastic constants, the freezing of microstructures into ice lenses was considered. However, it was found that an accurate approach needs to be developed to distinguish distribution problems concerning pore ice and ice lens volume. The mixing rule model should be adopted for individual elastic constants estimations of the soil layers with dispersive pore ice. Hence, series models and parallel models should be further employed for finding the equivalent elastic behavior of frozen soil that contains ice lenses and soil layers. However, in freezing fine-grained soils, the soil layers between ice lenses showed dewatering rather than a constant saturation during decreasing temperatures. Therefore, this influence was not considered in the present study.
7.2 Quantitative analysis of transversely isotropic elastic constants and ice contents
A comparison of E1 in Eq. 23 and the mixing rule calculation, Eq. 45, shows that the first two terms in both equations are identical, but Eq. 23 contains the correction term of the elastic constants and volumes for the ice and soil. A dimensional analysis revealed that this value was slightly smaller than the square (1%) of the difference of the soil–ice Poisson’s ratios. The removal of this correction term led to a negligible error when compared with the elastic modulus (MPa) of the soil matrix, Em. Similarly, a comparison of υ12 in Eqs. 24 and 45 showed that the equivalent Poisson’s ratio obtained using the mixing rule equation was identical to that of the first two terms in the υ12 equation. The difference was also the square of υ. However, compared with υ, it bore the same weight and thus should not be omitted. In contrast, a greater difference of the elastic constants was obtained in other main directions.
Figure 8 illustrates the relationship among the change of ice content, θi, the TISO elastic modulus, and Poisson’s ratio when Em = 46 MPa, υm = 0.4, and Ei = 6000 MPa, υm = 0.3. Figure 8a shows that the curve of the elastic modulus, E1, is parallel to the direction of the ice lenses, which increases linearly with the ice content. As the correction term of E1 is omissible, based on the mixing rule model, there is an overlap between E1 and the equivalent elastic modulus EISO. The curve of E2, which is vertical to the direction of ice lenses, performs as an S-shaped function and increases with the ice content, θi. In this case, the two inflection points appeared at θi = 0.05 and θi = 0.8, respectively. Within the range of θi from 0.05 to 0.8, E1 ≫ E2 and had no significant change.
Relations between the elastic constants of frozen soils and ice content described using the ISO and TISO models with a soil elastic modulus Em = 46 MPa, Poisson’s ratio υm = 0.4, and ice with Ei = 6000 MPa, υi = 0.4. a A comparison of the elastic moduli with increasing ice content. b A comparison of Poisson’s Ratio with increasing ice content. ISO isotropic, TISO transversely isotropic
Similarly, Fig. 8b shows that Poisson’s ratio, υ12, first increases and then slowly decreases to the value of the ice Poisson’s ratio, υi. υ21 quickly dropped to υi when θi < 0.2 and thereafter showed no significant change as θi increases. The variation magnitude for υ13 is maximized for increasing θi, and υ13 quickly decreases when θi < 0.2. When θi is between 0.2 and 0.8, υ13 exhibits minimal change (almost a straight line), quickly regressing to υi when θi > 0.8. The equivalent Poisson’s ratio, υISO, based on the mixing rule model decreases linearly to the Poisson’s ratio of ice as θi increases. When θi = 0.1, υISO has maximum difference with the Poisson’s ratio obtained in the present study. The maximum difference between υISO and υ13 is approximately 0.32.
When θi is between 0.2 and 0.8, Poisson’s ratio of the ice lens, υ13, reflects a horizontal straight line. This result matches well with the results given by Arenson et al. [1] who reported that frozen soil can be considered a TISO material when ice makes up 10–90% of the soil. Therefore, additional verification is required to judge the feasibility of determining the value of υ13 using Eq. 25 to make sure the frost-susceptible soil easily forms ice lenses, or to analyze the problem of distinguishing pore ice and ice lenses by using the initial and final points of the horizontal section of a curve.
7.3 Interaction between ice and soil layers
The assumption of an ideal bond between the ice layers and soil layers is essential for the derivation of elastic constants in this study. In fact, the clay characteristics of frozen soil (e.g., unfrozen water content) and temperature directly influence the bond and coordinated deformation. Hence, when frozen soil temperature and unfrozen water content are high during the initial freezing stage, the ice lens is affected by unfrozen water film, which may result in a minimal nonsynchronous slip or cause soil particles to move. This slip process deviates somewhat from this assumption. However, when frozen soil is constrained by overburden pressure and ice crystals of the freezing fringe, the effect of this slight deviation is negligible.
When the stress of the frozen soil is greater than the yield stress, failure (bend, fold, and fracture) of ice lenses in the soil easily occurs, with a possible slip between ice lenses and the soil bodies. In fact, the mechanism of the interaction between ice lenses and soil is complex. Therefore, a reasonable approach should be developed to examine and establish a standard thermal–moisture–deformation coupled transversely ISO nonlinear constitutive model.
7.4 Frost heave partition coefficient ξ
Uneven frost heaving of frozen soil involves complex coupling of multiple physical fields and is closely related to the particle grade of soil and the interaction between soil particles and ice crystals. The mechanism of uneven frost heaving has never been reported. Estimations of frost heave partition coefficients can only be obtained by using specific tests or parameter inversion.
The calculation results of case I show that the frost heave partition coefficient is not sensitive to the cooling rate for a specified type of soil. In case II, the frost heave partition coefficient can be approximated as a constant in the two-dimensional frost heaving analysis of complex temperature boundaries.
8 Conclusions
Based on the natural frost heaving deformation process and mesoscopic composition of fine–grained soil, with the assumption of an ideal bond between ice and soil, a typical micro-soil–ice series model and parallel model for frozen soil with ice lenses were established in this study by using deformation coordination, force equilibrium, and Hooke’s law. Subsequently, the TISO constitutive model of frozen soil was presented, and the expressions for the five independent elastic constants were derived on the basis of mechanics of composites. The following conclusions were drawn.
First, an improved theoretical method for solving TISO elastic constants was improved in this study. It overcame the disadvantage in the mixing rule theory, which can only approximately describe the elastic constant in symmetry in the plane (planes 1–3), but fails to reflect the other four elastic constants of transversely ISO frozen soil.
Second, a preliminary elastoplastic model for TISO frozen soil was established based on Hill plastic theory.
Third, a TISO frost heave model and numerical method for frozen soils were established based on the thermal–moisture–deformation coupling theory. Synchronous coupling and uniformity of the TISO constitutive model and the TISO frost heave model were realized for frozen soils with alternately laminated ice lenses structures. This approach overcame the drawbacks of previously used models, such as the rigid ice and segregated ice models, which are only applicable for one-dimensional freezing of saturated soil. Therefore, this approach bridged the research gap of the hydraulic frost heave model, which cannot consider the TISO mesoscopic composition of frozen soil and the uneven frost heave evolution.
Fourth, a standard indoor ramped freezing test together with the freezing process of a prototype canal freezing process was simulated using the thermal–moisture–deformation coupling finite element method. Results indicated that the TISO constitutive model for freezing fine-grained soil was more accurate than the ISO constitutive model. The analytical expressions of the elastic constants for frozen soil with ice lenses derived in this study are essential for deeply understanding the interaction between freezing fine-grained soils and buildings in a complex environment and with complex boundaries.
Finally, the stress equations for ice lenses and soil pressure were proposed for estimating ice pressure in frozen soil.
References
Arenson LU, Springman SM, Sego DC (2007) The rheology of frozen soils. Appl Rheol 17(1):12147. https://doi.org/10.3933/ApplRheol-17-12147
Beskow G (1935) Soil freezing and frost heaving with special application to roads and railroads. Soil Sci 65(4):355
Celia MA, Bouloutas ET, Zarba RL (1990) A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour Res 26(7):1483–1496. https://doi.org/10.1029/WR026i007p01483
de Vries DA (1963) Thermal properties of soils. North-Holland Publishing Company, Amsterdam
Guymon GL, Luthin JN (1974) A coupled heat and moisture transport model for arctic soils. Water Resour Res 10(5):995–1001. https://doi.org/10.1029/WR010i005p00995
Harlan R (1973) Analysis of coupled heat–fluid transport in partially frozen soil. Water Resour Res 9(5):1314–1323. https://doi.org/10.1029/WR009i005p01314
Hill R (1948) A theory of the yielding and plastic flow of anisotropic metals. Proc R Soc A 193(1033):281–297. https://doi.org/10.1098/rspa.1948.0045
Jame YW, Norum DI (1980) Heat and mass transfer in a freezing unsaturated porous medium. Water Resour Res 16(4):811–819. https://doi.org/10.1029/WR016i004p00811
Karra S, Painter S, Lichtner P (2014) Three-phase numerical model for subsurface hydrology in permafrost-affected regions. Cryosphere 8(5):1935–1950. https://doi.org/10.5194/tc-8-1935-2014
Kay BD, Groenevelt PH (1974) On the interaction of water and heat transport in frozen and unfrozen soils: I. Basic theory; the vapor phase 1. Soil Sci Soc Am J 38(3):395–400. https://doi.org/10.2136/sssaj1974.03615995003800030011x
Kelleners TJ (2013) Coupled water flow and heat transport in seasonally frozen soils with snow accumulation. Vadose Zone J. https://doi.org/10.2136/vzj2012.0162
Konrad JM, Morgenstern NR (1980) A mechanistic theory of ice lens formation in fine-grained soils. Can Geotech J 17(4):473–486. https://doi.org/10.1139/t80-056
Konrad JM, Morgenstern NR (1982) Prediction of frost heave in the laboratory during transient freezing. Can Geotech J 19(3):250–259. https://doi.org/10.1139/t82-032
Ladanyi B (1972) An engineering theory of creep of frozen soils. Can Geotech J 9(1):63–80. https://doi.org/10.1139/t72-005
Lai Y, Yang Y, Chang X, Li S (2010) Strength criterion and elastoplastic constitutive model of frozen silt in generalized plastic mechanics. Int J Plast 26(10):1461–1484. https://doi.org/10.1016/j.ijplas.2010.01.007
Lai Y, Zhang X, Yu W, Zhang S, Liu Z, Xiao J (2005) Three-dimensional nonlinear analysis for the coupled problem of the heat transfer of the surrounding rock and the heat convection between the air and the surrounding rock in cold-region tunnel. Tunn Undergr Space Technol 20(4):323–332. https://doi.org/10.1016/j.tust.2004.12.004
Li A (1987) Frost heave in big U-shaped concrete canals. Yellow River 4:8
Li N, Chen B, Chen F, Xu X (2000) The coupled heat–moisture-mechanic model of the frozen soil. Cold Reg Sci Technol 31(3):199–205. https://doi.org/10.1016/S0165-232X(00)00013-6
Li S, Lai Y, Zhang M, Pei W, Zhang C, Yu F (2018) Centrifuge and numerical modeling of the frost heave mechanism of a cold-region canal. Acta Geotech. https://doi.org/10.1007/s11440-018-0710-1
Liu J, Wang T, Tai B, Lv P (2018) A method for frost jacking prediction of single pile in permafrost. Acta Geotech. https://doi.org/10.1007/s11440-018-0711-0
Liu Z, Yu X (2011) Coupled thermo-hydro-mechanical model for porous materials under frost action: theory and implementation. Acta Geotech 6(2):51–65. https://doi.org/10.1007/s11440-011-0135-6
Michalowski RL, Zhu M (2006) Frost heave modelling using porosity rate function. Int J Numer Anal Methods Geomech 30(8):703–722. https://doi.org/10.1002/nag.497
Miller R (1972) Freezing and heaving of saturated and unsaturated soils. In: 51st Annual meeting of the Highway Research Board, Washington District of Columbia, 17–21, January, Highway Research Board, United States
Ning J, Zhu Z (2007) Constitutive model of frozen soil with damage and numerical simulation of the coupled problem. Chin J Theor Appl Mech 23(7):70–76. https://doi.org/10.6052/0459-1879-2007-1-2006-177
Niu F, Zheng H, Li A (2018) The study of frost heave mechanism of high-speed railway foundation by field-monitored data and indoor verification experiment. Acta Geotech. https://doi.org/10.1007/s11440-018-0740-8
Nixon J (1991) Discrete ice lens theory for frost heave in soils. Can Geotech J 28(6):843–859. https://doi.org/10.1139/t91-102
Nixon JF (1975) The role of convective heat transport in the thawing of frozen soils. Can Geotech J 12(3):425–429. https://doi.org/10.1139/t75-046
O’Neill K, Miller RD (1985) Exploration of a rigid ice model of frost heave. Water Resour Res 21(3):281–296. https://doi.org/10.1029/WR021i003p00281
Owen DRJ, Hinton E (1980) Finite elements in plasticity, theory and practice. Pineridge Press Limited, Swansea. https://doi.org/10.1002/nme.1620170712
Penner E (1986) Aspects of ice lens growth in soils. Cold Reg Sci Technol 13(1):91–100. https://doi.org/10.1016/0165-232X(86)90011-X
Shang S, Li X, Mao X, Lei Z (2004) Simulation of water dynamics and irrigation scheduling for winter wheat and maize in seasonal frost areas. Agric Water Manag 68(2):117–133. https://doi.org/10.1016/j.agwat.2004.03.009
Sheng D, Axelsson K, Knutsson S (1995) Frost heave due to ice lens formation in freezing soils: 1. Theory and verification. Hydrol Res 26(2):125–146. https://doi.org/10.2166/nh.1995.0009
Taber S (1930) The mechanics of frost heaving. J Geol 38(4):303–317. https://doi.org/10.1086/623720
Taylor GS, Luthin JN (1978) A model for coupled heat and moisture during soil freezing. Can Geotech J 15(4):548–555. https://doi.org/10.1139/t78-058
Van Genuchten MT (1980) A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci Soc Am J 44(5):892–898. https://doi.org/10.2136/sssaj1980.03615995004400050002x
Wang W, Lu TH, Sun BX (2007) Mathematical model for shear stress-strain relationship of soil-concrete interface during shear fracture process. Key Eng Mater 348–349:881–884. https://doi.org/10.4028/www.scientific.net/KEM.348-349.881
Wang Z, Zhang C (1999) Nonlinear finite element analysis of interaction of orthotropic frozen ground and construction. Chin Civ Eng J 32(3):55–60
Wang ZZ, Mu S-Y, Niu YH, Chen LJ, Liu J, Liu XD (2008) Predictions of elastic constants and strength of transverse isotropic frozen soil. Rock Soil Mech 29(s1):475–480
Wang ZZ, Yuan S, Chen T (2007) Study on the constitutive model of transversely isotropic frozen soil. Chin J Geotech Eng 29(8):1215–1218
Wei M, Guodong C, Qingbai W (2009) Construction on permafrost foundations: lessons learned from the Qinghai–Tibet railroad. Cold Reg Sci Technol 59(1):3–11. https://doi.org/10.1016/j.coldregions.2009.07.007
Zhang C, Liu Z (2018) Freezing of water confined in porous materials: role of adsorption and unfreezable threshold. Acta Geotech 13(5):1203–1213. https://doi.org/10.1007/s11440-018-0637-6
Zhang T, Barry RG, Knowles K, Ling F, Armstrong RL (2003) Distribution of seasonally and perennially frozen ground in the Northern Hemisphere. In: 8th International conference on permafrost, Zürich, 21–25 July, Switzerland, AA Balkema Publishers, pp 1289–1294
Zhi W, Yu S, Wei M, Jilin Q, Wu J (2005) Analysis on effect of permafrost protection by two-phase closed thermosyphon and insulation jointly in permafrost regions. Cold Reg Sci Technol 43(3):150–163. https://doi.org/10.1016/j.coldregions.2005.04.001
Zhou GQ, Zhou Y, Hu K, Wang YJ, Shang XY (2018) Separate-ice frost heave model for one-dimensional soil freezing process. Acta Geotech 13(1):207–217. https://doi.org/10.1007/s11440-017-0579-4
Zhu YL (1980) Fiber reinforce plastic structural design. China Architecture and Building Press, Beijing
Acknowledgments
This work was supported by the State Key Research and Development Plan “Water Resource Efficient Development And Utilization” Key Special Project of China (Grant No. 2017YFC0405101); the National Natural Science Foundation of China (Grant No. 51279168); the 12th Five-Year Science and Technology Support Plan of China (Grant No. 2012BAD10B02); the Ministry of Education Doctoral Funds of China (Grant No. 20120204110024); the Postdoctoral Science Foundation of China (Grant No. 2014M552494); and the Postdoctoral Science Foundation of Shaanxi Province of China. We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, Q., Wang, Z., Li, Z. et al. Transversely isotropic frost heave modeling with heat–moisture–deformation coupling. Acta Geotech. 15, 1273–1287 (2020). https://doi.org/10.1007/s11440-019-00774-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-019-00774-1