1 Introduction

The Lane–Emden (LE) equation [3, 5, 10] is one of the simplest nonlinear equations appearing in astrophysics. It describes balance in gaseous medium described by polytropic equation, between gravity that tries to squeeze it and internal pressure that try to prevent such collapse.

It is used in astrophysics as a first approximation to the more complicated star structure models [3, 5, 7, 10] and recently for describing molecular cloud cores [22]. Some exact solutions [19] are known and are useful in solving (matching) problems in which the interior is described by LE equation and the exterior area by some other equation. Such exact solutions appear also for higher space dimensions [15] and can be used for representation of symmetric Riemannian manifold with constant curvature as conformal flat model [20].

However, apart from applications, the LE equation is the simplest nonlinear equation that arises from the radial part of the Laplace operator in flat space with a nonlinear term. Therefore, it serves also as a building block for more complicated nonlinear differential equations, e.g., nonlinear wave equation with power-type nonlinearity [1, 13]. There are various kinds of generalization for this equation described (e.g., in [8, 11, 16, 17]). These solutions pose an interesting structure of movable singularities (singularities of analytic solutions) [14, 17, 17] and some flavor of the Painlevé analysis for them was provided in [8].

The main aim of this paper is to perturb the generalized Lane–Emden equation [4, 7, 16, 17, 17]:

$$ \frac{d^{2}u(x)}{dx^{2}}+\frac{\alpha} {x} \frac{du(x)}{dx}+\delta u(x)^{p}=0, $$
(1)

where α and δ are positive real constants and p > 1 is a natural number.

It is assumed that the perturbed equation of Eq. 1 is in the following form:

$$ \begin{array}{c} p(x)\frac{d^{2}u(x)}{dx^{2}}+q(x)\frac{du(x)}{dx}+ r(x)u(x)+\delta u(x)^{p}=0, \\ p(x) = (1+a_{-1}x+a_{0}x^{2}+\ldots+a_{n}x^{n+2}), \\ q(x) = \left( \frac{\alpha}{x}+b_{-1}+b_{0}x+\ldots+b_{n}x^{n+1}\right),\\ r(x) = \left( c_{-1}\frac{1}{x}+c_{0}+\ldots+c_{n}x^{n}\right), \end{array} $$
(2)

where n > − 1 is a natural number, and α > 0 and δ≠ 0 are real constants. The restriction imposed on the coefficients \(\{a_{k}\}_{k=-1}^{n}\), \(\{b_{k}\}_{k=-1}^{n}\) and \(\{c_{k}\}_{k=-1}^{n}\) will be given below. The polynomials p,q, and r are introduced into equations as new (fixed) singularities in the complex plane, and by a suitable change of coordinates, we can assume that the closest singularity to the origin is located at x = 1, which results in:

$$ p(x)=(1-x)\bar{p}(x)=(1-x)(1+\bar{a}_{-1}x+\ldots+\bar{a}_{n-1}x^{n}+\bar{a}_{n}x^{n+1}), $$
(3)

where \(\bar {p}(x)\) has zeros in the complex plane that are farther from the origin than 1. The coefficient correspondence is given by \(\bar {a}_{-1}=a_{-1}\), \(a_{k}=\bar {a}_{k+1}-\bar {a}_{k}\) for k ∈{0,…,n − 1} and \(a_{n}=-\bar {a}_{n}\).

It will be explained how to find the solution of boundary problem - find analytic solution(s) which connect these two fixed singularities atx = 0 andx = 1. The procedure that constructs such kind of analytic solutions and therefore provides a solution for this nonlinear (singular) boundary value problem will be the main topic of this paper.

This problem can be used to construct solutions of Eq. 2 on the unit interval and match it for some x > 1 with a solution to some other equation due to analyticity and therefore it is important in applications.

By deformation of the unit interval onto some smooth curve in the complex plane we will get a general problem of finding analytic solutions on such a curve that connects two (not necessary closest) fixed singularities of the deformed equation (1). The assumption on the smoothness of the curve is important as we do not want to introduce additional singularities along it.

Equation 2 is general enough to describe many problems that arise in mathematical physics. For example, the equation:

$$ (1-x^{2})\frac{d^{2}u(x)}{dx^{2}} + \left( \frac{\alpha}{x}+\beta x\right)\frac{du(x)}{dx} - \gamma u(x) + \delta u(x)^{p}=0, $$
(4)

appears in [1, 13, 14] for some special values of parameters as the equation for self-similar (analytic) profiles of nonlinear wave equation in flat spacetime on the unit interval. In this paper, the general theory for such a kind of equations will be provided and Eq. 4 will be analyzed as an example for real parameters: α > 0, β, γ and δ≠ 0.

The paper is organized as follows: In the next section, the existence of some special singular solution at x = 0, which is a crucial ingredient for global analytic solution on the interval [0;1], will be given, and then the local existence of the analytic solutions around the singular point x = 0 and x = 1 will be proved. Then, the next section presents the general discussion of the existence of global solutions on the unit interval. Finally, an example of the application of the results of the paper will be presented in Eq. 4. In Appendix, some technical results are collected for the reader’s convenience.

2 Local Existence

2.1 Local Solution at x = 0

For the existence of the global analytic solutions on the unit interval, the following singular solution at x = 0 will be of paramount importance:

$$ u_{\infty}(x)=b_{\infty}x^{a}, \quad b_{\infty}=\left( \frac{2[\alpha(p-1)-(p+1)]}{\delta(p-1)^{2}}\right)^{1/(p-1)}, \quad a=\frac{1}{1-p}. $$
(5)

Therefore, first, the class of Eq. 2 which has the solution (5) is singled out by the following:

Proposition 1

If Eq. 2allows the solution (5) then the coefficients have to fulfill the followingconditions:

$$ a(a-1) a_{k}+ab_{k}+c_{k}=0, \quad k \in \{-1,\ldots,n\}, $$
(6)

whereais defined in Eq. 5.

Proof

The proof is straightforward. Substituting (5) into (2) and collecting terms of the same order in x, we obtain:

$$ [b_{\infty}(a(a-1)+\alpha a) + \delta b_{\infty}^{p}]x^{a-2}+\sum\limits_{k=-1}^{n}b_{\infty}[a(a-1)a_{k}+a b_{k}+c_{k}]x^{a+k}=0. $$
(7)

The term at xa− 2 vanishes, which is exactly the definition of b∞. In addition, if Eq. 5 is the solution of Eq. 2, then all the other coefficient terms have to vanish, which gives the condition (6). □

Hereafter, we assume that Eq. 2 fulfills (6), and therefore (5) is a solution.

The next proposition shows the existence of local analytic solutions at x = 0 for Eq. 2 and their behavior for large initial data u(0) = c.

Proposition 2

There exist analytic solutions of Eq. 2atx = 0 with initial datau(0) = c.

For large c, the asymptotic of this analytic solution of Eq. 2at fixedx0within its radius of convergence is described by scaled asymptotics of thegeneralized Lane–Emden equation, namely (see also Eq. 46in Appendix):

$$ u_{\pm}(x_{0},c)\approx b_{\infty} x_{0}^{-2/(p-1)}(1 \pm A_{0} c^{-\frac{\alpha+3+p(1-\alpha)}{4}} x_{0}^{\frac{\alpha+3+p(1-\alpha)}{2(p-1)}}\sin(\omega \ln(c^{\frac{p-1}{2}}x_{0})+\phi), $$
(8)

wherep ≠ pQ, odd andf(p, α) < 0, where:

$$ p_{Q}:=\frac{\alpha+3}{\alpha-1}, $$
(9)
$$ f(p,\alpha):=(-1+\alpha)^{2}+p^{2}(9-10\alpha + \alpha^{2})-2p(-3-6\alpha+\alpha^{2}), $$
(10)

and where:

$$ \omega(p,\alpha)=i\frac{\sqrt{-f(p,\alpha)}}{2(p-1)}. $$
(11)

Here, A0 and ϕ are constants.

Proof

First, we have to prove that there exists a local analytic solution at x = 0. If we rewrite (2) in the form:

$$ \left\{ \begin{array}{l} xu^{\prime} = xv \\ xv^{\prime} = \frac{-1}{1+{\sum}_{k=-1}^{n}a_{k}x^{k+2}}\left( \alpha +v{\sum}_{k=-1}^{n}b_{k}x^{k+2}+ u{\sum}_{k=-1}^{n}c_{k+1}x^{k+1}+x\delta u^{p}\right) \end{array} \right. $$
(12)

The second equation has the following form:

$$ xv^{\prime} = -\alpha v + x g(x,u,v), $$
(13)

where g is analytic at x = 0. Therefore, using Proposition 5 from Appendix, we conclude that there is an analytic solution at x = 0 expressible in a power series form, in which the first term is initial data c = u(0). It can be found by a formal procedure of substituting a formal power series \(u(x)={\sum }_{k=0}^{\infty }h_{k}x^{k}\) into Eq. 2 and obtaining recurrence for the coefficients hk of this series. Then, the above statement assures us that this formal series is convergent—it is a solution.

For proving the asymptotic (8), Eq. 2 will be transformed into the generalized Lane–Emden (1) and Proposition (7) of Appendix will be used. We use the substitution from [1, 13]:

$$ u = c w, \qquad y=c^{\gamma}x,\qquad \gamma = (p-1)/2 $$
(14)

which transform Eq. 2 into (\('=\frac {d}{dy}\))

$$ w^{\prime\prime}+\frac{\alpha}{y}w^{\prime}+\delta w^{p}=-\frac{1}{c^{p}}\left( w^{\prime\prime}\sum\limits_{k=-1}^{n}a_{k}\frac{y}{c^{k\gamma+1}}+w^{\prime}\sum\limits_{k=-1}^{n}b_{k}\frac{y^{k+1}}{c^{k\gamma+1}}+\sum\limits_{k=-1}^{n}c_{k}\frac{y^{k}}{c^{k\gamma+1}} \right). $$
(15)

In the limit c →∞, the RHS of Eq. 15 vanishes and we are left with the Lane–Emden (1). To make the limiting process precise, we start from the analytic solution at a point x0 within its circle of convergence of analytic solution. Then, we perform c →∞ limit termwise which transform the analytic solution into the series solution (43) for the LE —the solution of Eq. 15 with vanishing RHS and initial condition w(0) = 1. Using large y asymptotic of the LE (1) of the form (46) from Appendix, and returning to the original variables u and x, we obtain exactly (8), as claimed. □

The asymptotic (8) is analogous to Proposition 7 of Appendix, and results from the appearance of the LE (1) as a basic building block of Eq. 2. Loosely speaking, Proposition 2 shows that when the phase plane (u(x0);u′(x0)) fixed at x0 is considered, then the analytic solution of Eq. 2 behaves as the spiral (8) parametrized by c that wraps around the limit point:

$$ P_{\infty} = \left( b_{\infty} x_{0}^{-2/(p-1)}, -\frac{2}{p-1}b_{\infty} x_{0}^{-2/(p-1)}\right). $$
(16)

The same behavior shows the special case of Eq. 2 and it was described in [1, 13].

One can note that the proof does not depend on the condition (6).

An obvious Corollary for the Proposition 2 is:

Corollary 1

For a largeu(0) = cvalue, the analytic solutions have movable singularities located as for the analyticsolutions of the LE (1), among other movable singularities.

Proof

Since (15) for c →∞ goes to Eq. 1, therefore during this process, the movable singularities of the analytic solution of Eq. 2 approach the movable singularities of Eq. 1 described in [17], i.e., they are located symmetrically around the origin on the rays connecting the origin with all p roots of − 1. □

This result ends our discussion of behavior of local analytic solutions at x = 0. We now pass on to the existence of the local solution at x = 1.

2.2 Local Existence at x = 1

In order to consider the local analytic solutions around x = 1, the new variable y = 1 − x is introduced. Equation 2 has now the form:

$$ \begin{array}{c} y\bar{p}(y)\frac{d^{2}u(y)}{dy^{2}}-q(y)\frac{du(y)}{dy}+ r(y)u(y)+\delta u(y)^{p}=0, \\ \bar{p}(y) = (A+A_{-1}y+A_{0}y^{2}+\ldots+A_{n}y^{n+2}), \\ q(y) = \left( \frac{\alpha}{1-y}+B_{-1}+B_{0}y+\ldots+B_{n}y^{n+1}\right),\\ r(y) = \left( c_{-1}\frac{1}{1-y}+C_{0}+\ldots+C_{n}x^{n}\right), \end{array} $$
(17)

where \(A= 1+ {\sum }_{l=-1}^{n}a_{l}\) and \(B_{-1}=b_{-1}-{\sum }_{l=0}^{n}b_{n}\).

On substituting formal powers series \(u(y)={\sum }_{l=0}^{\infty }d_{l}y^{l}\) and using the well-known Cauchy formula (42) from Appendix, the recurrence for dl coefficients is obtained:

$$ \begin{array}{c} d_{0}=b, \\ (l+1)(Al-B)d_{l+1}=f_{l+1}(d_{0},\ldots,d_{l}), \quad l>-1, \end{array} $$
(18)

where, as before, \(A= 1+ {\sum }_{l=-1}^{n}a_{l}\), B = α + B− 1 and fl+ 1is a polynomial function and b = u(y = 0) is the initial data at x = 1. Defining:

$$ k=\frac{B}{A}, $$
(19)

we have the following two cases:

  1. 1.

    k < 0 or k > 0, noninteger: There is infinite recurrence relations for the coefficients dl;

  2. 2.

    k ∈N (resonance condition): There is formal solution of the form u(y) = d0 + … + dkyk + dk+ 1(d0,…,dk,b)yk+ 1 + …, where the coefficients \(\{d_{l}\}_{l=k+1}^{\infty }\) are derived from the recurrence relation and the first k + 1 coefficients have fixed values that result from the set of polynomial equations:

    $$ \left\{ \begin{array}{c} f_{0}(d_{0})=d_{0}(C+d_{0}^{p-1})=0, \\ f_{1}(d_{0},d_{1})=0, \\ {\ldots} \\ f_{k}(d_{0},\ldots, d_{k})=0, \end{array} \right. $$
    (20)

    where C = c− 1 + C0. In principle, such a system can have complex-valued solutions.

The next step is to prove that these formal solutions are in fact solutions, i.e., they are convergent. It is immediate for finite-form solutions of the second case (when b is selected in such a way that dk+ 1 = 0). The structure of the formal solutions is similar to those for Eq. 4 with some specially selected values of parameters, and the convergence of this special case was given in the Appendix of [13]. Therefore, the proof for the convergence of formal power series of Eq. 17 is similar. The only difference is the multiplicity of coefficients. Therefore, we have:

Proposition 3

Formal analytic solutions of Eq. 17aty = 0 obtained above are in fact the solutions, i.e.,they are convergent in some neighborhood ofy = 0.

Proof

The idea of the proof is to transform (17) into the form required by Proposition 5 from [2] cited in Appendix. The proof is similar to those in the Appendix of [13] and therefore the sketch is only provided.

The proof depends on the value of k.

For k < 0, Eq. 17 can be transformed into:

$$ \left\{ \begin{array}{c} yu^{\prime}=yv \\ yv^{\prime}= kv-Cu-\delta u^{p}+yf(y,u,v), \end{array} \right. $$
(21)

where f(y,u,v) is some analytic function of arguments and k is given by Eq. 19. Introducing new variable \(\tilde {v}\) via:

$$ v=\tilde{v}+\frac{1}{kC}u+\frac{\delta}{k}u^{p}, $$
(22)

we get:

$$ \left\{ \begin{array}{c} yu^{\prime}=yg(y,u,v) \\ yv^{\prime}= kv+y\tilde{f}(y,u,v), \end{array} \right. $$
(23)

where again g and \(\tilde {f}\) are some analytic functions. Since k < 0, we can apply the aforementioned proposition which guarantees convergence of formal power series.

For non-integer \(\llcorner k \lrcorner < k < \ulcorner k \urcorner \), the general idea of the proof is as follows. First, the new function w(y) via:

$$ u(y)=d_{0}+{\ldots} + (d_{\llcorner k \lrcorner} + yw(y))y^{\llcorner k \lrcorner}, $$
(24)

is defined, where \(\{d_{l}\}_{l=0}^{\llcorner k \lrcorner }\) coefficients are given by the recurrence relation (18). Then, switching to the first order system of ODEs, removing constant terms, and diagonalizing linear parts, we arrive into the system required by Proposition 5.

The last part of the proof is also valid for k ∈N. □

The idea of the proof resembles the transformation to the normal form [12, 21]. As for x = 0, one can note that the proof does not depend on the condition (6) and therefore it is a general result for Eq. 2.

In the next section, a general discussion on the existence of global analytic solutions on unit interval will be given.

3 Global Existence of Analytic Solutions

In order to get global solution, generalization of the method proposed in [1] and developed in [13] will be used. For such general class as Eq. 2, we present only steps that can be done and not a strict algorithm—these steps have to be adjusted to the concrete equation under consideration. The steps are as follows:

  • Construct local analytic solutions at x = 0 (existence proved in Proposition 2) and prove that they can be extended toward x = 1.

  • Construct local analytic solutions at x = 1 (existence proved in Proposition 3) and prove that they can be extended toward x = 0.

  • Match theses local solutions at some point inside the unit interval to obtain the global solution.

For proving that there is no singularities along the unit interval, one can use some global methods, e.g., Lyapunov function (see [6, 21] for general reference on Lyapunov functions). If this is proved, then the local analytic solution can be extended along the real axis from x = 0 toward x = 1. Usually, the similar proof can be performed for the local analytic solution that starts from x = 1, and it can be shown that it can be extended to x = 0 along the real axis.

The proof of analytic continuation of local analytic solutions will be provided for a restricted class of Eq. 2, namely, we have:

Proposition 4

For\(\left (\frac {p^{\prime }(x)}{2}-q(x)\right ) < 0\),p(x) > 0 inx ∈ [0;1],a constantr(x) = r,and odd p, the local analytic solutions of Eq. 2aroundx = 0 andx = 1 described in the previous section can be extended along the unit interval,i.e., there is no (movable) singularities of the extended solutions in[0;1].

The assumption p(x) > 0 in the unit interval is not restrictive since the whole equation can be multiplied by − 1. There is p(x)≠ 0 in the unit interval since there is no (fixed) singularity of Eq. 2 in this interval by assumption.

Proof

The proof goes along the same line as in [1, 13] and based on the Lyapunov function

$$ H(x)=\frac{p(x)}{2}u^{\prime}(x)^{2}+\frac{\delta}{p+1}u(x)^{p+1}+\frac{r}{2}u(x)^{2}. $$
(25)

Its derivative on the solutions of Eq. 2 is:

$$ H^{\prime}= \left( \frac{p^{\prime}(x)}{2}-q(x)\right) u^{\prime 2} <0. $$
(26)

Since H is monotone on solutions, therefore denoting \(V_{min}=min_{u} \left (\frac {\delta }{p+1}u^{p+1}+\frac {r}{2}u^{2} \right )\) (p is odd and therefore global minimum exists), we have from H(x) ≤ H(0) the following estimate:

$$ \frac{p(x)}{2}u^{\prime}(x)^{2} < H(0) - V_{min}, $$
(27)

and therefore, since p(x) > 0 in [0;1], we get that |u′(x)| is bounded and the analytic solution extended from x = 0 toward x = 1 is also bounded.

For extension of the analytic solution at x = 1 toward 0, the following inequality will be used:

$$ \frac{-H^{\prime}}{1+H}\leq - \frac{p^{\prime}(x)-2q(x)}{p(x)}. $$
(28)

Integrating from x = 1 to some \(0<\bar {x} << 1\) and using the fact that the RHS is regular in this interval, we get that H is bounded and therefore u and u′ are finite as well. □

In the last step, analytic solutions extended from both endpoints have to be matched at some intermediate point x0 ∈ [0;1], as is presented in Fig. 1.

Fig. 1
figure 1

Matching of two local analytic solutions extended to x0 point

Full size image

The matching can be intuitively visualized when we analyze the situation on the phase plane at x0. Figure 2 presents the situation.

Fig. 2
figure 2

Matching of two local analytic solutions extended to x0 point. The cases 1, 2, and 3 belong to the same type of the equation with different values of coefficients. Case 4, topologically different from the previous ones, corresponds to the different equation. Wrapping point of C0 curve moves when the values of the equation’s coefficients are changing

Full size image

If we will vary c initial data of the solution starting from x = 0 then, as Proposition 2 states, we obtain the spiral that wraps around P∞, which is C0 curve. The second curve C1 is the image of the solution extended from x = 1, and it is parametrized by u(1) = b—the initial data at this endpoint. Each intersection of these curves is exactly C1 matching condition; moreover, it is analytical matching, because we match two analytic solutions.

Going along C1 curve, we start from b = 0—the trivial solution. Increasing b, we can get a few possibilities for the number of intersections:

  1. 1.

    In the first case, the C1 curve passes exactly through the wrapping point of the spiral—P∞. In this case, we obtain countable family of analytic solutions on unit interval (case 1 in the figure). For this case, the existence of u∞ solution, i.e., the condition (6), is required. It is obvious to explain why it is the case if we use continuous dependence of solutions on initial conditions with initial data that are slightly shifted from singular points x = 0 and x = 1, which however match these analytic solutions for some initial data specified at these singular points. The x = 0 solution “wraps around” (5). The second solution from x = 1 stays close to this point if we vary initial data b around b∞ value, therefore, also around (5).

  2. 2.

    The second curve can cross C0 in a finite number of points—a finite number of global solutions (case 2 in the figure). In this case, the condition (6) is slightly perturbed.

  3. 3.

    If there are some special solutions, like constant ones for the case of resonances for x = 1 solution (see also the next section for the example), then the second curve can cross C0 at one point which corresponds to this special solution (case 3 in the figure).

  4. 4.

    The second curve can also have only one point (0;0) (which corresponds to the trivial solution) with the C0 curve (case 4 in the figure).

The statements of this qualitative discussion will now be explained in the example in the following section.

4 Example

In this section, a simple example (4) that illustrates the above results and discussion is presented. It is a generalization of the equation analyzed in [1, 13, 14]. The other example of the class (2) is discussed in [18].

It is assumed that α > 0, β, γ and δ≠ 0 are real parameters for Eq. 4.

The condition for the existence of the solution (5) is of the form:

$$ \gamma = \frac{2}{1-p}\left( \frac{p+1}{p-1}+\beta\right), $$
(29)

and it is assumed that it is hereafter fulfilled. In addition, there exists the constant solution:

$$ u_{0}=\left( \frac{\gamma}{\delta}\right)^{1/(p-1)}:=b_{0}, $$
(30)

providing that γ > 0 (δ > 0 was assumed previously).

We start from analyzing local power series solution at x = 0, in which Proposition 2 assures to exist. On substituting formal power series \(u(x)={\sum }_{k=0}^{\infty }a_{k}x^{k}\) into Eq. 4, we get unique recurrence for the coefficients:

$$ a_{0}=c=\text{arbitrary}, \quad a_{1}=0,\quad a_{k+2}=\frac{[(k(k-1-\beta)+\gamma]a_{k}-\delta c_{k}}{(k+2)(k+1+\alpha)}, $$
(31)

where k ≥ 0 and ck can be computed from bk ones using Eq. 42 formula. This power series can be analytically continued from x = 0 to the vicinity of x = 1 along the real line without encountering any singularities. It can be proved by repeating the proof of Proposition 4 with additional assumptions, that p is odd, and δ > 0. To this end, we use the following Lyapunov function:

$$ H(u,u^{\prime};x)=(1-x^{2})\frac{u^{\prime 2}}{2}-\gamma \frac{u^{2}}{2}+\frac{\delta}{p+1}u^{p+1}. $$
(32)

We can shift this function by a constant (the minimum of polynomial in u consisting of the last two terms) to make it positively defined. Taking derivative and replacing u″ with the help of Eq. 4, we obtain:

$$ H^{\prime}= - \left( (1+\beta)x +\frac{\alpha}{x}\right) u^{\prime 2}. $$
(33)

the term in the bracket is positive on the unit interval when β > − 1 or β = 0 or when β < − 1 and α + β > − 1. Assuming this, we have that H′ < 0, therefore, H(0) > H(x) for 0 < x < 1. From this, we obtain immediately, as in [1, 13], that solution which is regular at x = 0 stays finite along the unit interval.

The solution at x = 1 can be obtained by introducing the variable y = 1 − x into Eq. 4, to obtain (′ = d/dy):

$$ y(2-y)u^{\prime\prime}-\left( \frac{\alpha}{1-y}+\beta (1-y) \right) u^{\prime} -\gamma u+\delta u^{p}=0. $$
(34)

Introducing a power series ansatz \(u(y)={\sum }_{k=0}^{\infty }b_{k}y^{k}\), we obtain the following recurrence for the coefficients:

$$ \begin{array}{@{}rcl@{}} &&b_{0}=b=\text{arbitrary}, \quad b_{1}=\frac{\gamma b_{0}-\delta c_{0}}{-(\alpha + \beta)},\\ &&b_{k+1}=\frac{k(3(k-1)-2\beta)b_{k}+\gamma b_{k}-\delta c_{k}+(k-1)(\beta+2-k)b_{k-1}-\gamma b_{k-1}+\delta c_{k-1}}{(k+1)(2k-\alpha-\beta)}), \end{array} $$
(35)

where ck can be computed from bk ones employing (42) formula. When α + β = 2k, where k ≥ 0 is a natural number, we obtain the resonance condition, which leads, as in [13], to the special class of the solutions described in Section 2.2. We will not discuss this class as it is analogous to the analysis in [13]. Therefore, we assume that − 1 < α + β < 0.

The convergence proof for the solution with the coefficients (35) is given by Proposition 3; however, it is instructive to provide the special case of this proof. To prove that this power series has nonzero radius of convergence, we rewrite it as a system of first-order ODEs:

$$ \left\{ \begin{array}{l} yu^{\prime}=yv \\ yv^{\prime} = \frac{1}{(2-y)(1-y)} ((\alpha +\beta (1+y^{2}-2y))v +\gamma(1-y)u-\delta (1-y)u^{p}. \end{array} \right. $$
(36)

We are allowed to use Proposition 5 if we remove the terms of u and up with constant coefficients. This can be done using the following change of variables:

$$ v = \bar{v} - \frac{\gamma}{\alpha+\beta}u +\frac{\delta}{\alpha+\beta}u^{p}, $$
(37)

which transforms (36) into:

$$ \left\{ \begin{array}{l} yu^{\prime}=yf(y,u,v) \\ yv^{\prime} = 2(\alpha+\beta) + yg(y,u,v), \end{array} \right. $$
(38)

where f and g are functions analytic in all of its variables around y = 0. From the fact that α + β < 0 and Proposition 5, we conclude that the solution (35) is convergent in some neighborhood of y = 0 (x = 1).

When 2k < α + β < 2(k + 1) or when a resonance condition occurs, namely α + β = 2k, for natural k, then the general proof is a simple modification of those from the Appendix of [13].

In next step, we show that the solution form x = 1 can be extended along the real line to x = 0. We use, as in [1] and [13], the following easy to check bound:

$$ \frac{-H^{\prime}}{H+1} < \frac{2\alpha}{x}, $$
(39)

from which it occurs, by integrating both sides, that u and u′ are bounded inside the unit interval if we start from solution (35) bounded at x = 1.

These results assure us that these two local solutions can be matched at some x0 inside the unit interval. This matching fits exactly the general scheme presented in the previous section: On the phase plane at x0, the solution form x = 0 gives a spiral which wraps around (5) solution. The second curve for solution at x = 1 crosses this spiral, such that every intersection gives a global solution. We can note that there will be at least two such intersections, which correspond to the u = 0 and u0 solution.

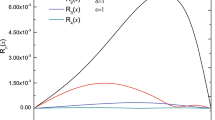
Figure 3 presents the case with many countable global solutions. For this case, condition (29) is fulfilled. If we now slightly perturb the equation coefficients that this condition is not fulfilled, then we get a finite number of intersections/global solutions, and in the end we are left only with two constant solutions. This is presented in Figs. 4 and 5.

Fig. 3
figure 3

Plot for α = 2, β = − 25/12, γ = 1/4, δ = 1. In this case, matching point x0 = 0.5, and wrapping point \(P_{\infty }=(\frac {\sqrt {2}}{\sqrt [3]{3}}; -\frac {2 \sqrt {2}}{3 \sqrt [3]{3}})\). The curve starts from (0;0) point and passes through \(P_{\infty }\) and integration was terminated at (b0;0) point

Full size image
Fig. 4
figure 4

Plot for α = 2, β = − 29/12, γ = 1/4, δ = 1. In this case, the matching point x0 = 0.5, and wrapping point \(P_{\infty }=(\frac {\sqrt {2}}{\sqrt [3]{3}}; -\frac {2 \sqrt {2}}{3 \sqrt [3]{3}})\). The curve starts from (0;0) point but does not pass through \(P_{\infty }\) as condition (29) is not fulfilled. Integration was terminated again at (b0;0) point

Full size image
Fig. 5
figure 5

Plot for α = 2, β = − 31/12, γ = 1/4, δ = 1. In this case, the matching point x0 = 0.5, and wrapping point \(P_{\infty }=(\frac {\sqrt {2}}{\sqrt [3]{3}}; -\frac {2 \sqrt {2}}{3 \sqrt [3]{3}})\). The curve starts from (0;0) point but does not pass through \(P_{\infty }\) as condition (29) is not fulfilled. Integration was terminated again at (b0;0) point. Now, we only get two global solutions—the trivial one and u0

Full size image

This example shows that for the specific case presented in [1, 13] the coefficients appear perfectly to fulfill the matching condition (29).

5 Conclusions

A general method of matching using a singular solution at one of the fixed singularity of the second-order differential equation that generalizes the Lane–Emden equation was presented. The method is constructive and shows under what circumstances countable the family of analytic solutions that interpolate between fixed singularities of the equation exists. This is a significant generalization of the idea presented in [1] and [13].

This theory was used to describe a matching problem for the differential equation generalizing the equations for self-similar profiles of nonlinear wave equations with power-type nonlinearity. This example sheds a new light on the special case presented in [13].

The boundary value problem and equations of the type presented in the paper are very common in applications since they arise from the radial part of the Laplace operator and power-type nonlinearity; therefore, these results are useful in applied sciences and technical problems.