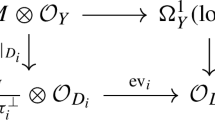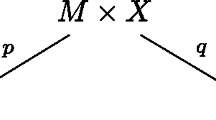Skip to main content
SpringerLink
Log in

Spectral Hirzebruch–Milnor classes of singular hypersurfaces

  • Published:
Mathematische Annalen Aims and scope Submit manuscript

Abstract

We introduce spectral Hirzebruch–Milnor classes for singular hypersurfaces. These can be identified with Steenbrink spectra in the isolated singularity case, and may be viewed as their global analogues in general. Their definition uses vanishing cycles of mixed Hodge modules and the Todd class transformation. These are compatible with the pushforward by proper morphisms, and the classes can be calculated by using resolutions of singularities. Formulas for Hirzebruch–Milnor classes of projective hypersurfaces in terms of these classes are given in the case where the multiplicity of a generic hyperplane section is not 1. These formulas using hyperplane sections instead of hypersurface ones are easier to calculate in certain cases. Here we use the Thom–Sebastiani theorem for the underlying filtered D-modules of vanishing cycles, from which we can deduce the Thom–Sebastiani type theorem for spectral Hirzebruch–Milnor classes. For the Chern classes after specializing to \(y=-\,1\), we can give a relatively simple formula for the localized Milnor classes, which implies a new formula for the Euler numbers of projective hypersurfaces, using iterated hyperplane sections. Applications to log canonical thresholds and Du Bois singularities are also explained; for instance, the latter can be detected by using Hirzebruch–Milnor classes in the projective hypersurface case.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aluffi, P.: Grothendieck classes and Chern classes of hyperplane arrangements. Int. Math. Res. Not. 2013, 1873–1900 (2013)

    MathSciNet  MATH  Google Scholar 

  2. Baum, P., Fulton, W., MacPherson, R.: Riemann–Roch for singular varieties. Inst. Hautes Etudes Sci. Publ. Math. 45, 101–145 (1975)

    MathSciNet  MATH  Google Scholar 

  3. Berthelot, P., Grothendieck, A., Illusie, L.: Théorie des intersections et théorème de Riemann–Roch, SGA 6. Lecture Notes in Mathematics, vol. 225. Springer, Berlin (1971)

    MATH  Google Scholar 

  4. Brasselet, J.-P., Schürmann, J., Yokura, S.: Hirzebruch classes and motivic Chern classes of singular spaces. J. Topol. Anal. 2, 1–55 (2010)

    MathSciNet  MATH  Google Scholar 

  5. Brieskorn, E.: Die Monodromie der isolierten Singularitäten von Hyperflächen. Manuscr. Math. 2, 103–161 (1970)

    MATH  Google Scholar 

  6. Budur, N.: On Hodge spectrum and multiplier ideals. Math. Ann. 327, 257–270 (2003)

    MathSciNet  MATH  Google Scholar 

  7. Budur, N., Saito, M.: Multiplier ideals, \(V\)-filtration, and spectrum. J. Algebr. Geom. 14, 269–282 (2005)

    MathSciNet  MATH  Google Scholar 

  8. Budur, N., Saito, M.: Jumping coefficients and spectrum of a hyperplane arrangement. Math. Ann. 347, 545–579 (2010)

    MathSciNet  MATH  Google Scholar 

  9. Cappell, S.E., Maxim, L., Schürmann, J., Shaneson, J.L.: Characteristic classes of complex hypersurfaces. Adv. Math. 225, 2616–2647 (2010)

    MathSciNet  MATH  Google Scholar 

  10. Deligne, P.: Théorie de Hodge II. Publ. Math. IHES 40, 5–58 (1971)

    MATH  Google Scholar 

  11. Deligne, P.: SGA7 XIII and XIV Lecture Notes in Mathematics 340. Le formalisme des cycles évanescents, in SGA7 XIII and XIV, pp. 82–115 and 116–164. Springer, Berlin (1973)

  12. Denef, J., Loeser, F.: Motivic exponential integrals and a motivic Thom–Sebastiani theorem. Duke Math. J. 99, 285–309 (1999)

    MathSciNet  MATH  Google Scholar 

  13. Dimca, A., Maisonobe, Ph, Saito, M., Torrelli, T.: Multiplier ideals, \(V\)-filtrations and transversal sections. Math. Ann. 336, 901–924 (2006)

    MathSciNet  MATH  Google Scholar 

  14. Fulton, F.: Intersection Theory. Springer, Berlin (1984)

    MATH  Google Scholar 

  15. Fulton, W., Johnson, K.: Canonical classes on singular varieties. Manuscr. Math. 32, 381–389 (1980)

    MathSciNet  MATH  Google Scholar 

  16. Guibert, G., Loeser, F., Merle, M.: Iterated vanishing cycles, convolution, and a motivic analogue of a conjecture of Steenbrink. Duke Math. J. 132, 409–457 (2006)

    MathSciNet  MATH  Google Scholar 

  17. Hartshorne, R.: Algebraic Geometry. Springer, New York (1977)

    MATH  Google Scholar 

  18. Hirzebruch, F.: Topological Methods in Algebraic Geometry. Springer, Berlin (1966)

    MATH  Google Scholar 

  19. Ishii, S.: On isolated Gorenstein singularities. Math. Ann. 270, 541–554 (1985)

    MathSciNet  MATH  Google Scholar 

  20. Kashiwara, M.: Lecture Notes in Mathematics. Vanishing cycle sheaves and holonomic systems of differential equations, vol. 1016, pp. 136–142. Springer, Berlin (1983)

    Google Scholar 

  21. Kovács, S., Schwede, K.: Hodge Theory Meets the Minimal Model Program: A Survey of Log Canonical and Du Bois Singularities, vol. 58, pp. 51–94. Cambridge University Press, Cambridge (2011)

    MATH  Google Scholar 

  22. Lazarsfeld, R.: Positivity in Algebraic Geometry II. Springer, Berlin (2004)

    MATH  Google Scholar 

  23. MacPherson, R.D.: Chern classes for singular algebraic varieties. Ann. Math. (2) 100, 423–432 (1974)

    MathSciNet  MATH  Google Scholar 

  24. Malgrange, B.: Polynôme de Bernstein-Sato et cohomologie évanescente. Astérisque 101–102, 243–267 (1983)

    MATH  Google Scholar 

  25. Maxim, L., Saito, M., Schürmann, J.: Hirzebruch–Milnor classes of complete intersections. Adv. Math. 241, 220–245 (2013)

    MathSciNet  MATH  Google Scholar 

  26. Maxim, L., Saito, M., Schürmann, J.: Hirzebruch-Milnor classes and Steenbrink spectra of certain projective hypersurfaces. Arbeitstagung Bonn 2013. Progress Mathematics, vol. 319, pp. 265–287. Birkhäuser, Cham (2016)

    Google Scholar 

  27. Maxim, L., Saito, M., Schürmann, J.: Thom–Sebastiani theorems for filtered \({\cal{D}}\)-modules and for multiplier ideals. Int. Math. Res. Not. https://doi.org/10.1093/imrn/rny032. arXiv:1610.07295

  28. Navarro Aznar, V.: On the Chern classes and the Euler characteristic for nonsingular complete intersections. Proc. Am. Math. Soc. 78, 143–148 (1980)

    MathSciNet  MATH  Google Scholar 

  29. Ohmoto, T., Yokura, S.: Product formulas for the Milnor class. Bull. Pol. Acad. Sci. Math. 48, 387–401 (2000)

    MathSciNet  MATH  Google Scholar 

  30. Orlik, P., Solomon, L.: Combinatorics and topology of complements of hyperplanes. Inv. Math. 56, 167–189 (1980)

    MathSciNet  MATH  Google Scholar 

  31. Parusiński, A., Pragacz, P.: Characteristic classes of hypersurfaces and characteristic cycles. J. Algebr. Geom. 10, 63–79 (2001)

    MathSciNet  MATH  Google Scholar 

  32. Saito, M.: On the exponents and the geometric genus of an isolated hypersurface singularity. In: Singularities, Part 2, Proceedings of Symposia in Pure Mathematics, vol. 40, pp. 465–472. AMS, Providence (1983)

  33. Saito, M.: Modules de Hodge polarisables. Publ. RIMS Kyoto Univ. 24, 849–995 (1988)

    MathSciNet  MATH  Google Scholar 

  34. Saito, M.: Duality for vanishing cycle functors. Publ. RIMS Kyoto Univ. 25, 889–921 (1989)

    MathSciNet  MATH  Google Scholar 

  35. Saito, M.: Mixed Hodge modules. Publ. RIMS Kyoto Univ. 26, 221–333 (1990)

    MathSciNet  MATH  Google Scholar 

  36. Saito, M.: On Steenbrink’s conjecture. Math. Ann. 289, 703–716 (1991)

    MathSciNet  MATH  Google Scholar 

  37. Saito, M.: On \(b\)-function, spectrum and rational singularity. Math. Ann. 295, 51–74 (1993)

    MathSciNet  MATH  Google Scholar 

  38. Saito, M.: On microlocal \(b\)-function. Bull. Soc. Math. France 122, 163–184 (1994)

    MathSciNet  MATH  Google Scholar 

  39. Saito, M.: On the Hodge filtration of Hodge modules. Mosc. Math. J. 9, 161–191 (2009)

    MathSciNet  MATH  Google Scholar 

  40. Saito, M.: Thom–Sebastiani theorem for Hodge modules (preprint)

  41. Scherk, J., Steenbrink, J.H.M.: On the mixed Hodge structure on the cohomology of the Milnor fibre. Math. Ann. 271, 641–665 (1985)

    MathSciNet  MATH  Google Scholar 

  42. Schürmann, J.: A generalized Verdier-type Riemann–Roch theorem for Chern–Schwartz–MacPherson classes. arXiv:math/0202175

  43. Schürmann, J.: Topology of Singular Spaces and Constructible Sheaves. Birkhäuser, Basel (2003)

    MATH  Google Scholar 

  44. Schürmann, J.: Topology of Stratified Spaces. Characteristic Classes of Mixed Hodge Modules, vol. 58, pp. 419–471. Cambridge University Press, Cambridge (2011)

    MATH  Google Scholar 

  45. Schürmann, J.: Specialization of motivic Hodge–Chern classes. arXiv:0909.3478

  46. Schürmann, J.: IRMA Lectures in Mathematics and Theoretical Physics. Nearby Cycles and Characteristic Classes of Singular Spaces, pp. 181–205. European Mathematical Society, Zurich (2012)

    Google Scholar 

  47. Schürmann, J.: Chern classes and transversality for singular spaces. Singularities in Geometry, Topology, Foliations and Dynamics. Trends in Mathematics, pp. 207–231. Birkhäuser, Cham (2017)

    MATH  Google Scholar 

  48. Steenbrink, J.H.M.: Limits of Hodge structures. Inv. Math. 31, 229–257 (1975/76)

  49. Steenbrink, J.H.M.: Hodge, mixed, structure on the vanishing cohomology. In: Real and Complex Singularities. Proceedings of Ninth Nordic Summer School, Oslo 1977. Alphen aan den Rijn, Sijthoff and Noordhoff, pp. 525–563 (1976)

  50. Steenbrink, J.H.M.: Mixed Hodge structures associated with isolated singularities. In: Singularities, Part 2, Proceedings of Symposia in Pure Mathematics, vol. 40, pp. 513–536. AMS, Providence (1983)

  51. Varchenko, A.N.: Asymptotic mixed Hodge structure in vanishing cohomologies. Math. USSR Izv. 18, 469–512 (1982)

    MATH  Google Scholar 

  52. Verdier, J.-L.: Le théorème de Riemann–Roch pour les intersections complètes. Astérisque 36–37, 189–228 (1976)

    MATH  Google Scholar 

  53. Yokura, S.: A generalized Grothendieck–Riemann–Roch theorem for Hirzebruch’s \(\chi _y\)-characteristic and \(T_y\)-characteristic. Publ. RIMS Kyoto Univ. 30, 603–610 (1994)

    MathSciNet  MATH  Google Scholar 

  54. Yokura, S.: On characteristic classes of complete intersections. In: Algebraic Geometry: Hirzebruch 70 (Warsaw, 1998). Contemporary Mathematics, vol. 241, pp. 349–369. American Mathematical Society, Providence (1999)

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Wisconsin-Madison, 480 Lincoln Drive, Madison, WI, 53706-1388, USA

    Laurentiu Maxim

  2. RIMS Kyoto University, Kyoto, 606-8502, Japan

    Morihiko Saito

  3. Mathematische Institut, Universität Münster, Einsteinstr. 62, 48149, Münster, Germany

    Jörg Schürmann

Authors
  1. Laurentiu Maxim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Morihiko Saito
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jörg Schürmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Laurentiu Maxim.

Additional information

Communicated by Ngaiming Mok.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maxim, L., Saito, M. & Schürmann, J. Spectral Hirzebruch–Milnor classes of singular hypersurfaces. Math. Ann. 377, 281–315 (2020). https://doi.org/10.1007/s00208-018-1750-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00208-018-1750-4

Search

Navigation