Abstract
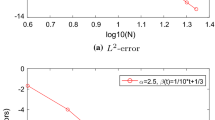
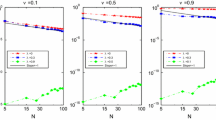
Our aim in this paper is to develop a Legendre-Jacobi collocation approach for a nonlinear system of two-point boundary value problems with derivative orders at most two on the interval (0,T). The scheme is constructed based on the reduction of the system considered to its equivalent system of Volterra-Fredholm integral equations. The spectral rate of convergence for the proposed method is established in both L2- and \( L^{\infty } \)- norms. The resulting spectral method is capable of achieving spectral accuracy for problems with smooth solutions and a reasonable order of convergence for non-smooth solutions. Moreover, the scheme is easy to implement numerically. The applicability of the method is demonstrated on a variety of problems of varying complexity. To the best of our knowledge, the spectral solution of such a nonlinear system of fractional differential equations and its associated nonlinear system of Volterra-Fredholm integral equations has not yet been studied in literature in detail. This gap in the literature is filled by the present paper.



Similar content being viewed by others
References
Zaky, M.A.: Recovery of high order accuracy in Jacobi spectral collocation methods for fractional terminal value problems with non-smooth solutions. J. Comput. Appl. Math. 357, 103–122 (2019)
Stynes, M., Gracia, J.L.: A finite difference method for a two-point boundary value problem with a Caputo fractional derivative. IMA J. Numer. Anal. 35(2), 698–721 (2015)
Pedas, A., Tamme, E., Vikerpuur, M.: Smoothing transformation and spline collocation for nonlinear fractional initial and boundary value problems. J. Comput. Appl. Math. 317, 1–16 (2017)
Gracia, J.L., Stynes, M.: Central difference approximation of convection in Caputo fractional derivative two-point boundary value problems. J. Comput. Appl. Math. 273, 103–115 (2015)
Cen, Z., Huang, J., Xu, A.: An efficient numerical method for a two-point boundary value problem with a Caputo fractional derivative. J. Comput. Appl. Math. 336, 1–7 (2018)
Podlubny, I.: Fractional Differential Equations, Mathematics in Science and Engineering, vol. 198 Academic Press (1999)
Zaky, M.A.: An improved tau method for the multi-dimensional fractional Rayleigh–Stokes problem for a heated generalized second grade fluid. Comput. Math. Appl. 75, 2243–2258 (2018)
Mokhtary, P.: Numerical treatment of a well-posed Chebyshev tau method for Bagley-Torvik equation with high-order of accuracy. Numer. Algor. 72(4), 875–891 (2016)
Bhrawy, A.H., Doha, E.H., Baleanu, D., Ezz-eldein, S.S.: A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 293, 142–156 (2015)
Doha, E.H., Zaky, M.A., Abdelkawy, M.: Spectral Methods Within Fractional Calculus, Handbook of Fractional Calculus with Applications, vol. 8 Part B, pp 207–232. De Gruyter, Berlin (2019)
Mokhtary, P.: Numerical analysis of an operational Jacobi tau method for fractional weakly singular integro-differential equations. Appl. Numer. Math. 121, 52–67 (2017)
Yarmohammadi, M., Javadi, S., Babolian, E.: Spectral iterative method and convergence analysis for solving nonlinear fractional differential equation. J. Comput. Phys. 359, 436–450 (2018)
Wei, Y., Chen, Y.: A Jacobi spectral method for solving multidimensional linear Volterra integral equation of the second kind. J. Sci. Comput. 79(3), 1801–1813 (2019)
Ezz-Eldien, S.S.: On solving systems of multi-pantograph equations via spectral tau method. Appl. Math. Comput. 321, 63–73 (2018)
Bhrawy, A.H., Zaky, M.A.: A method based on the Jacobi tau approximation for solving multi-term time-space fractional partial differential equations. J. Comput. Phys. 281, 876–895 (2015)
Bhrawy, A.H., Zaky, M.A.: Shifted fractional-order Jacobi orthogonal functions: application to a system of fractional differential equations. Appl. Math. Model. 40, 832–845 (2016)
Pezza, L., Pitolli, F.: A multiscale collocation method for fractional differential problems. Math. Comput. Simul. 147, 210–219 (2018)
Ghanbari, F., Ghanbari, K., Mokhtary, P.: Generalized Jacobi–Galerkin method for nonlinear fractional differential algebraic equations. Comp. Appl. Math. 37, 5456–5475 (2018)
Dabiri, A., Butcher, E.A.: Numerical solution of multi-order fractional differential equations with multiple delays via spectral collocation methods. Appl. Math. Model. 56, 424–448 (2018)
Mokhtary, P., Ghoreishi, F., Srivastava, H.M.: The Müntz-Legendre Tau method for fractional differential equations. Appl. Math. Model. 40(2), 671–684 (2016)
Kopteva, N., Stynes, M.: An efficient collocation method for a Caputo two-point boundary value problem. BIT Numer. Math. 55, 1105–1123 (2015)
Pedas, A., Tamme, E.: Piecewise polynomial collocation for linear boundary value problems of fractional differential equations. J. Comput. Appl. Math. 236, 3349–3359 (2012)
Sheng, C., Shen, J.: A hybrid spectral element method for fractional two-point boundary value problems. Numer. Math. Theory Methods Appl. 10(2), 437–464 (2017)
Wang, J., Xu, T.-Z., Wei, Y.-Q., Xie, J.-Q.: Numerical simulation for coupled systems of nonlinear fractional order integro-differential equations via wavelets method. Appl. Math. Comput. 324, 36–50 (2018)
Wang, C., Wang, Z., Wang, L.: A spectral collocation method for nonlinear fractional boundary value problems with a Caputo derivative. J. Sci. Comput. 76(1), 166–188 (2018)
Gu, Z.: Piecewise spectral collocation method for system of Volterra integral equations. Adv. Comput. Math. 43, 385–409 (2017)
Graef, J.R., Kong, L., Wang, M.: A Chebyshev spectral method for solving Riemann–Liouville fractional boundary value problems. Appl. Math. Comput. 241, 140–150 (2014)
Li, C., Zeng, F., Liu, F.: Spectral approximations to the fractional integral and derivative. Frac. Cal. Appl. Anal. 15.3, 383–406 (2012)
Doha, E.H., Bhrawy, A.H., Ezz-Eldien, S.S.: A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl. 62(5), 2364–2373 (2011)
Ezz-Eldien, S.S., Doha, E.H.: Fast and precise spectral method for solving pantograph type Volterra integro-differential equations. Numer. Algor. 81(1), 57–77 (2019)
Doha, E.H., Abdelkawy, M.A., Amin, A.Z.M., Lopes, A.M.: Shifted Jacobi–Gauss-collocation with convergence analysis for fractional integro-differential equations. Commun. Nonlinear Sci. Numer. Simulat. 72, 342–359 (2019)
Mokhtary, P., Moghaddam, B.P., Lopes, A.M., Tenreiro Machado, J.A.: A computational approach for the non-smooth solution of non-linear weakly singular Volterra integral equation with proportional delay. Numer Algor. https://doi.org/10.1007/s11075-019-00712-y (2019)
Zaky, M.A.: Existence, uniqueness and numerical analysis of solutions of tempered fractional boundary value problems. Appl. Numer. Math. https://doi.org/10.1016/j.apnum.2019.05.008 (2019)
Bai, Z., Lü, H.: Positive solutions for boundary value problem of nonlinear fractional differential equation. J. Math. Anal. Appl. 311, 495–505 (2005)
Su, X.: Boundary value problem for a coupled system of nonlinear fractional differential equations. Appl. Math. Lett. 22, 64–69 (2009)
Zhao, Y., Sun, S., Han, Z., Li, Q.: The existence of multiple positive solutions for boundary value problems of nonlinear fractional differential equations. Commun. Nonlinear Sci. Numer. Simulat. 16, 2086–2097 (2011)
Xu, X., Jiang, D., Yuan, C.: Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation. Nonlinear Anal. 71(10), 4676–4688 (2009)
Goodrich, C.: Existence of a positive solution to systems of differential equations of fractional order. Comput. Math. Appl. 62, 1251–1268 (2011)
Rehman, M., Khan, R.A.: A note on boundary value problems for a coupled system of fractional differential equations. Comput. Math. Appl. 62, 1251–1268 (2011)
Ouyang, Z., Chen, Y., Zou, S.: Existence of positive solutions to a boundary value problem for a delayed nonlinear fractional differential system. Bound. Value Probl. 2011(1), 475126 (2011)
Szegö, G.: Orthogonal Polynomials, 4th edn. AMS Coll Publ. (1975)
Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)
Shen, J., Tang, T., Wang, L.: Spectral Method Algorithms, Analysis and Applications. Springer, Berlin (2011)
Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods: Fundamentals in Single Domains. Springer, Berlin (2006)
Mastroianni, G., Occorsto, D.: Optimal systems of nodes for Lagrange interpolation on bounded intervals: a survey. J. Comput. Appl. Math. 134, 325–341 (2001)
Acknowledgments
The authors wish to thank the referees for their constructive comments and suggestions, which greatly improved the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Existence of the approximate solution
Appendix: Existence of the approximate solution
We consider the following iteration process:
Let \( \overrightarrow {\mathbf {U}}_{N}^{m}(x) = \mathbf {U}_{N}^{m}(x)-\mathbf {U}_{N}^{m-1}(x) \). Then, we have from (A.1) and (4.24) that
where
We obtain from the Cauchy-Schwarz inequality that
Hence, by (4.25), (5.14) and the Lipschitz condition, we obtain that
It remains to estimate the term \( \left \|\boldsymbol {B}_{2} \right \| \). By the Cauchy-Schwarz inequality, we have
The previous result, along with (2.8) and Lipschitz condition, yields
Hence,
since
we have \( \left \| \overrightarrow {\mathbf {U}}_{N}^{m} \right \| \longrightarrow 0 \) as \( m\longrightarrow \infty . \) It implies the existence of solution of (3.10).
Rights and permissions
About this article
Cite this article
Zaky, M.A., Ameen, I.G. A priori error estimates of a Jacobi spectral method for nonlinear systems of fractional boundary value problems and related Volterra-Fredholm integral equations with smooth solutions. Numer Algor 84, 63–89 (2020). https://doi.org/10.1007/s11075-019-00743-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-019-00743-5
Keywords
- System of fractional differential equations
- Fredholm integral equations
- Boundary value problems
- Convergence analysis