A new recursive formulation of the Tau method for solving linear Abel–Volterra integral equations and its application to fractional differential equations

Abstract

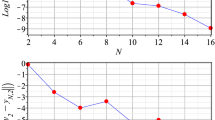
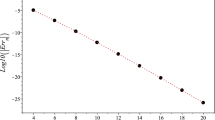
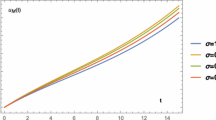
In this paper, the recursive approach of the Tau method is developed for numerical solution of Abel–Volterra type integral equations. Due to the singular behavior of solutions of these equations, the existing spectral approaches suffer from low accuracy. To overcome this drawback we use Müntz–Legendre polynomials as basis functions which have remarkable approximation to functions with singular behavior at origin and express Tau approximation of the exact solution based on a sequence of basis canonical polynomials that is generated by a simple recursive formula. We also provide a convergence analysis for the proposed method and obtain an exponential rate of convergence regardless of singularity behavior of the exact solution. Some examples are given to demonstrate the effectiveness of the proposed method. The results are compared with those obtained by existing numerical methods, thereby confirming the superiority of our scheme. The paper is closed by providing application of this method to approximate solution of a linear fractional integro-differential equation.

Appendix

Here we give definition of the well-known Beta function and some of its properties along with more details about the relation (39).

Beta function and its properties For $\alpha , \beta \in {\mathbf {R}}_{+}$, the beta function is defined by

$$\begin{aligned} B(\alpha , \beta )=\int _{0}^{1}t^{\alpha -1}(1-t)^{\beta -1}dt, \end{aligned}$$

and for all $m\in {\mathbf {N}}$ and $0< \alpha < 1$, we have

$$\begin{aligned} B(m\alpha +1,\alpha )= & {} \int _{0}^{1}t^{m\alpha }(1-t)^{\alpha -1}dt\le \int _{0}^{1}t^{\alpha }(1-t)^{\alpha -1}dt=B(\alpha +1,\alpha ).\nonumber \\ \end{aligned}$$

(58)

Details of (39) and (40) Here we give more details of the Eqs. (39) and (40).

Landau’s order notation [37] If f(t) and g(t) are two functions for $t\in {\mathbf {R}}$ and if $t_{0}\in {\mathbf {R}}$, we say that $f(t)=O(g(t))$ near $t_{0}$ if there exists a constant $\kappa \in {\mathbf {R}}$ such that

$$\begin{aligned} \lim _{t\rightarrow t_{0}} \frac{f(t)}{g(t)}=\kappa . \end{aligned}$$

Throughout the paper, we took all order near $+\infty .$

Theorem 7

[38] (Dirichlet’s test for convergence) If the sequence $\{a_{i}\}$ has bounded partial sums $s_{N}=\sum \nolimits _{i=1}^{N}a_{i}$ and $b_{i}\rightarrow 0$ with $b_{0}\ge b_{1} \ge b_{2} \ge \cdots$, then the series $\sum \nolimits _{i=0}^\infty {a_i b_i}$ is convergent.

Now, we use this theorem to show that the relation (39) is satisfied, i.e.,

$$\begin{aligned} \sum \limits _{i=0}^{N+j}c_{N+j,i}\vartheta _{i,\ell }=O(c_{N+j,N+j}\vartheta _{N+j,\ell }) \end{aligned}$$

or equivalently

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{\sum \limits _{i=0}^{N+j}c_{N+j,i}\vartheta _{i,l}}{c_{N+j,N+j}\vartheta _{N+j,l}}=\kappa . \end{aligned}$$

By setting $a_{i}:=\frac{c_{N+j,i}}{c_{N+j,N+j}}$ and $b_{i}:=\frac{\vartheta _{i,l}}{\vartheta _{N+j,l}}$, from Eqs. (4), (34) and (58) we have

$$\begin{aligned} s_{N}=\sum _{i=1}^{N+j-1}\frac{c_{N+j,i}}{c_{N+j,N+j}}= & {} \frac{1-c_{N+j,N+j}}{c_{N+j,N+j}}=\frac{\alpha ^{N+j}(N+j)!}{\prod \limits _{l=0}^{N+j-1}((N+j+l)\alpha +1)}-1\rightarrow -1, \end{aligned}$$

where $N\rightarrow \infty$ and hence $\vert s_{N} \vert \le 2$, $b_{0}\ge b_{1}\ge \cdots$ and $b_{i}\rightarrow 0$, therefore $\sum \limits _{i=0}^\infty a_{i}b_{i}$ is convergent and

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{ \sum \limits _{i=0}^{N+j}c_{N+j,i} \vartheta _{i,l}}{c_{N+j,N+j} \vartheta _{N+j,l}}= & {} \lim _{N\rightarrow \infty } \left( 1+\sum _{i=0}^{N+j-1}\frac{c_{N+j,i}\vartheta _{i,l}}{c_{N+j,N+j}\vartheta _{N+j,l}}\right) \\ {}= & {} \lim _{N\rightarrow \infty } \left( 1+\sum _{i=0}^{N+j-1} a_{i}b_{i} \right) =\kappa . \end{aligned}$$