Energy-efficient real-time scheduling for two-type heterogeneous multiprocessors

Abstract

We propose three novel mathematical optimization formulations that solve the same two-type heterogeneous multiprocessor scheduling problem for a real-time taskset with hard constraints. Our formulations are based on a global scheduling scheme and a fluid model. The first formulation is a mixed-integer nonlinear program, since the scheduling problem is intuitively considered as an assignment problem. However, by changing the scheduling problem to first determine a task workload partition and then to find the execution order of all tasks, the computation time can be significantly reduced. Specifically, the workload partitioning problem can be formulated as a continuous nonlinear program for a system with continuous operating frequency, and as a continuous linear program for a practical system with a discrete speed level set. The latter problem can therefore be solved by an interior point method to any accuracy in polynomial time. The task ordering problem can be solved by an algorithm with a complexity that is linear in the total number of tasks. The work is evaluated against existing global energy/feasibility optimal workload allocation formulations. The results illustrate that our algorithms are both feasibility optimal and energy optimal for both implicit and constrained deadline tasksets. Specifically, our algorithm can achieve up to 40% energy saving for some simulated tasksets with constrained deadlines. The benefit of our formulation compared with existing work is that our algorithms can solve a more general class of scheduling problems due to incorporating a scheduling dynamic model in the formulations and allowing for a time-varying speed profile.

1 Introduction

Efficient energy management has become an important issue for modern computing systems due to higher computational power demands in today’s computing systems, e.g. sensor networks, satellites, multi-robot systems, as well as personal electronic devices. There are two common schemes used in modern computing energy management systems. One is dynamic power management (DPM), where certain parts of the system are turned off during the processor idle state. The other is dynamic voltage and frequency scaling (DVFS), which reduces the energy consumption by exploiting the relation between the supply voltage and power consumption. In this work, we consider the problem of scheduling real-time tasks on heterogeneous multiprocessors under a DVFS scheme. The objective is to minimize energy consumption, while ensuring that both the execution cycle requirement and timeliness constraints of real-time tasks are satisfied. This problem is known to be NP-Complete, in general  (Ullman 1975). However, one of our algorithms involves solving an LP, for which a solution can be computed to an arbitrary accuracy in polynomial time using a suitably-chosen interior point method (Boyd and Vandenberghe 2004).

1.1 Terminologies and definitions

This section provides basic terminologies and definitions used throughout the paper.

Task $T_i$: An aperiodic task $T_i$ is defined as a triple $T_i:=(c_i,d_i,b_i)$; $c_i$ is the required number of CPU cycles needed to complete the task, $d_i$ is the task’s relative deadline and $b_i$ is the arrival time of the task. A periodic task $T_i$ is defined as a triple $T_i:=(c_i,d_i,p_i)$ where $p_i$ is the task’s period. If the task’s deadline is equal to its period, the task is said to have an ‘implicit deadline’. The task is considered to have a ‘constrained deadline’ if its deadline is not larger than its period, i.e. $d_i \le p_i$. In the case that the task’s deadline can be less than, equal to, or greater than its period, it is said to have an ‘arbitrary deadline’. Throughout the paper, we will refer to a task as an aperiodic task model unless stated otherwise, because a periodic task can be transformed into a collection of aperiodic tasks with appropriately defined arrival times and deadlines, i.e. the jth instance of a periodic task $T_i$, where $j\ge 1$, arrives at time $(j-1)p_i$, has the required execution cycles $c_i$ and an absolute deadline at time $(j-1)p_i+d_i$. Moreover, for a periodic taskset, we only need to find a valid schedule within its hyperperiod $\mathcal {L}$, defined as the least common multiple (LCM) of all task periods, i.e. the total number of job instances of a periodic task $T_i$ during the hyperperiod $\mathcal {L}$ is equal to $\mathcal {L}/p_i$. The taskset is defined as a set of all tasks. The taskset is feasible if there exists a schedule such that no task in the taskset misses the deadline.

Speed $s^r$: The operating speed $s^r$ is defined as the ratio between the operating frequency $f^r$ of processor type-r and the maximum system frequency $f_{max}$, i.e. $s^r:=f^r/f_{max}$, $f_{max}:=\max \left\{ \max \{f^r\mid r\in R\}\right\}$, where $R:=\{1,2,\ldots ,\kappa \}$ and $\kappa$ is the total number of processor types. Note that the superscript r is used to denote the type-r processor.

Minimum execution time ¹ $\underline{x}^r_i$: The minimum execution time $\underline{x}^r_i$ is the execution time of task $T_i$ when executed at the maximum system frequency $f_{max}$, i.e. $\underline{x}^r_i:=c^r_i/f_{max}$, where $c^r_i$ is the CPU cycles required to complete a task $T_i$ when executed on a processor of type r.

Task density ² $\delta _i(s_i)$: For a periodic task, a task density $\delta _i(s_i)$ is defined as the ratio between the task execution time and the minimum of its deadline and its period, i.e. $\delta _i(s_i):=c_i/(s_if_{max}\min \{d_i,p_i\})$, where $s_i$ is the task execution speed.

Taskset density $D(s_i)$: A taskset density $D(s_i)$ of a periodic taskset is defined as the summation of all task densities in the taskset, i.e. $D(s_i):=\sum _{i=1}^n \delta _i(s_i).$ The minimum taskset density D is given by $D:=\sum _{i=1}^n \delta _i(1).$

System capacity C: The system capacity C is defined as $C:=\sum _{r}s^r_{max}m_r$, where $s^r_{max}$ is the maximum speed of processor type-r, i.e. $s^r_{max}:=f^r_{max}/f_{max},$ $f^r_{max}:=\max f^r$, $m_r$ is the total number of processors of type-r.

Migration scheme: A global scheduling scheme allows task migration between processors and a partitioned scheduling scheme does not allow task migration.

Feasibility optimal: An algorithm is feasibility optimal if the algorithm is guaranteed to be able to construct a valid schedule such that no deadlines are missed, provided a schedule exists.

Energy optimal: An algorithm is energy optimal when it is guaranteed to find a schedule that minimizes the energy, while meeting the deadlines, provided such a schedule exists.

Step function: A function $f:X\rightarrow \mathbb {R}$ is a step (also called a piecewise constant) function, denoted $f\in \mathcal {PC}$, if there exists a finite partition $\{X_1,\ldots ,X_p\}$ of $X\subseteq \mathbb {R}$ and a set of real numbers $\{\phi _1,\ldots ,\phi _p\}$ such that $f(x) = \phi _i$ for all $x\in X_i$, $i\in \{1,\ldots ,p\}$.

1.2 Related work

Due to the heterogeneity of the processors, one should not only consider the different operating frequency sets among processors, but also the hardware architecture of the processors, since task execution time will be different for each processor type. In other words, the system has to be captured by two aspects: the difference in operating speed sets and the execution cycles required by different tasks on different processor types (Fig. 1).

With these aspects, fully-migration/global based scheduling algorithms, where tasks are allowed to migrate between different processor types, are not suitable in practice, since it will be difficult to identify how much computational work is executed on one processor type compared to another processor type due to differences in instruction sets, register formats, etc. Thus, most of the work related to heterogeneous multiprocessor scheduling are partition-based/non-preemptive task scheduling algorithms (Yu and Prasanna 2002; Leung et al. 2004; Yang et al. 2009; Goh et al. 2009; Chen et al. 2009; Li and Wu 2012; Awan and Petters 2013), i.e. tasks are partitioned onto one of the processor types and a well-known uniprocessor scheduling algorithm, such as Earliest Deadline First (EDF) (Liu and Layland 1973), is used to find a valid schedule. With this scheme, the heterogeneous multiprocessor scheduling problem is reduced to a task partitioning problem, which can be formulated as an integer linear program (ILP). Examples of such work are Yu and Prasanna (2002) and Chen et al. (2009).

However, with the advent of ARM two-type heterogeneous multicores architecture, such as the big.LITTLE architecture (ARM 2013), that supports task migrations among different core types, a global scheduling algorithm is possible. In Chwa et al. (2014, 2015), the first energy-aware global scheduling framework for this special architecture is presented, where an algorithm called Hetero-Split is proposed to solve a workload assignment and a Hetero-Wrap algorithm to solve a schedule generation problem. Their framework is similar to ours, except that we adopt a fluid model to represent a scheduling dynamic, our assigned operating frequency is time-varying and the CPU idle energy consumption is also considered.

Fig. 1

Fluid schedule and a practical schedule (Cho et al. 2006)

A fluid model is the ideal schedule path of a real-time task. The remaining execution time is represented by a straight line where the magnitude of the slope of the line is the task execution speed. However, a practical task execution path is nonlinear, since a task may be preempted by other tasks. The execution interval of a task is represented by a line with a negative slope and a non-execution interval is represented by a line with zero slope.

There are at least two well-known homogeneous multiprocessor scheduling algorithms that are based on a fluid scheduling model: Proportionate-fair (Pfair) (Baruah et al. 1993) and Largest Local Remaining Execution Time First (LLREF) (Cho et al. 2006). Both Pfair and LLREF are global scheduling algorithms. By introducing the notion of fairness, Pfair ensures that at any instant no task is one or more quanta (time intervals) away from the task’s fluid path. However, the Pfair algorithm suffers from a significant run-time overhead, because tasks are split into several segments, incurring frequent algorithm invocations and task migrations. To overcome the disadvantages of quantum-based scheduling algorithms, the LLREF algorithm splits/preempts a task at two scheduling events within each time interval (Cho et al. 2006). One occurs when the remaining time of an executing task is zero and it is better to select another task to run. The other event happens when the task has no laxity, i.e. the difference between the task deadline and the remaining execution time left is zero, hence the task needs to be selected immediately in order to finish the remaining workload in time.

The unified theory of the deadline partitioning technique and its feasibility optimal versions, called DP-FAIR, for periodic and sporadic tasks are given in Levin et al. (2010). Deadline Partitioning (DP) (Levin et al. 2010) is the technique that partitions time into intervals bounded by two successive task deadlines, after which each task is allocated the workload and is scheduled at each time interval. A simple optimal scheduling algorithm based on DP-FAIR, called DP-WRAP, was presented in Levin et al. (2010). The DP-WRAP algorithm partitioned time according to the DP technique and, at each time interval, the tasks are scheduled using McNaughton’s wrap around algorithm (McNaughton 1959). McNaughton’s wrap around algorithm aligns all task workloads along a real number line, starting at zero, then splits tasks into chunks of length 1 and assigns each chunk to the same processor. Note that the tasks that have been split migrate between the two assigned processors. The work of Levin et al. (2010) was extended in Funk et al. (2012) and Wu et al. (2012) by incorporating a DVFS scheme to reduce power consumption.

However, the algorithms that are based on the fairness notion (Cho et al. 2006; Funaoka et al. 2008a, b; Levin et al. 2010; Funk et al. 2012; Wu et al. 2012) are feasibility optimal, but have hardly been applied in a real system, since they suffer from high scheduling overheads, i.e. task preemptions and migrations. Recently, two feasibility optimal algorithms that are not based on the notion of fairness have been proposed. One is the RUN algorithm (Regnier et al. 2011), which uses a dualization technique to reduce the multiprocessor scheduling problem to a series of uniprocessor scheduling problems. The other is U-EDF (Nelissen et al. 2012), which generalises the earliest deadline first (EDF) algorithm to multiprocessors by reducing the problem to EDF on a uniprocessor.

Alternatively to the above methods, the multiprocessor scheduling problem can also be formulated as an optimization problem. However, since the problem is NP-hard (Lawler 1983), in general, an approximated polynomial-time heuristic method is often used. An example of these approaches can be found in  Chen et al. (2008) and Xian et al. (2007), which consider energy-aware multiprocessor scheduling with probabilistic task execution times. The tasks are partitioned among the set of processors, followed with computing the running frequency based on the task execution time probabilities. Among all of the feasibility assignments, an optimal energy consumption assignment is chosen by solving a mathematical optimization problem, where the objective is to minimize some energy function. The constraints are to ensure that all tasks will meet their deadlines and only one processor is assigned to a task. In partitioned scheduling algorithms, such as Chen et al. (2008) and Xian et al. (2007), once a task is assigned to a specific processor, the multiprocessor scheduling problem is reduced to a set of uniprocessor scheduling problems, which is well studied (Chen and Kuo 2007). However, a partitioned scheduling method cannot provide a feasibility optimal schedule.

For this work, we are interested in solving the scheduling problem of a two-type heterogeneous multiprocessor system, e.g. the ARM big.LITTLE architecture. Specifically, we formulate a real-time multiprocessor scheduling problem as an infinite-dimensional continuous-time optimal control problem. Three mathematical programming formulations to solve a hard real-time task scheduling problem on heterogeneous multiprocessor systems with DVFS capabilities are proposed. First is a mixed-integer nonlinear program (MINLP), which adopts the fluid model used in  Baruah et al. (1993), Cho et al. (2006), Funaoka et al. (2008a, b) to represent a scheduling dynamic. The MINLP formulation relies on the optimal control of a given system’s dynamic to globally solve for a valid schedule, while solutions are obtained by solving each instance of the time interval obtained using the DP technique (Cho et al. 2006; Funaoka et al. 2008a, b; Levin et al. 2010; Funk et al. 2012; Wu et al. 2012). By determining a percentage of a task’s execution time, rather than task assignments, the same scheduling problem can be divided into two sub-problems, i.e. a workload partitioning problem and a task ordering problem. A nonlinear program (NLP) and a linear program (LP) are proposed to solve the workload partitioning problem for a system with continuous operating speed and a practical system where a processor has a discrete operating speed set, respectively.

1.3 Contribution

The main contributions of this work are:

• The scheduling problem is decoupled into two sub-problems and the optimal control is adopted to solve the workload partitioning problem.

• We provide a generalised optimal speed profile solution to a uniprocessor scheduling problem with real-time taskset. That is, (i) for any given workload within the time interval, the optimal speed profile composes of at most two speed levels. (ii) For a processor with a convex power consumption model, the optimal speed profile is a constant. (iii) In general, the time-varying speed profile is better than a constant speed profile if the power function is not convex.

• The first multiprocessor scheduling algorithm that is both feasibility optimal and energy optimal.

• Our formulations are capable of solving a multiprocessor scheduling problem with any periodic tasksets as well as aperiodic tasksets, compared to existing work, due to the incorporation of a scheduling dynamic and a time-varying speed profile.

• Moreover, the proposed formulations can also be extended to a multicore architecture, which only allows frequency to be changed at a cluster-level, rather than at a core-level, as explained in Sect. 2.3.

1.4 Outline

This paper is organized as follows: Sect. 2 defines our feasibility scheduling problem in detail. Details on solving the scheduling problem with finite-dimensional mathematical optimization is given in Sect. 3. The optimality problem formulations are presented in Sect. 4. The simulation setup and results are presented in Sect. 5. Finally, conclusions and future work are discussed in Sect. 6.

2 Feasibility problem formulation

Though our objective is to minimize the total energy consumption, we will first consider a feasiblity problem before presenting an optimality problem.

2.1 System model

We consider a set of n real-time tasks that are to be partitioned on a two-type heterogeneous multiprocessor system composed of $m_r$ processors of type-$r,~r\in R$. We will assume that the system supports task migration among processor types, e.g. sharing the same instruction set and having a special interconnection for data transfer between processor types. Note that $c_i$ is the same for all processor types, since the instruction set is the same.

2.2 Task/processor assumptions

All tasks do not share resources, do not have any precedence constraints and are ready to start at the beginning of the execution. A task can be preempted/migrated between different processor types at any time. The cost of preemption and migration is assumed to be negligible or included in the minimum task execution times. Processors of the same type are homogeneous, i.e. having the same set of operating frequencies and power consumptions. Each processor’s voltage/speed can be adjusted individually. Additionally, for an ideal system, a processor is assumed to have a continuous speed range. For a practical system, a processor is assumed to have a finite set of operating speed levels.

2.3 Scheduling as an optimal control problem

Below, we will refer to the sets $I:=\{1,\ldots ,n\}$, $K^r:=\{1,\ldots ,m_r\}$ and $\Gamma :=[0,L]$, where L is the largest deadline of all tasks. Note that $\forall i,\forall k,\forall r,\forall t$ are short-hand notations for $\forall i\in I,\forall k\in K^r,\forall r\in R,\forall t\in \Gamma$, respectively. The scheduling problem can therefore be formulated as the following infinite-dimensional continous-time control problem:

(1a)

(1b)

(1c)

(1d)

(1e)

(1f)

(1g)

(1h)

where the state $x_{i}(t)$ is the remaining minimum execution time of task $T_{i}$ at time t, the control input $s_{k}^r(t)$ is the execution speed of the kth processor of type-r at time t and the control input $a_{ik}^r(t)$ is used to indicate the processor assignment of task $T_{i}$ at time t, i.e. $a_{ik}^r(t) = 1$ if and only if task $T_{i}$ is active on processor k of type-r. Notice that here we formulated the problem with speed selection at a core-level; a stricter assumption of a multicore architecture, i.e. a cluster-level speed assignment, is straightforward. Particularly, by replacing a core-level speed assignment $s_{k}^r$ with a cluster-level speed assignment $s^r$ in the above formulation.

The initial conditions on the minimum execution time of all tasks and task deadline constraints are specified in (1a) and (1b), respectively. The fluid model of the scheduling dynamic is given by the differential constraint (1c). Constraint (1d) ensures that each task will be assigned to at most one non-idle processor at a time. Constraint (1e) quarantees that each non-idle processor will only be assigned to at most one task at a time. The speeds are constrained by (1f) to take on values from $S^r\subseteq [0,1]$. Constraint (1g) emphasise that task assignment variables are binary. Lastly, (1h) denotes that the control inputs should be step functions.

Fact 1

A solution to (1) where (1c) is satisfied with equality can be constructed from a solution to (1).

Proof

Let (a, s, x) be a feasible point to (1). Let $t_i:=\min \{t\in [b_i,b_i+d_i]\mid x_i(t)\le 0\},~\forall i$. Choose $(\tilde{a},\tilde{s},\tilde{x})$ such that (i) $\tilde{a}_{ik}^r(t)\tilde{s}_{k}^r(t) = a_{ik}^r(t)s_{k}^r(t),~\forall i,k,r,$ $t\le t_i$ and (ii) $\tilde{a}_{ik}^r(t)\tilde{s}_{k}^r(t) = 0,~\forall i,k,r,t > t_i$. Choose $\tilde{x}_i(0)=\underline{x}_i,~\forall i$ and $\dot{\tilde{x}}_{i}(t) = -\sum _{r=1}^\kappa \sum _{k=1}^{m_r} \tilde{a}_{ik}^r(t)\tilde{s}_{k}^r(t),~\forall i,k,r,t$. It follows that $(\tilde{a},\tilde{s},\tilde{x})$ is a solution to (1) where (1c) is an equality. $\square$

3 Solving the scheduling problem with finite-dimensional mathematical optimization

The original problem (1) will be discretized by introducing piecewise constant constraints on the control inputs s and a. Let $\mathcal {T}:=\{\tau _0, \tau _1, \ldots , \tau _{N}\}$, which we will refer to as the major grid, denote the set of discretization time steps corresponding to the distinct arrival times and deadlines of all tasks within L, where $0=\tau _0< \tau _1< \tau _2< \cdots < \tau _{N} = L$.

3.1 Mixed-integer nonlinear program (MINLP-DVFS)

The above scheduling problem, subject to piecewise constant constraints on the control inputs, can be naturally formulated as an MINLP, defined below. Since the context switches due to task preemption and migration can jeopardize the performance, a variable discretization time step (Gerdts 2006) method is applied on a minor grid, so that the solution to our scheduling problem does not depend on the size of the discretization time step. Let $\{\tau _{\mu ,0},\ldots ,\tau _{\mu ,M}\}$ denote the set of discretization time steps on a minor grid on the interval $[\tau _\mu ,\tau _{\mu +1}]$ with $\tau _\mu = \tau _{\mu ,0} \le \ldots \le \tau _{\mu ,M} = \tau _{\mu +1}$, so that $\{\tau _{\mu ,1},\ldots ,\tau _{\mu ,M-1}\}$ is to be determined for all $\mu$ from solving an appropriately-defined optimization problem.

Let $\forall \mu$ and $\forall \nu$ be short notations for $\forall \mu \in U:=\{0,1,\ldots ,N-1\}$ and $\forall \nu \in V:=\{0,1,\ldots ,M-1\}$. Define the notation $[\mu ,\nu ]:= (\tau _{\mu ,\nu }),\forall \mu ,\nu$. Denote the discretized state and input sequences as

$$\begin{aligned}&x_{i}[\mu ,\nu ] := x_{i}(\tau _{\mu ,\nu }),&\forall i,\mu ,\nu \end{aligned}$$

(2a)

$$\begin{aligned}&s_{k}^r[\mu ,\nu ] := s_{k}^r(\tau _{\mu ,\nu }),&\forall k,r,\mu ,\nu \end{aligned}$$

(2b)

$$\begin{aligned}&a_{ik}^r[\mu ,\nu ] := a_{ik}^r(\tau _{\mu ,\nu }),&\forall i,k,r,\mu ,\nu \end{aligned}$$

(2c)

Let $s_{k}^r(\cdot )$ and $a_{ik}^r(\cdot )$ be step functions inbetween time instances on a minor grid, i.e.

$$\begin{aligned}&s_{k}^r(t) = s_{k}^r[\mu ,\nu ],&\forall t\in [\tau _{\mu ,\nu },\tau _{\mu ,\nu +1}),\mu ,\nu \end{aligned}$$

(3a)

$$\begin{aligned}&a_{ik}^r(t) = a_{ik}^r[\mu ,\nu ],&\forall t\in [\tau _{\mu ,\nu },\tau _{\mu ,\nu +1}),\mu ,\nu \end{aligned}$$

(3b)

Let $\Lambda$ denote the set of all tasks within L, i.e. $\Lambda :=\{T_{i}\mid i\in I\}$. Define a task arrival time mapping $\varPhi _b:\Lambda \rightarrow U$ by $\varPhi _b(T_{i}) := \mu$ such that $\tau _{\mu } = b_i$ for all $T_{i}\in \Lambda$ and a task deadline mapping $\varPhi _d:\Lambda \rightarrow U\cup \{N\}$ by $\varPhi _d(T_{i}):=\mu$ such that $\tau _{\mu } = b_i+d_i$ for all $T_{i}\in \Lambda$. Define $\mathcal {U}_i:=\{\mu \in U\mid \varPhi _b(T_i)\le \mu <\varPhi _d(T_i)\},~\forall i\in I$ and let $\forall \mu _i$ be short notation for $\forall \mu \in \mathcal {U}_i.$

By solving a first-order ODE with piecewise constant input, a solution of the scheduling dynamic (1c) has to satisfy the difference constraint

$$\begin{aligned} x_{i}[\mu ,\nu +1]\ge x_{i}[\mu ,\nu ]-h[\mu ,\nu ]\sum _{r=1}^\kappa \sum _{k=1}^{m_r}s_{k}^r[\mu ,\nu ]a_{ik}^r[\mu ,\nu ],\forall i,\mu _i,\nu . \end{aligned}$$

(4a)

where $h[\mu ,\nu ]:=\tau _{\mu ,\nu +1}-\tau _{\mu ,\nu },\forall \mu ,\nu .$

The discretization of the original problem (1) subject to piecewise constant constraints on the inputs (3) is therefore equivalent to the following finite-dimensional MINLP:

(4b)

(4c)

(4d)

(4e)

(4f)

(4g)

(4h)

(4i)

where (4h)–(4i) enforce upper and lower bounds on discretization time steps.

Theorem 2

Let the size of the minor grid $M \ge \underset{r}{\max }\{m_r\}$. A solution to (1) exists if and only if a solution to (4) exists.

Proof

Follows from the fact that if a solution exists to (1), then the Hetero-Wrap scheduling algorithm (Chwa et al. 2015) can find a valid schedule with at most $m_r-1$ migrations within the cluster. (Chwa et al. 2015, Lemma 2).

Next, we will show that $(\tilde{a}[\cdot ],\tilde{s}[\cdot ],\tilde{x}[\cdot ],\tilde{h}[\cdot ])$, a solution to (4), can be constructed from $(a(\cdot ),s(\cdot ),x(\cdot ))$, a solution to (1). Specifically, choose $\tilde{h}[\mu ,\nu ]=\tau _{\mu ,\nu +1}-\tau _{\mu ,\nu }$ as above and $\tilde{a}_{ik}^r[\mu ,\nu ]=a_{ik}^r(t)$ such that $a_{ik}^r(t)$ is a constant for all $t\in \tilde{h}[\mu ,\nu ]$ and

$$\begin{aligned} \tilde{h}[\mu ,\nu ]\tilde{a}_{ik}^r[\mu ,\nu ] =\int _{\tau _{\mu ,\nu }}^{\tau _{\mu ,\nu +1}}a_{ik}^r(t)dt,~\forall i,r,\mu ,\nu . \end{aligned}$$

(5)

Then (4a)–(4c) are satisfied with $\tilde{x}_i[\mu ,\nu ]=x_i(\tau _{\mu ,\nu }),~\forall i,\mu ,\nu$. It follows from (1d), (1e) and (1g) that (4d), (4e) and (4g) are satified, respectively. (4f) is satified with $\tilde{s}_k^r[\mu ,\nu ]=s_k^r(\tau _{\mu ,\nu })$.

Suppose now we have $(\tilde{a}[\cdot ],\tilde{s}[\cdot ],\tilde{x}[\cdot ],\tilde{h}[\cdot ])$, a solution to (4). We can choose $(a(\cdot ),s(\cdot ),x(\cdot ))$ to be a solution to (1) if the inputs are the step functions $a_{ik}^r(t) = \tilde{a}_{ik}^r[\mu ,\nu ]$ and $s_k^r(t) = \tilde{s}_k^r[\mu ,\nu ]$ when $\tilde{h}[\mu ,\nu ]\le t-\tau _{\mu ,\nu } < \tilde{h}[\mu ,\nu +1],~\forall i,k,r,\mu ,\nu$. It is simple to verify that (1) is satisfied by the above choice. $\square$

3.2 Computationally tractable multiprocessor scheduling algorithms

The time to compute a solution to problem (4) is impractical even with a small problem size. However, if we relax the binary constraints in (4g) so that the value of a can be interpreted as the percentage of a time interval during which the task is executed (this will be denoted as $\omega$ in later formulations), rather than the processor assignment, the problem can be reformulated as an NLP for a system with continuous operating speed and an LP for a system with discrete speed levels. The NLP and LP can be solved at a fraction of the time taken to solve the MINLP above. Particularly, the heterogeneous multiprocessor scheduling problem can be simplified into two steps:

STEP 1: :

Workload Partitioning Determine the percentage of task execution times and execution speed within a time interval such that the feasibility constraints are satisfied.

STEP 2: :

Task Ordering From the solution given in the workload partitioning step, find the execution order of all tasks within a time interval such that no task will be executed on more than one processor at a time.

3.2.1 Solving the workload partitioning problem as a continuous nonlinear program (NLP-DVFS)

Since knowing the processor on which a task will be executed does not help in finding the task execution order, the corresponding processor assignment subscript k of the control variables $\omega$ and s is dropped to reduce the number of decision variables. Moreover, partitioning time using only a major grid (i.e. $M = 1$) is enough to guarantee a valid solution, i.e. the percentage of the task exection time within a major grid is equal to the sum of all percentages of task execution times in a minor grid. Since we only need a major grid, we define the notation $[\mu ]:=\tau _\mu$ and $h[\mu ]:=\tau _{\mu +1}-\tau _\mu$. Note that we make an assumption that $h[\mu ]> 0,~\forall \mu$. We also assume that the set of allowable speed levels $S^r$ is a closed interval given by the lower bound $s_{min}^r$ and upper bound $s_{max}^r$.

Consider now the following finite-dimensional NLP:

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

(6g)

where $\omega ^r_{i}[\mu ]$ is defined as the percentage of the time interval $[\tau _{\mu },\tau _{\mu +1}]$ for which task $T_{i}$ is executing on a processor of type-r at speed $s_{i}^r[\mu ]$. (6d) guarantees that a task will not run on more than one processor at a time. The constraint that the total workload at each time interval should be less than or equal to the system capacity is specified in (6e). Upper and lower bounds on task execution speed and percentage of task execution time are given in (6f) and (6g), respectively.

3.2.2 Solving the workload partitioning problem as a linear program (LP-DVFS)

The problem (6) can be further simplified to an LP if the set of speed levels $S^r$ is finite, as is often the case for practical systems. We denote with $s^r_q$ the execution speed at level $q\in Q^r:=\{1,\ldots ,l_r\}$ of an r-type processor, where $l_r$ is the total number of speed levels of an r-type processor. Let $\forall q$ be short-hand for $\forall q\in Q^r$.

Consider now the following finite-dimensional LP:

(7a)

(7b)

(7c)

(7d)

(7e)

(7f)

where $\omega ^r_{iq}[\mu ]$ is the percentage of the time interval $[\tau _{\mu },\tau _{\mu +1}]$ for which task $T_{i}$ is executing on a processor of type-r at a speed level q. Note that all constraints are similar to (6), but the speed levels are fixed.

Theorem 3

A solution to (6) can be constructed from a solution to (7), and vice versa, if the discrete speed set $S^r$ is any finite subset of the closed interval $[s_{min}^r,s_{max}^r]$ with $s_{min}^r$ and $s_{max}^r$ in $S^r$ for all r.

Proof

Let $(\tilde{x},\tilde{\omega },\tilde{s})$ denote a solution to (6) and $(x,\omega )$ a solution to (7). The result follows by noting that one can choose $\lambda _q^r[\mu ]\in [0,1]$ such that $\sum _q\lambda _q^r[\mu ]s_q^r[\mu ]$ $=\tilde{s}_i^r[\mu ]$, $\omega _{iq}^r[\mu ]=\lambda _q^r[\mu ]\tilde{\omega }_i^r[\mu ]$ and $\sum _q\lambda _q^r[\mu ]=1,~\forall i,q,r,\mu$ are satisfied. $\square$

3.2.3 Task ordering algorithm

This section discusses how to find a valid schedule in the task ordering step for each time interval $[\tau _{\mu },\tau _{\mu +1}]$. Since the solutions obtained in the workload partitioning step are partitioning workloads of each task on each processor type within each time interval, one might think of using McNaughton’s wrap around algorithm (McNaughton 1959) to find a valid schedule for each processor within the processor type. However, McNaughton’s wrap around algorithm only guarantees that a task will not be executed at the same time within the cluster. There exists a possibility that a task will be assigned to more than one processor type (cluster) at the same time.

To avoid a parallel execution on any two clusters, we can adopt the Hetero-Wrap algorithm proposed in Chwa et al. (2015) to solve a task ordering problem of a two-type heterogeneous multiprocessor platform. The algorithm takes the workload partitioning solution to STEP 1 as its inputs and returns $(\sigma _{ik}^r,\eta _{ik}^r)\in [0,1]^2,~\forall i,k,r$, which is a task-to-processor interval assignment on each cluster. Note that, for a solution to problem (7), we define the total execution workload of a task $\omega _i^r:=\sum _q \omega _{iq}^r$ and assume that the percentage of execution times of each task at all frequency levels $\omega _{iq}^r$ will be grouped together in order to minimize the number of migrations and preemptions. In order to be self-contained, the Hetero-Wrap algorithm is given in Algorithm 1. Specifically, the algorithm classifies the tasks into four subsets: (i) a set $IM_a$ of migrating tasks with $\sum _r\omega _i^r = 1$, (ii) a set $IM_b$ of migrating tasks with $\sum _r\omega _i^r<1$, (iii) a set $CP_1$ of partitioned tasks on cluster of type-1, and (iv) a set $CP_2$of partitioned tasks on cluster of type-2. The algorithm then employs the following simple rules:

• For a type-1 cluster, tasks are scheduled in the order of $IM_a,~IM_b$ and $CP_1$ using McNaughton’s wrap around algorithm. That is, a slot along the number line is allocated, starting at zero, with the length equal to $m_1$ and the task is aligned with its assigned workload on empty slots of the cluster in the specified order starting from left to right.

• For a type-2 cluster, in the same manner, tasks are scheduled using McNaughton’s wrap around algorithm, but in the order of $IM_a, IM_b$ and $CP_2$ starting from right to left. Note that the order of tasks in $IM_a$ has to be consistent with the order in a type-1 cluster.

However, the algorithm requires a feasible solution to (6) or (7), in which $IM_b$ has at most one task, which we will call an inter-cluster migrating task. From Theorem 3, we can always transform a solution to (6) into a solution to (7). Therefore, we only need to show that there exists a solution to (7) with at most one inter-cluster migrating tasks that lies on the vertex of the feasible region by the following facts and lemma.

Fact 4

Among all the solutions to an LP, at least one solution lies at a vertex of the feasible region. In other words, at least one solution is a basic solution.

Proof

The Fundamental Theorem of Linear Programming, which states that if a feasible solution exists, then a basic feasible solution exists (Vanderbei 2001, p. 38). $\square$

Fact 5

A feasible solution to an LP that is not a basic solution can always be converted into a basic solution.

Proof

This follows from the Fundamental Theorem of Linear Programming (Vanderbei 2001, p. 38). $\square$

Fact 6

(Baruah 2004, Fact 2) Consider a linear program $\min \{c^T\chi \mid A\chi \le b, \chi \in \mathbb {R}^n\}$ for some $A\in \mathbb {R}^{(m+n)\times n}$, $b\in \mathbb {R}^{m+n}$, $c\in \mathbb {R}^{n}$. Suppose that n constraints are nonnegative constraints on each variable, i.e. $\chi _i\ge 0,~\forall i\in \{1,2,\ldots ,n\}$ and the rest are m linearly independent constraints. If $m<n$, then a basic solution will have at most m non-zero values.

Proof

A unique basic solution can be identified by any $n+m$ linearly independent active constraints. Since there are n nonnegative constraints and $m<n$, a basic solution will have at most m non-zero values. $\square$

Lemma 1

For a solution to (7) that lies on the vertex of the feasible region, there will be at most one inter-cluster partitioning task.

Proof

The number of variables $\omega$ subjected to nonnegative constraint (7f) at each time interval of (7) is $n(\sum _rl_r)$. The number of variables $\omega$ subjected to a set of necessary and sufficient feasibility constraints (7d)-(7e) is $n+2$. Note that we do not count the number of variables in (7c) because (7c) and (7d) are linearly dependent constraints for a given value of $\xi _i[\mu ]:= (x_{i}[\mu ]-x_{i}[\mu +1])/h[\mu ]$. If we assume that $n\ge 2$ and each processor type has at least one speed level, then it follows from Fact 6 that the number of non-zero values of variable $\omega$, a solution to (7) at the vertex of the feasible region, is at most $n+2$. Let $\gamma$ be the number of tasks assigned to two processor types. Therefore, there are $2\gamma +(n-\gamma )$ entries of variable $\omega$ that are non-zero. This implies that $\gamma < 2$, i.e. the number of inter-cluster partitioning tasks is at most one. $\square$

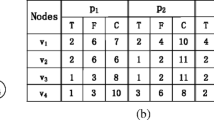
To illustrate how Algorithm 1 works, consider a simple taskset in which the percentage of execution workload partition at time interval $[\tau _{\mu },\tau _{\mu +1}]$ for each task is as shown in Table 1. A feasible schedule obtained by Algorithm 1 is shown in Fig. 2, where the numbers in a circle denote the order of tasks allocation. Notice that the processors of a cluster 1 are filled from left to right, while the processors of a cluster 2 are filled from right to left. For this example, $m_1 = m_2= 2$, $IM_a=\{T_1,T_2\},~IM_b=\{T_3\},~CP_1=\{T_4\}$ and $CP_2=\{T_5\}$.

Theorem 7

If a solution to (1) exists, then a solution to (6)/(7) exists. Furthermore, at least one valid schedule satisfying (1) can be constructed from a solution to problem (6)/(7) and the output from Algorithm 1.

Proof

The existence of a valid schedule is proven in Chwa et al. (2015, Thm 3). It follows from Facts 4–6 and Lemma 1 that one can compute a solution with at most one inter-cluster partitioning task. Given a solution to (6)/(7) and the output from Algorithm 1 for all intervals, choose a to be a step function such that $a_{ik}^r(t)=1$ when $\sigma _{ik}^r[\mu ,\nu ]h[\mu ,\nu ]\le t-\tau _{\mu ,\nu }<\eta _{ik}^r[\mu ,\nu ]h[\mu ,\nu +1]$ and $a_{ik}^r(t)=0$ otherwise, $\forall i,k,r,\mu ,\nu$. Specifically, one can verify that the following condition holds

$$\begin{aligned} h[\mu ,\nu ]\omega _i^r[\mu ]=\int _{\tau _{\mu ,\nu }}^{\tau _{\mu ,\nu +1}} {\sum _ka_{ik}^r(t)dt},~\forall i,r,\mu ,\nu . \end{aligned}$$

(8)

Then it is straightforward to show that (1) is satisfied. $\square$

Table 1 Workload partition example

Fig. 2

A feasible task schedule according to Algorithm 1

3.3 Computational complexity

Note that, although we need to solve the same multiprocessor scheduling problem with two steps in this section, the computation times to solve (6) or (7) is extremely fast compared to solving problem (4), i.e. even for a small problem, the times to compute a solution of (4) can be up to an hour, while (6) or (7) can be solved in milliseconds using a general-purpose desktop PC with off-the-shelf optimization solvers. In particular, great advances in LP solvers have been made in the last three decades and an LP can be solved to any specified accuracy in polynomial time using a suitably-chosen interior point method (Boyd and Vandenberghe 2004). Moreover, the optimization problems defined in this section are highly structured with sparse matrices. These facts can be exploited to develop efficient tailor-made solvers, as in the literature on real-time optimization-based or predictive control (Betts 2010; Boyd and Vandenberghe 2004; Mayne 2014), which can outperform general-purpose software by orders of magnitude. For example, custom optimization algorithms implemented on hardware accelerators, such as field-programmable gate arrays (FPGAs), can allow one to solve optimal control problems online in less than 1 $\upmu$s (Jerez et al. 2014). The solution to the optimization problems can also be precomputed as a lookup table by using methods in parametric programming that have been developed in the control community (Bemporad et al. 2002a, b).

A more detailed complexity analysis is possible for the problems considered here. Since the time taken to solve the NLP (6) and the LP (7) is orders of magnitude less than solving the MINLP (4), we restrict ourselves to the NLP (6) and LP (7). For simplicity, assume that an interior point method is used to solve these problems.

Consider first the complexity of computing Newton (search) directions. Note that the number of decision variables and constraints grow $\mathcal {O}(nN)$, hence it follows that the time to compute a Newton direction increases $\mathcal {O}(n^3N^3)$. However, the problem here as a very particular structure and one can do better than this naive analysis. If care is taken with the formulation of the optimization problem and sparse linear solvers are employed as in Betts (2010) and Kang et al. (2014), then the number of non-zeros in the KKT matrix increases $\mathcal {O}(nN)$. Hence, a Lanczos-based iterative linear solver, such as MINRES, will be able to solve the sparse symmetric KKT system in $\mathcal {O}(n^2N^2)$ time. We note that this is only an upper bound and it is possible to exploit structure even further. Using a similar method as in Kang et al. (2014), in Kasture (2017)³ it is shown that one can improve on this bound and that the Newton directions for the LP (7) can be computed in $\mathcal {O}(nN^2)$ time (note that $n\ge N$ for the problems in this paper). In practice, the method in Kasture (2017) scales better than this bound, suggesting that there is further structure to exploit; however, a detailed analysis is clearly beyond the scope of this paper and therefore left as an open research question.

Consider now the number of Newton steps required to compute a solution. It follows from established results that the number of Newton steps in an interior-point solver for an LP and certain classes of convex NLPs is bounded by $\mathcal {O}(\sqrt{nN})$ (Boyd and Vandenberghe 2004, Sect. 11.5). However, as is well-known, this bound is very conservative; in practice the number of steps hardly changes and is usually on the order of a few tens. This analysis clearly holds for the LP (7). However, we have so far been unable to derive a similar bound for the NLP (6), but have found that in practice the number of iterations of an interior-point solver is insensitive to the problem size if care is taken. An interesting open research question is therefore whether it is possible to reformulate the NLP (6) such that results on self-concordant functions (Boyd and Vandenberghe 2004, Sect. 11.5) can be used to derive a similar, scalable bound on the number of Newton iterations when solving the NLP (6).

Finally, note that the complexity of Algorithm 1 is $\mathcal {O}(n)$ (Chwa et al. 2015). Therefore, we expect that it would be feasible to execute the proposed algorithms online for certain taskets, but of course significant research on this topic still needs to be done in order to extend the scope and exploit the particular structure that arises in scheduling problems.

4 Energy optimality

4.1 Energy consumption model

A power consumption model can be expressed as a summation of dynamic power consumption $P_d$ and static power consumption $P_s$. Dynamic power consumption is due to the charging and discharging of CMOS gates, while static power consumption is due to subthreshold leakage current and reverse bias junction current (Rabaey et al. 2003). The dynamic power consumption of CMOS processors at a clock frequency $f=sf_{max}$ is given by

$$\begin{aligned} P_d(s) = C_{ef}V_{dd}^2sf_{max}, \end{aligned}$$

(9a)

where the constraint

$$\begin{aligned} sf_{max} \le \zeta \frac{(V_{dd}-V_t)^2}{V_{dd}} \end{aligned}$$

(9b)

has to be satisfied (Rabaey et al. 2003). Here $C_{ef} > 0$ denotes the effective switch capacitance, $V_{dd}$ is the supply voltage, $V_t$ is the threshold voltage ($V_{dd}>V_t>0$ V) and $\zeta > 0$ is a hardware-specific constant.

From (9b), it follows that if s increases, then the supply voltage $V_{dd}$ may have to increase (and if $V_{dd}$ decreases, so does s). In the literature, the total power consumption is often simply expressed as an increasing function of the form

$$\begin{aligned} P(s):=P_d(s)+P_s=\alpha s^\beta +P_s, \end{aligned}$$

(10)

where $\alpha >0$ and $\beta \ge 1$ are hardware-dependent constants, while the static power consumption $P_s$ is assumed to be either constant or zero (Li and Wu 2013).

The energy consumption of executing and completing a task $T_i$ at a constant speed $s_i$ is given by

$$\begin{aligned} E(s_i) := \frac{c_i}{f_{max}} \frac{(P_d(s_i)+P_s)}{s_i} =\frac{\underline{x}_i(P_d(s_i)+P_s)}{s_i}. \end{aligned}$$

(11a)

In the literature, it is often assumed that E is an increasing function of the operating speed. However, because $s\mapsto 1/s$ is a decreasing function, it follows that the energy consumed might not be an increasing function if $P_s$ is non-zero; Fig. 3 gives an example of when the energy is non-monotonic, even if the power is an increasing function of clock frequency.

Fig. 3

Example of a non-increasing active energy function, but where the active power consumption is an increasing function

This result implies the existence of a non-zero energy-efficient speed $s_{eff}$, i.e. the minimizer of (11) (Miyoshi et al. 2002; Chen et al. 2006; Aydin et al. 2006). Moreover, in the work of Zhai et al. (2004), the non-convex relationship between the energy consumption and processor speed can be observed as a result of scaling supply voltage.

The total energy consumption of executing a real-time task $T_i$ can be expressed as a summation of active energy consumption and idle energy consumption, i.e. $E = E_{active} + E_{idle}$, where $E_{active}$ is the energy consumption when the processor is busy executing the task and $E_{idle}$ is the energy consumption when the processor is idle. The energy consumption of executing and completing a task $T_i$ at a constant speed $s_i$ is

$$\begin{aligned} E(s_i)&= E_{active}(s_i) + E_{idle} \end{aligned}$$

(12a)

$$\begin{aligned}&=\frac{c_i}{f_{max}} \frac{(P_{active}(s_i)-P_{idle})}{s_i} + P_{idle}d_i \end{aligned}$$

(12b)

$$\begin{aligned}&=\frac{\underline{x}_i(P_{active}(s_i)-P_{idle})}{s_i} + P_{idle}d_i, \end{aligned}$$

(12c)

where $P_{active}(s):=P_{da}(s)+P_{sa}$ is the total power consumption in the active interval, $P_{idle}:=P_{di}+P_{si}$ is the total power consumption during the idle period. $P_{da} > 0$ and $P_{sa} \ge 0$ are dynamic and static power consumption during the active period, respectively. Similarly, $P_{di} > 0$ and $P_{si} \ge 0$ are the dynamic and static power consumption during the idle period. $P_{di}$ will be assumed to be a constant, since the processor is executing a nop (no operation) instruction at the lowest frequency $f_{min}$ during the idle interval. $P_{sa}$ and $P_{si}$ are also assumed to be constants where $P_{si} < P_{sa}$. Note that $P_{active}(s)-P_{idle}$ is strictly greater than zero.

4.2 Optimality problem formulation

The scheduling problem with the objective to minimize the total energy consumption of executing the taskset on a two-type heterogeneous multiprocessor can be formulated as the following optimal control problems:

$$\begin{aligned}&{\text {(I) Continuous Optimal Control Problem:}}\nonumber \\&\qquad {\mathop {\mathop {\text {minimize}}\limits _{x_{i}(\cdot ), a_{ik}^r(\cdot ),s_{k}^r(\cdot ),}}\limits _{\forall i\in I,k\in K^r,r\in R}} \quad \sum _{r,k,i}\int _0^{L} \ell ^r(a_{ik}^r(t),s_{k}^r(t))dt\end{aligned}$$

(13)

$$\begin{aligned}&\qquad \text {subject to}~(1). \nonumber \\&{\text {(II) MINLP-DVFS:}}\nonumber \\&\qquad {\mathop {\mathop {\text {minimize}} \limits _{x_{i}[\cdot ],a_{ik}^r[\cdot ],s_{k}^r[\cdot ],h[\cdot ],}} \limits _{\forall i\in I,k\in K^r,r\in R}} {\quad \sum _{r,\mu ,\nu ,k,i}h[\mu ,\nu ] \ell ^r(a_{ik}^r[\cdot ],s_{k}^r[\cdot ])} \end{aligned}$$

(14)

$$\begin{aligned}&\qquad \text {subject to}~(4). \nonumber \\&{\text {(III) NLP-DVFS:}}\nonumber \\&\qquad {\mathop {\mathop {\text {minimize}} \limits _{x_{i}[\cdot ],\omega _{i}^r[\cdot ],s_{i}^r[\cdot ],}} \limits _{\forall i\in I,r\in R}} \quad {\sum _{r,\mu ,\nu ,i}h[\mu ] \ell ^r(\omega _{i}^r[\cdot ],s_{i}^r[\cdot ])} \end{aligned}$$

(15)

$$\begin{aligned}&\qquad \text {subject to}~(6). \nonumber \\&{\text {(IV) LP-DVFS}:}\nonumber \\&\qquad {\mathop {\mathop {\text {minimize}}\limits _ {x_{i}[\cdot ],\omega _{iq}^r[\cdot ],}}\limits _ {\forall i\in I, q\in Q^r,r\in R}} \quad {\sum _{r,\mu ,\nu ,i,q}h[\mu ]\ell ^r(\omega _{iq}^r [\cdot ],s_q^r)}\nonumber \\&\text {subject to}~(7). \end{aligned}$$

(16)

where $\ell ^r(a,s):=a(P^r_{active}(s)-P^r_{idle})$. Note that (16) is an LP, since the cost is linear in the decision variables.

4.3 Constant or time-varying speed?

In this section, we present a result on a general speed selection trajectory for a uniprocessor scheduling problem with a real-time taskset. With this observation about optimal speed profile, we can formulate algorithms that are able to solve a more general class of scheduling problems than in the literature.

Consider the following simple example, illustrated in Fig. 4, where the power consumption model $P(\cdot )$ is a concave function of speed. Assume that $s_2$ is the lowest possible constant speed at which task $T_i$ can be finished on time, i.e. $\underline{x}_i=s_2d_i$. The energy consumed is $E(s_2) = P(s_2)d_i$ and the average power consumption $P(s_2)=:\bar{P}_c$. Let $\lambda \in [0,1]$ be a constant such that $s_2 = \lambda s_1 + (1-\lambda )s_3$, $s_1< s_2 < s_3$. Suppose $s(\cdot )$ is a time-varying speed profile such that $s(t) = s_1,~\forall t\in [0,t_1)$ and $s(t) = s_3,~\forall t\in [t_1,d_i)$. We can choose $t_1$ such that $\underline{x}_i=s_1t_1+s_3(d_i-t_1).$ The energy used in this case is $E(s_1,s_3)=t_1P(s_1)+(d_i-t_1)P(s_3)$. If we let $\lambda = t_1/d_i$, then the average power consumption $E(s_1,s_3)/d_i =: \bar{P}_{tv} = (t_1/d_i)P(s_1) + (1-(t_1/d_i))P(s_3) = \lambda P(s_1) + (1-\lambda )P(s_3).$ Since $P(\cdot )$ is concave, $P(s_2) \ge \lambda P(s_1) + (1-\lambda )P(s_3) = \bar{P}_{tv}.$ This result implies that a time-varying speed profile is better than a constant speed profile when the power consumption is concave. Notably, the result can be generalised to the case where the power model is non-convex, non-concave as well as discrete speed set.

Fig. 4

A time-varying speed profile is better than a constant speed profile if the power function is not convex

Theorem 8

Let a piecewise constant speed trajectory $s^*(\cdot )$ be given that maps every time instant in a closed interval $[t_0,t_f]$ to the domain S of a power function $P:S\rightarrow \mathbb {R}$. There exists a piecewise constant speed trajectory $s(\cdot )$ with at most one switch such that the amount of computations done and the energy consumed is the same as using $s^*(\cdot )$, i.e. $s(\cdot )$ is of the form

$$\begin{aligned} s(t):= {\left\{ \begin{array}{ll} \check{s} &{}\forall t\in [t_0,(t_f-t_0)\lambda +t_0)\\ \hat{s} &{} \forall t\in [t_0+(t_f-t_0)\lambda ,t_f] \end{array}\right. } \end{aligned}$$

where $\hat{s},\check{s}\in S$, $\lambda \in [0,1]$, such that the total amount of computations

$$\begin{aligned} c:= \int _{t_0}^{t_f}s^*(t)dt = \int _{t_0}^{t_f}s(t)dt \end{aligned}$$

and energy consumed

$$\begin{aligned} E:=\int _{t_0}^{t_f}P(s^*(t))dt = \int _{t_0}^{t_f}P(s(t))dt. \end{aligned}$$

Proof

Let $\{\mathcal {T}_1,\ldots ,\mathcal {T}_p\}$ be a partition of $[t_0,t_f]$ and ${\text {range}} s^*=:\{s_1,\ldots ,s_p\}\subseteq S$ such that $s^*(t)=s_i$ for all $t\in \mathcal {T}_i$, $i\in \mathcal {I}:=\{1,\ldots ,p\}$. Define $\varDelta _i:=\int _{\mathcal {T}_i}dt$ as the size of the set $\mathcal {T}_i$ and $\lambda _i:=\varDelta _i /(t_f-t_0)$, $\forall i \in \mathcal {I}$.

It follows that $c = \sum _is_i\varDelta _i$ and $E = \sum _iP(s_i)\varDelta _i$. Hence, the average speed $\bar{s}:=c/(t_f-t_0)= \sum _i\lambda _i s_i$ and average power $\bar{P}:=E/(t_f-t_0)= \sum _i\lambda _i P(s_i)$.

Note that $\sum _i\lambda _i = 1$. This implies that $(\bar{s},\bar{P})$ is in the convex hull of the finite set $G:=\{(s_i,P(s_i))\in S\times \mathbb {R}\mid i \in \mathcal {I}\}$ with ${\text {vert}}({\text {conv}}{G})\subseteq G$. Hence, there exists a $\lambda \in [0,1]$ and two points $\hat{s}$ and $\check{s}$ in S with $(\hat{s},P(\hat{s}))\in {\text {vert}}({\text {conv}}{G})$ and $(\check{s},P(\check{s}))\in {\text {vert}}({\text {conv}}{G})$ such that $\bar{s} = \lambda \check{s}+(1-\lambda )\hat{s}$ and $\bar{P}=\lambda P(\check{s})+(1-\lambda )P(\hat{s})$. If s is defined as above with these values of $\lambda$, $\hat{s}$ and $\check{s}$, then one can verify that $\int _{t_0}^{t_f}s(t)dt = (t_f-t_0)\bar{s}$ and $\int _{t_0}^{t_f}P(s(t))dt = (t_f-t_0)\bar{P}$. $\square$

The following result has already been observed in  Aydin et al. (2004, Prop. 1) and  Gerards et al. (2014, Cor. 1).

Corollary 1

Given a processor with a convex power model and required workload within a time interval, there exists a constant optimal speed profile if the set of speed levels S is a closed interval.

Proof

This is a special case of Theorem 8 and can be proven easily using Jensen’s inequality. $\square$

Corollary 2

An optimal speed profile to (13) can be constructed by switching between no more than two non-zero speed levels within each time interval defined by two consecutive time steps of the major grid $\mathcal {T}$.

Proof

The overall optimal speed profile can be obtained by connecting an optimal time-varying speed profile proven in Theorem 8 for each partitioned time interval. Specifically, the generalised optimal speed profile is a step function.$\square$

The result of the above Theorem and Corollaries can be applied directly to scheduling algorithms that adopt the DP technique such as, LLREF, DP-WRAP, as well as our algorithms in Sect. 3. Consider the problem of determining the optimal speeds at each time interval defined by two consecutive task deadlines. By subdividing time into such intervals, we can easily determine the optimal speed profile of four uniprocessor scheduling paradigms classified by power consumption and taskset models, i.e. (i) a convex power consumption model with implicit deadline taskset, (ii) a convex power consumption model with constrained deadline taskset, (iii) a non-convex power consumption model with implicit deadline taskset and (iv) a non-convex power consumption model with constrained deadline taskset. Specifically, if the taskset has an implicit deadline, then the required workloads (taskset density) are equal for all time intervals; the optimal speed profiles of all schedule intervals are the same as well. Therefore, the optimal speed profile is a constant for (i) (Cor. 1) and a combination of two speeds for (iii) (Cor. 8). However, for a constrained deadline taskset, the required workload varies from interval to interval, but is constant within the interval. Hence, even if the power function is (ii) convex or (iv) non-convex, the optimal speed profile is a (time-varying) piecewise constant function. In other words, for generality, a time-varying speed profile with two speed levels at each partitioned time interval is guaranteed to provide an energy optimal solution.

Theorem 9

Consider the optimization problems (13)–(16). An optimal speed profile for (13) can be constructed using any of the following methods:

• Compute a solution to (14) with the lower bound on M at least twice the bound in Theorem 2.

• If the active power function $P_{active}$ is convex and the speed level sets are closed intervals, compute a solution to (15). If there is more than one inter-cluster partitioning task, then the (finite) range of the optimal speed profile should be used to define and compute a solution to (16) with at most one inter-cluster partitioning task. This process is concluded with Algorithm 1.

• If the speed level sets are finite, compute a solution to (16) with at most one inter-cluster partitioning task, followed with Algorithm 1.

Proof

Follows from the choices of selecting a and s as in the proofs of Theorem 2 and Theorem 7. The cost of all problems are then equal. $\square$

5 Simulation results

5.1 System, processor and task models

The energy efficiency of solving the above optimization problems is evaluated on the ARM big.LITTLE architecture, where a big core provides faster execution times, but consumes more energy than a LITTLE core. The details of the ARM Cortex-A15 (big) and Cortex-A7 (LITTLE) core, which have been validated in Chwa et al. (2014), are given in Tables 2 and 3.

Table 2 ARM cortex-A15 (big) processor details (Chwa et al. 2014)

Table 3 ARM cortex-A7 (LITTLE) processor details (Chwa et al. 2014)

The active power consumption models, obtained by a polynomial curve fitting to the generic form (10), are shown in Table 4.

Table 4 ARM processor power consumption models

Fig. 5

Actual data versus fitted model

The plots of the actual data versus the fitted models are shown in Fig. 5. The idle power consumption was not reported, thus we will assume this to be a constant strictly less than the lowest active power consumption, namely $P_{idle}=70$ mW for the big core and $P_{idle}=12$ mW for the LITTLE core. To illustrate that our formulations are able to solve a broader class of multiprocessor scheduling problems than others optimal algorithms reported in the literature, we consider periodic taskset models with both implicit and constrained deadlines. However, a more general taskset model such as an arbitary deadline taskset, where the deadline could be greater than the period, a sporadic taskset model, where the inter-arrival time of successive tasks is at least $p_i$ time units, and an aperiodic taskset can be solved by our algorithms as well. To guarantee the existence of a valid schedule, the minimum taskset density has to be less than or equal to the system capacity. Moreover, a periodic task needs to be able to be executed on any processor type. Specifically, the minimum task density should be less than or equal to the lowest capacity of all processor types, i.e. $\delta _i(1)\le 0.375$ for this particular architecture.

5.2 Comparison between algorithms

For a system with a continuous speed range, four algorithms are compared: (i) MINLP-DVFS, (ii) NLP-DVFS, (iii) GWA-SVFS, which represents a global energy/feasibility-optimal workload allocation with constant frequency scaling scheme at a core-level and (iv) GWA-NoDVFS, which is a global scheduling approach without frequency scaling scheme. For a system with discrete speed levels, four algorithms are compared: (i) LP-DVFS, (ii) GWA-NoDVFS, (iii) GWA-DDiscrete and (iv) GWA-SDiscrete, which represent global energy/feasibility optimal workload allocation with time-varying and constant discrete frequency scaling schemes, respectively. Note that GWA-SVFS, GWA-NoDVFS, GWA-DDiscrete and GWA-SDiscrete are based on the mathematical optimization formulation proposed in Chwa et al. (2014), but adapted to our framework, for which details are given below.

GWA-SVFS/GWA-NoDVFS: Given $m_r$ processors of type-r and n periodic tasks, determine a constant operating speed for each processor $s^r_k$ and the workload ratio $y_{ik}^r$ for all tasks within hyperperiod $\mathcal {L}$ that solves:

(17a)

(17b)

(17c)

(17d)

(17e)

(17f)

(17g)

where $y_{ik}^r$ is the ratio of the workload of task $T_i$ on processor k of type-r, $\delta _{ik}^r(s^r_k)$ is the task density on processor k type-r defined as $\delta _{ik}^r(s^r_k):=y_{ik}^rc_{i}/(s^r_kf_{max}\min \{d_i,p_i\}$) and $\mathcal {L}_i:=\mathcal {L}\min \{d_i,p_i\}/p_i$. Note that when $d_i=p_i$ as in the case of an implicit deadline taskset $\mathcal {L}_i = \mathcal {L},~\forall i$. (17b) ensures that all tasks will be allocated the amount of required execution time. The constraint that a task will not be executed on more than one processor at the same time is specified in (17c). (17d) asserts that the assigned workload will not exceed processor type capacity. Upper and lower bounds on the workload ratio of a task are given in (17e). The difference between GWA-SVFS and GWA-NoDVFS lies in restricting a core-level operating speed $s^r_k$ to be either a continuous variable (17f) or fixed at the maximum value (17g).

GWA-DDiscrete: Given $m_r$ processors of type-r and n periodic tasks, determine a percentage of the task workload $y_{iq}^r$ at a specific speed level for all tasks within hyperperiod $\mathcal {L}$ that solves:

(18a)

(18b)

(18c)

(18d)

(18e)

where $y_{iq}^r$ is the percentage of workload of task $T_i$ on processor type-r at speed level q, $\delta _{iq}^r(y_{iq}^r)$ is the task density on processor type-r at speed level q, i.e. $\delta _{iq}^r(y_{iq}^r):=y_{iq}^rc_i/(s^r_qf_{max}\min \{d_i,p_i\}$). Constraint (18b) guarantees that the total execution workload of a task is allocated. Constraint (18c) assures that a task will be executed only on one processor at a time. Constraint (18d) ensures that each processor type workload capacity is not violated. Constraint (18e) provides upper and lower bounds on a percentage of task workload at specific speed level.

GWA-SDiscrete: Given $m_r$ processors of type-r and n periodic tasks, determine a percentage of task workload $y_{iq}^r$ at a specific speed level and a processor speed level selection $z_q^r$ for all tasks within hyperperiod $\mathcal {L}$ that solves:

(19a)

(19b)

(19c)

(19d)

(19e)

(19f)

(19g)

where $y_{ikq}^r$ is the workload partition of task $T_i$ of processor k of an r-type at speed level q, $z_{kq}^r$ is a speed level selection variable for processor k of an r-type , i.e. $z_{kq}^r = 1$ if a speed level q of an r-type processor is selected and $z_{kq}^r = 0$ otherwise. Constraint (19b), (19d)–(19f) are the same as the GWA-DDiscrete. Constraint (19c) assures that only one speed level is selected. Constraint (19g) emphasises that the speed level selection variable is a binary.

Note that GWA-SVFS and GWA-NoDVFS are NLPs, GWA-DDiscrete is an LP and GWA-SDiscrete is an MINLP. Moreover, the formulation of GWA-DDiscrete allows a processor to run with a time-varying combination of constant discrete speed levels, while GWA-SVFS and GWA-SDiscrete only allow a constant execution speed for each processor.

5.3 Simulation setup and results

For simplicity and without loss of generality, consider the case where independent real-time tasks are to be executed on two-type processor architectures, for which the details are given in Sect. 5.1. The MINLP formulations were modelled using ZIMPL (Koch 2004) and solved with SCIP (Achterberg 2009). The LP and NLP formulations were solved with SoPlex (Wunderling 1996) and Ipopt (Wächter and Biegler 2006), respectively. The value of the minor grid discretization step M is chosen according to Theorem 2.

For implict deadline tasksets, we consider the system composed of two big cores and six LITTLE cores, which has a system capacity of 4.25=(2+2.25). The total energy consumption of each taskset with a minimum taskset density varying from 0.5 to system capacity with a step of 0.25, given in Table 5, are evaluated. Note that, the first parameter of a task is $\underline{x}_i$; $c_i$ can be obtained by multiplying $\underline{x}_i$ by $f_{max}$. Since the task period is the same as the deadline, the last parameter of the task model is dropped.

Table 5 Implicit deadline tasksets for simulation

Figure 6a shows simulation results for scheduling a real-time taskset with implicit deadlines on an ideal system. The minimum taskset density D is represented on the horizontal axis. The vertical axis is the total energy consumption normalised by GWA-NoDVFS, where less than 1 means the algorithm does better than GWA-NoDVFS.

The three algorithms with a DVFS scheme, i.e. MINLP-DVFS, NLP-DVFS, and GWA-SVFS, produce the same optimal energy consumption, though both of our algorithms allow the operating speed to vary with time compared with a constant frequency scaling scheme, used by GWA-SVFS. The simulation results suggest that the optimal speed is a constant, rather than time-varying, for an implicit deadline taskset that has a constant workload over time. This result complies with Corollary 1. Moreover, the little core, which only has 37.5% computing power compared with the big core and consumes considerably less power even when running at full speed, will be selected by the optimizer before considering the big cores. This is why we can see two upwards parabolic curves in the figures, where the first one corresponds to the case where only little cores in the system are selected, while both core types are selected in the second, which happens when the minimum taskset density is larger than the little-core cluster’s capacity.

However, for a practical system, where a processor has discrete speed levels, the constant speed assignment is not an optimal strategy. As can be observed in Fig. 6b, the LP-DVFS and GWA-DDiscrete are energy optimal, while the GWA-SDiscrete is not. The results imply that to obtain an energy optimal schedule, a time-varying combination of discrete speed levels is necessary.

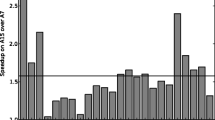
For a real-time taskset with constrained deadlines, we consider a system with one big core and one LITTLE core, i.e. a system capacity of $1.375=(1+0.375)$. The simulation results of executing each taskset, listed in Table 6, are shown in Fig. 7, where the total energy consumption normalised by GWA-NoDVFS is on the vertical axis.

Fig. 6

Simulation results for scheduling real-time tasks with implicit deadlines

Table 6 Constrained deadline tasksets for simulation

Fig. 7

Simulation results for scheduling real-time tasks with constrained deadlines

It can be seen from the plots that for a taskset with a piecewise constant and time-varying workload, i.e. constrained deadlines, our algorithms consume less energy than that of GWA-SVFS, GWA-DDiscrete and GWA-SDiscrete. This is because time is incorporated in our formulations, which provides benefits for solving a scheduling problem with a time-varying workload as well as a constant workload.

It has to be mentioned that the energy saving percentage varies with the taskset, which implies that the number on the plots shown here can be varied, but the significant outcomes stay the same. An example of how large the variability is illustrated in Fig. 8, where 5 constrained deadlines are randomly generated for each taskset density and are scheduled on a practical system composed of one of each processor type.

Lastly, although we had shown simulations with small tasksets in order to facilitate replicability, our proposed scheduling algorithms are scalable to large problems. (6)/(15) and (7)/(16) with large number of decision variables can be solved in milliseconds using a general-purpose PC with the off-the-self optimization solvers (Hei et al. 2008).

Fig. 8

Energy saving percentage box-plots of executing constrained deadline tasksets on a practical system

6 Conclusions

This work presents multiprocessor scheduling as an optimal control problem with the objective of minimizing the total energy consumption. We have shown that the scheduling problem is computationally tractable by first solving a workload partitioning problem, then a task ordering problem. The simulation results illustrate that our algorithms are both feasibility optimal and energy optimal when compared to an existing global energy/feasibility optimal workload allocation algorithm. Moreover, we have shown via proof and simulation that a constant frequency scaling scheme is enough to guarantee optimal energy consumption for an ideal system with a constant workload and convex power function, while this is not true in the case of a time-varying workload or a non-convex power function. For a practical system with discrete speed levels, a time-varying speed assignment is necessary to obtain an optimal energy consumption in general.

For future work, one could incorporate a DPM scheme and formulate the problem as a multi-objective optimization problem to further reduce energy consumption of a system. Extending the idea presented here to cope with uncertainty in a task’s execution time using feedback is also possible, as in our work on homogeneous multiprocessor systems (Thammawichai and Kerrigan 2016). Though our work has been focused on minimizing the energy consumption, the framework could be easily applied to other objectives such as leakage-aware, thermal-aware and communication-aware scheduling problems. Numerically efficient methods could also be developed to solve optimization problems defined here, since they are highly structured with sparse matrices. Lastly, although our proposed multiprocessor scheduling framework is designed for a real-time system, it can also be applied at a higher level of abstraction, such as a data center, server farm or cloud computing, as well as other generic scheduling problems such as multi-stage multi-machine problems.