Finite mixtures of multivariate scale-shape mixtures of skew-normal distributions

Abstract

Finite mixtures of multivariate skew distributions have become increasingly popular in recent years due to their flexibility and robustness in modeling heterogeneity, asymmetry and leptokurticness of the data. This paper introduces a novel finite mixture of multivariate scale-shape mixtures of skew-normal distributions to enhance strength and flexibility when modeling heterogeneous multivariate data that contain more extreme non-normal features. A computational tractable ECM algorithm which consists of analytically simple E- and CM-steps is developed to carry out maximum likelihood estimation of parameters. The asymptotic covariance matrix of parameter estimates is derived from the observed information matrix using the outer product of expected complete-data scores. We demonstrate the utility of the proposed approach through simulated and real data examples.

Appendices

Appendix A: Family of MSSMSN distributions

1.1 General formulation

Let $U_{1}$ be a N(0, 1) random variable and assumed to be independent of ${\varvec{U}}_{2}$, a p-dimensional random vector following a $N_{p}({\varvec{0}},{\varvec{I}}_{p})$ distribution. Let $\tau _{1}$ and $\tau _{2}$ be two independent positive random variables with a joint pdf $h(\tau _{1},\tau _{2};{\varvec{\nu }})$, where ${\varvec{\nu }}$ is a vector of parameters controlling the thickness of the tails. Further, we assume that ${\varvec{U}}=(U_{1},{\varvec{U}}_{2})$ and ${\varvec{\tau }}=(\tau _{1},\tau _{2})$ are independent. Let ${\varvec{Y}}$ be a random vector satisfying the specification of (4). We shall say that ${\varvec{Y}}$ follows a MSSMSN distribution, denoted by ${\varvec{Y}}\sim SSMSN_p({\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},{\varvec{\nu }})$. A stochastic representation of the MSSMSN distribution is given by

$$\begin{aligned} {\varvec{Y}}={\varvec{\xi }}+{\varvec{\varSigma }}^{1/2} \left[ \frac{\tau _{1}^{-1/2}{\varvec{\lambda }}}{\sqrt{f+{\varvec{\lambda }}^{\top }{\varvec{\lambda }}}} |U_{1}|+\tau _{2}^{-1/2}(f{\varvec{I}}_{p}+{\varvec{\lambda }}{\varvec{\lambda }}^{\top })^{-1/2}{\varvec{U}}_{2} \right] , \end{aligned}$$

(A.1)

where $f=\tau _{1}/\tau _{2}$.

Let $\gamma =\tau _{1}^{-1/2}(f+{\varvec{\lambda }}^{\top }{\varvec{\lambda }})^{1/2}|U_{1}|$ be a reparameterized latent variable. Alternatively, the MSSMSN distribution has a three-level hierarchical representation:

$$\begin{aligned} {\varvec{Y}}\mid (\gamma ,\tau _{1},\tau _{2})\sim & {} {N}_{p}\left( {\varvec{\xi }}+\frac{{\varvec{\varSigma }}^{1/2}{\varvec{\lambda }}\gamma }{f+{\varvec{\lambda }}^{\top }{\varvec{\lambda }}},\tau _{2}^{-1}{\varvec{\varSigma }}^{1/2}(f{\varvec{I}}_{p}+{\varvec{\lambda }}{\varvec{\lambda }}^{\top })^{-1}{\varvec{\varSigma }}^{1/2}\right) ,\nonumber \\ \gamma \mid (\tau _{1},\tau _{2})\sim & {} {TN}\left( 0,\frac{f+{\varvec{\lambda }}^{\top }{\varvec{\lambda }}}{\tau _{1}};(0,\infty )\right) ,\nonumber \\ (\tau _{1},\tau _{2})\sim & {} {h}(\tau _{1},\tau _{2};{\varvec{\nu }}), \end{aligned}$$

(A.2)

where $TN(\mu ,\sigma ^2; (a, b))$ represents the truncated normal distribution for $N(\mu ,\sigma ^2)$ whose support is bounded between interval (a, b). Combining all pdfs in (A.2), the joint pdf of ${\varvec{Y}}$, $\gamma$, $\tau _{1}$ and $\tau _{2}$ is

$$\begin{aligned} f({\varvec{y}},\gamma ,\tau _{1},\tau _{2})=h(\tau _{1},\tau _{2}\mid {\varvec{\nu }})\frac{2^{(1-p)/2} }{\pi ^{(p+1)/2}|{\varvec{\varSigma }}|^{1/2} }\tau _{1}^{p/2}\tau _{2}^{1/2} \exp \left\{ -\frac{\tau _{1}\Delta ^2}{2}-\frac{\tau _{2}(\gamma -\eta )^{2} }{2 }\right\} \end{aligned}$$

(A.3)

where $\Delta =\sqrt{({\varvec{y}}-{\varvec{\xi }})^{\top }{\varvec{\varSigma }}^{-1}({\varvec{y}}-{\varvec{\xi }})}$ and $\eta ={\varvec{\lambda }}^{\top }{\varvec{\varSigma }}^{-1/2}({\varvec{y}}-{\varvec{\xi }})$. Integrating out $\gamma$ in (A.3), we obtain

$$\begin{aligned} f({\varvec{y}},\tau _{1},\tau _{2})=2\frac{2^{(1-p)/2}\tau _{1}^{p/2} }{|{\varvec{\varSigma }}|^{1/2}\pi ^{(p-1)/2} } h(\tau _{1},\tau _{2}\mid {\varvec{\nu }}) \phi (\sqrt{\tau _{1}}\Delta ) \varPhi (\sqrt{\tau _{2} }\eta ), \end{aligned}$$

(A.4)

where $\phi (\cdot )$ denotes the pdf of N(0, 1). Subsequently, the marginal pdf of ${\varvec{Y}}$ is obtained as

$$\begin{aligned} \psi _{MSSMSN}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},{\varvec{\nu }})=\int ^{\infty }_{0}\int ^{\infty }_{0}f({\varvec{y}},\tau _{1},\tau _{2})\,d\tau _{1}\,d\tau _{2}. \end{aligned}$$

(A.5)

More details about members of the MSSMSN family are discussed later.

Dividing (A.3) by (A.4), we find that $\gamma$ and $\tau _{1}$ are conditionally independent given ${\varvec{Y}}={\varvec{y}}$, i.e., $f(\gamma \mid {\varvec{y}},\tau _{1},\tau _{2})=f(\gamma \mid {\varvec{y}},\tau _{2})$, and thereby

$$\begin{aligned} \gamma \mid ({\varvec{y}},\tau _{2})\sim {TN}\left( \eta ,\tau _{2}^{-1};(0,\infty )\right) . \end{aligned}$$

(A.6)

Moreover, dividing (A.4) by (A.5) gives

$$\begin{aligned} f(\tau _{1},\tau _{2}\mid {\varvec{y}})=2\frac{2^{(1-p)/2}\tau _{1}^{p/2}}{|{\varvec{\varSigma }}|^{1/2}\pi ^{(p-1)/2} } \frac{h(\tau _{1},\tau _{2}\mid {\varvec{\nu }}) \phi \left( \sqrt{\tau _{1}}\Delta \right) \varPhi \left( \sqrt{\tau _{2}}\eta \right) }{\psi _{MSSMSN}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},{\varvec{\nu }})}. \end{aligned}$$

(A.7)

Making use of the first two moments of MSN distribution and applying the law of iterated expectations, the mean vector and covariance matrix of ${\varvec{Y}}$ are given by

$$\begin{aligned} E({\varvec{Y}})={\varvec{\xi }}+\sqrt{\frac{2}{\pi }}\zeta _1{\varvec{\varSigma }}^{1/2}{\varvec{\lambda }}\quad \text{ and }\quad \mathrm{cov}({\varvec{Y}})=\zeta _0{\varvec{\varSigma }}-\frac{2\zeta ^{2}_1}{\pi }{\varvec{\varSigma }}^{1/2}{\varvec{\lambda }}{\varvec{\lambda }}^{\top }{\varvec{\varSigma }}^{1/2}, \end{aligned}$$

where $\zeta _0=E(\tau ^{-1}_{1})$ and $\zeta _1=E(\tau _{1}^{-1/2}(f+{\varvec{\lambda }}^{\top }{\varvec{\lambda }})^{-1/2})$, which can be exactly evaluated by numerical integration methods.

1.2 Multivariate skew-t-t distribution

Consider two independent random variables $\tau _{1}\sim \varGamma (\nu _{1}/2,\nu _{2}/2)$ and $\tau _{2}\sim \varGamma (\nu _{2}/2,\nu _{2}/2)$ with the joint pdf given by

$$\begin{aligned} h(\tau _{1},\tau _{2};{\varvec{\nu }})=g(\tau _{1};\nu _{1}/2,\nu _{1}/2)g(\tau _{2};\nu _{2}/2,\nu _{2}/2), \end{aligned}$$

where ${\varvec{\nu }}=(\nu _{1},\nu _{2})$ and $g(\cdot \mid \alpha ,\beta )$ stands for the pdf of a gamma distribution with mean $\alpha /\beta$. In this setting, we can derive the multivariate skew-t-t (MSTT) distribution, denoted by ${\varvec{Y}}\sim STT_p({\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\nu _{1},\nu _{2})$, with pdf

$$\begin{aligned} f_{MSTT}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\nu _{1},\nu _{2})=2t_{p}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},\nu _{1})T(\eta ;\nu _{2}). \end{aligned}$$

(A.8)

Remark that, when $\nu _1$ and $\nu _2$ are restricted to be equal, the MSTT density is very close to the MST density of (3), showing virtually indistinguishable performance of density estimation. The issue is examined numerically by a simulation study in Sect. 4.1.

Fig. 5

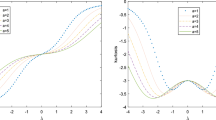
A comparison of MSN and MSTT contours by plotting $f_{MSTT}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\nu _1,\nu _2)=c$ for $c=0.1$ and 0.01, where ${\varvec{\xi }}=(0,0)^{\top },{\varvec{\varSigma }}={\varvec{I}}_{2}$, ${\varvec{\lambda }}=(3,3)^{\top }$, $\nu _{1}=4$ and various choices of $\nu _2$

If follows from (A.7) that $\tau _{1}\mid ({\varvec{Y}}={\varvec{y}})\sim \varGamma \left( (\nu _{1}+p)/2,(\nu _{1}+\Delta ^2)/2\right)$. Moreover, the conditional pdf of $\tau _{2}$ given ${\varvec{Y}}={\varvec{y}}$ is

$$\begin{aligned} f(\tau _{2}\mid {\varvec{y}})= \frac{(\frac{\nu _{2} }{2 })^{\frac{\nu _{2} }{2 } } }{\varGamma (\frac{\nu _{2}}{2}) } \frac{\tau _{2}^{\frac{\nu _{2} }{2 }-1 } \exp (-\frac{\nu _{2} }{2 }\tau _{2} ) \varPhi (\eta \sqrt{\tau _{2}}) }{T(\eta ;\nu _{2}) }. \end{aligned}$$

As a result, we have the following conditional expectations:

$$\begin{aligned} E(\tau _{1}\mid {\varvec{Y}}={\varvec{y}})= & {} \frac{\nu _{1}+p }{\nu _{1}+\Delta ^2 } ,\quad E(\tau _{2}\mid {\varvec{Y}}={\varvec{y}}) =\frac{T\left( \sqrt{ \frac{\nu _{2}+2 }{\nu _{2} }} \eta ;\nu _{2}+2 \right) }{T(\eta ;\nu _{2}) },\nonumber \\ E(\log \tau _{1}\mid {\varvec{Y}}={\varvec{y}})= & {} \mathrm{DG}\left( \frac{\nu _{1}+p }{2}\right) -\log \left( \frac{\nu _{1}+\Delta ^2}{2}\right) ,\nonumber \\ E(\log \tau _{2}|{\varvec{Y}}={\varvec{y}})= & {} \mathrm{DG}\left( \frac{\nu _{2}+1}{2}\right) -\log \left( \frac{\nu _{2}}{2}\right) +\frac{T\left( \sqrt{ \frac{\nu _{2}+2 }{\nu _{2} }} \eta ;\nu _{2}+2 \right) }{T(\eta ;\nu _{2}) } -1\nonumber \\&-\frac{\eta }{\nu _{2} } \frac{t(\eta ;\nu _{2}) }{T(\eta ;\nu _{2}) } -\frac{1}{T(\eta ;\nu _{2})} \int ^{\eta }_{-\infty }\log \left( 1+\frac{x^{2}}{\nu _{2}}\right) t(x;\nu _{2})d x,\nonumber \\ E(\gamma \tau _{2}\mid {\varvec{Y}}={\varvec{y}})= & {} \frac{1 }{T(\eta ;\nu _{2}) }\left[ T\left( \sqrt{\frac{\nu _{2}+2 }{\nu _{2} }}\eta ;\nu _{2}+2 \right) \eta \right. \nonumber \\&+\left. \frac{1}{a_{\nu _{2}+1}\sqrt{\pi (\nu _{2}+\eta ^{2})} }\left( \frac{\nu _{2}}{\nu _{2}+\eta ^{2}} \right) ^{\nu _{2}/2} \right] , \end{aligned}$$

(A.9)

where $a_{\nu }=\varGamma ((\nu -1)/2)/\varGamma (\nu /2)$ and $\mathrm{DG}(x)=d\log \varGamma (x)/dx$ is the digamma function.

Figure 5 displays the contour plots of bivariate densities given in (A.8), obtained with the solutions of $f_{MSTT}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\nu _{1},\nu _{2}) = c$, for $c=0.1$ and 0.01, where ${\varvec{\xi }}=(0,0)^{\top },{\varvec{\varSigma }}={\varvec{I}}_{2}$, ${\varvec{\lambda }}=(3,3)^{\top }$, $\nu _{1}=4$ and various choices of $\nu _{2}$. The MSN contours obtained by setting $\nu _1=\nu _2=\infty$ are also shown for the sake of comparison. Apparently, the MSN contour lies mostly outside the MSTT contours for $c=0.1$, while an opposite phenomenon happens for $c=0.01$. Note that the MSTT distribution contains two DOF parameters in which $\nu _1$ controls the main body kurtosis, while the $\nu _2$ is used to add flexibility in turning the extra kurtosis. As remarked previously, the contours drawn at $\nu _1=\nu _2=4$ correspond to a near of MST setting. It can be observed from Fig. 5(b) that a smaller value of $\nu _2$ enables a wider range of contour area, indicating that the MSST distribution is more flexible and should provide more robustness against extreme outliers than the MSN and MST distributions.

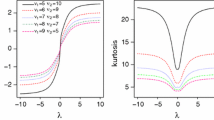
One thing worth noting is that the MSTT distribution includes the MSN, multivariate skew-t-normal (MSTN) and multivariate skew-normal-t (MSNT) distributions as particular members. The MSTN distribution is formulated by taking $\nu _1=\nu$ and $\nu _2=\infty$ with the pdf $f_{MSTN}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\nu )=2t_{p}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},\nu )\varPhi (\eta )$. More essential properties concerning the MSTN distribution can be found in Lin et al. (2014). In contrast, the MSNT distribution is obtained by letting $\nu _1=\infty$ and $\nu _2=\nu$ with the pdf taking the form of $f_{MSNT}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\nu )=2\phi _{p}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }})T(\eta ;\nu )$. Notably, the Fisher information of the shape and DOF parameters $({\varvec{\lambda }},\nu )$ is zero for both MSTN and MSNT distributions, indicating that their ML estimates are asymptotically uncorrelated. However, this is not the case for the MST distribution as considered by Azzalini and Capitaino (2003) and Pyne et al. (2009).

1.3 Multivariate skew generalized Laplace normal distribution

The multivariate generalized Laplace (MGL) distribution, as proposed by Kozubowski and Podgórski (2000), has the pdf:

$$\begin{aligned} f_{MGL}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},\alpha )=\frac{|{\varvec{\varSigma }}|^{-1/2} }{(2\pi )^{p/2}2^{\alpha -1}\varGamma (\alpha )}\Delta ^{(\alpha -p/2)} K_{p/2-\alpha }(\Delta ), \end{aligned}$$

where $K_{r}(a)$ denotes the modified Bessel function of the third kind of order $r\in \mathbb {R}$, also known as the MacDonald function, defined as

$$\begin{aligned} K_{r}(x)=\frac{1}{2}\int _{0}^{\infty }y^{r-1}\exp \left\{ -\frac{x}{2}\left( y+\frac{1}{y} \right) \right\} d y, \quad x>0. \end{aligned}$$

(A.10)

One important feature of $K_{r}(x)$ is symmetric with respect to r, namely $K_{r}(x)=K_{-r}(x)$. When $r=\pm 1/2$, it can be written in a simpler form of $K_{\pm 1/2}(x)=\sqrt{\pi /2}x^{-1/2}e^{-x}$. Moreover, the derivative of (A.10) with respect to r is

$$\begin{aligned} K'_{r}(x)=\frac{dK_{r}(x)}{dr}=\frac{1}{2}\int _{0}^{\infty }\log (y)y^{r-1}\exp \left\{ -\frac{x}{2}\left( y+\frac{1}{y} \right) \right\} d y, \quad x>0. \end{aligned}$$

(A.11)

For more properties and relations about the Bessel functions, one can refer to Barndorff-Nielsen and Biaesild (1981).

If we choose $\tau _{1}\sim \varGamma ^{-1}(\alpha ,1/2)$ and $\tau _{2}=1$ in (A.1), where $\varGamma ^{-1}(\alpha ,1/2)$ denotes the inverse gamma distribution with shape $\alpha$ and scale 1 / 2, it leads to a multivariate skew generalized Laplace normal (MSGLN) distribution, denoted by ${\varvec{Y}}\sim SGLN_p({\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\alpha )$. From (A.5), the pdf of ${\varvec{Y}}$ is

$$\begin{aligned} f_{MSGLN}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},\alpha )=2f_{MGL}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},\alpha )\varPhi (\eta ). \end{aligned}$$

(A.12)

A random variable X has the Generalized Inverse Gaussian (GIG) distribution (Good 1953) with parameters $\chi ,\psi \in \mathbb {R}^{+}$ and $\nu \in \mathbb {R}$, denoted by $X\sim GIG(q,\chi ,\psi )$, if it has the pdf:

$$\begin{aligned} f_{GIG}(x;q,\chi ,\psi )=\frac{\chi ^{-q}(\sqrt{\chi \psi })^{q} }{2K_{q}(\sqrt{\chi \psi }) }x^{q-1}\exp \left\{ -\frac{1}{2}(\chi x^{-1}+\psi x) \right\} , \end{aligned}$$

where $\chi$ and $\psi$ regulate both the concentration and scaling of the density, while q bears no concrete statistical meaning. The possible domains for the three parameters are (i) $\chi \ge 0,\psi >0$ if $q>0$; (ii) $\psi \ge 0,\chi >0$ if $q<0$; (iii) $\chi>0,\psi >0$ if $q=0$. The GIG distribution includes several special cases such as the inverse Gaussian if $q=-1/2$, the hyperbolic if $q=0$, the gamma distributions if $q=0,\chi =0$, and so on. More information about the GIG distribution and related statistical applications can be found in Jørgensen (1982) and Barndorff-Nielsen and Stelzer (2005) and the references therein.

Substituting $\tau _2=1$ into (A.6) and (A.7) results in $\gamma \mid ({\varvec{y}},\tau _{2})\sim TN(\eta ,1;(0,\infty ))$ and $\tau \mid ({\varvec{Y}}={\varvec{y}})\sim GIG(p/2-\alpha ,1,\Delta ^2)$. It is easy to see hat $\tau$ and $\gamma$ are independent conditional on ${\varvec{Y}}={\varvec{y}}$. In our developed EM-based algorithm, we need to exploit the following conditional expectations:

$$\begin{aligned} E(\tau \mid {\varvec{Y}}={\varvec{y}})=\Delta ^{-1}\frac{K_{p/2+1-\alpha }(\Delta )}{K_{p/2-\alpha }(\Delta )} \end{aligned}$$

and

$$\begin{aligned} E(\log \tau \mid {\varvec{Y}}={\varvec{y}})=-\log \Delta +\frac{K_{p/2-\alpha }^{'}(\Delta )}{K_{p/2-\alpha }(\Delta )}, \end{aligned}$$

(A.13)

where $K_{p/2-\alpha }^{'}(\Delta )$ is evaluated via (A.11).

Multivariate skew-slash-normal distribution

According to Wang and Genton (2006), the multivariate slash (MS) distribution can be stochastically represented by ${\varvec{Y}}={\varvec{\xi }}+{\varvec{\varSigma }}^{1/2}{\varvec{Z}} U^{-1/q}$, where ${\varvec{Z}}\sim N_{p}({\varvec{0}},{\varvec{I}}_{p})$ is independent of U, which is a uniform random variable on (0,1). The pdf of ${\varvec{Y}}$ is

$$\begin{aligned} f_{MS}({\varvec{y}};{\varvec{\xi }},{\varvec{\varSigma }},q)= {\left\{ \begin{array}{ll} \frac{q\varGamma (\frac{p+q}{2})|{\varvec{\varSigma }}|^{-1/2}2^{\frac{q}{2}-1}}{\pi ^{p/2} } \frac{G\big (\frac{\Delta ^2}{2};\frac{p+q}{2}\big ) }{\Delta ^{p+q} } ,&{} {\varvec{y}}\ne {\varvec{\xi }},\\ \frac{q }{(2\pi )^{p/2}(p+q) }|{\varvec{\varSigma }}|^{-1/2},&{} {\varvec{y}}= {\varvec{\xi }},\end{array}\right. } \end{aligned}$$

where $G(a;\alpha )=\int _{0}^a x^{\alpha -1}e^{-x\alpha }dx$ is the incomplete gamma function, and q is a tuning parameter controlling the thickness of tails. When $q\rightarrow \infty$, ${\varvec{Y}}$ approaches a $N_p({\varvec{\xi }},{\varvec{\varSigma }})$ distribution, indicating that the MS distribution has heavier tails than the MN distribution when q tends to be small.

Through setting $\tau _{1}\sim Beta(q/2,1)$ and $\tau _{2}=1$ in (A.1), we can generate a multivariate skew-slash-normal (MSSN) distribution. Using the result in (A.5), we obtain the MSSN density:

$$\begin{aligned} f_{MSSN}({\varvec{y}}\mid {\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},q)=2f_{MS}({\varvec{y}}\mid {\varvec{\xi }},{\varvec{\varSigma }},q)\varPhi (\eta ) \end{aligned}$$

(A.14)

and write ${\varvec{Y}}\sim SSN_p({\varvec{\xi }},{\varvec{\varSigma }},{\varvec{\lambda }},q)$ for short. Therefore, the MSSN distribution increases the flexibility of the MS distribution with an additional parameter vector ${\varvec{\lambda }}$ governing the shape of the distribution. It is worth noting that (A.14) is not identical to (9) of Wang and Genton (2006) obtained by setting $\tau _1=\tau _2=\tau$, where $\tau \sim Beta(q/2,1)$.

It follows from (A.7) that the conditional pdf of $\tau$ given ${{\varvec{Y}}}={{\varvec{y}}}$ is

$$\begin{aligned} h(\tau \mid {\varvec{y}})={\left\{ \begin{array}{ll} \frac{\Delta ^{p+q}\tau ^{\frac{p+q}{2}-1}\exp \{-\frac{1}{2}\tau \Delta ^2\} }{\varGamma (\frac{p+q}{2})2^{\frac{p+q}{2} }G(\frac{\Delta ^2}{2};\frac{p+q}{2}) }, &{}{\varvec{y}}\ne {\varvec{\xi }},\\ \frac{p+q}{2}\tau ^{\frac{p+q}{2}-1}, &{}{\varvec{y}}={\varvec{\xi }}.\end{array}\right. } \end{aligned}$$

Accordingly, we obtain

$$\begin{aligned} E(\tau \mid {\varvec{Y}}={\varvec{y}})={\left\{ \begin{array}{ll} \frac{p+q}{\Delta ^2} \frac{G(\frac{\Delta ^2}{2};\frac{p+q+2}{2}) }{G(\frac{\Delta ^2}{2};\frac{p+q}{2}) }, &{}{\varvec{y}}\ne {\varvec{\xi }},\\ \frac{p+q}{p+q+2}, &{}{\varvec{y}}={\varvec{\xi }},\end{array}\right. } \end{aligned}$$

(A.15)

and

$$\begin{aligned} E(\log \tau \mid {\varvec{Y}}={\varvec{y}})={\left\{ \begin{array}{ll} \log (2/\Delta ^2)+\frac{\int ^{\frac{\Delta ^2 }{2}}_{0}\log (x)x^{((p+q)/2-1)}\exp \{-x\}dx }{\varGamma (\frac{p+q}{2})G\left( \frac{\Delta ^2}{2};\frac{p+q}{2}\right) } &{},{\varvec{y}}\ne {\varvec{\xi }},\\ \frac{-2}{p+q} &{},{\varvec{y}}= {\varvec{\xi }}.\end{array}\right. } \end{aligned}$$

(A.16)

Formulae (A.15) and (A.16) are used when performing the EM-based algorithm. Besides, working the same with the MSGN distribution, we obtain $\gamma \mid ({\varvec{Y}}={\varvec{y}})\sim TN(\eta ,1;(0,\infty ))$ because of the independence between $\tau$ and $\gamma$ conditioning on ${\varvec{Y}}={\varvec{y}}$.

Appendix B: Detailed proof of partial derivatives in (15)

The partial derivatives of $\ell _{cj}=\ell _{cj}({\varvec{\varTheta }}\mid {\varvec{y}}_{j},{\varvec{\gamma }}_{j},{\varvec{\tau }}_{1j},{\varvec{\tau }}_{2j},{\varvec{Z}}_{j})$ defined in (14) with respect to each entry of parameters are given as follows:

$$\begin{aligned} \frac{\partial \ell _{cj}}{\partial \pi _{r}}= & {} \frac{Z_{rj}}{\pi _{r}}-\frac{Z_{Gj}}{\pi _{G}}\quad (r=1,\ldots ,G-1),\\ \frac{\partial \ell _{cj}}{\partial {\varvec{\xi }}_{i}}= & {} Z_{ij}\left[ \tau _{1j}{\varvec{F}}_{i}^{-1}{\varvec{u}}_{ij}-\tau _{2j}(\gamma _{j}-{\varvec{\lambda }}_{i}^{\top }{\varvec{u}}_{ij}){\varvec{F}}_{i}^{-1}{\varvec{\lambda }}_{i}\right] ,\\ \frac{\partial \ell _{cj}}{\partial {\varvec{f}}_{i}}= & {} Z_{ij}\text {vech}\Big \{-\left[ 2{\varvec{F}}_{i}^{-1}-\text {Diag}({\varvec{F}}_{i}^{-1})\right] +\tau _{1j}\left[ {\varvec{B}}_{ij}+{\varvec{B}}_{ij}^{\top }-\text {Diag}({\varvec{B}}_{ij}) \right] \\&-\,\tau _{2j}(\gamma _{j}-{\varvec{\lambda }}_{i}^{\top }{\varvec{u}}_{ij})\left[ {\varvec{C}}_{ij}+{\varvec{C}}_{ij}^{\top }-\text {Diag}({\varvec{C}}_{ij})\right] \Big \},\\ \frac{\partial \ell _{cj}}{\partial {\varvec{\lambda }}_{i}}= & {} Z_{ij}\left[ \tau _{2j}(\gamma _{j}-{\varvec{\lambda }}_{i}^{\top }{\varvec{u}}_{ij}){\varvec{u}}_{ij}\right] . \end{aligned}$$

Besides, the partial derivatives of (14) with respect to ${\varvec{\nu }}_i$ are discussed as follows:

Case 1::

For the FM-MSTT model, we have

$$\begin{aligned} \frac{\partial \ell _{cj}}{\partial \nu _{1i}}= & {} \frac{Z_{ij}}{2}\left[ \log \left( \frac{\nu _{1i}}{2}\right) +1+\log \tau _{1j}-\tau _{1j}-\mathrm{DG}\left( \frac{\nu _{1i}}{2}\right) \right] , \end{aligned}$$

and

$$\begin{aligned} \frac{\partial \ell _{cj}}{\partial \nu _{2i}}= & {} \frac{Z_{ij}}{2}\left[ \log \left( \frac{\nu _{2i}}{2}\right) +1+\log \tau _{2j}-\tau _{2j}-\mathrm{DG}\left( \frac{\nu _{2i}}{2}\right) \right] . \end{aligned}$$

Case 2::

For the FM-MSGLN model, we have

$$\begin{aligned} \frac{\partial \ell _{cj}}{\partial \alpha _{i}}= & {} Z_{ij}\left( -\log 2-\mathrm{DG}(\alpha _{i})-\log \tau _{j}\right) . \end{aligned}$$

Case 3::

For the FM-MSSN model, we have

$$\begin{aligned} \frac{\partial \ell _{cj}}{\partial q_{i}}= & {} Z_{ij}\left( \frac{1}{q_{i}}+\frac{1}{2}\log \tau _{j}\right) . \end{aligned}$$

Given the ML estimate $\hat{{\varvec{\varTheta }}}$, the gradients given in (15) can be obtained straightforwardly by taking the expectations of the above derivatives with respect to the conditional distribution of $({\varvec{\gamma }}_{j},{\varvec{\tau }}_{1j},{\varvec{\tau }}_{2j},{\varvec{Z}}_{j})$ given ${\varvec{Y}}_j={\varvec{y}}_j$. $\square$