Increasing risk aversion and life-cycle investing

Abstract

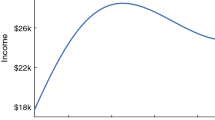
We derive the optimal portfolio for an investor with increasing relative risk aversion in a complete continuous-time securities market. The IRRA assumption helps to mitigate the criticism of constant relative risk aversion that it implies an unreasonably large aversion to large gambles, given reasonable aversion to small gambles. The model provides theoretical support for the common recommendation of financial advisors that older investors should reduce their allocations to risky assets, and it is consistent with empirical relations between age, wealth, and portfolios.

Appendices

Appendix A. Proof of Proposition 1

The function

$$\begin{aligned} \gamma \mapsto \mathsf {E}\int _0^T M_t (\gamma X_t - \xi )^+\,\mathrm {d}t \end{aligned}$$

is strictly monotone and maps $[0,\infty )$ onto $[0,\infty )$. Thus, there is a unique $\gamma$ such that

$$\begin{aligned} \mathsf {E}\int _0^T M_t (\gamma X_t - \xi )^+\,\mathrm {d}t = W_0. \end{aligned}$$

(A.1)

Let $C^*$ denote $(\gamma X_t - \xi )^+$, and let C be any other nonnegative consumption process satisfying the budget constraint

$$\begin{aligned} \mathsf {E}\int _0^T M_t C_t \mathrm {d}t \le W_0. \end{aligned}$$

(A.2)

By concavity,

$$\begin{aligned} u(C) \le u(C^*) + u'(C^*)(C-C^*), \end{aligned}$$

so

$$\begin{aligned} \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}u(C_t) \,\mathrm {d}t \le \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}u(C^*_t) \,\mathrm {d}t + \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}u'(C_t^*)(C_t-C_t^*)\,\mathrm {d}t. \end{aligned}$$

(A.3)

The second term on the right-hand side is the sum of

$$\begin{aligned} \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}u'(C_t^*)(C_t-C_t^*)1_{\{C^*_t>0\}}\,\mathrm {d}t \end{aligned}$$

(A.4)

and

$$\begin{aligned} \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}u'(C_t^*)(C_t-C_t^*)1_{\{C^*_t=0\}}\,\mathrm {d}t. \end{aligned}$$

(A.5)

The term (A.4) equals

$$\begin{aligned} \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}(\gamma X_t)^{-\rho } (C_t-C^*_t)1_{\{C^*_t>0\}} \,\mathrm {d}t = \gamma ^{-\rho } \mathsf {E}\int _0^T M_t (C_t-C^*_t) 1_{\{C^*_t>0\}}\,\mathrm {d}t. \end{aligned}$$

(A.6)

The term (A.5) equals

$$\begin{aligned} \mathsf {E}\int _0^T \mathrm {e}^{-\delta t} \xi ^{-\rho } (C_t-C^*_t)1_{\{C^*_t=0\}} \,\mathrm {d}t&\le \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}(\gamma X_t)^{-\rho } (C_t-C^*_t)1_{\{C^*_t=0\}} \,\mathrm {d}t \nonumber \\&= \gamma ^{-\rho } \mathsf {E}\int _0^T M_t (C_t-C^*_t) 1_{\{C^*_t=0\}}\,\mathrm {d}t, \end{aligned}$$

(A.7)

the inequality being due to the fact that $\xi \ge \gamma X_t$ when $C^*_t=0$. Adding (A.6) and (A.7) and using (A.1) and (A.2) yields

$$\begin{aligned} \mathsf {E}\int _0^T \mathrm {e}^{-\delta t}u'(C_t^*)(C_t-C_t^*)\,\mathrm {d}t \le 0. \end{aligned}$$

Hence, (A.3) implies that $C^*$ is optimal.

Because $C^*$ is the optimal consumption process, the expression (12)–which equals $f(t,X_t)$—is the optimal wealth process. We have

$$\begin{aligned} f(t,x)= & {} \int _t^T \mathrm {e}^{-\delta (u-t) }\mathsf {E}\left[ \left( \frac{X_u}{x}\right) ^{-\rho } (\gamma X_u-\xi )^+\mid X_t=x\right] \,\mathrm {d}u\nonumber \\= & {} \gamma x \int _t^T \mathrm {e}^{-\delta (u-t)}\mathsf {E}\left[ \left( \frac{X_u}{x}\right) ^{1-\rho } 1_{\{X_u>\xi /\gamma \}}\mid X_t = x\right] \,\mathrm {d}u\nonumber \\&- \xi \int _t^T \mathrm {e}^{-\delta (u-t)}\mathsf {E}\left[ \left( \frac{X_u}{x}\right) ^{-\rho } 1_{\{X_u>\xi /\gamma \}}\mid X_t = x\right] \,\mathrm {d}u \end{aligned}$$

(A.8)

Consider any constant $\alpha$ and dates $t<u$. Set $\tau = u-t$. Using the definition of X and the fact that M is the geometric Brownian motion (5), we have

$$\begin{aligned} \log X_u - \log X_t = \frac{(r-\delta +\lambda ^2/2)\tau }{\rho } + \frac{\lambda }{\rho }(B_u-B_t). \end{aligned}$$

(A.9)

Therefore,

$$\begin{aligned} \left( \frac{X_u}{X_t}\right) ^\alpha = \mathrm {e}^{\alpha (r-\delta + \lambda ^2/2) \tau /\rho } \mathrm {e}^{- \alpha \lambda \sqrt{\tau } \varepsilon / \rho }, \end{aligned}$$

where $\varepsilon =-(B_u-B_t)/\sqrt{u-t}$, which is a standard normal random variable. Furthermore,

$$\begin{aligned} X_u \ \ge \ \frac{\xi }{\gamma }&\quad \Leftrightarrow \quad \log X_t + \frac{(r-\delta +\lambda ^2/2)\tau }{\rho } - \frac{\lambda \sqrt{\tau } \varepsilon }{ \rho } \ \ge \ \log \left( \frac{\xi }{\gamma }\right) \\.&\quad \Leftrightarrow \quad \frac{\lambda \sqrt{\tau } \varepsilon }{ \rho } \ \le \ \log (\gamma X_t) - \log \xi + \frac{(r-\delta +\lambda ^2/2)\tau }{\rho } \\&\quad \Leftrightarrow \quad \varepsilon \ \le \ \omega , \end{aligned}$$

where we set

$$\begin{aligned} \omega = \frac{\rho [\log (\gamma X_t) - \log \xi ]}{\lambda \sqrt{\tau }} + \frac{(r-\delta +\lambda ^2/2)\sqrt{\tau }}{\lambda } . \end{aligned}$$

Therefore,

$$\begin{aligned}&\mathsf {E}\left[ \left( \frac{X_u}{x}\right) ^\alpha 1_{\{X_u>\xi /\gamma \}}\mid X_t = x\right] = \mathrm {e}^{\alpha (r-\delta + \lambda ^2/2) \tau /\rho } \frac{1}{\sqrt{2\pi }}\int _{-\infty }^\omega \mathrm {e}^{-y^2/2- \alpha \lambda \sqrt{\tau } y/ \rho } \,\mathrm {d}y\nonumber \\&\qquad = \mathrm {e}^{\alpha (r-\delta + \lambda ^2/2) \tau /\rho +\alpha ^2\lambda ^2\tau /2\rho ^2} \frac{1}{\sqrt{2\pi }}\int _{-\infty }^\omega \mathrm {e}^{-(y+\alpha \lambda \sqrt{\tau }/\rho )^2/2} \,\mathrm {d}y\nonumber \\&\qquad = \mathrm {e}^{\alpha (r-\delta + \lambda ^2/2) \tau /\rho +\alpha ^2\lambda ^2\tau /2\rho ^2} \frac{1}{\sqrt{2\pi }}\int _{-\infty }^{\omega + \alpha \lambda \sqrt{\tau }/\rho } \mathrm {e}^{-y^2/2} \,\mathrm {d}y\nonumber \\&\qquad = \mathrm {e}^{\alpha (r-\delta + \lambda ^2/2) \tau /\rho +\alpha ^2\lambda ^2\tau /2\rho ^2} {{\mathrm{N}}}\left( \omega + \frac{\alpha \lambda \sqrt{\tau }}{\rho }\right) . \end{aligned}$$

(A.10)

Substituting (A.10) with $\alpha = 1-\rho$ and $\alpha =-\rho$ into (A.8) verifies (16).

From the formula (16), it is straightforward to verify that f is continuously differentiable in t and twice continuously differentiable in x. Therefore, we can apply Itô’s formula to compute $\mathrm {d}f$. We compute the optimal portfolio $\pi$ by matching the stochastic part of $\mathrm {d}f$ to $W\pi \sigma \,\mathrm {d}B$, which is the stochastic part of $\mathrm {d}W$ implied by the intertemporal budget constraint. The drift parts will then match due to the fact that

$$\begin{aligned} \int _0^t M_sC_s\,\mathrm {d}s + M_tf(t,X_t) \end{aligned}$$

is a martingale (which implies that its drift is zero). From (A.9), X is a geometric Brownian motion with volatility $\lambda /\rho$. Therefore, the stochastic part of $\mathrm {d}f$ is $(\lambda /\rho )Xf_x \,\mathrm {d}B$. Matching this to $W\pi \sigma \,\mathrm {d}B$, we see that

$$\begin{aligned} \pi _t = \frac{\lambda }{\rho \sigma } \cdot \frac{X_tf_x(t,X_t)}{W_t} = \frac{\mu -r}{\rho \sigma ^2} \cdot \frac{X_tf_x(t,X_t)}{f(t,X_t)}. \end{aligned}$$

This verifies (17). The formula (16) for f and (17) directly imply (18).

If $\xi =0$, then the definition (14) simplifies to

$$\begin{aligned} f(t,x) = \gamma x \mathsf {E}\left[ \left. \int _t^T \mathrm {e}^{-\delta (u-t)}\left( \frac{X_u}{x}\right) ^{1-\rho } \,\mathrm {d}u \;\right| \; X_t = x\right] , \end{aligned}$$

which equals xa(t), where $a(\cdot )$ is the nonrandom function

$$\begin{aligned} a(t) = \mathsf {E}\left[ \left. \int _t^T \mathrm {e}^{-\delta (u-t)}\left( \frac{X_u}{x}\right) ^{1-\rho } \,\mathrm {d}u \;\right| \; X_t = x\right] . \end{aligned}$$

Therefore, $f(t,x) = xf_x(t,x)$ as claimed.

Appendix B. Negative consumption

Here we derive the optimum for an IRRA investor when negative consumption is allowed. The first order condition is

$$\begin{aligned} \mathrm {e}^{-\delta t}(\xi +C_t)^{-\rho } = \eta M_t \end{aligned}$$

As before, define $\gamma = \eta ^{-1/\rho }$ and define X as in (10). Then, the first order condition can be expressed as: $C_t = \gamma X_t-\xi$. Optimal wealth is

$$\begin{aligned} W_t&= \mathsf {E}_t\int _t^T\frac{M_u}{M_t}C_u\,\mathrm {d}u \\&= \gamma X_t\mathsf {E}_t\int _t^T\frac{M_u}{M_t}\frac{X_u}{X_t}\,\mathrm {d}u - \xi \mathsf {E}_t\int _t^T\frac{M_u}{M_t}\,\mathrm {d}u\\&= \gamma X_t\mathsf {E}_t\int _t^T\mathrm {e}^{-\delta (u-t)/\rho }\left( \frac{M_u}{M_t}\right) ^{(\rho -1)/\rho }\,\mathrm {d}u - \frac{\xi }{r}\left[ 1 - \mathrm {e}^{-r(T-t)}\right] \end{aligned}$$

Itô’s formula and the dynamics of M imply

$$\begin{aligned} \frac{\mathrm {d}M^{(\rho -1)/\rho }}{M^{(\rho -1)/\rho }}&= \frac{\rho -1}{\rho }\frac{\mathrm {d}M}{M} + \frac{1-\rho }{2\rho ^2}\left( \frac{\mathrm {d}M}{M}\right) ^2\\&= \frac{1-\rho }{\rho } r\,\mathrm {d}t + \frac{1-\rho }{\rho }\lambda \,\mathrm {d}B + \frac{1-\rho }{2\rho ^2}\lambda ^2\,\mathrm {d}t \end{aligned}$$

Therefore,

$$\begin{aligned} \mathsf {E}_t\left[ \left( \frac{M_u}{M_t}\right) ^{(\rho -1)/\rho }\right] = \mathrm {e}^{[(1-\rho )r/\rho + (1-\rho )\lambda ^2/2\rho ^2](u-t)}. \end{aligned}$$

It follows that

$$\begin{aligned} W_t = \frac{\gamma X_t}{\phi }\left[ 1-\mathrm {e}^{-\phi (T-t)}\right] - \frac{\xi }{r}\left[ 1 - \mathrm {e}^{-r(T-t)}\right] \end{aligned}$$

(B.1)

where

$$\begin{aligned} \phi \ = \ r \ - \ \frac{r - \delta }{\rho } \ - \ \frac{(1 - \rho )\lambda ^2}{2\rho ^2}. \end{aligned}$$

Define

$$\begin{aligned} \widehat{W}_t = W_t + \frac{\xi }{r}\left[ 1 - \mathrm {e}^{-r(T-t)}\right] . \end{aligned}$$

This is the investor’s wealth plus the proceeds that would be obtained by selling a claim that pays $\xi$ per unit of time from t to T. Equation (B.1) allows us to calculate $\gamma$ from $\widehat{W}_0$ as

$$\begin{aligned} \gamma = \frac{\phi \widehat{W}_0}{1-\mathrm {e}^{-\phi T}} \end{aligned}$$

(B.2)

The optimal consumption satisfies

$$\begin{aligned} C_t + \xi = \gamma X_t = \frac{\phi \widehat{W}_t}{1-\mathrm {e}^{-\phi (T-t)}} \end{aligned}$$

The optimal portfolio $\pi$ is such that $W\pi \sigma \,\mathrm {d}B$ equals the stochastic part of $\mathrm {d}W$, which is the stochastic part of $\mathrm {d}\widehat{W}$, which is the stochastic part of

$$\begin{aligned} \frac{\gamma }{\phi }\left[ 1-\mathrm {e}^{-\phi (T-t)}\right] \,\mathrm {d}X \end{aligned}$$

Thus,

$$\begin{aligned} W\pi \sigma&=\frac{\gamma \lambda }{\phi \rho }\left[ 1-\mathrm {e}^{-\phi (T-t)}\right] X_t\\&= \frac{\lambda }{\rho }\widehat{W}_t \end{aligned}$$

This implies

$$\begin{aligned} \pi = \frac{\widehat{W}_t}{W_t}\cdot \frac{\mu -r}{\rho \sigma ^2} \end{aligned}$$