Abstract
The Welge–JBN method for determining relative permeability from unsteady-state waterflood test is commonly used for two-phase flows in porous media. We discuss the theoretical criteria that limits application of the basic Buckley–Leverett model and Welge–JBN method and the operational criteria of the accuracy of measurements during core waterflood tests. The objective is determination of the waterflood test parameters (core length, flow velocity and effluent sampling frequency) that fulfil the theoretical and operational criteria. The overall set of criteria results in five inequalities in three-dimensional Euclidian space of these parameters. For known rock and fluid properties, a formula for minimum core length to fulfil Welge–JBN criteria is derived. For cases where the core length is given, formulae for test’s flow velocity and sampling period are provided to satisfy the test admissibility conditions. The application of the proposed methodology is illustrated by two coreflood tests.







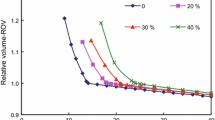
(adapted from Chatzis et al. 1983)









Similar content being viewed by others
Abbreviations
- f k :
-
Fractional flow during steady-state
- f min :
-
Minimum measured value of fractional flow
- J :
-
Capillary J-function
- k :
-
Permeability (m2)
- K r :
-
Relative permeability
- K rowi :
-
Relative permeability of oil at initial water saturation
- K rwor :
-
Relative permeability of water at residual oil saturation
- L :
-
Core length (m)
- l g :
-
Oil ganglion length (m)
- N c :
-
Capillary number
- N min :
-
Minimum number of samples
- n o :
-
Corey’s oil exponent
- n w :
-
Corey’s water exponent
- P c :
-
Capillary pressure (Pa)
- p :
-
Pressure (Pa)
- p min :
-
Minimum measured pressure (Pa)
- P :
-
Dimensionless pressure
- q w :
-
Water mass rate per unit area for linear flow (kg/m2 s)
- R :
-
Radius (m)
- r :
-
Pore throat radius
- s :
-
Water saturation
- t :
-
Time
- s f :
-
Frontal saturation during waterflooding
- S or :
-
Residual oil saturation
- S wi :
-
Connate water saturation
- U :
-
Velocity
- V min :
-
Minimum distinguishable volume
- x :
-
Distance (m)
- x D :
-
Dimensionless distance
- ε c :
-
Capillary–viscous ratio
- ε w :
-
Water-cut measurement accuracy
- ε p :
-
Pressure drop accuracy
- ε s :
-
Sampling period accuracy
- Δt :
-
Sampling period
- σ :
-
Interfacial tension (N/m)
- ϕ :
-
Porosity
- μ :
-
Viscosity (Pa s)
- ρ :
-
Density (kg/m3)
- σ :
-
Interfacial tension (N/m)
- θ :
-
Macroscopic contact angle
- λ :
-
Total mobility
- ξ :
-
Self-similar coordinate
- c:
-
Capillary
- m:
-
Maximum for velocity and for core length at maximum velocity
- min:
-
Minimum
- w:
-
Water
- o:
-
Oil
- i:
-
Initial
- D:
-
Dimensionless
- BL:
-
Buckley–Leverett
- BTC:
-
Breakthrough curve
- PDC:
-
Pressure drop curve
- RL:
-
Rapoport–Leas
- SS:
-
Steady-state
- USS:
-
Unsteady-state
References
Abbas, M.: An extension of Johnson, Bossler and Neumann JBN method for calculating relative permeabilities. In: SPE Annual Technical Conference and Exhibition 2016. Society of Petroleum Engineers (2016)
Adler, P.M.: Multiphase Flow in Porous Media. Springer, Amsterdam (1995)
Adler, P.: Porous Media: Geometry and Transports. Elsevier, Amsterdam (2013)
Adler, P.M., Thovert, J.-F.: Fractures and Fracture Networks, pp. 103–162. Springer, Berlin (1999)
Akin, S.: Estimation of fracture relative permeabilities from unsteady state corefloods. J. Pet. Sci. Eng. 30(1), 1–14 (2001)
Al Shalabi, E.W., Sepehrnoori, K., Delshad, M.: Mechanisms behind low salinity water flooding in carbonate reservoirs. In: SPE Western Regional & AAPG Pacific Section Meeting 2013 Joint Technical Conference 2013. Society of Petroleum Engineers (2013)
Arns, C., Adler, P.: Fast Laplace solver approach to pore-scale permeability. Phys. Rev. E 97(2), 023303 (2018)
Arns, J.-Y., Arns, C.H., Sheppard, A.P., Sok, R.M., Knackstedt, M.A., Pinczewski, W.V.: Relative permeability from tomographic images; effect of correlated heterogeneity. J. Pet. Sci. Eng. 39(3–4), 247–259 (2003)
Arns, C., Knackstedt, M., Mecke, K.: Boolean reconstructions of complex materials: integral geometric approach. Phys. Rev. E 80(5), 051303 (2009)
Aziz, K., Settari, A.: Petroleum Reservoir Simulation. Applied Science Publ. Ltd., London (1979)
Badalyan, A., Carageorgos, T., Bedrikovetsky, P., You, Z., Zeinijahromi, A., Aji, K.: Critical analysis of uncertainties during particle filtration. Rev. Sci. Instrum. 83(9), 095106 (2012)
Banchoff, T.F., Lovett, S.T.: Differential Geometry of Curves and Surfaces. Chapman and Hall/CRC, London (2016)
Barenblatt, G., Entov, V., Ryzhik, V.: Theory of Fluid Flows Through Natural Rocks. Kluwer, Dordrecht (1991)
Barenblatt, G., Patzek, T.W., Silin, D.: The mathematical model of nonequilibrium effects in water–oil displacement. SPE J. 8(04), 409–416 (2003)
Bartels, W.-B., Mahani, H., Berg, S., Hassanizadeh, S.: Literature review of low salinity waterflooding from a length and time scale perspective. Fuel 236, 338–353 (2019)
Bedrikovetsky, P.: Mathematical Theory of Oil and Gas Recovery: With Applications to Ex-USSR Oil and Gas Fields, vol. 4. Springer, Berlin (2013)
Borazjani, S., Behr, A., Genolet, L., Van Der Net, A., Bedrikovetsky, P.: Effects of fines migration on low-salinity waterflooding: analytical modelling. Trans. Porous Media 116(1), 213–249 (2017)
Borazjani, S., Behr, A., Genolet, L., Kowollik, P., Bedrikovetsky, P.: Ion-exchange inverse problem for low-salinity coreflooding. Trans. Porous Media 128(2), 571–611 (2019)
Buckley, S.E., Leverett, M.: Mechanism of fluid displacement in sands. Trans. AIME 146(01), 107–116 (1942)
Cao, J., James, L.A., Johansen, T.E.: Determination of two phase relative permeability from core floods with constant pressure boundaries. In: Society of Core Analysis Symposium, Avignon, France (2014)
Cao, J., Liu, X., James, L., Johansen, T.: Analytical interpretation methods for dynamic immiscible core flooding at constant differential pressure. In: Society of Core Analysis Symposium, St. John’s Newfoundland and Labrador, Canada, pp. 16–21 (2015)
Chatzis, I., Morrow, N.R., Lim, H.T.: Magnitude and detailed structure of residual oil saturation. Soc. Pet. Eng. J. 23(02), 311–326 (1983)
Chen, Z.: Reservoir Simulation: Mathematical Techniques in Oil Recovery, vol. 77. SIAM, Philadelphia (2007)
Chen, X., Kianinejad, A., DiCarlo, D.A.: An extended JBN method of determining unsteady-state two-phase relative permeability. Water Resour. Res. 52(10), 8374–8383 (2016)
Civan, F., Donaldson, E.: Relative permeability from unsteady-state displacements with capillary pressure included. SPE Form. Eval. 4(02), 189–193 (1989)
Dake, L.P.: Fundamentals of Reservoir Engineering, vol. 8. Elsevier, Amsterdam (1983)
Dos Santos, R.L., Bedrikovetsky, P., Holleben, C.R.: Optimal design and planning for laboratory corefloods. In: Latin American and Caribbean Petroleum Engineering Conference. Society of Petroleum Engineers (1997)
Farajzadeh, R., Ameri, A., Faber, M.J., Van Batenburg, D.W., Boersma, D.M., Bruining, J.: Effect of continuous, trapped, and flowing gas on performance of Alkaline Surfactant Polymer (ASP) flooding. Ind. Eng. Chem. Res. 52(38), 13839–13848 (2013)
Farajzadeh, R., Lotfollahi, M., Eftekhari, A., Rossen, W., Hirasaki, G.: Effect of permeability on implicit-texture foam model parameters and the limiting capillary pressure. Energy Fuels 29(5), 3011–3018 (2015)
Farajzadeh, R., Guo, H., van Winden, J., Bruining, J.: Cation exchange in the presence of oil in porous media. ACS Earth Space Chem. 1(2), 101–112 (2017)
Honarpour, M., Koederitz, F., Herbert, A.: Relative permeability of petroleum reservoirs. CRC Press, United States (1986)
Hussain, F., Cinar, Y., Bedrikovetsky, P.G.: Comparison of methods for drainage relative permeability estimation from displacement tests. In: SPE Improved Oil Recovery Symposium. Society of Petroleum Engineers (2010)
Hussain, F., Cinar, Y., Bedrikovetsky, P.: A semi-analytical model for two phase immiscible flow in porous media honouring capillary pressure. Trans. Porous Media 92(1), 187–212 (2012)
Hussain, F., Zeinijahromi, A., Bedrikovetsky, P., Badalyan, A., Carageorgos, T., Cinar, Y.: An experimental study of improved oil recovery through fines-assisted waterflooding. J. Pet. Sci. Eng. 109, 187–197 (2013)
Hussain, F., Pinczewski, W.V., Cinar, Y., Arns, J.-Y., Arns, C., Turner, M.: Computation of relative permeability from imaged fluid distributions at the pore scale. Trans. Porous Media 104(1), 91–107 (2014)
Islam, M.R., Bentsen, R.: A dynamic method for measuring relative permeability. J. Can. Pet. Technol. 25(01), 39–50 (1986)
Johansen, T.E., James, L.A.: Solution of multi-component, two-phase Riemann problems with constant pressure boundaries. J. Eng. Math. 96(1), 23–35 (2016)
Johnson, E., Bossler, D., Bossler, V.: Calculation of relative permeability from displacement experiments (1959)
Jones, S., Roszelle, W.: Graphical techniques for determining relative permeability from displacement experiments. J. Pet. Technol. 30(05), 807–817 (1978)
Katika, K., Ahkami, M., Fosbøl, P.L., Halim, A.Y., Shapiro, A., Thomsen, K., Xiarchos, I., Fabricius, I.L.: Comparative analysis of experimental methods for quantification of small amounts of oil in water. J. Pet. Sci. Eng. 147, 459–467 (2016)
Kianinejad, A., Chen, X., DiCarlo, D.A.: Direct measurement of relative permeability in rocks from unsteady-state saturation profiles. Adv. Water Resour. 94, 1–10 (2016)
Kim, C., Lee, J.: Experimental study on the variation of relative permeability due to clay minerals in low salinity water-flooding. J. Pet. Sci. Eng. 151, 292–304 (2017)
Krause, M.: Modeling and investigation of the influence of capillary heterogeneity on relative permeability. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers (2012)
Krause, M.H., Benson, S.M.: Accurate determination of characteristic relative permeability curves. Adv. Water Resour. 83, 376–388 (2015)
Kuo, C.-W., Benson, S.M.: Numerical and analytical study of effects of small scale heterogeneity on CO2/brine multiphase flow system in horizontal corefloods. Adv. Water Resour. 79, 1–17 (2015)
Kuo C.-w., Perrin J.-C., Benson, S.M.: Effect of gravity, flow rate, and small scale heterogeneity on multiphase flow of CO2 and brine. In: SPE Western Regional Meeting. Society of Petroleum Engineers (2010)
Lake, L.W., Johns, R., Rossen, W.R., Pope, G.A.: Fundamentals of enhanced oil recovery (2014)
Maplesoft™: Solver for a system of inequalities. https://www.maplesoft.com/support/help/maple/view.aspx?path=Task/SolveInequality (2019). Accessed 10 March 2019
MathWorks®: Meshgrid, Surf Commands https://au.mathworks.com/products/matlab.html (2019). Accessed 10 March 2019
McPhee, C., Reed, J., Zubizarreta, I.: Core Analysis: A Best Practice Guide, vol. 64. Elsevier, Amsterdam (2015)
Miller, M.A., Ramey Jr., H.: Effect of temperature on oil/water relative permeabilities of unconsolidated and consolidated sands. Soc. Pet. Eng. J. 25(06), 945–953 (1985)
Nasralla, R.A., Mahani, H., van der Linde, H.A., Marcelis, F.H., Masalmeh, S.K., Sergienko, E., Brussee, N.J., Pieterse, S.G., Basu, S.: Low salinity waterflooding for a carbonate reservoir: experimental evaluation and numerical interpretation. J. Pet. Sci. Eng. 164, 640–654 (2018)
Odeh, A., Dotson, B.: A method for reducing the rate effect on oil and water relative permeabilities calculated from dynamic displacement data. J. Pet. Technol. 37(11), 2051-052058 (1985)
Pereira, B.M.F., Shahverdi, H., Sohrabi, M.: Refinement of relative permeability measurements by accounting for viscous fingering in coreflood experiments. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers (2014)
Perrin, J.-C., Krause, M., Kuo, C.-W., Miljkovic, L., Charoba, E., Benson, S.M.: Core-scale experimental study of relative permeability properties of CO2 and brine in reservoir rocks. Energy Proc. 1(1), 3515–3522 (2009)
Rabinovich, A.: Estimation of sub-core permeability statistical properties from coreflooding data. Adv. Water Resour. 108, 113–124 (2017)
Rabinovich, A.: Analytical corrections to core relative permeability for low-flow-rate simulation. SPE J. (2018)
Rabinovich, A., Li, B., Durlofsky, L.J.: Analytical approximations for effective relative permeability in the capillary limit. Water Resour. Res. 52(10), 7645–7667 (2016)
Rapoport, L., Leas, W.: Properties of linear waterfloods. J. Pet. Technol. 5(05), 139–148 (1953)
Richmond, P., Watsons, A.: Estimation of multiphase flow functions from displacement experiments. SPE Reserv. Eng. 5(01), 121–127 (1990)
Sigmund, P., McCaffery, F.: An improved unsteady-state procedure for determining the relative-permeability characteristics of heterogeneous porous media (includes associated papers 8028 and 8777). Soc. Pet. Eng. J. 19(01), 15–28 (1979)
Sorop, T.G., Masalmeh, S.K., Suijkerbuijk, B.M.J.M., van der Linde, H.A., Mahani, H., Brussee, N.J., Marcelis, F.A.H.M., Coorn, A. Relative Permeability Measurements to Quantify the Low Salinity Flooding Effect at Field Scale (2015)
Tao, T., Watson, A.: Accuracy of JBN estimates of relative permeability: part 2-algorithms. Soc. Pet. Eng. J. 24(02), 215–223 (1984)
Torsæter, O., Abtahi, M.: Experimental Reservoir Engineering Laboratory Workbook. Department of Petroleum Engineering and Applied Geophysics, Norwegian University of Science and Technology (NTNU), Trondheim (2003)
Toth, J., Bodi, T., Szucs, P., Civan, F.: Direct determination of relative permeability from nonsteady-state constant pressure and rate displacements. In: SPE Production and Operations Symposium. Society of Petroleum Engineers (2001)
Toth, J., Bodi, T., Szucs, P., Civan, F.: Convenient formulae for determination of relative permeability from unsteady-state fluid displacements in core plugs. J. Pet. Sci. Eng. 36(1–2), 33–44 (2002)
Virnovsky, G., Guo, Y.: Relative permeability and capillary pressure concurrently determined from steady-state flow experiments. In: IOR 1995-8th European Symposium on Improved Oil Recovery (1995)
Virnovsky, G., Vatne, K., Skjaeveland, S., Lohne, A.: Implementation of multirate technique to measure relative permeabilities accounting. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers (1998)
Welge, H.J.: A simplified method for computing oil recovery by gas or water drive. J. Pet. Technol. 4(04), 91–98 (1952)
Zeinijahromi, A., Farajzadeh, R., Bruining, J.H., Bedrikovetsky, P.: Effect of fines migration on oil–water relative permeability during two-phase flow in porous media. Fuel 176, 222–236 (2016)
Zhou, K., Hou, J., Fu, H., Wei, B., Liu, Y.: Estimation of relative permeability curves using an improved Levenberg–Marquardt method with simultaneous perturbation Jacobian approximation. J. Hydrol. 544, 604–612 (2017)
Zou, S., Hussain, F., Arns, J.-Y., Guo, Z., Arns, C.H.: Computation of relative permeability from in situ imaged fluid distributions at the pore scale. SPE J. 23(03), 737–749 (2018)
Acknowledgements
The paper is dedicated to the memory of Eng. C. Holleben (Petrobras) who initiated the work by Dos Santos et al. (1997). The authors are grateful to Dr. A. Badalyan (The University of Adelaide) for fruitful discussions. Deep gratitude is due to Profs. M. Lurie and A. Kurbanov (Moscow Oil–Gas Gubkin University), who introduced PB to waterflood mathematics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Mathematical Model for Two-Phase Immiscible Displacement
Following Rapoport and Leas (1953), Barenblatt et al. (1991), Lake et al. (2014), here we present the mathematical model for two-phase flow of immiscible incompressible fluids in porous media. The modified Darcy’s law expresses the momentum balance for each phase
where k is the permeability, uw and uo are the water and oil velocities, respectively, Krw and Kro are the relative permeability for water and oil, s is the saturation, μw and μo are the viscosity for water and oil and Pw and Po are the phase pressures in water and oil.
Volumetric balance for water is:
Here ϕ is the porosity.
The total flux conservation follows from incompressibility of both phases:
where U is the total velocity.
The difference between phase pressures is equal to capillary pressure
Here Pc is the capillary pressure, σ is the interfacial tension, θ is the contact angle, and J is the capillary function.
Substituting Darcy’s law for both phases (1, 2) into the expression (4) for the total flux, expressing pressure in oil from Eq. (5) and also substituting it into Eq. (4) yield
Expressing pressure gradient in water and substituting it into Eq. (1) yields
where f is the fractional flow for water.
Substituting expression for water flux (A.6) into volume balance equation for water (A.2) results in one equations for unknown saturation s(x, t):
Introduce the following dimensionless variables and parameters:
Here xD is the dimensionless distance, L is the core length, tD is the dimensionless time, P is the dimensionless pressure, and εc is the capillary-viscous ratio.
Here λ(s) is the total mobility of two phases.
Equations (A.1) and (A.3) are decoupled, which means that the saturation distribution during the displacement s(xD, tD) is determined from Eq. (A.1). Afterwards, the pressure distribution p(xD, tD) is determined from Eq. (A.2) for the obtained saturation distribution.
Water flux in continuity Eq. (A.1) consists on the advective and capillary components, defined by Eq. (A.9).
The core is initially saturated with oil and connate water, i.e. the initial condition for Eq. (A.1) is:
Here Swi is the initial water saturation.
Only water flows through the inlet cross section, so the boundary condition at the inlet of the core is:
The boundary condition at the core outlet after the breakthrough is given by the condition of continuity of pressures in the both phases across the outlet interface, from which follows the continuity of the capillary pressure also. At the right-hand side of the core outlet, we assume a segregated flow regime, so the capillary pressure is zero. Therefore, the capillary pressure is zero behind the core outlet too. Thus, the boundary condition at the outlet of the core corresponds to zero capillary pressure:
and the outlet saturation after the breakthrough is equal to its maximum value s0 = 1 − Sor. Here Sor is the residual oil saturation.
Appendix B: Large-Scale Approximation of the Buckley–Leverett Equations
For small values of εc, one can neglect terms with εc in right-hand sides of Eqs. (A.9, A.10):
For this case, fractional flow function f(s) is the ratio between the water flux and the total flux.
Approaching εc > 0 in the boundary condition (A.6), we obtain:
The solution s(xD, tD) of the 1 − D capillary–pressure–free displacement problem (B.1), (A.5)–(A.7) is self-similar, depending only on the group ξ = xD/tD, i.e. s(xD, tD) = s(ξ):
The self-similarity of the solution is the only information which is required for inverse problem to have exact solution (see). In two following sections exact shape of s(xD, tD) will not be used, and only the fact of self-similarity will be exploited.
Appendix C: Welge’s Method for Determination of Fractional Flow Function
Let us discuss how to determine the fractional flow function f(s) from the water-cut history f(1, tD) measured during the coreflood.
Let us integrate Eq. (B.1) over the region Δ on the plane (xD, tD) which is limited by the triangle ∂Δ: (0, 0) → (1, 0) → (1, tD) → (0, 0) and apply the Green’s formula (Bedrikovetsky 2013):
Let us calculate the contour integral in (C.1) over the sides of triangle ∂Δ:
Substituting the expressions for the integrals over the sides of the triangle (C.2–C.4) into Eq. (C.1), we obtain the expression for the saturation on the core outlet:
Corresponding the saturation values, calculated by (C.5), to the water-cut values, which have been measured at the same moments, we obtain the dependence f = f(s).
Appendix D: JBN Method for Determination of Relative Permeability
Following the works by Johnson et al. (1959) and Jones and Roszelle (1978), let us calculate the pressure drop on the core during the waterflood:
Expressing the integral from (D.1) and taking its derivative with respect to the upper limit, we obtain the explicit expression for the total mobility
Corresponding the values of total mobility calculated by (D.2) to the values of saturations calculated by (C.5) for the coherent moments, we obtain the dependence λ = λ(s).
From the expression for the fractional flow function (A.9), the formulae for determination of relative permeabilities for both phases are:
It is important to emphasise that formulae (C.5) and (D.2), (D.3) deliver the solution f = f(s) and λ = λ(s) only for saturations which are realised during the displacement process. In the case of the displacement of oil with the connate water by water, the method provides with the fractional flow function and total mobility only for saturations higher than the frontal saturation sf and below the s0 and also in the initial point Swi.
Appendix E: Determination of the Frontal Saturation and Displacement Velocity from the Waterless Period Data
Let us calculate the pressure drop on the core, as in (D.1), but for the moment before the breakthrough. Acting by analogy to Eq. (D.1), we obtain
where initial saturation si can exceed connate water saturation Swi.
Let us transform Eq. (E.1) to the form
Equation (E.2) gives the straight line versus tD. The free constant in it is determined by the total mobility before the flood, which is known from the initial saturation process. The slope of the line together with the condition that the velocity D is the tangent of the fractional flow curve in the frontal saturation point makes it possible to determine the slope D and the frontal saturation sf. The slope of the pressure drop as defined by Eq. (E.2) and calculated from the measured data is an additional information for relative permeability tuning from the coreflood data.
Appendix F: Determination of Pore Throat Radius from Permeability and Porosity
Following Barenblatt et al. (1991), here we derive permeability and porosity for cubic lattice with the tube radius r and the bond length l. One cube is adjacent to 12 bonds and one bond belongs to four cubes, so each cube includes three bonds. The porosity is equal to
Flow through a cube side corresponds to flow through a single tube. Comparing Darcy and Poiseuille laws
we obtain the formula for permeability
From Eqs. (F.1) and (F.3) follows the expression for pore throat radius r
Rights and permissions
About this article
Cite this article
Al-Sarihi, A., You, Z., Behr, A. et al. Admissible Parameters for Two-Phase Coreflood and Welge–JBN Method. Transp Porous Med 131, 831–871 (2020). https://doi.org/10.1007/s11242-019-01369-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-019-01369-w