Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-25T17:57:04.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of finite-amplitude gravity–capillary progressive ring waves by an oscillating surface-piercing body

Published online by Cambridge University Press:  28 January 2020

Meng Shen  and
Yuming Liu Open the ORCID record for Yuming Liu [Opens in a new window]
Meng Shen
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA02139, USA
Yuming Liu*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA02139, USA
*
†Email address for correspondence: yuming@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

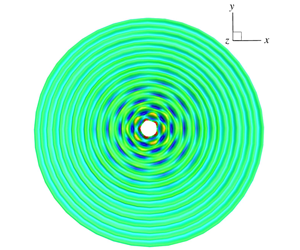
We investigate the instability of finite-amplitude progressive ring waves in deep water, which are radiated by the time-periodic oscillation of a half-submerged sphere (with radius $r_{1}$), under the influence of gravity and surface tension. We use direct numerical simulations of fully nonlinear wave–body interactions to quantify the temporal–spatial evolution of the base and perturbed outgoing ring wave fields, from which the stability of ring waves is analysed. The numerical simulation is based on a mixed Euler–Lagrangian quadratic boundary-element method and accounts for fully nonlinear wave–wave and wave–body interactions in the context of potential flow. We find that the progressive gravity–capillary ring waves (with frequency $2\unicode[STIX]{x1D714}_{0}$) become unstable to (small-amplitude) radial cross-wave disturbances when the body-motion parameter $k_{0}a$ exceeds the threshold value $\unicode[STIX]{x1D700}_{c}$, where $a$ is the amplitude of body oscillation and $k_{0}$ is the wavenumber of the ring wave at subharmonic frequency $\unicode[STIX]{x1D714}_{0}$. The predicted $\unicode[STIX]{x1D700}_{c}$ from nonlinear simulations under the assumption of ideal fluid, which decreases with increasing $k_{0}r_{1}$, is generally smaller than the experimental measurement of Tatsuno et al. (Rep. Res. Inst. Appl. Mech. Kyushu University, vol. 17, 1969, pp. 195–215) by approximately 50 %. When the viscous effects in body-surface and free-surface boundary layers are taken into account, the predicted $\unicode[STIX]{x1D700}_{c}$ matches the experimental data excellently. The unstable modes are characterized as the progressive radial cross-waves at the subharmonic frequency ($\unicode[STIX]{x1D714}_{0}$) with the growth rates generally increasing with $k_{0}a$. The maximum growth rate is achieved for the cross-wave mode with the azimuthal wavenumber $m^{\ast }\sim 1.2k_{0}r_{1}$. These distinctive features of instability obtained in numerical simulations are consistent with the experimental observations. From the comparison with the weakly nonlinear analysis of Shen & Liu (J. Fluid Mech., vol. 869, 2019, pp. 439–467), it is found that inclusion of finite-amplitude ring wave effects generally reduces the growth rate of unstable modes but has an insignificant influence on the shape of unstable modes and the value of $\unicode[STIX]{x1D700}_{c}$. Moreover, for moderately steep ring waves, nonlinear interactions of a few unstable modes can excite broadbanded unstable subharmonic cross-wave modes, leading to the formation/observation of distinctive non-axisymmetric wave patterns during long-time evolutions.

JFM classification

Waves/Free-surface Flows: Capillary waves Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 887 , 25 March 2020 , A16
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Becker, J. M. & Miles, J. M. 1991 Standing radial cross-waves. J. Fluid Mech. 222, 471–499.CrossRefGoogle Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wave trains on deep water. 1. Theory. J. Fluid Mech. 27, 395–397.CrossRefGoogle Scholar
Benney, D. J. & Roskes, G. J. 1969 Wave instabilities. Stud. Appl. Maths 48 (4), 377–385.CrossRefGoogle Scholar
Bogoliubonv, N. & Mitropolsryy, A. 1961 Asymptotic Methods in the Theory of Non-linear Oscillations. Hindustan.Google Scholar
Cho, Y., Diorio, J., Akylas, T. R. & Duncan, J. H. 2011 Resonantly forced gravity–capillary lumps on deep water. Part 2. Theoretical model. J. Fluid Mech. 672, 288–306.CrossRefGoogle Scholar
Coddington, D. A. & Levinson, N. 1955 Theory of Ordinary Differential Equations. McGraw-Hill.Google Scholar
Diorio, J., Cho, Y., Duncan, J. H. & Akylas, T. R. 2009 Gravity-capillary lumps generated by a moving pressure source. Phys. Rev. Lett. 103, 214502.CrossRefGoogle ScholarPubMed
Diorio, J., Cho, Y., Duncan, J. H. & Akylas, T. R. 2011 Resonantly forced gravity–capillary lumps on deep water. Part 1. Experiments. J. Fluid Mech. 672, 268–287.CrossRefGoogle Scholar
Dommermuth, D. G. & Yue, D. K. P. 1987 Numerical simulations of nonlinear axisymmetric flows with a free surface. J. Fluid Mech. 178, 195–219.CrossRefGoogle Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures, and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. A 121, 299–341.Google Scholar
Havelock, T. H. 1929 Forced surface waves on water. Phil. Mag. 8, 569–576.CrossRefGoogle Scholar
Hulme, A. 1982 The wave forces acting on a floating hemisphere undergoing forced periodic oscillations. J. Fluid Mech. 121, 443–463.CrossRefGoogle Scholar
Ingham, D. B., Ritchie, J. A. & Tayler, C. M. 1991 The linear boundary element solution of Laplace’s equation with Dirichlet boundary conditions. Math. Comput. Model. 15, 195–204.CrossRefGoogle Scholar
John, F. 1950 On the motion of floating bodies. II. Simple harmonic motions. Commun. Pure Appl. Maths 3, 45–101.CrossRefGoogle Scholar
von Kerczek, C. & Davis, S. H. 1976 Calculation of transition matrices. AIAA J. 13 (10), 1400–1403.CrossRefGoogle Scholar
Liu, Y., Xue, M. & Yue, D. K. P. 2001 Computations of fully nonlinear three-dimensional wave–wave and wave–body interactions – part 2. Nonlinear waves and forces on a body. J. Fluid Mech. 438, 41–66.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1978a The instabilities of gravity waves of finite amplitude in deep water I. Superharmonics. Proc. R. Soc. Lond. A 360, 471–488.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1978b The instabilities of gravity waves of finite amplitude in deep water II. Subharmonics. Proc. R. Soc. Lond. A 360, 489–505.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Cokelet, E. D. 1976 The deformation of steep surface waves on water – I. A numerical method of computation. Proc. R. Soc. Lond. A 350, 1–26.CrossRefGoogle Scholar
Marquardt, D. W. 1963 An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Indust. Appl. Maths 11, 431–441.CrossRefGoogle Scholar
McLean, J. W. 1982 Instabilities of finite-amplitude water waves. J. Fluid Mech. 114, 315–330.CrossRefGoogle Scholar
Mei, C. C. & Liu, L. F. 1973 The damping of surface gravity waves in a bounded liquid. J. Fluid Mech. 59 (2), 239–256.CrossRefGoogle Scholar
Mei, C. C., Stiassnie, M. & Yue, D. K. P. 2005 Theory and Applications of Ocean Surface Waves. Part 2: Nonlinear Aspects. World Scientific.Google Scholar
Mercer, G. N. & Roberts, A. J. 1992 Standing waves in deep water: their stability and extreme form. Phys. Fluids A 4 (2), 259–269.CrossRefGoogle Scholar
Miles, J. M. 1967 Surface-wave damping in closed basins. Proc. R. Soc. Lond. A 297, 459–475.Google Scholar
Milewski, P. A., Vanden-Broeck, J. M. & Wang, Z. 2010 Dynamics of steep two-dimensional gravity–capillary solitary waves. J. Fluid Mech. 186, 129–146.Google Scholar
Minorsky, N. 1974 Nonlinear Oscillations. Krieger Publishing.Google Scholar
Orlanski, I. 1975 A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 21 (3), 251–269.CrossRefGoogle Scholar
Pan, Y. & Yue, D. K. P. 2014 Direct numerical investigation of turbulence of capillary waves. Phys. Rev. Lett. 113, 094501.CrossRefGoogle ScholarPubMed
Park, B. & Cho, Y. 2017 Two-dimensional gravity–capillary solitary waves on deep water: generation and transverse instability. J. Fluid Mech. 834, 92–124.CrossRefGoogle Scholar
Rhodes-Robinson, P. F. 1971 On the forced surface waves due to a vertical wave-maker in the presence of surface tension. Proc. Camb. Phil. Soc. 70, 323–337.CrossRefGoogle Scholar
Shen, M.2019 The instability of axial-symmetric gravity–capillary waves generated by a vertically oscillating sphere. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Shen, M. & Liu, Y. 2019 Subharmonic resonant interaction of gravity–capillary progressive axially symmetric wave with radial cross-wave. J. Fluid Mech. 869, 439–467.CrossRefGoogle Scholar
Su, M. Y. 1982 Three-dimensional deep-water waves. Part 1. Experimental measurement of skew and symmetric wave patterns. J. Fluid Mech. 124, 73–108.CrossRefGoogle Scholar
Taneda, S. 1991 Visual observations of the flow around a half-submerged oscillating sphere. J. Fluid Mech. 227, 193–209.CrossRefGoogle Scholar
Tatsuno, M., Inoue, S. & Okabe, J. 1969 Transfiguration of surface waves. Rep. Res. Inst. Appl. Mech. Kyushu University 17, 195–215.Google Scholar
Thompson, J. F., Warsi, Z. U. A. & Mastin, C. W. 1985 Numerical Grid Generation Foundations and Applications. Elsevier.Google Scholar
Wang, Z. 2016 Stability and dynamics of two-dimensional fully nonlinear gravity–capillary solitary waves in deep water. J. Fluid Mech. 809, 530–552.CrossRefGoogle Scholar
Wang, Z., Vanden-Broeck, J. M. & Milewski, P. A. 2014 Asymmetric gravity–capillary solitary waves on deep water. J. Fluid Mech. 759, R2.CrossRefGoogle Scholar
Wu, G., Liu, Y. & Yue, D. K. P. 2006 A note on stabilizing the Benjamin–Feir instability. J. Fluid Mech. 556, 45–54.CrossRefGoogle Scholar
Xue, M., Xu, H., Liu, Y. & Yue, D. K. P. 2001 Computations of fully nonlinear three-dimensional wave–wave and wave–body interactions – part 1. Dynamics of three-dimensional steep waves. J. Fluid Mech. 438, 11–39.CrossRefGoogle Scholar
Yan, H. & Liu, Y. 2011 An efficient high-order boundary element method for nonlinear wave–wave and wave–body interactions. J. Comput. Phys. 230 (2), 402–424.CrossRefGoogle Scholar
Yung, T.-W., Standström, R. E., He, H. & Minta, M. K. 2010 On the physics of vapor/liquid interaction during impact on solids. J. Ship Res. 54 (3), 174–183.Google Scholar
Zhu, Q., Liu, Y. & Yue, D. K. P. 2003 Three-dimensional instability of standing waves. J. Fluid Mech. 496, 213–242.CrossRefGoogle Scholar