An Upscaled Model for Permeable Biofilm in a Thin Channel and Tube

Abstract

In this paper, we derive upscaled equations for modeling biofilm growth in porous media. The resulting macroscale mathematical models consider permeable multi-species biofilm including water flow, transport, detachment and reactions. The biofilm is composed of extracellular polymeric substances (EPS), water, active bacteria and dead bacteria. The free flow is described by the Stokes and continuity equations, and the water flux inside the biofilm by the Brinkman and continuity equations. The nutrients are transported in the water phase by convection and diffusion. This pore-scale model includes variations in the biofilm composition and size due to reproduction of bacteria, production of EPS, death of bacteria and shear forces. The model includes a water–biofilm interface between the free flow and the biofilm. Homogenization techniques are applied to obtain upscaled models in a thin channel and a tube, by investigating the limit as the ratio of the aperture to the length $\varepsilon$ of both geometries approaches to zero. As $\varepsilon$ gets smaller, we obtain that the percentage of biofilm coverage area over time predicted by the pore-scale model approaches the one obtained using the effective equations, which shows a correspondence between both models. The two derived porosity–permeability relations are compared to two empirical relations from the literature. The resulting numerical computations are presented to compare the outcome of the effective (upscaled) models for the two mentioned geometries.

1 Introduction

Biofilms are sessile communities of bacteria housed in a self-produced adhesive matrix consisting of extracellular polymeric substances (EPS), including polysaccharides, proteins, lipids and DNA (Aggarwal et al. 2015). The proportion of EPS in biofilms is 50–90% of the total organic matter (Donlan 2002; Vu et al. 2009). Water is by far the largest component of the matrix, giving biofilms the nickname "stiff water" (Flemming and Wingender 2010). Biofilms provoke chronic bacterial infection, infection on medical devices, deterioration of water quality and the contamination of food (Kokare et al. 2009). On the other hand, biofilms can be used for wastewater treatment and bioenergy production (Miranda et al. 2017). In microbial enhanced oil recovery (MEOR), one of the strategies is selective plugging, where bacteria are used to form biofilm in highly permeable zones to diverge the water flow and extract the oil located in low-permeability zones (Raiders et al. 1989). In wastewater treatment, one of the strategies consists of using biofilms to break down compounds which are not desirable to discharge into the natural environment (Capdeville and Rols 1992).

Two of the motivations to derive upscaled models are to accurately describe the average behavior of the system with relatively low computational effort compared to fully detailed calculations starting at the microscale (van Noorden et al. 2010) and to determine effective parameters (Helmig et al. 2002). The values of these effective parameters can be determined using known values from pore-scale experiments. Recent works have been carried out to derive upscaled models; for example, Collis et al. (2017) obtained a mathematical model describing macroscopic tumor growth, transport of drug and nutrient through homogenization and Jin and Chen (2019) upscaled a pore-scale model for primary fluid recovery and showed that the macroscopic equation for the water flux is fundamentally different from Darcys’ law. We also refer to Peszynska et al. (2016) where the authors upscale a pore-scale model for biofilm growth and compare to the experimental results and Schulz (2019a) where the author derives effective quantities for a permeable biofilm in a perforated domain. In contrast to Schulz (2019a), we consider different pore geometries and a multi-component biofilm.

The present work builds on Landa-Marbán et al. (2019), where a pore-scale model is discussed. The model includes permeable biofilm and evolution of different biofilm components: active bacteria, dead bacteria and EPS. The importance of including biofilm permeability is underlined by the fact that the dominated mechanism of nutrient transport within some biofilms is convection (Lewandowski and Beyenal 2003). This mathematical model is based on laboratory experiments performed by Liu et al. (2019), where the biofilm was grown in micro-channels. Here, we upscale this pore-scale model to derive effective equations, by investigating the limit as the ratio of the height to the length of the micro-channel approaches to zero.

In this general context, the objective of the research reported in the present article is to obtain core-scale models (also known as Darcy-scale or macroscale models) for permeable biofilm in two different pore geometries: a thin channel and a tube. The motivation for choosing these two geometries is because experiments are performed in the laboratory in micro-channels (Liu et al. 2019) and tubes (Bott and Miller 1983), they may represent a fracture in a core sample (Bringedal et al. 2015) and some porous media can be modeled as a stack of micro-tubes or micro-channels (van Noorden et al. 2010).

To summarize, the novel aspect in this work is the derivation of core-scale models from a pore-scale model for a biofilm which is permeable to the flow and has a variable (in time and space) height. The fluid flow in the biofilm is modeled by the Brinkman equation, whereas in the remaining pore space the Stokes model is adopted. This is done for two different geometries. We derive analytical expressions for the upscaled quantities and provide numerical simulations for the upscaled models in both cases.

The structure of this paper is as follows. In Sect. 2, we describe the pore-scale biofilm model. In Sect. 3, we present the dimensionless pore-scale biofilm model. In Sect. 4, we perform formal homogenization on the model equations and obtain upscaled equations. In Sect. 5, we compare the upscaled models with the upscaled model of van Noorden et al. (2010) and with the well-known core-scale model of Chen-Charpentier et al. (2009). We compare the derived porosity–permeability relations to empirical porosity–permeability relations from the literature. Also, we perform numerical simulations in the upscaled models and we compare the results for the biofilm height and nutrient concentration for the two different effective models. Finally, in Sect. 6 we present the conclusions.

2 Pore-Scale Model

The pore-scale mathematical model considered here follows ideas from Alpkvist and Klapper (2007) ,van Noorden et al. (2010) and Deng et al. (2013). A detailed description of this model can be found in Landa-Marbán et al. (2019), where a comparison of laboratory measurements and numerical simulations is also presented.

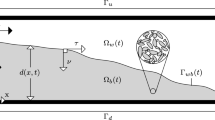
The biofilm has four components: water, EPS, active and dead bacteria ($j=\lbrace w,e,a,d\rbrace$). Let $\theta _j$ and $\rho _j$ denote the volume fraction and the density of component j. The sum of volume fractions is constraint to 1 ($\theta _w+\theta _e+\theta _a+\theta _d=1$). Given that biofilms are mostly water (Flemming and Wingender 2010), we assume that the volume fraction of water $\theta _w$ is constant. The biomass phases and water are assumed to be incompressible ($\partial _t\rho _j=0$), and the biofilm layer is attached to the pore walls. Figure 1 shows schematically the phenomena considered for the biofilm formation.

Fig. 1

Conceptual pore-scale model showing the processes for the biofilm dynamics

We consider two different pore geometries: a tube in cylindrical coordinates $\varvec{r}=(r,\varphi ,z)$ and a thin channel in Cartesian coordinates $\varvec{x}=(x,y,z)$. The z direction is taken along the length L of the tube and thin channel (see Figs. 2, 6). In the first case, the pore has circular cross section and in the second a rectangular one. In both cases, the length is much larger than the cross-sectional aperture. In both cases, we assume a certain symmetry. For the cylindrical pore, we assume that the processes are radially symmetric, and hence, there is no angular dependence (see Fig. 2). For the thin channel, there are no changes in the x direction, i.e., the width of the channel, so it can be reduced to a two-dimensional strip (see Fig. 6). This assumption is based on experiments, showing that when the width of the channel is much smaller than its height, the growth of the biofilm occurs only at the upper and lower walls along the channel (Liu et al. 2019). We present in detail the upscaling of the model equations on the tube geometry. The upscaling on the channel geometry is shown in “Appendix.” Figure 2 shows the different domains, boundaries and interface in the pore with tubular geometry.

Fig. 2

Pore of radius $\varrho$ and length L in cylindrical coordinates

We consider a thin tube of radius $\varrho$ and length L. We denote the biofilm height by d which only depends on z and time as a result of the symmetry assumption. The domain is occupied by the water $\varOmega _{T,w}(t)=\lbrace \varvec{r}|\;r\in [0,\varrho -d(z,t)),\varphi \in [0,2\pi ),z\in (0,L) \rbrace$ and biofilm $\varOmega _{T,b}(t)=\lbrace \varvec{r}|\;r\in (\varrho -d(z,t),\varrho ),\varphi \in [0,2\pi ),z\in (0,L) \rbrace$ phases with the biofilm located along the tube wall $\varGamma _{T,s}=\lbrace \varvec{r}|\;r=\varrho ,\varphi \in [0,2\pi ),z\in (0,L) \rbrace$. Clearly, $r=\varrho -d(z,t)$ separates the water and biofilm regions. The water domain has three boundary parts: the inflow $\varGamma _{T,{\mathrm {iw}}}(t) =\lbrace \varvec{r}|\;r\in [0,\varrho -d(z,t)),\varphi \in [0,2\pi ),z=0\rbrace$, the outflow $\varGamma _{T,{\mathrm {ow}}}(t) =\lbrace \varvec{r}|\;r\in [0,\varrho -d(z,t)),\varphi \in [0,2\pi ),z=L\rbrace$ and the interface between the water and the biofilm $\varGamma _{T,{\mathrm {wb}}}(t) =\lbrace \varvec{r}|\;r=\varrho -d(z,t),\varphi \in [0,2\pi ),z\in (0,L)\rbrace$. Similarly, for the biofilm we have the inflow $\varGamma _{T,{\mathrm {ib}}}(t)=\lbrace \varvec{r}|\;r\in (\varrho -d(z,t),\varrho ),\varphi \in [0,2\pi ),z=0\rbrace$ and outflow $\varGamma _{T,{\mathrm {ob}}}(t)=\lbrace \varvec{r}|\;r\in (\varrho -d(z,t),\varrho ),\varphi \in [0,2\pi )\;z=L\rbrace$ boundary parts, the water–biofilm interface $\varGamma _{T,{\mathrm {wb}}}(t)$ and the solid tube wall $\varGamma _{T,s}$. Although the tube is a three-dimensional domain, recalling the rotational symmetry, we only write the r- and z-components of the vectors in order to reduce the length of the mathematical expressions.

The unit normal $\boldsymbol{\nu }$ pointing into the biofilm and the normal velocity of the interface $\nu _n$ can be written in terms of the biofilm height d as (van Noorden et al. 2010)

$$\begin{aligned} \boldsymbol{\nu }=\left( 1,\partial _z d\right) ^T\big /\sqrt{1+\left( \partial _z d\right) ^2},\quad \nu _n =-\partial _t d\big /\sqrt{1+\left( \partial _z d\right) ^2}\quad {\text {at }}\;\varGamma _{T,{\mathrm {wb}}}(t). \end{aligned}$$

(1a,b)

The water flux outside the biofilm $\varOmega _{T,w}(t)$ is described by the Stokes and continuity equations

$$\begin{aligned} \mu \Delta \varvec{q}_w=\nabla p_w,\quad \nabla \boldsymbol{\cdot } \varvec{q}_w=0\quad \text {in }\;\varOmega _{T,w}(t) \end{aligned},$$

(2a,b)

while the water flux inside the biofilm $\varOmega _{T,b}(t)$ is described by the Brinkman and continuity equations

$$\begin{aligned} (\mu /\theta _w)\Delta \varvec{q}_b-(\mu /k)\varvec{q}_b=\nabla p_b,\quad \nabla \boldsymbol{\cdot } \varvec{q}_b=0\quad \text {in }\;\varOmega _{T,b}(t). \end{aligned}$$

(3a,b)

Here, $p_w$ and $p_b$ are the water pressures and $\varvec{q}_w$ and $\varvec{q}_b$ are the water velocities in the water domain and biofilm domain, respectively; $\mu$ is the water viscosity (constant, not dependent on biofilm species) and k is the permeability of the biofilm (assumed isotropic). The Brinkman model can be derived by upscaling, assuming that the volume of the porous medium skeleton is much smaller than the volume of the reference cell (Hornung 1997). As biofilms are mostly water, the Brinkman model is a good choice to model water flux inside biofilms. At the interface $\varGamma _{T,{\mathrm {wb}}}(t),$ one has the continuity of the velocity and of the normal stress tensor

$$\begin{aligned} \varvec{q}_{w}=\varvec{q}_{b},\boldsymbol{\nu }\boldsymbol{\cdot } \left[ \mu \left( \nabla \varvec{q}_{w}+\nabla \varvec{q}_{w}^T\right) -\mathbb {I}p_w\right] =\boldsymbol{\nu }\boldsymbol{\cdot } \left[ \left( \mu /\theta _w\right) \left( \nabla \varvec{q}_{b}+\nabla \varvec{q}_{b}^T\right) -\mathbb {I}p_b\right] \;{\text {at }}\;\varGamma _{T,{\mathrm {wb}}}(t) \end{aligned}$$

(4a,b)

where $\mathbb {I}$ is the identity matrix. At the wall $\varGamma _{T,s},$ we consider the no-slip boundary condition $\varvec{q}_b=\varvec{0}$.

To model the nutrient transport and consumption, we let $c_\alpha$$(\alpha \in \lbrace w,b\rbrace )$ stand for the nutrient concentration in water or biofilm (mass per total volume of biofilm), respectively, and D is the nutrient diffusion coefficient in water. Then, the nutrients in the water $\varOmega _{T,w}(t)$ satisfy the convection–diffusion equation

$$\begin{aligned} \partial _t c_{w}+\nabla \boldsymbol{\cdot }\varvec{J}_w=0,\quad \varvec{J}_w=-D\nabla c_{w}+\varvec{q}_wc_{w}\quad \text {in}\;\varOmega _{T,w}(t) \end{aligned}$$

(5a,b)

and in the biofilm $\varOmega _{T,b}(t)$ satisfy the convection–diffusion–reaction equation

$$\begin{aligned} \partial _t\left( \theta _w c_{b}\right) +\nabla \boldsymbol{\cdot }\varvec{J}_b=R_{b},\quad \varvec{J}_b=-\theta _w D\nabla c_{b}+\varvec{q}_{b}c_{b}\quad \text {in }\;\varOmega _{T,b}(t) \end{aligned}$$

(6a,b)

where $\varvec{J}_w$ and $\varvec{J}_b$ are the nutrient flux outside and inside the biofilm, respectively. Further at $\varGamma _{T,{\mathrm {wb}}}(t),$ we impose the mass conservation and continuity of nutrient concentration

$$\begin{aligned} (\varvec{J}_b-\varvec{J}_w)\boldsymbol{\cdot } \boldsymbol{\nu }=\nu _n(\theta _wc_b-c_w),\quad c_b=c_w\quad {\text {at }}\;\varGamma _{T,{\mathrm {wb}}}(t). \end{aligned}$$

(7a,b)

At the solid wall $\varGamma _{T,s},$ the normal flux is $\boldsymbol{\upsilon }\boldsymbol{\cdot }\varvec{J}_b=0$, where $\boldsymbol{\upsilon }$ is the normal vector at the pore wall. The reaction term $R_b$ for the consumption of nutrients is given by

$$\begin{aligned} R_b=-\mu _n\theta _a\rho _ac_{b}/(k_n+c_{b})\quad \text {in }\;\varOmega _{T,b}(t) \end{aligned}$$

(8)

where $\mu _n$ is the maximum rate of nutrient consumption and $k_n$ is the Monod-half nutrient velocity coefficient.

The movement of the biomass components $\theta _i$ in $\varOmega _{T,b}(t)$ due to reproduction, production of EPS and death of active bacteria can be modeled as a Darcy flow (Alpkvist and Klapper 2007). We denote by $\varvec{u}$ the velocity of the biomass and $\varPhi$ the growth velocity potential. Then, we consider the following equations (Alpkvist and Klapper 2007; Landa-Marbán et al. 2019)

$$\begin{aligned} \varvec{u}=-\nabla \varPhi ,\quad \nabla \boldsymbol{\cdot }\varvec{u}=(1-\theta _w)^{-1}\varSigma _i\left( R_i/\rho _i\right) ,\quad i\in \lbrace e,a,d\rbrace \quad \text {in }\;\varOmega _{T,b}(t). \end{aligned}$$

(9a,b)

The growth velocity potential is set to zero $\varPhi =0$ at the interface $\varGamma _{T,{\mathrm {wb}}}(t)$ and homogeneous Neumann boundary condition $\boldsymbol{\upsilon }\boldsymbol{\cdot }\nabla \varPhi =0$ on the wall $\varGamma _{T,s}$.

For each of the biomass components $\theta _i$ in $\varOmega _{T,b}(t)$, we impose mass conservation (Alpkvist and Klapper 2007)

$$\begin{aligned} \rho _i\partial _t\theta _i+\rho _i\nabla \boldsymbol{\cdot } (\theta _i \varvec{u})=R_i,\quad i\in \lbrace e,a,d\rbrace \quad \text {in }\;\varOmega _{T,b}(t) \end{aligned}$$

(10)

and Neumann condition $\boldsymbol{\nu }\boldsymbol{\cdot }\nabla \theta _i=0$ at the interface $\varGamma _{T,{\mathrm {wb}}}(t)$ and $\boldsymbol{\upsilon }\boldsymbol{\cdot }\nabla \theta _i=0$ on the wall $\varGamma _{T,s}$. The reaction terms for the biomass components are given by

$$\begin{aligned} R_d=k_{\mathrm {res}}\theta _a\rho _a,\quad R_e=-Y_eR_b,\quad R_a=-Y_aR_b-k_{\mathrm {res}}\theta _a\rho _a \quad \text {in }\;\varOmega _{T,b}(t) \end{aligned}$$

(11a,b,c)

where $Y_e$ and $Y_a$ are yield coefficients and $k_{\mathrm {res}}$ is the bacterial decay rate.

The water–biofilm interface changes in time due to changes inside the biofilm and the water flux provoking detachment of components which is known as erosion. Thus, the normal velocity of the interface $\varGamma _{T,{\mathrm {wb}}}(t)$ is given by van Noorden et al. (2010)

$$\begin{aligned} \nu _n=\left\{ \begin{array}{ll} f^{+}(\boldsymbol{\nu }\boldsymbol{\cdot }\varvec{u}), &{}\quad d=\varrho \\ \boldsymbol{\nu }\boldsymbol{\cdot }\varvec{u}+k_{\mathrm {str}}S, &{}\quad 0<d<\varrho \\ 0, &{}\quad d=0 \end{array} \right. \quad {\text {at }}\;\varGamma _{T,{\mathrm {wb}}}(t) \end{aligned}$$

(12)

where $f^{+}(x)=\max (0,x)$. Here, $k_{\mathrm {str}}$ is the stress coefficient and S is the tangential shear stress, given by van Noorden et al. (2010)

$$\begin{aligned} S=||(\mathbb {I}-\boldsymbol{\nu }{\boldsymbol{\nu }}^T)\mu (\nabla \varvec{q}_w+\nabla \varvec{q}_w^T)\boldsymbol{\nu }|| \quad {\text {at }}\;\varGamma _{T,{\mathrm {wb}}}(t). \end{aligned}$$

(13)

Advanced numerical schemes are necessary to solve this mathematical model as it involves a moving interface. When the pore is clogged, the active bacteria keep dying, consuming nutrients and producing EPS which leads to changes in the volume fractions of biomass components. In this model, we ensure that the biofilm–water interface does not overlap by taking the positive cut $f^{+}$ when $d=\varrho$. This pore-scale model can be extended to consider more complex systems. For example, one can add different kinds of nutrients, different active bacteria species in the biofilm or bacterial attachment.

3 Non-dimensional Model

Before seeking an effective model, we bring the mathematical equations to a non-dimensional form. To this aim, we introduce the reference time $t_{{\mathrm {ref}}}$, length $L_{{\mathrm {ref}}}$, radius $\varrho _{{\mathrm {ref}}}$, water velocity $q_{{\mathrm {ref}}}=L_{{\mathrm {ref}}}/t_{{\mathrm {ref}}}$, biomass velocity $u_{{\mathrm {ref}}}$, pressure $p_{{\mathrm {ref}}}$ and concentration $c_{{\mathrm {ref}}}$. The thin tube is characterized by the ratio of its radius to the length $\varepsilon =\varrho _{{\mathrm {ref}}}/L_{{\mathrm {ref}}}$, which is called the dimensionless aspect ratio. We define dimensionless coordinates and time as $\bar{r}=r/\varrho _{{\mathrm {ref}}}, \bar{z}=z/L_{{\mathrm {ref}}}$ and $\bar{t}=t/t_{{\mathrm {ref}}}$. The non-dimensional biofilm height is given by $\bar{d} =d/\varrho _{{\mathrm {ref}}}$. The non-dimensional unit normal (1) is given by $\boldsymbol{\bar{\nu }}(\bar{r},\bar{z})=(1,\varepsilon \partial _{\bar{z}} \bar{d})^T/\sqrt{1+(\varepsilon \partial _{\bar{z}} \bar{d})^2}.$ We notice that a factor of $\varepsilon$ appears in the second component of the non-dimensional unit normal, as a result of the transformation of the coordinates

$$\begin{aligned} \partial _z d= \frac{1}{L_{{\mathrm {ref}}}}\frac{\partial }{\partial \bar{z}}\left( \varrho _{{\mathrm {ref}}} \frac{d}{\varrho _{{\mathrm {ref}}}}\right) = \frac{1}{L_{{\mathrm {ref}}}}\frac{\partial }{\partial \bar{z}}(\varrho _{{\mathrm {ref}}} \bar{d})=\varepsilon \partial _{\bar{z}} \bar{d}. \end{aligned}$$

Note that we have omitted the dependence of the vector variables on $\varphi$ ($\boldsymbol{\bar{\nu }}(\bar{r},\varphi ,\bar{z})=\boldsymbol{\bar{\nu }}(\bar{r},\bar{z})$). This is justified by our assumption of the radial symmetry. The non-dimensional nutrient concentrations and densities are given by $\bar{c}_w=c_w/c_{{\mathrm {ref}}}$, $\bar{c}_b=c_b/c_{{\mathrm {ref}}}$ and $\bar{\rho }_i=\rho _i/c_{{\mathrm {ref}}}$$(i\in \lbrace e,a,d\rbrace )$. The water velocities are given by $\boldsymbol{\bar{q}}_w(\bar{r},\bar{z})=(\bar{q}_{w,\bar{r}},\bar{q}_{w,\bar{z}})^T =(q_{w,r}/(\varepsilon q_{{\mathrm {ref}}}),q_{w,z}/q_{{\mathrm {ref}}})^T$ and $\boldsymbol{\bar{q}}_{b}(\bar{r},\bar{z})=(\bar{q}_{b,\bar{r}},\bar{q}_{b,\bar{z}})^T =(q_{b,r}/(\varepsilon q_{{\mathrm {ref}}}),q_{b,z}/q_{{\mathrm {ref}}})^T$. The biomass velocity is given by $\boldsymbol{\bar{u}}(\bar{r},\bar{z}) =(\bar{u}_{\bar{r}},\bar{u}_{\bar{z}})^T=(u_r/(\varepsilon u_{{\mathrm {ref}}}),u_z/u_{{\mathrm {ref}}})^T$. We assume that the velocities in the radial direction are of the order $\rho _{{\mathrm {ref}}}/t_{{\mathrm {ref}}}$ (see van Noorden et al. 2010). Hence, they scale by $1/\varepsilon$ when compared to the longitudinal velocities. The biomass volume fractions are dimensionless; therefore, in the non-dimensional model we simply define $\bar{\theta }_i=\theta _i, i\in \lbrace w,e,a,d\rbrace$. Finally, the pressures and growth velocity potential become $\bar{p}_w=p_w/p_{{\mathrm {ref}}}$, $\bar{p}_{b} =p_{b}/p_{{\mathrm {ref}}}$, $\bar{\varPhi } =\varPhi /(\varepsilon ^2u_{{\mathrm {ref}}}L_{{\mathrm {ref}}})$. We observe that the growth velocity potential $\varPhi$ is scaled by $1/\varepsilon ^2$ in order to have the biomass velocities in the radial direction of the order $\rho _{{\mathrm {ref}}}/t_{{\mathrm {ref}}}$ (see van Noorden et al. 2010). We define the following dimensionless parameters ${\text {Pe}}=q_{{\mathrm {ref}}}L_{{\mathrm {ref}}}/D$, $\bar{\mu }_n=t_{{\mathrm {ref}}}\mu _{n}$, $\bar{k}_n=k_n/c_{{\mathrm {ref}}}$, $\bar{k}=k/\varrho _{{\mathrm {ref}}}^2$, $\bar{\mu }=\mu L_{{\mathrm {ref}}} q_{{\mathrm {ref}}}/(\varrho _{{\mathrm {ref}}}^2 p_{{\mathrm {ref}}})$, $\bar{k}_{\mathrm {str}}=p_{{\mathrm {ref}}}k_{\mathrm {str}}/u_{{\mathrm {ref}}}$ and $\bar{k}_{\mathrm {res}}=t_{{\mathrm {ref}}}k_{\mathrm {res}}$. The domains and boundaries are scaled accordingly.

In this way, the dimensionless system of equations for the water flux (2–4) is given by

$$\begin{aligned}&\frac{1}{\bar{r}}\partial _{\bar{r}}\left( \bar{r}\bar{q}_{w,\bar{r}}\right) +\partial _{\bar{z}}\bar{q}_{w,\bar{z}}=0\quad \text {in }\;\bar{\varOmega }_{T,w}(\bar{t}),\end{aligned}$$

(14)

$$\begin{aligned}&\bar{\mu }\left[ \frac{1}{\bar{r}}\partial _{\bar{r}}\left( \bar{r}\partial _{\bar{r}}\bar{q}_{w,\bar{r}}\right) +\varepsilon ^2\partial _{\bar{z}}^2 \bar{q}_{w,\bar{r}}-\frac{\bar{q}_{w,\bar{r}}}{\bar{r}^2}\right] =\varepsilon ^{-2}\partial _{\bar{r}} \bar{p}_w\quad \text {in}\;\bar{\varOmega }_{T,w}(\bar{t}),\end{aligned}$$

(15)

$$\begin{aligned}&\bar{\mu }\left[ \frac{1}{\bar{r}}\partial _{\bar{r}}\left( \bar{r}\partial _{\bar{r}}\bar{q}_{w,\bar{z}}\right) +\varepsilon ^2\partial _{\bar{z}}^2 \bar{q}_{w,\bar{z}}\right] =\partial _{\bar{z}} \bar{p}_w\quad \text {in }\;\bar{\varOmega }_{T,w}(\bar{t}),\end{aligned}$$

(16)

$$\begin{aligned}&\frac{1}{\bar{r}}\partial _{\bar{r}}\left( \bar{r}\bar{q}_{b,\bar{r}}\right) +\partial _{\bar{z}}\bar{q}_{b,\bar{z}}=0\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(17)

$$\begin{aligned}&\frac{\bar{\mu }}{\bar{\theta }_w}\left[ \frac{1}{\bar{r}}\partial _{\bar{r}}(\bar{r}\partial _{\bar{r}}\bar{q}_{b,\bar{r}})+\varepsilon ^2\partial _{\bar{z}}^2 \bar{q}_{b,\bar{r}}-\frac{\bar{q}_{b,\bar{r}}}{\bar{r}^2}\right] =\frac{\bar{\mu }}{\bar{k}}\bar{q}_{b,\bar{r}}+\varepsilon ^{-2}\partial _{\bar{r}} \bar{p}_b\quad \text {in}\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(18)

$$\begin{aligned}&\frac{\bar{\mu }}{\bar{\theta }_w}\left[ \frac{1}{\bar{r}}\partial _{\bar{r}}\left( \bar{r}\partial _{\bar{r}}\bar{q}_{b,{\bar{z}}}\right) +\varepsilon ^2\partial _{\bar{z}}^2 \bar{q}_{b,\bar{z}}\right] =\frac{\bar{\mu }}{\bar{k}}\bar{q}_{b,{\bar{z}}}+\partial _{\bar{z}} \bar{p}_b\quad \text {in}\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(19)

$$\begin{aligned}&2\bar{\mu }\partial _{\bar{r}} \bar{q}_{w,\bar{r}}-\varepsilon ^{-2}\bar{p}_w-2\frac{\bar{\mu }}{\bar{\theta }_w}\partial _{\bar{r}} \bar{q}_{b,\bar{r}}+\varepsilon ^{-2}\bar{p}_b=\partial _{\bar{z}} \bar{d}\left[ \frac{\bar{\mu }}{\bar{\theta }_w} \left( \partial _{\bar{r}}\bar{q}_{b,\bar{{z}}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{b,\bar{{r}}}\right) \right. \nonumber \\&\quad \left. -\bar{\mu }\left( \partial _{\bar{r}}\bar{q}_{w,\bar{z}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{w,\bar{r}}\right) \right] \quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(20)

$$\begin{aligned}\bar{\mu }\left( \partial _{\bar{r}}\bar{q}_{w,\bar{z}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{w,\bar{r}}\right) =&\partial _{\bar{z}} \bar{d}\left( 2\varepsilon ^{2}\frac{\bar{\mu }}{\bar{\theta }_w}\partial _{\bar{z}} \bar{q}_{b,\bar{z}} -\bar{p}_b-2\varepsilon ^{2}\bar{\mu }\partial _{\bar{z}} \bar{q}_{w,\bar{z}}+\bar{p}_w\right) \\&\quad+\frac{\bar{\mu }}{\bar{\theta }_w} \left( \partial _{\bar{r}}\bar{q}_{b,\bar{{z}}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{b,\bar{{r}}}\right) \quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(21)

$$\begin{aligned}&(\bar{q}_{w,\bar{r}},\bar{q}_{w,\bar{z}})=(\bar{q}_{b,\bar{r}},\bar{q}_{b,\bar{z}})\quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(22)

$$\begin{aligned}&(\bar{q}_{b,\bar{r}},\bar{q}_{b,\bar{z}})=(0,0)\quad \text {on }\;\bar{\varGamma }_{T,s} \end{aligned}$$

(23)

where (14–16) are the dimensionless Stokes and continuity equations, (17–19) are the dimensionless Brinkman and continuity equations, (20–22) are the dimensionless interface conditions and (23) is the dimensionless condition on the wall.

The dimensionless equations for the transport of nutrients (5–7) in the water and biofilm are given by

$$\begin{aligned}&\partial _{\bar{t}} \bar{c}_w-\frac{1}{{\text {Pe}}}\left[ \frac{\varepsilon ^{-2}}{{\bar{r}}}\partial _{\bar{r}}({\bar{r}}\partial _{\bar{r}} \bar{c}_w)+\partial _{\bar{z}}^2 \bar{c}_w\right] +\frac{1}{{\bar{r}}}\partial _{\bar{r}}(\bar{r}\bar{q}_{w,\bar{r}} \bar{c}_w)+\partial _{\bar{z}}(\bar{q}_{w,\bar{z}} \bar{c}_w)=0\quad \text {in }\;\bar{\varOmega }_{T,w}(\bar{t}),\end{aligned}$$

(24)

$$\begin{aligned}&\partial _{\bar{t}} (\bar{\theta }_w \bar{c}_b)- \frac{\bar{\theta }_w}{{\text {Pe}}}\left[ \frac{\varepsilon ^{-2}}{{\bar{r}}}\partial _{\bar{r}}({\bar{r}}\partial _{\bar{r}} \bar{c}_b)+\partial _{\bar{z}}^2 \bar{c}_b\right] +\frac{1}{{\bar{r}}}\partial _{\bar{r}}(\bar{r}\bar{q}_{b,\bar{r}} \bar{c}_b)+\partial _{\bar{z}}(\bar{q}_{b,\bar{z}} \bar{c}_b)=\bar{R}_b\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(25)

$$\begin{aligned}&\quad -\frac{\varepsilon ^{-2}}{{\text {Pe}}}(\partial _{\bar{r}} \bar{c}_w-\bar{\theta }_w \partial _{\bar{r}} \bar{c}_b)-(\bar{c}_b\bar{q}_{b,\bar{r}}-\bar{c}_w\bar{q}_{w,\bar{r}})+\partial _{\bar{t}} \bar{d}(\bar{\theta }_w\bar{c}_{b}-\bar{c}_w)\nonumber \\&\quad +\frac{\partial _{\bar{z}} \bar{d}}{{\text {Pe}}}(\partial _{\bar{z}} \bar{c}_w-\bar{\theta }_w\partial _{\bar{z}} \bar{c}_b)+\partial _{\bar{z}} \bar{d}(\bar{c}_b\bar{q}_{b,\bar{z}}-\bar{c}_w\bar{q}_{w,\bar{z}})=0\quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(26)

$$\begin{aligned}&\bar{c}_b=\bar{c}_w\quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(27)

$$\begin{aligned}&\partial _{\bar{r}}\bar{c}_b=0\quad \text {on }\;\bar{\varGamma }_{T,s} \end{aligned}$$

(28)

where (24) is the dimensionless transport equation of nutrients in the water domain, (25) is the dimensionless transport equation of nutrients in the biofilm domain, (26–27) are the dimensionless coupling conditions at the interface and (28) is the dimensionless condition on the wall. The dimensionless reaction rate (8) for the consumption of nutrients is given by $\bar{R}_b=-\bar{\mu }_n\bar{\theta }_a\bar{\rho }_a\bar{c}_b/(\bar{k}_n+\bar{c}_b)$.

The equations for the growth velocity potential (9) become

$$\begin{aligned}&\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}\left[ \frac{1}{{\bar{r}}}\partial _{\bar{r}}(\bar{r}\bar{u}_{\bar{r}})+\partial _{\bar{z}}\bar{u}_{\bar{z}}\right] =\bar{\varSigma }\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(29)

$$\begin{aligned}&(\bar{u}_{\bar{r}},\bar{u}_{\bar{z}})=-(\partial _{\bar{r}}\bar{\varPhi },\varepsilon ^2\partial _{\bar{z}}\bar{\varPhi })\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(30)

$$\begin{aligned}&\bar{\varPhi }=0\quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(31)

$$\begin{aligned}&\partial _{\bar{r}}\bar{\varPhi }=0\quad \text {on }\;\bar{\varGamma }_{T,s} \end{aligned}$$

(32)

where (29–30) are the dimensionless equations for the biomass growth velocity potential, (31) is the dimensionless reference potential at the interface and (32) is the dimensionless condition on the wall. We define the dimensionless sum of the biomass reaction terms as $\bar{\varSigma }=(1-\bar{\theta }_w)^{-1}[(Y_e\bar{\rho }_a/\bar{\rho }_e+Y_a)\bar{\mu }_n\bar{\theta }_a\bar{c}_b/(\bar{k}_n+\bar{c}_b)+(\bar{\rho }_a/\bar{\rho }_{d}-1)\bar{k}_{\mathrm {res}}\bar{\theta }_a].$

The equations for the biomass components (10) become

$$\begin{aligned}&\partial _{\bar{t}}\bar{\theta }_e+\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\bar{u}_{\bar{r}}\partial _{\bar{r}}\bar{\theta }_e+\bar{u}_{\bar{z}}\partial _{\bar{z}}\bar{\theta }_e)=Y_e\bar{\mu }_n\bar{\theta }_a\frac{\bar{\rho }_a}{\bar{\rho }_{e}}\frac{\bar{c}_b}{\bar{k}_n+\bar{c}_b}-\bar{\theta }_e\bar{\varSigma }\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(33)

$$\begin{aligned}&\partial _{\bar{t}}\bar{\theta }_a+\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\bar{u}_{\bar{r}}\partial _{\bar{r}}\bar{\theta }_a+\bar{u}_{\bar{z}}\partial _{\bar{z}}\bar{\theta }_a)=Y_a\bar{\mu }_n\bar{\theta }_a\frac{\bar{c}_b}{\bar{k}_n+\bar{c}_b}-\bar{k}_{\mathrm {res}}\bar{\theta }_a-\bar{\theta }_a\bar{\varSigma }\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(34)

$$\begin{aligned}&\partial _{\bar{t}}\bar{\theta }_d+\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\bar{u}_{\bar{r}}\partial _{\bar{r}}\bar{\theta }_d+\bar{u}_{\bar{z}}\partial _{\bar{z}}\bar{\theta }_d)=\bar{k}_{\mathrm {res}}\frac{\bar{\rho }_a}{\bar{\rho }_{d}}\bar{\theta }_a-\bar{\theta }_d\bar{\varSigma }\quad \text {in }\;\bar{\varOmega }_{T,b}(\bar{t}),\end{aligned}$$

(35)

$$\begin{aligned}&-\partial _{\bar{r}}\bar{\theta }_i+\varepsilon \partial _{\bar{z}} \bar{d}\partial _{\bar{z}} \bar{\theta }_i=0\quad i\in \lbrace e,a,d\rbrace \quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}),\end{aligned}$$

(36)

$$\begin{aligned}&\partial _{\bar{r}}\bar{\theta }_i=0\quad i\in \lbrace e,a,d\rbrace \quad \text {on }\;\bar{\varGamma }_{T,s} \end{aligned}$$

(37)

where (33–35) are the dimensionless conservation of mass equations for the biomass components, (36) is the dimensionless condition at the interface and (37) is the dimensionless condition on the wall.

The dimensionless biofilm height (12) is given by

$$\begin{aligned} \partial _{\bar{t}} \bar{d}=\left\{ \begin{array}{ll} f^{-}((-\bar{u}_{{\bar{r}}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}),&{}\quad \bar{d}=1\\ (-\bar{u}_{{\bar{r}}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}-\sqrt{1+(\varepsilon \partial _{\bar{z}} \bar{d})^2}\varepsilon \bar{k}_{\mathrm {str}}\bar{S} ,&{}\quad 0<\bar{d}<1\\ 0,&{}\quad \bar{d}=0\end{array} \right. \quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}) \end{aligned}$$

(38)

where $f^{-}$ is the negative cut ($f^{-}(x):=\min (0,x)$). The dimensionless tangential shear stress (13) is given by

$$\begin{aligned} \bar{S}=||(\mathbb {I}-\boldsymbol{\bar{\nu }}\boldsymbol{\bar{\nu }}^{T})\bar{\mu } (\mathbb {\bar{M}}+\mathbb {\bar{M}}^T)\boldsymbol{\bar{\nu }}||\quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}) \end{aligned}$$

(39)

where the matrix $\mathbb {\bar{M}}$ is given by

$$\begin{aligned} \mathbb {\bar{M}}&= \left( {\begin{array}{cc} \partial _{\bar{r}} \bar{q}_{w,\bar{r}} &{}\quad \varepsilon \partial _{\bar{z}} \bar{q}_{w,\bar{r}} \\ \varepsilon ^{-1}\partial _{\bar{r}} \bar{q}_{w,\bar{z}} &{}\quad \partial _{\bar{z}} \bar{q}_{w,\bar{z}} \end{array} } \right) \quad {\text {at }}\;\bar{\varGamma }_{T,{\mathrm {wb}}}(\bar{t}). \end{aligned}$$

(40)

4 Upscaling

The pore-scale mathematical model describes the biofilm formation in a three-dimensional domain. Under some model assumptions, when the length of the tube is much larger than its radius, it is possible to reduce the dimensionality of the problem from three to one dimension, letting the aspect ratio $\varepsilon$ approach to zero. We perform a formal asymptotic expansion of the variables depending on $\varepsilon$, namely $\bar{p}_w$, $\bar{p}_b$, $\bar{c}_w$, $\bar{c}_b$, $\boldsymbol{\bar{q}}_w$, $\boldsymbol{\bar{q}}_b$, $\boldsymbol{\bar{u}}$, $\bar{\varPhi }$, $\bar{\theta }_w$, $\bar{\theta }_e$, $\bar{\theta }_a$, $\bar{\theta }_d$ and $\bar{d}$. For all except $\bar{d},$ we assume $\bar{\chi }(\varvec{{\bar{r}}},{\bar{t}})=\bar{\chi }_{0}(\varvec{{\bar{r}}},{\bar{t}})+\varepsilon \bar{\chi }_{1}(\varvec{{\bar{r}}},{\bar{t}})+O(\varepsilon ^2)$. The corresponding asymptotic expansion of d is $\bar{d}({\bar{z}},{\bar{t}})=\bar{d}_{0}({\bar{z}},{\bar{t}})+\varepsilon \bar{d}_{1}({\bar{z}},{\bar{t}})+O(\varepsilon ^2)$. In van Noorden et al. (2010), Kumar et al. (2014) and Bringedal et al. (2015), the authors present upscaled models of pore-scale mathematical models for reactive flows. Following the same ideas, we can obtain the corresponding upscaled model in the tube pore geometry.

We define the average water velocity $\langle \bar{q} \rangle$ as the following integral

$$\begin{aligned} \langle \bar{q}\rangle ({\bar{z}},{\bar{t}})= \langle \bar{q}_w\rangle ({\bar{z}},{\bar{t}})+\langle \bar{q}_b\rangle ({\bar{z}},{\bar{t}}) =\frac{1}{\pi }\int _{0}^{2\pi }\left( \int _{0}^{1-\bar{d}_0}q_{w,\bar{z},0} \bar{r}\mathrm{d}{\bar{r}}+\int _{1-\bar{d}_0}^{1}q_{b,\bar{z},0}\bar{r}\mathrm{d}\bar{r}\right) \mathrm{d}\varphi . \end{aligned}$$

(41)

Notice that we divide by the cross-sectional area of the tube. We consider the following spatial regions in the tube:

$$\begin{aligned} \bar{\varXi }_w= & {} \lbrace \boldsymbol{\bar{r}}|\;0\le \bar{r}\le 1-\bar{d}\;\wedge \;0\le \varphi<2\pi \;\wedge \;z_1\le \bar{z} \le z_1+\delta z\rbrace ,\\ \bar{\varXi }_b= & {} \lbrace \boldsymbol{\bar{r}}|\;1-\bar{d}\le \bar{r} \le 1\;\wedge \;0\le \varphi <2\pi \;\wedge \;z_1\le \bar{z} \le z_1+\delta z\rbrace . \end{aligned}$$

These regions are a disk of radius $1-\bar{d}$ and a ring of thickness $\bar{d}$, respectively; both of length $\delta z$. Integrating (14) and (17) over the previous regions and using the Gauss’s theorem, we obtain

$$\begin{aligned} 0= & {} \int _{\bar{\varXi }_w}\bar{\nabla }\boldsymbol{\cdot } \boldsymbol{\bar{q}}_w \mathrm{d}\bar{V}+\int _{\bar{\varXi }_b}\bar{\nabla }\boldsymbol{\cdot } \boldsymbol{\bar{q}}_b \mathrm{d}\bar{V}=2\pi \int _{z_1}^{z_1+\delta z}(1-\bar{d})\boldsymbol{\bar{q}}_{w}\boldsymbol{\cdot }\boldsymbol{\bar{\nu }}\big |_{{\bar{r}}=1-\bar{d}}\mathrm{d}\bar{z}\\&\quad +2\pi \int _{0}^{1-\bar{d}}\left( \bar{q}_{w,\bar{z}}\big |_{{\bar{z}}=z_1+\delta z}-\bar{q}_{w,\bar{z}}\big |_{{\bar{z}}=z_1}\right) \bar{r}\mathrm{d}\bar{r}-2\pi \int _{z_1}^{z_1+\delta z}\left[ (1-\bar{d})\boldsymbol{\bar{q}}_{b}\boldsymbol{\cdot }\boldsymbol{\bar{\nu }}\big |_{{\bar{r}}= 1-\bar{d}}+\boldsymbol{\bar{q}}_{b}\boldsymbol{\cdot }\boldsymbol{\bar{\nu }}\big |_{{\bar{r}}=1}\right] \mathrm{d}\bar{z}\\&\quad +2\pi \int _{1-\bar{d}}^{1}\left( \bar{q}_{b,\bar{z}}\big |_{{\bar{z}}=z_1+\delta z}-\bar{q}_{b,\bar{z}}\big |_{\bar{z}=z_1}\right) \bar{r}\mathrm{d}\bar{r}. \end{aligned}$$

Recalling the no-slip condition for the water flux on the wall (23) and the continuity of fluxes at the interface (22), the previous equation becomes

$$\begin{aligned} \int _{0}^{1-\bar{d}}\left( \bar{q}_{w,\bar{z}}\big |_{{\bar{z}}=z_1+\delta z}-\bar{q}_{w,\bar{z}}\big |_{{\bar{z}}=z_1}\right) \bar{r}\mathrm{d}\bar{r}+\int _{1-\bar{d}}^{1}\left( \bar{q}_{b,\bar{z}}\big |_{{\bar{z}}=z_1+\delta z}-\bar{q}_{b,\bar{z}}\big |_{{\bar{z}}=z_1}\right) \bar{r}\mathrm{d}\bar{r}=0. \end{aligned}$$

Dividing the previous equation by $\delta z$ and in the limit where $\delta z$ approach to zero, we obtain for the lowest order terms in $\varepsilon$

$$\begin{aligned} \partial _{\bar{z}}\langle \bar{q}\rangle =\partial _{\bar{z}}\langle \bar{q}_w\rangle ({\bar{z}},{\bar{t}})+\partial _{\bar{z}}\langle \bar{q}_b\rangle ({\bar{z}},{\bar{t}})=0 \end{aligned}$$

where we use the definition of the average water velocity $\langle \bar{q}\rangle$ (41).

The lowest order terms in the Stokes model (14–16) lead to

$$\begin{aligned} \partial _{\bar{r}}(\bar{r}\bar{q}_{w,\bar{r},0})/\bar{r}+\partial _{\bar{z}}\bar{q}_{w,\bar{z},0}=0,\quad \partial _{\bar{r}} \bar{p}_{w,0}=0,\quad \bar{\mu }\partial _{\bar{r}}({\bar{r}}\partial _{\bar{r}}\bar{q}_{w,\bar{z},0})/\bar{r}=\partial _{\bar{z}} \bar{p}_{w,0}. \end{aligned}$$

(42a,b,c)

From (42b), we conclude that $\bar{p}_{w,0}$ does not depend on the ${\bar{r}}$ coordinate. Analogously, for the Brinkman model (17–19), the lower-order terms in $\varepsilon$ give

$$\begin{aligned} \partial _{\bar{r}}(\bar{r}\bar{q}_{b,\bar{r},0})/\bar{r}+\partial _{\bar{z}}\bar{q}_{b,\bar{z},0}=0,\quad \partial _{\bar{r}} \bar{p}_{b,0}=0,\quad \bar{\mu }\partial _{\bar{r}}({\bar{r}}\partial _{\bar{r}} \bar{q}_{b,\bar{z},0})/(\bar{r}\bar{\theta }_w)-\bar{\mu }\bar{q}_{b,\bar{z},0}/\bar{k}=\partial _{\bar{z}} \bar{p}_{b,0}. \end{aligned}$$

(43a,b,c)

From (43b), we conclude that $\bar{p}_{b,0}$ also does not depend on the ${\bar{r}}$ coordinate. Since neither $\bar{p}_{w,0}$ nor $\bar{p}_{b,0}$ depend on the ${\bar{r}}$ coordinate and from the lowest order terms in (20), we have that $\bar{p}_{w,0}=\bar{p}_{b,0}$ at the biofilm–water interface, and we obtain that $\bar{p}_{w,0}({\bar{z}},{\bar{t}})=\bar{p}_{b,0}({\bar{z}},{\bar{t}})=\bar{p}_0({\bar{z}},{\bar{t}})$. We turn our attention to Eqs. (42c) and (43c). It is possible to find solutions for $q_{w,\bar{z},0}$ and $q_{b,\bar{z},0}$ integrating twice with respect to ${\bar{r}}$ both equations and in addition using the symmetry, interface and boundary conditions (21–23). After integration, we get

$$\begin{aligned} \bar{q}_{w,\bar{z},0}=(\bar{r}^2/4+E )\partial _{\bar{z}}\bar{p}_0/\bar{\mu },\quad \bar{q}_{b,\bar{z},0}=(FJ_0(\xi {\bar{r}})+GY_0(-\xi {\bar{r}})-\bar{k} )\partial _{\bar{z}}\bar{p}_0/\bar{\mu } \end{aligned}$$

(44a,b)

where $\xi = i\sqrt{\bar{\theta }_w/\bar{k}}$, i is the imaginary number and $J_\nu ({\bar{z}})$ and $Y_\nu ({\bar{z}})$ are the Bessel functions of order $\nu$ of first and second kind, respectively (see Olver 2012). The Bessel functions appear naturally when solving elliptic equations in cylindrical coordinates and are widely used in various areas such as nuclear physics, acoustics and hydrodynamics (Korenev 2002). The coefficients appearing in (44) are

$$\begin{aligned} E= & {} \frac{2w\bar{\theta }_w[J_0(\xi )Y_0(-\xi w)-J_0(\xi w)Y_0(-\xi )]+\xi \bar{k}[J_0(\xi w)Y_1(-\xi w)+Y_0(-\xi w)J_1(\xi w)]}{4[\xi J_0(\xi )Y_1(-\xi w)+\xi Y_0(-\xi )J_1(\xi w)]}\\&\quad -\frac{\xi (4\bar{k}+w^2)[J_0(\xi )Y_1(-\xi w)+Y_0(-\xi )J_1(\xi w)]}{4[\xi J_0(\xi )Y_1(-\xi w)+\xi Y_0(-\xi )J_1(\xi w)]},\\ F= & {} \frac{2\bar{k}\xi Y_1(-\xi w)+w\bar{\theta }_wY_0(-\xi )}{2[\xi J_0(\xi )Y_1(-\xi w)+\xi Y_0(-\xi )J_1(\xi w)]},\quad G=\frac{2\bar{k}\xi J_1(\xi w)+w\bar{\theta }_wJ_0(\xi )}{2[\xi J_0(\xi )Y_1(-\xi w)+\xi Y_0(-\xi )J_1(\xi w)]} \end{aligned}$$

where $w=1-\bar{d}_0$. We remark that most of the mathematical commercial software includes Bessel functions; therefore, it is easy to use the above expression. Although the Bessel functions are evaluated with complex numbers, both fluxes $q_{w,{\bar{z}},0}$ and $q_{b,\bar{z},0}$ are real numbers.

To obtain the water velocity defined in (41), we integrate (44) as follows

$$\begin{aligned} \langle \bar{q}\rangle&= {} \frac{\partial _{\bar{z}}\bar{p}_0}{\pi \bar{\mu }} \int _{0}^{2\pi }\left\{ \int _{0}^{1-\bar{d}_0}[\bar{r}^2/4+E]\bar{r}\mathrm{d}\bar{r} +\int _{1-\bar{d}_0}^{1}\left[ FJ_0\left( \bar{r}\xi \right) +GY_0\left( -\bar{r}\xi \right) -\bar{k}\right] \bar{r}\mathrm{d}\bar{r}\right\} \mathrm{d}\varphi \\&= {} 2\lbrace w^4/16+Ew^2/2-\xi ^{-1}[FY_1(-\xi )-GJ_1(\xi )-FwY_1(-w\xi )+GwJ_1(w\xi )]\\&\quad -\bar{k}(1-w^2)/2\rbrace \partial _{\bar{z}} \bar{p}_0/\bar{\mu }\\&= {} -\kappa _T(\bar{d}_0)\partial _{\bar{z}} p_0/\bar{\mu }. \end{aligned}$$

This gives the Darcy’s law $\langle \bar{q}\rangle =-\kappa _T(\bar{d}_0)\partial _{\bar{z}} p_0/\bar{\mu }$, where $\kappa _T(\bar{d}_0)$ is the effective permeability given by

$$\begin{aligned} \kappa _T(\bar{d}_0)=-\frac{w^4}{8}-w^2E+\frac{2[FY_1(-\xi )-GJ_1(\xi )-FwY_1(-w\xi )+GwJ_1(w\xi )]}{\xi }+\bar{k}(1-w^2) \end{aligned}$$

which changes according to the biofilm height ($w=1-\bar{d}_0$).

The growth velocity potential equations (29) and (30) for the lower-order terms in $\varepsilon$ are

$$\begin{aligned} u_{{\mathrm {ref}}} [\partial _{\bar{r}}(\bar{r}\bar{u}_{\bar{r},0})/\bar{r}+\partial _{\bar{z}}\bar{u}_{\bar{z},0}]/q_{{\mathrm {ref}}}=\bar{\varSigma }_0,\quad \bar{u}_{\bar{r},0}=-\partial _{\bar{r}}\bar{\varPhi }_{0},\quad \bar{u}_{\bar{z},0}=0 \end{aligned}$$

(45a,b,c)

where the boundary conditions for the interface (31) become $\bar{\varPhi }_{0}=0$ and wall (32) becomes $\partial _{\bar{r}} \bar{\varPhi }_{0}=0$.

In dimensionless form, the volume fraction equations (33–35) are

$$\begin{aligned} \partial _{\bar{t}}\bar{\theta }_i+u_{{\mathrm {ref}}}(\bar{u}_{\bar{r}}\partial _{\bar{r}}\bar{\theta }_i+\bar{u}_{\bar{z}}\partial _{\bar{z}}\bar{\theta }_i)/q_{{\mathrm {ref}}}=\bar{R}_i-\bar{\theta }_i\bar{\varSigma },\quad i=\lbrace e,a,d\rbrace . \end{aligned}$$

(46)

We focus on biofilms where the biomass components change slightly along the ${\bar{r}}$ direction, resulting in the approximation $\bar{\theta }_{i,0}({\bar{r}},{\bar{z}},{\bar{t}})=\bar{\theta }_{i,0}({\bar{z}},{\bar{t}})$. Using (45c), the lower-order terms in (46) are $\partial _{\bar{t}}\bar{\theta }_{i,0}=\bar{R}_{i,0}-\bar{\theta }_{i,0}\bar{\varSigma }_0$.

Integrating (45a) over ${\bar{r}}$ ($\bar{u}_{\bar{z},0}=0$ from (45c)), we get an expression for $\bar{u}_{\bar{r},0}$ which cannot fulfill both conditions at the same time: $\bar{u}_{\bar{r},0}=0$ on the wall and $\bar{u}_{\bar{r},0}<\infty$ when ${\bar{r}}=0$. For the channel, the solution is a function such that it fulfills the homogeneous Dirichlet condition on the wall and is equal to $(q_{{\mathrm {ref}}}/u_{{\mathrm {ref}}})\bar{\varSigma }_0$ when the channel is clogged. Then, we consider the following expression for the radial biomass velocity

$$\begin{aligned} \bar{u}_{\bar{r},0}=\frac{q_{{\mathrm {ref}}}}{u_{{\mathrm {ref}}}}\bar{\varSigma }_0({\bar{r}}^2-1) \end{aligned}$$

(47)

where the squared dependence on the radius honors the radial geometry, as it is shown for the nutrients below.

For the nutrients, integrating (24) and (25) over ${\bar{r}}$ and $\varphi$ yields

$$\begin{aligned}&2\pi \int _{0}^{1-\bar{d}}\left\{ \partial _{\bar{t}} \bar{c}_w-\frac{1}{{\text {Pe}}}\left[ \varepsilon ^{-2}\frac{1}{{\bar{r}}}\partial _{\bar{r}} ({\bar{r}}\partial _{\bar{r}} \bar{c}_w)+\partial _{\bar{z}}^2 \bar{c}_w\right] +\frac{1}{{\bar{r}}}\partial _{\bar{r}}(\bar{r}\bar{q}_{w,\bar{r}} \bar{c}_w)+\partial _{\bar{z}}(\bar{q}_{w,\bar{z}} \bar{c}_w)\right\} \bar{r}\mathrm{d}\bar{r}=0,\\&2\pi \int _{1-\bar{d}}^{1}\left\{ \partial _{\bar{t}} (\bar{\theta }_w \bar{c}_b)- \frac{\bar{\theta }_w}{{\text {Pe}}}\left[ \varepsilon ^{-2}\frac{1}{{\bar{r}}}\partial _{\bar{r}} ({\bar{r}}\partial _{\bar{r}} \bar{c}_b)+\partial _{\bar{z}}^2 \bar{c}_b\right] +\frac{1}{{\bar{r}}}\partial _{\bar{r}}(\bar{r}\bar{q}_{b,\bar{r}} \bar{c}_b)+\partial _{\bar{z}}(\bar{q}_{b,\bar{z}} \bar{c}_b)\right. \\&\quad \left. +\bar{\mu }_n\bar{\theta }_a\bar{\rho }_a \frac{\bar{c}_b}{\bar{k}_n+\bar{c}_b}\right\} \bar{r}\mathrm{d}\bar{r}=0. \end{aligned}$$

Interchanging the integration and the differentiation operators, these equations become

$$\begin{aligned}&\partial _{\bar{t}}\left( \int _{0}^{1-\bar{d}} \bar{c}_w\bar{r}\mathrm{d}\bar{r}\right) +\partial _{\bar{t}}\bar{d} (\bar{r}\bar{c}_w)\big |_{{\bar{r}}=1-\bar{d}} -\partial _{\bar{z}}\left[ \int _{0}^{1-\bar{d}}\left( \frac{1}{{\text {Pe}}}\partial _{\bar{z}} \bar{c}_w-\bar{q}_{w,\bar{z}}\bar{c}_w\right) \bar{r}\mathrm{d}\bar{r}\right] \\&\quad -\partial _{\bar{z}}\bar{d}\left( \frac{1}{{\text {Pe}}}{\bar{r}}\partial _{\bar{z}} \bar{c}_w-\bar{r}\bar{q}_{w,\bar{z}}\bar{c}_w\right) \bigg |_{{\bar{r}}=1-\bar{d}}-\left( \frac{1}{\varepsilon ^2{\text {Pe}}}{\bar{r}}\partial _{\bar{r}} \bar{c}_w-\bar{r}\bar{q}_{w,\bar{r}}\bar{c}_w \right) \bigg |_{{\bar{r}}=1-\bar{d}}=0,\\&\partial _{\bar{t}}\left( \int _{1-\bar{d}}^{1}\bar{\theta }_w \bar{c}_{b}\bar{r}\mathrm{d}\bar{r}\right) -\bar{\theta }_w\partial _{\bar{t}}\bar{d} (\bar{c}_b{\bar{r}})\big |_{{\bar{r}}=1-\bar{d}}-\partial _{\bar{z}}\left[ \int _{1-\bar{d}}^{1}\left( \frac{\bar{\theta }_w}{{\text {Pe}}}\partial _{\bar{z}} \bar{c}_b-\bar{q}_{b,\bar{z}}\bar{c}_b\right) \bar{r}\mathrm{d}\bar{r}\right] \\&\quad +\partial _{\bar{z}}\bar{d}\left( \frac{\bar{\theta }_w}{{\text {Pe}}}{\bar{r}}\partial _{\bar{z}} \bar{c}_b-\bar{r}\bar{q}_{b,\bar{z}}\bar{c}_b\right) \bigg |_{{\bar{r}}=1-\bar{d}}-\left( \frac{\bar{\theta }_w}{\varepsilon ^2{\text {Pe}}}{\bar{r}}\partial _{\bar{r}} \bar{c}_b-\bar{r}\bar{q}_{b,\bar{r}}\bar{c}_b \right) \bigg |_{{\bar{r}}=1}\\&\quad +\left( \frac{\bar{\theta }_w}{\varepsilon ^2{\text {Pe}}}{\bar{r}}\partial _{\bar{r}} \bar{c}_b-\bar{r}\bar{q}_{b,\bar{r}}\bar{c}_b \right) \bigg |_{{\bar{r}}=1-\bar{d}}+\bar{\mu }_n\bar{\rho }_a\bar{\theta }_a\int _{1-\bar{d}}^{1} \frac{\bar{c}_b}{\bar{k}_n+\bar{c}_b}\bar{r}\mathrm{d}\bar{r}=0. \end{aligned}$$

The lower-order terms in the equations for the conservation of nutrients (24) and (25) are $\partial _{\bar{r}}( {\bar{r}} \partial _{\bar{r}} \bar{c}_{w,0})=0$ and $\partial _{\bar{r}}({\bar{r}} \partial _{\bar{r}} \bar{c}_{b,0})=0$, respectively. The interface coupling condition (27) becomes $\bar{c}_{w,0}=\bar{c}_{b,0},$ while the boundary condition on the wall (28) becomes $\partial _{\bar{r}}\bar{c}_{b,0}=0$. From these equations, we conclude that $\bar{c}_{w,0}$ and $\bar{c}_{b,0}$ do not depend on r, yielding $\bar{c}_{w,0}({\bar{z}},{\bar{t}})=\bar{c}_{b,0}({\bar{z}},{\bar{t}})=\bar{c}_0({\bar{z}},{\bar{t}})$. Then, using the aforementioned results, the equations for the nutrients can be written as

$$\begin{aligned}&\frac{1}{2}\partial _{\bar{t}}[\bar{c}_0(1-\bar{d}_0)^2]-\partial _{\bar{z}}\left[ \frac{(1-\bar{d}_0)^2}{2{\text {Pe}}}\partial _{\bar{z}} \bar{c}_0\right] +\partial _{\bar{z}}\left( \bar{c}_0\int _{0}^{1-\bar{d}_0}\bar{q}_{w,\bar{r},0}\bar{r}\mathrm{d}\bar{r}\right) =0,\\&\frac{1}{2}\partial _{\bar{t}}\lbrace \bar{\theta }_w\bar{c}_{0}[1-(1-\bar{d}_0)^2]\rbrace -\partial _{\bar{z}}\left[ \frac{1-(1-\bar{d}_0)^2}{2{\text {Pe}}}\bar{\theta }_w\partial _{\bar{z}} \bar{c}_0\right] +\partial _{\bar{z}}\left( \bar{c}_0\int _{1-\bar{d}_0}^{1}\bar{q}_{b,\bar{z},0}\bar{r}\mathrm{d}\bar{r}\right) \\&\quad +\frac{1-(1-\bar{d}_0)^2}{2}\bar{\mu }_n\bar{\rho }_a\bar{\theta }_{a,0}\frac{\bar{c}_0}{\bar{k}_n+\bar{c}_{0}}=0 \end{aligned}$$

where we use the interface condition (26). Then, adding both previous equations we finally obtain

$$\begin{aligned} \partial _{\bar{t}}[\bar{c}_0\varTheta _T(\bar{d}_0,\bar{\theta }_w)]+\partial _{\bar{z}}\left[ \bar{c}_0\langle \bar{q} \rangle - \frac{\varTheta _T(\bar{d}_0,\bar{\theta }_w)}{{\text {Pe}}}\partial _{\bar{z}}\bar{c}_0\right] =-[1-(1-\bar{d}_0)^2]\bar{\mu }_n\bar{\theta }_{a,0}\bar{\rho }_a\frac{\bar{c}_0}{\bar{k}_n+\bar{c}_0} \end{aligned}$$

where we define $\varTheta _T(\bar{d}_0,\bar{\theta }_w)$ as

$$\begin{aligned} \varTheta _T(\bar{d}_0,\bar{\theta }_w)=(1-\bar{d}_0)^2+\bar{\theta }_w[1-(1-\bar{d}_0)^2]. \end{aligned}$$

We focus on the water–biofilm interface (38):

$$\begin{aligned} \partial _{\bar{t}} \bar{d}=\left\{ \begin{array}{ll} f^{-}(u_{{\mathrm {ref}}}(-\bar{u}_{\bar{r}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})/q_{{\mathrm {ref}}}),&{}\quad \bar{d}=1,\\ u_{{\mathrm {ref}}}(-\bar{u}_{\bar{r}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})/q_{{\mathrm {ref}}}-\sqrt{1+(\varepsilon \partial _{\bar{z}} \bar{d})^2}\varepsilon \bar{k}_{\mathrm {str}}\bar{S},&{}\quad 0<\bar{d}<1,\\ 0,&{}\quad \bar{d}=0.\end{array}\right. \end{aligned}$$

(48)

Following van Noorden et al. (2010), we regularize the formulation of (48). First, we let $H_{0}$ and $H_{1}$ be the set-valued Heaviside graphs

$$\begin{aligned} H_{0}(\bar{d})=\left\{ \begin{array}{ll} \lbrace 0 \rbrace , &{}\quad \bar{d}<0,\\ {[}0,1] , &{}\quad \bar{d}=0,\\ \lbrace 1 \rbrace , &{}\quad \bar{d}>0, \end{array}\right. \quad H_{1}(\bar{d})=\left\{ \begin{array}{ll} \lbrace 1 \rbrace , &{}\quad \bar{d}<1,\\ {[}0,1], &{}\quad \bar{d}=1,\\ \lbrace 0 \rbrace , &{}\quad \bar{d}>1, \end{array}\right. \end{aligned}$$

(49)

where we set $H_0(\bar{d}=0)=0$ and $H_{1}(\bar{d}=1)=0$. Observe that this choice guarantees that $\partial _{\bar{t}} \bar{d}$ never becomes negative whenever $\bar{d}=0$ and positive when $\bar{d}=1$. Then, (48) is written as

$$\begin{aligned}&\partial _{\bar{t}} \bar{d}\in H_0(\bar{d})H_1(\bar{d})\left\{ u_{{\mathrm {ref}}}(-\bar{u}_{\bar{r}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})/q_{{\mathrm {ref}}}-\sqrt{1+(\varepsilon \partial _{\bar{z}} \bar{d})^2}\varepsilon \bar{k}_{\mathrm {str}}\bar{\mu } ||(\mathbb {I}-\boldsymbol{\bar{\nu }}\boldsymbol{\bar{\nu }}^{T})(\mathbb {\bar{M}}+\mathbb {\bar{M}}^T)\boldsymbol{\bar{\nu }}|| \right\} \nonumber \\&\quad +[1-H_1(\bar{d})]f^{-}(u_{{\mathrm {ref}}}(-\bar{u}_{\bar{r}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})/q_{{\mathrm {ref}}}). \end{aligned}$$

(50)

For practical calculations, the multi-valued functions are replaced by regularized Heaviside functions, defined by

$$\begin{aligned} H_{\delta ,0}(\bar{d})=\left\{ \begin{array}{ll} 0, &{}\quad \bar{d}<0,\\ \bar{d}/\delta , &{}\quad \bar{d}\in [0,\delta ],\\ 1, &{}\quad \bar{d}>\delta , \end{array}\right. \quad H_{\delta ,1}(\bar{d})=\left\{ \begin{array}{ll} 1, &{}\quad \bar{d}<1,\\ (1+\delta -\bar{d})/\delta , &{}\quad \bar{d}\in [1,1+\delta ],\\ 0, &{}\quad \bar{d}>1+\delta , \end{array}\right. \end{aligned}$$

(51)

where $\delta$ is a small regularization parameter. Then, we can write (50) as

$$\begin{aligned} \partial _{\bar{t}} \bar{d}= & {} H_{\delta ,0}(\bar{d})H_{\delta ,1}(\bar{d})u_{{\mathrm {ref}}}(-\bar{u}_{\bar{r}}-\partial _{\bar{z}}\bar{d} \bar{u}_{\bar{z}})/q_{{\mathrm {ref}}}+[1-H_{\delta ,1}(\bar{d})]f^{-}(u_{{\mathrm {ref}}}(-\bar{u}_{\bar{r}}-\partial _{\bar{z}}\bar{d}\bar{u}_{\bar{z}})/q_{{\mathrm {ref}}})\nonumber \\&\quad -H_{\delta ,0}(\bar{d})H_{\delta ,1}(\bar{d})\sqrt{1+(\varepsilon \partial _{\bar{z}} \bar{d})^2}\varepsilon \bar{k}_{\mathrm {str}}\bar{\mu } ||(\mathbb {I}-\boldsymbol{\bar{\nu }}\boldsymbol{\bar{\nu }}^{T})(\mathbb {\bar{M}}+\mathbb {\bar{M}}^T)\boldsymbol{\bar{\nu }}||. \end{aligned}$$

(52)

Using (39–40, 45c, 47) for the lower-order terms, we have

$$\begin{aligned} \partial _{\bar{t}} \bar{d}_0= H_{\delta ,0}(\bar{d}_0)H_{\delta ,1}(\bar{d}_0)\lbrace [1-(1-\bar{d}_0)^2]\bar{\varSigma }_0-\bar{k}_{\mathrm {str}}\bar{\mu } |\partial _{\bar{r}}\bar{q}_{w,\bar{z},0}|\rbrace +[1-H_{\delta ,1}(\bar{d}_0)]f^{-}(\bar{\varSigma }_0). \end{aligned}$$

(53)

Using (44a), we obtain

$$\begin{aligned} \partial _{\bar{t}} \bar{d}_0= H_{\delta ,0}(\bar{d}_0)H_{\delta ,1}(\bar{d}_0)\lbrace [1-(1-\bar{d}_0)^2]\bar{\varSigma }_0-\bar{k}_{\mathrm {str}}(1-\bar{d}_0)|\partial _{\bar{z}}\bar{p}_0|/2\rbrace +[1-H_{\delta ,1}(\bar{d}_0)]f^{-}(\bar{\varSigma }_0). \end{aligned}$$

The original model is obtained when passing $\delta$ to zero (van Duijn and Pop 2004), obtaining finally

$$\begin{aligned}\partial _{\bar{t}} \bar{d}_0= \left\{ \begin{array}{ll} f^{-}(\bar{\varSigma }_0), &{}\quad \bar{d}_0=1,\\ -\bar{k}_{\mathrm {str}}(1-\bar{d}_0)|\partial _{\bar{z}}{\bar{p}_0}|/2+[1-(1-\bar{d}_0)^2]\bar{\varSigma }_0, &{}\quad 0<\bar{d}_0<1,\\ 0, &{}\quad \bar{d}_0=0.\\ \end{array}\right. \end{aligned}$$

5 Discussion and Comparison with Other Biofilm Models

The extension from a channel (tube) to a porous medium is done by considering a stack of channels (tubes) of void space and solid material (van Noorden et al. 2010), where we denote by $\phi$ the porosity of the porous medium. As Steefel and Lichtner (1994) and van Noorden et al. (2010), we assume that all tubes have the same diameter and are equally separated. Therefore, multiplying the upscaled model equations by $\phi$, the corresponding core-scale mathematical models are obtained. Table 1 shows the core-scale equations of the van Noorden model (van Noorden et al. 2010), the porous medium formed by channels and the porous medium formed by tubes, where $v=\phi q$ is the Darcy velocity. The van Noorden model accounts for water flux, transport of nutrients and bacteria, bacterial attachment, detachment of biomass due to erosion, growth of biomass due to nutrient consumption and death of bacteria. In our model, we do not include transport of bacteria and bacterial attachment. The reason is because the pore-scale model was built based on laboratory experiments, where only nutrients were continuously injected after inoculation of bacteria and biofilm re-attachment was not observed (Landa-Marbán et al. 2019). For the details of the upscaling on the thin channel domain, see “Appendix.”

Table 1 Core-scale equations for the $^\mathrm{a}$channel, $^\mathrm{b}$tube and $^\mathrm{c}$van Noorden models

From Table 1, we observe that for the Darcy flow, the permeability is different for the three models. A discussion of these relations is given below in this section. We observe that the channel and tube models include the effects of the biofilm porosity and thickness on the transport of nutrients. For the van Noorden model, the nutrient consumption depends on the biofilm height while for the channel and tube model, the nutrient consumption also depends on the volume fraction of active bacteria. Comparing the tube and channel model, we observe a different function of the biofilm height, due to the cylindrical geometry. For the biofilm height, the difference between the van Noorden and channel model is on the $\varSigma$ term, where for the van Noorden model the total sum of reactions accounts for bacterial reproduction and decay, while in the channel structure it also accounts for EPS. Finally, for the bacterial, EPS and dead bacterial volume fractions, the model equations are the same for the channel and tube models, while for the van Noorden model the active bacterial volume fraction is constant with value 1.

In van Noorden et al. (2010), the authors compared their upscaled model with a well-known macroscale model by Taylor and Jaffe (1990), where a mathematical model for an impermeable single-species biofilm including flow, transport and reactions is built. We compare the two derived upscaled models with a macroscale model by Chen-Charpentier et al. (2009), where a mathematical model for impermeable multi-species biofilm including water flow, transport of nutrients and reactions is built (Table 2). In this model, the authors considered a biofilm formed by two bacterial species which consume nutrients, reproduce and die. The porosity of the core decreases as the biofilm grows which decreases the permeability of the core.

Table 2 Core-scale equations for the model comparison (Chen-Charpentier et al. 2009)

In Table 2, K is the permeability, $\theta _B$, $\mu _B$, $k_B$, $\theta _K$, $\mu _K$ and $k_K$ are the volume fractions, maximum rates of nutrient utilization and Monod-half nutrient velocity coefficients of the contaminant-degrading microbe and the strong biofilm-forming microbe, respectively, $\phi _O$ and $K_O$ the clean surface porosity and initial permeability, respectively, and $\eta$ an experimentally determined parameter. In Chen-Charpentier et al. (2009), the porosity decreases as the component concentrations increase. In our models, the porosity in the porous medium decreases as the biofilm height increases. However, in Chen-Charpentier et al. (2009) the authors do not include the detachment effects. The permeability in both tube and channel models has different functions as a result of the different geometries and also because of the water flow inside the biofilm. Notice that there is a quartic function of the biofilm height in one of the permeability terms in the porous medium formed by tubes, as proposed in Suchomel et al. (1998) and Mostafa and van Geel (2007). Unlike the equation for the transport of nutrients in the Chen-Charpentier et al. (2009) model, the channel and tube models include the effects of the biofilm porosity and thickness.

Porosity–permeability relations for evolving pore space is an active research field (see Hommel et al. (2018) for a review of these relations and Schulz (2019b) for a recent study providing porosity–permeability relations depending only on the underlying pore geometry). Thullner et al. (2002) present the following relation which includes the biofilm permeability k

$$\begin{aligned} K=K_O\left[ \left( \frac{\phi -\phi _{\mathrm {crit}}}{\phi _O-\phi _{\mathrm {crit}}}\right) ^\eta +k\right] \frac{1}{1+k} \end{aligned}$$

(54)

where $\phi _{\mathrm {crit}}$ is the critical porosity at which the permeability becomes zero. Vandevivere (1995) proposed the following relation of permeability and porosity for a plugging model

$$\begin{aligned} K=K_O[\exp (-0.5(B/B_c)^2)]\left( \frac{\phi }{\phi _O}\right) ^2+[1-\exp (-0.5(B/B_c)^2)]\frac{k}{1-[(1-k/K_O)\phi /\phi _O]} \end{aligned}$$

(55)

where B is a relative porosity given by $B=1-\phi /\phi _O$ and $B_c$ is the critical point where biofilm begins to detach and form plugs. Figure 3 shows our derived porosity–permeability relations, the one derived by van Noorden and the two proposed relations by Thullner and Vandevivere for different values of biofilm permeability. The values of parameters are $\phi _{\mathrm {crit}}=0$, $\eta =1.76$, $B_c=0.1$ (Hommel et al. 2018) and $\theta _w=0.1$. For a biofilm with high permeability $k=10^{-1}$, we observe a faster reduction in permeability for Vandevivere. As the biofilm permeability k decreases, we observe that the van Noorden et al. (2010) model represents the limit case in the channel model for impermeable biofilms. In general, we observe different behaviors of the relations as the porosity decreases.

Fig. 3

Ratio of initial to reduce permeability of different porosity–permeability relations for two different biofilm permeability values k

We perform numerical simulations considering both effective models (channel and tube) to compare the biofilm height over time. We consider two different porous media of length $L=0.1$ m: The first one has pores formed by thin channels of height $2l=0.2$ mm and the second ones with tubes of diameter $2\varrho =0.2$ mm. For the inlet boundary, we set $p_i=2$ Pa. The injected nutrient concentration is $c_i=1\,{\text {kg m}}{}^{-3}$. The porosity $\varPhi$ is set to 0.4. Recalling that biofilms are mostly composed by water, we set the water volume fraction in the biofilm equal to 90%. We set the initial EPS and active bacterial volume fraction equal to 5%; thus, the initial dead bacterial volume fraction is 0. In Table 3, the values of parameters for the numerical simulations are presented.

Table 3 Model parameters for the numerical studies

We implement the model equations in the commercial software COMSOL Multiphysics (COMSOL 5.2a, Comsol Inc, Burlington, MA, www.comsol.com). A decoupled finite element algorithm is used to solve the mathematical model equations. First, we solve for the pressure and concentration. Then, we compute the volume fractions and biofilm height. We iterate between both steps until the difference between successive values of the solution drops below a given tolerance $\zeta$. We perform numerical simulations and we compare the results of the two upscaled mathematical models.

To check if there is a correspondence between the pore-scale and upscaled models as $\varepsilon$ is close to zero, numerical simulations can be done for both models to compare the average solution of one of the variables. Figure 4 compares the upscaled model with the pore-scale model in the channel for different values of $\varepsilon$, where the percentage of biofilm on the whole domain is plotted over time. We called this coverage area a and for the channel and tube is given by

$$\begin{aligned} a_C(t)=\left[ \frac{1}{lL}\int \limits _0^L d(z,t)\mathrm{d}z\right] 100,\quad a_T(t)=\left[ 1-\frac{1}{\varrho ^2 L}\int \limits _0^L(\varrho -d(z,t))^2\mathrm{d}z\right] 100, \end{aligned}$$

(56)

respectively.

For all numerical simulations, we fix the value of the height of the channel 2l, where we set the initial biofilm height as $d=l/5$. Then, the length of the channel is changed accordingly to match the value of $\varepsilon$. We observe that the coverage area in the pore-scale simulations approaches the one computed from the upscaled model as $\varepsilon$ gets smaller.

Fig. 4

Percentage of biofilm coverage area over time for the upscaled model and for decreasing values of epsilon

Figure 5a shows the biofilm height along the length for both porous media for an injected nutrient concentration of $c_i=0.1\,{\text {kg m}}^{-3}$$(c_i/k_n=10^3)$. Initially, the left part ($0<z<L/2$) has a biofilm height of $d=l/2$ ($d=\varrho /2$ for the tubular pores) while the right part ($L>z>L/2$) has a height of $d=l/4$ ($d=\varrho /4$ for the tubular pores). This initial condition is given to study the biofilm development after clogging. We observe that the biofilm keeps growing even though the left part of the pore is clogged. This result cannot be observed using the van Noorden model because the water flux stops once the channel is clogged. Figure 5b shows the biofilm coverage area for different ratios of injected nutrients and Monod-half nutrient velocity coefficient. Initially, the biofilm height is $d=0.1l$ for the tubular pores and $d=0.19l$ for the channel pores. This initial condition is given to study the biofilm development in both porous media for the same initial biofilm coverage area. We observe that the biofilm grows faster in the tubes when we inject enough nutrients and it grows faster in the channels when we lower the injected nutrient concentration. To give a physical explanation of this result, let us consider the case when the biofilm thickness is half value of the aperture ($d=0.5$). Then, 50% of the cross-sectional area is biofilm for the channel while 75% for the tube. This implies that in the tube, the biofilm needs to consume more nutrients to have this thickness in comparison with the channel.

Fig. 5

Biofilm height (a) and coverage area (b) in the porous medium formed by channels and tubes

6 Conclusions

In this work, we upscale a mathematical model for permeable biofilm considering a thin channel and tubular pore geometries. The upscaled models differ mainly in the effective permeability terms which are functions of the biofilm height. As $\varepsilon$ gets smaller, we obtain that the percentage of biofilm coverage area over time predicted by the pore-scale model approaches the one obtained using the effective equations, which shows a correspondence between both models. After comparing with the model proposed by van Noorden et al. (2010), it is possible to derive this model as a particular case of the channel model. The derived upscaled models and the Chen-Charpentier et al. (2009) model are very similar. In this manner, the upscaling provides additional support for this model. The numerical simulations show a faster increase in coverage area in the porous medium formed by tubes than the one formed by channels when a large nutrient concentration is injected ($c_i/k_n=10^4$). These two upscaled models could be used to model porous media where the geometries of the fractures are similar to thin channels or tubes. To validate the core-scale upscaled models, designed laboratory experiments are necessary which is the subject of our future research.

Appendix: Upscaling of the Mathematical Model in a Thin Channel

In Sect. 4, we show with details how to obtain the upscaled model equations in a tube. Following the same ideas, in this “Appendix” we show how to upscale the model equations in a channel. We consider a thin channel with height 2l, width w and length L. When the width is much smaller than the height, experiments show that the growing of the biofilm occurs only in the upper and lower walls along the channel (Liu et al. 2019). Therefore, we can model the biofilm in the thin channel in a two-dimensional domain. Figure 6 shows the different domains, boundaries and interface in the rectangular geometry.

Fig. 6

Pore of length L, height 2l and width w in Cartesian coordinates

To achieve non-dimensional quantities, we use the reference values defined in Sect. 4 ($t_{{\mathrm {ref}}}$, $L_{{\mathrm {ref}}}$, $q_{{\mathrm {ref}}}$, $u_{{\mathrm {ref}}}$, $p_{{\mathrm {ref}}}$ and $c_{{\mathrm {ref}}}$), where we consider the height of the channel $l_{{\mathrm {ref}}}$ instead of the radius of the tube $\varrho _{{\mathrm {ref}}}$. We define dimensionless coordinates and time as $\tilde{y}=y/l_{{\mathrm {ref}}}, \tilde{z}=z/L_{{\mathrm {ref}}}$ and $\tilde{t}=t/t_{{\mathrm {ref}}}$. The thin channel is characterized by the ratio of its height to the length $\epsilon =l_{{\mathrm {ref}}}/L_{{\mathrm {ref}}}$. All dimensionless variables and quantities are analogously defined as in Sect. 3, where we use $l_{{\mathrm {ref}}}$ instead of $\varrho _{{\mathrm {ref}}}$ and we denote the dimensionless variables with $\;\tilde{}\;$ instead of $\;\bar{}$.

The dimensionless system of equations for the water flux is given by

$$\begin{aligned}&\partial _{\tilde{y}}\tilde{q}_{w,\tilde{y}}+\partial _{\tilde{z}}\tilde{q}_{w,\tilde{z}}=0\quad \text {in }\;\tilde{\varOmega }_{C,w}(\tilde{t}), \end{aligned}$$

(57)

$$\begin{aligned}&\tilde{\mu }(\epsilon ^2\partial _{\tilde{z}}^2 \tilde{q}_{w,\tilde{y}}+\partial _{\tilde{y}}^2 \tilde{q}_{w,\tilde{y}})=\epsilon ^{-2}\partial _{\tilde{y}} \tilde{p}_w\quad \text {in }\;\tilde{\varOmega }_{C,w}(\tilde{t}), \end{aligned}$$

(58)

$$\begin{aligned}&\tilde{\mu }(\epsilon ^2\partial _{\tilde{z}}^2 \tilde{q}_{w,\tilde{z}}+\partial _{\tilde{y}}^2 \tilde{q}_{w,\tilde{z}})=\partial _{\tilde{z}} \tilde{p}_w\quad \text {in }\;\tilde{\varOmega }_{C,w}(\tilde{t}), \end{aligned}$$

(59)

$$\begin{aligned}&\partial _{\tilde{y}}\tilde{q}_{b,\tilde{y}}+\partial _{\tilde{z}}\tilde{q}_{b,\tilde{z}}=0\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(60)

$$\begin{aligned}&\frac{\tilde{\mu }}{\tilde{\theta }_w}(\epsilon ^2\partial _{\tilde{z}}^2 \tilde{q}_{b,\tilde{y}}+\partial _{\tilde{y}}^2 \tilde{q}_{b,\tilde{y}})=\epsilon ^{-2}\partial _{\tilde{y}} \tilde{p}_b+\frac{\tilde{\mu }}{\tilde{k}}\tilde{q}_{b,\tilde{y}}\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(61)

$$\begin{aligned}&\frac{\tilde{\mu }}{\tilde{\theta }_w}(\epsilon ^2\partial _{\tilde{z}}^2 \tilde{q}_{b,\tilde{z}}+\partial _{\tilde{y}}^2 \tilde{q}_{b,\tilde{z}})=\partial _{\tilde{z}} \tilde{p}_b+\frac{\tilde{\mu }}{\tilde{k}}\tilde{q}_{b,\tilde{z}}\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(62)

$$\begin{aligned}&2\bar{\mu }\partial _{\bar{y}} \bar{q}_{w,\bar{y}}-\varepsilon ^{-2}\bar{p}_w-2\frac{\bar{\mu }}{\bar{\theta }_w}\partial _{\bar{y}} \bar{q}_{b,\bar{y}}+\varepsilon ^{-2}\bar{p}_b=\partial _{\bar{z}} \bar{d}\left[ \frac{\bar{\mu }}{\bar{\theta }_w} \left( \partial _{\bar{y}}\bar{q}_{b,\bar{{z}}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{b,\bar{{y}}}\right) \right. \nonumber \\&\quad \left. -\bar{\mu }\left( \partial _{\bar{y}}\bar{q}_{w,\bar{z}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{w,\bar{y}}\right) \right] \quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(63)

$$\begin{aligned}&\bar{\mu }\left( \partial _{\bar{y}}\bar{q}_{w,\bar{z}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{w,\bar{y}}\right) =\partial _{\bar{z}} \bar{d}\left( 2\varepsilon ^{2}\frac{\bar{\mu }}{\bar{\theta }_w}\partial _{\bar{z}} \bar{q}_{b,\bar{z}}-\bar{p}_b\right. \nonumber \\&\quad \left. -2\varepsilon ^{2}\bar{\mu }\partial _{\bar{z}} \bar{q}_{w,\bar{z}}+\bar{p}_w\right) \nonumber \\&\quad +\frac{\bar{\mu }}{\bar{\theta }_w} \left( \partial _{\bar{y}}\bar{q}_{b,\bar{{z}}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{b,\bar{{y}}}\right) \quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(64)

$$\begin{aligned}&(\tilde{q}_{w,\tilde{y}},\tilde{q}_{w,\tilde{z}})=(\tilde{q}_{b,\tilde{y}},\tilde{q}_{b,\tilde{z}})\quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(65)

$$\begin{aligned}&(\tilde{q}_{b,\tilde{y}},\tilde{q}_{b,\tilde{z}})=(0,0)\quad \text {on }\;\tilde{\varGamma }_{C,s}. \end{aligned}$$

(66)

The equations for the nutrients become

$$\begin{aligned}&\partial _{\tilde{t}} \tilde{c}_w-\frac{1}{{\text {Pe}}}(\epsilon ^{-2}\partial _{\tilde{y}}^2 \tilde{c}_w+\partial _{\tilde{z}}^2 \tilde{c}_w)+\partial _{\tilde{y}}(\tilde{q}_{w,\tilde{y}} \tilde{c}_w)+\partial _{\tilde{z}}(\tilde{q}_{w,\tilde{z}} \tilde{c}_w)=0\quad \text {in }\;\tilde{\varOmega }_{C,w}(\tilde{t}), \end{aligned}$$

(67)

$$\begin{aligned}\bar{\mu }\left( \partial _{\bar{y}}\bar{q}_{w,\bar{z}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{w,\bar{y}}\right) =&\partial _{\bar{z}} \bar{d}\left( 2\varepsilon ^{2}\frac{\bar{\mu }}{\bar{\theta }_w}\partial _{\bar{z}} \bar{q}_{b,\bar{z}}-\bar{p}_b -2\varepsilon ^{2}\bar{\mu }\partial _{\bar{z}} \bar{q}_{w,\bar{z}}+\bar{p}_w\right) \nonumber \\&\quad +\frac{\bar{\mu }}{\bar{\theta }_w} \left( \partial _{\bar{y}}\bar{q}_{b,\bar{{z}}}+\varepsilon ^2\partial _{\bar{z}}\bar{q}_{b,\bar{{y}}}\right) \quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(68)

$$\begin{aligned}&-\frac{1}{{\text {Pe}}\epsilon ^{2}}(\partial _{\tilde{y}} \tilde{c}_w-\tilde{\theta }_w \partial _{\tilde{y}} \tilde{c}_b)-(\tilde{c}_b\tilde{q}_{b,\tilde{y}}-\tilde{c}_w\tilde{q}_{w,\tilde{y}})+\partial _{\tilde{t}} \tilde{d}(\tilde{\theta }_w\tilde{c}_{b}-\tilde{c}_w)\nonumber \\&\quad +\frac{\partial _{\tilde{z}} \tilde{d}}{{\text {Pe}}}(\partial _{\tilde{z}} \tilde{c}_w-\tilde{\theta }_w\partial _{\tilde{z}} \tilde{c}_b)+\partial _{\tilde{z}} \tilde{d}(\tilde{c}_b\tilde{q}_{b,\tilde{z}}-\tilde{c}_w\tilde{q}_{w,\tilde{z}})=0\quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(69)

$$\begin{aligned}&\tilde{c}_b=\tilde{c}_w\quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(70)

$$\begin{aligned}&\partial _{\tilde{y}}\tilde{c}_b=0\quad \text {on }\;\tilde{\varGamma }_{C,s} \end{aligned}$$

(71)

where $\tilde{R}_b=-\tilde{\mu }_n\tilde{\theta }_a\tilde{\rho }_a\tilde{c}_b/(\tilde{k}_n+\tilde{c}_b)$.

The dimensionless equations for the growth velocity potential are given by

$$\begin{aligned}&\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\partial _{\tilde{y}}\tilde{u}_{\tilde{y}}+\partial _{\tilde{z}}\tilde{u}_{\tilde{z}})=\tilde{\varSigma }\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(72)

$$\begin{aligned}&(\tilde{u}_{\tilde{y}},\tilde{u}_{\tilde{z}})=-(\partial _{\tilde{y}}\tilde{\varPhi },\epsilon ^2\partial _{\tilde{z}}\tilde{\varPhi })\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(73)

$$\begin{aligned}&\tilde{\varPhi }=0\quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(74)

$$\begin{aligned}&\partial _{\tilde{y}}\tilde{\varPhi }=0\quad \text {on }\;\tilde{\varGamma }_{C,s} \end{aligned}$$

(75)

where $\tilde{\varSigma }=(1-\tilde{\theta }_w)^{-1}[(Y_e\tilde{\rho }_a/\tilde{\rho }_e+Y_a)\tilde{\mu }_n\tilde{\theta }_a\tilde{c}_b/(\tilde{k}_n+\tilde{c}_b)+(\tilde{\rho }_a/\tilde{\rho }_{d}-1)\tilde{k}_{\mathrm {res}}\tilde{\theta }_a]$.

The equations for the biomass components become

$$\begin{aligned}&\partial _{\tilde{t}}\tilde{\theta }_e+\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\tilde{u}_{\tilde{y}}\partial _{\tilde{z}}\tilde{\theta }_e+\tilde{u}_{\tilde{z}}\partial _{\tilde{y}}\tilde{\theta }_e)=Y_e\tilde{\mu }_n\tilde{\theta }_a \frac{\tilde{\rho }_a}{\tilde{\rho }_{e}}\frac{\tilde{c}_b}{\tilde{k}_n+\tilde{c}_b}-\tilde{\theta }_e\tilde{\varSigma }\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(76)

$$\begin{aligned}&\partial _{\tilde{t}}\tilde{\theta }_a+\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\tilde{u}_{\tilde{y}}\partial _{\tilde{z}}\tilde{\theta }_a+\tilde{u}_{\tilde{z}}\partial _{\tilde{y}}\tilde{\theta }_a)=Y_a\tilde{\mu }_n\tilde{\theta }_a \frac{\tilde{c}_b}{\tilde{k}_n+\tilde{c}_b}-\tilde{k}_{\mathrm {res}}\tilde{\theta }_a-\tilde{\theta }_a\tilde{\varSigma }\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(77)

$$\begin{aligned}&\partial _{\tilde{t}}\tilde{\theta }_d+\frac{u_{{\mathrm {ref}}}}{q_{{\mathrm {ref}}}}(\tilde{u}_{\tilde{y}}\partial _{\tilde{z}}\tilde{\theta }_d+\tilde{u}_{\tilde{z}}\partial _{\tilde{y}}\tilde{\theta }_d)=\tilde{k}_{\mathrm {res}}\frac{\tilde{\rho }_a}{\tilde{\rho }_{d}}\tilde{\theta }_a-\tilde{\theta }_d\tilde{\varSigma }\quad \text {in }\;\tilde{\varOmega }_{C,b}(\tilde{t}), \end{aligned}$$

(78)

$$\begin{aligned}&-\partial _{\tilde{y}}\tilde{\theta }_i+\epsilon \partial _{\tilde{z}} \tilde{d}\partial _{\tilde{z}} \tilde{\theta }_i =0\quad i\in \lbrace e,a,d\rbrace \quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}), \end{aligned}$$

(79)

$$\begin{aligned}&\partial _{\tilde{y}}\tilde{\theta }_i =0\quad i\in \lbrace e,a,d\rbrace \quad \text {on }\;\tilde{\varGamma }_{C,s}. \end{aligned}$$

(80)

For the biofilm height, we have

$$\begin{aligned} \partial _{\tilde{t}} \tilde{d}=\left\{ \begin{array}{ll} f^{-}((\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}),&{}\quad \tilde{d}=1\\ -\sqrt{1+(\epsilon \partial _{\tilde{z}} \tilde{d})^2}\epsilon \tilde{k}_{\mathrm {str}}\tilde{S}+(\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}},&{}\quad 0<\tilde{d}<1\\ 0,&{}\quad \tilde{d}=0\end{array}\right. \quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}) \end{aligned}$$

(81)

where

$$\begin{aligned} \tilde{S}=||(\mathbb {I}-\boldsymbol{\tilde{\nu }}\boldsymbol{\tilde{\nu }}^{T})\tilde{\mu }( \mathbb {\tilde{M}}+\mathbb {\tilde{M}}^T)\boldsymbol{\tilde{\nu }}^\epsilon ||\quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}) \end{aligned}$$

(82)

and

$$\begin{aligned} \mathbb {\tilde{M}}&= \left( {\begin{array}{cc} \partial _{\tilde{y}} \tilde{q}_{w,\tilde{y}} &{}\quad \epsilon \partial _{\tilde{z}} \tilde{q}_{w,\tilde{y}} \\ \epsilon ^{-1}\partial _{\tilde{y}} \tilde{q}_{w,\tilde{z}} &{}\quad \partial _{\tilde{z}} \tilde{q}_{w,\tilde{z}} \end{array} } \right) \quad {\text {at }}\;\tilde{\varGamma }_{C,{\mathrm {wb}}}(\tilde{t}). \end{aligned}$$

(83)

We define the average water velocity $\langle \tilde{q}\rangle$ as the following integral

$$\begin{aligned} \langle \tilde{q}\rangle (\tilde{z},\tilde{t})=\langle \tilde{q}_w\rangle (\tilde{z},\tilde{t})+\langle \tilde{q}_b\rangle (\tilde{z},\tilde{t}) =\frac{1}{2}\left( \int _{-(1-\tilde{d}_0)}^{1-\tilde{d}_0}\tilde{q}_{w,\tilde{z},0}\mathrm{d}\tilde{y}+\int _{-1}^{-(1-\tilde{d}_0)}\tilde{q}_{b,\tilde{z},0}\mathrm{d}\tilde{y}+\int _{1-\tilde{d}_0}^{1}\tilde{q}_{b,\tilde{z},0}\mathrm{d}\tilde{y}\right) . \end{aligned}$$

(84)

We define the following space regions in the channel

$$\begin{aligned} \tilde{\varXi }_u= & {} \lbrace \boldsymbol{\tilde{x}}|\;1-\tilde{d}\le \tilde{y}\le 1 \;\wedge \; z_1\le \tilde{z} \le z_1+\delta z\rbrace ,\\ \tilde{\varXi }_m= & {} \lbrace \boldsymbol{\tilde{x}}|\;|\tilde{y}|\le 1-\tilde{d}\;\wedge \; z_1\le \tilde{z} \le z_1+\delta z\rbrace ,\\ \tilde{\varXi }_l= & {} \lbrace \boldsymbol{\tilde{x}}|\;-1\le \tilde{y}\le -(1-\tilde{d})\;\wedge \; z_1\le \tilde{z} \le z_1+\delta z\rbrace . \end{aligned}$$

Integrating (57) and (60) over the previous regions and using the Gauss’s theorem yield

$$\begin{aligned} 0= & {} \int _{\tilde{\varXi }_u}\tilde{\nabla }\boldsymbol{\cdot } \boldsymbol{\tilde{q}}_b d\tilde{V}+\int _{\tilde{\varXi }_m}\tilde{\nabla }\boldsymbol{\cdot } \boldsymbol{\tilde{q}}_w d\tilde{V}+\int _{\tilde{\varXi }_l}\tilde{\nabla }\boldsymbol{\cdot } \boldsymbol{\tilde{q}}_b \mathrm{d}\tilde{V}\\= & {} 2\int _{z_1}^{z_1+\delta z}\boldsymbol{\tilde{q}}_{w}\boldsymbol{\cdot }\boldsymbol{\tilde{\nu }}\big |_{\tilde{y}=1-\tilde{d}}\mathrm{d}\tilde{z}+\int _{-(1-\tilde{d})}^{1-\tilde{d}}\left( \tilde{q}_{w,\tilde{z}}\big |_{\tilde{z}=z_1+\delta z}-\tilde{q}_{w,\tilde{z}}\big |_{\tilde{z}=z_1}\right) \mathrm{d}\tilde{y}\\&\quad -\int _{z_1}^{z_1+\delta z}\left( \boldsymbol{\tilde{q}}_b\boldsymbol{\cdot }\boldsymbol{\tilde{\nu }}\big |_{\tilde{y}=-(1-\tilde{d})}+\boldsymbol{\tilde{q}}_b\boldsymbol{\cdot }\boldsymbol{\tilde{\nu }}\big |_{\tilde{y}=-1}\right) \mathrm{d}\tilde{z}+\int _{-1}^{-(1-\tilde{d})}\left( \tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1+\delta z}-\tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1}\right) \mathrm{d}\tilde{y}\\&\quad -\int _{z_1}^{z_1+\delta z}\left( \boldsymbol{\tilde{q}}_b\boldsymbol{\cdot }\boldsymbol{\tilde{\nu }}\big |_{\tilde{y}=1}+\boldsymbol{\tilde{q}}_b\boldsymbol{\cdot }\boldsymbol{\tilde{\nu }}\big |_{\tilde{y}=1-\tilde{d}}\right) \mathrm{d}\tilde{z}+\int _{1-\tilde{d}}^{1}\left( \tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1+\delta z}-\tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1}\right) \mathrm{d}\tilde{y}. \end{aligned}$$

Recalling the no-slip condition for the water flux on the wall (66) and the continuity of fluxes at the interface (65), the previous equation becomes

$$\begin{aligned}&\int _{-(1-\tilde{d})}^{1-\tilde{d}}\left( \tilde{q}_{w,\tilde{z}}\big |_{\tilde{z}=z_1+\delta z}-\tilde{q}_{w,\tilde{z}}\big |_{\tilde{z}=z_1}\right) \mathrm{d}\tilde{y}+\int _{-1}^{-(1-\tilde{d})}\left( \tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1+\delta z}-\tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1}\right) \mathrm{d}\tilde{y}\\&\quad +\int _{1-\tilde{d}}^{1}\left( \tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1+\delta z}-\tilde{q}_{b,\tilde{z}}\big |_{\tilde{z}=z_1}\right) \mathrm{d}\tilde{y}=0. \end{aligned}$$

Dividing the previous equation by $\delta z$ and letting $\delta z$ approach zero, we obtain for the lowest order terms in $\epsilon$

$$\begin{aligned} \partial _{\tilde{z}}\langle \tilde{q}\rangle =\partial _{\tilde{z}}\langle \tilde{q}_w\rangle (\tilde{z},\tilde{t})+\partial _{\tilde{z}}\langle \tilde{q}_b\rangle (\tilde{z},\tilde{t})=0 \end{aligned}$$

where we use the definition of the water velocity $\langle \tilde{q}\rangle$ (84).

The lowest order terms in the Stokes model (57–59) lead to

$$\begin{aligned} \partial _{\tilde{y}}\tilde{q}_{w,\tilde{y},0}+\partial _{\tilde{z}}\tilde{q}_{w,\tilde{z},0}=0,\quad \partial _{\tilde{y}} \tilde{p}_{w,0}=0,\quad \tilde{\mu }\partial ^2_{\tilde{y}}\tilde{q}_{w,\tilde{z},0}=\partial _{\tilde{z}} \tilde{p}_{w,0}. \end{aligned}$$

(85a,b,c)

From (85b), we conclude that $\tilde{p}_{w,0}$ does not depend on the $\tilde{y}$ coordinate. Analogously, for the Brinkman model (60–62), the lower-order terms in $\epsilon$ give

$$\begin{aligned} \partial _{\tilde{y}}\tilde{q}_{b,\tilde{y},0}+\partial _{\tilde{z}}\tilde{q}_{b,\tilde{z},0}=0,\quad \partial _{\tilde{y}} \tilde{p}_{b,0}=0,\quad \tilde{\mu }\partial ^2_y\tilde{q}_{b,\tilde{z},0}/\tilde{\theta }_w-\tilde{\mu }\tilde{q}_{b,\tilde{z},0}/\tilde{k}=\partial _{\tilde{z}} \tilde{p}_{b,0}. \end{aligned}$$

(86a,b,c)

From (86b), we obtain that $\tilde{p}_{b,0}$ does not depend on the $\tilde{y}$ coordinate and from the lowest order terms in (63), we conclude that $\tilde{p}_{w,0}(\tilde{z},\tilde{t})=\tilde{p}_{b,0}(\tilde{z},\tilde{t})=\tilde{p}_0(\tilde{z},\tilde{t})$. Integrating twice (85) and (86) with respect to $\tilde{y}$ and using the symmetry, interface and boundary conditions (64–66)

$$\begin{aligned} \tilde{q}_{w,\tilde{z},0}=\left( \frac{\tilde{y}^2}{2}+V\right) \frac{\partial _{\tilde{z}}\tilde{p}_0}{\tilde{\mu }},\quad \tilde{q}_{b,\tilde{z},0}=\left( We^{\tilde{y}\lambda }+Xe^{-\tilde{y}\lambda }-\tilde{k}\right) \frac{\partial _{\tilde{z}}\tilde{p}_0}{\tilde{\mu }}, \end{aligned}$$

(87a,b)

where $\lambda =\sqrt{\tilde{\theta }_w/\tilde{k}}$ and the coefficients are given by

$$\begin{aligned} V= & {} -\frac{(\frac{h^2}{2}+\tilde{k})(e^{-\tilde{d}_0\lambda }+e^{\tilde{d}_0\lambda })-\sqrt{\tilde{k}\tilde{\theta }_w}h(e^{-\tilde{d}_0\lambda }-e^{\tilde{d}_0\lambda })-2\tilde{k}}{e^{-\tilde{d}_0\lambda }+e^{\tilde{d}_0\lambda }},\\ W= & {} \frac{\tilde{k}e^{h\lambda }-\sqrt{\tilde{k}\tilde{\theta }_w}he^{\lambda }}{e^{-\tilde{d}_0\lambda }+e^{\tilde{d}_0\lambda }},\quad X=\frac{\tilde{k}e^{-h\lambda }+\sqrt{\tilde{k}\tilde{\theta }_w}he^{-\lambda }}{e^{-\tilde{d}_0\lambda }+e^{\tilde{d}_0\lambda }}\\ \end{aligned}$$

where $h=1-\tilde{d}_0$.

To obtain the water velocity defined in (84), we integrate (87) as follows

$$\begin{aligned} \langle \tilde{q}\rangle= & {} \frac{\partial _{\tilde{z}}\tilde{p}_0}{2\tilde{\mu }}\left[ \int _{-(1-\tilde{d}_0)}^{1-\tilde{d}_0}\left( \frac{\tilde{y}^2}{2}+V\right) \mathrm{d}\tilde{y}+2\int _{-1}^{-(1-\tilde{d}_0)}\left( We^{\tilde{y}\lambda }+Xe^{-\tilde{y}\lambda }-\tilde{k}\right) \mathrm{d}\tilde{y}\right] \\= & {} \left[ \frac{\lambda ^3}{6}+V\lambda +\frac{We^{-\lambda }\left( e^{\tilde{d}_0\lambda }-1\right) -Xe^{\lambda }\left( e^{-\tilde{d}_0\lambda }-1\right) }{\lambda }-\tilde{k}\tilde{d}_0 \right] \frac{\partial _{\tilde{z}} \tilde{p}_0}{\tilde{\mu }}\\= & {} -\frac{\kappa _C(\tilde{d}_0)}{\tilde{\mu }}\partial _{\tilde{z}} \tilde{p}_0. \end{aligned}$$

This is the Darcy’s law $\langle \tilde{q}\rangle =-\kappa _C(\tilde{d}_0)\partial _{\tilde{z}} \tilde{p}_0/\tilde{\mu }$, where $\kappa _C(\tilde{d}_0)$ is the effective permeability given by

$$\begin{aligned} \kappa _C(\tilde{d}_0)=-\frac{\lambda ^3}{6}-\lambda V-\frac{We^{-\lambda }\left( e^{\tilde{d}_0\lambda }-1\right) -Xe^{\lambda }\left( e^{-\tilde{d}_0\lambda }-1\right) }{\lambda }+\tilde{k}\tilde{d}_0. \end{aligned}$$

The growth velocity potential equations (72) and (73) for the lower-order terms in $\epsilon$ are

$$\begin{aligned} u_{{\mathrm {ref}}}(\partial _{\tilde{y}}\tilde{u}_{\tilde{y},0}+\partial _{\tilde{z}}\tilde{u}_{\tilde{z},0})/q_{{\mathrm {ref}}}=\tilde{\varSigma }_0,\quad \tilde{u}_{\tilde{y},0}=-\partial _{\tilde{y}}\tilde{\varPhi }_0,\quad \tilde{u}_{\tilde{z},0}=0 \end{aligned}$$

(88)

where the conditions at the interface (74) become $\tilde{\varPhi }_0=0$ and wall (75) becomes $\partial _{\tilde{y}} \tilde{\varPhi }_{0}=0$.

In dimensionless form, the volume fraction equations (76–78) are

$$\begin{aligned} \partial _{\tilde{t}}\tilde{\theta }_i+u_{{\mathrm {ref}}}(\tilde{u}_{\tilde{y}}\partial _{\tilde{y}}\tilde{\theta }_i+\tilde{u}_{\tilde{z}}\partial _{\tilde{z}}\tilde{\theta }_i)/q_{{\mathrm {ref}}}=\tilde{R}_i-\tilde{\theta }_i\tilde{\varSigma } \end{aligned}$$

(89)

with $i=\lbrace e,a,d\rbrace$. We focus on biofilms where the biomass components change slightly along the $\tilde{y}$ direction, resulting in the approximation $\tilde{\theta }_{i,0}(\tilde{y},\tilde{z},\tilde{t})=\tilde{\theta }_{i,0}(\tilde{z},\tilde{t})$. Using (88c), the lower-order terms in (89) are

$$\begin{aligned} \partial _{\tilde{t}}\tilde{\theta }_{i,0}=\tilde{R}_{i,0}-\tilde{\theta }_{i,0}\tilde{\varSigma }_0. \end{aligned}$$

(90)

Integrating (88a) over $\tilde{y}$ and using the boundary conditions (74–75), one gets

$$\begin{aligned} \tilde{u}_{\tilde{y},0}=q_{{\mathrm {ref}}}\tilde{\varSigma }_0(\tilde{y}+1)/u_{{\mathrm {ref}}}. \end{aligned}$$

(91)

For the nutrients, integrating (67) and (68) yields

$$\begin{aligned}&\int _{-(1-\tilde{d})}^{1-\tilde{d}}\left[ \partial _{\tilde{t}} \tilde{c}_w-\frac{1}{{\text {Pe}}}\left( \epsilon ^{-2}\partial _{\tilde{y}}^2 \tilde{c}_w+\partial _{\tilde{z}}^2 \tilde{c}_w\right) +\partial _{\tilde{y}}(\tilde{q}_{w,\tilde{y}} \tilde{c}_w)+\partial _{\tilde{z}}(\tilde{q}_{w,\tilde{z}} \tilde{c}_w)\right] \mathrm{d}\tilde{y}=0,\\&2\int _{-1}^{-(1-\tilde{d})}\left[ \partial _{\tilde{t}} (\tilde{\theta }_w \tilde{c}_b)- \frac{\tilde{\theta }_w}{{\text {Pe}}}\left( \epsilon ^{-2}\partial _{\tilde{y}}^2 \tilde{c}_b+\partial _{\tilde{z}}^2 \tilde{c}_b\right) +\partial _{\tilde{y}}(\tilde{q}_{b,\tilde{y}} \tilde{c}_b)+\partial _{\tilde{z}}(\tilde{q}_{b,\tilde{z}} \tilde{c}_b)\right. \\&\quad \left. +\tilde{\mu }_n\tilde{\theta }_a\tilde{\rho }_a \frac{\tilde{c}_b}{\tilde{k}_n+\tilde{c}_b}\right] \mathrm{d}\tilde{y}=0. \end{aligned}$$

Interchanging the integration and the differentiation operators, these equations become

$$\begin{aligned}&\partial _{\tilde{t}}\left( \int _{-(1-\tilde{d})}^{1-\tilde{d}} \tilde{c}_w\mathrm{d}\tilde{y}\right) +2\partial _{\tilde{t}}\tilde{d} \tilde{c}_w\big |_{\tilde{y}=-(1-\tilde{d})}-\partial _{\tilde{z}}\left[ \int _{-(1-\tilde{d})}^{1-\tilde{d})}\left( \frac{1}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_w-\tilde{q}_{w,\tilde{z}}\tilde{c}_w\right) \mathrm{d}\tilde{y}\right] \end{aligned}$$

(92)

$$\begin{aligned}&-2\partial _{\tilde{z}}\tilde{d}\left( \frac{1}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_w-\tilde{q}_{w,\tilde{z}}\tilde{c}_w\right) \bigg |_{\tilde{y}=-(1-\tilde{d})}-2\left( \frac{1}{\epsilon ^2{\text {Pe}}}\partial _{\tilde{y}} \tilde{c}_w-\tilde{q}_{w,\tilde{y}}\tilde{c}_w \right) \bigg |_{\tilde{y}=-(1-\tilde{d})}=0,\nonumber \\&\quad 2\partial _{\tilde{t}}\left( \int _{-1}^{-(1-\tilde{d})}\tilde{\theta }_w \tilde{c}_b\mathrm{d}\tilde{y}\right) -2\tilde{\theta }_w\partial _{\tilde{t}}\tilde{d} \tilde{c}_b\big |_{\tilde{y}=-(1-\tilde{d})}\nonumber \\&\quad -2\partial _{\tilde{z}}\left[ \int _{-1}^{-(1-\tilde{d})}\left( \frac{\tilde{\theta }_w}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_b-\tilde{q}_{b,\tilde{z}}\tilde{c}_b\right) \mathrm{d}\tilde{y}\right] +2\partial _{\tilde{z}}\tilde{d}\left( \frac{\tilde{\theta }_w}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_b-\tilde{q}_{b,\tilde{z}}\tilde{c}_b\right) \bigg |_{\tilde{y}=-(1-\tilde{d})}\nonumber \\&\quad +2\left( \frac{\tilde{\theta }_w}{\epsilon ^2{\text {Pe}}}\partial _{\tilde{y}} \tilde{c}_b-\tilde{q}_{b,\tilde{y}}\tilde{c}_b \right) \bigg |_{\tilde{y}=-(1-\tilde{d})}+2\tilde{\mu }_n\tilde{\rho }_a\int _{-1}^{-(1-\tilde{d})}\tilde{\theta }_a \frac{\tilde{c}_b}{\tilde{k}_n+\tilde{c}_b}\mathrm{d}\tilde{y}=0. \end{aligned}$$

(93)

Next, the lower-order terms in the equations for the conservation of nutrients (67–68) are $\partial _{\tilde{y}}^2\tilde{c}_{w,0}=0$ and $\partial _{\tilde{y}}^2\tilde{c}_{b,0}=0$. The interface coupling condition (70) becomes $\tilde{c}_{b,0}=\tilde{c}_{w,0},$ while the boundary condition on the wall (71) becomes $\partial _{\tilde{y}}\tilde{c}_{b,0}=0$. The symmetry in $\tilde{y}$ implies that both nutrient concentrations do not depend on $\tilde{y}$, resulting in $\tilde{c}_{w,0}(\tilde{z},\tilde{t})=\tilde{c}_{b,0}(\tilde{z},\tilde{t})=\tilde{c}_0(\tilde{z},\tilde{t})$. Using the aforementioned results, both equations (92) and (93) can be written as

$$\begin{aligned}&\partial _{\tilde{t}}[\tilde{c}_0(2-2\tilde{d}_0)]-\partial _{\tilde{z}}\left( \frac{2-2\tilde{d}_0}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_0\right) +\partial _{\tilde{z}}\left( \tilde{c}_0\int _{-(1-\tilde{d}_0)}^{1-\tilde{d}_0}\tilde{q}_{w,\tilde{z},0}\mathrm{d}\tilde{y}\right) =0,\\&\partial _{\tilde{t}}(2\tilde{d}_0\tilde{\theta }_w\tilde{c}_0)-\partial _{\tilde{z}}\left( 2\tilde{d}_0\frac{\tilde{\theta }_w}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_0\right) +\partial _{\tilde{z}}\left( \tilde{c}_0\int _{-1}^{-(1-\tilde{d}_0)}\tilde{q}_{b,\tilde{z},0}\mathrm{d}\tilde{y}\right) +2\tilde{d}_0\tilde{\mu }_n\tilde{\rho }_a\tilde{\theta }_{a,0}\frac{\tilde{c}_0}{\tilde{k}_n+\tilde{c}_0}=0 \end{aligned}$$

where we use the interface condition (69). Then, adding both equations we finally obtain

$$\begin{aligned} \partial _{\tilde{t}}[\tilde{c}_0\varTheta _C(\tilde{d}_0,\tilde{\theta }_w)]+\partial _{\tilde{z}}\left[ \tilde{c}_0\langle \tilde{q}\rangle -\frac{\varTheta _C(\tilde{d}_0,\tilde{\theta }_w)}{{\text {Pe}}}\partial _{\tilde{z}} \tilde{c}_0\right] =-\tilde{d}_0\tilde{\mu }_n\tilde{\theta }_{a,0}\tilde{\rho }_a\frac{\tilde{c}_0}{\tilde{k}_n+\tilde{c}_0} \end{aligned}$$

where we define $\varTheta _C(\tilde{d}_0,\tilde{\theta }_w)$ as

$$\begin{aligned} \varTheta _C(\tilde{d}_0,\tilde{\theta }_w)=1-\tilde{d}_0+\tilde{\theta }_w\tilde{d}_0. \end{aligned}$$

We focus on the water–biofilm interface (81):

$$\begin{aligned} \partial _{\tilde{t}} \tilde{d}=\left\{ \begin{array}{ll} f^{-}((\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}),&{}\quad \tilde{d}=1,\\ -\sqrt{1+(\epsilon \partial _{\tilde{z}} \tilde{d})^2}\epsilon \tilde{k}_{\mathrm {str}}\tilde{\mu } \tilde{S}+(\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}},&{}\quad 0<\tilde{d}<1,\\ 0,&{}\quad \tilde{d}=0.\end{array}\right. \end{aligned}$$

Using the set-valued Heaviside graphs (49), we can write the previous equations as

$$\begin{aligned}&\partial _{\tilde{t}} \tilde{d}\in H_0(\tilde{d})H_{1}(\tilde{d}) \left\{ -\sqrt{1+(\epsilon \partial _{\tilde{z}} \tilde{d})^2}\epsilon \tilde{k}_{\mathrm {str}}\tilde{\mu } ||(\mathbb {I}-\boldsymbol{\tilde{\nu }}\boldsymbol{\tilde{\nu }}^T)(\mathbb {\tilde{M}}+\mathbb {\tilde{M}}^T)\boldsymbol{\tilde{\nu }}||\right. \nonumber \\&\quad \left. +[\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}}]u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}\right\} +[1-H_{1}(\tilde{d})]f^{-}((\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}). \end{aligned}$$

(94)

Using the regularized Heaviside functions (51), we can write (94) as

$$\begin{aligned} \partial _{\tilde{t}} \tilde{d}= & {} H_{\delta ,0}(\tilde{d})H_{\delta ,1}(\tilde{d}) \left\{ -\sqrt{1+(\epsilon \partial _{\tilde{z}} \tilde{d})^2}\epsilon \tilde{k}_{\mathrm {str}}\tilde{\mu } ||(\mathbb {I}-\boldsymbol{\tilde{\nu }}\boldsymbol{\tilde{\nu }}^T)(\mathbb {\tilde{M}}+\mathbb {\tilde{M}}^T)\boldsymbol{\tilde{\nu }}||\right. \\&\quad \left. +[\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}}]u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}\right\} +[1-H_{\delta ,1}(\tilde{d})]f^{-}((\tilde{u}_{\tilde{y}}-\partial _{\tilde{z}}\tilde{d} \tilde{u}_{\tilde{z}})u_{{\mathrm {ref}}}/q_{{\mathrm {ref}}}). \end{aligned}$$

Using (82–83, 87a, 88a, 91), for the lower-order terms in $\epsilon$ we have

$$\begin{aligned} \partial _{\tilde{t}} \tilde{d}_0= H_{\delta ,0}(\tilde{d}_0)H_{\delta ,1}(\tilde{d}_0)[-\tilde{k}_{\mathrm {str}}(1-\tilde{d}_0)|\partial _{\tilde{z}}\tilde{p}_0|+\tilde{d}_0\tilde{\varSigma }_0]+[1-H_{\delta ,1}(\tilde{d}_0)]f^{-}(\tilde{\varSigma }_0). \end{aligned}$$

Letting $\delta$ go to zero in order to return to the non-regularized formulation, we get

$$\begin{aligned}\partial _{\tilde{t}} \tilde{d}_0= \left\{ \begin{array}{ll} f^{-}(\tilde{\varSigma }_0) &{}\quad \tilde{d}_0=1,\\ -\tilde{k}_{\mathrm {str}}(1-\tilde{d}_0)|\partial _{\tilde{z}}{\tilde{p}_0}|+\tilde{d}_0\tilde{\varSigma }_0, &{}\quad 0<\tilde{d}_0<1,\\ 0, &{}\quad \tilde{d}_0=0.\\ \end{array}\right. \end{aligned}$$