Skip to main content
SpringerLink
Log in

Reversals of period doubling, coexisting multiple attractors, and offset boosting in a novel memristive diode bridge-based hyperjerk circuit

  • Published:
Analog Integrated Circuits and Signal Processing Aims and scope Submit manuscript

Abstract

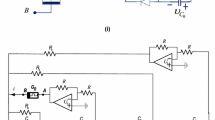
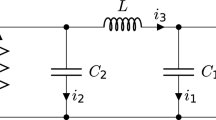
In this paper, a new memristive diode bridge-based RC hyperjerk circuit is proposed. This new memristive hyperjerk oscillator (MHO) is obtained from the autonomous 4-D hyperjerk circuit (Leutcho et al. in Chaos Solitons Fractals 107:67–87, 2018) by replacing the nonlinear component (formed by two antiparallel diodes) with a first order memristive diode bridge. The circuit is described by a fifth-order continuous time autonomous (‘elegant’) hyperjerk system with smooth nonlinearities. The dynamics of the system is investigated in terms of equilibrium points and stability, phase portraits, bifurcation diagrams and two-parameter Lyapunov exponents diagrams. The numerical analysis of the model reveals interesting behaviors such as period-doubling, chaos, offset boosting, symmetry recovering crisis, antimonotonicity (i.e. concurrent creation and destruction of periodic orbits) and several coexisting bifurcations as well. One of the most attractive features of the new MHO considered in this work is the presence of several coexisting attractors (e.g. coexistence of two, three, four, five, six, seven, or nine attractors) for some suitable sets of system parameters, depending on the choice of initial conditions. Accordingly, the distribution of initial conditions related to each coexisting attractor is computed to highlight different basins of attraction. Laboratory experimental measurements are carried out to verify the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  1. Chua, L. O. (1971). Memristor-The missing circuit element. IEEE Transactions on Circuit Theory,Ct-18(5), 507–519.

    Article  Google Scholar 

  2. Strukov, D. B., Snider, G. S., Stewart, G. R., & Williams, R. S. (2008). The missing memristor found. Nature,453, 80–83.

    Article  Google Scholar 

  3. Adhikari, S. P., Sah, M. P., Kim, H., & Chua, L. O. (2013). Three fingerprints of memristor. IEEE Transactions on Circuit Systems I,60(11), 3008–3021.

    Article  Google Scholar 

  4. Buscarino, A., Fortuna, L., Frasca, M., & Gambuzza, L. V. (2012). A chaotic circuit based on Hewlett–Packard memristor. Chaos,22, 023136.

    Article  MathSciNet  MATH  Google Scholar 

  5. Bao, B., Zhong, L., & Jian-Ping, X. (2010). Transient chaos in smooth memristor oscillator. Chinese Physics B,19(3), 030510.

    Article  Google Scholar 

  6. Buscarino, A., Fortuna, L., Frasca, M., & Gambuzza, L. V. (2013). A gallery of chaotic oscillators based on HP memristor. International Journal of Bifurcation and Chaos,23(5), 1330015.

    Article  MathSciNet  MATH  Google Scholar 

  7. Budhathoki, R. K., Sah, M. P. D., Yang, C., Kim, H., & Chua, L. O. (2014). Transient behavior of multiple memristor circuits based on flux charge relationship. International Journal of Bifurcation and Chaos,24(2), 1430006.

    Article  MathSciNet  MATH  Google Scholar 

  8. Bao, B., Zou, X., Liu, Z., & Hu, F. (2013). Generalized memory element and chaotic memory system. International Journal of Bifurcation and Chaos,23(8), 1350135.

    Article  MathSciNet  MATH  Google Scholar 

  9. Muthuswamy, B., & Chua, L. O. (2010). Simplest chaotic circuit. International Journal of Bifurcation and Chaos,20(5), 1567–1580.

    Article  Google Scholar 

  10. Wang, G. Y., He, J. L., Yuan, F., & Peng, C. J. (2013). Dynamical behaviour of a TiO2 memristor oscillator. Chinese Physics Letters,30, 110506.

    Article  Google Scholar 

  11. Itoh, M., & Chua, L. O. (2008). Memristor oscillators. International Journal of Bifurcation and Chaos,18, 3183–3206.

    Article  MathSciNet  MATH  Google Scholar 

  12. Muthuswamy, B. (2010). Implementing memristor based chaotic circuits. International Journal of Bifurcation and Chaos,20, 1335–1350.

    Article  MATH  Google Scholar 

  13. Bao, B., Xu, J. P., Zhou, G. H., Ma, Z. H., & Zou, L. (2011). Chaotic memristive circuit: Equivalent circuit realization and dynamical analysis. Chinese Physics B,20, 120502.

    Article  Google Scholar 

  14. Bao, B., Yu, J., Hu, F., & Liu, Z. (2014). Generalized memristor consisting of diode bridge with first order parallel RC filter. International Journal of Bifurcation and Chaos,24(11), 1450143.

    Article  MATH  Google Scholar 

  15. Chen, M., Li, M., Yu, Q., Bao, B., Xu, Q., & Wang, J. (2015). Dynamics of self-excited and hidden attractors in generalized memristor-based Chua’s circuit. Nonlinear Dynamics,81, 215–226.

    Article  MathSciNet  Google Scholar 

  16. Chen, M., Yu, J., Yu, Q., Li, C., & Bao, B. (2014). A memristive diode bridge-based canonical Chua’s circuit. Entropy,16, 6464–6476.

    Article  Google Scholar 

  17. Pisarchik, A. N., & Feudel, U. (2014). Control of multistability. Physics Reports,540(4), 167–218.

    Article  MathSciNet  MATH  Google Scholar 

  18. Masoller, C. (1994). Coexistence of attractors in a laser diode with optical feedback from a large external cavity. Physical Review A,50, 2569–2578.

    Article  Google Scholar 

  19. Cushing, J. M., Henson, S. M., & Blackburn, C. C. (2007). Multiple mixed attractors in a competition model. Journal of Biological Dynamics,1, 347–362.

    Article  MathSciNet  MATH  Google Scholar 

  20. Upadhyay, R. K. (2003). Multiple attractors and crisis route to chaos in a model of food-chain. Chaos, Solitons & Fractals,16, 737–747.

    Article  MathSciNet  MATH  Google Scholar 

  21. Massoudi, A., Mahjani, M. G., & Jafarian, M. (2010). Multiple attractors in Koper–Gaspard model of electrochemical. Journal of Electroanalytical Chemistry,647, 74–86.

    Article  Google Scholar 

  22. Li, C., & Sprott, J. C. (2014). Coexisting hidden attractors in a 4-D simplified Lorenz system. International Journal of Bifurcation and Chaos,24, 1450034.

    Article  MathSciNet  MATH  Google Scholar 

  23. Leipnik, R. B., & Newton, T. A. (1981). Double strange attractors in rigid body motion with linear feedback control. Physics Letters A,86, 63–87.

    Article  MathSciNet  Google Scholar 

  24. Guan, Z. H., Lai, Q., Chi, M., Chen, X. M., & Liu, F. (2014). A new three-dimensional system with multiple chaotic attractors. Nonlinear Dynamics,75, 331–343.

    Article  MathSciNet  MATH  Google Scholar 

  25. Lai, Q., & Chen, S. (2016). Generating multiple chaotic attractors from Sprott B system. International Journal of Bifurcation and Chaos,26(11), 1650177.

    Article  MathSciNet  MATH  Google Scholar 

  26. Lai, Q., & Chen, S. (2016). Coexisting attractors generated from a new 4D smooth chaotic system. International Journal on Control, Automation and Systems,14(4), 1124–1131.

    Article  Google Scholar 

  27. Kengne, J., Njitacke, Z. T., & Fotsin, H. B. (2016). Dynamical analysis of a simple autonomous jerk system with multiple attractors. Nonlinear Dynamics,83, 751–765.

    Article  MathSciNet  Google Scholar 

  28. VaithianathanVandVeijun, J. (1998). Coexistence of four different attractors in a fundamental power system model. IEEE Transactions on Circuits Systems-I,46, 405–409.

    Google Scholar 

  29. Kengne, J., NguomkamNegou, A., & Tchiotsop, D. (2017). Antimonotonicity, chaos and multiple attractors in a novel autonomous memristor-based jerk circuit. Nonlinear Dynamics,88, 2589–2608.

    Article  Google Scholar 

  30. Kuznetsov, A. P., Kuznetsov, S. P., Mosekilde, E., & Stankevich, N. V. (2015). Co-existing hidden attractors in a radio-physical oscillator. Journal of Physics A: Mathematical and Theoretical,48, 125101.

    Article  MathSciNet  MATH  Google Scholar 

  31. Kengne, J., Njitacke, Z. T., NguomkamNegou, A., FouodjiTsotsop, M., & Fotsin, H. B. (2015). Coexistence of multiple attractors and crisis route to chaos in a novel chaotic jerk circuit. International Journal of Bifurcation and Chaos,25(4), 1550052.

    Article  MathSciNet  Google Scholar 

  32. Njitacke, Z. T., Kengne, J., Fotsin, H. B., Nguomkam Negou, A., & Tchiotsop, D. (2016). Coexistence of multiple attractors and crisis route to chaos in a novel memristive diode bidge-based Jerk circuit. Chaos, Solitons & Fractals,91, 180–197.

    Article  MATH  Google Scholar 

  33. Kengne, J., Folifack Signing, V. R., Chedjou, J. C., & Leutcho, G. D. (2017). Nonlinear behavior of a novel chaotic jerk system: antimonotonicity, crises, and multiple coexisting attractors. International Journal of Dynamics and Control. https://doi.org/10.1007/s40435-017-0318-6.

    Article  MathSciNet  Google Scholar 

  34. Bao, B., Jiang, T., Xu, Q., Chen, M., Wu, H., & Hu, Y. (2017). Coexisting infinitely many attractors in active band-pass filter-based memristive circuit. Nonlinear Dynamics,86(3), 1711–1723.

    Article  Google Scholar 

  35. Li, C., Hu, W., Sprott, J. C., & Wang, X. (2015). Multistability in symmetric chaotic systems. The European Physical Journal Special Topics,224, 1493–1506.

    Article  Google Scholar 

  36. Xu, Q., Lin, Y., Bao, B., & Chen, M. (2016). Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos, Solitons & Fractals,83, 186–200.

    Article  MathSciNet  MATH  Google Scholar 

  37. Maggio, G. M., DeFeo, O., & Kennedy, M. P. (1999). Nonlinear analysis of the Colpitts oscillator and application to design. IEEE Transactions on Circuits and Systems I Fundamental Theory and Applications,46, 1118–1130.

    Article  MATH  Google Scholar 

  38. Leutcho, G. D., Kengne, J., & Kamdjeu Kengne, L. (2018). Dynamical analysis of a novel autonomous 4-D hyperjerk circuit with hyperbolic sine nonlinearity: Chaos, antimonotonicity and a plethora of coexisting attractors. Chaos, Solitons & Fractals,107, 67–87.

    Article  MathSciNet  MATH  Google Scholar 

  39. Klouverakis, K. E., & Sprott, J. C. (2006). Chaotic hyperjerk systems. Chaos, Solitons & Fractals,28, 739–746.

    Article  MathSciNet  MATH  Google Scholar 

  40. Linz, S. J. (2008). On hyperjerk systems. Chaos, Solitons & Fractals,37, 741–747.

    Article  MathSciNet  MATH  Google Scholar 

  41. Zeraoulia, E., & Sprott, J. C. (2013). Transformation of 4-D dynamical systems to hyperjerk form. Palestine Journal of Mathematics,2, 38–45.

    MathSciNet  MATH  Google Scholar 

  42. Munmuangsaen, B., & Srisuchinwong, B. (2011). Elemetary chaotic snap flows. Chaos, Solitons & Fractals,44, 995–1003.

    Article  Google Scholar 

  43. Dalkiran, F. Y., & Sprott, J. C. (2016). Simple chaotic hyperjerk systems. International Journal of Bifurcation and Chaos,26(11), 1550052.

    Article  MathSciNet  Google Scholar 

  44. Wang, X., Vaidyanathan, S., Volos, C., Pham, V.-T., & Kapitaniak, T. (2017). Dynamics, circuit realization, control and synchronization of a hyperchaotic hyperjerk system with coexisting attractors. Nonlinear Dynamics. https://doi.org/10.1007/s11071-017-3542-x.

    Article  MathSciNet  MATH  Google Scholar 

  45. Sundarapandian, V., Volos, C., Pham, V.-T., & Madhavan, K. (2015). Analysis, adaptive control and synchronization of a novel 4-D hyperchaotic hyperjerk system and its SPICE implementation. Archives of Control Sciences,25, 135–158.

    Article  MathSciNet  Google Scholar 

  46. Daltzis, P., Vaidyanathan, S., & Pham, V. (2017). Hyperchaotic attractor in a novel hyperjerk system with two nonlinearities. Circuits Systems Signal Processing. https://doi.org/10.1007/s00034-017-0581-y.

    Article  MathSciNet  MATH  Google Scholar 

  47. Fautso Kuiate, G., Karthikeyan, R., Kingni, S. T., Kamdoum Tamba, V., & Jafari, S. (2017). Autonomous Van der Pol-Duffing snap oscillator: analysis, synchronization and application to real-time image encryption. International Journal of Dynamics Control. https://doi.org/10.1007/s40435-017-0373-z.

    Article  MathSciNet  Google Scholar 

  48. Jafari, S., Ahmadi, A., Panahi, S., & Rajagopal, K. (2018). Extreme multi-stability: When imperfection changes quality. Chaos, Solitons & Fractals,108, 182–186.

    Article  Google Scholar 

  49. Jafari, S., Sprott, J. C., & Nazarimehr, F. (2015). Recent new examples of hidden attractors. European Physical Journal Special Topics,224, 1469–1476.

    Article  Google Scholar 

  50. Jafari, S., Pham, V. T., & Kapitaniak, T. (2016). Multiscroll chaotic sea obtained from a simple 3D system without equilibrium. International Journal of Bifurcation Chaos,26, 1650031.

    Article  MathSciNet  MATH  Google Scholar 

  51. Jafari, S., Sprott, J. C., & Molaie, M. (2016). A simple chaotic flow with a plane of equilibria. International Journal of Bifurcation Chaos,26, 1650098.

    Article  MathSciNet  MATH  Google Scholar 

  52. Jafari, S., Sprott, J. C., Pham, V. T., Volos, K., & Li, C. (2016). Simple chaotic 3D flows with surfaces of equilibria. Nonlinear Dynamics,86, 1349–1358.

    Article  Google Scholar 

  53. Leutcho, G. D., & Kengne, J. (2018). A unique chaotic snap system with a smoothly adjustable symmetry and nonlinearity: chaos, offset-boosting, antimonotonicity, and coexisting multiple attractors. Chaos, Solitons & Fractals,113, 275–293.

    Article  MathSciNet  Google Scholar 

  54. Leutcho, G. D., Kengne, J., & Kengne, R. (2018). Remerging Feigenbaum trees, and multiple coexisting bifurcations in a novel hybrid diode-based hyperjerk circuit with offset boosting. International Journal of Dynamic Control. https://doi.org/10.1007/s40435-018-0438-7.

    Article  Google Scholar 

  55. Strogatz, S. H. (1994). Nonlinear dynamics and chaos. Reading: Addison-Wesley.

    Google Scholar 

  56. Argyris, J., Faust, G., & Haase, M. (1994). An exploration of chaos. Amsterdam: North-Holland.

    MATH  Google Scholar 

  57. Nayfeh, A. H., & Balachandran, B. (1995). Applied nonlinear dynamics: Analytical, computational and experimental methods. New York: Wiley.

    Book  MATH  Google Scholar 

  58. Leonov, G. A., Kuznetsov, N. V., & Mokaev, T. N. (2015). Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. European Physical Journal Special Topics,224, 1421–1458.

    Article  Google Scholar 

  59. Li, C., Wang, X., & Chen, G. (2017). Diagnosing multistability by offset boosting. Nonlinear Dynamics. 017-3729-1.

  60. Li, C., Sprott, J. C., Akgul, A., Lu Herbert, H. C., & Zhao, Y. (2017). A new chaotic oscillator with free control. Chaos,27, 083101.

    Article  MathSciNet  MATH  Google Scholar 

  61. Pham, V.-T., Wang, X., Jafari, S., Volos, K., & Kapitaniak, T. (2017). From Wang-Chen system with only one stable equilibrium to a new chaotic system without equilibrium. International Journal of Bifurcation and Chaos,27, 1750097.

    Article  MathSciNet  MATH  Google Scholar 

  62. Pham, V. T., Volos, C., Kingni, S. T., Jafari, S., & Kapitaniak T. Coexistence of hidden chaotic attractors in a novelno-equilibrium system. Nonlinear Dyn.2016; 3170-x.

  63. Nguomkam Negou, A., & Kengne, J. (2018). Dynamic analysis of a unique Jerk system with a smoothly adjustable symmetry and nonlinearity: Reversals of period doubling, offset boosting and coexisting bifurcations. International Journal of Electronics and Communications. https://doi.org/10.1016/j.aeue.2018.04.003.

    Article  Google Scholar 

  64. Li, C., Sprott, J. C., Mei, Y. (2017). An infinite 2-D lattice of strange attractors. Nonlinear Dynamics. 017-3612-0.

  65. Li, C., & Sprott, J. C. (2016). Variable-boostable chaotic flows. Optik,127, 10389–10398.

    Article  Google Scholar 

  66. Li, C., Sprott, J. C., Hu, W., & Xu, Y. (2017). Infinite multistability in a self-reproducing Chaotic System. International Journal of Bifurcation and Chaos,27, 1750160.

    Article  MathSciNet  MATH  Google Scholar 

  67. Li, C., Sprott, J. C., Kapitaniak, T., & Lu, T. (2018). Infinite lattice of hyperchaotic strange attractors. Chaos, Solitons & Fractals,109, 76–82.

    Article  MathSciNet  MATH  Google Scholar 

  68. Li, C., & Sprott, J. C. (2018). An infinite 3-D quasiperiodic lattice of chaotic attractors. Physics Letters A,382, 581–587.

    Article  MathSciNet  MATH  Google Scholar 

  69. Stegemann, C., Albuquerque, H. A., Rubinger, R. M., & Rech, P. C. (2011). Lyapunov exponent diagrams of a 4 dimensional chua system. Chaos: An Interdisciplinary Journal of Nonlinear Science, 21(3):033105.

  70. Rech, P. C. (2017). Hyperchaos and quasiperiodicity from a four-dimensional system based on the lorenz system. European Physics Journal B,90(12), 251.

    Article  MathSciNet  Google Scholar 

  71. FozinFonzin, T., Srinivasan, K., Kengne, J., & Pelap, F. B. (2018). Coexisting bifurcations in a memristive hyperchaotic oscillator. International Journal of Electronics and Communications (AEÜ),90, 110–112.

    Article  Google Scholar 

  72. Kengne, R., Tchitnga, R., Mabekou, S., WafoTakam, B. R., Soh, G. B., & Fomethe, A. (2018). On the relay coupling of three fractional-order oscillations with time-delay consideration: Global and cluster synchronizations. Chaos, Solitons & Fractals,111, 6–17.

    Article  MathSciNet  MATH  Google Scholar 

  73. Alombah, H. N., Fotsin, H., & Kengne, R. (2017). Coexistence of Multiple attractors, metastable chaos and bursting oscillations in a multiscroll memristive chaotic circuit. Int. J. of Bifurcation and Chaos,27, 1750067.

    Article  MathSciNet  MATH  Google Scholar 

  74. Dawson, S. P., Grebogi, C., Yorke, J. A., Kan, I., & Koçak, H. (1992). Antimonotonicity: inevitable reversals of period-doubling cascades. Physics Letters A,162, 249–254.

    Article  MathSciNet  Google Scholar 

  75. Parlitz, U., & Lauterborn, W. (1985). Superstructure in the bifurcation set of the Duffing equation ẍ + dẋ + x + x3 = f cos (ωt). Physics Letters A,107, 351–355.

    Article  MathSciNet  Google Scholar 

  76. Kocarev, L., Halle, K., Eckert, K., & Chua, L. (1993). Experimental observation of antimonotonicity in Chua’s circuit. International Journal of Bifurcation and Chaos,3, 1051–1055.

    Article  MATH  Google Scholar 

  77. Ogawa, T. (1988). Quasiperiodic instability and chaos in the bad-cavity laser with modulated inversion: Numerical analysis of a Toda oscillator system. Physical Review A,37, 4286.

    Article  MathSciNet  Google Scholar 

  78. Manimehan, I., & Philominathan, P. (2012). Composite dynamical behaviors in a simple series–parallel LC circuit. Chaos, Solitons & Fractals,45, 1501–1509.

    Article  Google Scholar 

  79. Kyprianidis, I., Stouboulos, I., Haralabidis, P., & Bountis, T. (2000). Antimonotonicity and chaotic dynamics in a fourth-order autonomous nonlinear electric circuit. International Journal of Bifurcation and Chaos,10, 1903–1915.

    Article  Google Scholar 

  80. Bier, M., & Bountis, T. C. (1984). Remerging Feigenbaum trees in dynamical systems. Physics Letters A,104, 239–244.

    Article  MathSciNet  Google Scholar 

  81. Akgul, A., Moroz, I., Pehlivan, I., & Vaidyanathan, V. (2016). A new four-scroll chaotic attractor and its engineering applications. Optik,127(13), 5491–5499.

    Article  Google Scholar 

  82. Volos, C., Akgul, A., Pham, V. T., Stouboulos, I., & Kyprianidis, I. (2017). A simple chaotic circuit with a hyperbolic sine function and its use in a sound encryption scheme. Nonlinear Dynamics,89, 1047–1061.

    Article  Google Scholar 

  83. Elwakil, A. S., & Ozoguz, S. (2003). Chaos in a pulse-excited resonator with self feedback. Electronics Letters,39, 831–833.

    Article  Google Scholar 

  84. Akif, A., Shafqat, H., & Ihsan, P. (2016). A new three-dimensional chaotic system, its dynamical analysis and electronic circuit applications. Optik -International Journal for Light and Electron Optics,127, 7062–7071.

    Article  Google Scholar 

  85. Vaidyanathan, S., Akgul, A., Kaçar, S., & Çavusoglu, U. (2018). A new 4-D chaotic hyperjerk system, its synchronization, circuit design and applications in RNG, image encryption and chaos-based steganography. European Physical Journal Plus,133, 46.

    Article  Google Scholar 

  86. Ren, S., Panahi, S., Rajagopal, K., Akgul, A., Pham, V.-T., & Jafari, S. (2018). A new chaotic flow with hidden attractor: The first hyperjerk system with no equilibrium. Zeitschrift für Naturforschung. http://doi.org/10.1515/zna-2017-0409.

    Article  Google Scholar 

  87. Akif, A., Li, C., & Pehlivan, I. (2017). Amplitude control analysis of a four-wing chaotic attractor, its electronic circuit designs and microcontroller-based random number generator. Journal of Circuits Systems and Computers,26, 1750190.

    Article  Google Scholar 

  88. Pham, V.-T., Akgul, A., Volos, C., Jafari, S., & Kapitaniake, T. (2017). Dynamics and circuit realization of a no-equilibrium chaotic system with a boostable variable. International Journal of Electronics and Communications. https://doi.org/10.1016/j.aeue.2017.05.034.

    Article  Google Scholar 

  89. Sprott, J. C. (2011). A proposed standard for the publication of new chaotic systems. International Journal of Bifurcation and Chaos,21(9), 2391–2394.

    Article  Google Scholar 

  90. Maggio, G. M., De Feo, O., & Kennedy, M. P. (1999). Nonlinear analysis of the Colpitts oscilator and application to design. IEEE Transactions on Circuits and Systems,45, 1118–1130.

    Article  MATH  Google Scholar 

  91. Sprott, J. C. (2010). Elegant chaos: Algebraically siple flow. Singapore: Wold Scientific.

    Book  Google Scholar 

Download references

Acknowledgements

The authors would like to thank both the editor and the reviewers for their comments and suggestions that helped to greatly improve the presentation of the present manuscript.

Author information

Authors and Affiliations

  1. Research Unit of Laboratory of Automation and Applied Computer (LAIA), Electrical Engineering Department of IUT-FV, University of Dschang, P.O. Box 134, Bandjoun, Cameroon

    Jacques Kengne, Gervais Dolvis Leutcho & Adélaïde Nicole Kengnou Telem

  2. Research Unit of Laboratory of Condensed Matter, Electronics and Signal Processing (URMACETS), Department of Physics, Faculty of Sciences, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Jacques Kengne, Gervais Dolvis Leutcho & Adélaïde Nicole Kengnou Telem

Authors
  1. Jacques Kengne
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gervais Dolvis Leutcho
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Adélaïde Nicole Kengnou Telem
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jacques Kengne.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kengne, J., Leutcho, G.D. & Telem, A.N.K. Reversals of period doubling, coexisting multiple attractors, and offset boosting in a novel memristive diode bridge-based hyperjerk circuit. Analog Integr Circ Sig Process 101, 379–399 (2019). https://doi.org/10.1007/s10470-018-1372-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10470-018-1372-5

Keywords

Search

Navigation